Abstract
Purpose
The standard of care for treating patients with pancreatic adenocarcinomas includes gemcitabine (2′,2′-difluorodeoxycytidine). Gemcitabine primarily elicits its response by stalling the DNA replication forks of cells in the S phase of the cell cycle. To provide a quantitative framework for characterizing the cell cycle and apoptotic effects of gemcitabine, we developed a pharmacodynamic model in which the activation of cell cycle checkpoints or cell death is dependent on gemcitabine exposure.
Methods
Three pancreatic adenocarcinoma cell lines (AsPC-1, BxPC-3, and MiaPaca-2) were exposed to varying concentrations (0-100,000 ng/mL) of gemcitabine over a period of 96 h in order to quantify proliferation kinetics and cell distributions among the cell cycle phases. The model assumes that the drug can inhibit cycle-phase transitioning in each of the 3 phases (G1, S, and G2/M) and can cause apoptosis of cells in G1 and G2/M phases. Fitting was performed using the ADAPT5 program.
Results
The time course of gemcitabine effects was well described by the model, and parameters were estimated with good precision. Model predictions and experimental data show that gemcitabine induces cell cycle arrest in the S phase at low concentrations, whereas higher concentrations induce arrest in all cell cycle phases. Furthermore, apoptotic effects of gemcitabine appear to be minimal and take place at later time points.
Conclusion
The pharmacodynamic model developed provides a quantitative, mechanistic interpretation of gemcitabine efficacy in 3 pancreatic cancer cell lines, and provides useful insights for rational selection of chemotherapeutic agents for combination therapy.
Keywords: Modeling, Gemcitabine, Cell cycle, Cytotoxicity, Pharmacodynamics
Introduction
Pancreatic adenocarcinomas are malignant tumors that are associated with poor prognosis despite aggressive surgical and chemotherapeutic intervention. The standard of care for patients with these tumors is based on gemcitabine, which is a cytidine analog that is incorporated into DNA during replication in the S phase of the cell cycle [1]. Gemcitabine incorporation results in inactivation of DNA polymerases, cell cycle arrest, and eventually apoptosis [1]. However, the efficacy of gemcitabine remains modest against the highly resistant pancreatic adenocarcinomas [2].
Gemcitabine enters cells via nucleoside transporters and is deaminated by cytidine deaminase to form difluorodeoxyuridine (dFdU). dFdU is subsequently phosphorylated to form dFdUTP, which is incorporated into DNA. Alternatively, gemcitabine is phosphorylated initially by deoxycytidine kinase to form the monophosphate and subsequent phosphorylations result in the formation of the triphosphate metabolite, dFdCTP. Because of its structural similarity with deoxycytidine triphosphate, dFdCTP is incorporated into DNA during replication [3].
Gemcitabine exerts its activity primarily by inducing cell cycle arrest and cell death [4, 5]. The precise molecular mechanisms determining tumor cell responses to gemcitabine, and the impact of mechanistic interactions with other chemotherapeutic agents, remain to be elucidated. An improved understanding of the effect of gemcitabine on tumor cell cycle dynamics and apoptosis may provide insights into optimization of dose scheduling, rational selection of other chemotherapeutic agents for combination therapy, and ultimately improvement of treatment efficacy.
Pharmacodynamic models describing the effects of cell cycle-specific and non-specific chemotherapeutic agents have shown that efficacy depends on the fraction of proliferating cells, as well as on dose and exposure time [6-8]. Subsequent models that integrate the effect of chemotherapeutic agents on tumor cell progression through successive phases of the cell cycle have been utilized to provide a mechanistic interpretation of tumor cell growth kinetics following drug exposure [9-12]. Building upon previously reported models, we adopted a cell cycle-structured framework and extended it to incorporate pharmacological relationships governing the activation of cell cycle checkpoints that result in cell cycle arrest and cell death. The model is fitted to data obtained for cell proliferation and cell cycle distribution during gemcitabine exposure of three lines of pancreatic adenocarcinoma cells in vitro.
Materials and methods
Materials
Gemcitabine hydrochloride was purchased from Sequoia Research Products (Pangbourne, UK). Stock concentrations of 10 mg/mL in sterile, double-distilled water were stored at −20 °C until use.
Cell lines
Human pancreatic cancer cell lines AsPC-1, BxPC-3, and MiaPaca-2 were purchased from American Type Culture Collection (Manassas, VA). AsPC-1 and BxPC-3 cells were cultured in RPMI 1640 (Invitrogen, Carlsbad, CA) supplemented with 10 % fetal bovine serum (Cellgro, Manassas, VA), 4 mM l-glutamine, and 1 mM sodium pyruvate (GIBCO). MiaPaca-2 cells were cultured in DMEM (Invitrogen) supplemented as with the other cells. Cells were cultured at 37 °C in 5 % CO2 and a humidified atmosphere.
Cell growth assay
Cells were suspended in culture medium at a concentration of 1 × 104 (AsPC-1) or 2 × 104cells/mL (BxPC-3 and MiaPaca-2), and 1 mL of cell suspension was added to each well of a 24-well plate. Cells were allowed to attach for 18 h before treatment with a wide range of gemcitabine concentrations (0–100,000 ng/mL) to obtain full pharmacologic response profiles. Sterile double-distilled water was used as the vehicle control. Cells were counted at 24, 48, 72, and 96 h using a Coulter counter (Beckman Coulter, Brea, CA). To avoid any effects that are not specific to gemcitabine, care was taken to avoid confluence and cells were harvested in the exponential growth phase. At designated time points, cells were washed twice with PBS to remove dead cells and resuspended in 1 mL of Dulbecco’s phosphate-buffered saline (PBS) containing 0.025 % EDTA to promote cell detachment. Triplicate wells were counted for each drug concentration.
Flow cytometry
Propidium iodide (PI) staining (Sigma-Aldrich, St. Louis, MO) was performed to determine the cell cycle-phase distribution based on DNA content. Cells were seeded in 24-well plates as described above. BxPC-3 and MiaPaca-2 cells were incubated with 0, 0.1, 1, or 100 ng/mL gemcitabine, whereas AsPC-1 cells were incubated with 0, 10, 1,000, or 10,000 ng/mL. Cells were harvested in the exponential growth phase at 0, 24, 48, 72, and 96 h. At each time point, cells were washed with PBS and fixed in 70 % ice-cold ethanol. Cells were centrifuged at 300×g for 6 min at 4 °C, and the cell pellet was washed twice with PBS and then stained for 15 min at room temperature in the dark with 20 lg/mL PI in PBS containing 0.1 % (v/v) Triton X-100 (Bio-Rad Laboratories, Hercules, CA) and 0.2 mg/mL RNase A (Qiagen, Valencia, CA). Analysis was performed with a FACScan flow cytometer (Becton–Dickinson, Mansfield, MA). Cell cycle distributions, generated by CellQuest (Becton–Dickinson), were imported into ModFit software (Verity Software House, Topsham, ME) to quantify the fraction of viable cells in each phase of the cell cycle. Triplicate samples were used for every time point. The number of subG1 events was quantified in CellQuest as an indication of the number of apoptotic events.
Mathematical model
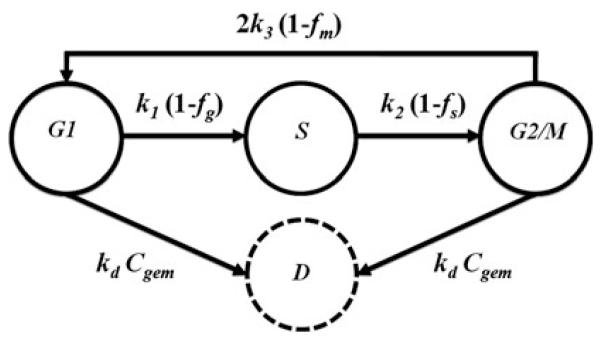
A compartmental model was used to follow the distribution of cells among the various phases of the cell cycle (Fig. 1). Each compartment represents a phase of cell cycle; however, G2 and M phases were combined as they are indistinguishable by DNA content in flow cytometric analysis. First-order rate constants (k1, k2, and k3) reflect rates of transition among consecutive phases. Cell cycle arrest in each of the phases is modeled as the activation of phase checkpoints that inhibit transitions among phases and are governed by three pharmacologic functions: fg, fs, and fm. In addition, cells in G1 and G2/M phases may commit to apoptosis as a result of drug exposure, which is treated as a second-order process, with rate constant kd. The balance of cells in each compartment is represented with:
| (1) |
| (2) |
| (3) |
| (4) |
Fig. 1.
Compartmental model of gemcitabine effects on cell cycle and apoptosis. Symbols are defined in the text and Table 1
The initial conditions in Eqs. (1–3) represent the number of cells in each phase of the cell cycle (G1, S, M) at steady state at initiation of treatment. The initial condition in Eq. (4) represents the number of cells committed to apoptosis (D) at time zero, when drug exposure was initiated and was assumed to be zero. The initial number of cells was estimated by fitting the growth curve of each cell line under no-drug conditions to an exponential equation. The number of cells in each phase of the cell cycle at time zero was then estimated by multiplying the total number of cells by the fraction of cells in each phase.
Experimental quantities of interest include the total number of viable cells (Ctot), calculated as the sum of the first three model compartments, and the total number of viable cells in each compartment, calculated for various time points and drug concentrations by multiplying the total number of viable cells by the fraction of cells in each phase (XG1, XS, XM), as determined by flow cytometry:
| (5) |
| (6) |
| (7) |
| (8) |
The effects of drug on cell cycle checkpoint activation and hence cell cycle arrest were modeled with saturation equations. In addition, the maximum effect constant was assumed to be equal to one for each checkpoint; thus, fg, fs, and fm are a function of the drug concentration (Cgem) and the cycle-phase sensitivity parameters (IC50g, IC50s, and IC50m). The cell death rate constant, kd, is assumed to depend upon drug concentration and number of viable cells in G1 and G2/M phases. Thus,
| (9) |
| (10) |
| (11) |
In the absence of drug, model Eqs. (1–4) reduce as follows with the same initial conditions:
| (12) |
| (13) |
| (14) |
Model Eqs. (12–14) were fitted to growth curves and cell cycle distributions of untreated cells to determine the transition rate constants (k1, k2, and k3) that govern the growth of each cell line. These parameters were set as constants in the full model in Eqs. (1–4). The model parameters (IC50g, IC50s, IC50m, and kd) were fitted to growth curves and cell cycle distributions of drug-treated cells using the maximum likelihood estimation algorithm in ADAPT5 [13]. A constant and proportional model was used to parameterize error variance. Model simulations were run in MATLAB (Mathworks, Natick, MA) using the ode15s solver.
Results
Pancreatic adenocarcinoma cell responses to gemcitabine
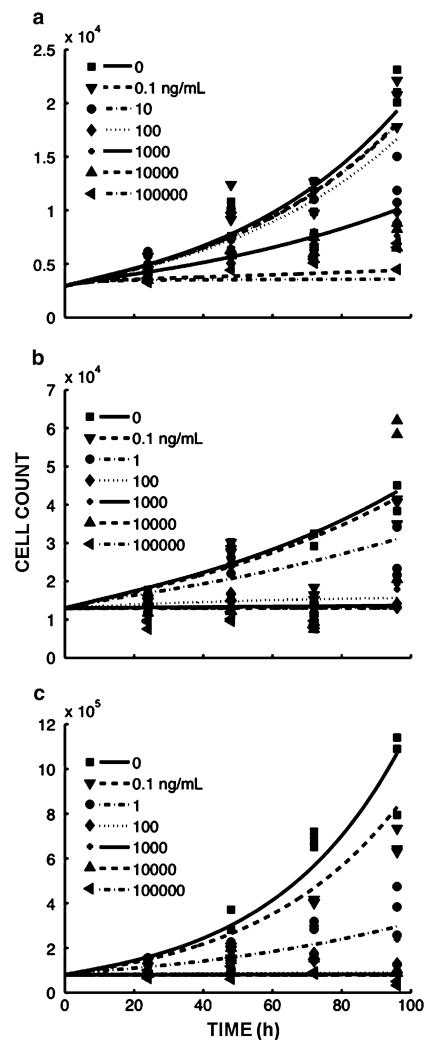
The AsPC-1, BxPC-3, and MiaPaca-2 cell lines were exposed to a wide range of gemcitabine concentrations (0–100,000 ng/mL) for up to 96 h. Gemcitabine was found to inhibit the growth of all cell lines in a concentration-dependent manner (Fig. 2). At lower concentrations (0.1 and 1 ng/mL), BxPC-3 and MiaPaca-2 cells continued to proliferate at a reduced rate. At higher concentrations (C100 ng/mL), proliferation ceased at 24–48 h. The AsPC-1 cell line was less sensitive compared to the other cell lines and continued to proliferate at 10 ng/mL. AsPC-1 proliferation ceased at ≥10,000 ng/mL. By 72–96 h, there was a net loss of cells to numbers lower than the initial cell number at time zero for BxPC-3 and MiaPaca-2 (Fig. 2b, c). AsPC-1 cell counts did not decrease below the initial values, even at the highest drug concentrations (Fig. 2a).
Fig. 2.
Cell numbers as a function of time and gemcitabine concentration for a AsPC-1, b BxPC-3, and c MiaPaca-2 cells. Symbols depict experimental data and lines represent the corresponding model fittings. Units of the ordinate are cells per well ×104 or 105. Each time point included three replicates
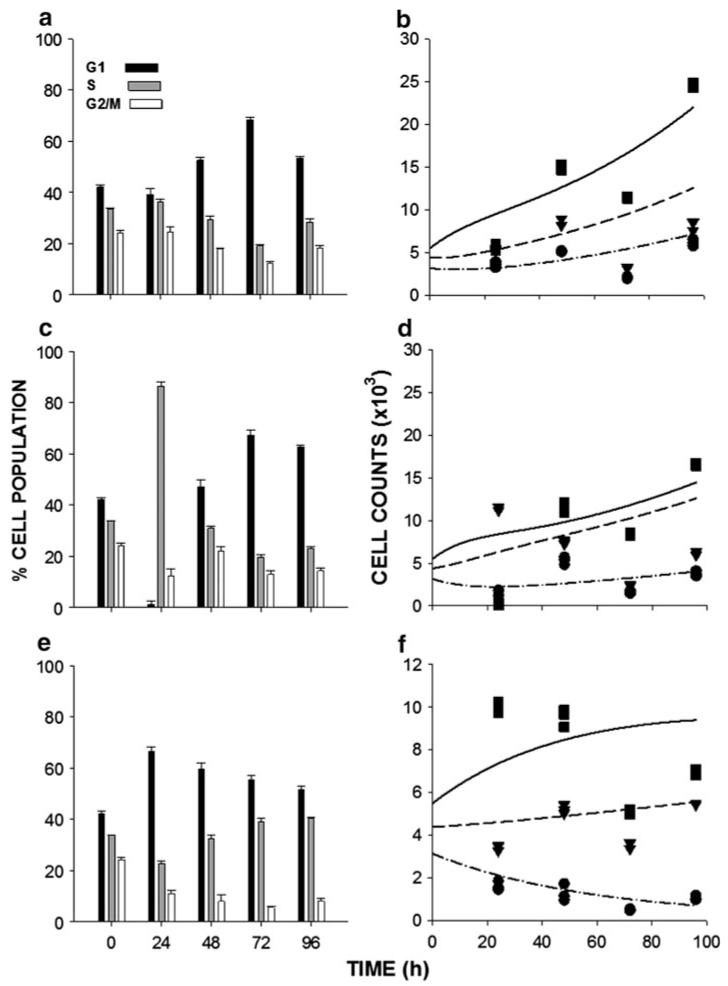
The inhibition of cell proliferation results from the cycle-phase-specific effects of gemcitabine metabolite incorporation into DNA during S phase [1]. Gemcitabine elicits its response through activation of cell cycle checkpoints, cell cycle arrest, and eventually cell death [4, 5]. To monitor the effects of gemcitabine on cell cycle progression, cells were exposed to a range of drug concentrations that produced low, moderate, and strong effects on cell proliferation, and the cell cycle distribution was monitored at 24, 48, 72, and 96 h after initiation of drug exposure. Figure 3 shows data for BxPC-3 cells, which is representative of the three cell lines. For low and moderate concentrations of gemcitabine, there was a transient accumulation of cells in S phase (Fig. 3a, c), which was dose-dependent. For high drug concentrations, cell cycle progression was minimal for all cycle phases, at all observation times (Fig. 3e), and for all of the cell lines compared to the distribution observed at 0 h (the initiation of drug treatment) and to untreated controls that were evaluated at each time point (not shown). Diminished cell progression through all cycle phases at the highest drug concentration indicates that cell cycle checkpoint activation can occur in all phases and is not specific to S phase only. The results also suggest that lower concentrations of gemcitabine induce cell cycle arrest in the S phase, whereas total arrest of cell cycle progression in all phases is produced at high drug concentrations.
Fig. 3.
Cell cycle-phase distributions of BxPC-3 exposed to a 0.1 ng/mL, c 1 ng/mL, and e 100 ng/mL gemcitabine for up to 96 h. b, d, and f show the corresponding number of cells per well in each cycle phase (squares-G1, triangles-S, circles-G2/M) and the model fittings (lines). Units of the ordinate are cells per well ×103. Each time point consisted of three replicates
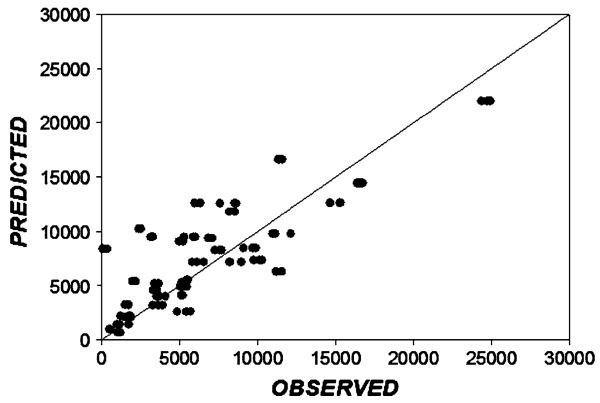
Figure 4 demonstrates the overall agreement between the fitted and observed BxPC-3 cell culture data. The values distribute well about the line of identity indicating the reasonable quality of model fitting.
Fig. 4.
Relationship between model-fitted and observed BxPC-3 cell culture data in the absence and presence of various concentrations of gemcitabine (data from Fig. 3). The diagonal is the line of identity
Cell cycle model
Cell cycle models have been used previously to describe the effects of chemotherapeutic agents on cancer cell lines, predict dose and exposure regimens to maximize drug efficacy [14, 15], and to distinguish cell cycle arrest versus cell killing in concentration–response curves [16]. We hypothesized that the effects of gemcitabine upon cellular proliferation and cell cycle checkpoint activation in pancreatic adenocarcinoma cells could be represented with a cell cycle-structured model (Fig. 1).
For the sake of model parsimony, the effect of drug on each of the cell cycle checkpoints and on cell death is represented with a one-parameter equation. Four parameters (IC50g, IC50s, IC50m, and kd) affect the proliferation of cells upon exposure to chemotherapy. The two parameters that alter cell cycle redistribution, and therefore proliferation, are IC50s and kd. In order to investigate how each parameter affects cell proliferation and cell cycle redistribution, we performed a simulation in which the magnitude of each parameter was varied individually with the others set to constant values.
When the cell death rate constant kd is set to a constant value, the fraction of cells in the S phase increases as drug concentrations are increased relative to IC50s, IC50g, and IC50m. Cell cycle distribution changes are more evident as the S phase checkpoint sensitivity increases (i.e., lower IC50s values) (not shown). kd also affects the distribution of cells among the different phases: with increasing values of kd, cell cycle distribution dynamics resulting from drug exposure are more rapid; with very low values of kd, phase distribution changes are less drastic, even at the highest drug concentration (not shown).
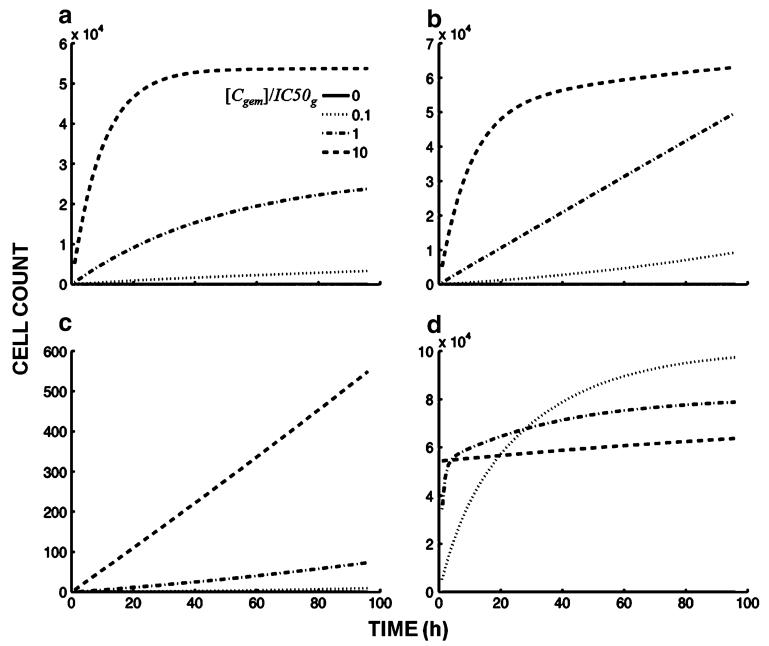
In terms of cell death, the cumulative number of dead cells as a function of time and drug concentration shifts, at later times, from a plateau to linear with increasing values of IC50s (Fig. 5a, b). The reason for this effect is that the number of cells in G1 and G2/M (i.e., cells undergoing death) is lower with a lower value for IC50s. This result suggests that arrest in S phase could act as a shield against cell death and thus contributes to drug resistance, and is consistent with reports linking increased chemotherapy resistance with increased efficiency of cell cycle arrest [17-19]. Increasing the value of kd results in a shift from a linear increase in the number of dead cells with time (Fig. 5c) to a constant value, at later times, in which a plateau results from the depletion of cells from G1 and G2/M (Fig. 5d). Increasing drug concentration also contributes to the shift from linear increase in the number of dead cells with time to a constant number (Fig. 5b).
Fig. 5.
Model simulations of the effects of varying IC50s and kd on cell death. The panels show simulations with different relative values for parameters IC50s, (a) and (b), and kd, (c) and (d), and within each panel, the drug concentration is varied relative to IC50g: [Cgem] = 0 (no drug), [Cgem] 10 % of IC50g, [Cgem] equal to IC50g, and [Cgem] 10-fold higher than IC50g. a Effect of highly drug-sensitive (100-fold lower) IC50s relative to IC50 of other cycle phases: IC50g = IC50m = 1,000 ng/mL, IC50s = 10 ng/mL, kd = 10−5 h−1 mL/ng, b IC50s equal to IC50 of other cycle phases, kd same as in a: IC50g = IC50s = IC50m = 1,000 ng/mL, kd = 10−5 h−1 mL/ng, c IC50 of cycle phases equal (same as in b), kd 1,000-fold lower than in a and b: IC50g = IC50s = IC50s = IC50m 1,000 ng/mL, kd = 10−8 h− mL/ng, and d IC50 of cycle phases equal (same as in b, c), kd 1,000-fold higher than in a and b: IC50g = IC50s = IC50m = 1,000 ng/mL, kd = 10−2 h−1 mL/ng
The effects of checkpoint activation parameters and cell death are reflected in the total number of viable cells. With high drug concentrations and high values of kd, growth curves are slightly concave downward, and cell counts fall to numbers lower than the initial number at time zero because of cell killing. However, despite high drug concentrations, low values of kd result in a flat growth curve and cell numbers do not fall below initial values (not shown). This prediction from simulation with the model is also consistent with the concept that cells are protected from cell death at high drug concentrations (Fig. 5d) because of arrest in S phase.
Model comparison with experimental results
The profiles simulated with the model of cell proliferation and cell cycle-phase distribution in response to low and high drug concentrations appear similar to experimental data obtained from exposing the pancreatic adenocarcinoma cell lines to low and high concentrations of gemcitabine. In order to obtain a quantitative estimation of the effect of gemcitabine on cell cycle checkpoint activation and death, data for cell proliferation and cell cycle distributions in the presence of varying concentrations of drug were fitted to the model. A single set of parameters (IC50g, IC50s, IC50m, and kd) jointly characterized the ensemble of data for each cell line. Experimental data were captured well in terms of drug concentration and time course (Figs. 2, 3b, d, f).
For all cell lines, the analysis suggested that the value of IC50s was markedly lower than for IC50g and IC50m, indicating higher sensitivity of the S phase checkpoint to gemcitabine compared to the G1 and G2/M checkpoints (Table 1). Furthermore, estimated values of the overall IC50 for cell growth inhibition were significantly higher for AsPC-1 cells compared to the other cell lines, in agreement with experimental data: after 72 h of exposure to varying concentrations of gemcitabine, the IC50 for growth inhibition was ~50 ng/mL for AsPC-1, compared to 0.24 ng/mL for BxPC-3 and 3.75 ng/mL for MiaPaca-2 (data not shown).
Table 1.
Model parameter estimates for different cell lines
| Cell line | Parameter | Definition | Value | CV (%) |
|---|---|---|---|---|
| AsPC-1 | k1 (h−1) | G1–S first-order rate transition | 0.04779 | 7.464 |
| k2 (h−1) | S–G2/M first-order rate transition | 0.06607 | 8.163 | |
| k3 (h−1) | G2/M–G1 first-order rate transition | 0.1381 | 10.09 | |
| IC50g (ng/mL) | G1 checkpoint sensitivity | 2,326 | 27.51 | |
| IC50s (ng/mL) | S checkpoint sensitivity | 1,066 | 21.84 | |
| IC50m (ng/mL) | G2/M checkpoint sensitivity | 5.71 × 106 | 4.79 × 104 | |
| kd (h−1 mL/ng) | Second-order rate transition into apoptosis | 8.22 × 10−13 | 4.14 × 108 | |
| BxPC-3 | k1 (h−1) | G1–S first-order rate transition | 0.03312 | 8.259 |
| k2 (h−1) | S–G2/M first-order rate transition | 0.05036 | 9.101 | |
| k3 (h−1) | G2/M–G1 first-order rate transition | 0.06779 | 9.572 | |
| IC50g (ng/mL) | G1 checkpoint sensitivity | 5.614 | 54.15 | |
| IC50s (ng/mL) | S checkpoint sensitivity | 0.8912 | 23.15 | |
| IC50m (ng/mL) | G2/M checkpoint sensitivity | 33.86 | 16.68 | |
| kd (h−1 mL/ng) | Second-order rate transition into apoptosis | 2.63 × 10−14 | 1.9 × 108 | |
| MiaPaca-2 | k1 (h−1) | G1–S first-order rate transition | 0.06315 | 4.49 |
| k2 (h−1) | S–G2/M first-order rate transition | 0.1202 | 6.27 | |
| k3 (h−1) | G2/M–G1 first-order rate transition | 0.1703 | 6.86 | |
| IC50g (ng/mL) | G1 checkpoint sensitivity | 4.445 | 57.21 | |
| IC50s (ng/mL) | S checkpoint sensitivity | 0.3097 | 17.50 | |
| IC50m (ng/mL) | G2/M checkpoint sensitivity | 6.546 | 30.75 | |
| kd (h−1 mL/ng) | Second-order rate transition into apoptosis | 4.69 × 10−13 | 6.75 × 108 |
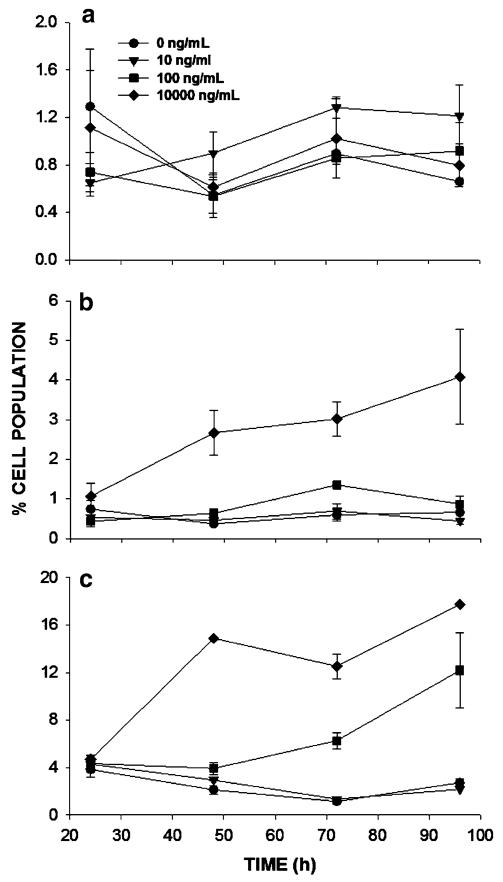
The estimates for kd were very low with high coefficients of variation, indicating that gemcitabine exposure had minimal effect on cell death, the rates of cellular proliferation, and on the distribution of cells among the cell cycle phases. To test these model predictions experimentally, the effect of gemcitabine on apoptosis of pancreatic cancer cells was measured experimentally for the three cell lines with various drug concentrations and varying times after initiation of drug exposure. The fraction of cells in subG1 is an indication of cells undergoing apoptosis: cells display hallmark changes including chromosomal fragmentation and diminishing DNA content. For BxPC-3 and MiaPaca-2 cells, subG1 populations exhibited trends similar to model simulations when kd values were very small (Fig. 5c); under such conditions, low drug concentrations produced baseline levels of dead cells and higher drug concentrations resulted in linear increases in dead cells with time (Fig. 6b, c). The AsPC-1 cell line showed no significant increase in the fraction of apoptotic cells, even at the highest concentration (Fig. 6a). This finding is in agreement with cell growth data, which shows that BxPC-3 and MiaPaca-2 cells (Fig. 2b, c) exhibit depletion of cells at higher drug concentrations and later time points, and the proliferation curves appear concave downward, whereas AsPC-1 cells exhibit no decrease in cell numbers and proliferation curves are flat at the highest drug concentrations (Fig. 2a).
Fig. 6.
Percent of apoptotic cells versus time as a function of gemcitabine concentration. Cells were exposed to the indicated concentration of gemcitabine starting at 0 h. Apoptosis was determined at each time point based upon the fraction of cells in subG1 phase, as determined by flow cytometry. a AsPC-1, b BxPC-3, and c MiaPaca-2 cells
Discussion
Pharmacodynamic models describing the effect of chemotherapeutic agents on tumor cells have been described previously. Many have been structured on cell cycle dynamics [9-12, 14, 15] and the cell cycle-phase specificity of the agent of interest [7, 8]. These models captured the effect of chemotherapeutic agents as a change in the rate parameters governing transitions among the successive phases of cell cycle or cellular elimination. Cell death and cell cycle arrest have been incorporated in subsequent models through simple pharmacological equations to ascribe mechanistic interpretations to the drug effects [16]. The effect of cell cycle arrest previously has been lumped into a single parameter without distinguishing the effects of chemotherapeutic agents on the individual cell cycle checkpoints.
In the current work, we investigated the effects of drug exposure on the activation of cell cycle checkpoints leading to cell cycle arrest and apoptosis. In the final model, cell cycle arrest was assumed to take place in each phase of the cell cycle, but with varying sensitivities. In addition, apoptosis was assumed to initiate in the G1 and G2/M phases, which is in agreement with experimental results showing that DNA damage delays cells in S phase, rather than causing a sustained arrest [20]. In the model developed, apoptosis was assumed to be the primary mode of cell death and the model structure was based on the relationship between G1 and G2/M checkpoint activation and apoptotic pathways [21, 22].
We fitted the model to pooled (i.e., without averaging) cell cycle distribution and proliferation data collected every 24 h for a total of 96 h after exposure to multiple concentrations of gemcitabine in order to gain a quantitative assessment of the checkpoint sensitivities of pancreatic adenocarcinoma cells. The 24-h sampling frequency is shorter than the cell cycle time of the panel of cells in this study, 30 h for MiaPaca-2 to 60 h for AsPC-1 cells, and allowed for estimating cell cycle transition parameters with good precision in the case of no-drug treatment as well as with drug exposure. The effect of gemcitabine on cell cycle checkpoint activation was represented as a saturable process without cooperativity (Eqs. 9–11) and cell death was represented as a second-order process. A single set of parameters was fit to the ensemble of data for each cell line. While there are some features of the data—for example, overprediction of cells in S phase (Fig. 3d)—that are not captured by the model, the combined concentration and time dependencies are fitted well. Model parameters were estimated with good precision (Table 1), with the exception of IC50m for AsPC-1 cells. Poor precision for this parameter is probably due to the slow cell cycle kinetics and prolonged stagnation of cells in G2/M relative to the sampling interval. In addition, kd was estimated with poor precision for all cell lines due to the minimal effects of gemcitabine on cell death during the time span of the experiment.
Several model structures for representing cell death were investigated, in which cells were allowed to undergo apoptosis from all compartments with a single kd value, a different kd value for each compartment, different kd values for the G1 and G2/M compartments, an additional exponential term (to account for increased cell death at later time points), or no death terms at all. In all cases and for all cell lines, the present model minimized the AIC [23] score. Interestingly, and in agreement with the observed drug-mediated apoptotic behavior (Fig. 6a), the “no death” model performed best for AsPC-1, which was experimentally the most drug-resistant line. However, the remaining parameter estimates obtained for all 3 cell lines were not significantly different between the various models. Thus, we chose the final model for its consistency in modeling data for multiple cell lines, and the fact that it appears to be more realistic physiologically. Interestingly, the value of kd derived for all cell lines suggests that cell death by apoptosis is not the primary mode of action of gemcitabine.
Gemcitabine has been shown to induce S phase cell cycle checkpoint activation as a result of DNA damage and stalled DNA replication forks [24]. In mammalian cells, replication stress during S phase results in phosphorylation of ATM (Ataxia Telangiectasia Mutated) kinase and subsequent activation of the Chk1 and Chk2 protein kinases, which ultimately results in cell cycle arrest [25]. In addition, the activation of Chk1 and Chk2 signaling pathways activates G1 and G2/M checkpoints [17-19, 25]. Consistent with prevailing concepts, gemcitabine was found to induce G1, S, and G2/M checkpoint activation in pancreatic cancer cells through the activation of Chk1 and Chk2 pathways, which results in Cdc25A (cell division cycle 25 phosphatase) degradation and cell cycle arrest [26]. In agreement with our results, Cappella et al. showed that gemcitabine induced transient S phase arrest in ovarian cancer cells at low and moderate concentrations, whereas higher concentrations resulted in total cessation of cell cycle progression [4]. Similar results were obtained with gemcitabine in bladder and lung cancer cells [27].
In addition to its effects upon the cell cycle, gemcitabine has been shown to induce caspase-3-mediated apoptosis [28]. Consistent with our results, the apoptotic effect was more evident at later time points (72 and 96 h), as evidenced by increased subG1 cell populations [4, 5, 28]. The modest apoptotic effect of gemcitabine on pancreatic cancer cells could be attributed to intrinsic resistance of these highly aggressive tumors, especially given that many survival pathways such as NFκB, K-ras, and MAPK are constitutively activated in these cells [29, 30].
Mechanistic pharmacodynamic models incorporating the molecular and cellular characteristics of tumors are becoming increasingly relevant to decision making for personalized cancer treatment. The traditional in vitro pharmacological characterization of chemotherapeutic agents ignores the dynamics of cellular proliferation and cell cycle effects. In the context of gemcitabine, cell cycle checkpoint activation could be viewed as a mechanism of cellular defense against the apoptotic effects of the drug, such that cell cycle progression is arrested so that DNA damage may be repaired before proliferation resumes. In agreement with this notion, several studies have shown that combination of gemcitabine with agents that abrogate cell cycle checkpoints enhances gemcitabine cytotoxicity significantly, by forcing the cells into mitotic catastrophe [26,31-35]. The model presented here could be utilized to inform selection of the correct agent and dosing schedule for combination with gemcitabine or possibly other DNA damaging agents. For example, the model suggests that with low and moderate concentrations of gemcitabine, the use of agents that override G1 or G2/M checkpoints (e.g., MK-1775) may not improve efficacy, whereas an agent that abrogates S phase checkpoint inhibition (e.g., UCN-01) could be more beneficial.
In a similar vein, the model presented here could be extended to highlight interesting dosing regimens for gemcitabine monotherapy. For instance, cells synchronized in S phase are more susceptible to gemcitabine cytotoxicity [36]. In theory, an initial “priming” low dose of gemcitabine, which synchronizes cells in S phase, can increase the efficacy of subsequent doses, whereas a high initial dose may arrest cell cycle progression completely, without sufficient cell kill, and ultimately decrease efficacy. This reasoning is in agreement with studies in preclinical [37] as well as clinical settings [38, 39] elaborating the increased efficacy and decreased toxicity of low and more frequent gemcitabine exposure in comparison with the conventional high and less frequent exposure.
The model developed here makes simplifying assumptions that are inherent to in vitro studies, e.g., that cells are treated as a homogenous population and there are no-drug perfusion limitations. In vivo, however, tumors are heterogeneous populations of cells having varying degrees of sensitivity to any given chemotherapeutic agent. In addition, drug penetration and tumor deposition clearly is an important factor in determining treatment efficacy, as shown by studies that have correlated the efficacy of gemcitabine in pancreatic cancers with the degree of stromal elaboration in these tumors [40]. To apply the model developed here to gemcitabine-based therapy in vivo, mechanistic models can be incorporated that account for cellular heterogeneity in drug responsiveness as well as tumor perfusion [41, 42], so as to provide a more comprehensive evaluation of tumor response to chemotherapy. Such integrated models will allow for testing treatment options in silico as a prelude to preclinical testing of personalized cancer therapies.
Acknowledgments
This work is supported by Grant GM57980 from the National Institutes of Health. SSH was supported by a Fellowship from Hoffmann-La Roche Inc.
References
- 1.Hui YF, Reitz J. Gemcitabine: a cytidine analogue active against solid tumors. Am J Health Syst Pharm. 1997;54:162–170. doi: 10.1093/ajhp/54.2.162. [DOI] [PubMed] [Google Scholar]
- 2.Hilbig A, Oettle H. Gemcitabine in the treatment of metastatic pancreatic cancer. Expert Rev Anticancer Ther. 2008;8:511–523. doi: 10.1586/14737140.8.4.511. [DOI] [PubMed] [Google Scholar]
- 3.Heinemann V, Hertel LV, Grindey GB, Plunkett W. Comparison of the cellular pharmacokinetics and toxicity of 2′,2′-difluorodeoxycytidine and 1-b-arabinofuranosylcytosine. Cancer Res. 1988;48:4024–4031. [PubMed] [Google Scholar]
- 4.Carpenelli G, Bucci G, D’Agnano I, Canese R, Caroli F, Raus L, Brunetti E, Giannarelli E, Podo F, Carapella CM. Gemcitabine treatment of experimental C6 glioma: the effects on cell cycle and apoptotic rate. Anticancer Res. 2006;26:3017–3024. [PubMed] [Google Scholar]
- 5.Cappella P, Tomasoni D, Faretta M, Lupi M, Montalenti F, Viale F, Banzato F, D’Incalci M, Ubezio P. Cell cycle effects of gemcitabine. Int J Cancer. 2001;93:401–408. doi: 10.1002/ijc.1351. [DOI] [PubMed] [Google Scholar]
- 6.Jusko WJ. Pharmacodynamics of chemotherapeutic effects: dose-time-response relationships for phase-nonspecific agents. J Pharm Sci. 1971;60:892–895. doi: 10.1002/jps.2600600618. [DOI] [PubMed] [Google Scholar]
- 7.Jusko WJ. A pharmacodynamic model for cell-cycle-specific chemotherapeutic agents. J Pharmacokinet Biopharm. 1973;1:175–200. [Google Scholar]
- 8.Gardner SN. A mechanistic, predictive model of dose–response curves for cell cycle phase-specific and -nonspecific drugs. Cancer Res. 2000;60:1417–1425. [PubMed] [Google Scholar]
- 9.Basse B, Baguley BC, Marshall ES, Joseph WR, van Brunt B, Wake G, Wall DJ. Modelling cell death in human tumour cell lines exposed to the anticancer drug paclitaxel. J Math Biol. 2004;49:329–357. doi: 10.1007/s00285-003-0254-2. [DOI] [PubMed] [Google Scholar]
- 10.Kozusko F, Chen P, Grant SG, Day BW, Panetta JC. A mathematical model of in vitro cancer cell growth and treatment with the antimitotic agent curacin A. Math Biosci. 2001;170:1–16. doi: 10.1016/s0025-5564(00)00065-1. [DOI] [PubMed] [Google Scholar]
- 11.Panetta JC, Evans WE, Cheok MH. Mechanistic mathematical modelling of mercaptopurine effects on cell cycle of human acute lymphoblastic leukaemia cells. Br J Cancer. 2006;94:93–100. doi: 10.1038/sj.bjc.6602893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gardner SN. Modeling multi-drug chemotherapy: tailoring treatment to individuals. J Theor Biol. 2002;214:181–207. doi: 10.1006/jtbi.2001.2459. [DOI] [PubMed] [Google Scholar]
- 13.D’Argenio DZ, Schumitzky A, Wang X. ADAPT 5 user’s guide: pharmacokinetic/pharmacodynamic systems analysis software. Biomedical Simulations Resource; Los Angeles: 2009. [Google Scholar]
- 14.Florian JA, Eiseman JL, Parker RS. Accounting for quiescent cells in tumour growth and cancer treatment. Syst Biol (Stevenage) 2005;152:185–192. doi: 10.1049/ip-syb:20050041. [DOI] [PubMed] [Google Scholar]
- 15.Sherer E, Hannemann RE, Rundell A, Ramkrishna D. Analysis of resonance chemotherapy in leukemia treatment via multi-staged population balance models. J Theor Biol. 2006;240:648–661. doi: 10.1016/j.jtbi.2005.11.017. [DOI] [PubMed] [Google Scholar]
- 16.Hamed SS, Roth CM. Mathematical modeling to distinguish cell cycle arrest and cell killing in chemotherapeutic concentration response curves. J Pharmacokinet Pharmacodyn. 2001;38:385–403. doi: 10.1007/s10928-011-9199-z. [DOI] [PubMed] [Google Scholar]
- 17.Batista LF, Roos WP, Kaina B, Menck CF. p53 mutant human glioma cells are sensitive to UV-C-induced apoptosis due to impaired cyclobutane pyrimidine dimer removal. Mol Cancer Res. 2009;7:237–246. doi: 10.1158/1541-7786.MCR-08-0428. [DOI] [PubMed] [Google Scholar]
- 18.Ruan S, Okcu MF, Ren JP, Chiao P, Andreeff M, Levin V, Zhang W. Overexpressed WAF1/Cip1 renders glioblastoma cells resistant to chemotherapy agents 1,3-bis(2-chloroethyl)-1-nitrosourea and cisplatin. Cancer Res. 1998;58:1538–1543. [PubMed] [Google Scholar]
- 19.Xu GW, Nutt CL, Zlatescu MC, Keeney M, Chin-Yee I, Cairncross JG. Inactivation of p53 sensitizes U87MG glioma to 1,3-bis(2-chloroethyl)-1-nitrosourea. Cancer Res. 2001;61:4155–4159. [PubMed] [Google Scholar]
- 20.Damia G, Broggini M. Improving the selectivity of cancer treatments by interfering with cell response pathways. Eur J Cancer. 2004;40:2550–2559. doi: 10.1016/j.ejca.2004.07.020. [DOI] [PubMed] [Google Scholar]
- 21.Damia G, Broggini M. Cell cycle checkpoint proteins and cellular response to treatment by anticancer agents. Cell Cycle. 2004;3:46–50. [PubMed] [Google Scholar]
- 22.Senderowicz AM. Targeting cell cycle and apoptosis for the treatment of human malignancies. Curr Opin Cell Biol. 2004;16:670–678. doi: 10.1016/j.ceb.2004.09.014. [DOI] [PubMed] [Google Scholar]
- 23.Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974;19:716–723. [Google Scholar]
- 24.Ewald B, Sampath D, Plunkett W. H2AX phosphorylation marks gemcitabine-induced stalled replication forks and their collapse upon S-phase checkpoint abrogation. Mol Cancer Ther. 2007;6:1239–1248. doi: 10.1158/1535-7163.MCT-06-0633. [DOI] [PubMed] [Google Scholar]
- 25.Zhou BB, Elledge SJ. The DNA damage response: putting checkpoints in perspective. Nature. 2000;408:433–439. doi: 10.1038/35044005. [DOI] [PubMed] [Google Scholar]
- 26.Azorsa DO, Gonzales IM, Basu GD, Choudhary A, Arora S, Bisanz KM, Kiefer JA, Henderson MC, Trent JM, Von Hoff DD, Mousses S. Synthetic lethal RNAi screening identifies sensitizing targets for gemcitabine therapy in pancreatic cancer. J Transl Med. 2009;7:43. doi: 10.1186/1479-5876-7-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pauwels B, Korst AE, Pattyn GG, Lambrechts HA, Van Bockstaele DR, Vermeulen K, Lenjou M, de Pooter CM, Vermorken JB, Lardon F. Cell cycle effect of gemcitabine and its role in the radiosensitizing mechanism in vitro. Int J Radiat Oncol Biol Phys. 2003;57:1075–1083. doi: 10.1016/s0360-3016(03)01443-3. [DOI] [PubMed] [Google Scholar]
- 28.Chandler NM, Canete JJ, Callery MP. Caspase-3 drives apoptosis in pancreatic cancer cells after treatment with gemcitabine. J Gastrointest Surg. 2004;8:1072–1078. doi: 10.1016/j.gassur.2004.09.054. [DOI] [PubMed] [Google Scholar]
- 29.Arora S, Bhardwaj A, Srivastava SK, Singh S, McClellan S, Wang B, Singh AP. Honokiol arrests cell cycle, induces apoptosis, and potentiates the cytotoxic effect of gemcitabine in human pancreatic cancer cells. PLoS One. 2011;6:e21573. doi: 10.1371/journal.pone.0021573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Holcomb B, Yip-Schneider MT, Matos JM, Dixon J, Kennard J, Mahomed J, Shanmugam R, Sebolt-Leopold J, Schmidt CM. Pancreatic cancer cell genetics and signaling response to treatment correlate with efficacy of gemcitabine-based targeting strategies. J Gastrointest Surg. 2008;12:288–296. doi: 10.1007/s11605-007-0406-6. [DOI] [PubMed] [Google Scholar]
- 31.Matsumoto K, Nagahara T, Okano J, Murawaki Y. The growth inhibition of hepatocellular and cholangiocellular carcinoma cells by gemcitabine and the roles of extracellular signal-regulated and checkpoint kinases. Oncol Rep. 2008;20:863–872. [PubMed] [Google Scholar]
- 32.Morgan MA, Parsels LA, Parsels JD, Mesiwala AK, Maybaum J, Lawrence TS. Role of checkpoint kinase 1 in preventing premature mitosis in response to gemcitabine. Cancer Res. 2005;65:6835–6842. doi: 10.1158/0008-5472.CAN-04-2246. [DOI] [PubMed] [Google Scholar]
- 33.Rajeshkumar NV, De Oliveira E, Ottenhof N, Watters J, Brooks D, Shumway SD, Mizuarai S, Hirai H, Maitra A, Hidalgo M. MK-1775, a potent Wee1 inhibitor, synergizes with gemcitabine to achieve tumor regression selectively in p53-deficient pancreatic cancer xenografts. Clin Cancer Res. 2011;17:2799–27806. doi: 10.1158/1078-0432.CCR-10-2580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Walton MI, Eve PD, Hayes A, Valenti M, De Haven Brandon A, Box G, Boxall KJ, Aherne GW, Eccles SA, Raynoud FI, Williams DH, Reader JC, Collins I, Garrett MD. The preclinical pharmacology and therapeutic activity of the novel CHK1 inhibitor SAR-020106. Mol Cancer Ther. 2010;9:89–100. doi: 10.1158/1535-7163.MCT-09-0938. [DOI] [PubMed] [Google Scholar]
- 35.Xu H, Cheung IY, Wei XX, Tran H, Gao X, Cheung NK. Checkpoint kinase inhibitor synergizes with DNA-damaging agents in G(1) checkpoint-defective neuroblastoma. Int J Cancer. 2011;129:153–162. doi: 10.1002/ijc.25842. [DOI] [PubMed] [Google Scholar]
- 36.Tonkinson JL, Worzalla JF, Tseng CH, Mendelsohn LG. Cell cycle modulation by a multitargeted antifolate, LY231514, increases the cytotoxicity and antitumor activity of gemcitabine in HT29 colon carcinoma. Cancer Res. 1999;59:3671–3676. [PubMed] [Google Scholar]
- 37.Pratt SE, Durland-Busbice S, Shepard RL, Donoho GP, Starling JJ, Wickremsinhe ER, Perkinks EJ, Dantzig AH. Efficacy of low-dose oral metronomic dosing of the prodrug of gemcitabine, LY2334737, in human xenografts. Mol Cancer Ther. 2013;12:481–490. doi: 10.1158/1535-7163.MCT-12-0654. [DOI] [PubMed] [Google Scholar]
- 38.Sakamoto H, Kitano M, Suetomi Y, Takeyama Y, Ohyanagi H, Nakai T, Yasuda C, Kudo M. Comparison of standard-dose and low-dose gemcitabine regimens in pancreatic adenocarcinoma patients: a prospective randomized trial. J Gastroenterol. 2006;41:70–76. doi: 10.1007/s00535-005-1724-7. [DOI] [PubMed] [Google Scholar]
- 39.Tempero M, Plunkett W, van Haperen VR, Hainsworth J, Hochester H, Lenzi R, Abbruzzese J. Randomized phase II comparison of dose-intense gemcitabine: thirty-minute infusion and fixed dose rate infusion in patients with pancreatic adenocarcinoma. J Clin Oncol. 2003;21:3402–3408. doi: 10.1200/JCO.2003.09.140. [DOI] [PubMed] [Google Scholar]
- 40.Olive KP, Jacobetz MA, Davidson CJ, Gopinathan A, McIntyre D, Honess D, Madhu B, Goldgraben MA, Caldwell ME, Allard D, Frese KK, Denicola G, Feig C, Combs C, Winter SP, Ireland-Zecchini H, Reicheld S, Howat WJ, Chang A, Dhara M, Wang L, Ruckert F, Grutzmann R, Pilarsky C, Izeradjene K, Hingorani SR, Huang P, Davies SE, Plunkett W, Egorin M, Hruban RH, Whitebread N, McGovern K, Adams J, Iacobuzio-Donahue C, Griffiths J, Tuveson DA. Inhibition of Hedgehog signaling enhances delivery of chemotherapy in a mouse model of pancreatic cancer. Science. 2009;324:1457–1461. doi: 10.1126/science.1171362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Venkatasubramanian R, Henson MA, Forbes NS. Integrating cell-cycle progression, drug penetration and energy metabolism to identify improved cancer therapeutic strategies. J Theor Biol. 2008;253:98–117. doi: 10.1016/j.jtbi.2008.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ribba B, Colin T, Schnell S. A multiscale mathematical model of cancer, and its use in analyzing irradiation therapies. Theor Biol Med Model. 2006;3:7. doi: 10.1186/1742-4682-3-7. [DOI] [PMC free article] [PubMed] [Google Scholar]