A k-Space Method for Moderately Nonlinear Wave Propagation

Abstract

A k-space method for moderately nonlinear wave propagation in absorptive media is presented. The Westervelt equation is first transferred into k-space via Fourier transformation, and is solved by a modified wave-vector time-domain scheme. The present approach is not limited to forward propagation or parabolic approximation. One- and two-dimensional problems are investigated to verify the method by comparing results to analytic solutions and finite-difference time-domain (FDTD) method. It is found that to obtain accurate results in homogeneous media, the grid size can be as little as two points per wavelength, and for a moderately nonlinear problem, the Courant–Friedrichs–Lewy number can be as large as 0.4. Through comparisons with the conventional FDTD method, the k-space method for nonlinear wave propagation is shown here to be computationally more efficient and accurate. The k-space method is then employed to study three-dimensional nonlinear wave propagation through the skull, which shows that a relatively accurate focusing can be achieved in the brain at a high frequency by sending a low frequency from the transducer. Finally, implementations of the k-space method using a single graphics processing unit shows that it required about one-seventh the computation time of a single-core CPU calculation.

I. Introduction

A prevalent numric approach to nonlinear acoustic problems involves solving the Kuznetsov–Zabolotskaya–Khokhlov (KZK) equation [1]–[7]. Developed as a modification of the Burgers equation to include absorption and diffraction [8], the KZK equation [1] can also be derived as the parabolic approximation to the Westervelt equation [9]. Despite its utility, the equation is limited in validity to cases of quasi-planar wave propagation and is accurate for directional fields close to the axis of propagation and far from the source [10]. More general methods based on the Westervelt equation have been reported, but have primarily been limited to forward propagation [11], thus neglecting reverberation, or otherwise restricting nonlinear distortion to the normal direction [12]–[14].

Recently, several methods have been proposed to solve the Westervelt equation without such restrictions [15]–[19]. Likewise, the present work investigates a new wave-vector time-domain (k-space) based numerical algorithm [20]–[23] that can be applied to a wide range of nonlinear applications. The overall goal is to develop a computationally efficient method that is well-suited for heterogeneous media. The described approach is similar to the so-called pseudo-spectral method [24] in that both methods calculate the spatial differentiation in the k-space by Fourier transformation. However, the proposed method employs a straightforward time-stepping scheme that has been shown to be more accurate and less complex [21], [22]. In addition, the proposed approach is based on the second-order nonlinear wave equation, whereas the pseudo-spectral method [24] is based on a first-order nonlinear wave equation, which requires extra computation and storage of the particle displacement vector. As a result, the present method is less demanding in terms of storage and computation.

The paper proceeds as follows: section II presents the derivation of the k-space method followed by the description of an absorbing layer devised to eliminate the problem of transformation-induced phase wrapping. Section III concerns numerical simulations. The k-space method is compared with the analytic solution and FDTD method. Criteria for choosing spatial and temporal step-size are revealed. An application of the proposed method for studying nonlinear wave propagation through the skull is presented. Finally, implementations of the algorithm using graphics processing units (GPUs) are also discussed. Section IV concludes the paper.

II. Theory

For a fluid medium with inhomogeneous acoustic properties, the nonlinear acoustic wave equation (Westervelt equation) is written as [7]

$$\rho \nabla \cdot (\frac{1}{\rho }\nabla p)-\frac{1}{c^2}\frac{{\mathrm{\partial }}^{2}p}{\mathrm{\partial }{t}^2}+\frac{\delta }{c^4}\frac{{\mathrm{\partial }}^{3}p}{\mathrm{\partial }{t}^3}+\frac{\beta }{\rho c^4}\frac{{\mathrm{\partial }}^2{p}^2}{\mathrm{\partial }{t}^2}=0,$$ (1)

where p is the sound pressure, c is the sound speed, δ is the sound diffusivity, β is the nonlinearity coefficient, and ρ is the ambient density. All materials are assumed to be spatially varying functions. The equation inherently assumes a thermoviscous fluid, because the relaxation mechanism is not considered. However, the following algorithm can be readily modified to include power-law absorption and dispersion [25]. It is also noted that the lagrangian density [8], which was shown to be negligible [18], has been dropped from (1).

By using the normalized wave field $f=p/\sqrt{\rho }$ [21], the first-order derivative term is eliminated and the nonlinear wave equation becomes

$${\nabla }^{2}f-\frac{1}{c_0^2}\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{t}^2}=f\sqrt{\rho }{\nabla }^2\frac{1}{\sqrt{\rho }}+\frac{1}{c_0^2}(\frac{c_0^2}{c^2}-1)\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{t}^2}-\frac{\delta }{c^4}\frac{{\mathrm{\partial }}^{3}f}{\mathrm{\partial }{t}^3}-\frac{\beta }{\sqrt{\rho }{c}^4}\frac{{\mathrm{\partial }}^2{f}^2}{\mathrm{\partial }{t}^2},$$ (2)

where c₀ is the background speed of sound.

By defining an auxiliary field w = f + v, where $v=(c_0^2/c^2-1)f,$ (2) can be reduced to

$$-\frac{1}{c_0^2}\frac{{\mathrm{\partial }}^{2}w}{\mathrm{\partial }{t}^2}={\nabla }^{2}v-{\nabla }^{2}w+(q-h-d)/c_0^2,$$ (3)

where

$$q=c_0^{2}f\sqrt{\rho }{\nabla }^2\frac{1}{\sqrt{\rho }},h=c_0^2\frac{\beta }{\sqrt{\rho }{c}^4}\frac{{\mathrm{\partial }}^2{f}^2}{\mathrm{\partial }{t}^2},d=c_0^2\frac{\delta }{c^4}\frac{{\mathrm{\partial }}^{3}f}{\mathrm{\partial }{t}^3}.$$ (4)

Fourier transformation of (3) in the spatial domain yields the k-space equation

$$\frac{{\mathrm{\partial }}^{2}W}{\mathrm{\partial }{t}^2}=c_0^2{k}^2(V-W)-(Q-H-D),$$ (5)

Where $k=\sqrt{k_x^2+k_y^2+k_z^2}$, and W, V, Q, H, and D are the spatial Fourier transforms of w, v, q, h, and d, respectively which can be calculated using a fast Fourier transform (FFT).

Eq. (5) can be solved in a nonstandard finite difference approach [21], [22],

$$W(t+\mathrm{\Delta }t)-2W(t)+W(t-\mathrm{\Delta }t)=4{sin}^2\left(\frac{c_{0}k\mathrm{\Delta }t}{2}\right)[V-W-\frac{1}{c_0^2{k}^2}(Q-H-D)],$$ (6)

where Δt is the temporal step size. For a homogeneous medium or a weakly inhomogeneous medium, this harmonic oscillator equation guarantees small dispersion error with a large temporal step, as opposed to the conventional leap-frog scheme,

$$W(t+\mathrm{\Delta }t)-2W(t)+W(t-\mathrm{\Delta }t)={(c_{0}k\mathrm{\Delta }t)}^2[V-W-\frac{1}{c_0^2{k}^2}(Q-H-D)],$$ (7)

or even higher order time integration, such as the fourth-order Adams-Bashforth time integration [24].

comparing (6) with [21, Eq. (9)], one can see that two new terms have been added, H and D, which are the contributions from the nonlinearity and diffusivity. This approach can then be viewed as a straightforward extension to a previous k-space method described by Mast et al.[21] with nonlinearity and absorption included. In addition, because the coefficients of the third and fourth terms in (1) are small compared with the coefficient of the second term, the stability condition should be similar to the linear k-space method,

$$sin\left(\frac{\text{CFL}{c}_0\pi }{{2c}_{max}}\right)\le \frac{c_0}{c_{max}},$$ (8)

where CFL is the courant-Friedrichs–Lewy number c_maxΔt/Δx. (note that the definition is somewhat different from that used in [21].) clearly, the algorithm is unconditionally stable for media with c(r) < c₀ everywhere.

To calculate H (or h), the following backward difference approximation was employed [26]:

$$\frac{{\mathrm{\partial }}^2{f}^2}{\mathrm{\partial }{t}^2}=(45f^2(t)-154f^2(t-\mathrm{\Delta }t)+214f^2(t-2\mathrm{\Delta }t)-156f^2(t-3\mathrm{\Delta }t)+61f^2(t-4\mathrm{\Delta }t)-10f^2(t-5\mathrm{\Delta }t))/(12\mathrm{\Delta }{t}^2).$$ (9)

This backward difference approximation has a fourth-order accuracy. It has the disadvantage of requiring the storage of six time steps. However, if this is problematic, the second-order backward difference approximation [26] can be used at the expense of a significantly reduced time step,

$$\frac{{\mathrm{\partial }}^2{f}^2}{\mathrm{\partial }{t}^2}=\frac{2f^2(t)-5f^2(t-\mathrm{\Delta }t)+4f^2(t-2\mathrm{\Delta }t)-f^2(t-3\mathrm{\Delta }t)}{\mathrm{\Delta }{t}^2}.$$ (10)

Conversely, if the memory is not limited, a higher order, e.g., a sixth-order approximation might be a good alternative. In this study, however, only the fourth-order approximation was used. The pressure field for the initial six steps can be either roughly calculated using the linear k-space method, assuming that the nonlinearity does not significantly build up in these six steps, or more precisely calculated using nonlinear projection methods. In this study, the former approach was used.

Similarly, to calculate D (or d), the following third-order backward difference approximation was used [6]:

$$\frac{{\mathrm{\partial }}^{3}f}{\mathrm{\partial }{t}^3}=(17f(t)-71f(t-\mathrm{\Delta }t)+118f(t-2\mathrm{\Delta }t)-98f(t-3\mathrm{\Delta }t)+41f(t-4\mathrm{\Delta }t)-7f(t-5\mathrm{\Delta }t))/(4\mathrm{\Delta }{t}^3).$$ (11)

Because an FFT implies periodicity, the k-space method inherently has a wrapping artifact problem: the wave enters one boundary and exits from the other side. The easiest way to overcome this is to enlarge the computational domain; however, this inevitably increases the calculation time. The well-known perfectly matched layer (PML) approach [22] has been shown to be a good solution to this problem. In this study, an absorbing layer [27], [28] was used to minimize the spurious reflections from the boundary. The equation for the absorbing layer can be written in f as

$${\mathrm{\nabla }}^{2}f-\frac{1}{c_0^2}\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{t}^2}=2U\frac{\mathrm{\partial }f}{\mathrm{\partial }t}+U^{2}f.$$ (12)

It is noted that the nonlinearity and absorption terms should still be considered in the absorption layer to prevent sudden medium change. They are only ignored here to emphasize the newly added term in the absorption layer, i.e., U, which is an absorption term (frequency independent) and its derivative should be kept as small as possible. In this study, we have used [28]

$$U=U_0/{cos\mathrm{h}}^2(\alpha n),$$ (13)

where U₀ is a constant (2.0 in the present study), α is a decay factor (0.1 in the present study), and n denotes the distance in number of grid points from the boundary. Although this equation was proposed for the linear acoustic equation, it has been found in this study to also be suitable for the nonlinear acoustic equation. Numerical simulations have shown that, for a normal incident wave, the refection from the absorption layer can be reduced by more than 50 dB.

After applying the Fourier transform, (12) can be written in terms of W as

$$\frac{{\mathrm{\partial }}^{2}W}{\mathrm{\partial }{t}^2}=c_0^2{k}^2(-W)-M,$$ (14)

where M is the Fourier transform of m, and

$$m=c_0^2(2U\frac{\mathrm{\partial }f}{\mathrm{\partial }t}+U^{2}f).$$ (15)

The first-order time derivative can be calculated by the second-order approximation

$$\frac{\mathrm{\partial }f}{\mathrm{\partial }t}=\frac{3f(t)-4f(t-\mathrm{\Delta }t)+f(t-2\mathrm{\Delta }t)}{2\mathrm{\Delta }t}.$$ (16)

A higher-order approximation can also be employed, but in this study, (16) was found to be sufficient. Finally, (14) can be solved in a manner similar to (6), and the complete time stepping algorithm is written as

$$W(t+\mathrm{\Delta }t)-2W(t)+W(t-\mathrm{\Delta }t)=4{sin}^2\left(\frac{c_{0}k\mathrm{\Delta }t}{2}\right)[V-W-\frac{1}{c_0^2{k}^2}(Q-H-D+M)],$$ (17)

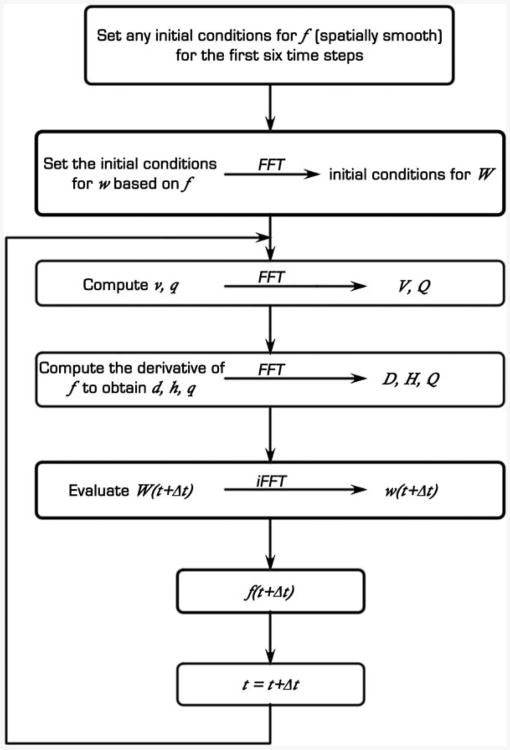
To close this section, it is reiterated that the present nonlinear k-space algorithm is very similar to the linear k-space algorithm and can now be summarized as in Fig. 1.

Fig. 1.

The algorithm for the k-space method.

III. Simulations

A. A 1-D Homogeneous Medium Problem

To verify the present k-space algorithm, as well as to determine the requirement for the spatial and temporal steps to achieve accurate results, we initially tested 1-d propagation in a homogeneous medium. The incident wave pi was defined as a plane wave with Gaussian temporal shape [21]:

$$p_i=p_{0}sin({\omega }_0\tau )e^{{-\tau }^2/(2{\sigma }^2)},$$ (18)

where p₀ is the pressure amplitude, ω₀ is the center angular frequency, τ is the retarded time τ = t − (x − x₀)/c₀, and x₀ is the center of the pulse. In this section, p₀ was chosen to be 2 MPa, ω₀ was 1 MHz × 2π, and σ was 5 × 10⁻¹². This gave a nominal maximum frequency of 1.5 MHz, corresponding to the spectral point 95 dB down from the center frequency. The speed of sound was 1500 m/s, the density was 1000 kg/m³, and the nonlinearity was 3.5. No attenuation was considered. With (18), the sound field is known for the first six temporal steps, with the assumption that the nonlinearity is negligible for these six steps. This accomplishes step 1 in the algorithm described in the previous section. Note that, because a second order time-domain equation is solved, two initial conditions are needed, one for the pressure and one for the pressure derivative with regard to time t. Because the sound field for the first six temporal steps can be obtained from (18), these two initial conditions are explicitly given.

To investigate the computational efficiency of the k-space method, a fourth-order finite-difference time-domain (FDTD) method [29] was implemented for comparison. A benchmark solution was also obtained using the analytic Poisson solution. Details of this solution are not repeated here, but can be found in [8].

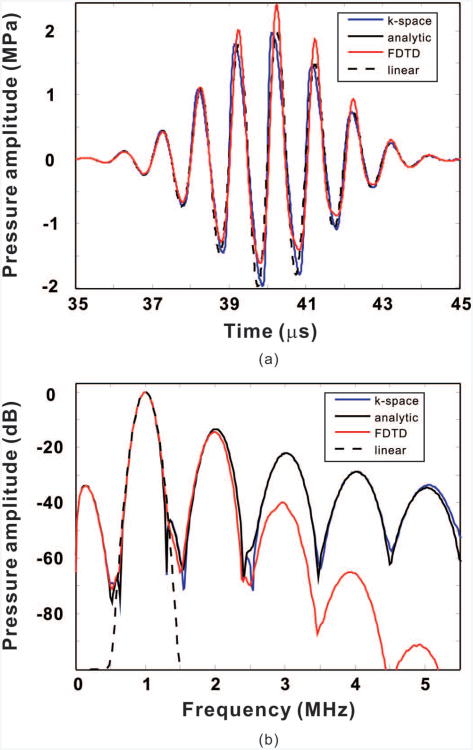
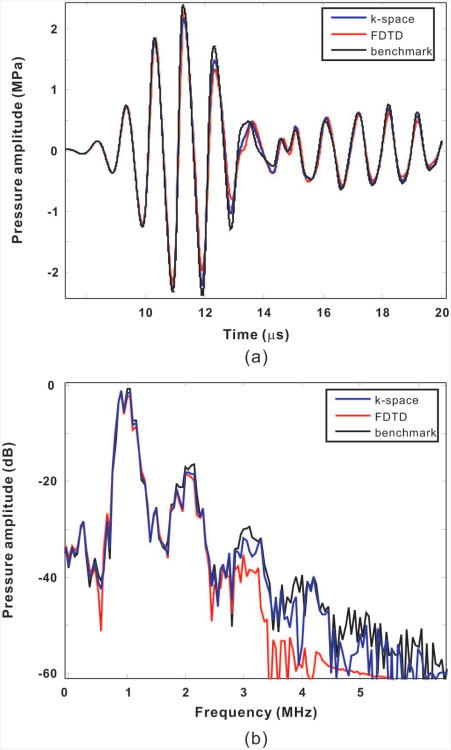
In the first case, the spatial steps were both 1/8 of the wavelength at the nominal maximum frequency for the k-space method and FDTD method. The CFL number were also the same, i.e., 0.1. Fig. 2(a) shows the time-domain signal of the pulse after a distance of 50 mm, which corresponds to 0.65 of the theoretical plane wave shock formation distance σ_s for a sinusoidal wave at 1 MHz. Fig. 2(b) shows the results in the frequency domain. Results for linear propagation are shown in both plots for reference. It can be clearly seen from Fig. 2(b) that even though the two approaches used the same numerical configuration, the k-space method agrees well with the analytic solution up to the fifth harmonics, with a maximum difference of around 2 dB, whereas the FDTD method completely deviates from the analytic solution starting from the third harmonics. This is because for the k-space method, only two grid points are needed for one wavelength at the frequency of interest to satisfy the Nyquist rate condition. On the other hand, the fourth-order FDTD method is well known to require approximately 8 to 10 grid points per wavelength to acquire accurate results. For a moderately nonlinear problem, if the third harmonics are of interest, then the k-space method theoretically requires 6 grid points at the wavelength of the fundamental frequency, whereas the FDTD method requires 24 to 30 grid points. The computational efficiency difference becomes more pronounced if a 3-D problem is considered. Finally, in this case, the k-space and FDTD method took about the same computation time.

Fig. 2.

Comparison between the analytical solution and the k-space method for a one-dimensional homogeneous medium at a distance of approximately 0.65σ. (a) Frequency-domain results with spatial step varied. (b) Frequency-domain results with courant–Friedrichs–lewy number varied.

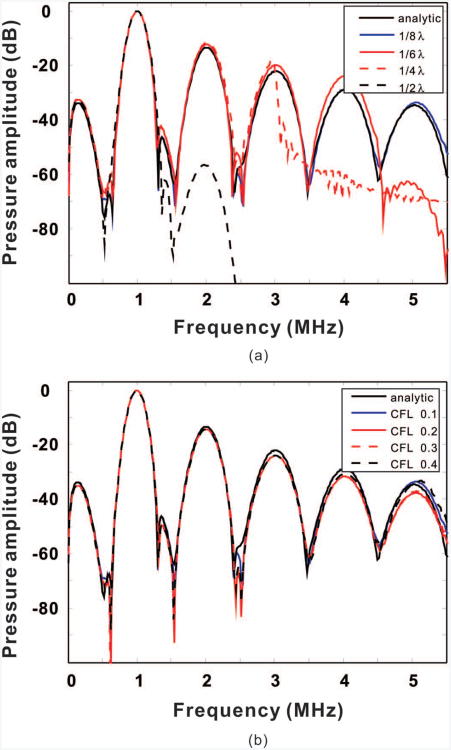
Next, the k-space method is tested with spatial step and CFL number varied. More specifically, two cases were studied. In the first case, the spatial step was chosen to be 1/2, 1/4, 1/6, and 1/8 of the wavelength at the nominal maximum frequency, with the CFL number fixed at 0.1. In the second case, the temporal criteria was evaluated by fixing the step size at 1/8 of the wavelength and varying the CFL number from 0.1 to 0.4. Simulation results in the frequency domain are shown in Figs. 3(a) and 3(b), respectively. We have the following observations:

1. The accuracy of the k-space method quickly decreases at the frequency where the Nyquist rate condition is not met. In this example, the k-space method is valid approximately up to 1.5, 3, 4.5, and 6 MHz for step sizes of 1/2, 1/4, 1/6, and 1/8 wavelength, respectively. Therefore, in a weakly nonlinear problem, in which the fundamental and second harmonics are of concern, the k-space method only needs to employ 4 points per wavelength at the maximum frequency to capture accurate wave propagation for a homogeneous medium.

2. The accuracy of the k-space method also depends on the CLF number; however, the change in the accuracy is not as significant as in the case in which the spatial step is varied. As expected, the smaller the CFL number is, the more accurate is the result. In this specific case, in which a moderately nonlinear wave propagation is modeled (the second harmonics are about 1/5 of the fundamental in amplitude), fairly accurate results can be obtained up to the fourth harmonics (maximum derivation around 2 dB) even with a CFL number of 0.4. It is expected that for a weakly nonlinear problem, the required CFL number can be even larger than 0.4, because the nonlinearity can then be viewed as a small perturbation imposed upon the linear wave equation. For a linear problem, the CFL number in the k-space algorithm can be arbitrarily large in a homogeneous medium as long as the Nyquist rate is satisfied [22], [23].

Fig. 3.

Comparison between the analytic solution and the k-space method for a one-dimensional homogeneous medium at a distance of approximately 0.65σ. (a) Frequency-domain results with spatial step varied. (b) Frequency-domain results with courant–Friedrichs–lewy number varied.

Finally, note that the k-space method is not optimum when applied to simulations of strongly nonlinear wave propagation, e.g., shock waves. This is because spectral methods suffer from discontinuities existing in the solution, which can be seen in a shock wavefront. The gibbs phenomenon, i.e., numerical oscillations near the discontinuity, is expected to be seen when applying k-space method to shock wave simulations. However, by utilizing an artificial attenuation in the algorithm [12], the numerical oscillations can be reduced. A recent study also reports on the use of gegenbauer reconstructions for shock wave modeling [30].

B. Two 2-D Inhomogeneous Medium Problems

In this section, two 2-d inhomogeneous medium problems are discussed. In the first problem, a cylindrical object with radius 4.0 mm was added into the center of the medium as a scatterer. The background medium has the same acoustic properties as in the 1-d homogenous medium problem; i.e., the speed of sound was 1500 m/s, the density was 1000 kg/m³, the nonlinearity was 3.5, and the medium was lossless. The acoustic properties in the cylindrical object were different; the speed of sound was 1575 m/s, the density was 1050 kg/m³, the nonlinearity was 4, and the diffusivity was 1 × 10⁻⁴ m²≥s⁻¹. Clearly this is a weak contrast problem, which can occur, for example, in soft tissue [11]. Assuming that the nonlinearity and diffraction effects are not significant within the first six steps, the initial sound field was again employed (18). The center frequency was 1 MHz, x₀ = −0.012, σ = 3e⁻¹². These result in a nominal maximum frequency of 1.5 MHz. The pressure amplitude p₀ was 3 MPa. In addition, this initial condition only applied to the domain | y | ≤ 0.01. The calculation domain was 5 × 5 cm, where 9 elements per minimum wavelength were used. The CFL number was 0.3. For comparison, FDTD was also implemented with the same spatial resolution and CFL number. The benchmark solutions were also obtained from an FDTD simulation, with a fine spatial resolution of 27 elements per minimum wavelength and a CFL number of 0.1.

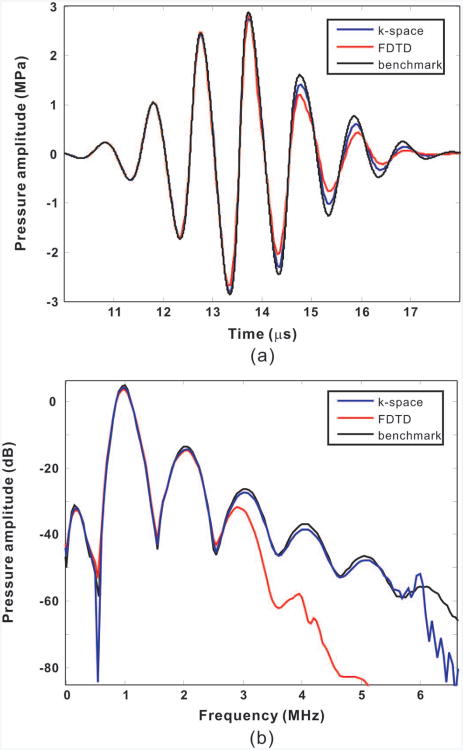
Fig. 4 presents three sets of snapshots of the sound field computed from the k-space method at times 6.23, 9.80, and 13.38 μs. The area shown in each figure is 2.5 × 2.5 cm. The benchmark solution is not shown here because the difference is visually indistinguishable. To assess the accuracy of the k-space method, Fig. 5(a) illustrates all three results: benchmark solution, FDTD, and k-space, at the location (8.25, 0) mm (shown in Fig. 4(a) as the receiver) in the time domain; Fig. 5(b) shows the results in the frequency domain. The k-space result agrees well with the benchmark solution. The derivation at the second and third harmonic are both around 1 dB. On the other hand, the accuracy of the FDTD method quickly deteriorates after the third harmonic, because of the insufficient spatial resolution. For example, the derivation at the third harmonic is about 8 dB.

Fig. 4.

Sound field computed in a two-dimensional strongly inhomogeneous medium. Pressure at (a) 6.23 μs, (b) 9.80 μs, and (c) 13.28 μs obtained from the k-space method. The solid line shows the cylinder.

Fig. 5.

Sound field computed in a two-dimensional weakly inhomogeneous medium. The k-space method and finite-difference time-domain (FDTD) method are compared with the benchmark solution. (a) Time-domain results at the location (8.25, 0) mm. (b) Frequency-domain results at the same location.

For this weakly inhomogeneous problem, the k-space method is shown to have fairly good performance, as was the case for the 1-D homogeneous problems. This has been found also in linear acoustic problems [20]–[22].

In the second example, the amplitude for the initial acoustic field was increased to 7 MPa. The acoustic properties in the cylindrical object were changed; the speed of sound was 3000 m/s, the density was 2000 kg/m³, and the nonlinearity was kept at 4. This example allowed verification of the present method for strong-contrast problems, which can occur, for example, in scattering from human bones [21] and phononic band gaps [31]. Fig. 6 presents three snapshots of the sound field at times 6.23, 9.80, and 13.38 μs. Fig. 7(a) shows the results at the same location (8.25, 0) mm in the time domain; Fig. 7(b) shows the results in the frequency domain. The k-space method again outperforms the FDTD in terms of accuracy, but is slightly less accurate compared with the weak contrast case. This is in correspondence with previous findings in linear acoustic problems [20]–[22]; i.e., the k-space method becomes less accurate for strongly inhomogeneous problems. For the k-space method, the derivations at the second and third harmonics are both approximately 2 dB, whereas for FDTD, they are 3 dB and 9 dB, respectively.

Fig. 6.

Sound field computed in a two-dimensional strongly inhomogeneous medium. Pressure at (a) 6.23 μs, (b) 9.80 μs, and (c) 13.28 μs obtained from the k-space method. The solid line shows the cylinder.

Fig. 7.

Sound field computed in a two-dimensional strongly inhomogeneous medium. The k-space method and finite-difference time-domain (FDTD) method are compared with the benchmark solution. (a) Time-domain results at the location (8.25, 0) mm. (b) Frequency-domain results at the same location.

It has been shown that the accuracy of the k-space method for large-contrast problems can be improved by using a smoothing approach [21]. However, this requires the analytic Fourier transforms of the inhomogeneities, which are typically not available. For this reason, the smoothing approach is not used in this study.

C. Harmonic Focusing

This section studies transcranial nonlinear ultrasound focusing inside the brain. It is well known that the skull introduces strong phase aberration during high-intensity focused ultrasound (HIFU) therapy [32]; thus, the focusing can be shifted outside the focal zone, potentially damaging the surrounding tissue. Methods have been developed to correct this phase distortion [33], [32] which require skull images from computed tomography (CT). The images are registered with both the magnetic resonance image and the ultrasound therapy device, and a computer algorithm predicts the amplitude and phasing pattern of a treatment array necessary to restore a distorted focus. However, this approach suffers from its high complexity, because it requires an extra imaging modality (CT) and typically a clinical system with a 500-element array as well as 500 dedicated driving channels [34]. On the other hand, the phase aberration is also strongly frequency-dependent. It has been shown that a focus can be achieved at a low frequency of 250 kHz [35], because of its long wavelength compared with the thickness and inhomogeneity of the skull. Nevertheless, for a low frequency, its ability to be focused and transformed into thermal energy at the target is significantly diminished compared with higher frequencies. For these reasons, ideally, a low frequency is desired in the near field to propagate through the distorting layers (skull), and a high frequency is desired at the focal point. This can be potentially realized by nonlinear wave propagation.

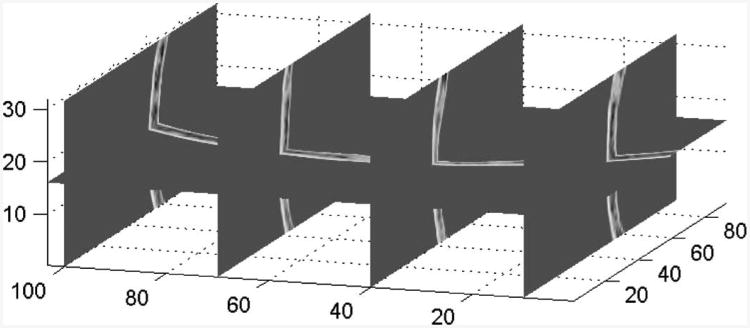
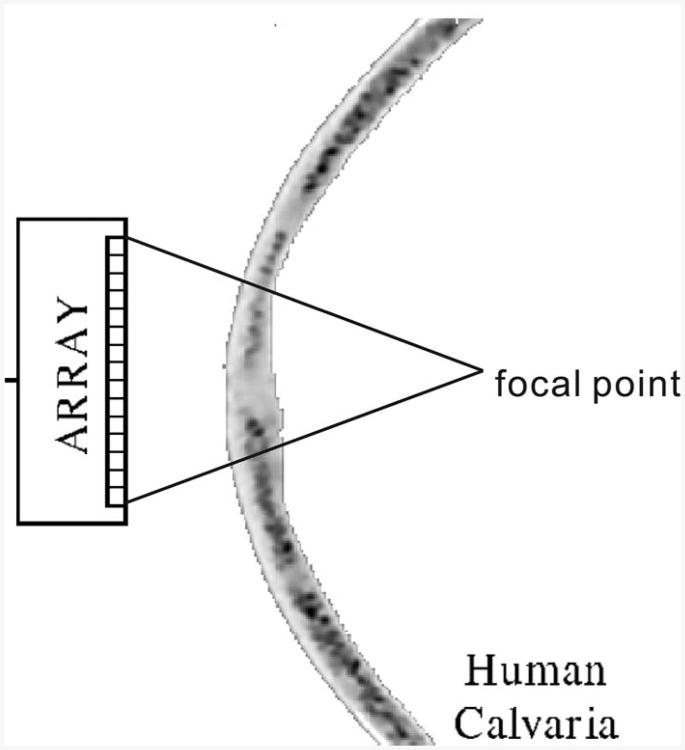
A full k-space 3-D simulation was implemented. The density of the skull was obtained from a CT scan. The speed of sound was calculated using empirical equations [32]. The absorption was neglected for simplicity because it is not expected to significantly impact the phase aberration. The nonlinearity coefficient of the skull was assumed to be homogeneous and was 3.5 (the same as water), this value was expected to at least give qualitative results. The spatial resolution (grid size) was 0.58 mm. The grid numbers are 171, 191, and 59 along the x, y, and z-axes, respectively. The CFL number was 0.2. Fig. 8 shows the portion of the 3-D skull used for the simulation. a phased array was placed close to the skull. For simplicity, each grid is considered as an element and the phase can be adjusted to achieve a focus. The focal point was about 10 cm away from the array. Fig. 9 illustrates a simple diagram of the simulation setup. The size of the array was relatively small, 3 × 10 cm, to minimize the computation time. Three separate simulations were carried out. The phased array emitted three pulses that centered at 250, 500, and 750 kHz, respectively, with a peak amplitude of 1 MPa. at 250 kHz, nonlinear wave propagation was modeled and harmonics at 500 and 750 kHz were generated. For the other two frequencies, linear propagations were assumed. The computation time was on the order of 10 min, and the memory required for the computation was about 10 GB. The detailed configuration of the computer can be found in the next subsection.

Fig. 8.

A 3-D spatial representation of the sound speed distribution deduced from computed tomography scans and used as input data for the full 3-D simulation. The axes are in millimeters.

Fig. 9.

A diagram of the numerical simulation setup for the skull and transducer array.

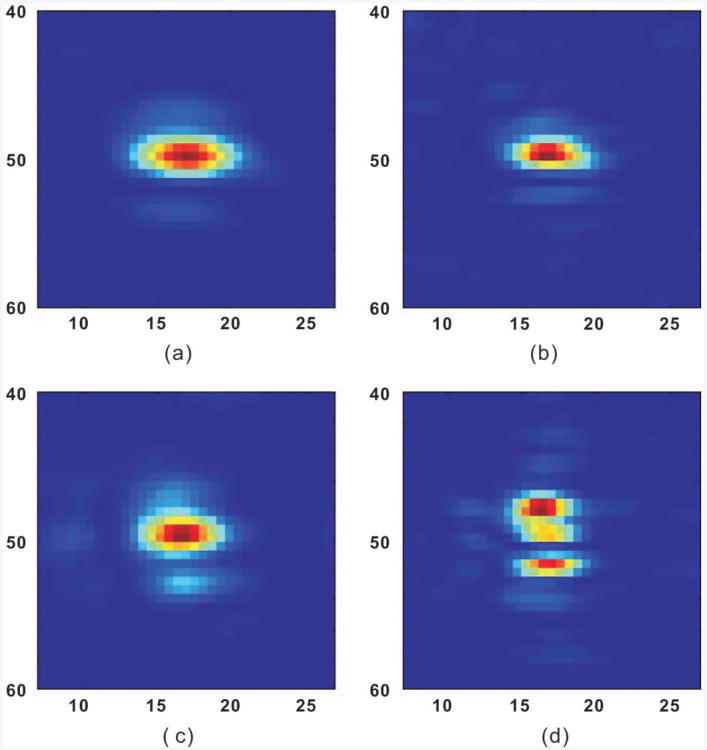
Fig. 10 shows the acoustic intensity distribution [36] on the focal plane. The focal point is designated at (0.017, 0.05) m. Figs. 10(a) and (b) show the intensity at the second and third harmonics generated from acoustic emission at 250 kHz. Figs. 10(c) and (d) show the intensity at the fundamental frequency, generated by higher frequencies at 500 and 750 kHz, respectively. It is evident that harmonic focusing using nonlinear wave propagation has lower side lobes and more accurate focusing compared with directly sending the acoustic signal at higher frequencies. Quantifications of the distortion of focused beams can be achieved through methods discussed in [37] and [38]. However, they are not pursued here because the purpose of this section is only to show that the k-space method can be effectively applied to simulating nonlinear wave propagation through skulls.

Fig. 10.

Acoustic intensity distribution on the focal plane. (a) second harmonics, f₂ = 500 kHz; (b) third harmonics, f₃ = 750 kHz; (c) fundamental, f₁ = 500 kHz; (d) fundamental, f₁ = 750 kHz. The axes are in millimeters.

The ultimate goal is to minimize the fundamental frequency and maximize the harmonics (second or higher harmonics) at the focal point, because the fundamental frequency has a larger focal zone and lower cavitation threshold. a preliminary solution [39] was proposed in which alternating array elements are driven out of phase, so that the fundamental frequency vanishes at the focal point, but the second harmonic would still be in phase at the focal point. Future work will follow along this line and further minimize the fundamental frequency, not only at the focal point, but also throughout the whole brain area.

D. GPU Implementations

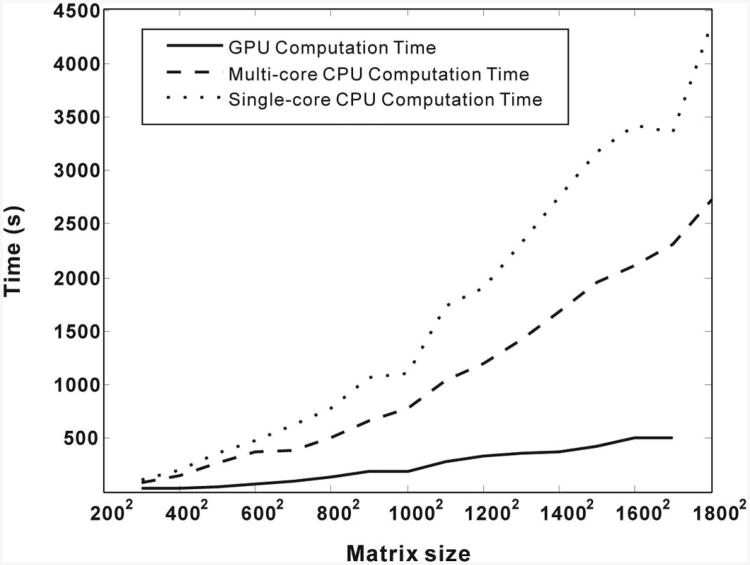
During the simulation, it was found that the majority of the computational time was spent on forward and inverse FFT routines. There was also a large amount of time spent on the matrix point-wise manipulations. All of these computations are inside the time-step and are candidates to be dispatched to GPUs for an increase in speed. We adopted a third-party Matlab (The MathWorks Inc., Natick, Ma) GPU computing toolbox named Jacket (AccelerEyes, Atlanta, GA) to achieve the GPU computing. Specifically, Jacket's forward and inverse FFT overload functions were employed to improve the computation speed. To test the algorithm performance on the GPU, we ran a set of 2-d simulations with 1600 time steps using Matlab r2011a on a 64-bit Pc.

Fig. 11 shows the comparison of the amount of time to run the 2-d simulation for different matrix sizes (number of grid points on x- and y-axis) on a multi-core CPU, a single-core CPU, and a GPU. The CPU calculations were implemented on a quad-core 3.60-gHz Intel Xeon 5687 CPU (Intel corp., Santa Clara, CA) with 192 GB of RAM. For the single CPU computational time test, we closed the multi-core function in the BIOS. The same amount of computation was also implemented on an Nvidia Quadro FX4000 with 2 GB of memory (Nvidia Corp., Santa Clara, CA). The comparison result shows that the computational time for the single-core and multi-core CPU computing increase dramatically as the matrix size increases, whereas the increase of the GPU computation time is much less. For a matrix size of 1700 × 1700, the GPU finished the computation in 505 s, which is about one-fifth of the multi-core CPU's 2731 s computation time and one-seventh of the single-core CPU's 3359 s. For a matrix size that is larger than 1800 × 1800, our GPU failed the computation because it exceeded the GPU memory.

Fig. 11.

Comparison of the total computation time for a 2-d 1600-time-step simulation on a graphics processing unit (GPU), a multi-core CPU, and a single-core CPU, with different matrix sizes.

It is noted that the distinction between multi-core CPU time and single-core CPU time is expected to be slightly larger if the code was implemented in c++ or Fortran. Nevertheless, the purpose of this section is more focused on demonstrating the perceived difference rather than a very precise numeric difference among different processing fashions. a similar study for the computational efficiency on GPUs and CPUs for k-space linear acoustic simulation was reported by a recent paper [40].

IV. Conclusions and Discussions

This paper reports on a newly developed algorithm for nonlinear wave propagation based on the k-t space scheme [21]. The validity of the present method is tested by comparing it with analytical solutions and a fourth-order FDTD method, and good agreements have been found. The present approach can be viewed as an extension to a previously reported linear k-space method [21], which has been expanded to include the effects of nonlinearity and attenuation. The method takes inhomogeneity into account and, unlike standard methods, does not employ the parabolic approximation or assume one-way propagation. Thus, it can be applied to a wide range of nonlinear acoustic problems. Furthermore, many commonly used approaches solve the Westervelt equation by assuming that nonlinear distortions occur along the direction normal to the source plane, which is not a valid assumption for highly focusing transducers. This method solves the full Westervelt equation without neglecting the nonlinear distortions in other directions, and thus might be a useful tool for studying the nonlinear sound field for highly focusing transducers.

The present method is highly efficient for moderately nonlinear problems, because it is essentially a spectral approach and thus only requires two nodes per minimum wavelength, as set by the Nysquist rate. In addition, because the method uses an extremely accurate time-stepping algorithm [21], the temporal step (or CFL number) can be fairly large compared with other approaches. As shown in the simulation results, more accurate results can be obtained using the proposed method in comparison with the FDTD method. compared with homogeneous or weakly inhomogeneous media, less accurate results were obtained in strongly inhomogeneous media. It is expected that this is caused in part by aliasing, which occurs from Fourier transformation of discontinuities in the medium [22]. In addition, the second-order wave equation incorporates the density within a second-order derivative term, which can be difficult to represent numerically [22]. One possible way to avoid this problem would be to employ the coupled first-order nonlinear wave equations [24], [22], which have already shown significant improvement for linear wave propagation in inhomogeneous media.

A set of simulations showed the feasibility of using nonlinear effects in HIFU propagation to strategically reduce the effects of near-field layers (skull) that distort the ultrasound field. Future studies will focus on maximizing the harmonic amplitudes and minimizing the fundamental frequency amplitude on the focal plane. Finally, implementations of the k-space method on a single GPU demonstrated a significant reduction of computation time over CPU implementations.

Biographies

Yun Jing received a B.S. degree in electronic science and engineering from Nanjing University, China, in 2006 and an M.S. degree from Rensselaer Polytechnic Institute in 2007. He received his Ph.D. degree in architectural acoustics from Rensselaer Polytechnic Institute in 2009. Before joining the North Carolina State University faculty as an assistant professor, he was a research fellow at Brigham and Women's Hospital, Harvard Medical School. He specializes in the development of analytical and numerical methods for linear and nonlinear wave propagation in fluids.

Tianren Wang is a graduate student in the department of Mechanical and Aerospace Engineering of North Carolina State University, Raleigh, NC. His current research interests include ultrasound tomography. T. Wang received a B.S. degree in optical engineering from Dalian University of Technology, China, in 2007 and an M.S. degree in computer science from the University of North Carolina (UNC) at Chapel Hill, NC, in 2011.

Greg T. Clement's photograph and biography were unavailable at time of publication.