Canonical microcircuits for predictive coding

Summary

This review considers the influential notion of a canonical (cortical) microcircuit in light of recent theories about neuronal processing. Specifically, we conciliate quantitative studies of microcircuitry and the functional logic of neuronal computations. We revisit the established idea that message passing among hierarchical cortical areas implements a form of Bayesian inference – paying careful attention to the implications for intrinsic connections among neuronal populations. By deriving canonical forms for these computations, one can associate specific neuronal populations with specific computational roles. This analysis discloses a remarkable correspondence between the microcircuitry of the cortical column and the connectivity implied by predictive coding. Furthermore, it provides some intuitive insights into the functional asymmetries between feedforward and feedback connections and the characteristic frequencies over which they operate.

Introduction

The idea that the brain actively constructs explanations for its sensory inputs is now generally accepted. This notion builds on a long history of proposals that the brain uses internal or generative models to make inferences about the causes of its sensorium (Helmholtz, 1860; Gregory 1968, 1980; Dayan et al., 1995). In terms of implementation, predictive coding is, arguably, the most plausible neurobiological candidate for making these inferences (Srinivasan et al., 1982; Mumford, 1992; Rao and Ballard, 1999). This review considers the canonical microcircuit in light of predictive coding. We focus on the intrinsic connectivity within a cortical column and the extrinsic connections between columns in different cortical areas. We try to relate this circuitry to neuronal computations by showing the computational dependencies – implied by predictive coding – recapitulate the physiological dependencies implied by quantitative studies of intrinsic connectivity. This issue is important as distinct neuronal dynamics in different cortical layers are becoming increasingly apparent (de Kock et al., 2007; Sakata and Harris, 2009; Maier et al., 2010; Bollimunta et al., 2011). For example, recent findings suggest that the superficial layers of cortex show neuronal synchronization and spike-field coherence predominantly in the gamma frequencies, while deep layers prefer lower (alpha or beta) frequencies (Roopun et al., 2006, 2008; Maier et al., 2010; Buffalo et al., 2011). Since feedforward connections originate predominately from superficial layers and feedback connections from deep layers, these differences suggest that feedforward connections use relatively high frequencies, compared to feedback connections, as recently demonstrated empirically (Bosman et al., 2012). These asymmetries call for something quite remarkable: namely, a synthesis of spectrally distinct inputs to a cortical column and the segregation of its outputs. This segregation can only arise from local neuronal computations that are structured and precisely interconnected. It is the nature of this intrinsic connectivity – and the dynamics it supports – that we consider. The aim of this review is to speculate about the functional roles of neuronal populations in specific cortical layers in terms of predictive coding. Our long-term aim is to create computationally informed models of microcircuitry that can be tested with dynamic causal modelling (David et al., 2006; Moran et al., 2008, 2011).

This review comprises three sections. We start with an overview of the anatomy and physiology of cortical connections – with an emphasis on quantitative advances. The second section considers the computational role of the canonical microcircuit that emerges from these studies. The third section provides a formal treatment of predictive coding and defines the requisite computations in terms of differential equations. We then associate the form of these equations with the canonical microcircuit to define a computational architecture. We conclude with some predictions about intrinsic connections and note some important asymmetries in feedforward and feedback connections that emerge from this treatment.

The anatomy and physiology of cortical connections

This section reviews laminar-specific connections that underlie the notion of a canonical microcircuit (Douglas et al., 1989; Douglas and Martin, 1991, 2004). We first focus on mammalian visual cortex and then consider whether visual microcircuitry can be generalized to a canonical circuit for the entire cortex. Both functional and anatomical techniques have been applied to study intrinsic (intracortical) and extrinsic connections. We will emphasise the insights from recent studies that combine both techniques.

Intrinsic connections and the canonical microcircuit

The seminal work of Douglas and Martin (1991), in the cat visual system, produced a model of how information flows through the cortical column. Douglas and Martin recorded intracellular potentials from cells in primary visual cortex during electrical stimulation of its thalamic afferents. They noted a stereotypical pattern of fast excitation, followed by slower and longer-lasting inhibition. The latency of the ensuing hyperpolarisation distinguished responses in supragranular and infragranular layers. Using conductance-based models, they showed that a simple model could reproduce these responses. Their model contained superficial and deep pyramidal cells with a common pool of inhibitory cells. All three neuronal populations received thalamic drive and were fully interconnected. The deep pyramidal cells received relatively weak thalamic drive but strong inhibition (Figure 1). These interconnections allowed the circuit to amplify transient thalamic inputs to generate sustained activity in the cortex, while maintaining a balance between excitation and inhibition, two tasks that must be solved by any cortical circuit. Their circuit, although based on recordings from cat visual cortex, was also proposed as a basic theme that might be present and replicated, with minor variations, throughout the cortical sheet (Douglas et al., 1989).

Figure 1.

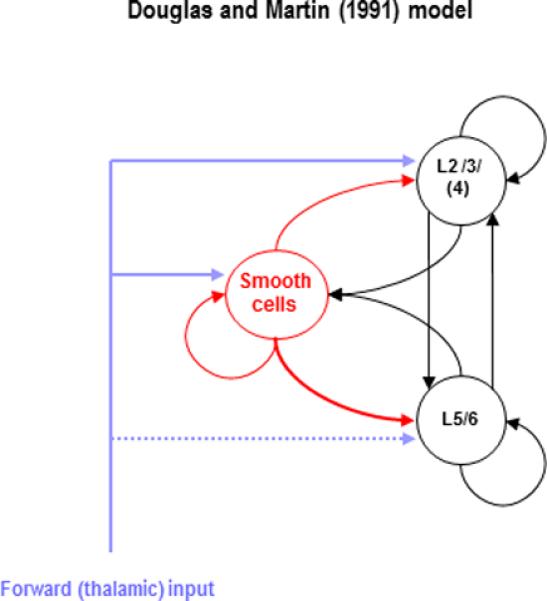
This is a schematic of the classical microcircuit adapted from Douglas and Martin (1991). This minimal circuitry comprises superficial (layers 2 and 3) and deep (layers, 5 and 6) pyramidal cells and a population of smooth inhibitory cells. Feedforward inputs – from the thalamus – target all cell populations, but with an emphasis on inhibitory interneurons and superficial and granular layers. Note the symmetrical deployment of inhibitory and excitatory intrinsic connections that maintain a balance of excitation and inhibition.

Subsequent studies have used intracellular recordings and histology to measure spikes (and depolarisation) in pre and post-synaptic cells, whose cellular morphology can be determined. This approach quantifies both the connection probability – defined as the number of observed connections divided by total number of pairs recorded – and connection strength – defined in terms of post-synaptic responses. Thomson et al (2002) used these techniques to study layers 2 to 5 (L2 to L5) of the cat and rat visual systems. The most frequently connected cells were located in the same cortical layer, where the largest interlaminar projections were the ‘feedforward’ connections from L4 to L3 and from L3 to L5. Excitatory reciprocal ‘feedback’ connections were not observed (L3 to L4) or less commonly observed (L5 to L3), suggesting that excitation spreads within the column in a feedforward fashion. Feedback connections were typically seen when pyramidal cells in one layer targeted inhibitory cells in another (see Thomson and Bannister, 2003 for a review).

While many studies have focused on excitatory connections, a few have examined inhibitory connections. These are more difficult to study, because inhibitory cells are less common than excitatory cells, and because there are at least seven distinct morphological classes (Salin and Bullier, 1995). However, recent advances in optogenetics have made it possible to more easily target inhibitory cells: Kätzel and colleagues combined optogenetics and whole-cell recording to investigate the intrinsic connectivity of inhibitory cells in mouse cortical areas M1, S1, and V1 (Kätzel et al., 2010). They transgenically expressed channelrhodopsin in inhibitory neurons and activated them, while recording from pyramidal cells. This allowed them to assess the effect of inhibition as a function of laminar position relative to the recorded neuron.

Several conclusions can be drawn from this approach (Kätzel et al., 2010): first, L4 inhibitory connections are more restricted in their lateral extent, relative to other layers. This supports the notion that L4 responses are dominated by thalamic inputs, while the remaining laminae integrate afferents from a wider cortical patch. Second, the primary source of inhibition originates from cells in the same layer, reflecting the prevalence of inhibitory intralaminar connections. Third, several interlaminar motifs appeared to be general – at least in granular cortex: principally, a strong inhibitory connection from L4 onto supragranular L2/3 and from infragranular layers onto L4. For more information on the cell-type specificity of inhibitory connections, see Yoshimura and Callaway, (2005). Figure 2 provides a summary of key excitatory and inhibitory intralaminar connections.

Figure 2.

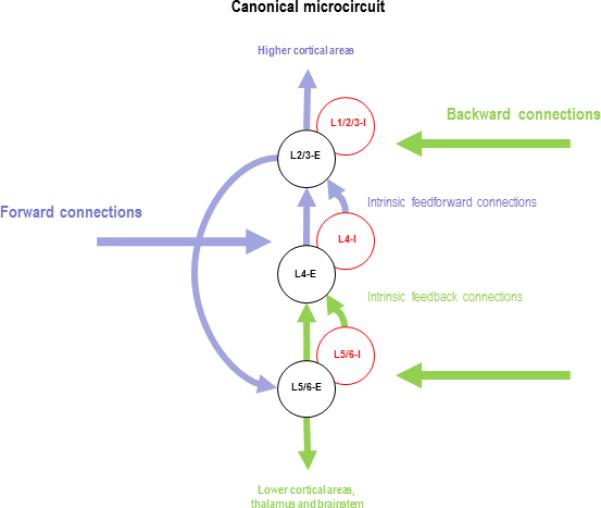
This is a simplified schematic of the key intrinsic connections among excitatory (E) and inhibitory (I) populations in granular (L4), supragranular (L1/2/3) and infragranular (L5/6) layers. The excitatory interlaminar connections are based largely on Gilbert and Wiesel (1983). Forward connections denote feedforward extrinsic corticocortical or thalamocortical afferents that are reciprocated by backward or feedback connections. Anatomical and functional data suggest that afferent input enters primarily into L4 and is conveyed to superficial layers L2/3 that are rich in pyramidal cells, which project forward to the next cortical area, forming a disynaptic route between thalamus and secondary cortical areas (Callaway, 1998). Information from L2/3 is then sent to L5 and L6, which sends (intrinsic) feedback projections back to L4 (Usrey and Fitzpatrick, 1996). L5 cells originate feedback connections to earlier cortical areas as well as to the pulvinar, superior colliculus, and brain stem. In summary, forward input is segregated by intrinsic connections into a superficial forward stream and a deep backward stream. In this schematic, we have juxtaposed densely interconnected excitatory and inhibitory populations within each layer.

Microcircuits in the sensorimotor cortex

Do the features of visual microcircuits generalize to other cortical areas? Recently, two studies have mapped the intrinsic connectivity of mouse sensory and motor cortices: Lefort and colleagues (2009) used multiple whole-cell recordings in mouse barrel cortex to determine the probability of monosynaptic connections – and the corresponding connection strength. As in visual cortex, the strongest connections were intralaminar and the strongest interlaminar connections were the ascending L4 to L2, and descending L3 to L5.

One puzzle about canonical microcircuits is whether motor cortex has a local circuitry that is qualitatively similar to sensory cortex. This question is important because motor cortex lacks a clearly defined granular L4 (a property that earns it the name “agranular cortex”). Weiler and colleagues combined whole-cell recordings in mouse motor cortex with photo-stimulation to uncage Glutamate (Weiler et al., 2008). This allowed them to systematically stimulate the cortical column in a grid – centred on the pyramidal neuron from which they recorded. By recording from pyramidal neurons in L2-6 (L1 lacks pyramidal cells), the authors mapped the excitatory influence that each layer exerts over the others. They found that the L2/3 to L5A/B was the strongest connection – accounting for one-third of the total synaptic current in the circuit. The second strongest interlaminar connection was the reciprocal L5A to L2/3 connection. This pathway may be homologous to the prominent L4/5A to L2/3 pathway in sensory cortex. Also – as in sensory cortex – recurrent (intralaminar) connections were prominent, particularly in L2, L5A/B and L6. The largest fraction of synaptic input arrived in L5A/B, consistent with its key role in accumulating information from a wide range of afferents – before sending its output to the corticospinal tract. In summary, strong input-layer to superficial, and superficial to deep connectivity, together with strong intralaminar connectivity, suggests that the intrinsic circuitry of motor cortex is similar to other cortical areas.

The anatomy and physiology of extrinsic connections

Clearly, an account of microcircuits must refer to the layers of origin of extrinsic connections and their laminar targets. Although the majority of presynaptic inputs arise from intrinsic connections, cortical areas are also richly interconnected, where the balance between intrinsic and extrinsic processing mediates functional integration among specialised cortical areas (Engel et al., 2010). By numbers alone, intrinsic connections appear to dominate – 95% of all neurons labelled with a retrograde tracer lie within about 2 mm of the injection site (Markov et al., 2011). The remaining 5% represent cells giving rise to extrinsic connections, which – although sparse – can be extremely effective in driving their targets. A case in point is the LGN to V1 connection: although it is only the sixth strongest connection to V1, LGN afferents have a substantial effect on V1 responses (Markov et al., 2011).

Hierarchies and functional asymmetries

Current dogma holds that the cortex is hierarchically organized. The idea of a cortical hierarchy rests on the distinction between three types of extrinsic connections: feedforward connections, that link an earlier area to a higher area, feedback connections, that link a higher to an earlier area, and lateral connections, that link areas at the same level (reviewed in Felleman and Van Essen, 1991). These connections are distinguished by their laminar origins and targets. Feedforward connections originate largely from superficial pyramidal cells and target L4, while feedback connections originate largely from deep pyramidal cells and terminate outside of L4 (Felleman and van Essen 1991). Clearly, this description of cortical hierarchies is a simplification and can be nuanced in many ways: for example, as the hierarchical distance between two areas increases, the percentage of cells that send feedforward (resp. feedback) projections from a lower (resp. higher) level becomes increasingly biased towards the superficial (resp. deep) layers (Barone et al., 2000; Vezoli, 2004) .

In addition to the laminar specificity of their origins and targets, feedforward and feedback connections also differ in their synaptic physiology. The traditional view holds that feedforward connections are strong and driving, capable of eliciting spiking activity in their targets and conferring classical receptive field properties – the prototypical example being the synaptic connection between LGN and V1 (Sherman and Guillery, 1998). Feedback connections are thought to modulate (extra-classical) receptive field characteristics according to the current context; e.g., visual occlusion, attention, salience, etc. The prototypical example of a feedback connection is the cortical L6 to LGN connection. Sherman and Guillery identified several properties that distinguish drivers from modulators. Driving connections tend to show a strong ionotropic component in their synaptic response, evoke large EPSPs, and respond to multiple EPSPs with depressing synaptic effects. Modulatory connections produce metabotropic and ionotropic responses when stimulated, evoke weak EPSPs, and show paired-pulse facilitation (Sherman and Guillery, 1998; 2011). These distinctions were based upon the inputs to the LGN, where retinal input is driving and cortical input is modulatory. Until recently, little data were available to assess whether a similar distinction applies to cortico-cortical feedforward and feedback connections. However, recent studies show that cortical feedback connections express not only modulatory but also driving characteristics:

Are feedback connections driving, modulatory or both?

Although it is generally thought that feedback connections are weak and modulatory (Crick and Koch, 1998; Sherman and Guillery, 1998), recent evidence suggests that feedback connections do more than modulate lower level responses: Sherman and colleagues recorded cells in mouse area V1/V2 and A1/A2, while stimulating feedforward or feedback afferents. In both cases, driving-like responses as well as modulatory-like responses were observed (Covic and Sherman, 2011; De Pasquale and Sherman, 2011). This indicates that – for these hierarchically proximate areas – feedback connections can drive their targets just as strongly as feedforward connections. This is consistent with earlier studies showing that feedback connections can be driving: Mignard and Malpeli (1991) studied the feedback connection between areas 18 and 17, while layer A of the LGN was pharmacologically inactivated. This silenced the cells in L4 in area 17 but spared activity in superficial layers. However, superficial cells were silenced when area 18 was lesioned. This is consistent with a driving effect of feedback connections from area 18, in the absence of geniculate input. In summary, feedback connections can mediate modulatory and driving effects. This is important from the point of view of predictive coding, because top-down predictions have to elicit obligatory responses in their targets (cells reporting prediction errors):

In predictive coding, feedforward connections convey prediction errors, while feedback connections convey predictions from higher cortical areas to suppress prediction errors in lower areas. In this scheme, feedback connections should therefore be capable of exerting strong (driving) influences on earlier areas to suppress or counter feedforward driving inputs. However, as we will see later, these influences also need to exert nonlinear or modulatory effects. This is because top-down predictions are necessarily context sensitive: e.g., the occlusion of one visual object by another. In short, predictive coding requires feedback connections to drive cells in lower levels in a context sensitive fashion, which necessitates a modulatory aspect to their postsynaptic effects.

Are feedback connections excitatory or inhibitory?

Crucially, because feedback connections convey predictions – that serve to explain and thereby reduce prediction errors in lower levels – their effective (polysynaptic) connectivity is generally assumed to be inhibitory. An overall inhibitory effect of feedback connections is consistent with in vivo studies. For example, electrophysiological studies of the mismatch negativity suggest that neural responses to deviant stimuli – that violate sensory predictions established by a regular stimulus sequence – are enhanced relative to predicted stimuli (Garrido et al., 2009). Similarly, violating expectations of auditory repetition causes enhanced gamma-band responses in early auditory cortex (Todorovic et al., 2011). These enhanced responses are thought to reflect an inability of higher cortical areas to predict, and thereby suppress, the activity of populations encoding prediction error (Garrido et al., 2007; Wacongne et al., 2011). The suppression of predictable responses can also be regarded as repetition suppression, observed in single unit recordings from the inferior temporal cortex of macaque monkeys (Desimone, 1996). Furthermore, neurons in monkey inferotemporal cortex respond significantly less to a predicted sequence of natural images, compared to an unpredicted sequence (Meyer and Olson, 2011).

The inhibitory effect of feedback connections is further supported by neuroimaging studies (Murray et al., 2002; Murray, 2005; Harrison et al., 2007; Summerfield et al., 2008, 2011; Alink et al., 2010). These studies show that predictable stimuli evoke smaller responses in early cortical areas. Crucially, this suppression cannot be explained in terms of local adaptation, because the attributes of the stimuli that can be predicted are not represented in early sensory cortex (e.g., Harrison et al. 2007). It should be noted that the suppression of responses to predictable stimuli can coexist with (top-down) attentional enhancement of signal processing (Wyart et al., 2012): in predictive coding, attention is mediated by increasing the gain of populations encoding prediction error (Spratling, 2008; Feldman and Friston, 2010). The resulting attentional modulation (e.g., Hopfinger et al., 2000) can interact with top-down predictions to override their suppressive influence – as demonstrated empirically (Kok et al., 2011). See Buschman and Miller, (2007), Saalmann et al., (2007), Anderson et al. (2011), and Armstrong et al. (2012) for further discussion of top-down connections in attention.

Further evidence for the inhibitory (suppressive) effect of feedback connections comes from neuropsychology: Patients with damage to the prefrontal cortex (PFC) show disinhibition of event related potential responses (ERP) to repeating stimuli (Knight et al., 1989; Yamaguchi and Knight, 1990; but see Barceló et al., 2000). In contrast, they show reduced-amplitude P300 ERPs in response to novel stimuli – as if there were a failure to communicate top-down predictions to sensory cortex (Knight, 1984). Furthermore, normal subjects show a rapid adaptation to deviant stimuli as they become predictable – an effect not seen in prefrontal patients.

Several invasive studies complement these human studies in suggesting an overall inhibitory role for feedback connections. In a recent seminal study, Olsen et al. studied corticothalamic feedback between L6 of V1 and the LGN using transgenic expression of channel rhodopsin in L6 cells of V1. By driving these cells optogenetically – while recording units in V1 and the LGN – the authors showed that deep L6 principal cells inhibited their extrinsic targets in the LGN and their intrinsic targets in cortical layers 2 to 5 (Olsen et al., 2012). This suppression was powerful – in the LGN, visual responses were suppressed by 76%. Suppression was also high in V1, around 80-84% (Olsen et al., 2012). This evidence is in line with classical studies of corticogeniculate contributions to length tuning in the LGN, showing that cortical feedback contributes to the surround suppression of feline LGN cells: without feedback, LGN cells are disinhibited and show weaker surround suppression (Murphy and Sillito, 1987; Sillito et al., 1993; but see Alitto and Usrey, 2008).

While these studies provide convincing evidence that cortical feedback to the LGN is inhibitory, the evidence is more complicated for corticocortical feedback connections (Sandell and Schiller, 1982; Johnson and Burkhalter, 1996, 1997). Hupé and colleagues cooled area V5/MT while recording from areas V1, V2, and V3 in the monkey. When visual stimuli were presented in the classical receptive field (CRF), cooling of area V5/MT decreased unit activity in earlier areas, suggesting an excitatory effect of extrinsic feedback (Hupé et al., 1998). However, when the authors used a stimulus that spanned the extra-classical RF the responses of V1 neurons were – on average – enhanced after cooling area V5, consistent with the suppressive role of feedback connections. These results indicate that the inhibitory effects of feedback connections may depend on (natural) stimuli that require integration over the visual field. Similar effects were observed when area V2 was cooled and neurons were measured in V1: when stimuli were presented only to the CRF, cooling V2 decreased V1 spiking activity; however, when stimuli were present in the CRF and the surround, cooling V2 increased V1 activity (Bullier et al., 1996). Finally, others have argued for an inhibitory effect of feedback based on the timing and spatial extent of surround suppression in monkey V1 – concluding that the far surround suppression effects were most likely mediated by feedback (Bair et al., 2003).

The empirical finding that feedback connections can both facilitate and suppress firing in lower hierarchical areas – depending on the content of classical and extra-classical receptive fields – is consistent with predictive coding: Rao and Ballard (1999) trained a hierarchical predictive coding network to recognise natural images. They showed that higher levels in the hierarchy learn to predict visual features that extend across many CRFs in the lower levels (e.g. tree trunks or horizons). Hence, higher visual areas come to predict that visual stimuli will span the receptive fields of cells in lower visual areas. In this setting, a stimulus that is confined to a CRF would elicit a strong prediction error signal (because it cannot be predicted). This provides a simple explanation for the findings of Hupé et al (1998) and Bullier et al (1996): when feedback connections are deactivated, there are no top-down predictions to explain responses in lower areas – leading to a disinhibition of responses in earlier areas, when – and only when – stimuli can be predicted over multiple CRFs.

Feedback connections and layer 1

How might the inhibitory effect of feedback connections be mediated? The established view is that extrinsic corticocortical connections are exclusively excitatory (using glutamate as their excitatory neurotransmitter) – although recent evidence suggests that inhibitory extrinsic connections exist and may play an important role in synchronizing distant regions (Melzer et al., 2012). However, one important route by which feedback connections could mediate selective inhibition is via their termination in L1 (Anderson and Martin, 2006; Shipp, 2007): layer 1 is sometimes referred to as acellular due to its pale appearance with Nissl staining (the classical method for separating layers that selectively labels cell bodies). Indeed, a recent study concluded that L1 contains less than 0.5% of all cells in a cortical column (Meyer et al., 2011). These L1 cells are almost all inhibitory and interconnect strongly with each other, via electrical connections and chemical synapses (Chu et al., 2003). Simultaneous whole cell patch clamp recordings show that they provide strong monosynaptic inhibition to L2/3 pyramidal cells, whose apical dendrites project into L1 (Chu et al., 2003; Wozny and Williams, 2011). This means L1 inhibitory cells are in a prime position to mediate inhibitory effects of extrinsic feedback. The laminar location highlighted by these studies – the bottom of L1 and the top of L2/3 – has recently been shown to be a “hotspot” of inhibition in the column (Meyer et al., 2011). Indeed, a study of rat barrel cortex – that stimulated (and inactivated) L1 – showed that it exerts a powerful inhibitory effect on whisker-evoked responses (Shlosberg et al., 2006). These studies suggest that corticocortical feedback connections could deliver strong inhibition, if they were to recruit the inhibitory potential of L1.

In terms of the excitatory and modulatory effect of feedback connections, predictive input from higher cortical areas might have an important impact via the distal dendrites of pyramidal neurons (Larkum et al., 2009). Furthermore, there is a specific type of GABAergic neuron that appears to control distal dendritic excitability, gating top down excitatory signals differentially during behavior (Gentet et al., 2012). Table 1 summarises the studies we have discussed in relation to the role of feedback connections.

Table 1.

Electrophysiological and neuroimaging findings consistent with predictive coding.

Prediction violated	Area studied	Neuronal expression of Prediction-error	Study
Learned visual object pairings	Monkey inferotemporal cortex (IT)	Enhanced firing rate	Meyer and Olson, 2011
Natural image statistics	Monkey V1, V2, V3	Enhanced firing rate	Hupé et al., 1998; Bullier et al., 1996; Bair et al., 2003
Repetitive auditory stream	Early human auditory cortex	Enhanced Event Related Potentials (ERPs), enhanced gamma-band power	Garrido et al., 2007, 2009; Todorovic et al., 2011
Coherence of visual form and motion	Human V1, V2, V3, V4, V5/MT	Enhanced BOLD response	Murray et al 2002; Murray et al 2005; Harrison et al., 2007
Audio-visual congruence of speech	Visual and auditory cortex	Gamma-band oscillatory activity	Arnal et al., 2011
Predictability of visual stimuli as a function of attention	Human V1, V2, V3	Enhanced BOLD response when unattended, reduced BOLD when attended	Kok et al., 2011
Hierarchical expectations in auditory sequences	Human temporal cortex	Enhanced Event Related Potentials (ERPs)	Wacongne et al., 2011
Expected repetition (or alternation) of face stimuli	FFA in fMRI, parietal and central electrodes of EEG	Enhanced BOLD response, diminished repetition suppression of ERP	Summerfield et al., 2008, 2011
Apparent motion of visual stimulus	V1	Enhanced BOLD response	Alink et al., 2010

Feedforward and transthalamic connections

While the evidence for an inhibitory effect of feedback connections has to be evaluated carefully, the evidence for an excitatory effect of feedforward connections is unequivocal. For example, in the monkey, V1 projects monosynaptically to V2, V3, V3a, V4, and V5/MT (Zeki, 1978; Zeki and Shipp, 1988). In all cases – when V1 is reversibly inactivated through cooling – single-cell activity in target areas is strongly suppressed (Girard and Bullier, 1989; Girard et al., 1991a, 1991b, 1992). In the cases of V2 and V3, the result of cooling area V1 is a near-total silencing of single unit activity. These studies illustrate that activity in higher cortical areas depends on driving inputs from earlier cortical areas that establish their receptive field properties.

Finally, while many studies have focused on extrinsic connections that project directly from one cortical area to the next, there is mounting evidence that feedforward driving connections (and perhaps feedback) in the cortex could be mediated by transthalamic pathways (Sherman and Guillery, 1998, 2011). The strongest evidence for this claim comes from the somatosensory system, where it was shown recently that the posterior medial nucleus of the thalamus (POm) – a higher-order thalamic nucleus that receives direct input from cortex – can relay information between S1 and S2 (Theyel et al., 2009). In addition, the thalamic reticular nucleus has been proposed to mediate the inhibition that might underlie cross-modal attention or top-down predictions (Yamaguchi and Knight, 1990; Crick, 1984; Wurtz et al., 2011). Furthermore, computational considerations and recent experimental findings point to a potentially important role for higher-order thalamic nuclei in coordinating and synchronizing cortical responses (Vicente et al., 2008; Saalmann et al., 2012). The degree to which cortical areas are integrated directly via corticocortical or indirectly via cortico-thalamo-cortical connections – and the extent to which transthalamic pathways dissociate feedforward from feedback connections in the same way as we have proposed for the cortico-cortical connections – are open questions.

The canonical microcircuit

Central to the idea of a canonical microcircuit is the notion that a cortical column contains the circuitry necessary to perform requisite computations, and that these circuits can be replicated with minor variations throughout the cortex. One of the clearest examples of how cortical circuits process simple inputs – to generate complex outputs – is the emergence of orientation tuning in V1. Orientation tuning is a distinctly cortical phenomenon because geniculocortical relay cells show no orientation preferences. A further elaboration of cortical responses can be found in the distinction between simple and complex cells – while simple cells possess spatially confined receptive fields, complex cells are orientation-tuned but show less preference for the location of an oriented bar. Hubel and Wiesel proposed a model for how intrinsic and extrinsic connectivity could establish a circuit explaining these receptive field properties. They proposed that orientation tuning in simple cells could be generated by a single cortical cell receiving input from several ON centre – OFF surround geniculate cells arranged along a particular orientation, thereby endowing it with a preference for bars oriented in a particular direction (Hubel and Wiesel, 1962). Complex cells were hypothesized to receive inputs from several simple cells – with the same orientation preference and slightly varying receptive field locations. Thus, complex cells were thought not to receive direct LGN input but to be higher order cells in cortex. Subsequent findings supported these predictions, showing that input layer 4Cα and 4Cβ contained the largest proportion of cells receiving monosynaptic geniculate input, while superficial and deep layer cells contain a larger number of cells receiving disynaptic or polysynaptic input (Bullier and Henry, 1980). Furthermore, simple cells project monosynaptically onto complex cells, where they exert a strong feedforward influence (Alonso and Martinez, 1998; Alonso, 2002). These models suggest that intrinsic cortical circuitry allows processing to proceed along discrete steps that are capable of producing response properties in outputs that are not present in inputs.

Segregation of processing streams

A key property of canonical circuits is the segregation of parallel streams of processing. For example, in primates, parvocellular input enters the cortex primarily in layer 4Cβ, whereas magnocellular inputs enter in 4Cα. The corticogeniculate feedback pathway from L6 maintains this segregation, as upper L6 cells preferentially synapse onto parvocellular cells in the LGN, while lower L6 cells target the magnocellular LGN layers (Fitzpatrick et al., 1994; Briggs and Usrey, 2009). Further examples of stream segregation are also present in the dorsal “where” and the ventral “what” pathways, and in the projection from V1 to the thick, thin, and inter-stripe regions of V2 (Zeki and Shipp, 1988; Sincich and Horton, 2005).

Superficial and deep layers are anatomically interconnected, but mounting evidence suggests that they constitute functionally distinct processing streams: in an elegant experiment, Roopun et al. (2006) showed that L2/3 of rat somatomotor cortex shows prominent gamma oscillations that are co-expressed with beta oscillations in L5. Both rhythms persisted, when superficial and deep layers were disconnected at the level of L4. Maier and colleagues (2010) used multilaminar recordings to show strong LFP coherence amongst sites within the superficial layers (the superficial compartment), as well as strong coherence amongst sites in deep layers (the deep compartment), but weak inter-compartment coherence. These studies indicate a segregation of – potentially autonomous – supragranular and infragranular dynamics. Maier et al., found that supragranular sites had higher broadband gamma power than infragranular sites. This pattern was reversed in the alpha and beta range; with greater power in the infragranular and granular layers. Finally, the spiking activity of neurons in the superficial layers of visual cortex are more coherent with gamma frequency oscillations in the local field potential, while neurons in deep layers are more coherent with alpha frequency oscillations (Buffalo et al., 2011). This finding is consistent with an earlier study by Livingstone (1996) showing that 50% of cells in L2/3 of squirrel monkey V1 expressed gamma oscillations, compared to less than 20% of cells in L4C and infragranular layers. The different spectral behaviour of superficial and deep layers has led to the interesting proposal that feedforward and feedback signalling may be mediated by distinct (high and low) frequencies (reviewed in Wang, 2010, see also Buschman and Miller, 2007 in the context of attention), a proposal that has recently received experimental support - at least for the feedforward connections (Bosman et al., 2012; see also Gregoriou et al., 2009).

Integration and segregation within canonical circuits

Given this functional and anatomical segregation into parallel streams, the question naturally arises, how are these streams integrated? It has been previously suggested that integration occurs through the synchronized firing of multiple neurons that form a neural ensemble (Gray et al., 1989; Singer, 1999), while others have emphasized inter-areal phase-synchronization or coherence (Varela et al., 2001; Fries, 2005; Fujisawa and Buzsáki, 2011). While a full treatment of this question is beyond the scope of the current review, we propose that the canonical microcircuit contains a clue for how the dialectic between segregation and integration might be resolved. While top-down and bottom-up inputs and outputs may be segregated in layers, streams, and frequency bands, the canonical microcircuit specifies the circuitry for how the basic units of cortex are interconnected and therefore how the intrinsic activity of the cortical column is entrained by extrinsic inputs. This intrinsic connectivity specifies how the cells of origin and termination of extrinsic projections are interconnected, and thus determine how top-down and bottom-up streams are integrated within each cortical column.

Spatial segregation and cortical columns

The notion of a canonical microcircuit implicitly assumes that each circuit is distinct from its neighbours; that could presumably carry out computations in parallel. Therefore, the canonical microcircuit specifies the spatial scale over which processing is integrated. The most likely candidate for this spatial scale is the cortical column – that can vary over three orders of magnitude between minicolumns, columns, and hypercolumns. Minicolumns are only a few cells wide, estimated to be about 50-60 micrometers in diameter by Mountcastle (1997) and are seen in Nissl sections of cortex as slight variations in cell density. Minicolumns were originally proposed as elementary units of cortex by Lorente de No (1949) and appear to reflect the migration of cells from the ventricular zone to the cortical sheet during foetal development (reviewed in Horton and Adams, 2005). Hubel and Wiesel estimated that orientation columns were on this order of magnitude, about 25-50 micrometers wide, although they failed to establish a correspondence between orientation columns observed physiologically and the minicolumns seen in Nissl sections (Hubel and Wiesel, 1974). A cortical column was classically defined as a vertical alignment of cells containing neurons with similar receptive field properties, such as orientation preference and ocular dominance in V1; or touch in somatosensory cortex (Mountcastle, 1957; Hubel and Wiesel, 1972). These columns were suggested by Mountcastle to encompass a number of minicolumns, with a width of 300-400 micrometers (Mountcastle, 1997). Finally, Hubel and Wiesel defined a hypercolumn to be the unit of cortex necessary to traverse all possible values of a particular receptive field property, such as orientation or eye dominance – estimated to be between 0.5 to 1 mm wide (Hubel and Wiesel, 1974).

Columns, connections and computations

So is the cortical column the basic unit of cortical computation? Some authors emphasize that even within a dendrite, there are all the necessary biophysical mechanisms for performing surprisingly advanced computations, such as direction selectivity, coincidence detection, or temporal integration (Häusser and Mel, 2003; London and Häusser, 2005). Others argue that single neurons can process their inputs at the dendrite, soma, and initial segment, such that the output spike trains of just two interconnected cells could mediate computations like independent components analysis (Klampfl et al., 2009). Others posit that cortical columns form the basic computational unit (Mountcastle, 1997; Hubel and Wiesel, 1972) but see (Horton and Adams, 2005). Donald Hebb proposed that neurons distributed over several cortical areas could form a functional computational unit called a neural assembly (Hebb, 1949). This view has re-emerged in recent years, with the development of the requisite recording and analytic techniques for evaluating this proposal (Buzsáki, 2010; Canolty et al., 2010; Singer et al., 1997; Lopes-dos-Santos et al., 2011).

Computational modelling studies indicate that cortical columns with structured connectivity are computationally more efficient than a network containing the same number of neurons but with random connectivity (Haeusler and Maass, 2007). Others suggest that this circuitry allows the cortex to organize and integrate bottom-up, lateral, and top-down information (Ullman, 1995; Raizada and Grossberg, 2003). Douglas and Martin suggest that the rich anatomical connectivity of L2/3 pyramidal cells allows them to collect information from top-down, lateral, and bottom-up inputs, and – through processing in the dendritic tree – select the most likely interpretation of its inputs. More recently, George and Hawkins have suggested that the canonical microcircuit implements a form of Bayesian processing (George and Hawkins, 2009). In the following section, we pursue similar ideas, but ground them in the framework of predictive coding, and propose a cortical circuit that could implement predictive coding through canonical interconnections. In particular, we find that the proposed circuitry agrees remarkably well with quantitative characterisations of the canonical microcircuit (Haeusler and Maass, 2007).

A canonical microcircuit for predictive coding

This section considers the computational role of cortical microcircuitry in more detail. We try to show that the computations performed by canonical microcircuits can be specified more precisely than one might imagine and that these computations can be understood within the framework of predictive coding. In brief, we will show that (hierarchical Bayesian) inference about the causes of sensory input can be cast as predictive coding. This is important because it provides formal constraints on the dynamics one would expect to find in neuronal circuits. Having established these constraints, we then attempt to match them with the neurobiological constraints afforded by the canonical microcircuit. The endpoint of this exercise is a canonical microcircuit for predictive coding.

Predictive coding and the free energy principle

It might be thought impossible to specify the computations performed by the brain. However, there are some fairly fundamental constraints on the basic form of neuronal dynamics. The argument goes as follows – and can be regarded as a brief summary of the free energy principle (see Friston, 2010 for details):

• Biological systems are homoeostatic (or allostatic), which means that they minimise the dispersion (entropy) of their interoceptive and exteroceptive states.

• Entropy is the average of surprise over time, which means biological systems minimise the surprise associated with their sensory states at each point in time.

• In statistics, surprise is the negative logarithm of Bayesian model evidence, which means biological systems – like the brain – must continually maximise the Bayesian evidence for their (generative) model of sensory inputs.

• Maximising Bayesian model evidence corresponds to Bayesian filtering of sensory inputs. This is also known as predictive coding.

These arguments mean that by minimising surprise, through selecting appropriate sensations, the brain is implicitly maximising the evidence for its own existence – this is known as active inference. In other words, to maintain a homoeostasis the brain must predict its sensory states on the basis of a model. Fulfilling those predictions corresponds to accumulating evidence for that model – and the brain that embodies it. The implicit maximisation of Bayesian model evidence provides an important link to the Bayesian brain hypothesis (Hinton and van Camp, 1993; Dayan et al., 1995; Knill and Pouget, 2004) and many other compelling proposals about perceptual synthesis – including analysis by synthesis (Neisser, 1967; Yuille and Kersten, 2006) epistemological automata (MacKay, 1956), the principle of minimum redundancy (Attneave, 1954; Barlow, H.B., 1961; Dan et al., 1996), the Infomax principle (Linsker, 1990; Atick, 1992; Kay and Phillips, 2011), and perception as hypothesis testing (Gregory, 1968; 1980).

The most popular scheme – for Bayesian filtering in neuronal circuits – is predictive coding (Srinivasan et al., 1982; Buchsbaum and Gottschalk, 1983; Rao and Ballard, 1999). In this context, surprise corresponds (roughly) to prediction error. In predictive coding, top-down predictions are compared with bottom-up sensory information to form a prediction error. This prediction error is used to update higher-level representations – upon which top-down predictions are based. These optimised predictions then reduce prediction error at lower levels.

To predict sensations, the brain must be equipped with a generative model of how its sensations are caused (Helmholtz, 1860). Indeed, this led Geoffrey Hinton and colleagues to propose that the brain is an inference (Helmholtz) machine (Hinton and Zemel, 1994; Dayan et al., 1995). A generative model describes how variables or causes in the environment conspire to produce sensory input. Generative models map from (hidden) causes to (sensory) consequences. Perception then corresponds to the inverse mapping from sensations to their causes, while action can be thought of as the selective sampling of sensations. Crucially, the form of the generative model dictates the form of the inversion – for example, predictive coding. Figure 3 depicts a general model as a probabilistic graphical model. A special case of these models are hierarchical dynamic models (see Figure 4), which grandfather most parametric models in statistics and machine learning (see Friston, 2008). These models explain sensory data in terms of hidden causes and states. Hidden causes and states are both hidden variables that cause sensations but they play slightly different roles: hidden causes link different levels of the model and mediate conditional dependencies among hidden states at each level. Conversely, hidden states model conditional dependencies over time (i.e., memory) by modelling dynamics in the world. In short, hidden causes and states mediate structural and dynamic dependencies respectively.

Figure 3.

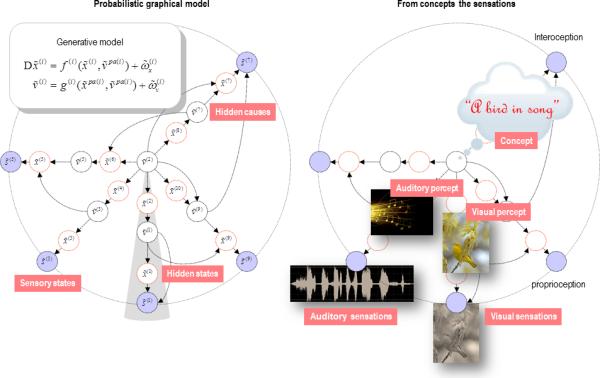
This schematic shows an example of a generative model. Generative models describe how (sensory) data are caused. In this figure, sensory states (blue circles on the periphery) are generated by hidden variables (in the centre). The left panel shows the model as a probabilistic graphical model, where unknown variables (hidden causes and states) are associated with the nodes of a dependency graph and conditional dependencies are indicated by arrows. Hidden states confer memory on the model by virtue of having dynamics, while hidden causes connect nodes. A graphical model describes the conditional dependencies among hidden variables generating data. These dependencies are typically modelled as (differential) equations with nonlinear mappings and random fluctuations ${\tilde{\omega }}^{\left(i\right)}$ with precision (inverse variance) Π⁽ⁱ⁾ (see the equations in the insert on the left). This allows one to specify the precise form of the probabilistic generative model and leads to a simple and efficient inversion scheme (predictive coding; see next figure). Here ${\tilde{v}}^{pa\left(i\right)}$ denotes the set of hidden causes that constitute the parents of sensory s̃⁽ⁱ⁾ or hidden x̃⁽ⁱ⁾ states. The ~ indicates states in generalised coordinates of motion: x̃ = (x, x′, x″,...). An intuitive version of the model is shown on the right: here, we imagine that a singing bird is the cause of sensations, which – through a cascade of dynamical hidden states – produces modality-specific consequences (e.g., the auditory object of a bird song and the visual object of a song bird). These intermediate causes are themselves (hierarchically) unpacked to generate sensory signals. The generative model therefore maps from causes (e.g., concepts) to consequences (e.g., sensations), while its inversion corresponds to mapping from sensations to concepts or representations. This inversion corresponds to perceptual synthesis – in which the generative model is used to generate predictions. Note that this inversion implicitly resolves the binding problem - by explaining multisensory cues with a single cause.

Figure 4.

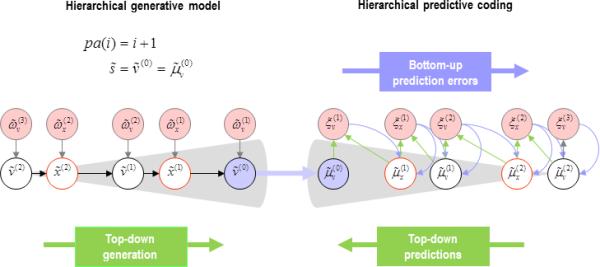
This figure describes the predictive coding scheme associated with a simple hierarchical model shown on the left. In this model each node has a single parent. The ensuing inversion or generalised predictive coding scheme is shown on the right. The key quantities in this scheme are (conditional) expectations of the hidden states and causes and their associated prediction errors. The basic architecture – implied by the inversion of the graphical (hierarchical) model – suggests that prediction errors (caused by unpredicted fluctuations in hidden variables) are passed up the hierarchy to update conditional expectations. These conditional expectations now provide predictions that are passed down the hierarchy to form prediction errors. We presume that the forward and backward message passing between hierarchical levels is mediated by extrinsic (feedforward and feedback) connections. Neuronal populations encoding conditional expectations and prediction errors now have to be deployed in a canonical microcircuit to understand the computational logic of intrinsic connections – within each level of the hierarchy – as shown in the next figure.

The details of the graph in Figure 3 are not important; it just provides a way of describing conditional dependencies among hidden states and causes responsible for generating sensory input. These dependencies mean that we can interpret neuronal activity as message passing among the nodes of a generative model, where each canonical microcircuit contains representations or expectations about hidden states and causes. In other words, the form of the underlying generative model defines the form of the predictive coding architecture used to invert the model. This is illustrated in Figure 4, where each node has a single parent. We will deal with this simple sort of model because it lends itself to an unambiguous description in terms of bottom-up (feedforward) and top-down (feedback) message passing. We now look at how perception or model inversion – recovering the hidden states and causes of this model given sensory data – might be implemented at the level of a microcircuit:

Predictive coding and message passing

In predictive coding, representations (or conditional expectations) generate top-down predictions to produce prediction errors. These prediction errors are then passed up the hierarchy in the reverse direction, to update conditional expectations. This ensures an accurate prediction of sensory input and all its intermediate representations. This hierarchal message passing can be expressed mathematically as a gradient descent on the (sum of squared) prediction errors ${\xi }^{\left(i\right)}={\Pi }^{\left(i\right)}{\tilde{\epsilon }}^{\left(i\right)}$, where the prediction errors are weighted by their precision (inverse variance).

$$\begin{array}{cc}\hfill {\dot{\tilde{\mu }}}_v^{\left(i\right)}& =\mathrm{D}{\tilde{\mu }}_v^{\left(i\right)}-{\partial }_{\tilde{v}}{\tilde{\epsilon }}^{\left(i\right)}\cdot {\xi }^{\left(i\right)}-{\xi }_v^{(i+1)}\hfill \\ \hfill {\dot{\tilde{\mu }}}_x^{\left(i\right)}& =\mathrm{D}{\tilde{\mu }}_x^{\left(i\right)}-{\partial }_{\tilde{x}}{\tilde{\epsilon }}^{\left(i\right)}\cdot {\xi }^{\left(i\right)}\hfill \\ \hfill {\xi }_v^{\left(i\right)}& ={\Pi }_v^{\left(i\right)}{\tilde{\epsilon }}_v^{\left(i\right)}={\Pi }_v^{\left(i\right)}({\tilde{\mu }}_v^{(i-1)}-g^{\left(i\right)}({\tilde{\mu }}_x^{\left(i\right)},{\tilde{\mu }}_v^{\left(i\right)}))\hfill \\ \hfill {\xi }_x^{\left(i\right)}& ={\Pi }_x^{\left(i\right)}{\tilde{\epsilon }}_x^{\left(i\right)}={\Pi }_x^{\left(i\right)}(\mathrm{D}{\tilde{\mu }}_x^{\left(i\right)}-f^{\left(i\right)}({\tilde{\mu }}_x^{\left(i\right)},{\tilde{\mu }}_v^{\left(i\right)}))\hfill \end{array}$$ (1)

The first pair of equalities just says that conditional expectations about hidden causes and states $({\tilde{\mu }}_v^{\left(i\right)},{\tilde{\mu }}_x^{\left(i\right)})$ are updated based upon the way we would predict them to change – the first term – and subsequent terms that minimise prediction error. The second pair of equations simply expresses prediction error $({\xi }_v^{\left(i\right)},{\xi }_x^{\left(i\right)})$ as the difference between conditional expectations about hidden causes and (the changes in) hidden states and their predicted values, weighed by their precisions $({\Pi }_v^{\left(i\right)},{\Pi }_x^{\left(i\right)})$. These predictions are nonlinear functions of conditional expectations (g⁽ⁱ⁾, f⁽ⁱ⁾) at each level of the hierarchy and the level above.

It is difficult to overstate the generality and importance of Equation (1) – it grandfathers nearly every known statistical estimation scheme, under parametric assumptions about additive noise. These range from ordinary least squares to advanced Bayesian filtering schemes (see Friston 2008). In this general setting, Equation (1) minimises variational free energy and corresponds to generalised predictive coding. Under linear models, it reduces to linear predictive coding, also known as Kalman-Bucy filtering (see Friston et al, 2010 for details).

In neuronal network terms, Equation (1) says that prediction error units receive messages from the same level and the level above. This is because the hierarchical form of the model only requires conditional expectations from neighbouring levels to form prediction errors, as can be seen schematically in Figure 4. Conversely, expectations are driven by prediction error from the same level and the level below – updating expectations about hidden states and causes respectively. These constitute the bottom-up and lateral messages that drive conditional expectations to provide better predictions – or representations – that suppress prediction error. This updating corresponds to an accumulation of prediction errors – in that the rate of change of conditional expectations is proportional to prediction error. Electrophysiologically, this means that one would expect to see a transient prediction error response to bottom-up afferents (in neuronal populations encoding prediction error) that is suppressed to baseline firing rates by sustained responses (in neuronal populations encoding predictions). This is the essence of recurrent message passing between hierarchical levels to suppress prediction error (see Friston 2008 for a more detailed discussion).

The nature of this message passing is remarkably consistent with the anatomical and physiological features of cortical hierarchies. An important prediction is that the nonlinear functions of the generative model – modelling context sensitive dependencies among hidden variables – appear only in the top-down and lateral predictions. This means, neurobiologically, we would predict feedback connections to possess nonlinear or neuromodulatory characteristics; in contrast to feedforward connections that mediate a linear mixture of prediction errors. This functional asymmetry is exactly consistent with the empirical evidence reviewed above. Another key feature of Equation (1) is that the top-down predictions produce prediction errors through subtraction. In other words, feedback connections should exert inhibitory effects, of the sort seen empirically. Table 2 summarises the features of extrinsic connectivity (reviewed in the previous section) that are explained by predictive coding. In the remainder of this review, we focus on intrinsic connections and cortical microcircuits.

Table 2.

The functional (computational) correlates of the anatomy and physiology of cortical hierarchies and their extrinsic connections.

Anatomy and physiology	Functional correlates
Hierarchical organisation of cortical areas (Zeki and Shipp 1988; Felleman and Van Essen, 1991; Barone et al., 2000; Vezoli, 2004)	Encoding of conditional dependencies in terms of a graphical model (Mumford, 1992; Rao and Ballard, 1999; Friston 2008).
Distinct (laminar-specific) neuronal responses (Douglas et al., 1989; Douglas and Martin, 1991)	Encoding expected states of the world (superficial pyramidal cells) and prediction errors (deep pyramidal cells) (Mumford, 1992; Friston 2008).
Distinct (laminar-specific) extrinsic connections (Zeki and Shipp 1988; Felleman and Van Essen, 1991; Barone et al., 2000; Vezoli, 2004; Markov et al., 2011).	Forward connections convey prediction error (from superficial pyramidal cells) and backward connections convey predictions (from deep pyramidal cells) (Mumford, 1992; Friston 2008).
Reciprocal extrinsic connectivity (Zeki and Shipp 1988; Felleman and Van Essen, 1991; Barone et al., 2000; Vezoli, 2004; Markov et al., 2011)	Recurrent dynamics are intrinsically stable because they are trying to suppress prediction error (Crick and Koch 1998;; Friston 2008).
Feedback extrinsic connections are (driving and) modulatory (Mignard and Malpeli 1991; Bullier et al., 1996; Sherman and Guillery 1998; Covic and Sherman, 2011; De Pasquale and Sherman, 2011).	Forwards (driving) and backwards (driving and modulatory) connections mediate the (linear) influence of prediction errors and the (linear and non-linear) construction of predictions (Friston 2008; 2010).
Feedback extrinsic connections are inhibitory (Murphy and Sillito, 1987; Sillito et al., 1993; Chu et al., 2003; Olsen et al. 2012; Meyer et al., 2011; Wozny and Williams, 2011).	Top-down predictions suppress or counter prediction errors produced by bottom up inputs (Mumford, 1992; Rao and Ballard, 1999; Friston 2008).
Differences in neuronal dynamics of superficial and deep layers (de Kock et al., 2007; Sakata and Harris, 2009; Maier et al., 2010; Bollimunta et al., 2011; Buffalo et al., 2011).	Principal cells elaborating predictions (deep pyramidal cells) may show distinct (low-pass) dynamics, relative to those encoding error (superficial pyramidal cells) (Friston 2008).
Dense intrinsic and horizontal connectivity (Thomson and Bannister, 2003; Katzel et al., 2010).	Lateral predictions and prediction errors mediating winnerless competition and competitive lateral dependencies (Desimone, 1996; Friston 2010).
Predominance of nonlinear synaptic (dendritic and neuromodulatory) infrastructure in superficial layers (Häusser and Mel, 2003; London and Häusser, 2005; Gentet et al., 2012).	Required to scale prediction errors, in proportion to their precision, affording a form of cortical bias or gain control that encodes uncertainty (Feldman and Friston 2010; Spratling, 2008)

The cortical microcircuit and predictive coding

We now try to associate the variables in Equation (1) with specific populations in the canonical microcircuit. Figure 5 illustrates a remarkable correspondence between the form of Equation (1) and the connectivity of the canonical microcircuit. Furthermore, the resulting scheme corresponds almost exactly to the computational architecture proposed by Mumford (1992). This correspondence rests upon the following intuitive steps:

• First, we divide the excitatory cells in the superficial and deep layers into principal (pyramidal) cells and excitatory interneurons. This accommodates the fact that (in macaque V1) a significant percentage of superficial L2/3 cells (about half) and deep L5 excitatory cells (about 80%) do not project outside the cortical column (Callaway and Wiser, 1996; Briggs and Callaway, 2005).

• Second, we know that the superficial and deep pyramidal cells provide feedforward and feedback connections respectively. This means that superficial pyramidal cells must encode and broadcast prediction errors on hidden causes ${\xi }_v^{(i+1)}$, while deep pyramidal cells must encode conditional expectations $({\tilde{\mu }}_v^{\left(i\right)},{\tilde{\mu }}_x^{\left(i\right)})$ so that they can elaborate feedback predictions.

• Third, we know that the (spiny stellate) excitatory cells in the granular layer receive feedforward connections encoding prediction errors ${\xi }_v^{\left(i\right)}$ on the hidden causes of the level below.

• This leaves the inhibitory interneurons in the granular layer, which, for symmetry, we associate with prediction errors on the hidden states.

• The remaining populations are the excitatory and inhibitory interneurons in the supragranular layer, to which we assign expectations about hidden causes and states respectively. These are mapped through descending (intrinsic) feedforward connections to cells in the deep layers that generate predictions. We do not suppose that this is a simple one-to-one mapping – rather it mediates the nonlinear transformation of expectations to predictions required by the earlier cortical level.

Figure 5.

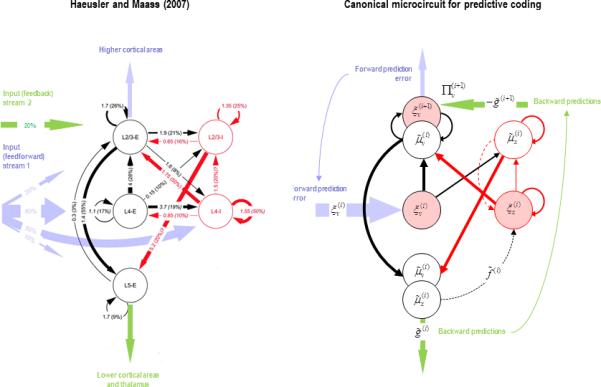
The left hand panel is the canonical microcircuit based on Haeusler and Maass (2007), where we have removed inhibitory cells from the deep layers – because they have very little interlaminar connectivity. The numbers denote connection strengths (mean amplitude of PSPs measured at soma in mV) and connection probabilities (in parentheses) according to Thomson et al. (2002). The right panel shows the proposed cortical microcircuit for predictive coding, where the quantities of the previous figure have been associated with various cell types. Here, prediction error populations are highlighted in pink. Inhibitory connections are shown in red, while excitatory connections are in black. The dotted lines refer to connections that are not present in the microcircuit on the left (but see Figure 2). In this scheme, expectations (about causes and states) are assigned to (excitatory and inhibitory) interneurons in the supragranular layers, which are passed to infragranular layers. The corresponding prediction errors occupy granular layers, while superficial pyramidal cells encode prediction errors that are sent forward to the next hierarchical level. Conditional expectations and prediction errors on hidden causes are associated with excitatory cell types, while the corresponding quantities for hidden states are assigned to inhibitory cells. Dark circles indicate pyramidal cells. Finally, we have placed the precision of the feedforward prediction errors against the superficial pyramidal cells. This quantity controls the postsynaptic sensitivity or gain to (intrinsic and top-down) pre-synaptic inputs. We have previously discussed this in terms of attentional modulation, which may be intimately linked to the synchronisation of pre-synaptic inputs and ensuing postsynaptic responses (Fries et al 2001; Feldman and Friston, 2010).

This arrangement accommodates the fact that the dependencies among hidden states are confined to each node (by the nature of graphical models), which means that their expectations and prediction errors should be encoded by interneurons. Furthermore, the splitting of excitatory cells in the upper layers into two populations (encoding expectations and prediction errors on hidden causes) is sensible, because there is a one-to-one mapping between the expectations on hidden causes and their prediction errors.

The ensuing architecture bears a striking correspondence to the microcircuit in (Haeusler and Maass, 2007) in the left panel of Figure 5 – in the sense that nearly every connection required by the predictive coding scheme appears to be present in terms of quantitative measures of intrinsic connectivity. However, there are two exceptions that both involve connections to the inhibitory cells in the granular layer (shown as dotted lines in Figure 5). Predictive coding requires that these cells (that encode prediction errors on hidden states) compare the expected changes in hidden states with the actual changes. This suggests that there should be interlaminar projections from supragranular (inhibitory) and infragranular (excitatory) cells. In terms of their synaptic characteristics, one would predict that these intrinsic connections would be of a feedback sort – in the sense that they convey predictions. Although not considered in this Haeusler and Maass scheme, feedback connections from infragranular layers are an established component of the canonical microcircuit (see Figure 2).

Functional asymmetries in the microcircuit

The circuitry in Figure 5 appears consistent with the broad scheme of ascending (feedforward) and descending (feedback) intrinsic connections: feedforward prediction errors from a lower cortical level arrive at granular layers and are passed forward to excitatory and inhibitory interneurons in supragranular layers, encoding expectations. Strong and reciprocal intralaminar connections couple superficial excitatory interneurons and pyramidal cells. Excitatory and inhibitory interneurons in supragranular layers then send strong feedforward connections to the infragranular layer. These connections enable deep pyramidal cells and excitatory interneurons to produce (feedback) predictions, which ascend back to L4 or descend to a lower hierarchical level. This arrangement recapitulates the functional asymmetries between extrinsic feedforward and feedback connections and is consistent with the empirical characteristics of intrinsic connections.

If we focus on the superficial and deep pyramidal cells, the form of the recognition dynamics in Equation (1) tells us something quite fundamental: We would anticipate higher frequencies in the superficial pyramidal cells, relative to the deep pyramidal cells. One can see this easily by taking the Fourier transform of the first equality in Equation (1)

$$\left(j\omega \right){\tilde{\mu }}_v^{\left(i\right)}\left(\omega \right)=\mathrm{D}{\tilde{\mu }}_v^{\left(i\right)}\left(\omega \right)-{\partial }_{\tilde{v}}{\tilde{\epsilon }}^{\left(i\right)}\cdot {\xi }^{\left(i\right)}\left(\omega \right)-{\xi }_v^{(i+1)}\left(\omega \right)$$ (2)

This equation says that the contribution of any (angular) frequency ω in the prediction errors (encoded by superficial pyramidal cells) to the expectations (encoded by the deep pyramidal cells) is suppressed in proportion to that frequency (Friston 2008). In other words, high frequencies should be attenuated when passing from superficial to deep pyramidal cells. There is nothing mysterious about this attenuation – it is a simple consequence of the fact that conditional expectations accumulate prediction errors, thereby suppressing high-frequency fluctuations to produce smooth estimates of hidden causes. This smoothing – inherent in Bayesian filtering – leads to an asymmetry in frequency content of superficial and deep cells: for example, superficial cells should express more gamma relative to beta, and deep cells should express more beta relative to gamma (Roopun et al., 2006, 2008; Maier et al., 2010).

Figure 6 provides a schematic illustration of the spectral asymmetry predicted by Equation 2. Note that predictions about the relative amplitudes of high and low frequencies in superficial and deep layers pertain to all frequencies – there is nothing in predictive coding per se to suggest characteristic frequencies in the gamma and beta ranges. However, one might speculate the characteristic frequencies of canonical microcircuits have evolved to model and – through active inference – create the sensorium (Friston, 2010; Berkes et al., 2011; Engbert et al., 2011). Indeed, there is empirical evidence to support this notion; in the visual (Lakatos et al., 2008; Meirovithz et al., 2012; Bosman et al., 2009) and motor domain (Gwin and Ferris, 2012).

Figure 6.

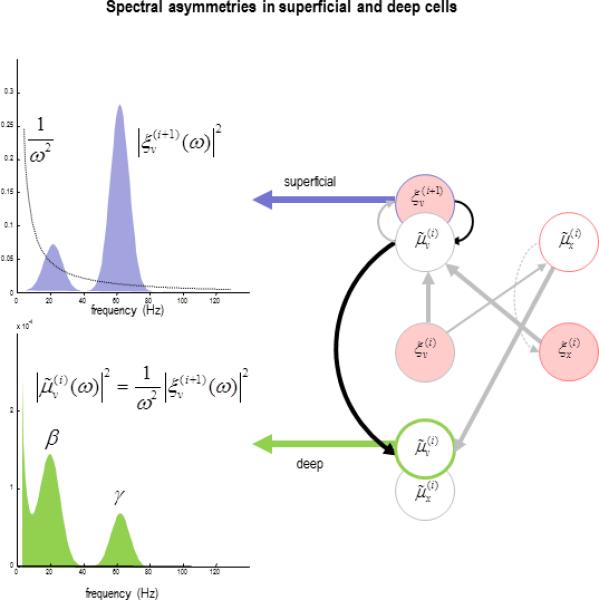
This schematic illustrates the functional asymmetry between the spectral activity of superficial and deep cells predicted theoretically. In this illustrative example, we have ignored the effects of influences on the expectations of hidden causes (encoded by deep pyramidal cells), other than the prediction error on causes (encoded by superficial pyramidal cells). The lower panel shows the spectral density of deep pyramidal cell activity, given the spectral density of superficial pyramidal cell activity in the upper panel. The equation expresses the spectral density of the deep cells as a function of the spectral density of the superficial cells; using Equation (2). This schematic is meant to illustrate how the relative amounts of low (beta) and high (gamma) frequency activity in superficial and deep cells can be explained by the evidence accumulation implicit in predictive coding.

In summary, predictions are formed by a linear accumulation of prediction errors. Conversely, prediction errors are nonlinear functions of predictions. This means that the conversion of prediction errors into predictions (Bayesian filtering) necessarily entails a loss of high frequencies. However, the nonlinearity in the mapping from predictions to prediction errors means that high frequencies can be created (consider the effect of squaring a sine wave, which would convert beta into gamma). In short, prediction errors should express higher frequencies than the predictions that accumulate them. This is another example of a potentially important functional asymmetry between feedforward and feedback message passing that emerges under predictive coding. It is particularly interesting given recent evidence that feedforward connections may use higher frequencies than feedback connections (Bosman et al., 2012).

Conclusion

In conclusion, there is a remarkable correspondence between the anatomy and physiology of the canonical microcircuit and the formal constraints implied by generalised predictive coding. Having said this, there are many variations on the mapping between computational and neuronal architectures: Even if predictive coding is an appropriate implementation of Bayesian filtering, there are many variations on the arrangement shown in Figure 5. For example, feedback connections could arise directly from cells encoding conditional expectations in supragranular layers. Indeed, there is emerging evidence that feedback connections between proximate hierarchical levels originate from both deep and superficial layers (Markov et al 2011). Note that this putative splitting of extrinsic streams is only predicted in the light of empirical constraints on intrinsic connectivity.

One of our motivations – for considering formal constraints on connectivity – was to produce dynamic causal models of canonical microcircuits. Dynamic causal modelling enables one to compare different connectivity models, using empirical electrophysiological responses (David et al, 2006; Moran et al, 2008, 2011). This form of modelling rests upon Bayesian model comparison and allows one to assess the evidence for one microcircuit relative to another. In principle, this provides a way to evaluate different microcircuit models, in terms of their ability to explain observed activity. One might imagine that the particular circuits for predictive coding presented in this paper will be nuanced as more anatomical and physiological information becomes available. The ability to compare competing models or microcircuits – using optogenetics, local field potentials and electroencephalography – may be important for refining neurobiologically informed microcircuits. In short, many of the predictions and assumptions we have made about the specific form of the microcircuit for predictive coding may be testable in the near future.