Principles of Contour Information: Reply to Lim and Leek (2012)

Abstract

Lim and Leek (2012) presented a formalization of information along object contours, which they argued was an alternative to the approach taken in our article (Feldman & Singh, 2005). Here, we summarize the 2 approaches, showing that—notwithstanding Lim and Leek's (2012) critical rhetoric—their approach is substantially identical to ours, except for the technical details of the formalism. Following the logic of our article point by point, Lim and Leek (a) defined probabilistic expectations about the geometry of smooth contours (which they based on differential contour geometry, while we used a discrete approximation—the only essential difference in their approach), (b) assumed that information along the contour was proportional to the negative logarithm of probability, following standard information theory, and then (c) extended this formulation to closed contours. We analyze what they described as errors in our approach, all of which rest on mathematical misunderstandings or bizarre misreadings of our article. We also show that their extension to 3-dimensional surfaces and their “modified minima rule” contain fatal deficiencies.

In Feldman and Singh (2005), we presented a formal answer to a question first posed by Attneave (1954): Which portions of a visual contour convey the most information? This problem lies at the foundation of the psychological representation of visual shape, as it depends on the way the brain encodes the geometry of the bounding contours of objects. But aside from an important contribution by Resnikoff (1985), this problem had not received a coherent mathematical answer in the decades since Attneave's article.¹ In recent years, however, an increasingly sophisticated understanding of the probabilistic representation of visual properties has made an effective approach to this problem possible. In our 2005 article, we proposed a framework for contour information based on a set of very simple ideas, which boil down the following three points.

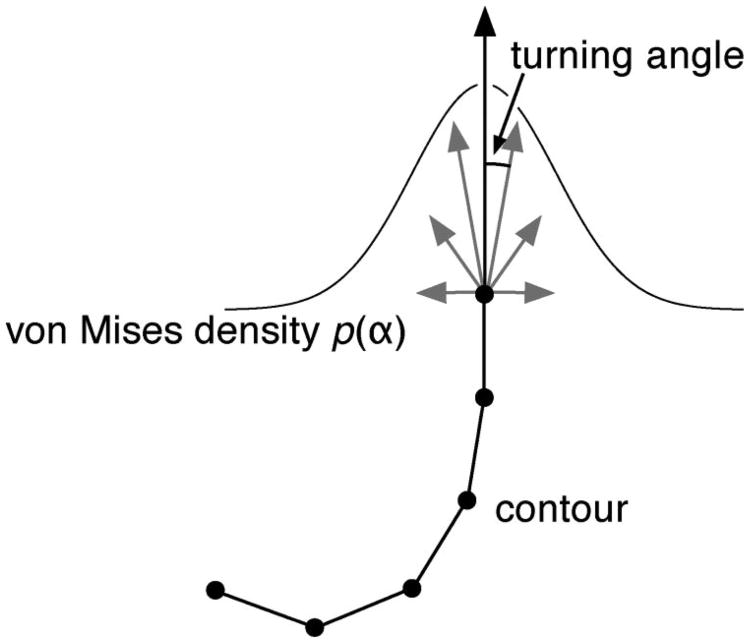
1. We define probabilistic expectations about the geometry of smooth contours, based on the assumption that smooth contours are most likely to continue to be straight at each point, with a decreasing likelihood of larger turning angles (see Figure 1). We expressed this idea mathematically by assuming that the turning angle α follows a von Mises density (similar to a normal or Gaussian density²), p(α) ∝ exp(β cos α). (We also considered several weaker or more general assumptions; see discussion below.) That is, we assumed that contours tend to continue to be straight with some random deviation about this direction.

2. Following the principles of standard information theory, we assume that the information at each contour point corresponds to the surprisal of its turning angle α, defined as −log p(α). In other words, the shape information at each contour point depends on how “surprising” the geometry at the point is, given our probabilistic expectations p(α) about how the contour will continue. This leads directly to Attneave's (1954) claim that information content increases with the curvature of the bounding contour.

3. Information along closed contours (e.g., object boundaries) can be understood by modifying the distribution of the turning angles p(α) based on the constraint that the contour must eventually close. This yields the mathematical result that points of negative curvature (concavities) convey more information than do points of positive curvature (convexities) because they are more “surprising.” This extends Attneave's (1954) original claim and is consistent with the psychological finding that convexities and concavities play different roles in shape perception (e.g., Barenholtz & Feldman, 2003; Cohen & Singh, 2007; de Winter & Wagemans, 2008a, 2008b; Hoffman & Richards, 1984; Hoffman & Singh, 1997; Koenderink & Van Doorn, 1982; Panis, de Winter, Vandekerckhove, & Wagemans, 2008) and that changes to shapes are easier to detect at concavities than at convexities (e.g., Barenholtz, Cohen, Feldman, & Singh, 2003; Bertamini & Farrant, 2005; Cohen, Barenholtz, Singh, & Feldman, 2005; Vandekerckhove, Panis, & Wagemans, 2008).

Figure 1.

In the Feldman and Singh (2005) approach, a contour is assumed to continue with a turning angle that is distributed as a von Mises (approximately normal) distribution with a mean of 0° (i.e., straight). The information at a point depends on the surprisal of the turning angle, −log p(α).

This approach is mathematically coherent and consistent with standard information theory, and moreover, it can easily be extended in several ways. One that we mentioned in the original article is that information along an extended contour C can be understood by integrating suprisal along that contour, yielding a natural measure of contour complexity −Σ_C log p(α). Another is that information can be extended to include the contribution of higher derivatives of the contour—for example, changes in curvature—merely by placing analogous probabilistic assumptions on those derivatives, such as the assumption that the change in the turning angle (like the turning angle itself) is most likely to be zero. This corresponds to an expectation of cocircularity, that is, a tendency to continue contour curvature, which is supported by empirical evidence in the context of contour integration (e.g., Feldman, 1997; Pizlo, Salach-Goyska, & Rosenfeld, 1997) and the visual extrapolation of contours behind occluders (Singh & Fulvio, 2005, 2007).

Lim and Leek's (2012) Approach

Lim and Leek (2012) presented what they describe as an alternative approach to formalizing contour information, and identified what they describe as errors in our development of the formalism. Notwithstanding their critical rhetoric, their approach echoed our framework 1–3, point by point. The only substantive difference, detailed below, was that their formulation started from probabilistic assumptions about the curvature κ of a smooth contour (a differential property, defined in the limit as arc length goes to zero), while ours began with probabilistic assumptions about the turning angle (a discrete quantity, measurable in the image). Specifically, they assumed a probability density function over curvature, p(κ)—analogous to our density over turning angle p(α). From there on, their development proceeded in a manner exactly parallel to ours:

• 1′. Assume contour curvature has distribution p(κ) that peaks at zero curvature (i.e., “straight”) and decreases with increasing curvature magnitude.

• 2′. Assume that information depends on the corresponding surprisal, −log p(κ).

• 3′. Show that the above formulation can be modified for the case of closed contours by modifying the distribution p(κ) to reflect the constraint that the contour must eventually close.

Lim and Leek (2012) then extended this formulation to three dimensions (see below). Regardless of arguments about the benefits of their continuous formulation versus our discrete one, it is important to recognize that beyond this technical distinction (curvature vs. turning angle), their approach was essentially conceptually identical to ours—hardly the “novel approach” their article promises.

Discrete Versus Continuous Foundations

Contour curvature is a differential property of smooth curves, technically the derivative of the tangent direction with respect to arc length (and therefore determined by the second derivative of the curve). As such, it is defined as a limiting value as one considers the abstract smooth curve in a neighborhood of diminishing size—in effect, it quantifies how rapidly the curve is bending in an infinitesimal neighborhood. By contrast, the turning angle α measures how much the curve has actually “turned” in a given nonzero interval. Basing a theory of shape information on a differential property may be appealing to a mathematician concerned primarily with differential geometry, but we choose to base our approach on discrete quantities that are actually measurable in the image because this ties our work to problems faced by the biological visual system, which can only measure contours with finite resolution. This also allowed us to connect our analysis to the extensive psychophysical and physiological literature on contour integration, which has been an active area of research at least since the early 1970s (e.g., Elder & Goldberg, 2002; Field, Hayes, & Hess, 1993; Geisler, Perry, Super, & Gallogly, 2001; Geisler & Perry, 2009; Lamote & Wagemans, 1999; Smits & Vos, 1987; Uttal, 1973).

In the literature on contour integration, researchers have examined how the visual system groups discrete local elements (e.g., dots, oriented edges, or Gabor patches) into representations of extended contours. Among other things, this literature has documented the geometric relations—most importantly, the turning angles between neighboring discrete elements—that support the percept of an extended contour. (Indeed, by definition, one cannot actually study empirical properties of contour curvature without going via a discrete approximation such as turning angle.) These psychophysical findings have led to the important idea of an “association field” (Field et al., 1993; Geisler et al., 2001), have been linked to the statistics of natural images (Elder & Goldberg, 2002; Geisler & Perry, 2009; Geisler et al., 2001), and have informed physiological findings about long-range horizontal connections between orientation-sensitive units in the primary visual cortex (e.g., Bosking, Zhang, & Fitzpatrick, 1997). Performance on contour integration tasks has also allowed researchers to estimate the distribution of the turning angles that the visual system implicitly expects. Specifically, the Gaussian or von Mises distribution of the turning angle has been documented in a number of studies (Feldman, 1996, 1997, 2001). Hence, our assumption of such a distribution, unlike Lim and Leek's (2012) adoption of a distribution over curvature itself, was not simply a mathematical abstraction but a scientifically documented premise.

Moreover, as Lim and Leek (2012) eventually acknowledged, unlike turning angle, curvature is not scale invariant. This means that any information theoretic treatment would, likewise, have information varying with the scale, or overall size, of the object. Lim and Leek only mentioned this late in their development and asserted that it can be patched, but their solution is ad hoc—repairing a problem that stems from the foundation of the theory—and without empirical support.

Technical Discrepancies

In previous articles on turning angle, Feldman (1996, 1997, 2001) found psychophysical evidence for a Gaussian or von Mises density for the turning angle α, which is corroborated by physiological work on the tuning properties of orientation-selective neurons in the primary visual cortex (Swindale, 1998). But in Feldman and Singh (2005), we noted that certain key claims about contour information do not depend on the specific form of the distribution but, instead, were guaranteed as long as the distribution p(α) peaked at zero (in the open-contour case) and decreased monotonically with increasing turning angle. Indeed, as we stated in the original article, the fact that contour information rises with turning angle stems directly from the assumption of decreasing probability with larger turning angles, via the very basic relation that surprisal is simply −log p(α), an assumption that Lim and Leek (2012) explicitly adopted. Indeed this basic observation—that information along contours depends on probabilistic expectations about how curves continue—was the principal contribution of our article, and this seems to have been embraced wholeheartedly by Lim and Leek (2012).

Lim and Leek (2012) did dispute our more specific claim that there is a bound on information as a function of curvature regardless of distributional form, which stems from a much more technical argument. Our claim was that the probability of more extreme turning angles is bound by a limit that diminishes with the increasing turning angle because of what is called the Chebyshev bound. The Chebyshev bound shows that the tail area of any probability distribution must diminish as one goes further out in the tails, regardless of the form of the distribution. What this means in our context is that the probabilities of turning angles fall under a bound that decreases monotonically as they get more extreme. Lim and Leek (2012) described our derivation as mathematically flawed, but their argument stems from a puzzling confusion between the terms “probability” and “probability density.” Probability density is a quantity associated with a continuous random variable, such as the turning angle, which must be integrated over some nonzero interval in order to yield a nonzero probability. Unlike probability, probability density can take values higher than 1, so long as the integral over any interval—the probability itself—does not exceed 1. For smooth densities over continuous random variables (like the one over turning angle considered in our article), the “probability” per se of a single point value—say, 45°—is automatically 0 (because, again, it must be integrated across some nonzero interval to amount to a nonzero value). Hence, an expression such as “the probability of an angle α₀” really means “the integral of the probability density function in a small neighborhood of α₀,” more properly notated ${\int }_{{\alpha }_0}^{{\alpha }_0+\varepsilon }f(\alpha )d\alpha$, where f(x) is the probability density function—a notation we avoided in our article as pedantic and potentially confusing. In words, what this means is that the probability of a given angle corresponds to the area under the density curve over a small range (e.g., the probability that the turning angle falls between 45° and 46°)—an area that is a subset of the tail and thus necessarily smaller than the tail, which Chebyshev showed is itself bounded in size. This was our original argument, and it is correct. Lim and Leek's suggestion that it leads to an absurd conclusion—that there is no bound on the magnitude of probability—depends entirely on perversely interpreting p(α) as density rather than probability, which results only in showing that probability density can be larger than 1—which is correct, but trivial. Once one distinguishes correctly between probability and probability density, Lim and Leek's Equation 3, which stated that the area under the curve in the neighborhood near a given angle, p(t + Δt)Δt in their notation, is limited by the Chebyshev bound, becomes precisely equivalent to our assertion that they claim to dispute. In sum, the only way our claim could appear to be invalid is if one misreads the notation p(α) to mean probability density at an infinitesimal point—an interpretation that is no way supported by our article and is very unlikely to be drawn by any mathematically knowledgeable reader. The authors' point is therefore most charitably understood as a pedantic criticism about notation and less charitably understood as a deliberate obfuscation intended to create the appearance of an error.

Returning to the main issue, the primary contribution of our original article was the observation that information along contours can be understood as Shannon surprisal (−log p), once one adopts a suitable probability model for contours. One can make a range of assumptions about this probability model, with concomitant constraints on the resulting surprisal. We can divide these assumptions into three basic cases, all of which were mentioned at various points in our original article, but which Lim and Leek (2012) conflated in their discussion:

Strongest Assumption

One can assume a particular distribution of turning angle, such as that it is Gaussian or von Mises. As documented above and in our original article, such an assumption is well supported by the psychological literature. In this case, surprisal clearly increases with turning angle. Lim and Leek (2011) did not dispute this.

Weaker Assumption

Instead of assuming a particular functional form for the distribution, we can simply assume that the distribution has a probability that is monotonically decreasing with the increasing turning angle. In this case, the increase in suprisal −log p with increasing turning angles again follows immediately.

Weakest Assumption

Finally, instead of assuming a monotonically decreasing probability distribution, we can instead make no assumptions about the functional form of the distribution, in which case (the Chebyshev argument shows) one can still make a surprisingly strong claim about angle probability, namely that it is bound by a monotonically decreasing function (and hence that contour information is bound by a monotonically increasing function). Lim and Leek (2012) disputed this argument, but in so doing, they repeatedly conflated it with one of the above assumptions. (They also conflate “probability” and “probability density,” as we noted above.) The fact that the bound decreases monotonically obviously does not mean that the function itself decreases (which is why our original article asserted only that the bound decreases in this case). Of course, in practice, a decreasing bound places a strong constraint on likely angles since it implies that the range of possible angle probabilities gets tighter as the angle gets larger.

Another point of criticism raised by Lim and Leek (2012) is that as the sampling density of the contour is increased, the effect of the turning angle on information content gets progressively smaller. This criticism is equally misplaced. For any finite-resolution measurement system, it must be the case that the smaller the window through which one examines a smooth contour, the closer to linear it looks. If this microscopic view of the contour is all that is available to the system, it would indeed have to conclude that that contour segment is (locally) flatter. Their criticism thus simply boils down to the fact that in a sufficiently small neighborhood, all smooth curves approximate straight lines. From the point of view of perception, this is uninteresting because the visual system does not have access to an arbitrarily fine view.³ Moreover, their criticism presupposes that when the separation between consecutive sample points is decreased, the dispersion (or spread) of the von Mises distribution on turning angle will remain unchanged. This assumption is unjustified. Simple considerations of the geometry of smooth contours suggest that the distribution of turning angles would be expected to be tighter (smaller spread) when the contour is examined through smaller apertures. This criticism of Lim and Leek's (2012) is thus based on a straw man—a patently invalid extension of our framework, which serves only to confuse. Finally, Lim and Leek's complaint about our visualization code is trivial—analogous to complaining about the scale of the y-axis in a data plot.

Lim and Leek's (2012) Three-Dimensional Extension and the “Modified Minima Rule”

Later in their article, Lim and Leek (2012) attempted to generalize their approach from two-dimensional contours to three-dimensional (3D) surfaces. Unfortunately, their proposed 3D extension fails several basic tests of plausibility.

Curvature on a 3D surface is substantially more complex than for a contour, and several alternative formulations of curvature are possible (Koenderink, 1990). At any given point on a surface, the curvature of a path depends on the direction in which it is taken; there is a different curvature value for each possible direction. Of these directions, one has maximal curvature and one has minimal curvature, and these form an orthogonal basis for describing surface curvature. These two directions determine the so-called principal curvatures, κ₁ and κ₂, which must be combined in some way in order to characterize “the curvature” of the surface at that point. Different measures of surface curvature combine them in different ways: Gaussian curvature takes their product and mean curvature takes their average, whereas curvedness and shape index use more complex combination functions (Koenderink, 1990). A central challenge in defining information content for surfaces is to determine how exactly the two principal curvatures contribute to the surprisal. Lim and Leek (2012) unfortunately disregarded this deep issue altogether and simply adopted Gaussian curvature as a basis for their information measure—giving no motivation or principled reason for their choice and indeed not even mentioning that alternative measures of surface curvature exist.

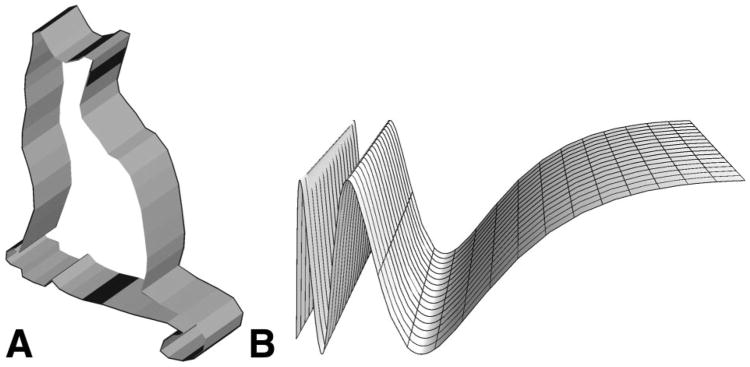
Unfortunately, Gaussian curvature is not in our view an adequate basis upon which to quantify information. Most obviously, Gaussian curvature is zero if either of the two principal curvatures is zero—such as everywhere along the curved surface of a cylinder. More generally, Gaussian curvature is zero everywhere along the surface of a generalized cylinder with a straight axis but an arbitrary (though fixed) cross-section—regardless of the curvature profile of the cross-section (e.g., the cookie-cutter cat in Figure 2A). This means that Lim and Leek's (2012) formalism predicts that all points on such a curved surface convey identical—and minimal—shape information. Similarly, the surface in Figure 2B, although it has ridges and valleys of varying strengths, nevertheless has zero Gaussian curvature everywhere (because one of the two principal curvatures is consistently zero). That these variations in surface geometry convey no variation in shape information blatantly contradicts intuition, and this is not supported by any empirical finding of which we are aware. It is disappointing that these rather obvious defects in the formulation are not acknowledged, much less addressed, in Lim and Leek's article.⁴

Figure 2.

Examples of 3D shapes with zero Gaussian curvature everywhere and thus—in Lim and Leek's (2012) account—constant, minimal, shape information everywhere. In both shapes, Gaussian curvature is zero everywhere because one of the two principal curvatures is zero. Under Lim and Leek's account, the cookie-cutter cat in A, unlike Attneave's (1954) cat, would have no variation in the concentration of shape information; similarly, in B, the variations in the strengths of the ridges and valleys would convey no variation in shape information. These predictions blatantly contradict intuition.

Lim and Leek (2012) went on to argue that their measure of 3D surface information implies a constraint on 3D part boundaries, namely, that they can only occur within regions of negative Gaussian curvature (saddle-shaped regions). Indeed, the tendency for such regions to contain part boundaries was observed almost three decades ago in a well-known article by Koenderink and van Doorn (1982), which Lim and Leek did not cite. Lim and Leek gave no argument whatsoever for any mathematical connection between shape information as they have quantified it and part boundary status—which makes it difficult to evaluate its intended scope.

In any case, it is readily apparent that part boundaries need not fall only within negative Gaussian curvature regions, as Lim and Leek's (2012) “modified minima rule” asserts. Many biological limbs have boundaries that do not fall exclusively within negative Gaussian curvature regions but are nevertheless perceived as psychological parts of objects (see, e.g., de Winter & Wagemans, 2006; Singh, Seyranian, & Hoffman, 1999). An example is the human shoulder joint, which has negative Gaussian curvature underneath but positive Gaussian curvature above. Thus, Lim and Leek's definition of part would seem to exclude human arms, as well as legs and most animal limbs. Indeed, it is well established that the loci of negative minima are by themselves insufficient to segment shapes into parts, and various researchers have proposed geometric factors beyond negative minima for part decomposition (e.g., de Winter & Wagemans, 2006; Siddiqi, Tresness, & Kimia, 1996; Singh & Hoffman, 2001; Singh et al., 1999). By contrast, Lim and Leek's proposal simply added a further constraint on which negative minima should be used (namely, those that lie in hyperbolic regions). It does nothing to address the limitations of negative minima that have been discussed in the parts literature, and thus, it contributes little to our understanding of part decomposition.

The surfaces in Figure 2 illustrate another shortcoming of limiting part boundaries to negative Gaussian curvature regions: These surfaces contain no negative Gaussian curvature regions at all but do contain several fairly salient part boundaries (e.g., at the base of the ears or tail of the cookie-cutter cat and along the valleys of “wave”).

Conclusion

In summary, we are gratified that Lim and Leek (2012) seem to agree with the major elements of the approach we proposed in our 2005 article, though we are somewhat baffled by the negative way in which they have framed their agreement. Our approach is simple, is internally coherent, agrees with both intuition as well as psychophysical and physiological data on contour perception, and harmonizes with the growing literature on probabilistic approaches to visual perception. The defects that Lim and Leek listed stem either from mathematical misunderstandings or from bizarre misreadings of our article—some of which we hope we have clarified above. Unfortunately, while the prospect of extending this approach to 3D is appealing, the simplistic manner they propose to do so, based solely on Gaussian curvature, is unconvincing. Still, we welcome attention to this important problem and look forward to what we hope will be more edifying developments in the future.