Evaluating multicenter DTI data in Huntington's disease on site specific effects: An ex post facto approach

Abstract

Purpose

Assessment of the feasibility to average diffusion tensor imaging (DTI) metrics of MRI data acquired in the course of a multicenter study.

Materials and methods

Sixty-one early stage Huntington's disease patients and forty healthy controls were studied using four different MR scanners at four European sites with acquisition protocols as close as possible to a given standard protocol. The potential and feasibility of averaging data acquired at different sites was evaluated quantitatively by region-of-interest (ROI) based statistical comparisons of coefficients of variation (CV) across centers, as well as by testing for significant group-by-center differences on averaged fractional anisotropy (FA) values between patients and controls. In addition, a whole-brain based statistical between-group comparison was performed using FA maps.

Results

The ex post facto statistical evaluation of CV and FA-values in a priori defined ROIs showed no differences between sites above chance indicating that data were not systematically biased by center specific factors.

Conclusion

Averaging FA-maps from DTI data acquired at different study sites and different MR scanner types does not appear to be systematically biased. A suitable recipe for testing on the possibility to pool multicenter DTI data is provided to permit averaging of DTI-derived metrics to differentiate patients from healthy controls at a larger scale.

Highlights

► Alternative procedure to evaluate prerequisites for multicenter DTI data pooling. ► Procedure may serve as reference for future multicenter MRI-DTI trials in HD. ► FA differences between HD and controls consistent with single center reports.

1. Introduction

In the last decade the necessity for multicenter studies has arisen in order to increase sample sizes and therefore reliability of results. This multicenter approach is particularly important for rare disorders, such as Huntington's disease (HD), because it permits collecting data from a sufficiently large number of participants in a reasonable time frame.

Cerebral white matter (WM) changes in HD have been reported in a number of studies (for reviews see Bohanna et al. (2008) and Klöppel et al. (2009)), mainly using MR-based diffusion weighted imaging (DWI) and diffusion tensor imaging (DTI) (Douaud et al., 2009; Rosas et al., 2006). These techniques use diffusion directions of water molecules to calculate a tensor, which can be converted into metrics such as fractional anisotropy (FA) (Basser and Jones, 2002; Pierpaoli et al., 1996), a dimensionless scalar ranging from a value of zero (isotropy) to a value of one (high directionality, anisotropy). There is, however, a downside to multicenter imaging studies focusing on DTI, in that scanner and environmental noise, as well as systematic inter-subject variables may contribute to the variability of DTI results. Some effort has already been made to investigate the influence of these variables on scanning results. Pagani and colleagues demonstrated between-center differences in DTI repeatedly scanning a number of subjects (between 7 and 13) at 8 different scanner sites (Pagani et al., 2010). By contrast, other authors reported only small differences in DTI metrics between sites when scanning a physical phantom (Teipel et al., 2011; Walker et al., 2012). Other studies focused on comparability of DTI metrics from different scanners by region of interest (ROI) analyses of coefficients of variation (CV). They found that FA is the most comparable measure across different scanners and that nonlinear co-registration of FA maps reduced average inter-site CV (Fox et al., 2012; Vollmar et al., 2010).

A common way to reduce variability is to calibrate all scanners involved in a multicenter study, with the optimal procedure being to scan a number of participants as a reference group at each study center. However, this is a time consuming and expensive procedure, and not viable for many important but underfunded studies. Therefore, other equally valid ways of ensuring comparability of DTI results from different scanners should be explored.

As a proof of concept, we used DTI data from early HD and control participants acquired from four different scanners. For comparison, we defined five ROIs based on previous findings in DTI studies with HD patients, i.e. basal ganglia, external and internal capsules, thalamic region and corpus callosum (Douaud et al., 2009; Rosas et al., 2006). These five structures have been identified as being particularly affected in people with manifest HD with a specific pattern of decreases and increases in FA values. The regions most affected were the basal ganglia with an increase in FA and the internal and external capsules and the thalamic regions which showed FA decreases (Rosas et al., 2006). It should be noted that these studies were not multicenter studies and that all participants were scanned with the same MRI scanner.

The aim of our study was to provide an evaluating framework for combining DTI data acquired from different study centers without time- and cost-intensive repeated scanning of the same reference group at each study site. As the primary outcome variable the present study focused on FA data as the relevant DTI metric since FA differences between HD subjects and controls have already been reported (Douaud et al., 2009; Fox et al., 2012; Rosas et al., 2006). For analysis, we suggest a three-step procedure as outlined in Fig. 1. In the first step we tested whether the CV of FA values in predefined ROIs differed between centers. In this step we used data from control participants to estimate potential influences independent of disease related factors. In the second step we tested whether group differences between patients and controls differed between centers. In the third step patient and control data from different study sites were pooled and a voxel-wise whole-brain analysis was performed to assess whether putative group differences were present in the selected ROIs. This procedure may also help to monitor multi-center (DTI) studies.

Fig. 1.

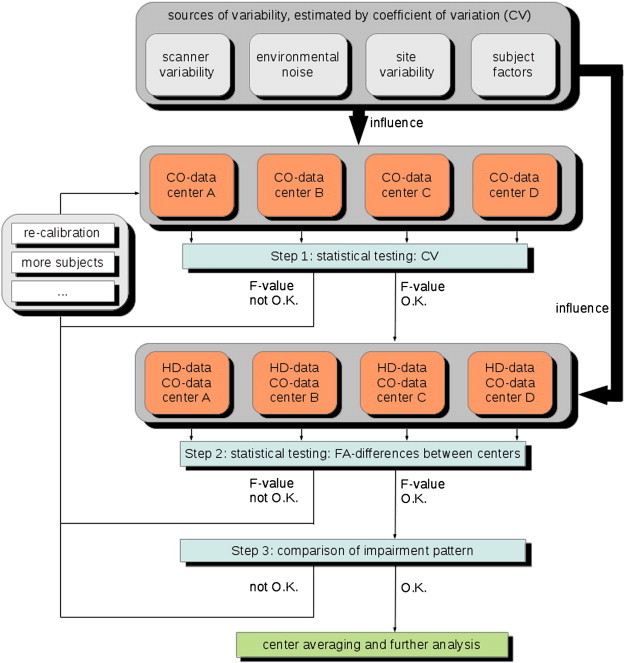
Different sources of variability may contribute to the diffusion data of control subjects (CO) and patients with Huntington's disease (HD). Although the contribution of each source of variation cannot be singled out, the coefficient of variance (CV) from the CO data of each center serves as an estimate whether one or more centers contributed systematically biased data. Investigating FA group differences between patients and controls on systematic between-center differences is a further criterion to decide whether pooling across centers is permitted. The calibration procedure as well as the inclusion of more subjects is an option and is an alternative if the various checks do not permit pooling the data.

2. Methods

2.1. Data collection and participants

Data in this study were collected as part of the European PADDINGTON project at four study sites in Europe (Leiden, the Netherlands; London, UK; Paris, France; Ulm, Germany). The PADDINGTON project, which involves five partners (Siena Biotech SpA, University of Ulm, University College London, the London School of Hygiene and Tropical Medicine and KCR Poland), is an international initiative that aims to provide pharmacodynamic approaches for disease-modifying clinical trials. The work package 2 of this project entails the collection of volumetric 3 Tesla MRI and DTI scans acquired with standardized acquisition protocols from patients with HD in an early disease stage and from healthy control participants, with the objective of identifying biomarkers of disease progression. DTI data from work package 2 were used to evaluate our three-step procedure.

All participants gave written informed consent. Subjects were at least 18 years old. HD patients had a genetically confirmed diagnosis with a trinucleotide (CAG) repeat length of 36 or higher, and had clinical features of mild HD at least of stage I based on the Unified Huntington's Disease Rating Scale (UHDRS) with a total functional capacity (TFC) score of 11–13. All participants were ambulatory and agreed to volunteer for MRI scanning. Subjects with claustrophobia and conditions not permitting MR scanning were excluded from the study. In total 61 HD and 40 control subjects (CO) were scanned (DTI acquisition time is approximately 7 min per subject). The acquisition parameters for the different sites are listed in Table 1, and sample sizes are listed in Table 2.

Table 1.

Acquisition parameters of the 4 different centers. N of (b = 1000 s/mm²) reflects the number of gradient directions used at each site.

Center	Vendor	Coil	Slices	Slice thickness (mm)	In-plane matrix	In-plane resolution (mm2)	N of (b = 1000 s/mm2) acquisitions	N of (b = 0) acquisitions	TR/TE (ms)
A	Philips Achieva 3.0 T	SENSE-8	55	2.0	112 × 112	2.0 × 2.0	42	1	8077/56
B	Siemens TIMTRIO 3.0 T	8 channel	65	2.0	96 × 128	2.0 × 2.0	41	7	7600/84
C	Siemens Verio 3.0 T	8 channel	76	2.0	128 × 128	2.0 × 2.0	42	7	7600/84
D	Siemens Allegra 3.0 T	Head-coil	52	2.2	96 × 128	2.2 × 2.2	47	1	7600/85

Table 2.

Demographic parameters and distribution of patients with Huntington's disease (HD) and controls (CO) investigated at the 4 different centers (mean ± standard deviation).

	N of subjects		Age (years)		Sex (m/f)
	CO	HD	CO	HD	CO	HD
Center A	10	17	50 ± 4	48 ± 10	6/4	3/14
Center B	10	16	53 ± 8	52 ± 9	5/5	5/11
Center C	10	13	57 ± 8	46 ± 15	3/7	7/6
Center D	10	15	48 ± 9	48 ± 10	4/6	11/4
All	40	61	52 ± 8	49 ± 11	18/22	26/35

2.2. Data analysis — post-processing

The in-house developed DTI analysis software Tensor Imaging and Fibre Tracking (TIFT; Müller et al., 2007a, 2007b) with additional routines for eddy current correction was used for post-processing and statistical analysis. Prior to FA-calculation motion artifacts were eliminated in each volume and each subject separately by a recently described procedure (Müller et al., 2007a, 2007b).

In order to perform spatial normalization to a common space (Brett et al., 2002) a study-specific b0-template and an FA-template were created (Müller et al., 2007a; Müller et al., 2009; Unrath et al., 2010). Normalization to an FA-template was further included into the process of normalization because a non-affine registration to an FA-template has the advantage of providing more contrast in comparison to b0-images (Smith et al., 2006).

In a next step a non-linear normalization of the DTI data sets was performed by minimizing the squared differences of regional intensities between the normalized FA-maps and the FA-template (following the basic ideas of Ashburner and Friston (1999)).

The whole normalization process was iterative. Scanner- and sequence specific b0- and FA-templates were created by arithmetically averaging data sets of all participants for each site after linear transformation according to manually set landmarks. After initial normalization, templates were created during an iterative step to further optimize the normalization matrices. This process was repeated until the correlation was > 0.7 between the individual FA-maps and the FA-template, which was achieved by one iteration.

According to standard methods (Basser and Jones, 2002), the second-rank diffusion tensor $\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{D}}$, the eigenvalues (λ₁, λ₂, λ₃), the eigenvectors (${\stackrel{\rightharpoonup }{\nu }}_1,{\stackrel{\rightharpoonup }{\nu }}_2,{\stackrel{\rightharpoonup }{\nu }}_3$), and the FA for quantification of the diffusion anisotropy were calculated after normalization of individual DTI data sets.

Since filter size may influence the results of the DTI data analysis (Henley et al., 2010; Jones et al., 2005), the ideal adjustment of the smoothing kernel requires application of the matched filter theorem which states that the filter size should be tailored to the size of the expected difference (Rosenfeld and Kak, 1982). Based on results from previous studies that had already tested several filter sizes between 6 and 10 mm full width at half maximum (FWHM) in DTI analysis of FA and mean diffusivity values (Müller et al., 2012; Unrath et al., 2010) and informed by previous voxel-based morphometry studies of T1-weighted data (Henley et al., 2010; Kassubek et al., 2004) we used an estimated Gaussian filter size of 8 mm FWHM for smoothing to balance the trade-off between sensitivity and specificity.

2.3. Coefficients of variation (CV)

The CV is defined as the ratio of the standard deviation of the measurements divided by the mean multiplied by 100. It is an intuitive estimate of measurement variance expressed as relative percentage regardless of the absolute measurement value and reflects the inverse of the signal-to-noise ratio. In previous studies on DTI test–retest reliability the CV is a frequently reported statistical measure (Vollmar et al., 2010). Since testing whether or not differences between centers are beyond chance imposes a comparable reliability problem, we decided to use this measure for reliability tests in controls. CV values of FA data were computed in different ROIs. Using previous reference studies (Douaud et al., 2009; Rosas et al., 2006) these a priori defined anatomical ROIs were located in the basal ganglia, the external capsule, the thalamus, the internal capsule, and the corpus callosum (Fig. 2). CVs were averaged per ROI and subject and were then tested on significant center effects using a one-way analysis of variance with main factor center (4 levels).

Fig. 2.

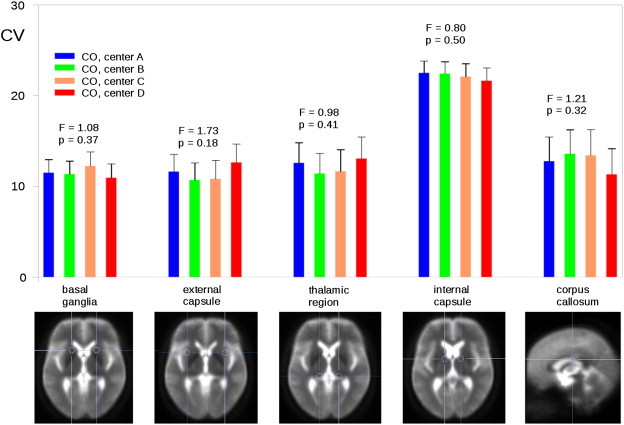
Coefficients of variation (corrected for age) for different ROIs calculated for control subjects (CO) from each center.

2.4. ROI based comparisons between HD and control participants

For each ROI used in the between-center comparisons of the CVs, averages of FA values were computed for each individual and entered into an analysis of variance with main factors group (2 levels: controls, patients) and center (4 levels). In this analysis, the group-by-center interaction is particularly informative because it permits inference whether or not group differences of the mean FA values would significantly differ between centers.

2.5. Whole brain-based statistical analyses

Voxel-wise statistical comparison between HD and control subjects was performed by Student's t-tests implemented in the TIFT software (Müller et al., 2007a) to infer significant differences of FA maps between both groups. FA values below 0.2 were not considered for calculation since cortical gray matter may show FA values of up to 0.2 (Kunimatsu et al., 2004). Correction for multiple comparisons used the false-discovery-rate (FDR) algorithm at a nominal level of p < 0.05 (Genovese et al., 2002). To further reduce alpha error a spatial correlation algorithm was used for eliminating isolated voxels or small isolated groups of voxels. This has led to a threshold cluster size of 512 contiguously significant voxels.

3. Results

The Results section follows the outline of the suggested three-step procedure by first analyzing CV in control participants and then analyzing differences of FA values between HD and control participants. These two steps were based on pre-defined regions of interest. In the third step, a voxel-wise analysis of FA maps is performed, to see whether the overall pattern of impairments matches the expected one (Fig. 1).

3.1. Step 1: a) age and sex distribution in controls

To control for subject factors (see Fig. 1) as a potential source of variability in control participants we first examined the distribution of demographic variables of age and sex between sites. An analysis of variance (ANOVA) on age showed a significant center effect (F(3,36) = 3.99, p = 0.02). Post-hoc Newman–Keuls tests (nominal alpha level of p < 0.05) revealed that control participants at center C were significantly older than control participants at center D (p = 0.01). No other pairwise comparison was significant. Distribution of sex (chi² = 2.02; degrees of freedom (d.f.) = 3; p = 0.57) did not differ between study centers (center-specific demographic details are summarized in Table 2).

3.2. Step 1: b) testing on center effects in controls

Due to the results above, age was added as a covariate to the ANOVA when testing for center effects on CV. One-way ANOVAs with age as a covariate showed no significant differences of CV between centers for the five predefined ROIs (highest F-value: F(3,35) 1.73, p = 0.18; external capsule). Results are shown in Fig. 2 (F-values and associated p-values are shown above the bars; d.f. was 3.35 for each analysis). One-way ANOVAs without age as covariate did not change the pattern of results (highest F-value: F(3,36) = 2.47; p = 0.08; external capsule).

At one specific site it had become necessary to scan subjects with shorter echo times (TE) than at the three other sites (see Table 1). Since diffusion quantification may change with TE (e.g. Qin et al., 2009) we used TE as a second covariate. With this, the overall pattern of insignificant center effects remained stable for each ROI (highest F-value: F(3,34) = 2.03; p = 0.13; external capsule).

Finally, the same analysis was repeated but now on FA values. Center effects were again not significant for all ROIs (basal ganglia: F(3,34) = 0.35; p = 0.79; external capsule: F(3,34) = 1.94; p = 0.14; thalamus: F(3,34) = 1.45; p = 0.25; internal capsule: F(3,34) = 1.74; p = 0.18; corpus callosum: F(3,34) = 1.54; p = 0.22).

3.3. Step 2: a) age and sex distribution in patients and controls

As for the CV statistics, the demographic variables age and sex distribution were tested for significant group-by-center interactions by two separate analyses. An ANOVA with age as the dependent variable did not show a significant effect for group (F(1,93) = 2.34; p = 0.13) or center (F(3,93) = 1.48; p = 0.23), and no significant interaction thereof (F(3,93) = 1.89; p = 0.14). Sex distribution, however, differed across centers (chi² = 16.06; d.f. = 7; p = 0.03), in that centers A, B and D included unequal numbers of male and female HD participants (Table 2).

3.4. Step 2: b) testing on center effects of FA differences between patients and controls

Statistical tests for significant group-by-center interactions were computed with FA as the dependent variable and sex as covariate. For each of the five ROIs we found a significant effect of group (Table 3) indicating differences in mean FA values between patients and controls for each region when averaging across centers. The group-by-center interactions (Table 3) were far from significance for all ROIs, supporting that group differences between patients and controls were not systematically influenced by being collected at a specific center (see Fig. 3). Removing the covariate sex from the analysis did not change the pattern of results (see Table 3 and Fig. 3 for details).

Table 3.

Results of analyses of variance on ROI averaged FA values with and without the covariate sex; the anatomical location of the five different ROIs is depicted in Fig. 2; the degrees of freedom (d.f.) of each F-statistic is given in brackets. The listed values were obtained for differences between the HD and the control group.

	In the presence of the covariate sex				No covariates
	Group		Group-by-center		Group		Group-by-center
	F(1,92)	p	F(3,92)	p	F(1,93)	p	F(3,93)	p
Basal ganglia	28.22	< 0.001	1.54	0.209	27.56	< 0.001	2.42	0.071
External capsule	11.26	0.001	0.45	0.717	11.40	0.001	0.49	0.693
Thalamic region	19.14	< 0.001	0.84	0.475	19.38	< 0.001	1.27	0.288
Internal capsule	18.56	< 0.001	0.17	0.915	18.72	< 0.001	0.16	0.922
Corpus callosum	11.68	0.001	0.31	0.816	11.75	0.001	0.29	0.835

Fig. 3.

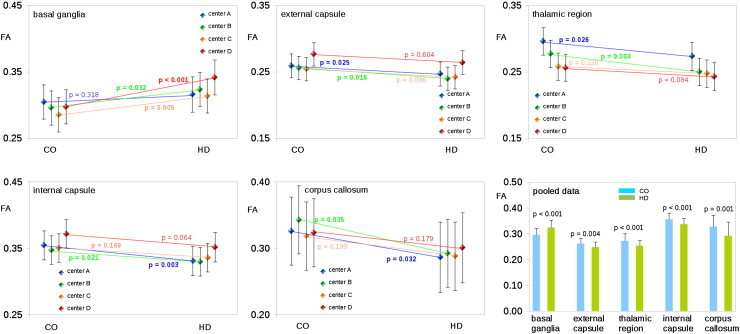
FA differences (corrected for influences of sex) from controls (CO) and patients with Huntington's disease (HD) in different ROIs for different centers. Lower panel right: FA differences in different ROIs for data pooled across centers.

3.5. Step 3: voxel-wise whole brain analysis of group differences

Whole brain-based spatial statistics for pooled FA data showed patterns of significant group differences encompassing all five ROIs (Fig. 4). Basal ganglia FA was significantly increased in HD patients compared to controls, whereas decreases of FA were found in the thalamic region, the internal and external capsules and the corpus callosum in HD patients.

Fig. 4.

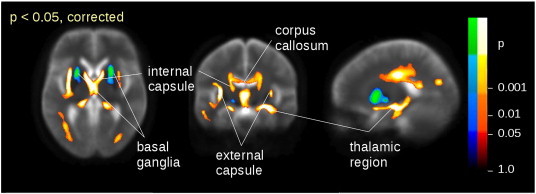
Whole-brain spatial statistic demonstrating clusters of significant FA differences between patients with HD and controls encompassing those predefined ROIs used for the calculation of preceding test statistics (compare Fig. 2). Hot colors indicate FA decrease from controls to HD, and cold colors indicate FA increase.

4. Discussion

In order to comply with the requirements for increased statistical power and consistency of results in clinical imaging studies, it is necessary to scan increasingly larger sample sizes. This demands data to be collected across multiple study sites, since one single center is unlikely to be able to acquire such sample sizes in a reasonable timeframe. Ideally, measured diffusion metrics should be identical across different MR scanners after their calibration. In reality, however, differences between scanning parameters at different sites and with various scanner types can influence the homogeneity of diffusion-derived dependent variables. Further sources of variation include environmental noise and inter-site and inter-subject variability. Also, since one single voxel covers multiple axon bundles, slight differences in positioning may result in averaging different FA values of the same voxel because even a slight shift in the voxel position could lead to a different coverage of axon bundles. This cannot be completely compensated by spatial smoothing of the FA maps.

The variability of diffusion data has already been extensively studied in previous research (Pagani et al., 2010; Teipel et al., 2011; Vollmar et al., 2010; Walker et al., 2012). Nevertheless, a specific multicenter study may not have the resources to repeatedly scan a large number of participants at each site and will have to develop a procedure to overcome potential problems associated with between-site variability within practical and financial constraints unique to that project. Therefore, the aim of the present study was to provide an alternative approach to evaluate the feasibility of pooling multicenter data in a valid and robust fashion.

Within the framework of a three-step testing procedure we observed that in control participants CVs calculated in different a priori selected ROIs did not significantly differ between study sites. Although the specific contribution of any individual source of variation cannot be detected by this approach, the consistency of this measure across centers suggests that a systematic bias due to one or more centers is unlikely. Especially when controlling for influences of control participants' age all F-values in the present analyses of center effects on CV data were clearly below the critical threshold of F(3,35) = 2.25 which would have indicated effects at a level of p < 0.10, hereby also ruling out the idea that keeping the null-hypothesis may have been an issue of insufficient power.

In a next step we tested whether ROI based group differences between patients and controls would differ between centers. Again, all F-values of the group-by-center interactions of interest were clearly below the critical value of F(3,91) = 2.15 (associated p = 0.10) when controlling for additional effects of unbalanced sex distributions across groups and centers. In the absence of this covariate only one (basal ganglia; Table 3) of the five analyses of variances showed an F-value above the critical threshold of F(3,93) = 2.14 (p = 0.10) which however was still beyond significance, thus supporting the conclusion that none of the study centers had contributed systematically biased differences.

The results of our analysis demonstrate that multicenter pooling of DTI data can be performed in a valid manner. The resulting voxelwise pattern of FA group differences between patients and controls showed a high consistency with previous reports performed at single centers (Douaud et al., 2009; Rosas et al., 2006; Weaver et al., 2009) and also encompassed all ROIs from which previous test statistics had been derived. Rosas et al. (2006) compared FA maps of HD subjects against controls on a single center level, and they found decreases in the internal and external capsules, the corpus callosum and the thalamic region, whereas an increase was found in the basal ganglia. This increase in the basal ganglia appears to be a main feature of HD pathology probably reflecting a decline of medium spiny neurons. In healthy participants, the complex neural connectivity of the basal ganglia results in a net diffusion with low FA values. However, the disease related atrophy of those medium spiny neurons which have a distinct orientation results in a net increase of FA values for the basal ganglia because other neurons with a different orientation remain unaffected. Therefore, an increase of directionality of water molecules' diffusion within the basal ganglia most likely indicates a disturbance in this region (Douaud et al., 2009). Anatomical structures affected by the disease process in HD were also identified by structural MRI studies (for review see Bohanna et al. (2008) and Klöppel et al. (2009)) as well as by functional MRI studies (for review see Albin et al. (1995)). The identified key structures were again the basal ganglia, the thalamus, the external and internal capsules as well as the corpus callosum. Accordingly, the clinical symptoms in HD most likely result from an abnormal functioning of the basal-ganglia-thalamo-cortical circuitry that may originate from striatal degeneration (Albin et al., 1995; Douaud et al., 2009; Rosas et al., 2006).

5. Conclusion

Patterns of changes in fractional anisotropy associated with early HD need to be reproduced at larger scales in order to improve reliability and to meet the requirements of clinical trials, which imposes the necessity of multicenter studies. In the present study we present a new approach for assessing feasibility and validity of pooling DTI data from different centers if time or cost limitations do not permit scanning of a reference sample at each study site. This study may serve as a reference for future multicenter trials employing MRI to measure disease-specific progression independent of site specific conditions. Another technical application of this methodological framework may be the interim quality control of DTI data during an ongoing multicenter imaging trial.