Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2013 May 14;35(5):1801–1814. doi: 10.1002/hbm.22295

Characterization of disease‐related covariance topographies with SSMPCA toolbox: Effects of spatial normalization and PET scanners

Shichun Peng 1,†, Yilong Ma 1,✉, Phoebe G Spetsieris 1,†, Paul Mattis 1, Andrew Feigin 1, Vijay Dhawan 1, David Eidelberg 1
PMCID: PMC3778048  NIHMSID: NIHMS469784  PMID: 23671030

Abstract

To generate imaging biomarkers from disease‐specific brain networks, we have implemented a general toolbox to rapidly perform scaled subprofile modeling (SSM) based on principal component analysis (PCA) on brain images of patients and normals. This SSMPCA toolbox can define spatial covariance patterns whose expression in individual subjects can discriminate patients from controls or predict behavioral measures. The technique may depend on differences in spatial normalization algorithms and brain imaging systems. We have evaluated the reproducibility of characteristic metabolic patterns generated by SSMPCA in patients with Parkinson's disease (PD). We used [18F]fluorodeoxyglucose PET scans from patients with PD and normal controls. Motor‐related (PDRP) and cognition‐related (PDCP) metabolic patterns were derived from images spatially normalized using four versions of SPM software (spm99, spm2, spm5, and spm8). Differences between these patterns and subject scores were compared across multiple independent groups of patients and control subjects. These patterns and subject scores were highly reproducible with different normalization programs in terms of disease discrimination and cognitive correlation. Subject scores were also comparable in patients with PD imaged across multiple PET scanners. Our findings confirm a very high degree of consistency among brain networks and their clinical correlates in PD using images normalized in four different SPM platforms. SSMPCA toolbox can be used reliably for generating disease‐specific imaging biomarkers despite the continued evolution of image preprocessing software in the neuroimaging community. Network expressions can be quantified in individual patients independent of different physical characteristics of PET cameras. Hum Brain Mapp 35:1801–1814, 2014. © 2013 Wiley Periodicals, Inc.

Keywords: spatial covariance analysis, principal component analysis, Parkinson's disease, emission tomography, brain imaging

OVERALL DESCRIPTION OF THE PROCEDURE

It is often a challenge to diagnose and assess neurological disorders on clinical criteria alone. Functional brain imaging methods can provide an objective basis for discriminating patients from controls and for differential diagnosis of clinically similar neuropsychiatric syndromes [Habeck et al., 2008; Spetsieris et al., 2009; Tang et al., 2010]. Likewise, statistical mapping approaches can be used to assess disease progression and the effects of novel interventions on resting brain function [Eidelberg, 2009; Feigin et al., 2007a; Hirano et al., 2008]. In general, two analytical techniques have been used to identify and validate disease‐related biomarkers in functional and anatomical neuroimaging data. Mass‐univariate general linear models [e.g. statistical parametric mapping (SPM)] provide a widely used approach to delineate regional abnormalities that are specific to a given illness. By contrast, multivariate approaches based on spatial covariance mapping [e.g., scaled subprofile model (SSM)/principal component analysis (PCA)] provide a reliable means to characterize disease‐related network abnormalities and quantify these changes in individual subjects.

We have implemented a general toolbox (The software freely available to the neuroimaging community at http://www.fil.ion.ucl.ac.uk/spm/ext/) to rapidly perform SSM/PCA operation on brain images from patients and normals. The underlying algorithm and its assumptions were introduced in the early 1990s for use in volume‐of‐interest (VOI) data [Alexander and Moeller, 1994; Eidelberg et al., 1994; Moeller and Strother, 1991; Petersson et al., 1999] and was subsequently extended for voxel‐level whole brain analysis [Asanuma et al., 2005; Habeck et al., 2008; Ma et al., 2007; Moeller et al., 1999]. This SSMPCA toolbox was developed to provide automated voxel‐wise computations with an improved user‐interface, and optimized efficiency for general applications. It can identify characteristic abnormal covariance patterns from principal components whose expression in individual subjects (i.e., subject scores) either discriminate patients from controls or correlate with independent descriptors of disease severity or behavior performance. In addition, an inverse algorithm called topographic profiling rating (TPR) has been devised to prospectively quantify expressions of a given covariance pattern for new subjects on a single case basis.

Spatial covariance analysis with SSMPCA toolbox has been used extensively in the study of Parkinson's disease (PD) and other neurodegenerative disorders [Eidelberg, 2009; Ma et al., 2009; Poston and Eidelberg, 2009; Tang et al., 2010]. We have found with [18F]fluorodeoxyglucose (FDG) PET that PD is associated with two specific covariance patterns for motor and cognitive symptoms. Subject scores of the PD motor‐related pattern (PDRP) have been shown to correlate with independent measures of disease severity, with changes in PDRP expression correlating with clinical outcome following antiparkinsonian interventions [Asanuma et al., 2006; Fukuda et al., 2001; Poston and Eidelberg, 2009]. By contrast, subject scores for the PD cognition‐related pattern (PDCP) have been found to correlate with the degree of cognitive impairment noted in these patients [Eidelberg, 2009; Huang et al., 2007a, 2008]. Furthermore, characteristic metabolic covariance patterns have also been identified to aid diagnosis of atypical [Eckert et al., 2008; Tang et al., 2010] and tremor‐related [Mure et al., 2011] parkinsonism in a clinical setting.

One key prerequisite for univariate or multivariate brain mapping studies at the voxel level is spatial registration and normalization of individual images. This is usually performed using commonly available computing tools implemented in SPM software [Friston, 2007]. Over the last decade this software has evolved steadily (four officially released versions from spm99 to spm8) to provide more powerful solutions for inferential statistics. In particular, optimized algorithms are incorporated into these routines to improve the accuracy of image preprocessing. Parallel to these developments in the neuroimaging field, SSMPCA can be run using different preprocessing methods, which are likely to introduce a degree of inconsistency into the results. Thus, it may be difficult to compare or interpret the results of SSMPCA without knowing the comparability of covariance patterns using these different image preprocessing tools. Network expressions may also depend on differences in PET cameras and image reconstruction algorithms given the variation of imaging systems among many nuclear medicine facilities.

In this study, we evaluated the performance of the SSMPCA toolbox in generating characteristic disease‐specific patterns with the use of different versions of the SPM program. This was based on both PDRP and PDCP which have been generated and validated extensively with spm99 [Asanuma et al., 2006; Hirano et al., 2008; Huang et al., 2007a, 2007b; Ma et al., 2007; Mattis et al., 2011; Spetsieris and Eidelberg, 2011; Trost et al., 2006]. We observed an error of 5–7% in the diagnostic accuracy when evaluating these brain networks with images normalized using newer versions of SPM software. By preprocessing FDG PET images with different spatial normalization algorithms, we assessed the stability of metabolic covariance patterns in discriminating patients from controls and in correlating with behavioral measures in independent populations. The reproducibility of subject scores for these patterns was also assessed using images from different PET scanners and SPM normalization programs.

SUMMARY OF THE MATERIALS AND EQUIPMENT USED

The SSMPCA toolbox was implemented in MATLAB (Mathworks, Natick, MA), a common software platform used by researchers in the neuroimaging field. Brain images from the scanner database are extracted into DICOM format and transformed into standard Analyze or NIfTI‐1 file format. Imaging volumes of all subjects are then mapped to the same physical space by spatial transformation to a standardized brain template. This normalization procedure allows automated data‐driven processing in both VOI‐ and voxel‐based analyses over the whole brain. User‐defined threshold criteria, smoothing and masking constraints are also applied uniformly over all image data to enhance signal‐to‐noise ratio prior to statistical analysis.

For network analysis and diagnosis, we use an implementation of SSM in conjunction with PCA that includes automated TPR diagnostic tools [Ma et al., 2007; Spetsieris et al., 2006]. SSMPCA can be applied to brain images for a combined group of patients and controls or a single subject group (Fig. 1). Each input VOI dataset or spatially normalized brain image undergoes a natural log‐transformation if imaging data have positive values and multiplicative variability (e.g. PET). In contrast, this transformation is not suitable if imaging data have negative values or additive variability (e.g. fMRI). The resulting data from all subjects are then entered into a PCA after applying an offset to remove subject‐ and voxel‐specific mean effects. It is this two‐step centering procedure that ensures that the estimated topographic pattern is a direct measure of the spatial covariation among widely distributed brain regions. Although the log‐transformation is not always essential, the use of double‐centered log‐transformed PCA [Joliffe, 2002] is known to minimize the effect of any subject‐ and/or group‐dependent differences in global brain function on pattern topography (c.f. [Spetsieris and Eidelberg, 2011]). SSM analysis outputs a set of principal components (PCs) along with the fraction of the variance accounted for (VAF) by each PC. This operation also generates subject scores that reflect the degree to which a subject expresses the associated network topology in each PC.

Figure 1.

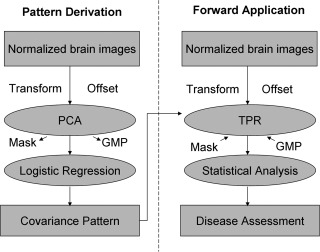
Figure 1

Open in a new tab

Flow chart for the multivariate covariance analysis with SSMPCA toolbox. (A) Pattern derivation: principal component analysis (PCA) can be performed on brain images for two subject groups or one single group. Input data may be log‐transformed and then offset to remove subject‐specific measures of global scaling factors and region‐specific effects termed group mean profile (GMP). PCA is done within a brain mask defined by the input imaging data. Logistic regression is conducted on subject scalar factors for a subset of PCs for optimizing the discrimination between the two subject groups or behavioral correlation in the single subject group. (B) Forward application: topographic profiling rating (TPR) can be applied prospectively to brain images from any number of subject groups or conditions. The computation is carried out using a brain mask and GMP either come from the original sample for the PCA operation or defined by the user in the prospective sample of any new population. Subject scores of each covariance pattern are usually transformed into z‐scores for prospective analysis.

The PCs resulting from a single SSM/PCA run represent a set of regional vectors or voxel maps of Group Invariant Subprofile (GIS) that may result from functional abnormality in relevant brain disorders. Each GIS pattern consists of voxels with both positive and negative values that are termed region weights [Eidelberg, 2009; Ma et al., 2009]. The values of the region weight measure the degree and direction of regional covariance and the relative contribution to a GIS pattern by each voxel. Positive voxel weights indicate that as pattern expression increases, relative metabolic activity in the positively weighted voxels increases as well. Likewise, negative voxel weights indicate decreases in relative local metabolic activity with increasing pattern expression.

To obtain a clinically relevant covariance pattern it is necessary to examine a subset of PCs (e.g. 1–6) with the total voxel‐subject variance exceeding 50%. Subject scores for individual PCs can be linearly combined by logistical regression to identify the optimal combination that best separates patients from controls or predicts behavior correlates in a single subject group. Consequently, a disease‐specific covariance pattern can be defined by either a single PC or a linear combination of these PCs using the same parameters determined by the logistic regression. In the forward application, subject scores were determined by TPR from the dot product between the covariance pattern and individual brain images with or without the natural log‐transformation. Hence, subjects will have higher scores for a pattern if their brain images contain more regions with concomitantly more increased and/or more decreased relative brain activity. Likewise, subjects will have lower scores following the restoration of regional brain function.

To derive a robust covariance pattern one has to assess the reliability of the region‐weight that is significantly different from zero at each voxel. The SSMPCA toolbox uses a bootstrapping algorithm to estimate the reliability of each covariance pattern as described elsewhere [Habeck et al., 2003]. In this module, PCA procedure is repeated iteratively for a large number of iterations (e.g. 500–1,000) by resampling the original sets of brain images with replacement. A three‐dimensional (3D) map of inverse coefficient of variation (ICV) is produced on a voxel basis by dividing the region–weight of the original covariance pattern by the standard deviation of covariance patterns generated from all iterations in the bootstrapping. This map allows the user to define a statistic for measuring the reliability by selecting a z‐threshold for both positive and negative region–weights of a particular covariance pattern.

STEP‐BY‐STEP DESCRIPTION OF THE RESEARCH PROTOCOL

In this study, we used brain scans of cerebral glucose metabolism from several cohorts of patients and normal controls for pattern derivation and prospective validation. FDG PET images were acquired in 3D mode using a GE Advance tomograph (GE Medical Systems, Milwaukee, WI) at North Shore University Hospital. On a fast since the night before, all subjects remained at rest in a quiet and dimly‐lit room during radiotracer uptake and imaging. The procedure involved taking one single blood sample at 20 min post‐injection, followed by a sequential transmission and emission scanning protocol [Ma et al., 2007]. Table 1 provides the demographic and clinical information of all subjects. For studies on the motor‐related PDRP network, two independent cohorts were created randomly from the FDG PET images in 33 patients with PD and 33 age‐matched controls that were originally used to generate the PDRP in the test–retest study [Ma et al., 2007]. The patients had a total motor score of 31.3 ± 16.4 (mean ± SD) as evaluated by the Unified Parkinson's Disease Rating Scale (UPDRS). For PDRP identification, we used images in the first cohort of 20 patients with PD (age 55 ± 5 year; Hoehn and Yahr [H&Y] stages: 2–4) and 20 normal controls (age 55 ± 9 year). For prospective validation, subject scores were determined in the second cohort of 13 patients with PD (age 61 ± 11 year; H&Y stages 2–4) and 13 normal controls (age 55 ± 19 year). There were no significant differences in age (ANOVA: F 3,62 = 1.11, P = 0.35) among these four subject groups.

Table 1.

Clinical characteristics in patients with PD and normal controls

Group Derivation sample Validation sample
PD NC PD NC
PDRP
Number 20 20 13 13
Age (year) 54.7 ± 4.9 55.1 ± 9.0 61.1 ± 10.6 54.9 ± 18.7
PDCP
Number 15 – 15 15
Age (year) 58.6 ± 9.5 – 62.1 ± 5.2 56.8 ± 9.5
UPDRS 31.3 ± 15.4 – 33.7 ± 16.3 –
MMSE 28.3 ± 2.1 – 28.2 ± 1.6 –
CVLT 35.0 ± 15.3 – 34.6 ± 9.5 –
Trails B 138.1 ± 63.9 – 134.0 ± 63.2 –
HVOT 19.2 ± 4.5 – 19.6 ± 4.5 –
Open in a new tab

UPDRS, Unified Parkinson's Disease Rating Scale; MMSE, Minimal Mental Status Examination; CVLT, California Verbal Learning Test; Trails B, Trail Making Test Part B; HVOT, Hooper Visual Organization Test.

All values are given as mean ± SD.

To derive the cognition‐related PDCP network, we used FDG scans from a single group of 15 nondemented PD patients (age 59 ± 10 year; H&Y stages 2–4; MMSE 28.2 ± 2.1) [Huang et al., 2007a]. Fifteen age‐matched healthy subjects (age 57 ± 13 year) served as normal controls. Furthermore, an independent sample of 15 patients with PD (age 62 ± 5 year; H&Y stages 2–4; MMSE 28.2 ± 1.6) was used for prospective validation of this pattern [Huang et al., 2008]. Age did not differ across these three subject groups (ANOVA: F 2,42 = 1.16, P = 0.32). All patients with PD were assessed with UPDRS and a battery of neuropsychology tests on their cognitive performance as described previously [Huang et al., 2007a, 2008]. Patients in the validation sample had been diagnosed to have single domain mild cognitive impairment (MCI) but were otherwise similar to those in the derivation sample (P ≥ 0.23; Student's t‐test; Table 1). Ethical permission for this study had been given by the local Institutional Review Board. Written informed consent had been obtained from each subject with detailed explanation of the procedures and in accordance with the Code of Ethics of the World Medical Association (Declaration of Helsinki).

All images were preprocessed using four different versions (spm99, spm2, spm5, and spm8) of SPM software (Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK; http://www.fil.ion.ucl.ac.uk/spm). Individual images were spatially normalized into Talairach brain space. This standard anatomical space was defined by a series of image‐modality specific brain templates. The normalization used linear and nonlinear registration algorithms in each of four SPM versions [Ashburner and Friston, 1999; Ashburner et al., 1997]. The default registration was not regularized sufficiently in spm99. The algorithms were more refined from spm2 onwards, with increased regularization and optimization in the iterative registration algorithm. These algorithms perform better in reducing the effect of potential brain atrophy (e.g. in the PDCP network) on the normalization accuracy compared to the previous method implemented in spm99. The normalized images were then smoothened by a 10mm Gaussian filter over a 3D space to increase signal to noise ratio before statistical analysis.

PDRP and PDRP topographies were generated from images spatially normalized by each version of SPM software. Differences across four versions of PDRP or PDCP were separately assessed by visual inspection and by quantitative pairwise comparison. For qualitative inspection, the four versions of each pattern were overlaid onto a standard MRI brain template on three orthogonal views using the same thresholds. For quantitative analysis, the four versions of each pattern were compared by computing the region–weights in a set of 30 VOIs covering the whole brain, including only voxels ≥±80% of the maxima within each VOI. The comparisons were also made voxelwise to evaluate topographic patterns more accurately. In addition, subject scores for PDRP/PDCP were computed for the images in the validation sample. All subject scores were z‐transformed individually by subtracting control mean and dividing by pooled standard deviation in the original derivation sample. This made the mean value of the derivation controls equal to zero and ensured the comparability of subject scores across different populations.

MULTICENTER REPRODUCIBILITY OF NETWORK EXPRESSIONS

To assess the reproducibility of PDRP/PDCP scores across multiple PET scanners, we used FDG PET scans acquired at baseline from 23 nondemented patients with advanced PD who belonged originally to the sham group in a randomized double‐blind gene therapy trial [Lewitt et al., 2011]. All subjects (age 61 ± 7 year; H&Y stages 2–4; UPDRS 39.0 ± 8.7) were scanned over 35–45 min post‐injection in five medical centers in the USA with five different PET cameras (Supporting Information Table I). These cameras included four PET alone machines and one PET/CT scanner made by two major vendors, with a 3D resolution of 4–6 mm at the center and 5–7 mm at 10 cm from the center. PET images were reconstructed with one of four different methods commonly used at each site. Subject scores of PDRP/PDCP networks were then determined as described earlier.

STATISTICAL ANALYSIS

Data analyses for PDRP and PDCP networks were performed separately and in parallel. All comparisons were made in reference to the results from spm99‐processed images which have been validated rigorously as noted in the Introduction. For the four versions of each pattern, region weights were correlated pairwise using both VOI‐ and voxel‐based regression analyses. Between‐group differences in subject scores for each version of the PDRP were evaluated with two‐sample t‐tests and receiver operating characteristic (ROC) analyses in both cohorts of patients with PD and healthy controls. To assess the single‐case diagnostic power of PDRP score from spm99‐normalized images, an optimal threshold was chosen to give high sensitivity and specificity of 95% in the derivation cohort and then applied to the validation cohort. In each cohort, the reproducibility of diagnostic accuracy was further tested by subject scores from the other three versions of the PDRP using the same optimal threshold chosen above. In addition, subject scores for each version of the PDCP were correlated with age, UPDRS motor ratings, and neuropsychological measures in patients. Within each group of patients and controls, subject scores were also correlated among the four versions of PDRP or PDCP network. All statistical computations were performed using SPSS software (SPSS, Chicago, IL) running on PCs and were considered significant with P < 0.05.

RESULTS

PDRP

The PDRP topography was identified as the first PC that accounted for at least 18.3% subject × voxel variance in the four derivation analyses (Fig. 2), each using a different version of the SPM normalization software. Subject scores for each of the four resulting versions were elevated in the patients with PD relative to the healthy controls (P < 0.0001). These four PDRPs were very similar in terms of metabolic topographies of increased and decreased regional covariation (Fig. 3) and reliable at P < 0.005 according to the bootstrapping estimation (Supporting Information Fig. 1A). The major results for the four PDRP versions were summarized in Table 2. Region‐weights of these patterns from images normalized by spm2, spm5, and spm8 were highly intercorrelated (P < 0.0001) with those from spm99 (R ≥ 0.998; Supporting Information Fig. 2) and almost identical among themselves (R = 1.0).

Figure 2.

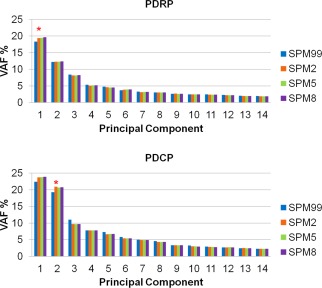
Figure 2

Open in a new tab

Eigenvalue distributions produced for the derivations of PDRP and PDCP using FDG PET images normalized by spm99, spm2, spm5, and spm8. Variance accounted for (VAF) was plotted for each of major principal components from SSMPCA network analyses. Each of the PDRPs was identified by the first PC (asterisk) from 20 patients with PD and 20 age‐matched normal volunteers in the original derivation sample. Each of the PDCPs was identified by the second PC (asterisk) from 15 nondemented patients with PD with mild to moderate motor symptoms in the original derivation sample. Asterisks denoted the optimal PC that gave rise to the maximum group separation (PDRP) or behavioral correlation (PDCP). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 3.

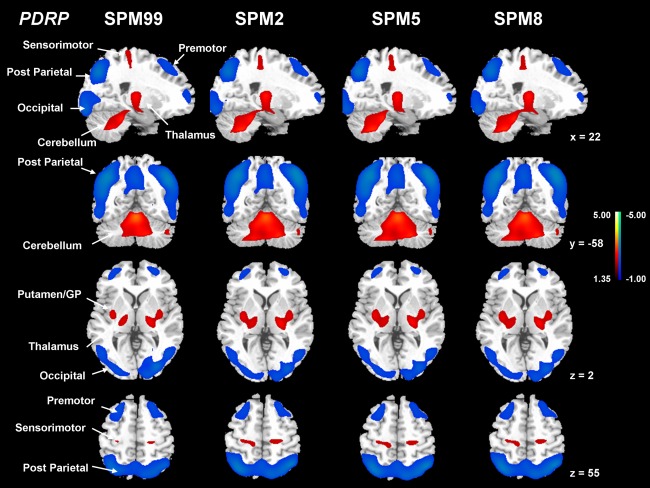
Figure 3

Open in a new tab

Comparisons of PDRP from FDG PET images normalized by spm99, spm2, spm5, and spm8. Each of the PDRPs was identified by network analysis of FDG PET scans from 20 patients with PD and 20 age‐matched normal volunteers in the original derivation sample. This covariance pattern was characterized by relative pallidal, thalamic, sensorimotor, pontine, and cerebellar hypermetabolism, associated with covarying metabolic decrements in the lateral premotor and posterior parietal areas. PDRP expression (subject scores) for this pattern was significantly (P < 0.001) increased in the patients with PD relative to the normal control subjects. [The displays are on a standard single‐subject MRI brain template and represent voxels that contribute significantly (P < 0.005) to the network based on a bootstrapping estimation algorithm. Red/blue colors indicate brain regions with concurrently increased/decreased covariation between regional glucose metabolism.]

Table 2.

Comparisons of PDRP network and subject scores with FDG PET images normalized by four versions of SPM software

SPM99 SPM2 SPM5 SPM8
VAF (%) 18.33 19.43 19.46 19.61
GIS weightsa 1.000/1.000 0.998/0.987 0.998/0.986 0.998/0.986
PCA derivation sample
20 NC 0.000 ± 0.099 0.000 ± 0.096 0.000 ± 0.096 0.000 ± 0.097
20 PDb 1.486 ± 0.186 1.473 ± 0.190 1.471 ± 0.191 1.469 ± 0.191
AUC (CI) 0.993 (0.974, 1.011) 0.985 (0.959, 1.011) 0.985 (0.959, 1.011) 0.984 (0.956, 1.012)
Sensitivity 0.95 0.90 0.90 0.90
Specificity 0.95 0.90 0.90 0.90
TPR validation sample
13 NC 0.000 ± 0.118 0.000 ± 0.117 0.000 ± 0.117 0.000 ± 0.117
13 PDb 1.462 ± 0.239 1.436 ± 0.246 1.434 ± 0.247 1.434 ± 0.247
AUC (CI) 0.970 (0.914, 1.027) 0.959 (0.892, 1.025) 0.959 (0.892, 1.025) 0.959 (0.892, 1.025)
Sensitivity 0.92 0.85 0.85 0.85
Specificity 0.92 0.92 0.92 0.92
Subject score correlationa
20 NC 1.000 0.972 0.971 0.971
20 PD 1.000 0.995 0.995 0.995
13 NC 1.000 0.966 0.968 0.969
13 PD 1.000 0.995 0.996 0.996
Open in a new tab

AUC, area under the curve in the receiver operating characteristic analysis; CI, 95% confidence of intervals (lower bound, upper bound); sensitivity, true positive rate (TPR); specificity, true negative rate (TNR); VAF, variance accounted for in principal component analysis; GIS, Group Invariant Subprofile from the derivation sample of PD and control subjects.

The correlations of the GIS weights were performed over a standard 30 VOI template with a threshold of 80 % or over all voxels of the brain with non‐zero values.

All average values are given as mean ± SE.

a

P < 0.0001; Pearson correlation coefficient from regression analysis.

b

P < 0.0001; with respect to normal controls (Student's unpaired t‐tests).

The subject scores for each version of the four PDRPs were significantly higher in the patients versus the controls in the two separate cohorts (P < 0.0001; Fig. 4). These scores exhibited excellent discriminating accuracy in the original derivation (AUC ≥ 0.984, 95% confidence of interval [CI] = 0.956–1.012) and the prospective validation (AUC ≥ 0.959, 95% CI = 0.892–1.027) cohorts. For single‐case diagnosis, the specificity and sensitivity were excellent in the derivation cohort, but slightly better for the spm99‐processed images than for the other three versions. In the validation cohort, despite high specificity overall, the sensitivity was also better for the former than for the latter. PDRP scores from four SPM‐normalization programs were highly inter‐correlated (P < 0.0001; Supporting Information Fig. 2) for the controls and the patients in the derivation (R ≥ 0.971) and the validation (R ≥ 0.966) cohorts.

Figure 4.

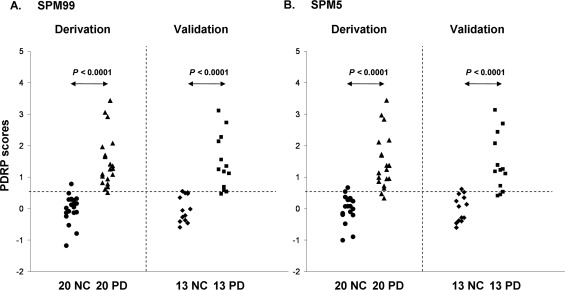
Figure 4

Open in a new tab

Disease differentiations by subject scores of the PDRP networks from FDG PET images normalized by spm99 (A) and spm5 (B). In both cases, PDRP scores were elevated (P < 0.00001) in the 20 patients with PD relative to the 20 controls in the original derivation sample. This excellent disease discrimination is similar to that from subject scores computed prospectively between the 13 patients with PD and the 13 controls in the validation sample. The dash‐lines indicate the optimal threshold defined from PDRP scores in the derivation cohort using spm99‐normalized images. The performance figures by the subject scores of the PDRP in both derivation sample and validation sample are highly equivalent between images normalized by the four versions of SPM program (see text).

PDCP

PDCP was identified in separate analyses in which subject differences in the expression of each PC were correlated with the behavioral measures [Huang et al., 2007a]. The PDCP topography was determined as the second PC (accounting for at least 19.3% of subject × voxel variance; Fig. 2) using images from each version of the SPM programs. Subject scores for each of the resulting PDCPs correlated (P < 0.01) with the degree of cognitive impairment measured by California verbal learning test (CVLT). These four PDCPs were also highly similar (Fig. 5) and reliable at P < 0.005 according to the bootstrapping estimation (Supporting Information Fig. 1B). The major results for the four PDCPs were summarized in Table 3. Region‐weights of the PDCPs from images normalized by spm2, spm5, and spm8 were also highly intercorrelated (P < 0.0001) with those from spm99 (R ≥ 0.968; Supporting Information Fig. 2) and almost identical among themselves (R = 1.0).

Figure 5.

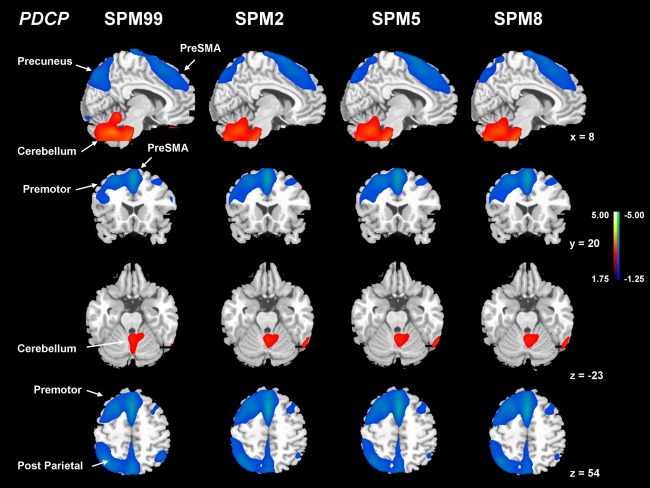
Figure 5

Open in a new tab

Comparisons of PDCP from FDG PET images normalized by spm99, spm2, spm5, and spm8. Each of the PDCPs was identified by network analysis of FDG PET scans from 15 nondemented patients with PD with mild to moderate motor symptoms in the original derivation sample. This covariance pattern was marked by bilateral metabolic reductions in the rostral supplementary motor area (preSMA) and precuneus, the dorsal premotor cortex, the inferior parietal lobule, as well as in the left prefrontal region, covarying with relative metabolic increases in the cerebellar vermis and dentate nuclei. Subject scores for this pattern correlated significantly (P < 0.01) with psychometric indices of verbal learning performance. [The displays are on a standard single‐subject MRI brain template and represent voxels that contribute significantly (P < 0.01) to the network based on a bootstrapping estimation algorithm. Red/blue colors indicate brain regions with concurrently increased/decreased covariation between regional glucose metabolism.]

Table 3.

Comparisons of PDCP network and subject scores with FDG PET images normalized by four versions of SPM software

SPM99 SPM2 SPM5 SPM8
VAF (%) 19.28 20.92 20.65 20.81
GIS weightsa 1.000/1.000 0.976/0.949 0.968/0.940 0.970/0.943
PCA derivation sample
15 PD 0.864 ± 0.312 0.640 ± 0.325 0.608 ± 0.326 0.617 ± 0.325
CVLT −0.727b −0.661c −0.645c −0.650c
TPR validation sample
15 PD2 1.087 ± 0.236 0.883 ± 0.225 0.851 ± 0.222 0.856 ± 0.222
CVLT −0.503d −0.610d −0.612d −0.610d
CVLT 30 PD −0.650a −0.642a −0.632a −0.635a
Subject score correlationa
15 PD 1.000 0.965 0.957 0.959
15 NC 1.000 0.948 0.947 0.952
15 PD2 1.000 0.975 0.970 0.973
Open in a new tab

VAF, variance accounted for in principal component analysis; GIS, Group Invariant Subprofile from the derivation sample of patients with PD.

The correlations of the GIS weights were performed over a standard 30 VOI template with a threshold of 80% or over all voxels of the brain with non‐zero values.

All average values are given as mean ± SE.

a

P < 0.0001; Pearson correlation coefficient from regression analysis.

b

P < 0.005.

c

P < 0.01.

d

P < 0.05.

Subject scores from each version of the four PDCPs correlated negatively with individual values of CVLT in the original derivation (R ≤ −0.645, P < 0.01; Supporting Information Fig. 3) and prospective validation (R ≤ −0.503, P = 0.056) patients with PD. The correlations in the combined sample were similar (R ≤ −0.632, P < 0.001; Fig. 6) with comparable magnitudes among four versions of the PDCP. In other words, a higher PDCP score predicted a worsening ability in verbal learning and memory. However, the same subject scores did not correlate with UPDRS motor scores in each of the two patient groups (P ≥ 0.83). In addition, PDCP scores from the four SPM‐normalization programs were highly correlated (R ≥ 0.948, P < 0.0001; Supporting Information Fig. 2) in the derivation and validation groups.

Figure 6.

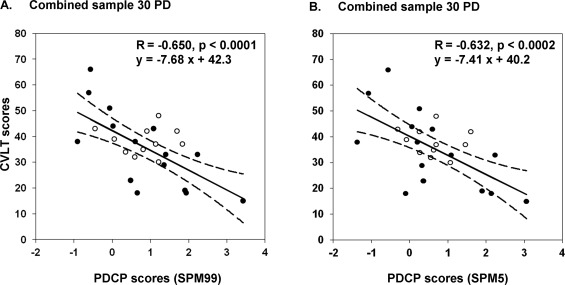
Figure 6

Open in a new tab

Behavioral correlations by subject scores of the PDCP networks from FDG PET images normalized by spm99 (A) and spm5 (B). In both cases, subject scores were negatively correlated with individual values of California Verbal Learning Test (CVLT) in the 15 patients with PD in the original derivation sample (closed circles) and in the 15 patients with PD in the validation sample (open circles). Each graph included a linear regression fit (solid line) and 95% confidence of intervals (dash lines) in the combined sample of 30 patients with PD. The performance figures by the subject scores of the PDCP in individual samples and in the combined sample are highly equivalent between images normalized by the four versions of SPM program (see text).

Multicenter Reproducibility of Network Expressions

Network scores of patients with PD in Sites A (the Feinstein Institute), B, C, D, and E were presented in Table 4 and Figure 7. UPDRS motor ratings or PDRP scores were comparable for the patients across the five sites, with no differences between the 10 subjects from Site A and the 13 subjects from all other Sites (P > 0.32). PDCP network scores were similar to those for the PDRP network scores. PDRP/PDCP scores were also analogous between spm99‐ and spm5‐processed images for individual subjects at each of the five Sites (Supporting Information Fig. 4).

Table 4.

Subject scores of PDRP and PDCP networks with FDG images from multiple PET scanners

Site (no.) PDRP PDCP
SPM99 SPM5 SPM99 SPM5
All (n = 23) 1.23 ± 0.14 1.27 ± 0.15 1.08 ± 0.14 0.84 ± 0.13
Site A (n = 10) 1.07 ± 0.21 1.13 ± 0.22 1.02 ± 0.19 0.83 ± 0.19
Others (n = 13) 1.36 ± 0.19 1.38 ± 0.21 1.12 ± 0.21 0.84 ± 0.19
Open in a new tab

All average values are given as mean ± SE.

Subject scores were computed using multicenter FDG PET images normalized by two different versions of SPM software.

Scanner information for all participating sites is available in Supporting information Table I.

Figure 7.

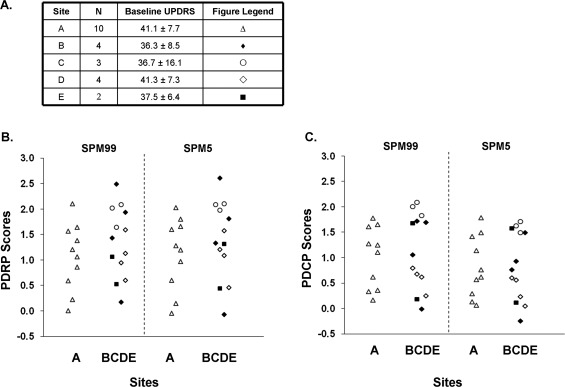
Figure 7

Open in a new tab

Reproducibility of disease‐related brain network expressions in patients with PD using FDG images acquired with five different PET scanners and normalized by spm99 and spm5. (A) UPDRS motor ratings in patients at each of the five participating sites. (B) Subject scores of the PDRP network. (C) Subject scores of the PDCP network. Network scores for patients from the Feinstein Institute (Site A) were similar to those from all other Sites (B–E). Specific information on the PET scanner at each site is listed in Supporting Information Table I. Network scores were highly comparable among multiple PET cameras and image reconstruction methods using different versions of SPM normalization program (see text).

DISCUSSION

PD results from progressive losses of dopaminergic neurons in the nigrostriatal system, as well as nondopaminergic neurons of serotonergic and norepinephrinergic origins in the related neural pathways. Cortical brain atrophy and Lewy body deposition may also underlie cognitive dysfunction. It is this complex neuropathology that leads ultimately to widespread motor symptoms and cognitive impairment in PD [Caballol et al., 2007]. We have established that motor and cognitive dysfunction in PD are associated with specific spatial covariance patterns involving distinct metabolic abnormalities in subcortico‐cortical pathways [Eidelberg, 2009; Huang et al., 2007a; Lozza et al., 2004; Ma et al., 2007]. Both patterns included large areas not normally associated with PD, reflecting the nature of covariance analysis for revealing distal brain regions within a widely distributed network. Widespread cortical abnormalities in metabolism and perfusion have also been described with PET and SPECT using other analysis methods [Bohnen et al., 2011; Hsu et al., 2007]. Indeed, PDRP expression correlated with the increasing severity of motor symptoms and was modulated with successful pharmacologic and stereotaxic surgical interventions for PD [Feigin et al., 2001; Fukuda et al., 2001]. By contrast, PDCP expression correlated with independent measures of cognitive dysfunction in PD and did not exhibit such characteristics seen in the PDRP network [Hirano et al., 2008; Huang et al., 2007b]. PDRP and PDCP expressions in individual patients may be useful in selecting candidates for clinical trials and track their response and prognosis over long‐term follow‐up.

We have previously shown the excellent reliability of these two characteristic patterns within and between imaging sessions. By using functional brain images preprocessed with spm99, we validated PDRP/PDCP expressions as disease‐related biomarkers in prospective patient cohorts scanned at rest with FDG and H2 15O PET techniques [Huang et al., 2007a; Ma et al., 2007]. Subject scores obtained from regional cerebral glucose metabolism (rCMRglc) and blood flow (rCBF) data in the same cohort of patients and controls were highly comparable for both PDRP and PDCP. We also demonstrated the stability of these measures in test–retest studies of patients scanned at different disease stages in the untreated condition and during pharmacological or neurosurgical interventions. This information is useful in the design of interventional imaging studies of novel therapies for PD and related neurodegenerative disorders.

We have now demonstrated that the results obtained from FDG PET images spatially normalized by spm2, spm5, and spm8 are highly consistent with those in the previous studies with spm99. Indeed, the motor‐related PDRPs were strongly correlated among four versions of SPM program in terms of the region‐weights assessed over the whole brain (R > 0.98; Table 2). The topography of these PDRP networks was very similar to that from multivariate independent component analysis of SPECT brain perfusion data [Hsu et al., 2007]. PDRP expression reliably distinguished patients with PD from normal controls with a high degree of accuracy in two independent cohorts and across four versions of SPM software. Nevertheless, there was a small decline in the discrimination power in the validation cohort due to the reduced number of subjects. Furthermore, subject scores in PD patients from spm99‐normalized images were slightly higher than those from other versions of SPM program, consistent with the marginally better discrimination power in the corresponding PDRP. Subject scores of all PDRPs were strongly correlated in the two independent groups of PD patients or normal controls.

The determination of disease‐specific patterns with SSMPCA may depend on the selection of optimal PCs, image smoothing, and sample size. We compared the distribution of subject scores in the derivation of PDRP or PDCP with different sets of combinations of contiguous PCs (1–2 until 1–6), using PET images normalized with both spm99 and spm5. For each combination of PCs, the total VAF was comparable with subject scores in each group highly correlated between the two versions of SPM (Supporting Information Tables II and III). The first PC consistently gave the maximum group discrimination in subject scores. The second PC produced the strongest behavioral correlation in the reference condition of spm99. Hence, the first/second PC was used to define the PDRP/PDCP as described in this article. The effect of image smoothing remains to be fully assessed.

The PDRP network reported here with 20 patients with PD and 20 control subjects was very similar to that derived from a large sample of patients and controls. Indeed, PDRP networks generated from the whole groups of 33 patients with PD and 33 controls were also highly correlated (R ≥ 0.94; P < 0.0001) with the former in terms of the region‐weights and subject scores with spm99‐ or spm5‐normalized images. Discrimination power was also comparable among different groups of patients and controls. To test the effect of the sample size on PDRP, a series of empirical studies were conducted by randomly selecting a smaller number of subjects in the derivation sample. The results indicated that reliable variance patterns may be identified with as few as 10 patients and 10 controls.

The cognition‐related PDCP topographies were also highly reproducible among four versions of SPM normalization program, with very strong pair‐wise correlations in the region‐weights (R ≥ 0.94; Table 3). The PDCP network was almost identical to the topography obtained from another voxel‐based multivariate analysis method using brain‐behavior partial least squares [Mentis et al., 2002]. PDCP expression reliably predicted objective measures of cognitive dysfunction in two independent groups of PD patients across four versions of SPM software. However, the predictive power of the PDCP score was marginally better in spm99‐normalized images than those preprocessed with other versions of SPM in the 15 derivation patients. PDCP scores from the former were higher (but not significantly) than those from the latter in both patient groups. Lower PDCP scores in spm2‐8 were attributed to the normalization methods which tend to minimize the spread of hypometabolic brain regions (predominate in the PDCP). Consistent with a diagnosis of MCI the validation sample had higher (nonsignificant) PDCP scores relative to the derivation sample. Given that the behavioral correlations in the combined sample were comparable in magnitudes and directionality with those in the derivation or validation groups (Table 3), the effects of sample size were also estimated empirically. These results all showed high similarity among four versions of SPM normalization program, suggesting that a sample size of 15 is adequate in such a network analysis in a single group of subjects.

PDRP/PDCP topographies and subject scores were almost identical using FDG PET images spatially normalized by spm2, spm5, and spm8, suggesting the very high degree of similarity in the standard brain template and spatial normalization algorithms in these three latest versions of SPM software. We noted that the PDRP was mostly symmetrical in terms of abnormal relative regional metabolism reflecting bilateral motor symptoms in our patients with PD. In contrast, the relative cortical hypometabolism in the PDCP appears to be more pronounced on the left hemisphere, attributed to the stringent threshold used to display the pattern, although a left‐sided dominance of cortical hypometabolism could not be excluded in PD patients with verbal learning dysfunction.

We have demonstrated that network expressions in patients with PD were highly comparable across multiple PET scanners in the context of a multicenter clinical trial. Indeed, PDRP/PDCP scores in this sample did not differ from those in the derivation and validation patients described earlier, in line with similar degrees of motor symptoms or cognitive dysfunction among different cohorts of patients with PD. Despite the small numbers of subjects available per site this result agreed well with our recent study in which PD‐related networks were found to be reproducible in many multicenter studies using different PET cameras and reconstruction algorithms [Niethammer and Eidelberg, 2012].

The methods implemented in the SSMPCA toolbox have been applied to many neurodegenerative disorders using a variety of multimodality brain imaging data at resting‐state. In addition to many studies that employ FDG and H2 15O PET imaging [Hirano et al., 2008; Ma et al., 2007], PD‐related brain networks can be derived or quantified by using rCBF data acquired by SPECT [Eckert et al., 2007; Feigin et al., 2002] and perfusion‐weighted MRI [Ma et al., 2010; Melzer et al., 2011]. We also revealed a spatial covariance pattern related with MPTP‐induced parkinsonism using FDG PET in macaques [Ma et al., 2008, 2012]. This pattern was topographically similar to the PDRP network in patients and was modulated by experimental therapy.

Specific spatial covariance patterns were also reported in normal aging [Moeller et al., 1996; Zuendorf et al., 2003], Huntington's disease [Feigin et al., 2007b], and torsion dystonia [Asanuma et al., 2005; Trost et al., 2002] using FDG PET, and in patients with Alzheimer's disease (AD) using rCMRglc or rCBF data from PET [Habeck et al., 2008; Kerrouche et al., 2006; Scarmeas et al., 2004] as well as from the perfusion‐weighted MRI [Asllani et al., 2008]. Furthermore, these multivariate techniques were useful in identifying structural covariance patterns based on anatomical MRI data. These included atrophy‐related regional covariance patterns associated with normal aging [Bergfield et al., 2010; Brickman et al., 2008] and AD [Chen et al., 2004] in human subjects, along with the aging‐related pattern in the rhesus macaque [Alexander et al., 2008]. Therefore, SSMPCA provides a valuable methodology for generating specific brain networks with both functional and anatomical imaging markers.

CONCLUSION

PCA‐based network analysis with SSMPCA toolbox can be used to identify disease‐related covariance patterns associated with motor and cognitive functioning. PDRP and PDCP brain networks have been generated to describe the characteristic abnormal metabolism in PD using FDG PET images spatially normalized by four different versions of SPM program developed over the last decade. All results replicate our previous work independent of the normalization algorithms implemented in different SPM software. Network expressions are also reproducible in patients with PD of similar clinical severity despite the use of different PET cameras or image reconstruction methods. SSMPCA toolbox allows fast multivariate statistical analysis of functional and anatomical brain images in a variety of neurodegenerative disorders. Disease‐specific patterns may be used as imaging biomarkers to enhance diagnostic accuracy and track disease progression, improve patient screening, and treatment evaluation in clinical trials.

Supporting information

Supporting Information Figure 1. Reliability at each voxel for the PDRP and the PDCP networks from FDG PET images normalized by spm99. Both maps represent the inverse coefficient of variation (ICV) thesholded at p < 0.005 following a voxelwise bootstrapping estimation algorithm (1000 iterations) over the whole brain (Habeck, et al. 2003). [The displays are on a standard single‐subject MRI brain template and represent voxels that are reliable from the bootstrapping estimation algorithm. Red/blue colors indicate brain regions with concurrently increased/decreased covariation between regional glucose metabolism.]

Click here for additional data file. (3.1MB, tif)

Supporting Information Figure 2. Correlations between region‐weights and subject scores of the PDRP or PDCP networks from FDG PET images normalized by spm99 and spm5. Regression analyses revealed that the region‐weights of the PDRP were highly correlated with each other between the two versions of SPM normalization program (A); the subject scores of the PDRP were also significantly correlated with each other in the 20 PD patients in the derivation sample (B) and in the 13 PD patients in the validation sample (C). The strong correlations were also evident for the PDCP between the region‐weights (D) and subject scores in the 15 PD patients in the derivation sample (E) and in the 15 PD patients in the validation sample (F). These results were highly equivalent between images normalized by the four versions of SPM program (see text).

Click here for additional data file. (7.3MB, tif)

Supporting Information Figure 3. Behavioral correlations by subject scores of the PDCP networks from FDG PET images normalized by spm99 and spm5. In both cases, subject scores were negatively correlated with individual values of California Verbal Learning Test (CVLT) in the 15 PD patients in the original derivation sample (A, C) and in the 15 PD patients in the validation sample (B, D). The performance figures by the subject scores of the PDCP in both derivation sample and validation sample are highly equivalent between images normalized by the four versions of SPM program (see text).

Click here for additional data file. (6MB, tif)

Supporting Information Figure 4. Correlations between subject scores of the PRDR/PDCP networks from FDG PET images acquired with five different PET scanners and normalized by spm99 and spm5. Regression analyses revealed that subject scores of the PDRP (A) and the PDCP (B) in an independent validation sample of PD patients were significantly correlated between two versions of SPM normalization program, regardless of technical differences in PET cameras and image reconstruction methods.

Click here for additional data file. (4.4MB, tif)

Supporting Information Table

Click here for additional data file. (66KB, doc)

Supporting Information Cover Letter

Click here for additional data file. (1.8MB, doc)

ACKNOWLEDGMENTS

The acquisition of multicenter FDG PET images was funded by Neurologix, Fort Lee, NJ, USA. We appreciate Dr. Tom Chaly for radiochemistry support; David Bjelke and Claude Margouleff for their outstanding contributions in FDG PET imaging. We are grateful to a travel award from the OHBM to present part of this work at the 15th Annual Meeting on June 18–22, 2009 in San Francisco, CA, USA.

REFERENCES

  1. Alexander G, Moeller J (1994): Application of the scaled subprofile model to functional imaging in neuropsychiatric disorders: A principal component approach to modeling brain function in disease. Human Brain Mapp 2: 1–16. [Google Scholar]
  2. Alexander GE, Chen K, Aschenbrenner M, Merkley TL, Santerre‐Lemmon LE, Shamy JL, Skaggs WE, Buonocore MH, Rapp PR, Barnes CA (2008): Age‐related regional network of magnetic resonance imaging gray matter in the rhesus macaque. J Neurosci 28: 2710–2718. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Asanuma K, Ma Y, Huang C, Carbon M, Edwards C, Raymond D, Bressman S, Moeller JR, Eidelberg D (2005): The metabolic pathology of dopa‐responsive dystonia. Ann Neurol 57: 596–600. [DOI] [PubMed] [Google Scholar]
  4. Asanuma K, Tang C, Ma Y, Dhawan V, Mattis P, Edwards C, Kaplitt MG, Feigin A, Eidelberg D (2006): Network modulation in the treatment of Parkinson's disease. Brain 129: 2667–2678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ashburner J, Friston KJ (1999): Nonlinear spatial normalization using basis functions. Hum Brain Mapp 7: 254–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ashburner J, Neelin P, Collins DL, Evans A, Friston K (1997): Incorporating prior knowledge into image registration. Neuroimage 6: 344–352. [DOI] [PubMed] [Google Scholar]
  7. Asllani I, Habeck C, Scarmeas N, Borogovac A, Brown TR, Stern Y (2008): Multivariate and univariate analysis of continuous arterial spin labeling perfusion MRI in Alzheimer's disease. J Cereb Blood Flow Metab 28: 725–736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bergfield KL, Hanson KD, Chen K, Teipel SJ, Hampel H, Rapoport SI, Moeller JR, Alexander GE (2010): Age‐related networks of regional covariance in MRI gray matter: Reproducible multivariate patterns in healthy aging. Neuroimage 49: 1750–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bohnen NI, Koeppe RA, Minoshima S, Giordani B, Albin RL, Frey KA, Kuhl DE (2011): Cerebral glucose metabolic features of Parkinson disease and incident dementia: Longitudinal study. J Nucl Med 52: 848–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Brickman AM, Habeck C, Ramos MA, Scarmeas N, Stern Y (2008): A forward application of age associated gray and white matter networks. Hum Brain Mapp 29: 1139–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Caballol N, Marti MJ, Tolosa E (2007): Cognitive dysfunction and dementia in Parkinson disease. Mov Disord 22 (Suppl 17): S358–S366. [DOI] [PubMed] [Google Scholar]
  12. Chen K, Reiman EM, Alexander GE, Bandy D, Renaut R, Crum WR, Fox NC, Rossor MN (2004): An automated algorithm for the computation of brain volume change from sequential MRIs using an iterative principal component analysis and its evaluation for the assessment of whole‐brain atrophy rates in patients with probable Alzheimer's disease. Neuroimage 22: 134–143. [DOI] [PubMed] [Google Scholar]
  13. Eckert T, Van Laere K, Tang C, Lewis DE, Edwards C, Santens P, Eidelberg D (2007): Quantification of Parkinson's disease‐related network expression with ECD SPECT. Eur J Nucl Med Mol Imaging 34: 496–501. [DOI] [PubMed] [Google Scholar]
  14. Eckert T, Tang C, Ma Y, Brown N, Lin T, Frucht S, Feigin A, Eidelberg D (2008): Abnormal metabolic networks in atypical parkinsonism. Mov Disord 23: 727–733. [DOI] [PubMed] [Google Scholar]
  15. Eidelberg D (2009): Metabolic brain networks in neurodegenerative disorders: A functional imaging approach. Trends Neurosci 32: 548–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Eidelberg D, Moeller JR, Dhawan V, Spetsieris P, Takikawa S, Ishikawa T, Chaly T, Robeson W, Margouleff D, Przedborski S, et al (1994): The metabolic topography of parkinsonism. J Cereb Blood Flow Metab 14: 783–801. [DOI] [PubMed] [Google Scholar]
  17. Feigin A, Fukuda M, Dhawan V, Przedborski S, Jackson‐Lewis V, Mentis MJ, Moeller JR, Eidelberg D (2001): Metabolic correlates of levodopa response in Parkinson's disease. Neurology 57: 2083–2088. [DOI] [PubMed] [Google Scholar]
  18. Feigin A, Antonini A, Fukuda M, De Notaris R, Benti R, Pezzoli G, Mentis MJ, Moeller JR, Eidelberg D (2002): Tc‐99m ethylene cysteinate dimer SPECT in the differential diagnosis of parkinsonism. Mov Disord 17: 1265–1270. [DOI] [PubMed] [Google Scholar]
  19. Feigin A, Kaplitt MG, Tang C, Lin T, Mattis P, Dhawan V, During MJ, Eidelberg D (2007a): Modulation of metabolic brain networks after subthalamic gene therapy for Parkinson's disease. Proc Natl Acad Sci USA 104: 19559–19564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Feigin A, Tang C, Ma Y, Mattis P, Zgaljardic D, Guttman M, Paulsen JS, Dhawan V, Eidelberg D (2007b): Thalamic metabolism and symptom onset in preclinical Huntington's disease. Brain 130(Pt 11): 2858–2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Friston K (2007): Statistical Parametric Mapping: The Analysis of Functional Brain Images. London:Academic Press. [Google Scholar]
  22. Fukuda M, Mentis MJ, Ma Y, Dhawan V, Antonini A, Lang AE, Lozano AM, Hammerstad J, Lyons K, Koller WC, et al. (2001): Networks mediating the clinical effects of pallidal brain stimulation for Parkinson's disease: A PET study of resting‐state glucose metabolism. Brain 124(Pt 8): 1601–1609. [DOI] [PubMed] [Google Scholar]
  23. Habeck C, Hilton HJ, Zarahn E, Flynn J, Moeller J, Stern Y (2003): Relation of cognitive reserve and task performance to expression of regional covariance networks in an event‐related fMRI study of nonverbal memory. Neuroimage 20: 1723–1733. [DOI] [PubMed] [Google Scholar]
  24. Habeck C, Foster NL, Perneczky R, Kurz A, Alexopoulos P, Koeppe RA, Drzezga A, Stern Y (2008): Multivariate and univariate neuroimaging biomarkers of Alzheimer's disease. Neuroimage 40: 1503–1515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hirano S, Asanuma K, Ma Y, Tang C, Feigin A, Dhawan V, Carbon M, Eidelberg D (2008): Dissociation of metabolic and neurovascular responses to levodopa in the treatment of Parkinson's disease. J Neurosci 28: 4201–4209. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hsu JL, Jung TP, Hsu CY, Hsu WC, Chen YK, Duann JR, Wang HC, Makeig S (2007): Regional CBF changes in Parkinson's disease: A correlation with motor dysfunction. Eur J Nucl Med Mol Imaging 34: 1458–1466. [DOI] [PubMed] [Google Scholar]
  27. Huang C, Mattis P, Tang C, Perrine K, Carbon M, Eidelberg D (2007a): Metabolic brain networks associated with cognitive function in Parkinson's disease. Neuroimage 34: 714–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Huang C, Tang C, Feigin A, Lesser M, Ma Y, Pourfar M, Dhawan V, Eidelberg D (2007b): Changes in network activity with the progression of Parkinson's disease. Brain 130(Pt 7): 1834–1846. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Huang C, Mattis P, Perrine K, Brown N, Dhawan V, Eidelberg D (2008): Metabolic abnormalities associated with mild cognitive impairment in Parkinson disease. Neurology 70(16 Pt 2): 1470–1477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Joliffe IT (2002): Springer Series in Statistics: Principal Components Analysis, 2nd ed. New York:Springer‐Verlag. [Google Scholar]
  31. Kerrouche N, Herholz K, Mielke R, Holthoff V, Baron JC (2006): 18FDG PET in vascular dementia: Differentiation from Alzheimer's disease using voxel‐based multivariate analysis. J Cereb Blood Flow Metab 26: 1213–1221. [DOI] [PubMed] [Google Scholar]
  32. Lewitt PA, Rezai AR, Leehey MA, Ojemann SG, Flaherty AW, Eskandar EN, Kostyk SK, Thomas K, Sarkar A, Siddiqui MS, et al. (2011): AAV2‐GAD gene therapy for advanced Parkinson's disease: A double‐blind, sham‐surgery controlled, randomised trial. Lancet Neurol 10: 309–319. [DOI] [PubMed] [Google Scholar]
  33. Lozza C, Baron JC, Eidelberg D, Mentis MJ, Carbon M, Marie RM (2004): Executive processes in Parkinson's disease: FDG‐PET and network analysis. Hum Brain Mapp 22: 236–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Ma Y, Tang C, Spetsieris PG, Dhawan V, Eidelberg D (2007): Abnormal metabolic network activity in Parkinson's disease: Test‐retest reproducibility. J Cereb Blood Flow Metab 27: 597–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Ma Y, Peng S, Flores J, Cornfeldt M, Mitrovic B, Eidelberg D, Doudet DJ (2008): Abnormal metabolic brain network in parkinsonian macaques: Modulation by retinal pigment epithelial (RPE) cell implantation. Neurology 71: 154–155 [abstract]. [Google Scholar]
  36. Ma Y, Tang C, Moeller JR, Eidelberg D (2009): Abnormal regional brain function in Parkinson's disease: Truth or fiction? Neuroimage 45: 260–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Ma Y, Huang C, Dyke JP, Pan H, Alsop D, Feigin A, Eidelberg D (2010): Parkinson's disease spatial covariance pattern: Noninvasive quantification with perfusion MRI. J Cereb Blood Flow Metab 30: 505–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ma Y, Peng S, Spetsieris PG, Sossi V, Eidelberg D, Doudet DJ (2012): Abnormal metabolic brain networks in a nonhuman primate model of parkinsonism. J Cereb Blood Flow Metab 32: 633–642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Mattis PJ, Tang CC, Ma Y, Dhawan V, Eidelberg D (2011): Network correlates of the cognitive response to levodopa in Parkinson disease. Neurology 77: 858–865. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Melzer TR, Watts R, MacAskill MR, Pearson JF, Rueger S, Pitcher TL, Livingston L, Graham C, Keenan R, Shankaranarayanan A, et al. (2011): Arterial spin labelling reveals an abnormal cerebral perfusion pattern in Parkinson's disease. Brain 134(Pt 3): 845–855. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Mentis MJ, McIntosh AR, Perrine K, Dhawan V, Berlin B, Feigin A, Edwards C, Mattis P, Eidelberg D (2002): Relationships among the metabolic patterns that correlate with mnemonic, visuospatial, and mood symptoms in Parkinson's disease. Am J Psychiatry 159: 746–754. [DOI] [PubMed] [Google Scholar]
  42. Moeller JR, Strother SC (1991): A regional covariance approach to the analysis of functional patterns in positron emission tomographic data. J Cerebral Blood Flow Metab 11: A121–A135. [DOI] [PubMed] [Google Scholar]
  43. Moeller JR, Ishikawa T, Dhawan V, Spetsieris P, Mandel F, Alexander GE, Grady C, Pietrini P, Eidelberg D (1996): The metabolic topography of normal aging. J Cereb Blood Flow Metab 16: 385–398. [DOI] [PubMed] [Google Scholar]
  44. Moeller JR, Nakamura T, Mentis MJ, Dhawan V, Spetsieres P, Antonini A, Missimer J, Leenders KL, Eidelberg D (1999): Reproducibility of regional metabolic covariance patterns: Comparison of four populations. J Nucl Med 40: 1264–1269. [PubMed] [Google Scholar]
  45. Mure H, Hirano S, Tang CC, Isaias IU, Antonini A, Ma Y, Dhawan V, Eidelberg D (2011): Parkinson's disease tremor‐related metabolic network: Characterization, progression, and treatment effects. Neuroimage 54: 1244–1253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Niethammer M, Eidelberg D (2012): Metabolic brain networks in translational neurology: Concepts and applications. Ann Neurol 72: 635–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Petersson KM, Nichols TE, Poline JB, Holmes AP (1999): Statistical limitations in functional neuroimaging. I. Non‐inferential methods and statistical models. Philos Trans R Soc Lond B Biol Sci 354: 1239–1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Poston KL, Eidelberg D (2009): Network biomarkers for the diagnosis and treatment of movement disorders. Neurobiol Dis 35: 141–147. [DOI] [PubMed] [Google Scholar]
  49. Scarmeas N, Habeck CG, Zarahn E, Anderson KE, Park A, Hilton J, Pelton GH, Tabert MH, Honig LS, Moeller JR, et al. (2004): Covariance PET patterns in early Alzheimer's disease and subjects with cognitive impairment but no dementia: Utility in group discrimination and correlations with functional performance. Neuroimage 23: 35–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Spetsieris PG, Eidelberg D (2011): Scaled subprofile modeling of resting state imaging data in Parkinson's disease: Methodological issues. Neuroimage 54: 2899–2914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Spetsieris P, Ma Y, Dhawan V, Moeller JR, Eidelberg D (2006): Highly automated computer‐aided diagnosis of neurological disorders using functional brain imaging. Proc SPIE: Med Imag 6144: 5M1–5M12. [Google Scholar]
  52. Spetsieris PG, Ma Y, Dhawan V, Eidelberg D (2009): Differential diagnosis of parkinsonian syndromes using PCA‐based functional imaging features. Neuroimage 45: 1241–1252. [DOI] [PubMed] [Google Scholar]
  53. Tang CC, Poston KL, Eckert T, Feigin A, Frucht S, Gudesblatt M, Dhawan V, Lesser M, Vonsattel JP, Fahn S, et al. (2010): Differential diagnosis of parkinsonism: A metabolic imaging study using pattern analysis. Lancet Neurol 9: 149–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Trost M, Carbon M, Edwards C, Ma Y, Raymond D, Mentis MJ, Moeller JR, Bressman SB, Eidelberg D (2002): Primary dystonia: Is abnormal functional brain architecture linked to genotype? Ann Neurol 52: 853–856. [DOI] [PubMed] [Google Scholar]
  55. Trost M, Su S, Su P, Yen RF, Tseng HM, Barnes A, Ma Y, Eidelberg D (2006): Network modulation by the subthalamic nucleus in the treatment of Parkinson's disease. Neuroimage 31: 301–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Zuendorf G, Kerrouche N, Herholz K, Baron JC (2003): Efficient principal component analysis for multivariate 3D voxel‐based mapping of brain functional imaging data sets as applied to FDG‐PET and normal aging. Hum Brain Mapp 18: 13–21. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information Figure 1. Reliability at each voxel for the PDRP and the PDCP networks from FDG PET images normalized by spm99. Both maps represent the inverse coefficient of variation (ICV) thesholded at p < 0.005 following a voxelwise bootstrapping estimation algorithm (1000 iterations) over the whole brain (Habeck, et al. 2003). [The displays are on a standard single‐subject MRI brain template and represent voxels that are reliable from the bootstrapping estimation algorithm. Red/blue colors indicate brain regions with concurrently increased/decreased covariation between regional glucose metabolism.]

Click here for additional data file. (3.1MB, tif)

Supporting Information Figure 2. Correlations between region‐weights and subject scores of the PDRP or PDCP networks from FDG PET images normalized by spm99 and spm5. Regression analyses revealed that the region‐weights of the PDRP were highly correlated with each other between the two versions of SPM normalization program (A); the subject scores of the PDRP were also significantly correlated with each other in the 20 PD patients in the derivation sample (B) and in the 13 PD patients in the validation sample (C). The strong correlations were also evident for the PDCP between the region‐weights (D) and subject scores in the 15 PD patients in the derivation sample (E) and in the 15 PD patients in the validation sample (F). These results were highly equivalent between images normalized by the four versions of SPM program (see text).

Click here for additional data file. (7.3MB, tif)

Supporting Information Figure 3. Behavioral correlations by subject scores of the PDCP networks from FDG PET images normalized by spm99 and spm5. In both cases, subject scores were negatively correlated with individual values of California Verbal Learning Test (CVLT) in the 15 PD patients in the original derivation sample (A, C) and in the 15 PD patients in the validation sample (B, D). The performance figures by the subject scores of the PDCP in both derivation sample and validation sample are highly equivalent between images normalized by the four versions of SPM program (see text).

Click here for additional data file. (6MB, tif)

Supporting Information Figure 4. Correlations between subject scores of the PRDR/PDCP networks from FDG PET images acquired with five different PET scanners and normalized by spm99 and spm5. Regression analyses revealed that subject scores of the PDRP (A) and the PDCP (B) in an independent validation sample of PD patients were significantly correlated between two versions of SPM normalization program, regardless of technical differences in PET cameras and image reconstruction methods.

Click here for additional data file. (4.4MB, tif)

Supporting Information Table

Click here for additional data file. (66KB, doc)

Supporting Information Cover Letter

Click here for additional data file. (1.8MB, doc)

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES