An Exponential Decay Model for Mediation

Abstract

Mediation analysis is often used to investigate mechanisms of change in prevention research. Results finding mediation are strengthened when longitudinal data are used because of the need for temporal precedence. Current longitudinal mediation models have focused mainly on linear change, but many variables in prevention change nonlinearly across time. The most common solution to nonlinearity is to add a quadratic term to the linear model, but this can lead to the use of the quadratic function to explain all nonlinearity, regardless of theory and the characteristics of the variables in the model. The current study describes the problems that arise when quadratic functions are used to describe all nonlinearity and how the use of nonlinear functions, such as exponential decay, addresses many of these problems. In addition, nonlinear models provide several advantages over polynomial models including usefulness of parameters, parsimony, and generalizability. The effects of using nonlinear functions for mediation analysis are then discussed and a nonlinear growth curve model for mediation is presented. An empirical example using data from a randomized intervention study is then provided to illustrate the estimation and interpretation of the model. Implications, limitations, and future directions are also discussed.

Not all relations in prevention research are linear, especially when modeling change across time. For example, in a longitudinal study of three classroom reading programs for 1^st and 2^nd graders, vocabulary changed linearly, but word reading changed quadratically (Foorman, Francis, Fletcher, Schatschneider, & Mehta, 1998). Ma and McClintock (2011) showed that taxable retail sales following a statewide smoking ban grow quadratically. And a longitudinal study of youth found the prevalence of both free-time and organized physical activity participation was quadratic for boys (Wall, Carlson, Stein, Lee, & Fulton, 2011).

Despite numerous nonlinear relations in prevention, linear (i.e., first-order polynomial) models are the default with which most researchers begin analyzing their data, including mediation models. Mediation occurs when the effect of a variable, X, on a second variable, Y, is transmitted through a third variable, M. The linear single mediator model can be represented using three ordinary-least-squares (OLS) regression equations

$$Y_i={\beta }_0+{cX}_i+r_i$$ (1)

$$M_i={\beta }_0+{aX}_i+r_i$$ (2)

$$Y_i={\beta }_0+c^{\prime }{X}_i+{bM}_i+r_i$$ (3)

where c is the total effect of X on Y, c′ is the direct effect of X on Y controlling for M, a is the effect of X on M, b is the effect of M on Y controlling for X, and ab is the mediated effect. One of the primary assumptions of the single mediator model, however, states that in order to produce unbiased estimates of a, b, and c′, the relations between X, M, and Y must be correctly specified (MacKinnon, 2008). This means that Equations 1 through 3 only give unbiased estimates of a, b, and c′ if the relations between X, M, and Y are in fact linear.

The Problem with Polynomials

When a nonlinear relation is present, a higher-order polynomial function can be used to model the nonlinearity. Higher-order polynomial functions are created by adding new terms to the linear model. For example, if the relation between M and X was quadratic (i.e., second-order; shown in Figure 1), then Equation 2 could be rewritten to capture this relation as

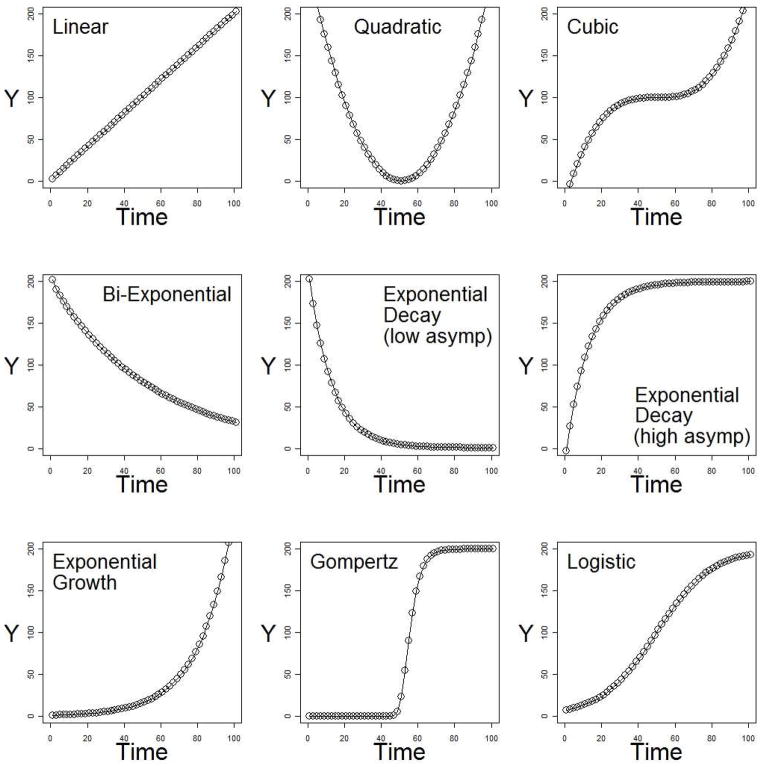
Figure 1.

The top three panels show common polynomial trajectories and the bottom six panels show common nonlinear trajectories.

$$M_i={\beta }_0+{\beta }_1{X}_i+{\beta }_2{X}_i^2+r_i$$ (4)

where β₀, β₁, and β₂ are the intercept, linear, and quadratic terms. If β₂ is significant, then there is second-order curvature in the relation between X and M. If there is no second-order curvature in the relation, then β₂ should be nonsignificant, but higher-order curvature could exist.

Cohen, Cohen, West, and Aiken (2003) state that the selection and testing of polynomial models should be based on theory, unless the analysis is exploratory, and that most theories in the social sciences can only support linear, quadratic, or cubic (i.e., third-order) relations. When nonlinearity in the relation between two variables present but the exact form is unknown, the appropriate polynomial is selected by adding higher-order terms until a nonsignificant term is found. Then the nonsignificant term is dropped and the previous model is used. For example, if β₂ in Equation 4 was significant, but a cubic term (i.e., β₃X³) added to the model was not, then the quadratic model would be used. Selecting models in this way, independent of theory, creates several problems. First, other even higher-order terms (e.g., β₄X⁴) may be significant. Second, unnecessary terms increase the probability of making a Type I error, while each additional term decreases in descriptive value; fourth-order and higher terms likely have little bearing on theory (Pinheiro & Bates, 2000). Third, highly-ordered polynomials can over fit the model to the original sample creating problems with cross-validation.

The largest problem with using polynomials to model nonlinearity, however, is that a quadratic model is often selected regardless of the variables being examined or the underlying theory. The reason for the dominance of the quadratic function is its ability to describe many different types of nonlinearity in addition to true quadratic relations. For instance, a quadratic model can be used to model many of the functions, or at least pieces of the functions, illustrated in Figure 1 such as the exponential, bi-exponential, and logistic functions. Because of this, quadratic has become synonymous with nonlinear and curvilinear for some researchers who may even use these terms interchangeably. The consequence is that quadratic models are being used to describe any deviation from linearity, regardless of theory. Although the quadratic function is versatile at describing nonlinearity, Cohen et al. (2003) “caution that polynomial equations may be only approximations to nonlinear relations” (p. 198). This means that while quadratic relations do exist, the quadratic function may only be an approximation for other relations that are better described by nonpolynomial functions.

Selecting the correct function to model nonlinearity is especially important for mediation models because of temporal precedence, another primary assumption of mediation where X must precede M and M must precede Y in time (MacKinnon, 2008). This means that in addition to meeting the assumption that the shape of the relations between X, M, and Y are correct, the change of X, M, and Y across time must also be correctly specified for the estimates of a, b, and c′ to be unbiased. Therefore, even when the selected model performs approximately as well as the true model, as the quadratic function does in the left panel of Figure 2, the estimates of the mediation parameters will still be biased. The true model can never be known, but theory, the characteristics of the variable in question, and the observed data should all be used to eliminate obviously incorrect models and to aid in selecting the model that gives the most unbiased estimates of the mediation parameters. Theory and the characteristics of the variables must also be used to address the assumption that X, M, and Y are measured at the correct times. For more on assumptions of the single mediator model see MacKinnon (2008).

Figure 2.

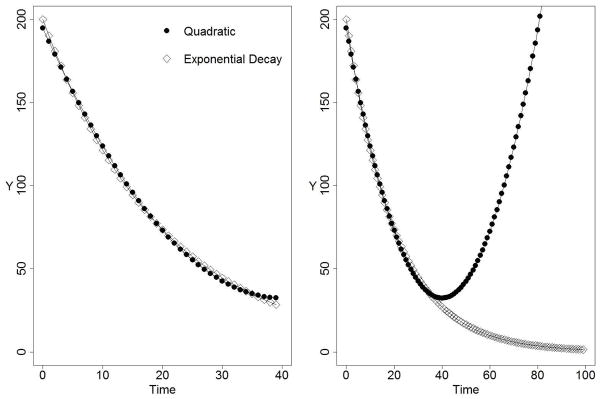
The left panel shows how over a short time span a quadratic function and an exponential decay function can be approximately equivalent. The right panel shows that over a longer time span an exponential decay function approaches an asymptote while the quadratic function approaches infinity.

Nonpolynomial Nonlinear Functions

In order to discuss mediation models that use nonpolynomial functions to model nonlinearity, a distinction needs to be made between nonlinear relations that can be described by polynomials and those that cannot. All polynomials, such as the quadratic function in Equation 4, are linear in the parameters, which means that the criterion score is equal to the sum of the predictors, each multiplied by a corresponding coefficient, and a residual (Cohen et al., 2003). This is why polynomials are often referred to as curvilinear models. Here the term nonlinear refers to functions that are not linear in the parameters such as the exponential decay function

$$Y_i={\beta }_2+({\beta }_0-{\beta }_2)exp[{\beta }_{1}t]+r_i$$ (5)

where t is time, β₀ is the initial value at t = 0, β₂ is the asymptote as t goes to infinity, and β₁, constrained to be less than zero, is the rate of change or how quickly the process decays from the initial value to the asymptote (Browne, 1993).

In addition to avoiding many of the problems associated with polynomial models, nonlinear models offer several other advantages. First, nonlinear models can be more parsimonious. Pinheiro and Bates (2000, pp. 274–275) show that for the same data, the fit of a logistic model and a fifth-order polynomial can be almost identical, but the logistic model has three parameters and the polynomial model has six. Parsimony also means that the nonlinear functions can often be estimated using fewer time points. For example, the exponential decay function can be estimated from as few as three time points, though using only three time points would cause the model to fit the data perfectly so more time points are preferred.

Second, nonlinear models often have parameters that are more useful for prevention scientists because they are mechanistic, meaning they are based on the physical or theoretical traits of the variables. For example, the three parameters in the exponential decay function are likely more useful for a prevention researcher than the three parameters in a quadratic function. Third, nonlinear functions can also improve generalizability by providing more realistic descriptions of constructs or behaviors. Figure 2 shows a quadratic function plotted against an exponential decay function. Over a short time span, the functions give similar predicted scores. But as time continues, the quadratic function changes direction and grows to infinity, while the exponential decay function approaches an asymptote. This illustrates the point that polynomials may only approximate the true nonlinear function. Few variables in prevention can realistically be hypothesized to approach infinity, so a nonlinear function is more realistic than a polynomial function in most circumstances. Even with nonlinear models, however, extrapolating beyond the range of the observed data is not advisable.

Selecting a Nonlinear Function

Nonlinear functions, several of which are illustrated in Figure 1, may be unfamiliar to researchers, but many variables in prevention are hypothesized to change nonlinearly. For example, the Gompertz function can model the growth of cancerous tumors (d’Onofrio, 2005). The biexponential function has been used to describe the relationship between drug concentration following an injection and time (Gibaldi & Perrier, 1982). And Zhang, Zhang, Li, Small, and Wang (2011) used nonlinear models to examine willingness to be vaccinated based on perceived probability of being infected. With so many nonlinear functions available, selecting an appropriate function requires consideration of theory, the observed data, and the characteristics of the different nonlinear functions. Exponential decay was selected here based on its general usefulness in modeling behavioral and psychological variables following an intervention. This is illustrated using data from the Athletes Training and Learning to Avoid Steroids (ATLAS; Goldberg et al., 2000) program. ATLAS, based on Social Learning Theory (Bandura, 1977), the Health Beliefs Model (Janz & Becker, 1984), and the Theory of Planned Action (Fishbein & Azjen, 1975), is designed to decrease anabolic steroid use in high school football players because of an increased risk of steroids use compared to other student athletes.

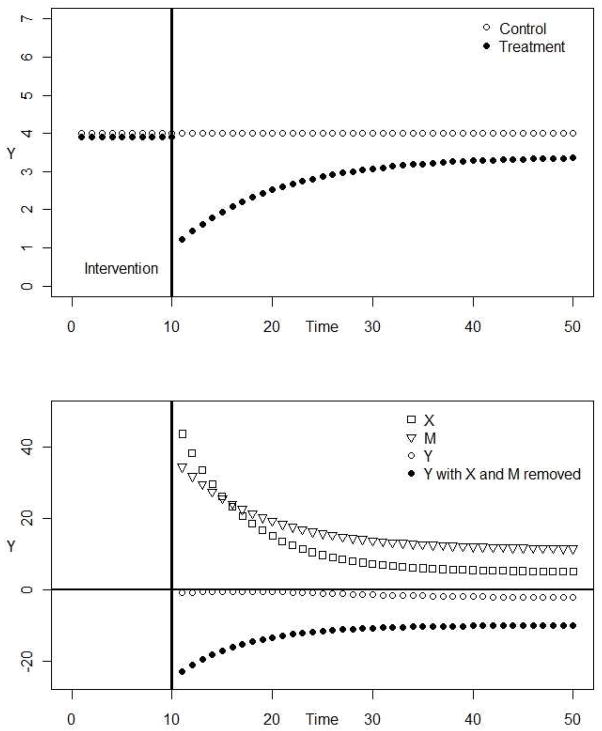
Consider a proposed mediator that ATLAS was designed to decrease, beliefs in media advertisements related to products designed to increase muscle mass and strength. Beliefs in media ads is equal to the mean of three 7-point scale items where higher scores indicate higher beliefs (e.g., I think that most products advertised in muscle magazines do what they claim to do) and had reliabilities of .746 or higher (MacKinnon et al., 2001). If ATLAS was effective, beliefs in media ads would be lower for students in the intervention condition immediately after the program than their pre-intervention level or the control group. The effect could diminish, however, with continued exposure to media ads without the continued benefit of the program as illustrated in the top of Figure 3.

Figure 3.

The top panel shows a treatment extinguishing over time to a level below the control group, which stays at the same level. In the bottom panel, Y appears to have a slightly negative linear trajectory until X and M are partialled out to reveal Y decays exponentially.

The theoretical reasoning for using the exponential decay function was supported by plotting belief in media ads for individual students which showed a proportion of students who received the ATLAS program had beliefs that dropped immediately following completion of the program but decayed back towards the pre-intervention level across time. Individuals in the control group, however, remained unchanged. Based on theory and the plots, most of the functions in Figure 1 can be eliminated including the linear, exponential growth, Gompertz, and logistic functions. The quadratic and cubic functions could still be used, but the quadratic implies that after leveling off beliefs would then begin to decrease to infinity and the cubic model implies that after leveling off, beliefs would begin to increase towards infinity.

Another reason to use the exponential decay function is the usefulness of the parameters. Using Equation 5 and the ATLAS example with t = 0 immediately after completion of the intervention, β₀ is belief in media ads immediately after the intervention, β₂ is belief in media ads expected to be continued in the long-term, and β₁ is how quickly students move between these two values. These values are likely more useful to a researcher than the parameters from a polynomial model. In addition, given the decay found in beliefs, a researcher would be interested in whether the intervention group maintained a lower level of beliefs in the long term, as illustrated in the top of Figure 3, or returned to the level of the control group. This could be tested using the exponential decay function by adding intervention group as a predictor of the asymptote value using a mixed effects model, which is described below. Finally, the exponential decay function was chosen because a variable can decay exponentially while appearing to change linearly. The bottom panel of Figure 3 shows the plots for the variables in a mediation model with a continuous X where the outcome variable Y appears to change linearly. When X and M are partialled out of Y, however, it can be seen that Y decays exponentially.

Exponential Decay Growth Curve Models

Polynomial growth can be modeled using a mixed effects growth curve model where Level 1 accounts for the variation of scores within a person and Level 2 accounts for the variation of scores between persons. The growth curve model for a quadratic function is

$$\begin{array}{ll}\text{Level}1:\hfill & Y_{it}={\beta }_{0i}+{\beta }_{1i}t+{\beta }_{2i}{t}^2+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+u_{2i}\hfill \end{array}$$ (6)

where t is time, and β_0i, β_1i, and β_2i are interpreted as in Equation 4, but are allowed to vary between persons using random effects, u_ji (Raudenbush & Bryk, 2002). Time-varying predictors are added to Level 1 to explain variance in the residual, r_it, and time-invariant predictors are added to Level 2 to explain variance in the u_ji’s. Polynomial growth curves are estimated using software such as MIXED (SAS Institute, 2012) and LME (R Core Development Team, 2012) which provide several indices of model fit including the −2 log likelihood (−LL), the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC).

Adapting notation from Raudenbush and Bryk (2002), Equation 6 can be rewritten for any nonlinear function by replacing the Level 1 equation with the appropriate nonlinear function (Davidian & Giltinan, 1995). The growth curve model for exponential decay is

$$\begin{array}{ll}\text{Level}1:\hfill & Y_{it}={\beta }_{2i}+({\beta }_{0i}-{\beta }_{2i})\ast exp[{\beta }_{1i}\ast t]+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+u_{2i}\hfill \end{array}$$ (7)

where t, β_0i, β_1i, and β_2i are interpreted as in Equation 5, while the u_ji‘s, and r_it are interpreted as in Equation 6. Predictors added at Level 2 would predict the initial value, asymptote, and rate of change of Y. As in the linear case, it is assumed that observations between persons are independent, the random effects are distributed ~ N(0, τ), the within person variances are independent of the random effects, and the within person variances are independent and distributed ~ N(0, σ²), though this assumption can be relaxed (Pinheiro & Bates, 2000). In the nonlinear case, most additional predictors are assumed to still have a linear relation with the criterion at the level in which they are entered, but nonlinear relations may be included at either level. Nonlinear growth curve models are estimated using software such as NLMIXED (SAS Institute, 2012) and NLME (R Core Development Team, 2012) which also provide the −2LL, AIC, and BIC indices of model fit.

Exponential Decay Mediation Models

An exponential decay mediation model requires changing Equations 2 and 3 to the form of Equation 7. When M decays exponentially, but X is time-invariant, such as random assignment to an intervention or control group, then Equation 2 becomes

$$\begin{array}{ll}\text{Level}1:\hfill & M_{it}={\beta }_{2i}+({\beta }_{0i}-{\beta }_{2i})exp[{\beta }_{1i}t]+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+a_0{X}_i+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+a_1{X}_i+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+a_2{X}_i+u_{2i}\hfill \end{array}$$ (8)

If X is coded [0,1], then γ₀₀, γ₁₀, and γ₂₀ are estimates of the initial value, the rate of change, and asymptote of M for the group coded 0 and a₀, a₁, and a₂ are the differences in the initial value, rate of change, and asymptote between the two groups in X.

There are several ways in which Equation 3 can be specified. If M is time-varying then it can be added at Level 1 as in Equation 9

$$\begin{array}{ll}\text{Level}1:\hfill & Y_{it}={\beta }_{2i}+({\beta }_{0i}-{\beta }_{2i})exp[{\beta }_{1i}{t}_i]+b_i{M}_{it}+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+{c^{\prime }}_0{X}_i+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+{c^{\prime }}_1{X}_i+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+{c^{\prime }}_2{X}_i+u_{2i}\hfill \\ \hfill & b_i={\gamma }_{30}\hfill \end{array}$$ (9)

where b_i is the average relation across time between M and Y at each corresponding time point, partialling out the effect of time (i.e., the exponential decay of Y). MacKinnon (2008) calls this a 2 → 1 → 1 model because X is in Level 2 while M and Y are in Level 1. If X is coded [0,1], γ₀₀, γ₁₀, and γ₂₀ are estimates of the initial value, rate of change, and asymptote of Y for the group coded 0, partialling out the effect of M and time, and c’₀, c’₁, and c’₂ are the differences in the initial value, rate of change, and asymptote between the two groups in X, partialling out the effect of M and time. Here, b_i is a fixed effect, but a random effect, u_3i, could be added; it would not change the interpretation of b_i, but it does indicate that the effect differs among persons. Similarly, if a Level 2 predictor was added that predicted b_i this would create a cross-level interaction between that predictor and M, meaning the predictor of b_i is a moderator of the effect of M on Y. For more information on moderation of a mediated effect see Fairchild and MacKinnon (2009).

Equation 9 violates the temporal precedence assumption because M predicts Y at the same time point. To address this, a lag could be introduced such that M predicts Y at a later time point. With a lag of one wave, M_it would change to M_i(t−1) and M would predict Y at the next time point. Then b_i would be the average relation across time between M at t and Y at (t + 1), partialling out the effect of time. Equal spacing is not an assumption of the model, but when the measurements are not equally spaced and the effect of M is lagged, then b_i represents the average effect of M across the different time lags. A specific value of M could also be entered as a Level 2 predictor of Y. For example, if X had a significant effect on the initial value of M, a₀ in Equation 8, which in turn predicted the rate of change and asymptote of Y, β_1i and β_2i in Equation 9, then the effect of X on the rate of change and asymptote of Y would be mediated through its initial effect on M. This does not completely satisfy temporal precedence since the initial value of Y is used to estimate the rate of change and asymptote of Y, but it does make a stronger case for mediation than in Equation 9.

When X is time-varying, it can be entered into Equations 8 and 9 using any of the three methods described for M. That is, X could be entered as a time-varying Level 1 predictor that predicted M and Y at the same time point, X_it, where the Level 1 parameter a_i is the average effect of X on M at each time point partialling out time and the Level 1 parameter c’_i is the average effect of X on Y at each time point partialling out M and time; as a time lagged Level 1 predictor, X_i(t−1), where a_i is the average effect of X on M at the next time point partialling out time and c’_i is the average effect of X on Y at the next time point partialling out M and time; or a specific value of X could be included as a Level 2 predictor. Random effects could be included at Level 2 for a_i, and c’_i if desired. However, entering X into Level 1 presents the same cross-level interaction issues for a_i and c’_i as previously described for b_i in Equation 9.

MacKinnon (2008) calls a model where X, M, and Y are all time-varying and entered at Level 1 a 1 → 1 → 1 model. Bauer, Preacher, and Gil (2006) list several assumptions for the linear 1 → 1 → 1 model that apply to the nonlinear case. First, the Level 1 residuals must be uncorrelated with each other and the random effects, within and across equations. Second, X and M must be uncorrelated with the random effects and residuals, within and across equations, though this assumption must be relaxed if either X or M is included at Level 2. The functional form assumption must now also be expanded to include correct relationships at each level of the model. For more information on mediation at different levels see Kenny, Korchmaros, and Bolger (2003), Krull and MacKinnon (2001), and Preacher, Zyphur, and Zhang (2010).

Although familiar, the causal steps approach (Baron & Kenny, 1986) can be difficult to extend to longitudinal models. For nonlinear longitudinal mediation models, two tests will be discussed: the joint significance test (MacKinnon, Lockwood, Hoffman, West, & Sheets, 2002) and the percentile bootstrap test (MacKinnon, Lockwood, & Williams, 2004; Shrout & Bolger, 2002). In the joint significance test, the a and b paths are tested for significance separately and if both are significant, then the mediated effect ab is significant. When X is time-invariant, as in Equation 8, the joint significance test becomes more complicated because there are now three separate effects of X on M, a₀, a₁, and a₂, each of which represents the effect of X on M. This means that three mediated effects can be estimated and tested, a₀b_i, a₁b_i, and a₂b_i, any or all of which may be of interest.

A criticism of the joint significance test is that the mediated effect ab is not directly tested. For linear mixed effects mediation models, a standard error can be computed for ab which can then be tested for significance (Bauer et al., 2006; Kenny et al., 2003), but ab is not normally distributed in most cases (MacKinnon et al., 2004). A method that does not assume normality of ab is the percentile bootstrap test which resamples from the original sample a large number of times with replacement. In each of the new bootstrap samples, ab is estimated and the estimates are ordered from smallest to largest creating an empirical distribution of ab. The values of the bootstrapped estimates of ab that correspond to the appropriate percentiles then form a confidence interval around the mediated effect. The bias-corrected bootstrap is a variation that has been shown to have higher power than the percentile bootstrap (e.g., Fritz & MacKinnon, 2007), but also elevated Type I error rates (Fritz, Taylor, & MacKinnon, 2012), so the percentile bootstrap will be used here. The percentile bootstrap can be implemented in software packages such as SAS and R, as well as Mplus (Muthen & Muthen, 2012).

An Empirical Example

The exponential decay mediation model is now illustrated using data from the ATLAS program (Goldberg et al., 2000). The data used here come from sophomores and juniors in the first cohort who had complete data for five measurements (N = 270): pre-intervention baseline (-3 months), at completion of the ATLAS program (0 months), and 9, 12, and 21 months after completion. Juniors graduating in the spring at month 18 were measured prior to graduation and these scores were used as their 21 month scores.

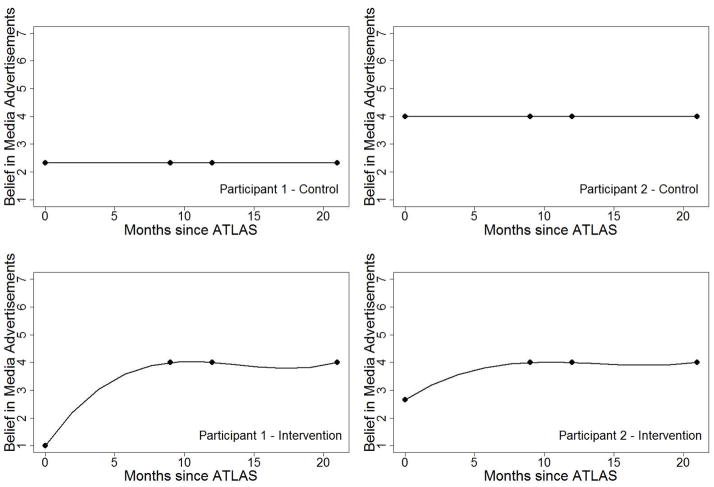
The relations of interest are the effect of the ATLAS program (X; Group: 0 = control, 1 = intervention) on intentions to use anabolic steroids (Y) through the mediator beliefs in media ads (M). Intentions to use anabolic steroids is equal to the mean of five 7-point scale items where higher scores indicate higher intent (e.g., I am curious to try anabolic steroids.) and had reliabilities of .918 or higher for the −3, 0, and 9 month measurements. Beliefs in media ads and intentions to use steroids were chosen because it was hypothesized that any program effects would decay slightly over time. In addition, plots showed a proportion of students in the ATLAS group had beliefs, shown in Figure 4, and intentions that appeared to decay exponentially while these variables showed no change for a proportion of those in the control group.

Figure 4.

Plots of beliefs in media advertisements against time with a loess line for four participants in ATLAS. The top two participants were in the control group, while the bottom two participants received the intervention.

Both the quadratic and bi-exponential functions could also be used to describe the nonlinearity shown in Figure 4. A bi-exponential function was not used because it is less parsimonious than exponential decay and the parameters is less useful for this example. The quadratic function does not make theoretical sense in this example because it is unlikely that the change in beliefs or intentions would change directions and grow towards infinity, especially since the variables are measured on a 7-point scale. Quadratic models were fit for statistical comparison, however, by replacing the Level 1 equation with a quadratic function. The AIC and BIC values indicated that the exponential decay models fit better than the quadratic models, as described, so the full results from the quadratic models are not presented.

The effect of ATLAS on beliefs in media ads controlling for the student’s pre-intervention baseline beliefs score were examined using the equation

$$\begin{array}{ll}\text{Level}1:\hfill & {\mathit{Perception}}_{it}={\beta }_{2i}+({\beta }_{0i}-{\beta }_{2i})\ast exp[{\beta }_{1i}\ast t]+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+a_0\ast {\mathit{Group}}_i+{\gamma }_{02}\ast {\mathit{BaseBelief}}_i+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+a_1\ast {\mathit{Group}}_i+{\gamma }_{12}\ast {\mathit{BaseBelief}}_i+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+a_2\ast {\mathit{Group}}_i+{\gamma }_{22}\ast {\mathit{BaseBelief}}_i+u_{2i}\hfill \end{array}$$ (10)

The effect of beliefs and ATLAS on intentions to use steroids was tested with two models. First, beliefs was added as a time-varying Level 1 predictor, while group was included at Level 2. In addition, baseline intentions was added as a predictor of the growth parameters β_0i, β_1i, and β_2i, and baseline beliefs was added as a predictor of b_i, in order to correct for pre-intervention differences. Baseline intentions was not added as a predictor of b_i because beliefs were hypothesized to change intentions, not the other way around, and baseline beliefs was not added as predictors of β_0i and β_1i because baseline differences were already being accounted for in b_i. The exception to this is the inclusion of baseline beliefs as a predictor of β_2i. This was necessary because including baseline beliefs as a predictor of b_i created a cross-level interaction between baseline beliefs and beliefs, necessitating the inclusion of baseline beliefs as a predictor of β_2i in order to include the lower order effect of baseline beliefs in the overall mixed effects model. A lagged approach was not used due to the unequal spacing of the measurements. No random effect was added to b_i because there was no reason to believe that this effect varied among individuals.

$$\begin{array}{ll}\text{Level}1:\hfill & {\mathit{Intent}}_{it}={\beta }_{2i}+({\beta }_{0i}-{\beta }_{2i})exp[{\beta }_{1i}{t}_t]+b_i{\mathit{Belieft}}_{i(t)}+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+{c^{\prime }}_0{\mathit{Group}}_i+{\gamma }_{02}\ast {\mathit{BaseIntent}}_i+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+{c^{\prime }}_1{\mathit{Group}}_i+{\gamma }_{12}\ast {\mathit{BaseIntent}}_i+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+{c^{\prime }}_2{\mathit{Group}}_i+{\gamma }_{22}\ast {\mathit{BaseIntent}}_i+{\gamma }_{23}\ast \mathit{BaseBelief}+u_{2i}\hfill \\ \hfill & b_i={\gamma }_{30}+{\gamma }_{31}\ast {\mathit{BaseBelief}}_i\hfill \end{array}$$ (11)

Second, the value of beliefs immediately following the intervention was included as a Level 2 predictor of β_0i, β_1i, and β_2i. Baseline intentions were included to correct for pre-intervention differences in the outcome variable.

$$\begin{array}{ll}\text{Level}1:\hfill & {\mathit{Intent}}_{it}={\beta }_{2i}+({\beta }_{0i}-{\beta }_{2i})exp[{\beta }_{1i}{t}_t]+r_{it}\hfill \\ \text{Level}2:\hfill & {\beta }_{0i}={\gamma }_{00}+{c^{\prime }}_0{\mathit{Group}}_i+{\gamma }_{02}\ast {\mathit{BaseIntent}}_i+b_0\ast {\mathit{Belief}}_{t=0,i}+u_{0i}\hfill \\ \hfill & {\beta }_{1i}={\gamma }_{10}+{c^{\prime }}_1{\mathit{Group}}_i+{\gamma }_{12}\ast {\mathit{BaseIntent}}_i+b_1\ast {\mathit{Belief}}_{t=0,i}+u_{1i}\hfill \\ \hfill & {\beta }_{2i}={\gamma }_{20}+{c^{\prime }}_2{\mathit{Group}}_i+{\gamma }_{22}\ast {\mathit{BaseIntent}}_i+b_2\ast {\mathit{Belief}}_{t=0,i}+u_{2i}\hfill \end{array}$$ (12)

All models were fit using NLMIXED, the variances of the random effects were freely estimated, and the covariances set to zero. Baseline beliefs (Mean = 2.72), baseline intentions (Mean = 1.63), and beliefs at 0 months (Mean = 2.39) were mean centered and group was coded [0,1].

The results for Equation 10, shown in Table 1, indicate that the control group’s initial, γ_00, and asymptote values, γ_20, are identical and the rate of change, γ₁₀, is not significantly different than zero, which matches the straight line for the control group individuals in Figure 4. The parameters a₀, a₁, and a₂ are the differences between the intervention and control group such that γ₀₀ + a₀, γ₁₀ + a₁, and γ₂₀ + a₂ are the initial value, rate of change, and asymptote of students receiving the intervention with the mean level of baseline beliefs. The results show that ATLAS decreased beliefs at 0 months and maintained these effects in the future. The fit indices showed that the exponential decay model (AIC = 3274.9, BIC = 3321.7) fit better than the quadratic model (AIC = 3329.3, BIC = 3340.1).

Table 1.

Results for the empirical example.

Equation 10		Equation 11		Equation 12
Parameter	Estimate (SE)	Parameter	Estimate (SE)	Parameter	Estimate (SE)
γ00	2.705** (0.072)	γ00	1.395** (0.086)	γ00	1.767** (0.055)
γ10	0.001 (0.006)	γ10	−0.030** (0.008)	γ10	−0.030** (0.010)
γ20	2.704** (0.075)	γ20	1.310** (0.089)	γ20	1.607** (0.077)
a0	−0.639** (0.138)	c’0	−0.106 (0.088)	c’0	−0.082 (0.091)
a1	−0.059 (0.042)	c’1	0.022** (0.007)	c’1	0.025** (0.009)
a2	−0.412* (0.189)	c’2	−0.146 (0.108)	c’2	−0.115 (0.101)
γ02	0.402** (0.042)	γ02	0.513** (0.043)	γ02	0.511** (0.043)
γ12	−0.004 (0.004)	γ12	−0.043** (0.010)	γ12	−0.024** (0.007)
γ22	0.396** (0.044)	γ22	0.300** (0.080)	γ22	0.328** (0.075)
		γ23	0.024 (0.018)	b0	0.225** (0.037)
		bi	0.147** (0.026)	b1	−0.012 (0.006)
		γ31	0.046** (0.012)	b2	0.148** (0.048)
σ2	0.808** (0.044)	σ2	0.559** (0.032)	σ2	0.558** (0.033)
τ00	0.579** (0.098)	τ00	0.208** (0.045)	τ00	0.230** (0.054)
τ11	0.240 (0.628)	τ11	0.199 (0.231)	τ11	0.128 (0.126)
τ22	0.327 (0.653)	τ22	1.827** (0.541)	τ22	1.252 (0.674)

Note. σ² is the Level 1 residual variance estimate, τ₀₀, τ₁₁, and τ₂₂ are the Level 2 random effect variance estimates for the initial value, rate of change, and asymptote, respectively.

^*p < .05.

^**p < .01.

The results for Equation 11 show that beliefs in media ads, b_i, is a significant predictor of intentions at the same time point when the effect of group and baseline intentions are partialled out. The effect of baseline beliefs is significant as well meaning this effect is stronger for students whose pre-intervention beliefs in media ads were higher. Using the joint significance test, a₀b_i and a₂b_i are significant, but a₁b_i is not, meaning that students who received ATLAS were lower than the control group in believing media ads at 0 month and at asymptote, and these changes predicted a student’s intentions to use steroids at the same time point. The model fit indices showed that the exponential decay model (AIC = 2929.5, BIC = 2987.1) fit better than the quadratic model (AIC = 3062.1, BIC = 3072.9).

The results for Equation 12 show that beliefs in media ads immediately after the intervention significantly predicted intentions to use steroids at 0 months and the asymptote such that an increase in beliefs was related to an increase in intentions. Using the joint significance test, a₀b₀, a₀b₂, a₂b₀, and a₂b₂ are significant. The most interesting mediated effect is a₀b₂ which indicates that the effect of ATLAS on intentions to use steroids worked by decreasing beliefs in media ads immediately following the intervention, which then decreased the asymptote of intentions to use steroids. The model fit indices showed that the exponential decay model (AIC = 2956.9, BIC = 3014.4) fit better than the quadratic model (AIC = 3088.5, BIC = 3099.3).

The models reported in the examples converged without difficulty, but creating percentile bootstrap confidence intervals of the indirect effects proved problematic. The sample was bootstrapped at the person-level (i.e., Level 2) and the nonconvergence rate of the pairs of models in the bootstrap samples was over 75%, too high to be able to report confidence intervals with any certainty. This instability indicates that the results presented here are for illustration purposes only and should not be generalized beyond that function. The problems with the bootstrap test are discussed in more detail in the discussion of study limitations.

Discussion

The true function describing the relation between two variables can never be known for certain using sampled data. Instead, competing models are examined and individual models are then eliminated based upon theory and the observed data, leaving the last model standing as the best model. But the final model is contingent on the initial pool of models considered. If only linear and quadratic functions are examined, then deviations from linearity will likely result in the quadratic model being used for all nonlinear relationships. Chen (1990) warns of the danger of this type of “step-by-step cookbook method of doing evaluations… [with] a set of predetermined research steps that are uniformly and mechanically applied to various programs without concern of the theoretical implications” (p. 18). This is not to say that quadratic relations do not exist, but that a quadratic model should not be used when other functions make more theoretical sense. Chen’s criticism was focused on program evaluators that only examined program outcomes and failed to investigate mediating variables. Prevention researchers have responded by using mediation analysis to explore the mechanisms that cause program outcomes, but if nonlinear functions are not considered, then researchers risk repeating the same mistake of ignoring theory and context, this time for mediation analyses.

Selecting a ‘correct’ model is difficult. There is a lack of diagnostic tests that statistically distinguish between polynomial and nonlinear functions, as well as between different nonlinear functions. Deviance statistics are unavailable because these models are rarely nested. Plots, significance tests of individual parameters, R² measures, and general fit indices such as the AIC and BIC do provide some information. These measures are not as useful, however, when several competing functions have the same approximate fit, such as the quadratic and exponential decay functions in Figure 2. Model selection is further complicated when the data at the ends of the observed range are sparse, making the shape of data unclear. In these cases, theory is needed to help select the best function, whether it is polynomial or nonlinear. If multiple functions match the underlying theory and the data, then consideration can be given to selecting the most parsimonious function with the most useful parameters.

The use of nonlinear models presents several implications for prevention researchers. First, in general, nonlinear models represent a more mechanistic, theory-based approach to longitudinal data than polynomial models. This gives nonlinear models several potential advantages for intervention designers and evaluators such as improved usefulness of parameters, parsimony, and better generalization outside the observed range of the data (Davidian & Giltinan, 1995). Exponential decay was specifically chosen here because there are many variables in prevention that decay exponentially and it is especially useful for intervention studies as illustrated in Figure 3.

Second, all polynomial models approach infinity, while many nonlinear models approach asymptotes, which is more likely for many variables in prevention. For instance, in the ATLAS example the variables were measured on a 7-point scale and cannot go to infinity, so a quadratic model is inappropriate. When theory cannot help with determining this, Cohen et al. (2003) suggest oversampling the ends of the observed range in order to get a better idea of the shape of the data at the ends of the range.

Third, it is likely that even if an intervention has an effect, the effect will decay some over time. Therefore, consideration needs to be given to how quickly the effects decay. Unless the decay takes several years to occur, measuring on an annual basis will likely miss most of the decay. This is important because if M approaches asymptote very quickly, it is possible that the asymptote value of M could predict the asymptote value of Y. If Y decays more quickly than M, it is unlikely the rate of change or asymptote of M could predict the asymptote of Y. As one reviewer pointed out, once an intervention has changed a mediator, the resulting effect of the mediator on the outcome may be almost instantaneous, which complicates when to measure M and Y to get the best estimate of the effect. Even more concerning is that the relation between M and Y may change over time. For a further discussion of the timing of effects in mediation see Fritz and MacKinnon (2012). Finally, X, M, and Y can have different trajectories. Other nonlinear functions, as well as combinations of functions, for example a linear mediator and a nonlinear outcome (Fritz & MacKinnon, 2009) may be included in the same mediation model.

Latent Variables

Latent variables can also be incorporated into Equations 8 and 9 by specifying separate exponential decay latent growth curve models for M and Y, and then regressing the Y scores on the corresponding or lagged M scores. Next, if X is time-invariant, the latent growth parameters for M and Y would be regressed directly on X. Browne (1993; see also Blozis, 2007; Grimm & Ram, 2009) developed a general method for nonlinear latent growth curve models using first partial derivatives. Two problems that occur when using this method are that one of the growth parameters’ means has to be set equal to zero and that in order to constrain the loadings correctly, the values of the growth parameters must be known prior to estimating the model. But these problems can be solved by using nonlinear constraints in a software package such as Mplus (Muthen & Muthen, 2012). Alternatively, the latent growth parameters for each continuous variable could be directly regressed onto the latent growth parameters for the other continuous variables, which is called a parallel process model. For example, the latent asymptote of Y could be regressed onto the latent initial value of M, similar to adding M as a Level 2 predictor, and both of these latent variables could be regressed on X. Cheong, MacKinnon, and Khoo (2003) described a linear parallel process mediation model that can be adapted for nonlinear functions.

Limitations

There are several limitations of the models presented here. First, researchers may be unfamiliar with nonlinear functions and the software necessary to fit these models. Second, data needs to be collected in a way that allows a specific nonlinear model to give good estimates. For exponential decay, if a variable is not measured immediately following an intervention, then the estimate of the initial value may be poor. By contrast, if a variable is not measured after a majority of the effect has decayed, then the estimate of the asymptote may be poor. And, if all of the decay occurs between two measurement occasions, the estimate of the rate of decay may be poor. Third, nonlinear mediation models suffer from the same issues regarding temporal precedence and the causal inference of the b path as polynomial mediation models.

Finally, in practice there may be issues with applying existing tests of mediation to nonlinear models. For instance, the percentile bootstrap test failed in the empirical example due to nonconvergence of the nonlinear models in the bootstrap samples. There is no theoretical reason for this, so the issues here are most likely data or model based. One possible explanation is that in the ATLAS data presented, students in the control group (n = 154) outnumbered those in the intervention group (n = 116). Since beliefs and intentions in the control group remained unchanged across time, with resampling it is possible that the bootstrap samples contained too high a percentage of scores that did not change across time, making the estimation of the rate of change parameter for the program group impossible. There were also some students in the intervention group whose scores did not change, which likely compounded this effect. Additionally, it is possible that the timing of the measurements caused problems or that the starting values supplied for the models for each bootstrap sample were insufficient. An attempt was made to improve convergence by adjusting the starting values for the models for each of the bootstrap samples, but this did not improve convergence, so more research in needed.

Future directions

There are several areas of future research for nonlinear mediation models. First is the need to investigate the effect of the spacing and number of repeated measurements on the estimation of the growth parameters for different nonlinear functions. In turn this will have an effect on the estimation of the mediation parameters. A second area involves investigating other nonlinear functions, adding a third-level to the model, or specifying nonlinear relations between other Level 1 predictors and the outcome variable, or the Level 2 predictors and the Level 1 parameters. Third, more research is needed to determine if the bootstrapping problems encountered here were a result of the data used or are endemic to nonlinear growth curve models. Finally, more research is needed on diagnostic tests to compare the fit of competing functions such as a quadratic and exponential decay function.