Why It Is Hard to Find Genes Associated With Social Science Traits: Theoretical and Empirical Considerations

Abstract

Objectives. We explain why traits of interest to behavioral scientists may have a genetic architecture featuring hundreds or thousands of loci with tiny individual effects rather than a few with large effects and why such an architecture makes it difficult to find robust associations between traits and genes.

Methods. We conducted a genome-wide association study at 2 sites, Harvard University and Union College, measuring more than 100 physical and behavioral traits with a sample size typical of candidate gene studies. We evaluated predictions that alleles with large effect sizes would be rare and most traits of interest to social science are likely characterized by a lack of strong directional selection. We also carried out a theoretical analysis of the genetic architecture of traits based on R.A. Fisher’s geometric model of natural selection and empirical analyses of the effects of selection bias and phenotype measurement stability on the results of genetic association studies.

Results. Although we replicated several known genetic associations with physical traits, we found only 2 associations with behavioral traits that met the nominal genome-wide significance threshold, indicating that physical and behavioral traits are mainly affected by numerous genes with small effects.

Conclusions. The challenge for social science genomics is the likelihood that genes are connected to behavioral variation by lengthy, nonlinear, interactive causal chains, and unraveling these chains requires allying with personal genomics to take advantage of the potential for large sample sizes as well as continuing with traditional epidemiological studies.

People differ in their intelligence, personality, and behavior, and a century of research in behavioral genetics has left little doubt that some of this variation is caused by differences in their genomes.^1–3 Nonzero (and sometimes substantial) heritability of psychological traits has been consistently established in twin, adoption, and family studies that have often had very large sample sizes. Beyond establishing that genes matter, however, such studies have said little about the detailed genetic architecture of psychological traits, that is, how many genetic polymorphisms affect a trait, how the polymorphisms interact, what they are, and what they do.

The recent advent of affordable genome-wide association studies (GWAS) offers the exciting opportunity to understand the genetic factors that influence psychological trait variation with far greater precision. GWAS have the potential to uncover some of a given trait’s genetic architecture, including the number, genomic locations, average effects, and allele frequencies of the DNA variants that affect the trait. Even an incomplete understanding of a trait’s genetic architecture could prove a boon to social scientists for at least 4 reasons.⁴

First, the presence of genetic variants can be detected with high reliability. Thus, they may constitute direct measures of constructs that were previously regarded as only latent. For example, some evidence has shown that a person’s genotype for the single-nucleotide polymorphism (SNP) in FTO associated with body mass index (BMI; defined as weight in kilograms divided by the square of height in meters) may indicate a preference for certain kinds of high-calorie foods,⁵ and one might speculate that other genes may affect how much body weight is produced from a person’s caloric intake. These genetic variants could then be used as variables of interest, or as controls, in testing models of the causation of obesity that formerly could only appeal loosely to genetic factors.

Second, the discovery of genetic associations may identify or clarify the actual biological mechanisms that underlie social and health behaviors. For example, a mechanistic role for the hormone oxytocin in trust-related behavior has been suggested by findings that variants in the oxytocin receptor gene (OXTR) are associated with differences in performance in a behavioral–economic trust game (albeit with mixed results so far).^6,7 Also, just as in medicine, for which genetic discoveries have suggested new pathways for understanding and treating disease (e.g., Crohn’s disease⁸), genetic discoveries may help social scientists decompose crude concepts such as risk aversion and time preference, both of which play roles in health behaviors, into biologically meaningful subcomponents.

Third, under very special circumstances, genetic variants could be used as instrumental variables that would identify causal relationships from nonexperimental data. For such analysis to be valid, the allele must reliably and exclusively affect a specific biological trait (and no other biological traits). If these strong conditions are met, then one can use the random assignment (during meiosis) of each person’s genotype at that allele as a natural experiment to test the hypothesis that the biological trait, in turn, causes variation in some behavioral phenotype. For example, Chen et al.⁹ showed that SNPs in ALDH2 that are known to increase alcohol metabolism are associated with decreased blood pressure, thus providing evidence that alcohol consumption in fact causes an increase in blood pressure—under the crucial, and perhaps implausible, condition that those SNPs are assumed not to also affect blood pressure through some other channel. Other studies of this type have been published,¹⁰ but it seems likely that the circumstances in which the instrumental variable approach can work are rare.

Fourth, knowledge of individuals’ genotypes could help in targeting social science interventions to those who stand to benefit from them the most—an application of concepts from personalized medicine to public health and policy. Such a benefit is particularly likely to help children because their abilities and preferences are less developed and harder to measure. For example, children with genotypes that confer a susceptibility to dyslexia might be offered personalized educational resources from a very early age.

The leap in precision from GWAS compared with twin studies promises to help not just working social and behavioral scientists but anyone interested in the evolutionary history and adaptive pressures that shaped the human species and its variation. Not only does an individual’s genome provide a partial recipe for the development of his or her unique phenome (set of phenotypes) forward in time, but our species’ array of genomic data provides a trace of our collective evolutionary history backward in time. For example, once it was discovered that mutations in the gene FOXP2 could cause a severe developmental deficit in speech and language, comparative genomic analyses showed that this gene’s sequence had changed at least twice since the separation of humans and chimpanzees from their common ancestor and that these changes predate the separation of humans from Neanderthals—all relevant to venerable and hitherto nearly unresolvable debates on the evolution of language.

MOLECULAR GENETIC RESEARCH ON BEHAVIORAL PHENOTYPES

Despite the extraordinary promise of extending genetic research to behavioral traits, results of studies that have searched for genetic variants associated with these traits have so far been disappointing: No strong, replicable associations have been discovered. Most of the claims of genetic associations with such traits have turned out to be false positives, or at best vast overestimates of true effect sizes. Chabris et al.¹¹ found that across 3 independent samples, only 1 of 12 published associations of particular genes with general intelligence replicated, and this association replicated in only 1 of the samples. Worse, the new samples were considerably larger than the originals, which suggests that all of these reports were probably false positives. Similarly, Benjamin et al.⁴ found a SNP associated with educational attainment and cognitive function but could not replicate it in 3 independent samples. Benjamin et al.^12a likewise found no significant associations with any member of a set of traits involving economic and political behavior. Finally, Beauchamp et al.^12b conducted a GWAS of educational attainment (i.e., years of education completed) and found no hits that met conventional genome-wide significance levels; those that approached significance did not replicate in a second sample.

Difficulty in finding specific genes that correlate with traits that are known to be heritable is not unique to the social sciences. It is also a problem in GWAS of medical traits such as psychiatric diagnoses and susceptibility to common diseases and even with certain physical traits, such as height. Table 1 summarizes the heritabilities estimated from twin studies of medical, physical, and social science traits, based on 3 review articles and some recent publications in behavioral economics; it shows that the heritabilities of physical and psychological traits are similar and substantial.

TABLE 1—

Heritabilities Estimated From Twin Studies of Selected Medical, Physical, and Behavioral Traits

Phenotype	Heritability, %	Source
Medical and physical traits
Lipoprotein A level (age 17 y)	95	Boomsma et al.13
LDL cholesterol level (age 44 y)	69	Boomsma et al.13
HDL cholesterol level (age 44 y)	67	Boomsma et al.13
Heart rate (age 17 y)	44	Boomsma et al.13
Respiration rate (age 44 y)	61	Boomsma et al.13
Testosterone level (age 17 y)		Boomsma et al.13
Boys	66
Girls	41
Birth weight	10	Boomsma et al.13
Height (ages 16 y–adult)	80a	Visscher14
Behavioral traits
Externalizing problem behavior (age 3 y)		Boomsma et al.13
Boys	49
Girls	73
Internalizing problem behavior (age 3 y)		Boomsma et al.13
Boys	61
Girls	66
Personality traits (adults)		Bouchard15
Neuroticism	48
Extraversion	54
Openness to experience	57
Agreeableness	42
Conscientiousness	49
General cognitive ability (age 18 y)	81	Boomsma et al.13
Boredom susceptibility (age 18 y)	50	Boomsma et al.13
Anxiety (age 18 y)	54	Boomsma et al.13
Depression (age 18 y)		Boomsma et al.13
Men	39
Women	53
Smoking (yes or no, age 18 y)		Boomsma et al.13
Men	66
Women	32
Alcohol use (yes or no, age 18 y)		Boomsma et al.13
Men	48
Women	75
Sports participation (age 18 y)	47	Boomsma et al.13
Religiosity (adults)	38	Bouchard15
Specific religion practiced (age 18 y)	0	Boomsma et al.,13 Bouchard15
Conservatism (adults)	55	Bouchard15
Risk attitudes		Cesarini et al.16
General willingness to take risk	21
Willingness to take financial risk	26
Risk aversion	34
Portfolio volatility	25	Cesarini et al.17
Cooperation		Cesarini et al.18
Trust	15
Trustworthiness	18
Income, single y	38	Taubman19
Income, single y		Benjamin et al.4
Men	37
Women	28
Education, y	28	Taubman19
Behavioral traits, estimates corrected for measurement error
Risk attitudes		Cesarini et al.16
General willingness to take risk	35
Willingness to take financial risk	37
Risk aversion	54
Income, 20-y average		Benjamin et al.4
Men	58
Women	46

Note. HDL = high-density lipoprotein; LDL = low-density lipoprotein. Estimates are averages of male and female heritabilities except when heritabilities are provided separately for both sexes (these are cases in which heritability differs by a large amount between males and females). Except in the third section, heritability estimates were not adjusted for differences in measurement error, longitudinal stability, or test–retest reliability of the phenotypes. Heritabilities may also vary with age; for example, general cognitive ability becomes more heritable with age. Summaries of heritabilities of these and other phenotypes may be found in Plomin et al.,²⁰ Boomsma et al.,¹³ Bouchard,¹⁵ and Barnea et al.²¹

^aEstimated from genome-wide single-nucleotide polymorphism data from twin and sibling pairs in Australia.

The discrepancy between the high heritability of both physical and psychological traits and the rarity of replicable discoveries of particular genes for those traits has been dubbed the problem of missing heritability.²² One possible resolution of this paradox is that each of the genes associated with a trait explains only a minuscule fraction of the total genetic variance—hence, these genes are difficult to identify statistically—but the number of such genes is huge, and the heritability estimate reflects their aggregated effects.

Zuk et al.²³ suggested that the discrepancy between heritability estimates from traditional biometrical studies of families and GWAS results thus far comes from the fact that biometrical studies will overestimate heritability if genes interact nonadditively. If this suggestion is correct, then it may be that GWAS approaches that do not grapple with the combinatorial explosion posed by the search for gene–gene interactions will not produce interesting results. This criticism of biometrical studies, however, only applies when such studies focus on only one type of kinship (e.g., twins reared together). Many human traits, including height and IQ, have been studied biometrically using many different kinds of kinships (twins reared together and apart, parents and offspring living together and apart, adoptive relatives who live together but are biologically unrelated). When these results are considered collectively, they converge on relatively large heritability values.

The evidence base for claims about heritability has been strengthened by a recently developed way to estimate heritability that examines genetic variation directly. The genomic-relatedness-matrix restricted maximum likelihood (GREML) technique²⁴ uses all of the genotypic data from SNP arrays to estimate, for each pair of participants in a data set, their degree of genetic similarity (relatedness) and then correlates genetic relatedness with phenotypic similarity across all of the pairs. This yields an estimate of additive genetic variance. Note that this technique does not require the participants to be related in the conventional genealogical sense of being siblings or cousins. It exploits the fact that all individuals within a population are distantly related and that the level of relatedness varies considerably among pairs of people. For example, Davies et al.²⁵ reported a GREML analysis with about 550 000 common SNPs and 3000 participants in which about 45% of the variance in general cognitive ability could be directly explained by the SNP variation; Chabris et al.¹¹ replicated this finding with a smaller sample. In the original application of GREML, Yang et al.²⁴ showed that 45% of the variance in height across 4000 participants could be explained by approximately 300 000 common SNPs. These estimates leave room for unmeasured genetic variation (e.g., uncommon SNPs, other non-SNP polymorphisms) to explain additional heritability.

In this context, a common variant is a polymorphic site at which the minor allele shows a frequency exceeding a certain threshold (say .05), and a rare variant is a site at which the frequency of the minor allele falls below this threshold. The GREML results finding substantial heritability owed to common variants have tended to discredit the hypothesis that missing heritability arises because common variants typically studied in GWAS are merely surrogates for rare variants of powerful effect that, if they could only be discovered, would account for much more heritability.²⁶ Furthermore, Wray et al.²⁷ provided a thorough analysis of the available GWAS results and showed that a model relying exclusively on rare causal variants cannot account for the data. It is important to note that, under any reasonable evolutionary model, most genetic variants affecting a given phenotype may be rare. All else being equal, however, a common variant contributes more variability than a rare variant, and thus it is not at all inconsistent to expect that common variants will be responsible for a substantial portion of heritability.

Although medical and behavioral geneticists are becoming increasingly sympathetic to the many-common-genes-of-small-effect answer to the missing heritability question, why such a diffuse polygenic architecture should be typical of quantitative traits is still not known. What might account for the exceptions that have been found is also not known.

A simple possible explanation invokes the length of the causal chain from genetic to phenotypic variation. For example, variation in pigmentation (e.g., of eyes, skin, and hair) arises from the number of melanosomes produced, as well as their size and shape, and the type of melanin synthesized.²⁸ These biochemical differences follow directly from changes in the composition or regulation of gene products, which are in turn strongly influenced by differences in DNA sequence. Indeed, a single SNP in HERC2 is largely responsible for blue eye color.²⁹

By contrast, changes at the molecular and cellular level must be remote from their ultimate effects on most behavioral phenotypes, and even from many physical phenotypes such as body mass index. Consider that BMI may depend on what a person likes to eat, how often the person eats, how much the person exercises, details of the person’s metabolism, and a host of other complex behaviors and physiological processes. Similarly, given that the physical basis of psychological attributes such as cognitive ability, conscientiousness, impulsivity, and risk aversion resides in intricate patterns of neural circuitry and interlocking biochemical feedback loops, one should perhaps expect any single genetic variant affecting such an attribute to contribute only a small fraction of the total variation in the phenotype.

FISHER'S GEOMETRIC MODEL OF NATURAL SELECTION

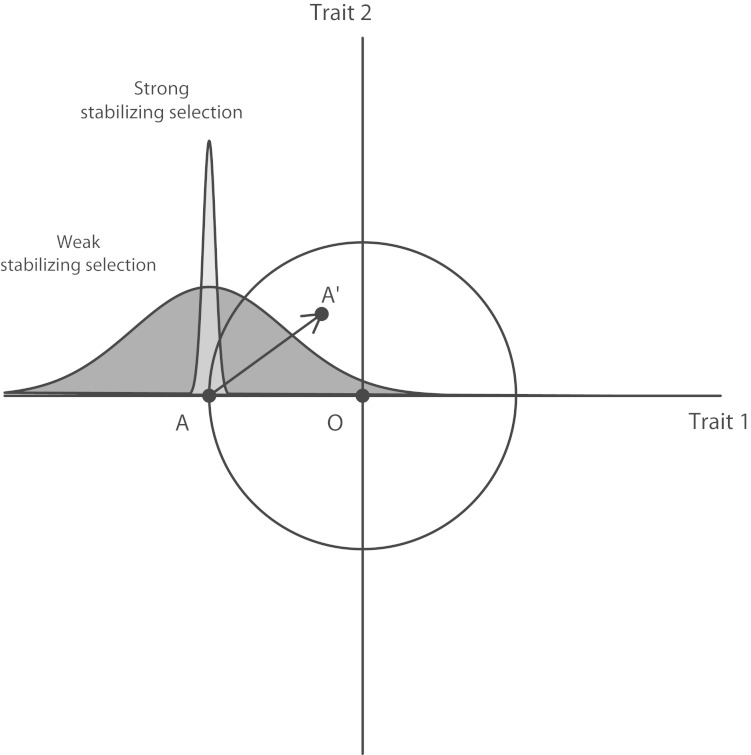
Here we offer a second explanation (which is not mutually exclusive with the first) that invokes the differential action of natural selection. More than 70 years ago, Fisher³⁰ proposed a geometric model of adaptation that is summarized in Figure 1, which depicts 2 quantitative traits as the vertical and horizontal dimensions on a 2-dimensional space (representing a slice of the vast multidimensional space of possible phenotypes). Point A represents the current mean phenotype of the species (in this example, a low value of trait 1 and an intermediate value of trait 2). Point O represents the optimum favored by natural selection. Suppose that A was once optimal because selection had pushed the population to its optimum value, but that O no longer coincides with A because of an abrupt environmental change that demands a different (in this case, higher) value of trait 1. What would have to happen for selection to adapt the organism to the new optimum?

FIGURE 1—

R. A. Fisher’s geometric model of adaptation.

Note. A is the current mean phenotype of the population, A′ is the mean phenotype that would result if the mutation denoted by the arrow were to be instantly fixed, and O is the new optimum favored by natural selection. The narrow distribution of trait 1 values around A is the situation that would prevail under strong stabilizing selection, whereas the broad distribution would prevail under weak stabilizing selection.

Source. Fisher.³⁰

One possibility is a new mutation arising in a single individual and, if beneficial, reaching fixation (100% allele frequency) in the population. In the model, the fixation of a mutation corresponds to adding a vector of random direction to the population’s current trait-space position at A. This feature of the model captures 2 key observations: (1) mutations have no inherent tendency to increase the fitness of their bearers, and (2) any single mutation may affect several distinct traits, and therefore this mutation could change the population’s mean values of both traits 1 and 2. The subset of new phenotypes that would result in an increased level of adaptation is depicted in Figure 1 as the interior of the circle centered on O, representing all the combinations of trait values that are closer to the optimum (using the Euclidean distance metric).

The diagram also helps one understand the fates of mutations with different effect sizes. Note that any mutation whose effect on the traits exceeds the diameter of the circle would not be fixed because it leaves the population farther from the optimum than when it started (point A). Selection would simply favor the status quo. In general, the smaller the mutation, the more likely it is to be beneficial, because many small moves can be made from A that stay within the circle, but few very large ones; most large moves will overshoot the circle or move away from it. The fact that a smaller move is more likely to take the population into the circle should already be evident from Figure 1. As the number of traits or dimensions increases to larger values (which cannot be depicted in a 2-dimensional figure), the greater ease with which smaller moves take the population into the “hypersphere” becomes quite dramatic. If the number of traits (n) is large, then the probability that a random mutation of length r takes the population into a hypersphere of radius z is 1 − Φ(x), where Φ is the cumulative distribution function of the standard normal distribution and x = r√n/(2z).³⁰

Fisher³⁰ argued that mutations of large effect are relatively unimportant in evolution because they will rarely move a population closer to O. The closer to the optimum the organism already is, the less likely large mutations are to be beneficial. Fisher draws an analogy to the process of focusing a microscope. When a microscope is already close to the correct focusing point, a small random perturbation of the knob is likelier than a larger perturbation to bring it closer to exact focus.

We now expand Fisher’s³⁰ argument to explain the puzzling contrast between some physical phenotypes such as skin or eye color on the one hand and social science and medical phenotypes on the other. Suppose that trait 1 was previously under strong stabilizing selection and thus has negligible genetic variation at the time of the environmental shift that makes O the new optimum (this state of affairs would correspond to a tight clustering of trait 1 values around point A). Because the rate of the approach to the optimum via existing genetic variation (i.e., variation that does not result from de novo mutations) is bounded above by trait 1’s heritability (per the breeder’s equation),³¹ a population with negligible genetic variability in that trait is unlikely to adapt quickly toward O unless a mutation of large effect arises and reaches fixation—for example, a mutation that took the population to A′, for which its new value for trait 1 is much closer to the optimum.

Alternatively, suppose that stabilizing selection on trait 1 had been much weaker, permitting the buildup of substantial genetic variation (leading to a wide scatter of trait 1 values around A). In this case, a mutation of large effect is far less likely to become common through positive selection. At the same time that this mutation is struggling to increase its frequency, the existing genetic variation is enabling the population to adapt toward O. If O lies within the current range of genetic variation (which is true for trait 1 under the assumption of the more variable population in Figure 1) and selection is even moderately strong, then the population mean shifts from A to O even without the arrival of a mutation of large effect. As the population evolves, the diameter of the circle bounding all points of higher adaptation continuously shrinks. Once the magnitude of the mutation that would have taken the population to A′ exceeds the diameter of the circle, the mutation is disfavored and is very likely to be eliminated from the population. A numerical example may help to illustrate our argument. Suppose that the fixation of a new mutation is the only means for the population to increase its level of adaptation—that is, no genetic variation initially exists along the selected direction. If the selective advantage of the new mutation is 5%, it will then take about 500 generations to increase from a frequency of 0.001 to a frequency of 0.999.³² A selective advantage of roughly this magnitude seems reasonable for many of the mutations affecting pigmentation. Now suppose that the population contains substantial genetic variability in the trait. In particular, suppose that the trait has a heritability of 100% and follows a standard normal distribution. If we stipulate that the old and new optima are separated by 2 phenotypic units (and that each unit continues to correspond to a 5% change in relative fitness; i.e., a 5% gain in offspring per generation), then standard quantitative genetic results^32,33 imply that the population will reach the new optimum in 40 generations. If the preexisting variants of small effect have pleiotropic effects, the adaptation time may be somewhat longer. Nevertheless, in a race between the fixation of a major mutation and polygenic adaptation, the latter will often have a profound advantage. Once polygenic adaptation has brought the population close to the new optimum, the major mutation will become disfavored while still at a low frequency.

To complete our explanation, we need to assume that the polymorphic sites contributing to existing genetic variation tend to be small in effect. Even under weak stabilizing selection, variants of large effect experience greater selection pressure and are consequently more likely to be found at a low minor allele frequency,^34–36 which implies that any common (i.e., high-frequency) variants contributing to standing genetic variation will typically be small in effect. Thus, we might expect many loci of small effect to explain most of the heritable variation underlying a quantitative trait—unless recent selection for the trait was strong relative to the initial variability. If a trait turns out to be associated with many genetic loci of small effect and few or no loci with large effects, then we would have evidence that this trait has not experienced such selection.

In the remainder of this article, we show how this evolutionary analysis can help epidemiologists and social scientists make sense of the genetics of behavior in the era of rapidly expanding genome scans. We report the results of our own GWAS of more than 100 human phenotypes—both physical phenotypes, such as body size and pigmentation, and behavioral phenotypes of great interest to social scientists, such as general intelligence, memory ability, verbal fluency, impulsivity, risk aversion, fairness, and utilitarianism. We measured a wide variety of cognitive, personality, and behavioral–economic traits so that we could generalize within types of traits and compare the behavioral phenotypes with the physical phenotypes. To our knowledge this study is the first to examine associations between a genome-wide panel of SNPs and such a broad spectrum of phenotypes; almost all previous association studies of behavioral traits have examined only 1 or a few candidate genes and phenotypes. In addition to including both physical and behavioral traits, we examined traits that are expected to be both monogenic and polygenic. An additional innovation is that the behavioral phenotyping was intensive, relying not just on standardized paper-and-pencil tests but on individual computerized tasks, sometimes administering 100s of trials to quantify a single trait. This step is essential because crude measurement of behavioral traits could lead to false negatives and thus would not help explain the puzzling failure to find associated genes. Thus, each of 419 participants was tested individually in a laboratory session lasting an average of 3.5 hours.

To preview the results, despite an adequate sample size for detecting large effects and despite high-precision measurements, we found few associations between SNPs and traits at an appropriately stringent significance threshold. Because many of our measured phenotypes (including our behavioral phenotypes) are known to be heritable,³⁷ the absence of strong associations in our data indicates that—aside from pigmentation—both physical and behavioral traits are mainly affected by numerous genes with small effects.

After presenting the results, we discuss their implications for future genetic association studies of behavioral traits, which are likely to become ever more common as the cost of genotyping and sequencing declines. In addition to our analysis of the evolutionary genetics of heritable variation, we introduce 2 other key issues in designing and interpreting such studies: the effects of selection bias for participant inclusion in such studies, and the trade-offs between measurement error and statistical power in selecting simple, fast, inexpensive assessments of traits versus the sort of complex, time-consuming, and potentially expensive assessments that we conducted.

METHODS

We recruited participants and collected data and samples at 2 sites: Harvard University in Cambridge, Massachusetts, and Union College in Schenectady, New York. We made efforts to recruit from the surrounding communities a more representative sample than the typical college student population: paper fliers were posted at various public locations, advertisements were placed in free newspapers and on Craigslist, and the study was made available to the Psychology Department Study Pool at Harvard.

Participants completed an online screening questionnaire that included items regarding age, medical history, and grandparental ethnicity. We excluded participants who were younger than 18 or older than 45 years or who reported a history of bipolar disorder, schizophrenia, or severe head trauma. To help control for ancestral confounding of genotypes and trait levels,³⁸ we recruited a sample of predominantly Western European ancestry, which was ascertained at the screening process by asking potential participants to list the country of origin or ancestry for each of their biological grandparents. A total of 419 participants provided complete, usable genetic and phenotypic data. Phenotyping took place from July 2007 through June 2009.

Eligible participants were invited to either the Harvard or the Union lab for a data collection session typically lasting from 3 to 4 hours. Participants gave informed consent after the nature of the procedure had been fully explained to them. We collected a diverse set of cognitive, personality, economic, attitude, demographic, and physical phenotypes via computerized tasks, paper-and-pencil surveys, and face-to-face interaction. DNA was collected via 2 mouthwash samples in the lab and then extracted and genotyped elsewhere. Population stratification was investigated and controlled for in all genetic analyses reported here. We used the program PLINK version 1.07 (Center for Human Genetic Research, Massachusetts General Hospital, Boston, MA, and Broad Institute of Harvard University and Massachusetts Institute of Technology, Cambridge, MA) for genotypic data cleaning and analyses.³⁹ (See supporting material, available as a supplement to the online version of this article at http://www.ajph.org, for a complete list of phenotypes, descriptions of select phenotypes, and details of DNA collection, extraction, genotyping, and analysis of population stratification.)

We performed logistic regression to test for association with dichotomous traits and linear regression for all polytomous and continuous traits. We chose the standard genome-wide significance threshold of 5 × 10⁻⁸ for declaring a SNP–trait association to be statistically significant.⁴⁰ Under a frequentist approach aiming to minimize the chance that even a single declared hit is a false positive, the large number of examined traits would require an even more stringent threshold. However, we adopted the generally accepted quasi-Bayesian justification of the Wellcome Trust Case Control Consortium⁴¹ for retaining the standard genome-wide significance threshold; it maintains a constant ratio of true to false positives as the number of markers and traits increases (as long as statistical power and prior probabilities for any given association do not change).

For any SNP showing an association with a trait at the significance threshold 5 × 10⁻⁸, we reran PLINK with our cognitive ability composite and revised NEO Personality Inventory (NEO–PI–R) openness, neuroticism, and agreeableness factor scores as additional covariates in an effort to control for selection bias.⁴² Selection bias may be an underappreciated contaminant in gene–trait association studies.⁴³ To understand this bias, consider this analogy: suppose that a driveway will be wet in the morning as the consequence of 2 possible causal mechanisms: whether it rained last night and whether a sprinkler was activated (Figure 2a). Suppose also that the 2 causal variables are independent; that is, taking all days into account, no correlation exists between whether it rains and whether the sprinkler turns on. If one only considers mornings on which the pavement is wet, however, one will spuriously conclude that the 2 causes are negatively correlated. For instance, if one sees that the pavement is wet and knows that it did not rain last night, one can be confident that the sprinkler was activated. One only sees the true noncorrelation when one considers all days. Suppose that the probability of rain and the probability of sprinkler activity are both 0.5 and are independent. If one checked the driveway every morning, wet or dry, then one would observe rain and no sprinkler a quarter of the mornings, sprinkler and no rain a quarter of the mornings, both sprinkler and rain a quarter of the mornings, and neither sprinkler nor rain a quarter of the mornings—the lack of association is apparent. Now suppose one checked only the mornings on which the driveway was wet. On a majority of the mornings (two thirds), one would discover either rain with no sprinkler or a sprinkler with no rain. In other words, one would find a negative correlation, but only because those mornings that would have diluted the correlation to zero were excluded. The basic principle emerging from this example is that if one inadvertently conditions an observation on the common effect (is the driveway wet?) of multiple causes (rain or sprinkler), one can create the illusion of a nonzero correlation among the causes.

FIGURE 2—

Examples of directed acyclic graphs containing a “collider” (the common effect of 2 or more causes) for (a) 2 uncorrelated causes of a wet driveway that can incorrectly appear to be correlated and (b) situation in which a gene is associated with a trait that is itself a cause of participation in the study.

Note. Conditioning on a collider alters the apparent covariation among the causes; for example, 2 independent causes that are uncorrelated when all observations are considered can appear to be negatively correlated when we consider only those observations where the collider assumes a certain value.

Source. Pearl.⁴²

An example using continuous variables may also help to illustrate the concept of selection bias and its generality. Suppose that intelligence and athletic ability (both continuous traits) are uncorrelated in the population at large. However, if one limits one’s observations to the students attending a university that uses both of these attributes as admissions criteria, then one will find that intelligence and athleticism are negatively correlated. If one encounters a student at this university with low intelligence, then it becomes more probable that the student is a good athlete. Otherwise the student would likely not have been admitted. This negative correlation between intelligence and athleticism among admitted students holds even if admission is not a deterministic function of these two attributes; other attributes (e.g., musical talent) and random noise may play a role. Geiger and Pearl⁴⁴ provided a rigorous mathematical proof that conditioning on a common effect induces dependence among the causes. The apparent dependence does not have to be a negative correlation as in these examples; an apparent positive correlation would result if, say, students high in both athleticism and intelligence were especially likely to be admitted.

This same principle applies in GWAS. Suppose that high levels of either trait 1 or 2 are independent causes of a person ending up as a participant in our study, either because the trait affects whether the person decides to volunteer or it affects whether we decide to include the person’s data (Figure 2b). Then we would spuriously find any gene that affects trait 2 to be associated with trait 1, even if trait 1 is not at all affected by genetic variation, because among people who participate in the study, traits 1 and 2 will appear to be (negatively) correlated, and therefore a cause of scoring high on trait 2 will appear to also be a cause of scoring low on trait 1. Controlling for the other traits affecting participation may not fully solve the problem (even if we know what these traits are) because the trait of interest may itself be connected to the other participation-related traits in a complex causal graph and therefore the decision to condition on the other traits could in principle introduce further bias. In practice, however, conditioning on traits that may affect study participation is likely to be a conservative procedure. For example, if 1 trait mediates the genetic effect of another, then controlling for the mediating trait will suppress the genuine effect of the genetic variant on the downstream trait of interest and is therefore unlikely to generate additional false positives.

We performed a numerical simulation to illustrate the extent to which selection bias may distort GWAS results. We stipulated 2 initially independent traits affecting participation in the study; the sum of an individual’s z scores on these traits needed to exceed 3 for the individual to be in the pool of participants, which corresponds to slightly less than 2% of the general population being available to participate. We believe that this simulated situation is not so farfetched as a model of some ongoing projects (e.g., the Personal Genome Project,⁴⁵ 23andMe⁴⁶). We stipulated that each trait has a heritability of 0.50 and is affected by loci all with an allele frequency of 0.50 and an average effect (regression coefficient) of 0.05; each causal locus thus accounts for 0.25% of the variance in its trait. The results were striking: The estimated effects of the true causal variants with respect to a given trait were centered at 0.03—off by 40%. Similarly, the effects of the variants on the wrong trait (of the 2 traits, the one that the variants did not affect) were centered at –0.02. In a situation in which it is important to distinguish miniscule effects from 0, a spurious effect of 0.02 cannot be considered trivial. Although more thorough numerical and analytical investigations are certainly worthwhile, this example illustrates that researchers performing GWAS of behavioral traits should be aware of the consequences of selection bias.

Table 2 includes the sample statistics for the Multidimensional Attribute Battery–II (MAB–II) and the NEO–PI–R, 2 instruments used in our study that have detailed population norms. Compared with the norming samples for the MAB–II, our participants showed much higher means and smaller standard deviations, suggesting that cognitively able individuals were more likely to participate in the study. The relationship between the NEO–PI–R personality traits and study participation was more complex. Our study participants showed conspicuously higher levels of openness than the norming samples. The trait of openness is defined by a willingness to examine new ideas and try new activities, and thus higher levels of this trait may plausibly be a cause of volunteering for scientific research. Our study participants also showed consistently lower levels of neuroticism and higher levels of agreeableness. (Of interest is that our study participants were more variable than the norming samples, perhaps because people with higher cognitive ability are more variable in their responses to personality questionnaires.⁴⁹) Furthermore, the fact that students were overrepresented among our participants indicates that the selection bias may already have operated extensively at an earlier point. That is, even if we could have taken a random sample of all students attending the top 200 colleges, for example, the process of college admissions would still have exerted considerable selection bias distinguishing this special population from its larger age cohort. As a reasonable attempt to control for selection bias, then, we used general cognitive ability, openness, neuroticism, and agreeableness as additional covariates whenever a novel SNP–trait association showed a significant P value. Without doing this, we might have spuriously found, for example, that a gene associated with greater openness was also negatively associated with all the traits that are correlated with openness, such as political liberalism (see the Results section).

TABLE 2—

Sample Age, Gender, General Cognitive Ability Characteristics, and Personality Traits: Genome-Wide Association Study; Harvard University, Cambridge, MA, and Union College, Schenectady, NY; July 2007–June 2009.

Tralit	Sample Statistics, Mean ±SD	Population Norms, Mean ±SD
Age, y	25.2 ±6.44
MAB–II
Arithmetic	0.797 ±0.836	0 ±1
Similarities	1.054 ±0.601	0 ±1
Vocabulary	1.386 ±0.891	0 ±1
NEO–PI–R neuroticism
College, female	21.90 ±8.38	25.83 ±7.59
Adult, female	18.71 ±9.13	20.54 ±7.61
College, male	18.53 ±10.04	22.49 ±7.92
Adult, male	18.84 ±10.46	17.60 ±8.61
NEO–PI–R extraversion
College, female	30.10 ±6.89	31.27 ±5.64
Adult, female	29.19 ±7.55	28.16 ±5.82
College, male	29.08 ±6.10	29.22 ±5.97
Adult, male	29.70 ±8.64	27.22 ±5.85
NEO–PI–R openness
College, female	34.02 ±6.57	27.94 ±5.72
Adult, female	34.42 ±5.57	26.98 ±5.87
College, male	31.79 ±6.57	27.62 ±6.08
Adult, male	31.36 ±7.04	27.09 ±5.82
NEO–PI–R agreeableness
College, female	33.80 ±5.51	31.00 ±5.33
Adult, female	34.42 ±4.71	33.76 ±4.74
College, male	31.46 ±6.05	28.76 ±5.24
Adult, male	32.00 ±5.70	31.93 ±5.03
NEO–PI–R conscientiousness
College, female	33.64 ±7.40	31.02 ±6.53
Adult, female	32.29 ±7.15	35.04 ±5.78
College, male	30.17 ±6.54	30.21 ±7.19
Adult, male	33.33 ±8.04	34.10 ±5.95

Note. MAB–II = Multi-Aptitude Battery–II; NEO–PI–R = Revised NEO Personality Inventory. The sample was 67.6% female. MAB–II scores were scaled as standard normal using the tables in the MAB–II manual.⁴⁷ We calculated NEO–PI–R summary statistics for participants aged between 18 and 22 for purposes of comparison with the college norms in the NEO–PI–R manual⁴⁸ and for participants aged 30 and older for comparison with the adult norms.

RESULTS

As can be seen in Table 3, we found at least a marginal signal for all SNPs previously found to be associated with eye color, hair color, freckling, and skin color^{28,46,50–53} (with the exception of SNPs identified in a study that digitally quantified eye color⁵⁴) and that were either present in our cleaned set of genotyped SNPs or represented by a proxy SNP with an r² > 0.60. Note that despite our relatively small sample size, the effects of the intronic SNP rs12913832 in HERC2 on eye and hair color were statistically significant at the stringent, standard GWAS threshold.

TABLE 3—

Association Results for Pigmentation Phenotypes: Genome-Wide Association Study; Harvard University, Cambridge, MA, and Union College, Schenectady, NY; July 2007–June 2009.

Trait and Reported SNP	Proxy SNP	r2	Minor Allele	Sample MAF	HapMap MAF	Effect Size	P	Gene
Eye color
rs12913832			A	0.222	0.208	0.998	2 × 10−68	HERC2
rs12896399	rs1075830	0.615	A	0.460	0.308	0.167	.003	SLC24A
rs1393350			A	0.266	0.192	–0.154	.02	TYR
rs1408799			T	0.313	0.300	0.095	.11	TYRP1
rs12913832			A	0.223	0.208	0.840	1 × 10−13	HERC2
rs12896399	rs1075830	0.640	A	0.460	0.308	0.372	9 × 10−5	SLC24A4
rs12821256			C	0.095	0.142	–0.352	.03	KITLG
Red hair
rs1805007			T	0.076	0.147	7.44	2 × 10−6	MC1R
rs1015362			T	0.278	0.233	0.507	.09	ASIP
Freckling
rs1805007			T	0.076	0.147	0.613	6 × 10−6	MC1R
rs1042602			A	0.346	0.417	–0.223	.005	TY R
rs2153271	rs1416742	0.949	G	0.384	0.373	–0.139	.07	BNC2
rs619865			A	0.098	0.108	0.178	.15	ASIP
Skin darkness
rs1805007			T	0.076	0.147	–0.267	.005	MC1R
rs1042602			A	0.346	0.417	–0.118	.03	TY R
rs619865			A	0.098	0.108	–0.156	.07	ASIP

Note. MAF = minor allele frequency; SNP = single-nucleotide polymorphism. Eye darkness was reported on a 3-point scale. Hair darkness was recorded on 9-point scale. Red hair was recorded as a dichotomous trait, and its effect size is reported as an odds ratio. Freckling and skin darkness were recorded on 5-point scales. All effect sizes for nondichotomous traits are reported as the expected change in trait value per each additional copy of the minor allele. All alleles are coded according to National Center for Biotechnology Information build 36 coordinates on the forward strand.

A meta-analysis has identified more than 180 genomic regions containing a variant affecting height.⁵⁵ Because of the weak effect of each individual variant, however, we did not replicate any of these loci with genome-wide significance. However, of the 94 loci either present in our set of SNPs or represented by a proxy, 65 had estimated effects with the correct sign, and 29 did not (binomial test P < .001). We also found an enrichment of low P values; whereas only 9 or 10 P values less than .1 were expected under the null distribution, we observed 16 (significantly more, according to a binomial test P < .05). These trends were consistent with most of these loci being true positives despite our inability to extract a strong signal from them. A selection of the height variants showing marginal significance in our data are shown in Table 4, along with the nonsynonymous SNP rs1815739 in ACTN3 that has been found to affect athletic performance.⁵⁶

TABLE 4—

Association Results for Physical Phenotypes and Behavioral Phenotypes with Previously Reported SNPs: Genome-Wide Association Study; Harvard University, Cambridge, MA, and Union College, Schenectady, NY; July 2007–June 2009

Trait and Reported SNP	Proxy SNP	r2	Minor Allele	Sample MAF	HapMap MAF	Effect Size	P	Gene
Physical Phenotypes
Standing height
rs7460090			C	0.134	0.117	–.188	.07	SDR16C5
rs237743			A	0.231	0.308	0.175	.04	ZNFX1
rs6439167			T	0.201	0.183	–.191	.03	C3orf47
rs889014			T	0.347	0.375	–.124	.1	BOD1
rs7274811	rs3213183	0.692	A	0.304	0.267	–140	.07	ZNF341
rs7759938	rs369065	1	C	0.332	0.364	.0172	.02	LIN28B
rs3764419	rs9890032	0.982	G	0.401	0.375	–188	.009	ATAD5/RNF135
rs3791675			T	0.228	0.275	–.305	4 × 10−4	EFEMP1
rs724016			G	0.428	0.483	0.121	.1	ZBTB38
rs1351394	rs7968682	0.983	T	0.499	0.517	–.120	.1	HMGA2
Strength: rs1815739	rs540874	1	A	0.428	0.458	0.252	.006	ACTN3
Behavioral Phenotypes
General cognitive ability
rs2760118	rs7775073	0.982	G	0.316	0.317	0.062a	.42	ALDH5A1
rs324650			T	0.464	0.467	0.026	.72	CHRM2
rs363050			G	0.444	0.475	–.027	.72	SNAP-25
rs17571	rs17834326	0.781	A	0.083	0.083	–.051a	.7	CTSD
rs760761	rs2619545	1	C	0.196	0.192	–.033a	.72	DTNBP1
Conscientiousness: rs2576037	rs7233515	0.879	A	0.400	0.408	–.038	.6	KATNAL2
Neuroticism: rs12883384			A	0.410	0.317	–.014a	.85	MAMDC1
Paired-associate recognition: rs17070145			T	0.338	0.267	0.065	.37	KIBRA
3-back accuracy: rs4680			A	0.449	0.517	0.027	.72	COMT

Note. MAF = minor allele frequency; SNP = single-nucleotide polymorphism. Effect sizes for height are reported in standard deviation units. Note that these effect sizes tend to be inflated because of the winner’s curse. Strength was reported on a 5-point scale.

^aThe estimated effect in our study had a sign opposite to what had been previously reported.

Another recent meta-analysis⁵⁷ has identified 32 genomic regions containing a variant affecting BMI. BMI, even more than height, seems to be affected by many loci of small effect. Consistent with this view, 11 of the 17 known BMI loci represented in our data had estimated effect sizes of the correct sign; however, the wrong-signed loci were the most statistically significant.

Table 4 shows our results for a selection of SNPs previously reported to be associated with general cognitive ability,^58–62 personality,^63,64 working memory,⁶⁵ and episodic memory,⁶⁶ all of which we measured extensively. We observed little evidence for these associations in our own data. In concordance with a previous study,⁶⁷ we did not replicate a reported association between a common SNP in the gene KIBRA and episodic memory, despite a putative functional validation in the original study both by an analysis of gene expression and by functional MRI,⁶⁶ which suggests that most of the SNPs reported in earlier association studies of behavioral traits may either have been false positives or have overestimated effect sizes. Applying a threshold of 5 × 10⁻⁸, we did not observe any loci significantly associated with the traits in Table 4.

We did find a significant association between political conservatism and rs10952668 (Table 5). This SNP lies in LOC642355, a pseudogene on chromosome 7. Not surprisingly, the SNP also showed an association with the highly correlated trait of Democrat versus Republican (b = 0.260, P < .02). We also observed a significant association between rs1402494, which lies in a gene desert on chromosome 4, and gambling frequency. These novel associations are the only 2 that reached genome-wide significance; besides these, only eye color and hair color also produced significant associations.

TABLE 5—

Novel Association Results for Behavioral Phenotypes: Genome-Wide Association Study; Harvard University, Cambridge, MA, and Union College, Schenectady, NY; July 2007–June 2009

Trait	Reported SNP	Minor Allele	Sample MAF	HapMap MAF	Effect Size	P
Liberal vs conservative	rs10952668	T	.458	.392	.552 (.478)	2 × 10−8 (1 × 10−6)
Gambling frequency	rs1402494	G	.206	.241	.278 (.276)	3 × 10−8 (6 × 10−8)

Note. MAF = minor allele frequency; SNP = single-nucleotide polymorphism. Liberal versus conservative was reported on a 7-point scale. Gambling frequency was reported on a 5-point scale. Effect sizes and P values after adjustment for general cognitive ability, Openness, Neuroticism, and Agreeableness are given parenthetically. Note that effect estimates may be inflated as a result of the winner’s curse.

An interesting finding was that the SNP associated with political conservatism, rs10952668, also showed marginal evidence for association with the personality traits openness (b = 0.142, P < .06) and agreeableness (b = 0.130, P  < .08), which are positively correlated with political liberalism.⁶⁸ Because the correlation is positive, contrary to findings from political psychology that conservatives tend to be less open and agreeable (in the sense of compassionate⁶⁹), these results raise the possibility that the association between rs10952668 and conservatism may be attributable to selection bias rather than the gene causing the personality traits typical of conservatives. (Because to our knowledge this potential selection artifact has not been discussed in the genetic epidemiology literature—although it has parallels in the effects of natural selection on linkage disequilibrium—we explore it at some length in the Discussion section.) After we added general cognitive ability, openness, neuroticism, and agreeableness as covariates in an attempt to control for selection bias, the association of rs10952668 and conservatism diminished and fell short of significance. The association of rs1402494 and gambling frequency appears robust against our attempts to control for selection bias. We conclude that both of these associations must be replicated in much larger samples before they are accepted as true positives.

DISCUSSION

The contrast between pigmentation and the other phenotypes examined in this study is striking (Tables 3–4). Given a significance threshold of 5 × 10⁻⁸, our study had statistical power approaching 0.80 to detect any locus accounting for more than 10% of the variance in any trait. We retained some power (0.12) for loci accounting for as little as 5% of the variance. The fact that we measured so many phenotypes implies that we should have obtained several hits if a large proportion of the phenotypes were indeed affected by such loci. Because we only obtained at most 2 new hits, however, loci with effects of this magnitude on the nonpigmentation traits we studied (see Table A, available as a supplement to the online-only version of this article at http://www.ajph.org) must be uncommon. In agreement with previous studies,^11,64,70,71 we conclude that cognitive ability, personality dimensions, social attitudes, and most other traits of interest to behavioral scientists are affected by numerous loci of small effect. In this respect, the behavioral traits we studied resemble height and BMI rather than pigmentation.

How can we explain the differences in genetic architecture between the pigmentation traits and the other physical and behavioral traits? One possibility is that the architecture hinges on the length of the causal chain between gene and phenotype. Pigments, after all, are molecules, and one can change a molecule, thereby giving a person a different eye color, by changing a single gene. It is not as easy to make a person more intelligent, utilitarian, altruistic, or impulsive by changing one gene, owing to the greater complexity in the mechanisms that lead a person to be intelligent or altruistic in the first place. With gross physical traits such as BMI and height, the problem may be that genes can directly affect the phenotype in too many ways; indeed, it may be hard for a genetic change not to affect them, just as most changes to the features of, say, a car or laptop computer have consequences for its size and weight, which engineers have to trade off with many minute compensations.

The other explanation invokes the evolutionary model of the causes of genetic architectures we outlined earlier, which relates the effect size of genetic polymorphisms to the magnitude and recency of changes in the adaptively optimal level of the trait. After the loss of body hair in our lineage, pigmentation probably came under strong stabilizing selection in our ancestors, who needed protection from the African sun. More recently, the out-of-Africa migrants ancestral to Europeans and East Asians experienced a sudden and drastic shift in the optimal level of pigmentation, perhaps because of the need to sustain cutaneous synthesis of vitamin D in northern climates,⁷² although others have implicated sexual selection or as-yet unidentified evolutionary pressures.^73–75 In any event, the result was that several depigmenting mutations of large effect increased rapidly in frequency.^76–78

No such recent environmental change—with clear consequences for the direction and magnitude of the optimum—is apparent for other phenotypes such as height, BMI, and the behavioral traits we examined. Although differences in climate and food availability may select for different optima in body size and shapes, they fluctuate rapidly across space and time and may not show the consistent selection pressure that changes in latitude, altitude, and cloud cover apparently exerted on pigmentation. Intelligence is a highly general and universally adaptive trait that can translate into fitness benefits (via successful problem solving) in any environment. If human populations have long been at the optimum, then existing variants are likely to be small in effect. Such variants are likely to be small in effect even if the optimum has changed over time—as may have happened in the cases of intelligence^79,80 and religiosity⁸¹—so long as the change occurred very gradually. In particular, intelligence may respond more to coevolutionary pressures exerted by language and sociality than to any sudden change in the physical environment. Personality traits, too, are far less predictably correlated with physical environments than are pigmentation traits. Evolutionary game theory has established theoretical rationales for the persistence of multiple behavioral phenotypes (e.g., hawk-and-dove strategies) in the same population.^82,83 Analogously, the selective environment for personality may consist of the local distributions of the personalities of other people,⁸³ and the mixture is unlikely to have changed in a systematic way with recent shifts in the human population.

Even if selection has acted on these traits since the dispersal of Homo sapiens from Africa, the new optima could have quickly been reached by small shifts in allele frequency at many minor loci, leaving any major mutants at the low frequencies determined by the interaction of mutation, drift, and stabilizing selection.⁸⁴ As discussed earlier, the result of such dynamics would be the observed absence of common variants with large effects.

Our 2 proposals for explaining the pattern in Tables 3 to 5 lead to the following suggestions for future GWAS of behavioral traits. First, to understand the causal chain between genetic and phenotypic variation, researchers should try to narrow the chasm from both sides. Doing so requires seeking and validating endophenotypes that lie closer on the causal chain to genetic variation than the coarse and easily measured phenotypes researchers are used to. Second, researchers seeking variants of large effect should ideally study populations in which directional selection may recently have produced a phenotypic change that is large relative to the initial standing variation. Recent studies of altitude adaptation in Tibetans exemplify both of these suggestions.^85–87 The genes successfully associated with red blood cell count and hemoglobin concentration in these studies would have been more difficult to identify if the phenotype had been characterized at a level as abstract as altitude tolerance. Moreover, the recent and rapid divergence of Han Chinese and Tibetans in altitude tolerance after the latter began to occupy a highland environment was plausibly driven by a selection differential large enough to pull variants of large effect away from the boundary of frequency zero. How many social science traits can be studied by looking for recent directional selection, however, is an open question.

As for traits with more typical evolutionary histories, the expectation of small effect sizes requires that much larger samples be ascertained than are common in social science genetics research. We see 2 promising approaches. One is for researchers to take advantage of the potential for large sample sizes by allying with the burgeoning field of personal genomics, in which a large base of volunteers or consumers provides genotype and phenotype information.^46,88,89 It is crucial, though, to check these samples for selection biases, because many phenotypes of interest are likely to be causes of participation in personal genomics itself. For example, an individual with a liability to a particular disease may be strongly motivated to participate in a personal genomics study by self-interest or altruism; participants must also be wealthy enough to afford the service. We conjecture that our findings of elevated cognitive ability and intellectual openness among research volunteers will generalize to future studies. If so, it is prudent to collect reliable measurements of these traits in all GWAS that are not based on population samples and to note any unusual sample distributions of these traits when reporting SNP–trait associations.

The other approach is the traditional epidemiological study, which attempts to minimize the impact of personal characteristics on study participation by recruiting a population-based sample. This type of study will remain an important complement to volunteer- and consumer-driven approaches. Recall that Chabris et al.¹¹ analyzed data from 3 population-based studies and found that only 1 of 12 published genetic associations with general intelligence could be replicated within them, and that was replicated only 1 of 3 times. One explanation is that the original associations came from small convenience samples similar to the one we studied here.

The Trade-off Between Sample Size and Phenotype Quality

There is an inherent trade-off, however, in using large population-based studies for gene discovery. Most of these projects are directed toward medical outcomes rather than social science traits (with some notable exceptions, such as the Health and Retirement Study, the Wisconsin Longitudinal Study, and the English Longitudinal Study of Aging; the first of these now has GWAS data available, and the others may soon). Data collection in these surveys, although often face-to-face and longitudinal, distributes time and effort across many phenotypes that are measured with short questionnaires (or even single questions). The disadvantage of such studies is that whenever the underlying trait of interest is continuous, quick or brief measures are inherently less reliable (i.e., are subject to more measurement error) than are more detailed ones.

Genetic association studies, then, present researchers with a trade-off between using high-quality or high-technology (e.g., neuroimaging) measures of each phenotype, which are often only feasible for small samples, and having a large sample in which the phenotype is measured poorly. In social science research, this dilemma is commonly resolved in favor of smaller samples with higher-quality measures—and perhaps for this reason, that has been the strategy in most of the social science genetic association studies conducted to date, including the one we reported here. Because the genetic architecture of behavioral traits is likely to feature very weak genetic associations, however, our intuitions regarding the appropriate research strategy may not be correct when carried over from nongenetic social science research, in which effect sizes are typically much larger. As yet, no straightforward way exists to calculate an expected effect size for genetic associations in social science, so the best we can do is to assume that effects will be similar to those found for other complex (polygenic) traits—tiny.

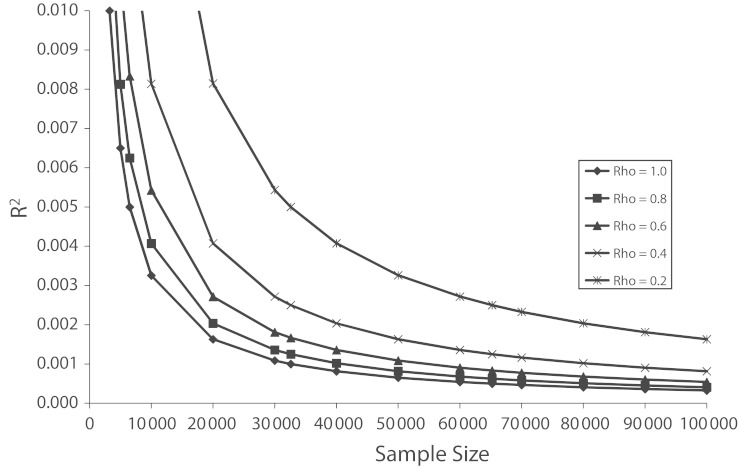
Figure 3 displays the results of a set of power calculations that quantify the trade-off. The phenotype is assumed to be normally distributed. The y-axis shows effect sizes in terms of R², the fraction of variance in the phenotype explained by variation in a single genotype, ranging from 0 to 0.01 (1%) in increments of 0.001 (one tenth of 1%). The x-axis is the sample size. Each curve graphs the locus of effect-size and sample-size pairs that gives 50% power to detect the association at P = 5 × 10⁻⁸ for a given phenotype reliability. The phenotype reliability is measured in terms of the test–retest correlation, that is, the correlation between 2 independent measurements of the phenotype. We consider the cases in which reliability is equal to 1.0, 0.8, 0.6, 0.4, and 0.2.

FIGURE 3—

Effect of the reliability (measurement error; Rho) of a phenotype on the relationship between effect size of a genetic association and the sample size required to achieve 50% statistical power to detect the effect at the genome-wide significance threshold of 5 × 10⁻⁸.

Note. For example, if one expects a genotype to explain 0.4% of the variance in a trait (R² = 0.004), then a sample of about 10 000 participants is required to achieve 50% power when reliability is 0.80, but a sample of 20 000 participants is required if reliability is 0.40. That is, with a sample of 20 000 instead of 10 000, instruments that are only one quarter as reliable provide the same power to detect the effect.

For the very small effect sizes that can be expected for behavioral traits, Figure 3 indicates that it will generally be better to sacrifice phenotype quality in favor of larger sample sizes. For example, consider an effect size of R² = 0.001 (0.1% of the variance), which is the size of the association found in a meta-analysis of the association between cognitive ability and variation in the COMT gene in 67 independent samples, and it is likely to be biased upward because the meta-analysis found evidence of publication bias.⁹⁰ Because cognitive ability is among the most reliably measured social science traits and because the meta-analysis found evidence of publication bias, such an effect size is likely to be representative of the largest associations we can expect for a behavioral trait. Given R² = 0.001, for a perfectly measured phenotype (reliability = 1.0) 50% power requires a sample size of 30 000 individuals. This is far too large a sample to obtain high-quality measures of behavioral traits, which generally requires bringing the research participants into a laboratory and conducting repeated tests spanning many minutes or hours. In contrast, for a phenotype with test–retest reliability of 0.6—which is typical of behavioral phenotypes measured by brief questionnaires—50% power requires a sample size of 50 000 individuals. Samples at least this large have recently become feasible. Medical data sets that have already collected GWAS data could much more easily add brief behavioral questionnaires to their ongoing data collections than onerous laboratory sessions. Because such medical data sets are in aggregate made up of hundreds of thousands of participants, such a research strategy should be possible.⁴ An important caveat, however, is that psychometric errors of measurement often represent stable characteristics of the study participants; unreliable measurements may therefore lead to spurious associations that do not replicate in studies that measure the chief phenotype of interest more accurately (in the sense of internal consistency). This potential problem might be addressed by using multiple parallel forms of a brief instrument across different studies.

Conclusions

We conducted a GWAS of more than 100 carefully measured phenotypes among more than 400 participants but found very few loci of large effect associated with any trait other than the pigmentation of eyes and skin, including a substantial proportion of the traits that have been of theoretical interest to behavioral scientists in recent decades. Four points emerge from our analysis:

1. The genetic architecture of trait variation cannot be taken as constant across traits, particularly the expectation that a single gene or a small number of genes will have a noticeable effect on the trait. First, the shortness of the causal chain between the DNA and the trait matters a great deal, with single-gene effects being more likely for traits generated by a single protein or regulatory shift. Second, the genetic architecture of a trait is intimately intertwined with its evolutionary history. The implications flow in both directions: the discovery of an association between a gene and a trait can illuminate the evolution of our species, and the evolutionary process determines which associations can most readily be discovered. In particular, stabilizing selection of moderate strength, which permits a substantial background of small-effect variants, supplies the fuel for polygenic adaptation and may obviate the need for mutations of large effect to arise after a sudden environmental change.

2. Many psychological traits of interest to researchers are themselves plausible causes of participation in scientific research, which raises the potential of spurious associations. Measuring such traits (e.g., cognitive ability and personality) and incorporating them into analyses is one strategy for dealing with this issue.

3. If there are 2 ways to measure a trait—a high-reliability measure that can be performed only on a small sample because of the required time, effort, and resources versus a lower reliability brief measure that can be administered to a large sample—power analyses suggest that using the lower-reliability measure with the larger sample size is likely to be the best strategy. Researchers interested in the genetic architecture of behavioral traits should therefore consider working with large-scale survey data sets such as the Health and Retirement Study, Wisconsin Longitudinal Study, and English Longitudinal Study of Ageing, as well as medical–genetic studies that are willing to conduct social science surveys among their participants.

4. Genetic associations with behavioral traits have proven notoriously difficult to replicate, not because the relevant traits are not heritable or the original studies were poorly designed or knowingly underpowered, but because researchers at the time lacked the resources to conduct more genotyping and assemble larger samples, and they were hoping to find common alleles with large effect size. Our discussion of Fisher’s model, and the empirical experience accumulated in the first 15 years of social science genetics, suggest that individual gene effect sizes for traits not under strong directional selection are likely to be extremely small and therefore require extremely large data sets to be detected.

The fact that faster, cheaper, and more powerful methods of genotyping have led to fewer, smaller, and less reliable findings on the connection between genes and behavior, despite the near-certainty that such connections exist, stands as a disappointment of 21st-century science. To make progress, researchers should shift away from the traditional model of epidemiology via statistical significance testing, in which large significant correlations are the standards of success and worthy of newspaper headlines and negative results are considered a failure and destined for the file drawer. It has become increasingly clear that this practice has led to mischief both in epidemiology and in social science,^91,92 and it may also be preventing the discovery of important scientific insights. If we have learned that behavioral genetic variation is caused by many genes with effects that are too small to currently measure, then we have also learned something important about the physiology and evolutionary history of such traits. With nature as with people, the Yiddish expression “No answer is also an answer” may apply.