Characterization of Dynamics in Complex Lyophilized Formulations: I. Comparison of Relaxation Times Measured by Isothermal Calorimetry with Data Estimated from the Width of the Glass Transition Temperature Region

Abstract

The purposes of this study are to characterize the relaxation dynamics in complex freeze dried formulations and to investigate the quantitative relationship between the structural relaxation time as measured by thermal activity monitor (TAM) and that estimated from the width of the glass transition temperature (ΔT_g). The latter method has advantages over TAM because it is simple and quick. As part of this objective, we evaluate the accuracy in estimating relaxation time data at higher temperatures (50°C and 60°C) from TAM data at lower temperature (40°C) and glass transition region width (ΔT_g) data obtained by differential scanning calorimetry. Formulations studied here were hydroxyethyl starch (HES)-disaccharide, HES-polyol and HES-disaccharide-polyol at various ratios. We also re-examine, using TAM derived relaxation times, the correlation between protein stability (human growth hormone, hGH) and relaxation times explored in a previous report, which employed relaxation time data obtained from ΔT_g. Results show that most of the freeze dried formulations exist in single amorphous phase, and structural relaxation times were successfully measured for these systems. We find a reasonably good correlation between TAM measured relaxation times and corresponding data obtained from estimates based on ΔT_g, but the agreement is only qualitative. The comparison plot showed that TAM data is directly proportional to the 1/3 power of ΔT_g data, after correcting for an offset. Nevertheless, the correlation between hGH stability and relaxation time remained qualitatively the same as found with using ΔT_g derived relaxation data, and it was found that the modest extrapolation of TAM data to higher temperatures using ΔT_g method and TAM data at 40°C resulted in quantitative agreement with TAM measurements made at 50 °C and 60 °C, provided the TAM experiment temperature is well below the T_g of the sample.

1 Introduction

Amorphous systems or glasses are an important class of pharmaceutical solids. Thermodynamically, amorphous solids are defined as ‘out of equilibrium’ states with reference to the crystalline state because of their excess free energy [1]. These high energy state solids are often used to improve solubility, dissolution and bioavailability of poorly soluble drugs [2]. Despite a significant amount of research input to understand the amorphous systems, the properties of glass dynamics are still not fully understood [3]. The “global” dynamics or relaxation dynamics of a glass is commonly described by the structural relaxation time, τ. Structural relaxation occurs when the amorphous system ‘relaxes’ towards the equilibrium supercooled state over time. During the process, the energy and free volume decreases. Structural relaxation is also known as enthalpy relaxation as heat is being released during the process [4]. In pharmaceutical development, one hypothesis is that pharmaceutical instability (i.e. degradation and crystallization) and structural relaxation should be correlated or ‘coupled’, since both processes requires some level of molecular mobility. Therefore a good understanding of structural relaxation may help to improve the stability of amorphous pharmaceutical solids [5], to the extent that this hypothesis is valid. This hypothesis is currently under investigation in several studies, and the data presented in this report is critical to these investigations.

The study of structural relaxation is often carried out using the calorimetry methods - differential scanning calorimetry (DSC) and isothermal microcalorimetry (i.e., the thermal activity monitor, TAM). In the DSC method, the enthalpy relaxation has been conventionally studied by measuring the enthalpy recovery of samples aged for various times at temperatures below the glass transition temperature, T_g. In TAM measurements, the enthalpy relaxation of a sample is directly measured during isothermal hold periods by monitoring the rate of heat release. These data (enthalpy recovery or relaxation) are then fitted with a decay function describing the kinetics of relaxation, either the Kohlrausch-William-Watts equation (KWW) or the alternative equation known as the modified stretch exponential (MSE), which normally provides a better representation of the data from TAM measurements. The application of KWW and MSE in relaxation studies have been well described and can be found in Kawakami et. al. [3] and Liu et. al. [4]. Although structural relaxation of amorphous systems have been successfully characterized using DSC and TAM, these techniques share one common disadvantage; that is the data acquisition times are very long, frequently on the order of days or longer, and particularly for TAM, large amount of sample are required.

In 2004, an alternative method was suggested by which one may estimate the relaxation time of amorphous systems below the T_g, using the T_g, change in heat capacity at the T_g and width of the T_g region (ΔT_g). The relationship (Section 2.2.4, Equation 1) was derived [6] by combining a series of equations based on observations by Moynihan [7], Angell [8] and the ‘modified’ Vogel-Tammann-Fulcher [9] equation. The advantage of Equation 1 is that structural relaxation of non-equilibrium glasses at any storage temperature of interest (below the T_g) can be estimated from a single DSC (or MDSC) run. Clearly, this method, if quantitative, would reduce the experimental time substantially, providing a quick and simple method to evaluate the dynamic parameters of pharmaceutical relevant amorphous systems. In the same report, the validity of Equation 1 was tested in single-component freeze dried disaccharides (trehalose and sucrose) at 30 °C, 40 °C and 50 °C, and PVP at 40 °C and 50 °C. Reasonably good quantitative agreement was found between the two relaxation time values for the disaccharide samples, but agreement was poorer for the PVP sample.

In a study of the correlation between glass dynamics and pharmaceutical stability in freeze dried amorphous human growth hormone [5], it was shown that the stability of human growth hormone (hGH) was superior in sucrose formulations than in the corresponding trehalose formulations, in spite of the observation that the relaxation time was found to be smaller in the sucrose formulations (i.e., global mobility greater in sucrose). Conversly, a comparison of “Fast Dynamics” in sucrose and trehalose formulations demonstrated that dynamics on a nanosecond timescale was dampened in sucrose relative to that in trehalose, suggesting that it is “Fast Dynamics” that is more predictive of pharmaceutical stability than is “global dynamics”. However, the relaxation times reported were evaluated from the width of the glass transition region (ΔT_g method). While the ΔT_g method was believed to be sufficiently accurate for the purpose, direct confirmation of this assumption is needed. Such is one objective of the present report.

Thus, the general objective of this study is to investigate the quantitative relationship between the two relaxation times obtained from the TAM and ΔT_g methodologies for a series of freeze dried hydroxyethyl starch (HES)-disaccharides, HES-polyol and HES-disaccharide-polyol mixtures. Such multiple components formulations are of interest because they have been shown to improve the stability of native structure of proteins in dried solids [10]. As part of this objective, we also evaluate the accuracy (and utility) of estimating relaxation data at 50 °C and 60 °C using TAM data obtained at 40 °C and ΔT_g data. Even if there are serious quantitative differences between TAM and ΔT_g data overall, our hypothesis is that accurate extrapolations of TAM data can be made over short temperature ranges, and if so, such methodology would be extremely useful in comparisons of global mobility data with pharmaceutical stability.

2 Materials and Methods

2.1 Materials

HES (Frensenius Kabi, Graz, Austria; L19700642/1708135101; mean molecular weight of 220 kDa), sucrose (Sigma Aldrich, St. Louis, MO; Lot 040M0073), trehalose (Pfannstiehl Laboratory Inc., Waukegan, IL; Lot 25654A), sorbitol (Pfannstiehl Laboratory Inc., Waukegan, IL; Lot 24832A), glycerol (ICN Biomedicals Inc., Aurora, OH; Lot 1905A) were used as received. Phosphate buffer salts were purchased from Fischer Scientific, Fairlawn, NJ. Human growth hormone was obtained and handled as previously described [5].

2.2 Methods

2.2.1 Composition of formulations

Overall, five categories of freeze dried formulations were prepared; (A) HES + disaccharide (trehalose or sucrose) at total solids content of 5%, (B) HES 5% + sorbitol or glycerol 0-1%, (C) HES 5% + trehalose 1% + sorbitol or glycerol 0-1%, (D) HES 5% + trehalose 3% + sorbitol or glycerol 0-1% and (E) HES 0.75% + trehalose:glycerol (total solid of 3.75%). Composition details of these formulations are shown in Table 1. Formulations (A-D) were prepared in 2 mM phosphate buffer at pH 7.0, while formulation (E) HES 0.75% + trehalose:glycerol systems where dissolved in deionised water.

Table 1.

Composition of HES, disaccharides and polyols in the freeze dried formulations.

Formulations	HES:Disacdiaride ratio
(A) HES + disaccharide (trehalose or sucrose) (Total solid of 5%)	5 : 0
	4 : 1
	2.5 : 2.5
	1 : 4
	0 : 5
	Amount of sorbitol or glycerol
(B) HES 5% + (C) HES 5% + trehalose 1% + (D) HES 5% + trehalose 3% + (Variable solid content, 5 – 9%)	none
	sorbitol 0.5 %
	sorbitol 1 %
	glycerol 0.5 %
	glycerol 1 %
	Trehalose:glycerol ratio, 3% total
(E) HES 0.75% + trehalose:glycerol (Total solid of 3.75%)	3 : 0
	2.91 : 0.09
	2.85 : 0.15
	2.70 : 0.30
	2.55 : 0.45

2.2.2 Freeze drying procedures

All formulations were filtered (0.22 micron) prior to vial filling and were then freeze dried using a FTS Durastop system. Daikyo Flurotec stoppers (West Pharmaceutical, Lititz, PA) were used for all the freeze drying in vials. Product temperatures (were targeted and maintained at ≈2 °C below the formulation with the lowest T_g’) were measured via copper-constantan thermocouples, placed in the bottom centre of a vial. Primary drying was judged complete when the product temperature equals the shelf temperature. After a delay time (~15% of primary drying time), the shelf temperature was increased for secondary drying. A summary of the freeze drying procedures, vial sizes and fill volumes are shown in Table 2. All samples have a fill depth of ≤1 cm. At the end of freeze drying cycle, the chamber was vented with dry nitrogen gas, the vials were sealed in the chamber, and then capped with an aluminium seal before storing it at –20 °C until analysis. In theory, at –20 °C, thermal history of the samples is ‘preserved’. Visual inspection was also carried out to confirm the absence of collapse. Residual moistures were <1% by Karl Fisher assay. The absence of birefringence under the polarized light microscopy (PLM) indicated the freeze dried formulations were amorphous.

Table 2.

Freeze drying parameters used for the series of formulations in this study.

Formulation	Fill volume (vial size)	Target product temperature	Chamber pressure	Freezing temperature (ramp rate)	Primary drying		Secondary drying
					Shelf temperature (ramp rate)	Drying Time	Shelf temperature (ramp rate)	Drying time
HES + disaccharide (i.e. Formulation A)	1 mL (5 cc)	–40 °C	70 mTorr	–45 °C (1 °C/min)	–20 °C (1.3 °C/min)	~12 h	+33 °C (0.3 °C/min)	2 h
Samples with sorbitol in formulation B, C and D	2 mL (5 cc)	–31 °C	100 mTorr	–40 °C (1 °C/min)	–18 °C (0.2 °C/min)	~43 h	+40 °C (0.1 °C/min)	6 h
Samples with glycerol in formulation B, C and D	2 mL (5 cc)	–40 °C	60 mTorr	–45 °C (1 °C/min)	–34 °C (0.2 °C/min)	~88 h	+40 °C (0.1 °C/min)	5 h
HES 0.75% + trehalose:glycerol (i.e. Formulation E)	5 mL (20 cc)	–40 °C	70 mTorr	–45 °C (1 °C/min)	–34 °C (0.2 °C/min)	~72 h	+40 °C (0.1 °C/min)	6 h

2.2.3 Characterization of freeze dried glasses

All sample handling of the freeze dried formulations were done in a dry bag purged with dry nitrogen gas to avoid moisture being taken up by the sample during sample preparation. A hygrometer was used to ensure the environment in the bag was essentially moisture free (RH of <5%).

2.2.3.1 Differential scanning calorimetry (DSC)

Modulated DSC Q1000 (v9.8, Build 296, TA Instrument, New Castle, DE) was used to determine the T_g and the change in the heat capacity (ΔC_p) at the T_g. The temperature and heat capacity were calibrated using indium and sapphire, respectively as calibration standards. Sample powders (3 to 10 mg) were compacted into disks and sealed in hermatic aluminum pans. The measurements were carried out at a heating rate of 1 °C per min from –30 up to 280 °C under a nitrogen gas flow of 50 mL/min. The modulation amplitude was 0.5 °C and the period was 100 s. The T_g was determined as the midpoint of the ΔC_p of the sample.

2.2.3.2 Isothermal microcalorimetry

Enthalpy relaxation of the freeze dried amorphous samples was measured using the Thermal Activity Monitor (TAM, Thermometric, Sweden). Two 4 mL stainless steel ampoules (one reference, one sample) were used for the analysis. Approximately 100-200 mg of sample was used for each measurement. Crystalline glycine (Sigma Aldrich, St. Louise, MO; batch 083K0160), a thermally inert sample was used as a reference for all TAM measurements. Samples were first equilibrated at the equilibration position for 30 min before being lowered down into the measurement position. Data acquisition was initiated from the time when the samples were placed into the TAM channels (i.e., the measurement position). Due to the disturbance during lowering of the ampoules from equilibration to measurement position, only TAM data after the first hour were used for analysis. Enthalpy relaxation data were acquired at 40 °C, 50 °C and 60 °C for at least 72 hr. The specific power-time curves were then fitted with KWW and MSE equations [3] to obtain the τ (hours) and β values. Due to systematic errors in τ and β values [3], the more accurate and robust result, τ^β is reported. Comparison of structural relaxation time is based on the natural log scale values; ln (τ^β)_KWW and/or ln (τ_D^β)_MSE.

2.2.4 Structural relaxation by the width of glass transition temperature, ΔT_g

The relationship between structural relaxation time, τ, T_g (in Kelvin) and ΔT_g was established previously [6],

$$\ln {\tau }^{\beta }\cong \ln {\left({\tau }^{\beta }\right)}_{{\mathrm{T}}_{\mathrm{g}}}+\frac{\mathrm{C}}{(\Delta {\mathrm{T}}_{\mathrm{g}}∕{\mathrm{T}}_{\mathrm{g}})}\cdot \left[1-\gamma \cdot \left(1-\frac{36.9\cdot \beta }{\mathrm{C}}\cdot \frac{\Delta {\mathrm{T}}_{\mathrm{g}}}{{\mathrm{T}}_{\mathrm{g}}}\right)\right]\cdot \left(1-\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{g}}}\right)$$ (1)

The value ln (τ^β)_Tg is roughly a constant and was found to be ≈ – 1.6 in a series of samples with different fragility [6]. The parameters in the bracket [...] is used to estimate the temperature dependence of the relaxation time constant at storage temperature of interest T (K), and is calculated using C, β, ΔT_g and γ. The value C is a constant related to DSC protocols used to probe the T_g data. For MDSC protocol at a heating rate of 1 °C per min, C was estimated to be 2.45 [6]. The symbol β is the stretch power in the KWW expression. The value of β is normally between 0.3 – 0.5 for most pharmaceutical relevant systems [6]; here we used β = 0.4. ΔT_g is calculated from the E = 0 method as described previously [6]. Briefly, the onset and offset of T_g are the intersection of a tangent line drawn from the inflection point at the T_g region (i.e. midpoint) with the tangent line of the ‘baseline’ before and above the T_g, respectively. The parameter, γ, can be estimate using the empirical relationship [5, 6]

$$\gamma \cong \frac{\Delta {\mathrm{C}}_{\mathrm{p}}}{\Delta {\mathrm{C}}_{\mathrm{p}}+0.00331\cdot \text{exp}(6.63\cdot \Delta {\mathrm{C}}_{\mathrm{p}})}$$ (2)

Errors in the calculated values of “ln(τ^β)_ΔTg” were estimated using the propagation of errors methodology, assuming errors in the input parameters for Equation 1 are all independent.

2.2.5 Estimating structural relaxation time at 50 °C and 60 °C using ΔT_g method and TAM relaxation data at 40 °C, (ln (τ^β)_TAM-ΔTg)

Here we examined the reliability of estimating the dynamics at other temperatures below the T_g by combining experimental TAM results and ΔT_g method using the expression as given below,

$$\ln {\left({\tau }^{\beta }\right)}_{\mathrm{TAM}-\Delta {\mathrm{T}}_{\mathrm{g}}(\mathrm{Y}°\mathrm{C})}=\ln {\left({\tau }_{\mathrm{D}}^{\beta }\right)}_{\mathrm{MSE}(\mathrm{X}°\mathrm{C})}+\lfloor \ln {\left({\tau }^{\beta }\right)}_{\Delta {\mathrm{T}}_{\mathrm{g}}(\mathrm{Y}°\mathrm{C})}-\ln {\left({\tau }^{\beta }\right)}_{\Delta {\mathrm{T}}_{\mathrm{g}}(\mathrm{X}°\mathrm{C})}\rfloor$$ (3)

where ln (τ^β)_TAM-ΔTg, ln (τ_D^β)_MSE and ln (τ^β)_ΔTg are structural relaxation times obtained from TAM-ΔTg method, TAM and ΔT_g approach, respectively, at two temperatures X and Y °C.

3 Results and discussion

3.1 Thermal parameters as characterized by MDSC

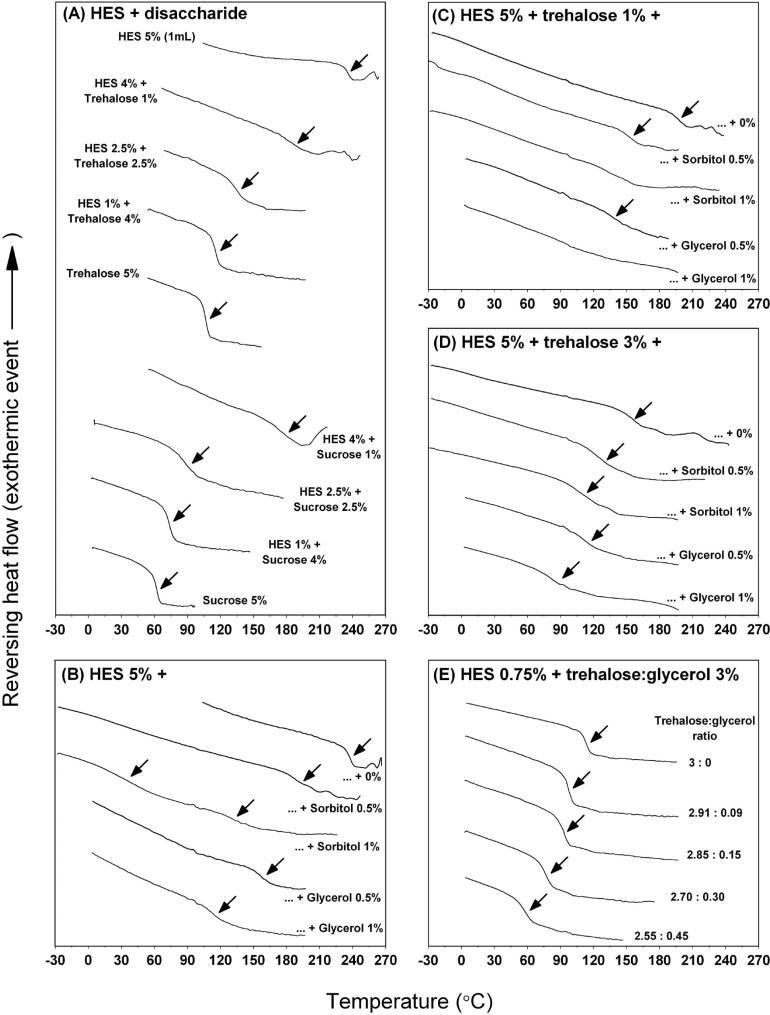
The MDSC thermograms of freeze dried HES-disaccharides, HES-polyol and HES-disaccharide-polyol formulations are shown in Figure 1. Overall, MDSC analysis of the formulations showed a single T_g (arrows as indicated in Figure 1) in the range of 64 °C to 237 °C with estimated ΔC_p at the T_g between 0.217 and 0.647 J/(g·°C) (Table 3). The single T_g observed in these formulations suggest that the freeze dried formulations exist as a single amorphous phase system. However in two samples, MDSC analysis was unable to detect a clear T_g, for HES 5% + trehalose 1% + sorbitol and glycerol at 1% systems (Figure 1C; mid and bottom thermogram, respectively). In another system (HES 5% + sorbitol 1%), MDSC analysis showed two T_gs at 36 °C and 134 °C (Figure 1B; mid thermogram), suggesting a two phase system.

Figure 1.

MDSC thermograms of the freeze dried formulations. (A) HES + disaccharide (trehalose or sucrose) at a total solid of 5%, (B) HES 5% + sorbitol or glycerol 0-1%; (C) HES 5% + trehalose 1% + sorbitol or glycerol 0-1%; (D) HES 5% + trehalose 3% + sorbitol or glycerol 0-1% and (E) HES 0.75% + trehalose:glycerol. The arrows indicate an observed T_g or T_gs. The y-axis of the thermograms is offset for clarity.

Table 3.

Thermal parameters (MDSC analysis) and water content for the freeze dried formulations (n ≥ 3) and predicted T_g (using Fox equation). Uncertainties are standard errors.

Formulation	Predicted Tg using Fox equation (°C)	MDSC analysis			Water content (%)d
		Tg (midpoint) (°C) ± SD	ΔCp at Tg (J/(g·°C)) ± SD	ΔTg ± SD
(A) HES + disaccharide
HES 5%	234a	234 ± 2	0.217 ± 0.021	9.5 ± 0.5	0.28
HES 4% + trehalose 1%	206	182 ± 4	0.206 ± 0.017	20.0 ± 1.3	0.20
HES 2.5% + trehalose 2.5%	169	127 ± 2	0.370 ± 0.011	15.4 ± 0.7	0.26
HES 1% + trehalose 4%	137	114 ± 1	0.454 ± 0.009	7.9 ± 1.1	0.19
Trehalose 5%	118b	105 ± 1	0.548 ± 0.025	6.4 ± 0.4	0.28
HES 4% + sucrose 1%	194	170 ± 3	0.274 ± 0.022	25.7 ± 1.8	0.10
HES 2.5% + sucrose 2.5%	140	87 ± 1	0.440 ± 0.024	8.7 ± 0.2	0.35
HES 1% + sucrose 4%	98	73 ± 1	0.576 ± 0.023	9.9 ± 0.6	0.30
Sucrose 5%	75c	64 ± 1	0.647 ± 0.012	6.9 ± 0.4	0.55
(B) HES + sorbitol or glycerol
HES 5%	234a	237 ± 1	0.217 ± 0.033	8.3 ± 0.9	not determined
+ sorbitol 0.5%	197	189 ± 2	0.226 ± 0.029	15.8 ± 1.5	not determined
+ sorbitol 1%	170	36 and 134	not determined	not determined	not determined
+ glycerol 0.5%	165	162 ± 4	0.199 ± 0.042	17.2 ± 2.5	not determined
+ glycerol 1%	121	116 ± 3	0.259 ± 0.056	25.6 ± 7.1	not determined
(C) HES + trehalose 1% + sorbitol or glycerol
HES 5% + trehalose 1%	210	197 ± 1	0.246 ± 0.021	19.8 ± 3.6	not determined
+ sorbitol 0.5%	183	156 ± 2	0.252 ± 0.003	25.8 ± 1.8	not determined
+ sorbitol 1%	162	not detected	not detected	not determined	not determined
+ glycerol 0.5%	157	138 ± 4	0.283 ± 0.075	26.1 ± 7.1	not determined
+ glycerol 1%	120	not detected	not detected	not determined	not determined
(D) HES + trehalose 3% + sorbitol or glycerol
HES 5% + trehalose 3%	183	151 ± 2	0.307 ± 0.046	20.0 ± 3.1	not determined
+ sorbitol 0.5%	166	125 ± 1	0.365 ± 0.077	23.7 ± 3.0	not determined
+ sorbitol 1%	151	102 ± 2	0.375 ± 0.068	23.0 ± 2.7	not determined
+ glycerol 0.5%	147	108 ± 3	0.360 ± 0.008	23.8 ± 1.6	not determined
+ glycerol 1%	120	81 ± 1	0.348 ± 0.042	24.8 ± 1.2	not determined
(E) HES 0.75% + trehalose:glycerol
HES 0.75% + trehalose 3%	137	114 ± 5	0.490 ± 0.033	8.8 ± 0.4	0.19
+ trehalose 2.91%; glycerol 0.09%	126	97 ± 1	0.504 ± 0.012	8.9 ± 0.5	0.24
+ trehalose 2.85%; glycerol 0.15%	119	91 ± 2	0.511 ± 0.030	11.6 ± 1.8	0.21
+ trehalose 2.70%; glycerol 0.30%	102	76 ± 1	0.503 ± 0.021	12.2 ± 0.9	0.21
+ trehalose 2.55%; glycerol 0.45%	87	62 ± 2	0.492 ± 0.027	13.3 ± 1.4	0.18

SD denotes standard deviation.

^aThe T_g (midpoint) of HES was obtained from reference 12.

^bThe T_g (midpoint) of amorphous trehalose was obtained from reference 13.

^cThe T_g (midpoint) of amorphous sucrose was obtained from reference 13.

^dThe average standard error of water content was 0.03

A summary of the thermal parameters for these formulation systems can be found in Table 3. Comparing between T_g predicted from the simple Fox equation (reciprocal of T_g of a mixture is the sum of the reciprocals of the component T_g's) and experimental T_g, for most formulations the difference is greater than 20 °C. Only a few formulations showed small difference (less than 10 °C) between experimental and predicted T_g value. It was interesting to note that while some formulations showed a sharp change at the T_g (i.e., small ΔT_g), other formulations yield a broad transition, especially samples containing a high proportion of HES. The values of ΔT_g vary between 6K and 26K, indicating a wide range of fragilities in the mixtures freeze dried.

3.2 Relaxation dynamics by TAM and ΔT_g

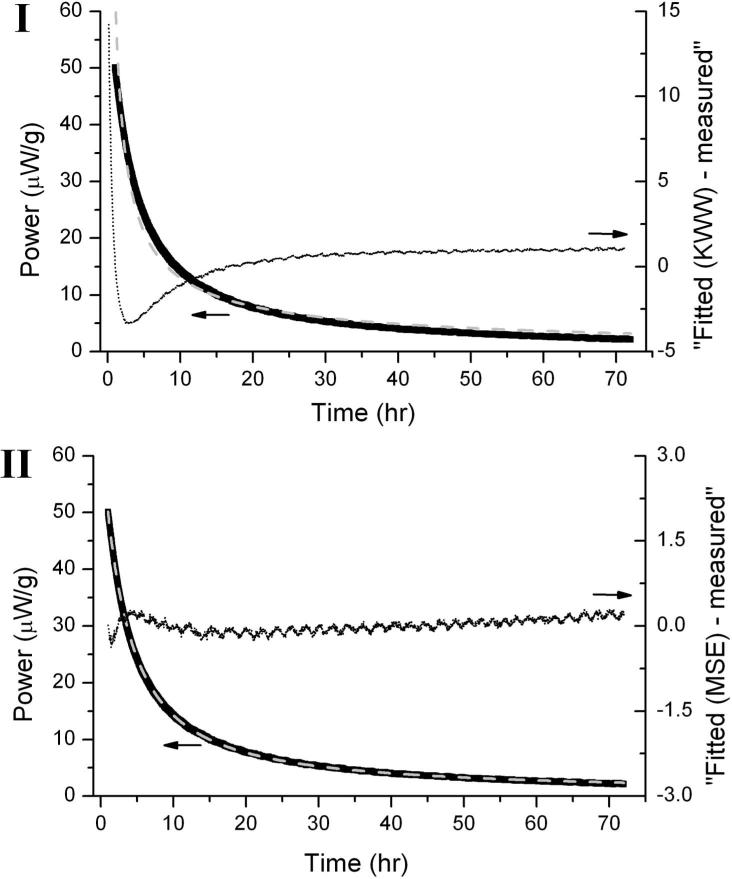
TAM relaxation time values obtained from KWW and MSE analysis are generally in good agreement for formulation category (B), (C), (D) and (E) (τ in hours). However in formulation (A), considerable differences in the ln(τ^β)_KWW and ln(τ_D^β)_MSE values were observed. In this series of formulations, the KWW analysis yields “unphysical” low beta values (i.e. < 0.1). In pharmaceutical systems, the beta value has been estimated to be between 0.3-0.5 [6]. This behavior is likely a result of systematic errors introduced, in part, by the fact that the KWW equation in power form (i.e., time derivative of energy) approaches infinity as time approaches zero. The MSE equation does not have this flaw [4]. Owing to the disadvantages of KWW equation, MSE analysis is generally the preferred methodology to evaluate the relaxation parameters for glassy systems from TAM data. Not only does the MSE analysis give a better fit than does the KWW power equation, as shown in an example in Figure 2, the error associated with ln(τ^β)_MSE (reported as standard deviation) is also lower compared to the error in ln(τ^β)_KWW (Table 4).

Figure 2.

An example showing the fitted curve (grey dash line) on the 72 h relaxation enthalpy data (black line) of HES 5% + trehalose 3% + sorbitol 1% formulation using (I) KWW and (II) MSE derivative expression (arrows indicating to the left). The difference between fitted and measured values (dotted line) as a function of time is also presented on the respective graphs (arrows indicating to the right). Note that MSE curve fitting gave a better fit compare to KWW.

Table 4.

Relaxation times (τ in hours) of freeze-dried formulations evaluated with the TAM and ΔT_g methods at 40 °C (n ≥ 3). KWW and MSE derivative expression were used to obtain the relaxation parameters from the TAM data, and Equation 1 was used to calculate for the relaxation parameters from the ΔT_g method (a β value of 0.4 was used for the calculation). The standard error is given for all structural relaxation times obtained by KWW, MSE and ΔT_g method. Note that the relaxation parameters (τ and τ_D (hr), β, τ^β, τ_D^β, ln (τ^β)_KWW, ln (τ_D^β)_MSE and ln (τ^β)_ΔTg) reported here represents the arithmetic mean of a number of independent experimental values. However, note that the mean of independent τ^β or τ_D^β values, as tabulated, are not exactly the same as the corresponding parameters calculated from the mean values of β and τ or β and τ_D. The tabulated τ^β or τ_D^β values should be used when making comparisons as these values are more accurate.

Formulations	KWW				MSE				ΔTg
	τ (hr)	β	τ β	ln (τβ) ± SD	τD (hr)	β	τ D β	ln (τDβ) ± SD	ln (τβ) ± SD; β = 0.4
(A) HES + disaccharide
HES 5%	3.4 E+14	0.05	5.8	1.6 ± 0.6	1.1 E+09	0.19	45.3	3.8 ± <0.1	6.7 ± 0.4
HES 4% + trehalose 1%	1.2 E+08	0.07	4.1	0.9 ± 0.9	1.3 E+08	0.20	26.2	3.3 ± 0.1	3.8 ± 0.4
HES 2.5% + trehalose 2.5%	1.9 E+07	0.08	4.2	1.1 ± 0.9	2.3 E+07	0.20	23.5	3.2 ± 0.1	2.6 ± 0.2
HES 1% + trehalose 4%	1.5 E+06	0.07	3.1	0.8 ± 0.8	4.5 E+07	0.19	21.3	3.1 ± 0.1	3.8 ± 0.7
Trehalose 5%	6.6 E+06	0.07	3.0	0.4 ± 0.9	6.0 E+07	0.19	21.3	3.1 ± 0.1	5.1 ± 0.4
HES 4% + sucrose 1%	4.5 E+02	0.04	0.9	-0.2 ± 0.4	1.6 E+09	0.17	22.8	3.1 ± <0.1	3.3 ± 0.3
HES 2.5% + sucrose 2.5%	2.2 E+01	0.10	1.2	0.1 ± 0.3	5.1 E+05	0.18	9.7	2.3 ± 0.2	1.7 ± 0.1
HES 1% + sucrose 4%	8.4 E+01	0.16	1.7	0.3 ± 0.6	2.3 E+04	0.19	6.7	1.9 ± 0.1	1.2 ± 0.2
Sucrose 5%	2.0 E+01	0.19	1.5	0.3 ± 0.4	2.7 E+03	0.21	5.0	1.6 ± 0.2	1.5 ± 0.2
(B) HES + sorbitol or glycerol
HES 5%	5.0 E+06	0.26	63.1	4.1 ± 0.1	9.9 E+06	0.29	94.3	4.5 ± 0.1	7.3 ± 0.9
+ sorbitol 0.5%	6.8 E+06	0.24	42.4	3.7 ± 0.2	7.6 E+07	0.24	58.2	4.1 ± 0.1	4.3 ± 0.6
+ sorbitol 1%	-	-	-	-	-	-	-	-	-
+ glycerol 0.5%	3.1 E+08	0.15	14.5	2.6 ± 0.5	7.3 E+07	0.20	34.4	3.5 ± 0.1	3.3 ± 0.7
+ glycerol 1%	1.1 E+08	0.11	9.6	2.2 ± 0.3	6.3 E+08	0.17	30.1	3.4 ± 0.1	1.6 ± 0.9
(C) HES + trehalose 1% + sorbitol or glycerol
HES 5% + trehalose 1%	2.9 E+07	0.22	44.9	3.8 ± 0.1	3.6 E+08	0.23	66.0	4.2 ± 0.1	4.3 ± 1.1
+ sorbitol 0.5%	6.4 E+05	0.27	35.6	3.6 ± 0.1	9.7 E+06	0.23	40.4	3.7 ± <0.1	2.8 ± 0.3
+ sorbitol 1%	-	-	-	-	-	-	-	-	-
+ glycerol 0.5%	1.5 E+06	0.21	18.7	2.9 ± 0.2	1.2 E+07	0.22	29.6	3.4 ± 0.1	2.3 ± 1.1
+ glycerol 1%	-	-	-	-	-	-	-	-	-
(D) HES + trehalose 3% + sorbitol or glycerol
HES 5% + trehalose 3%	1.3 E+06	0.28	48.3	3.9 ± <0.1	3.4 E+07	0.23	52.3	4.0 ± 0.1	3.0 ± 0.7
+ sorbitol 0.5%	2.6 E+05	0.29	37.9	3.6 ± 0.1	3.6 E+06	0.26	42.6	3.7 ± 0.1	2.1 ± 0.5
+ sorbitol 1%	3.3 E+04	0.34	30.9	3.4 ± 0.2	3.6 E+05	0.28	29.5	3.4 ± 0.1	1.2 ± 0.3
+ glycerol 0.5%	1.3 E+05	0.27	22.0	3.1 ± 0.1	2.0 E+10	0.20	22.7	3.1 ± 0.3	1.4 ± 0.2
+ glycerol 1%	5.2 E+03	0.25	8.4	2.1 ± 0.1	8.5 E+04	0.21	10.8	2.4 ± <0.1	0.3 ± 0.1
(E) HES 0.75% + trehalose:glycerol
HES 0.75% + trehalose 3%	1.3 E+07	0.24	39.4	3.6 ± 0.4	5.4 E+08	0.19	43.2	3.8 ± 0.1	3.9 ± 0.2
+ trehalose 2.91%; glycerol 0.09%	1.4 E+05	0.31	37.1	3.6 ± 0.1	2.3 E+07	0.22	32.5	3.5 ± 0.1	2.8 ± 0.2
+ trehalose 2.85%; glycerol 0.15%	1.0 E+05	0.31	32.6	3.5 ± 0.2	1.3 E+12	0.17	23.1	3.1 ± 0.3	1.9 ± 0.5
+ trehalose 2.70%; glycerol 0.30%	5.7 E+03	0.32	16.6	2.7 ± 0.5	3.6 E+05	0.21	13.1	2.5 ± 0.3	0.8 ± 0.2
+ trehalose 2.55%; glycerol 0.45%	5.1 E+02	0.39	11.0	2.4 ± 0.1	4.5 E+03	0.28	8.1	2.1 ± 0.2	–0.2 ± 0.2

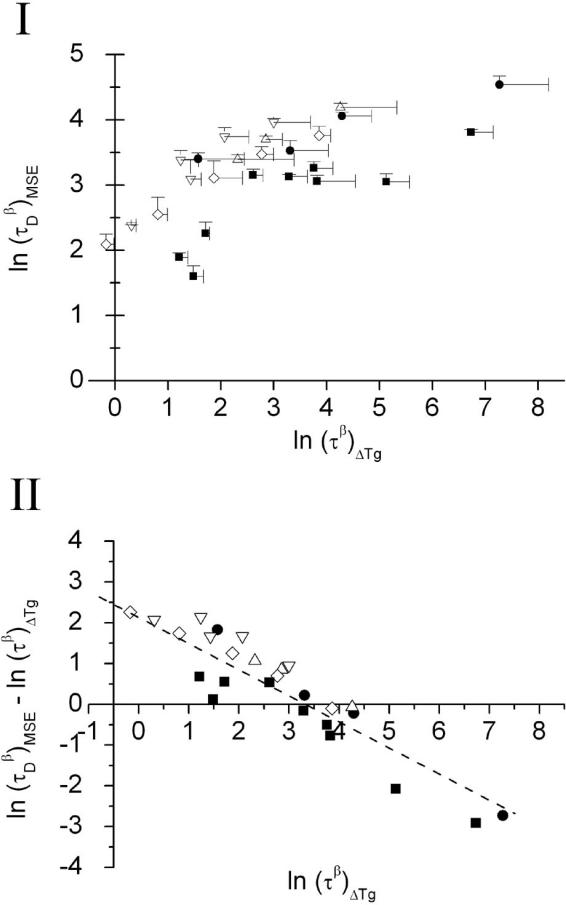
The ln(τ^β)_ΔTg values calculated from the ΔT_g method are also shown in Table 4. Comparison of ln(τ^β)_ΔTg values with ln(τ^β)_KWW or ln(τ^β)_MSE, results clearly shows that ln(τ^β)_ΔTg is closer to ln(τ_D^β)_MSE than ln(τ^β)_KWW. Figure 3(I) shows the comparison plot of ln(τ_D^β)_MSE versus ln(τ^β)_ΔTg. It is clear that while results from the two methods are correlated, agreement is only qualitative. A plot of [ln(τ_D^β)_MSE – ln(τ^β)_ΔTg] versus ln(τ^β)_ΔTg yield a linear plot, ln y = – 0.72 · ln x + 2.4 and R² = 0.86 (Figure 3(II)). This indicates ln(τ_D^β)_MSE is directly proportional to the 1/3 power of ln (τ^β)_ΔTg, after correcting for the offset. We note that the intercept observed here (y = 2.4) is similar to the offset observed with the PVP sample (extrapolated results) from a previous study [6].

Figure 3.

(I) Comparison of relaxation data determined from the TAM method at 40 °C (using MSE fitting) with the ΔT_g method for the series of freeze dried formulations. The standard deviations for both relaxation times are indicated by the error bars. (II) A plot of [(ln τ_D^β)_MSE – (ln τ^β)_ΔTg] versus ln (τ^β)_ΔTg. The dash line is the linearly fitted line (ln y = – 0.72 · ln x + 2.4; R² = 0.86). Symbol keys for formulations; ■ - (A) HES + disaccharide (trehalose or sucrose) at total solid of 5%; ● - (B) HES 5% + sorbitol or glycerol 0-1%; △ - (C) HES 5% + trehalose 1% + sorbitol or glycerol 0-1%; ▽ - (D) HES 5% + trehalose 3% + sorbitol or glycerol 0-1% and ◇ - (E) HES 0.75% + trehalose:glycerol.

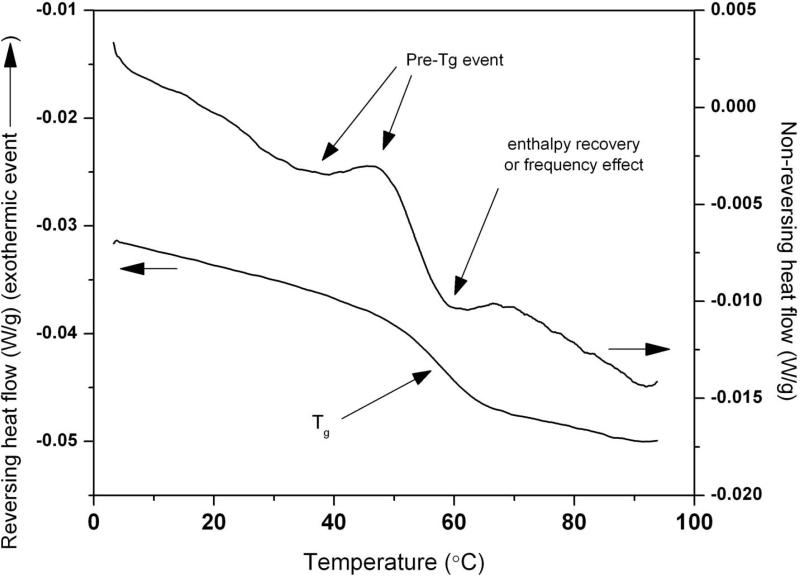
Generally, the range of relaxation times estimated by the ΔT_g method is larger than the TAM-MSE determined values. In some samples, very small relaxation times were predicted by the ΔT_g method (points that were very close to the y-axis). Based on the non reversing thermograms, a pre-T_g event (Figure 4) was observed in these samples, suggesting there are two relaxing populations. The precise impact of the pre-T_g event on the ΔT_g calculation is unknown. However as the theoretical rationale for the ΔT_g method (Equation 1) assumes a single distribution of states, and at least a bi-exponential distribution was observed here, it is perhaps not surprising that the use of Equation 1 may lead to significant systematic errors.

Figure 4.

Reversing and non-reversing MDSC thermograms of sample HES 0.75% + trehalose 2.55% + glycerol 0.45 % (coordinate (–0.17, 2.1) in Figure 3(I)). Note the small endo-exothermic wave-like event (i.e. a pre-T_g) prior to the enthalpy recovery or frequency effect on the non-reversing thermogram.

3.3 Estimating relaxation dynamics at 50 °C and 60 °C using the ΔT_g method and TAM relaxation data at 40 °C (TAM-ΔT_g method)

The stability of a pharmaceutical compound is commonly investigated at more than one storage temperature, and there is therefore also an interest in relaxation data at multiple temperatures. Thus, a simple and accurate method to extrapolate relaxation data from one temperature to another would have practical use. Thus, here we investigate the feasibility of obtaining, with useful accuracy, the structural relaxation times of HES-disaccharide systems estimated at 50 °C and 60 °C from TAM data measured at 40°C, using the ΔT_g method to enable the extrapolation (i.e., using equation 3). The comparison of estimated and directly measured (via TAM) structural relaxation times are shown in Table 5. Overall, structural relaxation times at 50 °C ‘calculated’ from TAM-ΔT_g method showed excellent agreement with the structural relaxation data measured by TAM, validating the extrapolation procedure for small extrapolations. The agreement at 60°C is generally acceptable, with the only exceptions being the trehalose 5% and sucrose 5% sample where a difference of 1-2 orders of magnitude was observed between the estimated and directly measured relaxation data at 60°C (Table 5). For trehalose 5% ln(τ_D^β)_MSE > ln(τ_β)_TAM-ΔTg, however ln(τ^β)_TAM-ΔTg > ln(τ_D^β)_MSE for the sucrose 5% sample. The discrepancy in the trehalose 5% could be due to heterogeneity of relaxation dynamics noted earlier (i.e., the pre-T_g thermal event), thus resulting in slower relaxation dynamics (i.e. larger ln(τ_D^β)_MSE value) as measured by the TAM method. An exo-/endothermic event prior to the T_g has been reported in an aspartame:trehalose freeze dried formulation at 1:10 w/w ratio [11]. For the sucrose 5% sample, a larger ln(τ_D^β)_MSE value is not surprising given the fact that the formulation has a T_g (midpoint) of 64 °C (Table 3). Clearly at 60 °C, the TAM experiment is being carried out at or close to the T_g region, essentially at the onset, and in this case, one questions the validity of the TAM measurement. Generally, due to excessive relaxation during the thermal equilibration period, one does not carry out TAM measurements this close to the T_g onset.

Table 5.

Comparison of structural relaxation times (τ in hours) of freeze dried HES-disaccharides formulations obtained by TAM and TAM-ΔT_g method at 50 °C and 60 °C (n = 2; n = 3 where SD is given). In TAM-ΔT_g method, TAM data at 40 °C was used.

HES + disaccharide formulations	Experimental; ln (τDβ)MSE (TAM and MSE derivative)		TAM-ΔTg method; ln (τβ)TAM-ΔTg (TAM at 40 °C, ΔTg using β value of 0.4)
	50 °C	60 °C	50 °C	60 °C
HES 5%	3.4	not done	3.4	2.9
HES 4% + trehalose 1%	2.8	2.7	2.8	2.4
HES 2.5% + trehalose 2.5%	2.7	2.4	2.6	2.1
HES 1% + trehalose 4%	2.6	not done	2.3	1.5
Trehalose 5%	2.5	2.5	2.0	0.9
HES 4% + sucrose 1%	2.8	not done	2.7	2.3
HES 2.5% + sucrose 2.5%	1.6	1.3	1.5	0.8
HES 1% + sucrose 4%	1.0 ± 0.1	0.6	1.0	0.2
Sucrose 5%	0.5 ± 0.1	-2.0	0.2	-1.1

SD denotes standard deviation

4 Directly Measured (TAM) Relaxation Times for hGH-Disaccharide Formulations and Comparison with Stability

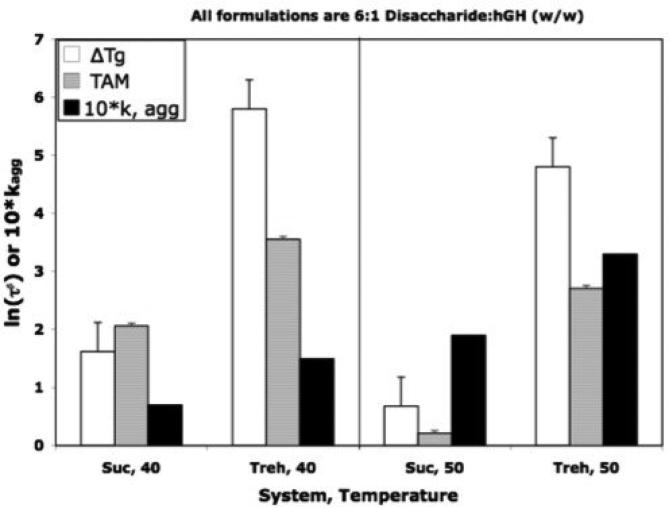
In a previous report [5], stability of sucrose formulations of human growth hormone (hGH) were compared with trehalose and stachyose formulations, where it was noted that sucrose formulations were significantly more stable than expected based on structural relaxation time constant data, τ^β. Specifically, sucrose formulations were about a factor of two more stable than corresponding trehalose formulations, in spite of the observation that the structural relaxation times for the sucrose formulations were much smaller (i.e., greater “molecular mobility” in sucrose). However, the structural relaxation data used were estimated from the ΔT_g procedure. As demonstrated in this report, the ΔT_g procedure does not necessarily provide quantitative estimates of the time constant, τ^β. Thus, here we present structural relaxation time constants directly measured by the TAM in an effort to validate the assumption that the structural relaxation time constants for these sucrose formulations are indeed signficantly less than those for the corresponding trehalose formulations. Figure 5 demonstrates that while quantitative agreement is not observed between ln(τ^β) values determined by the ΔT_g estimation (equations 1 and 2) and directly measured by TAM, the agreement is qualitative in the sense that the trends with both temperature and formulation are the same. The net result is that the sucrose formulations do indeed have greater “global” molecular mobility (i.e., smaller values of τ^β) but yet are more stable by about a factor of 2. As noted earlier [5], stability in these systems is sensibly correlated with “fast dynamics”, specifically amplitudes of motion of hydrogen over nanosecond time scales, as determined by neutron backscattering, but obviously (Figure 5) is not well correlated with “global” mobility as measured by enthalpy relaxation dyanamics.

Figure 5.

Comparison of Stability of hGH in Freeze Dried Sucrose and Trehalose Formulations with Relaxation Time Constants Directly Measured by TAM with those Estimated by the ΔT_g Procedure (equations 1 and 2). The formulations are 6:1 disaccharide:hGH, w/w), and stability is ten times the rate constant for aggregation, based on square root of time kinetics. Stability data and relaxation time constants, ln(τ^β) taken from reference 5.

5 Conclusion

Relaxation dynamics estimated using ΔT_g method, does not necessarily provide quantitative accuracy, but agreement is qualitative. We find a correlation between the two sets of data in that a cube root (1/3 power) relationship was observed between the relaxation times evaluated from TAM data and the ΔT_g estimation approach. However, the quantitative accuracy is sufficient to allow reliable extrapolations of TAM data measured at 40°C to temperatures of 50°C and in most cases to obtain extrapolations of useful accuracy event to 60°C, provided the glass transition temperature is well above 60°C. Further, while the agreement between TAM and ΔT_g estimated relaxation times for disaccharide formulations of hGH is found to be only qualitative, this agreement is sufficent to “validate” previous conclusions that the enthalpy relaxation times in sucrose formulations are indeed much smaller than in the corresponding trehalose formulations.