Dielectric Boundary Force in Molecular Solvation with the Poisson–Boltzmann Free Energy: A Shape Derivative Approach

Abstract

In an implicit-solvent description of molecular solvation, the electrostatic free energy is given through the electrostatic potential. This potential solves a boundary-value problem of the Poisson–Boltzmann equation in which the dielectric coefficient changes across the solute-solvent interface—the dielectric boundary. The dielectric boundary force acting on such a boundary is the negative first variation of the electrostatic free energy with respect to the location change of the boundary. In this work, the concept of shape derivative is used to define such variations and formulas of the dielectric boundary force are derived. It is shown that such a force is always in the direction toward the charged solute molecules.

1 Introduction

We consider electrostatic interactions in the solvation of molecules within the framework of widely used implicit-solvent or continuum-solvent modeling [9, 19, 24, 45, 53]. In such a model, the solvent molecules and ions are treated implicitly and their effects are coarse grained. Most of the existing implicit-solvent models are based on various kinds of fixed solute-solvent interfaces, such as the van der Waals surface, solvent-excluded surface, or solvent-accessible surface [17, 18, 35, 43, 44]. Such a predefined interface is used to compute the solvation free energy as the sum of two separate parts. One is the surface energy, proportional to the area of interface. The other is the electrostatic contribution determined by the Poisson–Boltzmann (PB) [1, 7, 20, 25–27, 30, 31, 36, 37, 39, 49, 58] or generalized Born (GB) [2, 3, 52] approach in which the solute-solvent interface is used as the dielectric boundary.

In recent years, a new class of implicit-solvent models, termed variational implicit-solvent models (VISM), have emerged [22, 23]. Coupled with the robust level-set numerical method [41, 42, 46], such models allow an efficient and quantitative description of molecular solvation [12, 13, 15]. Central in the VISM is a free-energy functional of all possible solute-solvent interfaces, or dielectric boundaries, that separate the continuum solvent from all solute atoms. In a simple setting, such a free-energy functional consists of surface energy of solute molecules, solute-solvent van der Waals interaction energy, and continuum electrostatic free energy, all coupled together and depending solely on a given solute-solvent interface. Minimizing the functional determines the solvation free energy and stable equilibrium solute-solvent interfaces. Initial applications of the level-set VISM to nonpolar molecular systems have demonstrated its success in capturing the hydrophobic interaction, multiple equilibrium states of hydration, and fluctuation between such states [12, 14, 15, 47, 57], all of which are difficult to be captured by a fixed-surface implicit-solvent model. See [4, 9, 10, 24, 56] for other related models and methods.

In this work, we study the dielectric boundary force—the normal component of such a force, to be more precisely—acting on a dielectric boundary or solute-solvent interface. Such a force is the negative variation of the electrostatic free energy with respect to the location change of the dielectric boundary. It is the electrostatic part of the total boundary force associated with the VISM free-energy functional, determining the conformation and dynamics of an underlying molecular system with an implicit solvent. Practically, it is also the electrostatic part of the “normal velocity” in the level-set relaxation of the free-energy functional.

For a given solvation system with a fixed charge density and dielectric coefficient, any given, possible dielectric boundary Γ determines the electrostatic potential ψ = ψ_Γ as the unique solution to the nonlinear PB equation, which in turn determines the electrostatic free energy G[Γ]. Appealing the notion and method of shape derivatives, we give a precise definition of the dielectric boundary force and derive formulas for such a force. We notice that in [57] the dielectric boundary force with the Coulomb-field approximation of electrostatic free energy is derived and implemented in the level-set VISM for charged molecules. In this approach, there is no need to estimate the GB radii as usually done in a GB model which is also based on the Coulomb-field approximation in a simple setting. In [11], the Yukawa-field approximation of the electrostatic free energy is proposed and the formula of the corresponding dielectric boundary force is derived. These approaches require no solutions to any partial differential equations. In comparison, our current approach is more accurate analytically but can be less efficient computationally. Related work on electrostatic forces in molecular systems can be found in [29, 32, 38].

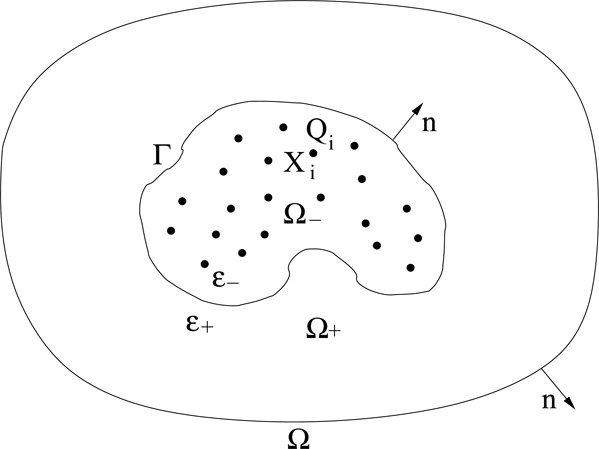
We assume that the entire solvation system occupies a bounded region Ω ⊂ ℝ³. It is divided into three disjoint parts: the region of solute Ω₋ (e.g., charged biomolecules such as proteins), the region of solvent Ω₊ (e.g., salted water), and the solute-solvent interface or the dielectric boundary Γ that separates Ω₋ and Ω₊. See Figure 1, where n denotes the unit normal to the boundary Γ pointing from Ω₋ to Ω₊ and also the exterior unit normal to ∂Ω, the boundary of Ω. The solute region Ω₋ is completely contained in the entire system region Ω, i.e., $\overline{{\mathrm{\Omega }}_{-}}\subset \mathrm{\Omega }$, where an over-line denotes the closure. The solute region Ω₋ contains all the solute atoms located at X₁, …, X_N, carrying charges Q₁, …, Q_N, respectively.

Figure 1.

The geometry of a solvation system with an implicit solvent. Dots represent solute atoms at X_i carrying charge Q_i (i = 1, …, N). The solute-solvent interface Γ separates the solute region Ω₋ and the solvent region Ω₊. The corresponding dielectric coefficients are denoted by ε₋ and ε₊, respectively. The unit normal at the interface Γ pointing from Ω₋ to Ω₊ and the exterior unit normal at the boundary of the entire solvation region Ω are both denoted by n.

In the PB theory, the electrostatic part of the solvation free energy—the electrostatic free energy—is given by

$$G[\mathrm{\Gamma }]={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}{|\nabla \psi |}^2+f\psi -{\chi }_{+}{\beta }^{-1}\sum _{j=1}^M{c}_j^{\infty }(e^{-\beta q_j\psi }-1)]dX$$ (1.1)

through the electrostatic potential ψ : Ω → ℝ [8, 20, 29, 37, 49]. Here, ε_Γ : Ω → ℝ is the dielectric coefficient defined by

$${\epsilon }_{\mathrm{\Gamma }}(X)=\{\begin{array}{cc}{\epsilon }_{-}\hfill & \text{if}X\in {\mathrm{\Omega }}_{-},\hfill \\ {\epsilon }_{+}\hfill & \text{if}X\in {\mathrm{\Omega }}_{+},\hfill \end{array}$$ (1.2)

where ε₋ and ε₊ are two positive constants. We have ${\epsilon }_{+}={\epsilon }_{+}^{\prime }{\epsilon }_0$ and ${\epsilon }_{-}={\epsilon }_{-}^{\prime }{\epsilon }_0$, respectively, where ε₀ is the vacuum permittivity, and ${\epsilon }_{+}^{\prime }$ and ${\epsilon }_{-}^{\prime }$ are the temperature-dependent relative permittivities. Typically, the value of ${\epsilon }_{-}^{\prime }$ is in between 1 and 10 for proteins and that of ${\epsilon }_{+}^{\prime }$ is close to 80 for water at normal conditions. The function f : Ω → ℝ is the fixed charge density of charged solute molecules. It is usually the sum of the point charges Q_i located at X_i (i = 1, …, N). Here we assume that f is an integrable function that approximates these point charges. The function χ₊ is the characteristic function of Ω₊ defined by χ₊(X) = 1 if X ∈ Ω₊ and χ₊(X) = 0 otherwise. The parameter β > 0 is the inverse thermal energy, M ≥ 2 is the number of ionic species in the solvent, and q_j ∈ ℝ and $c_j^{\infty }>0$ are the charge and bulk concentration, respectively, of the jth ionic species with j = 1, …, M. Note that all ε₊, ε₋, f, β, and q_j and $c_j^{\infty }(1\le j\le M)$ are input data. We use the SI units of electrostatics. The electrostatic potential ψ is the unique solution of a boundary-value problem of the nonlinear PB equation [1, 20, 25, 37, 48]

$$\nabla ·{\epsilon }_{\mathrm{\Gamma }}\nabla \psi +{\chi }_{+}\sum _{j=1}^M{q}_j{c}_j^{\infty }{e}^{-\beta q_j\psi }=-f\text{in}\mathrm{\Omega }.$$ (1.3)

See also [5, 34, 36, 37, 54, 55, 58] for generalized PB equations to include ionic excluded-volume effects. Eq. (1.3) is the Euler–Lagrange equation of the right-hand side of (1.1) viewed as a functional of ψ. Note that this functional is concave in ψ.

Let V : ℝ³ → ℝ³ be a smooth map vanishing outside a small neighborhood of the dielectric boundary Γ. Let x = x(t, X) be the solution map of the dynamical system [6, 21, 33, 51]

$$\frac{dx(t,X)}{dt}=V(x(t,X))\forall t>0\text{small and}x(0,X)=X\forall X\in {ℝ}^3.$$

The shape derivative of the electrostatic free energy G[Γ] in the direction of V : ℝ³ → ℝ³ is defined to be

$${\delta }_{\mathrm{\Gamma },V}G[\mathrm{\Gamma }]={\frac{d}{dt}G[{\mathrm{\Gamma }}_t(V)]|}_{t=0},$$

where Γ_t(V) = {x(t, X) : X ∈ Γ} and G[Γ_t(V)] is defined similarly using Γ_t(V) instead of Γ. It will be shown that δ_Γ,V G[Γ] is an integral of the product of V · n and some function on Γ that is independent of V, where n is the unit normal along Γ (cf. Theorem 4.1). We identify that function on Γ as the shape derivative of G[Γ] and denote it by δ_ΓG[Γ]. We define the dielectric boundary force, or more precisely the normal component of the dielectric boundary force, to be −δ_ΓG[Γ] and denote it by F_n. Notice that it is only the normal component, not the tangential components of the boundary force, that determines the motion of the boundary.

Our main result is the following formula of the shape derivative δ_ΓG[Γ] : Γ → ℝ of the electrostatic free energy G[Γ] with respect to the dielectric boundary Γ:

$${\delta }_{\mathrm{\Gamma }}G[\mathrm{\Gamma }]=\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }^{+}|}^2-\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }^{-}|}^2-{\epsilon }_{+}{|\nabla {\psi }^{+}·n|}^2+{\epsilon }_{-}{|\nabla {\psi }^{-}·n|}^2+B(\psi ),$$ (1.4)

where ψ is the electrostatic potential, a superscript + or − denotes the restriction onto Ω₊ or Ω₋, respectively, and

$$B(s)={\beta }^{-1}\sum _{j=1}^M{c}_j^{\infty }(e^{-\beta q_{j}s}-1)\forall s\in ℝ.$$ (1.5)

Note that ε₊∇ψ⁺ · n = ε₋∇ψ⁻ · n on Γ and this common value is denoted by ε_Γ∇ψ · n. The dependence on the direction of n is in V · n in the integral over Γ. See Theorem 4.1 for the details. A different but useful form of the shape derivative δ_ΓG[Γ] : Γ → ℝ is

$${\delta }_{\mathrm{\Gamma }}G[\mathrm{\Gamma }]=\frac{1}{2}(\frac{1}{{\epsilon }_{-}}-\frac{1}{{\epsilon }_{+}}){|{\epsilon }_{\mathrm{\Gamma }}\nabla \psi ·n|}^2+\frac{1}{2}({\epsilon }_{+}-{\epsilon }_{-}){|(I-n\otimes n)\nabla \psi |}^2+B(\psi ),$$ (1.6)

where I is the identity matrix. See Corollary 4.1. The vector (I − n ⊗ n)∇ψ is the tangential component of ∇ψ. It is continuous across the boundary Γ. The corresponding term, the middle term, in the boundary force (1.6), may not be small compared with the first term in (1.6), since a solute-solvent interface can be rough.

We remark that our results hold true for the function B : ℝ → ℝ that is more general than that defined in (1.5). Our formula (1.4) corrects that in [8] (cf. (3.13) in [8]). If we define E = −∇ψ and

$$T={\epsilon }_{\mathrm{\Gamma }}E\otimes E-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}{|E|}^{2}I-{\chi }_{+}B(\psi )I\text{in}\mathrm{\Omega },$$

then it is easy to verify by the formula (1.4) that

$$F_n=-{\delta }_{\mathrm{\Gamma }}G[\mathrm{\Gamma }]=n·T^{+}n-n·T^{-}n.$$

The quantity T is the Maxwell stress tensor of our underlying charged molecular system [29, 38, 40].

A direct consequence of our result (1.6) is that, under the assumption ε₋ < ε₊ which is true in general, we always have

$$F_n<0\text{on}\mathrm{\Gamma }.$$ (1.7)

See Corollary 4.1. This gives a quantitative interpretation, in the framework of implicit solvent, of the following phenomenon described by Debye in 1960s [16]: “Under the combined influence of electric field generated by solute charges and their polarization in the surrounding medium which is electrostatic neutral, an additional potential energy emerges and drives the surrounding molecules to the solutes.” A significant consequence of our mathematical statement (1.7) is as follows: A neutral cavity close to a charged solute (e.g., a protein) will move away from the solute due to the dielectric boundary force. This important charge effect to the hydrophobic interaction in biomolecules has been observed in the recent level-set variational implicit-solvent modeling of BphC, a two-domain protein [57].

In the proof of our main results, we use some uniform bounds of the potential ψ. Such bounds are obtained in the proof of the existence and uniqueness of the solution to the boundary-value problem of the PB equation. We also use the variational principle that the electrostatic free energy G[Γ] maximizes a corresponding functional of ψ for a fixed boundary Γ. In deriving the formula of boundary force, we do not use an abstract lemma as usually done [21,51]. Rather we give a direct and simpler derivation using the definition of shape derivatives. Notice that we assume in this work that the fixed charge density f is a compactly supported smooth function that approximates point charges. Numerically such approximation can be made by that of the Dirac delta function [50]. Our analysis does not directly extend to the case of point charges which can be in general more difficult to treat. In fact, with point charges in the PB model, a rigorous definition of the electrostatic free energy must be given with caution. This will be our future work.

The rest of the paper is organized as follows: In Section 2, we recall the boundary-value problem of the PB equation and the related electrostatic free energy. In Section 3, we define the dielectric boundary force using the notion of shape derivative. Finally, in Section 4, we derive our main formula of the dielectric boundary force and show that the force is always attractive to solutes.

2 The Poisson–Boltzmann Equation and Electrostatic Free Energy

We make the following assumptions throughout the rest of the paper:

• A1. All Ω, Ω₋, and Ω₊ are non-empty, bounded, and open subsets of ℝ³ with $\overline{{\mathrm{\Omega }}_{-}}\subset \mathrm{\Omega }$ and ${\mathrm{\Omega }}_{+}=\mathrm{\Omega }\backslash \overline{{\mathrm{\Omega }}_{-}}$. The boundary $\mathrm{\Gamma }=\partial {\mathrm{\Omega }}_{-}=\overline{{\mathrm{\Omega }}_{-}}\cap \overline{{\mathrm{\Omega }}_{+}}$. Both ∂ Ω and Γ are of C². The unit normal at Γ pointing from Ω₋ to Ω₊ is denoted by n. The unit exterior normal at the boundary of Ω is also denoted by n. See Figure 1.

• A2. M ≥ 2 is an integer. All β > 0, q_j ∈ ℝ and $c_j^{\infty }>0(1\le j\le M)$, ε₋ > 0, and ε₊ > 0 are constants. The function ε_Γ ∈ L^∞(Ω) is defined in (1.2). The parameters q_j and $c_j^{\infty }(1\le j\le M)$ satisfy the condition of charge neutrality: ${\sum }_{j=1}^M{q}_j{c}_j^{\infty }=0$.

• A3. The fixed charge density f : Ω → ℝ satisfies that f ∈ L²(Ω) and supp (f) ⊂ Ω₋. The boundary data in the Dirichlet boundary condition that we use is given by a function g ∈ W^2,∞(Ω). Moreover, we use the notation

  $$H_g^1(\mathrm{\Omega })=\{\varphi \in H^1(\mathrm{\Omega }):\varphi =g\text{on}\partial \mathrm{\Omega }\}.$$

  Here and below we use the standard notation for the Sobolev space W^k,p(Ω) which, for any fixed integer k ≥ 1 and any extended real number p : 1 ≤ p ≤ ∞, consists of all k-times (weakly) differentiable functions u : Ω → ℝ with the pth power of u or any of its derivatives of order ≤ k integral over Ω if 1 ≤ p < ∞ or with u and all its derivatives of order ≤ k essentially bounded in Ω.

• A4. There exists a smooth function B : ℝ → ℝ that satisfies B(s) > B(0) = 0 for all s ≠ 0, B′(0) = 0, inf_ℝ B″ > 0 and hence B is strictly convex, B(±∞) = ∞, and B′(∞) = ∞ and B′(−∞) = −∞.

In the usual PB theory, the function B : ℝ → ℝ is given by (1.5). One easily verifies using the charge neutrality and Jensen’s inequality that for this specific form of B, all the properties listed in A4 are satisfied. A general function B : ℝ → ℝ as we assumed in A4 above covers other cases such as those including ionic size effects [5, 34, 36, 37, 54, 55].

We define G[Γ, ·] : H¹(Ω) → ℝ ∪ {±∞} by

$$G[\mathrm{\Gamma },\varphi ]={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}{|\nabla \varphi |}^2+f\varphi -{\chi }_{+}B(\varphi )]dX.$$ (2.1)

We consider the maximization of the functional G[Γ, ·] and the boundary-value problem of the Poisson–Boltzmann (PB) equation

$$\nabla ·{\epsilon }_{\mathrm{\Gamma }}\nabla \psi -{\chi }_{+}B\prime (\psi )=-f\text{in}\mathrm{\Omega },$$ (2.2)

$$\psi =g\text{on}\partial \mathrm{\Omega }.$$ (2.3)

Theorem 2.1. (1) The functional $G[\mathrm{\Gamma },·]:H_g^1(\mathrm{\Omega })\to ℝ\cup \{\pm \infty \}$ has a unique maximizer ${\psi }_0\in H_g^1(\mathrm{\Omega })$, defined by

$$G[\mathrm{\Gamma },{\psi }_0]=\underset{\varphi \in H_g^1(\mathrm{\Omega })}{\text{max}}G[\mathrm{\Gamma },\varphi ].$$

Moreover, this maximum value is finite and

$${\Vert {\psi }_0\Vert }_{H^1(\mathrm{\Omega })}+{\Vert {\psi }_0\Vert }_{L^{\infty }(\mathrm{\Omega })}\le C_1$$

for some constant C₁ > 0 depending on ε₋, ε₊, f, g, B and Ω but not on Γ.

(2) The maximizer ψ₀ is the unique solution to the boundary-value problem of the PB equation (2.2) and (2.3).

We define the electrostatic free energy corresponding to the dielectric boundary Γ to be

$$G[\mathrm{\Gamma }]=\underset{\varphi \in H_g^1(\mathrm{\Omega })}{\text{max}}G[\mathrm{\Gamma },\varphi ]=G[\mathrm{\Gamma },{\psi }_0].$$ (2.4)

Proof of Theorem 2.1. Let $u_0\in H_g^1(\mathrm{\Omega })$ be such that

$${\int }_{\mathrm{\Omega }}{\epsilon }_{\mathrm{\Gamma }}\nabla u_0·\nabla \upsilon dX={\int }_{\mathrm{\Omega }}f\upsilon dX\forall \upsilon \in H_0^1(\mathrm{\Omega }).$$ (2.5)

Standard regularity theory implies that u₀ ∈ L^∞(Ω) and there exists a constant Ĉ₁ > 0, depending possibly on ε₋, ε₊, f, g, and Ω but not on Γ, such that

$${\Vert u_0\Vert }_{H^1(\mathrm{\Omega })}+{\Vert u_0\Vert }_{L^{\infty }(\mathrm{\Omega })}\le {Ĉ}_1,$$ (2.6)

cf. [28] (Chapter 8). Let $\varphi \in H_g^1(\mathrm{\Omega })$ and $u=\varphi -u_0\in H_0^1(\mathrm{\Omega })$. By (2.1), we have

$$G[\mathrm{\Gamma },\varphi ]=-I[\mathrm{\Gamma },u]+{\int }_{\mathrm{\Omega }}(f{u}_0-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}{|\nabla u_0|}^2)dX,$$

where

$$I[\mathrm{\Gamma },u]={\int }_{\mathrm{\Omega }}[\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}{|\nabla u|}^2+{\chi }_{+}B(u+u_0)]dX.$$

Hence the maximization of G[Γ, ϕ] over all $\varphi \in H_g^1(\mathrm{\Omega })$ is equivalent to the minimization of I[Γ, u] over all $u\in H_0^1(\mathrm{\Omega })$.

By the Poincaré inequality and the fact that B : ℝ → ℝ is non-negative, there exists a constant C > 0 such that

$$I[\mathrm{\Gamma },u]\ge C{\Vert u\Vert }_{H^1(\mathrm{\Omega })}^2\forall u\in H_0^1(\mathrm{\Omega }).$$

Thus $\alpha ≔{\text{inf}}_{u\in H_0^1(\mathrm{\Omega })}$ I[Γ, u] is finite. Let $u_k\in H_0^1(\mathrm{\Omega })$ (k = 1, 2…) be such that

$$\underset{k\to \infty }{\text{lim}}I[\mathrm{\Gamma },u_k]=\alpha .$$

Then {u_k} is bounded in H¹(Ω) and hence it has a subsequence, not relabeled, that weakly converges to some $u_{\infty }\in H_0^1(\mathrm{\Omega })$. Since the embedding H¹(Ω) ↪ L²(Ω) is compact, up to a further subsequence, again not relabeled, u_k → u_∞ a. e. in Ω. Therefore, since B : ℝ → ℝ is continuous and non-negative, Fatou’s lemma implies

$$\underset{k\to \infty }{\text{lim inf}}{\int }_{{\mathrm{\Omega }}_{+}}B(u_k)dX\ge {\int }_{{\mathrm{\Omega }}_{+}}B(u_{\infty })dX.$$

Since

$$u\mapsto {\int }_{\mathrm{\Omega }}{\epsilon }_{\mathrm{\Gamma }}{|\nabla u|}^{2}dX$$

is convex and H¹(Ω)-continuous, it is sequentially weakly lower semi-continuous. Consequently,

$$\underset{k\to \infty }{\text{lim inf}}I[\mathrm{\Gamma },u_k]\ge I[\mathrm{\Gamma },u_{\infty }].$$

Thus u_∞ is a minimizer of $I:H_0^1(\mathrm{\Omega })\to ℝ\cup \{\infty \}$ and the minimum value is clearly finite. The uniqueness of such a minimizer follows from the strict convexity of I[Γ, ·]. Therefore ${\psi }_0=u_0+u_{\infty }\in H_g^1(\mathrm{\Omega })$ is the unique maximizer of G[Γ, ·] over $H_g^1(\mathrm{\Omega })$ and the maximum value is finite.

We show now the boundedness of the minimizer u_∞ of I[Γ, ·] over $H_0^1(\mathrm{\Omega })$ and hence that of the maximizer ψ₀ = u₀ + u_∞ of G[Γ, ·] over $H_g^1(\mathrm{\Omega })$. By (2.6) and the assumption that B′(∞) = ∞ and B′(−∞) = −∞, there exists λ > 0 depending on Ĉ₁ and B such that

$$B\prime (u_0+\lambda )\ge 1\text{and}B\prime (u_0-\lambda )\le -1\mathrm{a}.\mathrm{e}.{\mathrm{\Omega }}_{+}.$$

Define u_λ : Ω → ℝ by

$$u_{\lambda }(X)=\{\begin{array}{cc}-\lambda \hfill & \text{if}{u}_{\infty }(X)<-\lambda ,\hfill \\ u_{\infty }(X)\hfill & \text{if}|u_{\infty }(X)|\le \lambda ,\hfill \\ \lambda \hfill & \text{if}{u}_{\infty }(X)>\lambda .\hfill \end{array}$$

Clearly $u_{\lambda }\in H_0^1(\mathrm{\Omega })$ and hence I[Γ, u_∞] ≤ I[Γ, u_λ]. This and the fact that |∇u_λ| ≤ |∇u_∞| a.e. in Ω imply

$${\int }_{{\mathrm{\Omega }}_{+}}B(u_0+u_{\infty })dX\le {\int }_{{\mathrm{\Omega }}_{+}}B(u_0+u_{\lambda })dX.$$

Consequently, we have by the convexity of B : ℝ → ℝ imply that

$$0\ge {\int }_{\{X\in {\mathrm{\Omega }}_{+}:u_{\infty }(X)>\lambda \}}[B(u_0(X)+u_{\infty }(X))-B(u_0(X)+\lambda )]dX+{\int }_{\{X\in {\mathrm{\Omega }}_{+}:u_{\infty }(X)<-\lambda \}}[B(u_0(X)+u_{\infty }(X))-B(u_0(X)-\lambda )]dX\ge {\int }_{\{X\in {\mathrm{\Omega }}_{+}:u_{\infty }(X)>\lambda \}}B\prime (u_0(X)+\lambda )[u_{\infty }(X)-\lambda ]dX+{\int }_{\{X\in {\mathrm{\Omega }}_{+}:u_{\infty }(X)<-\lambda \}}B\prime (u_0(X)-\lambda )[u_{\infty }(X)+\lambda ]dX\ge {\int }_{\{X\in {\mathrm{\Omega }}_{+}:u_{\infty }(X)>\lambda \}}[u_{\infty }(X)-\lambda ]dX-{\int }_{\{X\in {\mathrm{\Omega }}_{+}:u_{\infty }(X)<-\lambda \}}[u_{\infty }(X)+\lambda ]dX={\int }_{\{X\in {\mathrm{\Omega }}_{+}:|u_{\infty }(X)|>\lambda \}}[|u_{\infty }(X)|-\lambda ]dX\ge 0.$$

Hence the last integral is 0. This implies that the Lebesgue measure of the set {X ∈ Ω₊ : |u_∞(X)| > λ} is 0. Therefore |u_∞| ≤ λ a.e. Ω₊.

Since $u_{\infty }\in H_0^1(\mathrm{\Omega })$ is a minimizer of $I:H_0^1(\mathrm{\Omega })\to ℝ\cup \{\infty \}$, it is a weak solution of the corresponding Euler–Lagrange equation, which can be rewritten as

$$\nabla ·{\epsilon }_{\mathrm{\Gamma }}\nabla u_{\infty }={\chi }_{+}B\prime (u_{\infty }+u_0)\text{in}\mathrm{\Omega }.$$

The right-hand side of this equation is bounded in Ω by a constant depending only on Ĉ₁ and B but not on Γ. Thus, by the regularity theory, both the H¹(Ω) and L^∞(Ω) norms of u_∞ and hence those of ψ₀ = u_∞ + u₀ are bounded by a constant that only depends on Ĉ₁ and B but not on Γ. This proves the desired boundedness of ψ₀.

Now routine calculations lead to

$${\frac{d}{dt}|}_{t=0}G[\mathrm{\Gamma },{\psi }_0+t\varphi ]={\int }_{\mathrm{\Omega }}[-{\epsilon }_{\mathrm{\Gamma }}\nabla {\psi }_0·\nabla \varphi +f\varphi -{\chi }_{+}B\prime ({\psi }_0)\varphi ]dX\forall \varphi \in H_0^1(\mathrm{\Omega }).$$

Hence ψ₀ is a weak solution to the boundary-value problem of PB equation (2.2) and (2.3).

If ${\varphi }_0\in H_g^1(\mathrm{\Omega })$ is another weak solution to the boundary-value problem of PB equation (2.2) and (2.3), then

$${\int }_{\mathrm{\Omega }}\{{\epsilon }_{\mathrm{\Gamma }}\nabla ({\psi }_0-{\varphi }_0)·\nabla \eta +{\chi }_{+}[B\prime ({\psi }_0)-B\prime ({\varphi }_0)]\eta \}dX=0$$

for any $\eta \in H_0^1(\mathrm{\Omega })$. Choosing $\eta ={\psi }_0-{\varphi }_0\in H_0^1(\mathrm{\Omega })$ and using the convexity of B : ℝ → ℝ, we obtain ψ₀ = ϕ₀, proving the uniqueness.

We remark that the boundary-value problem of the PB equation (2.2) and (2.3) is equivalent to the elliptic interface problem

$$\{\begin{array}{cc}{\epsilon }_{-}\mathrm{\Delta }\psi =-f\hfill & \text{in}{\mathrm{\Omega }}_{-},\hfill \\ {\epsilon }_{+}\mathrm{\Delta }\psi -B\prime (\psi )=0\hfill & \text{in}{\mathrm{\Omega }}_{+},\hfill \\ 〚\psi 〛=〚{\epsilon }_{\mathrm{\Gamma }}\nabla \psi ·n〛=0\hfill & \text{on}\mathrm{\Gamma },\hfill \\ \psi =g\hfill & \text{on}\partial \mathrm{\Omega },\hfill \end{array}$$ (2.7)

where 〚u〛 = u|_Ω+−u|_Ω− denotes the jump across Γ of a function u from Ω₊ to Ω₋. See [37] for a proof. In particular, this equivalence implies the continuity of ε_Γ∂ψ/∂n across the boundary Γ.

3 Dielectric boundary forces as shape derivatives

Let V ∈ C^∞(ℝ³,ℝ³). Assume that V (x) = 0 if dist (x, Γ) > d for some d > 0 such that

$$d<\frac{1}{2}\text{min}(\text{dist}(\mathrm{\Gamma },\partial \mathrm{\Omega }),\text{dist}(\text{supp}(f),\mathrm{\Gamma })).$$ (3.1)

Let X ∈ ℝ³ and consider the dynamical system for x = x(t):

$$\{\begin{array}{cc}\frac{dx}{dt}=V(x)\hfill & \forall t>0,\hfill \\ x(0)=X.\hfill \end{array}$$ (3.2)

The solution of this dynamical system defines a smooth map from ℝ³ to ℝ³ at each t ≥ 0. We shall denote this map by x = x(t, X) = T_t(X) for all t ≥ 0 and X ∈ ℝ³. Each T_t : ℝ³ → ℝ³ is a homeomorphism with both T_t and $T_t^{-1}$ being smooth. Clearly T₀ is the identity map.

Notice that for t > 0 small we have by Taylor’s expansion that

$$T_t(X)=x(t,X)=x(0,X)+t{\partial }_{t}x(0,X)+O(t^2)=X+tV(x(0,X))+O(t^2)=X+tV(X)+O(t^2).$$

This means that the perturbation of identity defined by X ↦ X + tV (X) and the map T_t(X) = x(t, X) agree with each other up to the leading order term in t. Notice also that we only consider V = V (x) instead of a more general V = V (t, x), since the shape derivative defined via V = V (t, x) only depends on V (0, ·) by the Structure Theorem [21, 51].

For each t ≥ 0, we denote

$${\mathrm{\Omega }}_t=T_t(\mathrm{\Omega }),{\mathrm{\Omega }}_{t-}=T_t({\mathrm{\Omega }}_{-}),{\mathrm{\Omega }}_{t+}=T_t({\mathrm{\Omega }}_{+}),{\mathrm{\Gamma }}_t=T_t(\mathrm{\Gamma }).$$

Clearly, all Ω_t, Ω_t−, and Ω_t+ are open sets, and ${\mathrm{\Gamma }}_t=\partial {\mathrm{\Omega }}_{t-}=\overline{{\mathrm{\Omega }}_{t+}}\cap \overline{{\mathrm{\Omega }}_{t-}}$. To indicate the dependence on V, we also write Γ_t = Γ_t(V). Note that each T_t perturbs Γ locally: T_t(X) = X if dist (X, Γ) > d. Since d > 0 satisfies (3.1), we have T_t(X) = X if f(X) ≠ 0 or X ∈ ∂Ω. In particular, Ω_t = T_t(Ω) = Ω and T_t(∂Ω) = ∂T_t(Ω) = ∂Ω.

We recall that the electrostatic free energy G[Γ] is given by (2.4), where the functional G[Γ, ·] is given in (2.1) and ψ₀ is the weak solution to (2.2) and (2.3). For t > 0, we define

$$G[{\mathrm{\Gamma }}_t,\varphi ]={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{{\mathrm{\Gamma }}_t}}{2}{|\nabla \varphi |}^2+f\varphi -{\chi }_{t+}B(\varphi )]dx\forall \varphi \in H^1({\mathrm{\Omega }}_t)=H^1(\mathrm{\Omega }),$$ (3.3)

where ε_Γt : Ω → ℝ is defined by

$${\epsilon }_{{\mathrm{\Gamma }}_t}(x)=\{\begin{array}{cc}{\epsilon }_{-}\hfill & \text{if}x\in {\mathrm{\Omega }}_{t-},\hfill \\ {\epsilon }_{+}\hfill & \text{if}x\in {\mathrm{\Omega }}_{t+},\hfill \end{array}$$ (3.4)

and χ_t+ is the characteristic function of Ω_t+. By Theorem 2.1 there exists a unique ${\psi }_t\in H_g^1(\mathrm{\Omega })\cap L^{\infty }(\mathrm{\Omega })$ that maximizes G[Γ_t, ·] over $H_g^1(\mathrm{\Omega })$. The maximum is finite and is given by

$$G[{\mathrm{\Gamma }}_t]=\underset{\varphi \in H_g^1(\mathrm{\Omega })}{\text{max}}G[{\mathrm{\Gamma }}_t,\varphi ]=G[{\mathrm{\Gamma }}_t,{\psi }_t].$$ (3.5)

This is the electrostatic free energy corresponding to Γ_t. In addition, ψ_t is the unique weak solution to the corresponding boundary-value problem of the Poisson–Boltzmann equation

$$\nabla ·{\epsilon }_{{\mathrm{\Gamma }}_t}\nabla {\psi }_t-{\chi }_{t+}B\prime ({\psi }_t)=-f\text{in}\mathrm{\Omega },$$ (3.6)

$${\psi }_t=g\text{on}\partial \mathrm{\Omega }.$$ (3.7)

Finally,

$${\Vert {\psi }_t\Vert }_{H^1(\mathrm{\Omega })}+{\Vert {\psi }_t\Vert }_{L^{\infty }(\mathrm{\Omega })}\le C_1,$$ (3.8)

where C₁ is the same constant in Theorem 4.1. In particular, C₁ does not depend on Γ_t.

Definition 3.1. Let V and Γ_t(V) (t ≥ 0) be given as above. The shape derivative of G[Γ] in the direction of V is

$${\delta }_{\mathrm{\Gamma },V}G[\mathrm{\Gamma }]={\frac{d}{dt}G[{\mathrm{\Gamma }}_t(V)]|}_{t=0}=\underset{t\to 0^{+}}{\text{lim}}\frac{G[{\mathrm{\Gamma }}_t(V)]-G[\mathrm{\Gamma }]}{t},$$

if the limit exists.

In general, there exists w : Γ → ℝ such that

$${\delta }_{\mathrm{\Gamma },V}G[\mathrm{\Gamma }]={\int }_{\mathrm{\Gamma }}w(V·n)dS,$$

where n is the unit normal to Γ. We shall define

$${\delta }_{\mathrm{\Gamma }}G[\mathrm{\Gamma }]=w$$

and call it the shape derivative of G[Γ].

We recall some properties of the transformation T_t(X) defined by V = V (X). These properties can be proved by direct calculations, cf. [21] (Chapter 8 and Chapter 9).

1. Let X ∈ ℝ³ and t ≥ 0. Let ∇T_t(X) be the Jacobian matrix of T_t at X defined by ${(\nabla T_t(X))}_{ij}={\partial }_j{T}_t^i(X)$, where $T_t^i$ is the ith component of T_t (i = 1, 2, 3). Let

   $$J_t(X)=\text{det}\nabla T_t(X).$$

   Then for each X the function t → J_t(X) is in C^∞ and at X

   $$\frac{d{J}_t}{dt}=J_t(\nabla ·V)◦T_t,$$ (3.9)

   where ◦ denotes the composition of functions or maps. Clearly, ∇T₀ is the identity matrix and J₀ = 1. The continuity of J_t at t = 0 then implies that J_t > 0 for t > 0 small enough.
2. Define A(t) : Ω → ℝ for t ≥ 0 small enough by

   $$A(t)=J_t{(\nabla T_t)}^{-1}{(\nabla T_t)}^{-T},$$ (3.10)

   where a superscript T denotes the matrix transpose. We have at each point in Ω that

   $$A\prime (t)=[((\nabla ·V)◦T_t)-{(\nabla T_t)}^{-1}((\nabla V)◦T_t)\nabla T_t-{(\nabla T_t)}^{-1}{((\nabla V)◦T_t)}^T(\nabla T_t)]A(t).$$ (3.11)
3. For any u ∈ L²(Ω) and t ≥ 0, u ◦ T_t ∈ L²(Ω) and $u◦T_t^{-1}\in L^2(\mathrm{\Omega })$. Moreover,

   $$\underset{t\to 0}{\text{lim}}u◦T_t=u\text{and}\underset{t\to 0}{\text{lim}}u◦T_t^{-1}=u\text{in}{L}^2(\mathrm{\Omega }).$$ (3.12)
4. Let t ≥ 0 and u ∈ H¹(Ω). Then both u ↦ u◦T_t and $u\mapsto u◦T_t^{-1}$ are one-to-one and onto maps from H¹(Ω) (resp. $H_g^1(\mathrm{\Omega })$) to H¹(Ω_t) = H¹(Ω) (resp. $H_g^1(\mathrm{\Omega })$). Moreover, for any u ∈ H¹(Ω),

   $$\nabla (u◦T_t^{-1})={(\nabla T_t^{-1})}^T(\nabla u◦T_t^{-1})\text{and}\nabla (u◦T_t)={(\nabla T_t)}^T(\nabla u◦T_t).$$ (3.13)
5. For any u ∈ H¹(Ω) and t ≥ 0,

   $$\frac{d}{dt}(u◦T_t)=(\nabla u·V)◦T_t.$$ (3.14)

4 Formulas of the dielectric boundary force

Let V ∈ C^∞(ℝ³,ℝ³) be such that V (X) = 0 if dist (X, Γ) > d for some d > 0 that satisfies (3.1). Let the transformations T_t (t ≥ 0) be defined by (3.2). For t > 0, the electrostatic free energy G[Γ_t] is given by (3.5), where the functional G[Γ_t, ·] is given in (3.3) and ψ_t is the weak solution to (3.6) and (3.7), respectively. For t = 0, the electrostatic free energy G[Γ] is given by (2.4), where the functional G[Γ, ·] is given in (2.1) and ψ₀ is the weak solution to (2.2) and (2.3).

Theorem 4.1. Assume f ∈ H¹(Ω). Then the shape derivative of the electrostatic free energy G[Γ] in the direction of V is given by

$${\delta }_{\mathrm{\Gamma },V}G[\mathrm{\Gamma }]={\int }_{\mathrm{\Gamma }}[\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }_0^{+}|}^2-\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }_0^{-}|}^2-{\epsilon }_{+}{|\nabla {\psi }_0^{+}·n|}^2+{\epsilon }_{-}{|\nabla {\psi }_0^{-}·n|}^2+B({\psi }_0)](V·n)dS.$$ (4.1)

Proof. We divide our proof into four steps.

Step 1. Let t ≥ 0. Since each $\varphi \in H_g^1({\mathrm{\Omega }}_t)=H_g^1(\mathrm{\Omega })$ corresponds uniquely to $\varphi ◦T_t^{-1}\in H_g^1(\mathrm{\Omega })$, we have by (3.5) that

$$G[{\mathrm{\Gamma }}_t]=\underset{\varphi \in H_g^1(\mathrm{\Omega })}{\text{max}}G[{\mathrm{\Gamma }}_t,\varphi ◦T_t^{-1}].$$

Let ϕ ∈ H¹(Ω) ∩ L^∞(Ω) and t ≥ 0, and denote

$$z(t,\varphi )=G[{\mathrm{\Gamma }}_t,\varphi ◦T_t^{-1}].$$ (4.2)

We prove that ∂_tz(t, ϕ) exists for t ≥ 0 small and derive a formula for this derivative.

Recall that J_t(X) = det∇T_t(X). By the continuity of t ↦ J_t(X) and the fact that J₀(X) = 1 at each X ∈ Ω, there exists τ > 0 such that J_t(X) > 0 for all t ∈ [0, τ] and all X ∈ Ω. Now let t ∈ [0, τ] and ϕ ∈ H¹(Ω) ∩ L^∞(Ω). By the definition of G[Γ_t, ϕ] (cf. (3.3)), the change of variable x = T_t(X), and (3.13), we obtain

$$z(t,\varphi )=G[{\mathrm{\Gamma }}_t,\varphi ◦T_t^{-1}]={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{{\mathrm{\Gamma }}_t}}{2}{|\nabla (\varphi ◦T_t^{-1})|}^2+f(\varphi ◦T_t^{-1})-{\chi }_{t+}(B(\varphi )◦T_t^{-1})]dx={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A(t)\nabla \varphi ·\nabla \varphi +(f◦T_t)\varphi J_t-{\chi }_{+}B(\varphi )J_t]dX,$$ (4.3)

where A(t) is given in (3.10). By the properties of the transformations T_t (t ≥ 0), cf. (3.9), (3.11), and (3.14), each term in the above integral is differentiable with respect to t, and

$${\partial }_{t}z(t,\varphi )={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A\prime (t)\nabla \varphi ·\nabla \varphi +({\partial }_t(f◦T_t))\varphi J_t+(f◦T_t)\varphi {\partial }_t{J}_t-{\chi }_{+}B(\varphi ){\partial }_t{J}_t]dX={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A\prime (t)\nabla \varphi ·\nabla \varphi +((\nabla f·V)◦T_t)\varphi J_t+(f◦T_t)\varphi ((\nabla ·V)◦T_t)J_t-{\chi }_{+}B(\varphi )((\nabla ·V)◦T_t)J_t]dX={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A\prime (t)\nabla \varphi ·\nabla \varphi +((\nabla ·(fV))◦T_t)\varphi J_t-{\chi }_{+}B(\varphi )((\nabla ·V)◦T_t)J_t]dX.$$ (4.4)

Step 2. Let t ∈ (0, τ]. Since ${\psi }_t\in H_g^1(\mathrm{\Omega })\cap L^{\infty }(\mathrm{\Omega })$ and ${\psi }_0\in H_g^1(\mathrm{\Omega })\cap L^{\infty }(\mathrm{\Omega })$ maximize G[Γ_t, ·] and G[Γ, ·], respectively, over $H_g^1(\mathrm{\Omega })$ (cf. (3.5) and (2.4)), we have

$$G[{\mathrm{\Gamma }}_t,{\psi }_0◦T_t^{-1}]\le G[{\mathrm{\Gamma }}_t,{\psi }_t]=G[{\mathrm{\Gamma }}_t],G[\mathrm{\Gamma },{\psi }_t]\le G[\mathrm{\Gamma },{\psi }_0]=G[\mathrm{\Gamma }],G[\mathrm{\Gamma },{\psi }_t◦T_t]\le G[\mathrm{\Gamma },{\psi }_0]=G[\mathrm{\Gamma }].$$

Hence

$$\frac{G[{\mathrm{\Gamma }}_t,{\psi }_0◦T_t^{-1}]-G[\mathrm{\Gamma },{\psi }_0]}{t}\le \frac{G[{\mathrm{\Gamma }}_t]-G[\mathrm{\Gamma }]}{t}\le \frac{G[{\mathrm{\Gamma }}_t,{\psi }_t]-G[\mathrm{\Gamma },{\psi }_t◦T_t]}{t}.$$

Consequently, we obtain by (4.2) that

$$\frac{z(t,{\psi }_0)-z(0,{\psi }_0)}{t}\le \frac{G[{\mathrm{\Gamma }}_t]-G[\mathrm{\Gamma }]}{t}\le \frac{z(t,{\psi }_t◦T_t)-z(0,{\psi }_t◦T_t)}{t}.$$

From Step 1, there exist ξ(t), η(t) ∈ [0, t] for each t ∈ (0, τ] such that

$${\partial }_{t}z(\xi (t),{\psi }_0)\le \frac{G[{\mathrm{\Gamma }}_t]-G[\mathrm{\Gamma }]}{t}\le {\partial }_{t}z(\eta (t),{\psi }_t◦T_t)\forall t\in (0,\tau ].$$ (4.5)

Step 3. We prove

$$\underset{t\to 0}{\text{lim}}{\partial }_{t}z(\xi (t),{\psi }_0)={\partial }_{t}z(0,{\psi }_0),$$ (4.6)

$$\underset{t\to 0}{\text{lim}}{\partial }_{t}z(\eta (t),{\psi }_t◦T_t)={\partial }_{t}z(0,{\psi }_0).$$ (4.7)

We only prove (4.7). The proof of (4.6) is similar and in fact simpler.

Since V ∈ C^∞(ℝ³,ℝ³) is compactly supported in Ω, it is easy to see that

$$A\prime (\eta (t))\to A\prime (0),J_{\eta (t)}\to J_0=1,$$

uniformly on Ω as t → 0 which implies η(t) → 0 as t → 0. By (3.12), we also have as t → 0 that

$$(\nabla ·(fV))◦T_{\eta (t)}\to \nabla ·(fV)\text{in}{L}^2(\mathrm{\Omega }),(\nabla ·V)◦T_{\eta (t)}\to \nabla ·V\text{in}{L}^2(\mathrm{\Omega }).$$

We shall prove at the end of this step

$$\underset{t\to 0}{\text{lim}}{\Vert {\psi }_t◦T_t-{\psi }_0\Vert }_{H^1(\mathrm{\Omega })}=0.$$ (4.8)

Notice by Theorem 2.1 that ψ_t is uniformly bounded in L^∞(Ω) with respect to t ∈ [0, τ], cf. (3.8). Thus

$$B({\psi }_t◦T_t)-B({\psi }_0)=B\prime (\lambda (t))({\psi }_t◦T_t-{\psi }_0)\to 0\text{in}{H}^1(\mathrm{\Omega }),$$

as t → 0, where λ(t) : Ω → ℝ is in between ψ_t ◦T_t and ψ₀ at each point in Ω and hence λ(t) is uniformly bounded in L^∞(Ω) with respect to t ∈ [0, τ]. Applying all these convergence results, we obtain by (4.4) that

$${\partial }_{t}z(\eta (t),{\psi }_t◦T_t)={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A\prime (\eta (t))\nabla ({\psi }_t◦T_t)·\nabla ({\psi }_t◦T_t)+((\nabla ·(fV))◦T_{\eta (t)})({\psi }_t◦T_t)J_{\eta (t)}-{\chi }_{+}B(({\psi }_t◦T_t))((\nabla ·V)◦T_{\eta (t)})J_{\eta (t)}]dX\to -{\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A\prime (0)\nabla {\psi }_0·\nabla {\psi }_0+(\nabla ·(fV)){\psi }_0-{\chi }_{+}B({\psi }_0)(\nabla ·V)]dX={\partial }_{t}z(0,{\psi }_0)\text{as}t\to 0,$$

proving (4.7).

We now prove (4.8). Fix t > 0. Since ${\psi }_t\in H_g^1(\mathrm{\Omega })$ maximizes G[Γ_t, ·] over $H_g^1(\mathrm{\Omega })$, ψ_t ◦T_t maximizes $z(t,\varphi )=G[{\mathrm{\Gamma }}_t,\varphi ◦T_t^{-1}]$ over all $\varphi \in H_g^1(\mathrm{\Omega })$. Since ψ_t is bounded in Ω by (3.8), we obtain from (4.3) and

$${\frac{d}{d\sigma }|}_{\sigma =0}z(t,({\psi }_t+\sigma \eta ◦T_t^{-1})◦T_t)={\frac{d}{d\sigma }|}_{\sigma =0}z(t,{\psi }_t◦T_t+\sigma \eta )=0\forall \eta \in H_0^1(\mathrm{\Omega })$$

that

$${\int }_{\mathrm{\Omega }}[-{\epsilon }_{\mathrm{\Gamma }}A(t)\nabla ({\psi }_t◦T_t)·\nabla \eta +(f◦T_t)J_t\eta -{\chi }_{+}B\prime ({\psi }_t◦T_t)J_t\eta ]dX=0\forall \eta \in H_0^1(\mathrm{\Omega }).$$

Since ${\psi }_0\in H_g^1(\mathrm{\Omega })$ maximizes G[Γ, ·] over $H_g^1(\mathrm{\Omega })$,

$${\int }_{\mathrm{\Omega }}[-{\epsilon }_{\mathrm{\Gamma }}\nabla {\psi }_0·\nabla \eta +f\eta -{\chi }_{+}B\prime ({\psi }_0)\eta ]dX=0\forall \eta \in H_0^1(\mathrm{\Omega }).$$

Subtracting one of these two equations from the other and choosing $H_0^1(\mathrm{\Omega })$, we deduce by rearranging the terms that

$${\int }_{\mathrm{\Omega }}{\epsilon }_{\mathrm{\Gamma }}{|\nabla ({\psi }_t◦T_t)-\nabla {\psi }_0|}^{2}dX+{\int }_{{\mathrm{\Omega }}_{+}}[B\prime ({\psi }_t◦T_t)-B\prime ({\psi }_0)]({\psi }_t◦T_t-{\psi }_0)dX=-{\int }_{\mathrm{\Omega }}{\epsilon }_{\mathrm{\Gamma }}[(A(t)-I)\nabla ({\psi }_t◦T_t)]·[\nabla ({\psi }_t◦T_t)-\nabla {\psi }_0]dX+{\int }_{\mathrm{\Omega }}[(f◦T_t)J_t-f]({\psi }_t◦T_t-{\psi }_0)dX-{\int }_{{\mathrm{\Omega }}_{+}}B\prime ({\psi }_t◦T_t)(J_t-1)({\psi }_t◦T_t-{\psi }_0)dX.$$

Notice by the convexity of B that

$$[B\prime ({\psi }_t◦T_t)-B\prime ({\psi }_0)]({\psi }_t◦T_t-{\psi }_0)\ge 0\text{in}{\mathrm{\Omega }}_{+.}$$

Therefore, applying the Poincaré inequality to ${\psi }_t◦T_t-{\psi }_0\in H_0^1(\mathrm{\Omega })$ and using the Cauchy–Schwarz inequality, we obtain that

$${\Vert {\psi }_t◦T_t-{\psi }_0\Vert }_{H^1(\mathrm{\Omega })}^2\le C{\int }_{\mathrm{\Omega }}{\epsilon }_{\mathrm{\Gamma }}{|\nabla ({\psi }_t◦T_t)-\nabla {\psi }_0|}^{2}dX+C{\int }_{{\mathrm{\Omega }}_{+}}[B\prime ({\psi }_t◦T_t)-B\prime ({\psi }_0)]({\psi }_t◦T_t-{\psi }_0)dX\le C[{\Vert A(t)-I\Vert }_{L^{\infty }(\mathrm{\Omega })}{\Vert \nabla ({\psi }_t◦T_t)\Vert }_{L^2(\mathrm{\Omega })}+{\Vert (f◦T_t)J_t-f\Vert }_{L^2(\mathrm{\Omega })}+{\Vert B\prime ({\psi }_t◦T_t)(J_t-1)\Vert }_{L^{\infty }(\mathrm{\Omega })}]{\Vert {\psi }_t◦T_t-{\psi }_0\Vert }_{H^1(\mathrm{\Omega })}.$$

Here and below we denote by C > 0 a generic constant that can depend on ε₋, ε₊, Ω, B but not on t or ψ₀. Note that

$$(f◦T_t)J_t-f=(f◦T_t-f)J_t+f(J_t-1).$$

Consequently, the uniform boundedness of ψ_t in L^∞(Ω) and in H¹(Ω) for small t > 0 (cf. (3.8)), the uniform convergence A(t) → A(0) = I and J_t → 1 as t → 0, and the convergence f ◦ T_t → f in L²(Ω) (cf. (3.12)) imply that

$${\Vert {\psi }_t◦T_t-{\psi }_0\Vert }_{H^1(\mathrm{\Omega })}\le C[{\Vert A(t)-I\Vert }_{L^{\infty }(\mathrm{\Omega })}{\Vert \nabla ({\psi }_t◦T_t)\Vert }_{L^2(\mathrm{\Omega })}+{\Vert f◦T_t-f\Vert }_{L^2(\mathrm{\Omega })}{\Vert J_t\Vert }_{L^{\infty }(\mathrm{\Omega })}+{\Vert f\Vert }_{L^2(\mathrm{\Omega })}{\Vert J_t-1\Vert }_{L^{\infty }(\mathrm{\Omega })}+{\Vert B\prime ({\psi }_t◦T_t)\Vert }_{L^{\infty }(\mathrm{\Omega })}{\Vert J_t-1\Vert }_{L^{\infty }(\mathrm{\Omega })}]\to 0\text{as}t\to 0.$$

This is (4.8).

Step 4. It follows from (4.5)–(4.7) that

$${\delta }_{\mathrm{\Gamma },V}G[\mathrm{\Gamma }]={\frac{d}{dt}|}_{t=0}G[{\mathrm{\Gamma }}_t(V)]={\partial }_{t}z(0,{\psi }_0).$$

We now show that ∂_tz(0, ψ₀) is the right-hand side of (4.1).

It follows from (4.4) with t = 0 and ϕ = ψ₀, and (3.11) with t = 0 that

$${\partial }_{t}z(0,{\psi }_0)={\int }_{\mathrm{\Omega }}[-\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}A\prime (0)\nabla {\psi }_0·\nabla {\psi }_0+(\nabla ·(fV)){\psi }_0-{\chi }_{+}B({\psi }_0)(\nabla ·V)]dX=-{\int }_{\mathrm{\Omega }}\frac{{\epsilon }_{\mathrm{\Gamma }}}{2}(\nabla ·V)\nabla {\psi }_0·\nabla {\psi }_{0}dX+{\int }_{\mathrm{\Omega }}{\epsilon }_{\mathrm{\Gamma }}(\nabla V)\nabla {\psi }_0·\nabla {\psi }_{0}dX+{\int }_{\mathrm{\Omega }}(\nabla ·(fV)){\psi }_{0}dX-{\int }_{{\mathrm{\Omega }}_{+}}B({\psi }_0)(\nabla ·V)dX.$$

Denote by Vⁱ and n_i the ith components of V and n, respectively. Recall that the unit normal n to Γ points from Ω₊ to Ω₋. By integration by parts and the fact that V vanishes in a neighborhood of ∂ Ω, by (2.7) with ψ = ψ₀, and using the summation convention, we continue to have

$${\partial }_{t}z(0,{\psi }_0)=-{\int }_{{\mathrm{\Omega }}_{+}}\frac{{\epsilon }_{+}}{2}{\partial }_{X_i}{V}^i{\partial }_{X_j}{\psi }_0{\partial }_{X_j}{\psi }_{0}dX-{\int }_{{\mathrm{\Omega }}_{-}}\frac{{\epsilon }_{-}}{2}{\partial }_{X_i}{V}^i{\partial }_{X_j}{\psi }_0{\partial }_{X_j}{\psi }_{0}dX+{\int }_{{\mathrm{\Omega }}_{+}}{\epsilon }_{+}{\partial }_{X_j}{V}^i{\partial }_{X_j}{\psi }_0{\partial }_{X_i}{\psi }_{0}dX+{\int }_{{\mathrm{\Omega }}_{-}}{\epsilon }_{-}{\partial }_{X_j}{V}^i{\partial }_{X_j}{\psi }_0{\partial }_{X_i}{\psi }_{0}dX-{\int }_{\mathrm{\Omega }}f(V·\nabla {\psi }_0)dX+{\int }_{{\mathrm{\Omega }}_{+}}B\prime ({\psi }_0)(\nabla {\psi }_0·V)dX+{\int }_{\mathrm{\Gamma }}B({\psi }_0)(V·n)dX={\int }_{{\mathrm{\Omega }}_{+}}{\epsilon }_{+}{V}^i{\partial }_{X_j}{\psi }_0{\partial }_{X_j{X}_i}^2{\psi }_{0}dX+{\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }_0^{+}|}^2(V·n)dS+{\int }_{{\mathrm{\Omega }}_{-}}{\epsilon }_{-}{V}^i{\partial }_{X_j}{\psi }_0{\partial }_{X_j{X}_i}^2{\psi }_{0}dX-{\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }_0^{-}|}^2(V·n)dS-{\int }_{{\mathrm{\Omega }}_{+}}{\epsilon }_{+}{V}^i({\partial }_{X_j{X}_j}^2{\psi }_0{\partial }_{X_i}{\psi }_0+{\partial }_{X_j}{\psi }_0{\partial }_{X_i{X}_j}^2{\psi }_0)dX-{\int }_{\mathrm{\Gamma }}{\epsilon }_{+}{V}^i{n}_j{\partial }_{X_j}{\psi }_0^{+}{\partial }_{X_i}{\psi }_0^{+}dS-{\int }_{{\mathrm{\Omega }}_{-}}{\epsilon }_{-}{V}^i({\partial }_{X_j{X}_j}^2{\psi }_0{\partial }_{X_i}{\psi }_0+{\partial }_{X_j}{\psi }_0{\partial }_{X_i{X}_j}^2{\psi }_0)dX+{\int }_{\mathrm{\Gamma }}{\epsilon }_{-}{V}^i{n}_j{\partial }_{X_j}{\psi }_0^{-}{\partial }_{X_i}{\psi }_0^{-}dS-{\int }_{\mathrm{\Omega }}f(V·\nabla {\psi }_0)dX+{\int }_{{\mathrm{\Omega }}_{+}}B\prime ({\psi }_0)(\nabla {\psi }_0·V)dX+{\int }_{\mathrm{\Gamma }}B({\psi }_0)(V·n)dS={\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }_0^{+}|}^2(V·n)dS-{\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }_0^{-}|}^2(V·n)dS-{\int }_{\mathrm{\Gamma }}{\epsilon }_{+}(\nabla {\psi }_0^{+}·n)(V·\nabla {\psi }_0^{+})dS+{\int }_{\mathrm{\Gamma }}{\epsilon }_{-}(\nabla {\psi }_0^{-}·n)(V·\nabla {\psi }_0^{-})dS-{\int }_{{\mathrm{\Omega }}_{+}}[{\epsilon }_{+}\mathrm{\Delta }{\psi }_0+f-B\prime ({\psi }_0)](\nabla {\psi }_0·V)dX-{\int }_{{\mathrm{\Omega }}_{-}}({\epsilon }_{-}\mathrm{\Delta }{\psi }_0+f)(\nabla {\psi }_0·V)dX+{\int }_{\mathrm{\Gamma }}B({\psi }_0)(V·n)dS={\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }_0^{+}|}^2(V·n)dS-{\int }_{\mathrm{\Gamma }}\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }_0^{-}|}^2(V·n)dS-{\int }_{\mathrm{\Gamma }}{\epsilon }_{+}(\nabla {\psi }_0^{+}·n)(V·\nabla {\psi }_0^{+})dS+{\int }_{\mathrm{\Gamma }}{\epsilon }_{-}(\nabla {\psi }_0^{-}·n)(V·\nabla {\psi }_0^{-})dS+{\int }_{\mathrm{\Gamma }}B({\psi }_0)(V·n)dS.$$ (4.9)

Since ${\psi }_0^{+}={\psi }_0^{-}$ along Γ,

$$\nabla ({\psi }_0^{+}-{\psi }_0^{-})=(\nabla {\psi }_0^{+}·n-\nabla {\psi }_0^{-}·n)n\text{on}\mathrm{\Gamma }.$$

By (2.7),

$${\epsilon }_{+}\nabla {\psi }_0^{+}·n={\epsilon }_{-}\nabla {\psi }_0^{-}·n={\epsilon }_{\mathrm{\Gamma }}\nabla {\psi }_0·n\text{on}\mathrm{\Gamma }.$$ (4.10)

We thus have

$${\int }_{\mathrm{\Gamma }}{\epsilon }_{+}(\nabla {\psi }_0^{+}·n)(V·\nabla {\psi }_0^{+})dS-{\int }_{\mathrm{\Gamma }}{\epsilon }_{-}(\nabla {\psi }_0^{-}·n)(V·\nabla {\psi }_0^{-})dS={\int }_{\mathrm{\Gamma }}{\epsilon }_{\mathrm{\Gamma }}(\nabla {\psi }_0·n)V·\nabla ({\psi }_0^{+}-{\psi }_0^{-})dS={\int }_{\mathrm{\Gamma }}{\epsilon }_{\mathrm{\Gamma }}(\nabla {\psi }_0·n)V·(\nabla {\psi }_0^{+}·n-\nabla {\psi }_0^{-}·n)n={\int }_{\mathrm{\Gamma }}[{\epsilon }_{+}{|\nabla {\psi }_0^{+}·n|}^2-{\epsilon }_{-}{|\nabla {\psi }_0^{-}·n|}^2](V·n)dS.$$

This and (4.9) imply that ∂_tz(0, ψ₀) is the right-hand side of (4.1).

Corollary 4.1. Under the assumption of Theorem 4.1 we have

$${\delta }_{\mathrm{\Gamma }}G[\mathrm{\Gamma }]=\frac{1}{2}(\frac{1}{{\epsilon }_{-}}-\frac{1}{{\epsilon }_{+}}){|{\epsilon }_{\mathrm{\Gamma }}\nabla {\psi }_0·n|}^2+\frac{1}{2}({\epsilon }_{+}-{\epsilon }_{-}){|(I-n\otimes n)\nabla {\psi }_0|}^2+B({\psi }_0).$$ (4.11)

In particular, if ε₋ < ε₊ then the dielectric boundary force in the normal direction from Ω₋ to Ω₊ is always negative: F_n = −δ_ΓG[Γ] < 0 on Γ.

Proof. We have the orthogonal decomposition

$$\nabla {\psi }_0^{\pm }=(\nabla {\psi }_0^{\pm }·n)n+(I-n\otimes n)\nabla {\psi }_0^{\pm }\text{on}\mathrm{\Gamma }.$$

Moreover, since ψ₀ is continuous, its tangential derivatives along Γ are continuous. Hence

$$(I-n\otimes n)\nabla {\psi }_0^{+}=(I-n\otimes n)\nabla {\psi }_0^{-}\text{on}\mathrm{\Gamma }.$$

We denote this common value by (I − n ⊗ n)∇ψ₀. Notice that

$$n·(I-n\otimes n)\nabla {\psi }_0=0.$$

We thus have by (4.10) that

$$\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }_0^{+}|}^2-\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }_0^{-}|}^2-{\epsilon }_{+}{|\nabla {\psi }_0^{+}·n|}^2+{\epsilon }_{-}{|\nabla {\psi }_0^{-}·n|}^2=-\frac{{\epsilon }_{+}}{2}{|\nabla {\psi }_0^{+}·n|}^2+\frac{{\epsilon }_{-}}{2}{|\nabla {\psi }_0^{-}·n|}^2+\frac{{\epsilon }_{+}}{2}{|(I-n\otimes n)\nabla {\psi }_0^{+}|}^2-\frac{{\epsilon }_{-}}{2}{|(I-n\otimes n)\nabla {\psi }_0^{-}|}^2=\frac{1}{2}(\frac{1}{{\epsilon }_{-}}-\frac{1}{{\epsilon }_{+}}){|{\epsilon }_{\mathrm{\Gamma }}\nabla {\psi }_0·n|}^2+\frac{1}{2}({\epsilon }_{+}-{\epsilon }_{-}){|(I-n\otimes n)\nabla {\psi }_0|}^2.$$

This and (4.1) imply (4.11). If ε₋ < ε₊ then (4.11) implies F_n = −δ_ΓG[Γ] < 0.