Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Sep 20.
Published in final edited form as: Spine (Phila Pa 1976). 2012 Nov 1;37(23):E1438–E1443. doi: 10.1097/BRS.0b013e31826b39d7

Dynamic Biomechanical Examination of the Lumbar Spine with Implanted Total Disc Replacement (TDR) Utilizing a Pendulum Testing System

Alan H Daniels 1, David J Paller 1, Sarath Koruprolu 1, Matthew McDonnell 1, Mark A Palumbo 1, Joseph J Crisco 1
PMCID: PMC3778666  NIHMSID: NIHMS507973  PMID: 22869057

Abstract

Study Design

Biomechanical cadaver investigation

Objective

To examine dynamic bending stiffness and energy absorption of the lumbar spine with and without implanted Total Disc Replacement (TDR) under simulated physiologic motion.

Summary of background data

The pendulum testing system is capable of applying physiologic compressive loads without constraining motion of functional spinal units (FSUs). The number of cycles to equilibrium observed under pendulum testing is a measure of the energy absorbed by the FSU.

Methods

Five unembalmed, frozen human lumbar FSUs were tested on the pendulum system with axial compressive loads of 181N, 282N, 385N, and 488N before and after Synthes ProDisc-L TDR implantation. Testing in flexion, extension, and lateral bending began by rotating the pendulum to 5° resulting in unconstrained oscillatory motion. The number of rotations to equilibrium was recorded and bending stiffness (N-m/°) was calculated and compared for each testing mode.

Results

In flexion/extension, the TDR constructs reached equilibrium with significantly (p<0.05) fewer cycles than the intact FSU with compressive loads of 282N, 385N and 488N. Mean dynamic bending stiffness in flexion, extension, and lateral bending increased significantly with increasing load for both the intact FSU and TDR constructs (p<0.001). In flexion, with increasing compressive loading from 181N to 488N, the bending stiffness of the intact FSUs increased from 4.0N-m/° to 5.5N-m/°, compared to 2.1N-m/° to 3.6N-m/° after TDR implantation. At each compressive load, the intact FSU was significantly more stiff than the TDR (p<0.05).

Conclusion

Lumbar FSUs with implanted TDR were found to be less stiff, but also absorbed more energy during cyclic loading with an unconstrained pendulum system. Although the effects on clinical performance of motion preserving devices are not fully known, these results provide further insight into the biomechanical behavior of this device under approximated physiologic loading conditions.

INTRODUCTION

The ProDisc-L® TDR (Figure 1) achieved U.S. Food and Drug Administration approval for human use in 2006 and was designed to provide an alternative to fusion by reestablishing mobility to an affected segment of the lumbar spine. It is a semi-constrained arthroplasty device composed of a cobalt/chromium on polyethylene bearing surface. Short-to-midterm clinical follow-up of the ProDisc-L have been reported, with numerous studies indicating positive clinical outcomes1–3.

Figure 1.

Figure 1

Open in a new tab

ProDisc-L prosthesis (Courtesy of Synthes, West Chester, PA)

In addition to clinical studies, biomechanical investigations into motion preserving implants are essential to complete our understanding of their in vivo behavior. The biomechanical properties of the ligamentous cadaver lumbar spine with and without implanted motion-preserving devices have been studied utilizing a wide variety of experimental protocols including displacement-controlled testing, constrained load-controlled testing, unconstrained load-controlled testing, and unconstrained pure moment load-controlled testing4–19. More recently, finite element analysis has also been used to model spinal biomechanics both with and without motion preserving devices4,20–24. Yet, many of the previously used protocols were limited in their ability to apply physiologic compressive loads greater than 200N or to apply dynamic bending moments while allowing unconstrained three-dimensional motion.

To address the aforementioned limitations, we developed a novel pendulum testing system as a means to study the complex kinematics and the dynamic nature of the lumbar spine25. The pendulum apparatus is capable of applying physiologic compressive loads dynamically without constraining the motion of the functional spinal unit (FSU). Initial investigation utilizing the pendulum found that after an initial rotation, FSUs behaved as a dynamic, under-damped vibrating elastic system. Significant increases in bending stiffness and decreases in natural frequency were found with increasing compressive loading. The number of cycles to equilibrium observed under pendulum testing is a marker of the energy absorbed by the FSU. To our knowledge, energy absorption of motion preserving spinal implants under simulated physiologic motion and loading conditions has not previously been described.

In this study, we hypothesized that the lumbar spine with implanted Total Disc Replacement (TDR) would exhibit decreased dynamic stiffness and energy absorption compared to native lumbar FSUs under simulated physiologic motion when tested with the pendulum system. We aimed to determine the effects of various axial compressive loads on the dynamic biomechanical properties of native lumbar FSUs with implanted TDR as compared to native lumbar FSUs.

METHODS

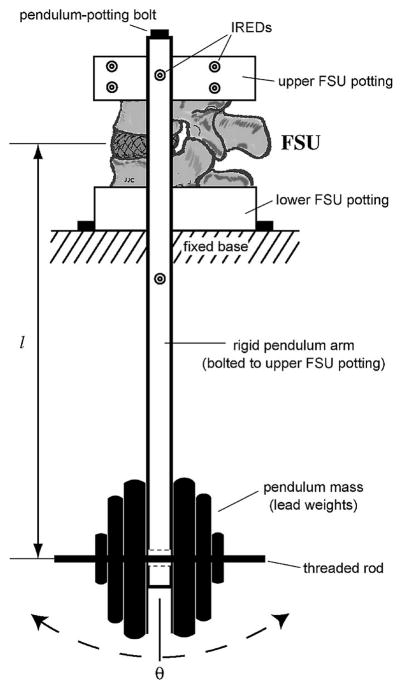
Five unembalmed, frozen human lumbar FSUs were obtained from 4 cadavers (average age 69.3 years, range 59–83). Radiographic screening was performed to eliminate any samples with previous surgery, trauma, or pathologic lesion. One FSU from L1/2, one from L2/3, two from L3/4, and one from L4/5 were utilized for testing. Biomechanical testing of the FSUs was performed on a pendulum apparatus as described previously25. The pendulum system consists of the lower lumbar vertebra mounted on a rigid platform via its potting cup, and the pendulum arm (0.55m) mounted to the upper vertebral body via its potting cup. The intervertebral disc or the TDR serves as an unconstrained fulcrum with dead weights fixed to the lower end of the pendulum arm directly below the FSU (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Pendulum testing apparatus

Each intact FSU was tested on the pendulum system with an axial compressive load of 181N, 282N, 385N, and 488N, chosen to represent physiologic loading26. Testing began by manually rotating the pendulum to an initial angle of 5° and then releasing the pendulum, resulting in unconstrained oscillatory motion of the superior vertebra. Testing was performed in flexion, extension, right lateral bending, and left lateral bending. The three-dimensional motion of the superior vertebra relative to the inferior vertebra was measured at 200Hz using an Optotrak 3020 (Northern Digital Inc., Ontario, Canada; RMS, accuracy to 0.1mm and three-dimensional resolution to 0.01 mm). Six infrared-emitting diode markers were attached to the upper potting cup, and six to the lower potting cup. Custom NDI First Principles (Northern Digital Inc., Ontario, Canada) software was used to track the marker position of the upper vertebral body with respect to the lower vertebral body. Each test was repeated twice.

The motion data as the spine oscillated was collected until angular motion was <0.1°, at which point the cycles from initial perturbation to equilibrium were collected. The number of cycles of each specimen at each compressive load was averaged for flexion, extension, right and left lateral bending.

The mean dynamic bending stiffness (N-m/°) was calculated from the time series for each specimen at each compressive load. The dynamic bending stiffness of each specimen at each compressive load was averaged for flexion, extension, right and left lateral bending.

After initial testing of the intact spines, the FSUs underwent ProDisc-L TDR implantation. The FSUs were then re-tested on the pendulum apparatus with the same loading protocol.

In addition to pendulum testing, pure moment testing was performed on all specimens before and after TDR implantation to determine quasi-static ROM and bending stiffnesses. A 400N follower load was used during moment applications (0 ± 6 Nm) at a test frequency of 0.1 Hz26 with a biaxial servohydraulic load frame (model 8521S; Instron Corp., Canton, MA). Specimen holders and attachment plates were indexed in 45° increments about two perpendicular axes so that the FSU could be positioned at the various moment axes. A six-channel load cell (model MC3-6-1000; AMTI, Watertown, MA) acquired load and moment data about three orthogonal axes while linear and rotary motions about the vertical axis were measured with the load frame transducers27. Testing of FSUs involved applying positive and negative pure moments (0 ±6 Nm sinusoidal waveform with 0.1 Hz frequency) in right and left axial rotation, flexion, extension, and right and left lateral bending using a standard flexibility protocol to apply pure moments using test methods and fixtures that were published by Spenciner et al27.

To compare statistical difference between the intact FSU and implanted TDR samples for average cycles to equilibrium and dynamic stiffness, a two factor (treatment and compressive load) repeated measures ANOVA was performed (SigmaPlot 12.0, SYSTAT, San Jose, CA). In the event of statistical differences, a Tukey post hoc test was administered. For the pure moment Instron testing, the significance of the differences for each load by outcome variable between the intact spine and TDR groups was calculated using a paired t-test. In all instances, statistical significance was set to p<0.05, a priori.

RESULTS

Average number of cycles to equilibrium

The motion of the intact FSUs with and without implanted TDR exhibited that of an under-damped, vibrating elastic system at each compressive load (Figure 3).

Figure 3.

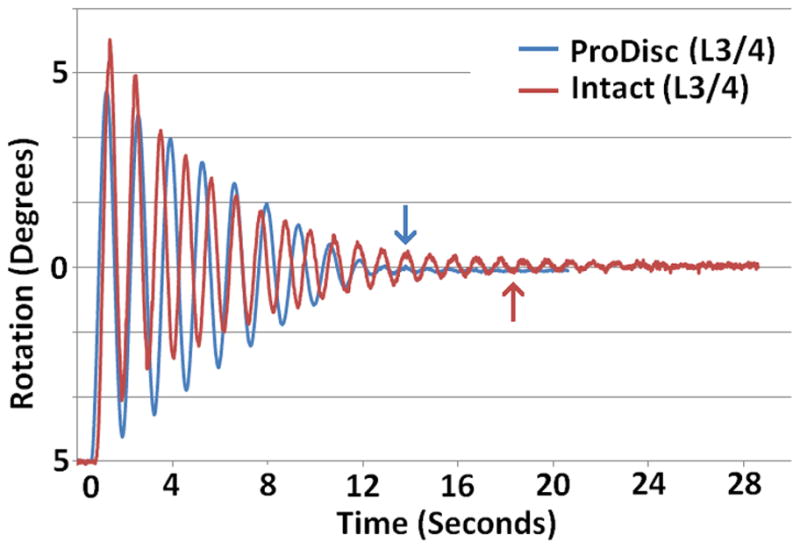
Figure 3

Open in a new tab

Typical rotation profile for an FSU before and after TDR implantation with a compressive pendulum load of 385N and an initial rotation of 5° in flexion. Arrows indicate point of cycles to equilibrium.

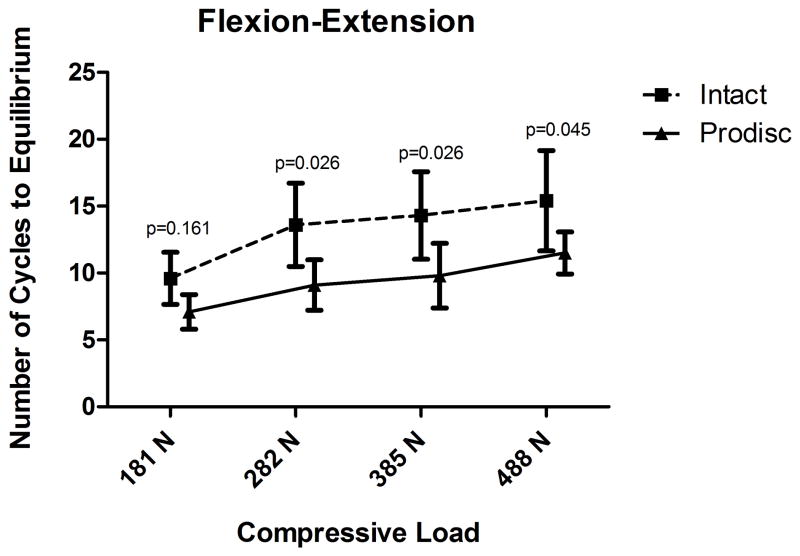
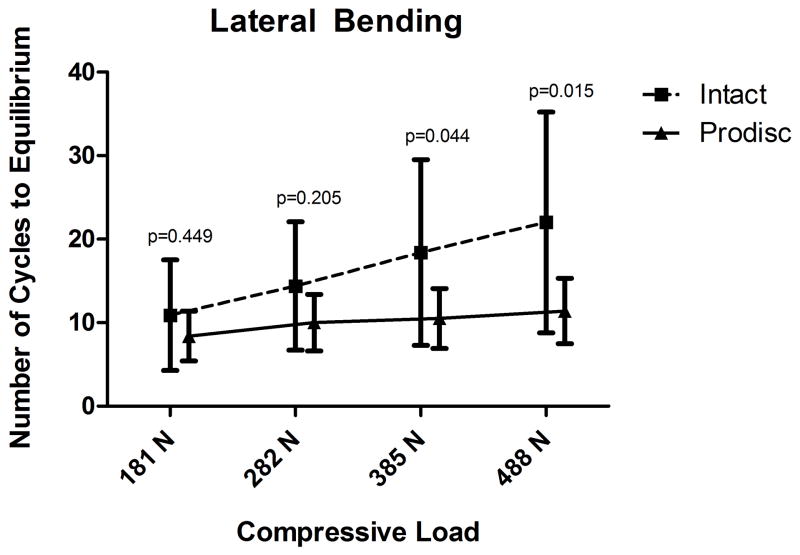
The average number of cycles to equilibrium increased with increasing compressive load for both flexion/extension testing, and lateral bending testing for the intact FSU and TDR specimens (Figure 4). In flexion/extension testing with increasing load from 181N to 488N, the average number of cycles to equilibrium of the intact FSU specimens increased from 9.6 to 15.4. After TDR implantation with increasing loads from 181N to 488N, the average number of cycles to equilibrium increased from 7.1 to 11.5. When compared to intact, The TDR exhibited significantly fewer cycles to equilibrium at loads of 282N, 385N, and 488N (p<0.05). There was no significant difference in the number of cycles to equilibrium between the intact FSU and the TDR at a load of 181N (p=0.161) (Figure 4a).

Figure 4.

Figure 4

Figure 4

Open in a new tab

Pendulum testing results in flexion (4a) and lateral bending (4b) for mean cycles to equilibrium comparing Intact FSU versus TDR. Results indicate higher energy absorption for the TDR compared to the intact FSU.

In lateral bending testing with increasing load from 181N to 488N, the average number of cycles to equilibrium of the intact FSU specimens increased from 10.2 to 22.0. After TDR implantation with increasing load from 181N to 488N, the average number of cycles to equilibrium increased from 8.4 to 11.4. The TDR exhibited significantly fewer cycles to equilibrium at 385N, and 488N (p<0.05), but was not significantly different at 181N or 282N (p>0.2) (Figure 4b).

Dynamic Bending Stiffness

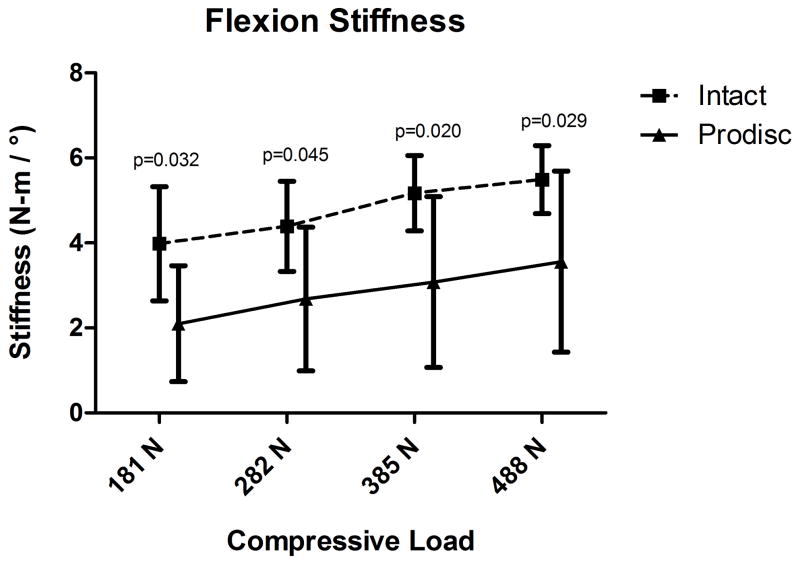
The mean dynamic bending stiffness determined by pendulum testing in flexion, extension, left lateral bending, and right lateral bending significantly increased with increasing load for both the intact FSU and TDR specimens (p<0.001). In flexion testing with increasing load from 181N to 488N, the mean bending stiffness of the intact FSU specimens increased from 4.0N-m/° to 5.5N-m/°. After TDR implantation with increasing load from 181N to 488N, the mean bending stiffness increased from 2.1N-m/° to 3.6N-m/°. When compared to the intact FSU, the TDR was significantly less stiff at all loads tested (p<0.05) (Figure 5a).

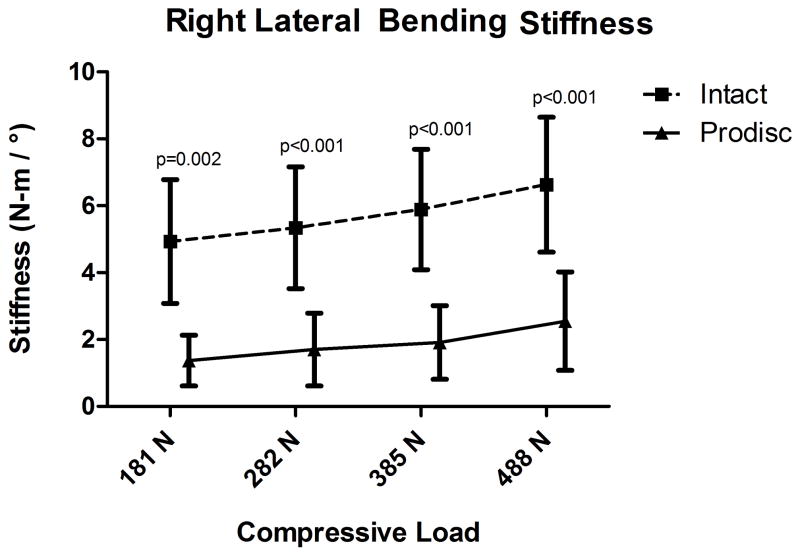
Figure 5.

Figure 5

Figure 5

Open in a new tab

Pendulum testing results in flexion (5a) and right lateral bending (5b) for mean bending stiffness (N-m/°) comparing the intact FSU versus TDR.

In extension testing, with increasing load from 181N to 488N, the mean bending stiffness of the intact FSU specimens increased from 3.6N-m/° to 5.6N-m/°. After TDR implantation with increasing load from 181N to 488N, the mean bending stiffness increased from 2.1N-m/° to 3.8N-m/°. When compared to the intact FSU, the TDR was significantly less stiff at 282N (p=0.012) and 488N (p=0.028), but was not significantly different at 181N (p=0.052) or 385N (p=0.096).

In right lateral bending testing with increasing load from 181N to 488N, the mean bending stiffness of the intact FSU specimens increased from 4.9N-m/° to 6.6N-m/°. After TDR implantation with increasing load from 181N to 488N, the mean bending stiffness increased from 1.4N-m/° to 2.5N-m/°. When compared to the intact FSU, the TDR exhibited significantly lower mean bending stiffness at all loads tested (p<0.001) (Figure 5b).

In left lateral bending testing, with increasing load from 181N to 488N, the mean bending stiffness of the intact FSU specimens increased from 5.1N-m/° to 5.9N-m/°. After TDR implantation, with increasing load from 181N to 488N, the mean bending stiffness increased from 1.4N-m/° to 2.2N-m/°. When compared to the intact FSU, the TDR exhibited significantly lower mean bending stiffness at all loads tested (p<0.001).

Quasi-Static ROM and Bending Stiffness

The range of motion of the intact FSU in flexion/extension was 5.2°, compared to 6.1° for the TDR (p=0.475). The stiffness in flexion for the intact FSU was 3.5N-m/°, which was similar to the TDR stiffness of 3.4N-m/° (p=0.943). The stiffness in extension for the intact FSU was equivalent to the TDR at 2.7N-m/°.

The range of motion of the intact FSU in lateral bending was 6.4°, compared to 16.9° for the TDR (p=0.007). The stiffness in right lateral bending for the intact FSU was 2.5N-m/°, which was statistically greater than the TDR stiffness of 1.4N-m/° (p=0.021).

The range of motion of the intact FSU in axial rotation was 5.1°, compared to 6.0° for the TDR (p=0.518). The stiffness in right axial rotation for the intact FSU was 4.4N-m/°, which was not significantly different from the TDR stiffness of 3.1N-m/° (p=0.270).

DISCUSSION

This study examined the dynamic biomechanical properties of cadaver FSUs with and without implanted TDR utilizing a pendulum testing apparatus and large compressive loads. Under pendulum testing with increasing axial loading, the bending stiffness and number of cycles to equilibrium increased for both the intact FSU and the TDR. At loading of 385N and above in flexion/extension and lateral bending, the number of cycles to equilibrium was significantly decreased for the TDR as compared to the intact FSU. This decrease in the number of cycle to equilibrium indicates greater energy absorption for the specimens with implanted TDR as compared to intact FSUs.

The stored elastic energy placed in the pendulum testing system dissipated during free swinging testing of the pendulum apparatus. The energy absorption presumably occurred within the native FSU structures and/or TDR device as damping of the pendulum swing occurred. The energy absorption characteristics of motion preserving implants have potential implications in the study of implant wear and particle formation, implant-bone interface reaction, and adjacent segment degeneration. This study did not evaluate where in the FSU that the energy absorption occurred. Energy absorption may occur at the bearing surface, the implant-bone interface, or in the native intact anatomical structures. The biomechanical and clinical effects of energy absorption of FSUs with implanted TDR are the subject of ongoing research and may help predict in vivo TDR long-term performance28–30.

Under pendulum testing, increasing axial loading was significantly associated (p<0.001) with increasing stiffness in flexion, extension, and lateral bending for both intact and TDR implanted FSUs. We found an increase in stiffness for intact FSUs from 3.6N-m/° to 6.6N-m/° with an increase in loading from 181N to 488N. This range falls within the previously reported range of stiffness under compressive loading7,8,14,25,26. Crisco et al25 reported an increase in stiffness of 1.7N-m/° to 3.5N-m/° with loads ranging from 78N to 488N, while Miller et al14 reported an increase in stiffness of 6N-m/° to 11N-m/° with bending loads ranging from 60N to 95N. Although Miller et al used compressive loads much lower than that we report in this investigation, it is interesting that both studies found an increase in stiffness of 83% following compressive loading.

In this study, we found that the bending stiffness of the TDR was significantly lower than the intact FSU in flexion and lateral bending. The effects of the bending stiffness of motion preserving devices on affected and adjacent segments are not completely understood. A primary theoretical advantage of lumbar TDR over spinal fusion is to prevent adjacent segment disease and preserve native motion patterns. Presumably, this can be accomplished through replication of intact FSU stiffness and motion parameters, although this effect has yet to be clinically proven1,31,32. Holm et al examined intradiscal pressure in a pig model of disc injury, and found increasing intradiscal pressure at discs adjacent to injured levels, presumable due to increasing stiffness at the injured disc33. This makes intuitive sense that a FSU with greater stiffness will cause increasing stress on adjacent levels. Our findings of the decreased stiffness of the TDR cannot be assumed to be protective of adjacent levels, and ongoing long-term clinical outcomes studies1,32 are needed to evaluate this theoretical advantage of TDR.

Simulating intact FSU motion and stiffness parameters with motion preserving devices may be protective to adjacent levels, yet there it not definitive long-term human evidence that this is true. Numerous studies utilizing finite element analysis have examined the effects of motion preserving implants, fusions, and cementation techniques on stiffness at the treated and adjacent levels.4,13,20–24,34,35. The optimal stiffness of motion preserving implants is not truly known, and may need to be individualized for the patient undergoing this type of surgery.

In addition to pendulum testing, we also performed pure moment testing in a quasi-static manner. Pure moment testing mimicked the pendulum results in some test modes, yet we did not perform a statistical comparison of the bending stiffness results due to differences in the range of motion tested and the methods by which we calculated stiffness. Although no direct comparison is valid, it is interesting to examine the data from both testing systems. Pendulum testing at 385N in flexion revealed a bending stiffness of 5.17N-m/° for the intact FSU and 3.08-m/° for the TDR (p=0.020), while pure moment testing at 400N revealed a bending stiffness of 3.49N-m/° for the intact FSU and 3.42N-m/° for the TDR (p=0.943). Pendulum testing at 385N in lateral bending revealed a bending stiffness of 5.89N-m/° for the intact FSU and 1.91N-m/° for the TDR (p<0.001), while pure moment testing at 400N revealed a bending stiffness of 2.46N-m/° for the intact FSU and 1.24N-m/° for the TDR (p=0.021). The results of the pendulum testing system and the pure moment testing system differed in exact value for bending stiffness, although the trends were similar providing evidence toward the validity of our methods. The larger difference between the intact FSU and the TDR in bending stiffness calculated from pendulum testing compared to pure moment testing suggests that the pendulum testing system may be able to detect small differences in stiffness not detected by pure moment testing.

Numerous other in vitro studies examining the ProDisc TDR have been performed18,19,30,36. Meyers et al19 examined FSUs with and without implanted ProDisc under pure bending moment testing with 600N and 1200N compressive loading, and reported very similar data to our pure moment data. Panjabi et al36 examined T12-S1 spinal segments with and without implanted ProDisc TDRs, and reported that the TDR preserved native physiologic motions at all levels, yet no stiffness or energy absorption data was reported. The results of this study provide additional data regarding the behavior of TDR technology.

The results from this investigation also compare favorably to the results reported in the initial investigation using the pendulum testing apparatus25. In the initial report25 the stiffness of intact FSUs in flexion increased from 2.3 to 3.5N-m/° when tested with 181N to 488N, while ours increased from 4.0 to 5.5N-m/°. It is interesting that we report stiffness values nearly twice that of the previous report. This may have been due to subtle differences in testing apparatus or the level of degeneration of individual cadaver specimens.

The pendulum testing system appears to be a useful tool for examining the motion and stiffness of single FSUs, yet its ability to test multiple adjacent FSUs may be limited and is yet unknown. The complex motion patterns of multi-level spinal units may make data interpretation challenging, as we calculated FSU stiffness based on the damping of the single FSU on the pendulum apparatus. Numerous experimental18,37 and computational21,22 methods for studying FSU motion adjacent to motion preserving technology have been developed, and although the pendulum testing system may be useful for this purpose, additional modifications such as motion tracking and intradiscal pressure monitoring will need to be utilized. Even with additional study tools, the complex interrelated motion of adjacent segments under a free swinging pendulum may limit the pendulum testing system’s ability to provide useful data regarding adjacent level motion. Similarly, the pendulum’s utility for studying fusion and instrumentation constructs is limited due to the necessity of motion for data collection.

This study had several limitations. This study did not assess the level of disc degeneration of the intact FSUs. Significant degeneration of the disc and facet joints affects FSU stiffness33, thus it is difficult to assess if the TDR in this study mimicked healthy or degenerated FSUs. Furthermore, this lack of degeneration assessment may have led to the discrepancy between stiffness values between this investigation and the first pendulum investigation. An additional study limitation was that our computations of stiffness were based on a dynamic response, thus are an average of the actual dynamic stiffness that occurs with physiologic motion. Lastly, environmental factors such as body temperature and lubrication may affect in vivo TDR performance, and this study did not examine any of these factors.

Further biomechanical study may examine where energy absorption in intact FSUs and motion preserving devices is occurring. In addition, clinical studies with long term follow-up are essential to monitor rates of adjacent segment degeneration and implant related complications in patients with implanted TDR devices.

This study examined the biomechanical performance of an implanted TDR in the cadaver lumbar spine on a pendulum testing system. Our data provide additional insight into the ability of the pendulum testing apparatus to evaluate motion preserving spinal implants in simulated physiologic loading situations. Lumbar FSUs with implanted TDR were found to be less stiff, but also absorbed more energy during cyclic loading with the unconstrained pendulum testing system. Studies such as this are important in the ongoing evaluation and development of spinal motion preserving implants.

Key points.

  1. Lumbar FSUs with implanted TDR were found to absorb more energy than intact FSUs during cyclic loading with an unconstrained pendulum system.

  2. Lumbar FSUs with implanted TDR were found to be less stiff in flexion, extension, and lateral bending compared to intact FSUs under pendulum testing.

  3. The pendulum testing system appears to be a useful method for examining lumbar spine motion preserving devices by applying physiologic compressive loads without constraining motion of functional spinal units.

  4. Although the effects of energy absorption and stiffness on clinical performance of motion preserving devices are not fully known, these results provide further insight into the biomechanical behavior of this device under approximated physiologic loading conditions.

Acknowledgments

No outside financial support was obtained for this study. Synthes provided the implants and instruments for the investigation.

ProDisc-L is FDA approved for single level disc replacement L3-S1.

References

  • 1.Delamarter R, Zigler JE, Balderston RA, Cammisa FP, Goldstein JA, Spivak JM. Prospective, randomized, multicenter Food and Drug Administration investigational device exemption study of the ProDisc-L total disc replacement compared with circumferential arthrodesis for the treatment of two-level lumbar degenerative disc disease: results at twenty-four months. J Bone Joint Surg Am. 2011 Apr 20;93(8):705–715. doi: 10.2106/JBJS.I.00680. [DOI] [PubMed] [Google Scholar]
  • 2.Markwalder TM, Wenger M, Marbacher S. A 6.5-year follow-up of 14 patients who underwent ProDisc total disc arthroplasty for combined long-standing degenerative lumbar disc disease and recent disc herniation. J Clin Neurosci. 2011 Dec;18(12):1677–1681. doi: 10.1016/j.jocn.2011.04.024. [DOI] [PubMed] [Google Scholar]
  • 3.Park CK, Ryu KS, Lee KY, Lee HJ. Clinical Outcome of Lumbar Total Disc Replacement Using ProDisc-L(R) in Degenerative Disc Disease: Minimum 5-year Follow-up Results at a Single Institute. Spine (Phila Pa 1976) 2011 Aug 18; doi: 10.1097/BRS.0b013e31822ecd85. [DOI] [PubMed] [Google Scholar]
  • 4.Chung SK, Kim YE, Wang KC. Biomechanical effect of constraint in lumbar total disc replacement: a study with finite element a nalysis. Spine (Phila Pa 1976) 2009 May 20;34(12):1281–1286. doi: 10.1097/BRS.0b013e3181a4ec2d. [DOI] [PubMed] [Google Scholar]
  • 5.Cunningham BW, Gordon JD, Dmitriev AE, Hu N, McAfee PC. Biomechanical evaluation of total disc replacement arthroplasty: an in vitro human cadaveric model. Spine (Phila Pa 1976) 2003 Oct 15;28(20):S110–117. doi: 10.1097/01.BRS.0000092209.27573.90. [DOI] [PubMed] [Google Scholar]
  • 6.Cunningham BW, Hu N, Beatson HJ, Serhan H, Sefter JC, McAfee PC. Revision strategies for single- and two-level total disc arthroplasty procedures: a biomechanical perspective. Spine J. 2009 Sep;9(9):735–743. doi: 10.1016/j.spinee.2009.03.011. [DOI] [PubMed] [Google Scholar]
  • 7.Edwards WT, Hayes WC, Posner I, White AA, 3rd, Mann RW. Variation of lumbar spine stiffness with load. J Biomech Eng. 1987 Feb;109(1):35–42. doi: 10.1115/1.3138639. [DOI] [PubMed] [Google Scholar]
  • 8.Gardner-Morse MG, Stokes IA. Structural behavior of human lumbar spinal motion segments. J Biomech. 2004 Feb;37(2):205–212. doi: 10.1016/j.jbiomech.2003.10.003. [DOI] [PubMed] [Google Scholar]
  • 9.Goel VK, Goyal S, Clark C, Nishiyama K, Nye T. Kinematics of the whole lumbar spine. Effect of discectomy. Spine (Phila Pa 1976) 1985 Jul-Aug;10(6):543–554. doi: 10.1097/00007632-198507000-00008. [DOI] [PubMed] [Google Scholar]
  • 10.Goel VK, Voo LM, Weinstein JN, Liu YK, Okuma T, Njus GO. Response of the ligamentous lumbar spine to cyclic bending loads. Spine (Phila Pa 1976) 1988 Mar;13(3):294–300. doi: 10.1097/00007632-198803000-00012. [DOI] [PubMed] [Google Scholar]
  • 11.Goel VK, Wilder DG, Pope MH, Edwards WT. Biomechanical testing of the spine. Load-controlled versus displacement-controlled analysis. Spine (Phila Pa 1976) 1995 Nov 1;20(21):2354–2357. doi: 10.1097/00007632-199511000-00017. [DOI] [PubMed] [Google Scholar]
  • 12.Grassmann S, Oxland TR, Gerich U, Nolte LP. Constrained testing conditions affect the axial rotation response of lumbar functional spinal units. Spine (Phila Pa 1976) 1998 May 15;23(10):1155–1162. doi: 10.1097/00007632-199805150-00016. [DOI] [PubMed] [Google Scholar]
  • 13.Izambert O, Mitton D, Thourot M, Lavaste F. Dynamic stiffness and damping of human intervertebral disc using axial oscillatory displacement under a free mass system. Eur Spine J. 2003 Dec;12(6):562–566. doi: 10.1007/s00586-003-0569-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Miller JA, Schultz AB, Warwick DN, Spencer DL. Mechanical properties of lumbar spine motion segments under large loads. J Biomech. 1986;19(1):79–84. doi: 10.1016/0021-9290(86)90111-9. [DOI] [PubMed] [Google Scholar]
  • 15.Panjabi MM. Experimental determination of spinal motion segment behavior. Orthop Clin North Am. 1977 Jan;8(1):169–180. [PubMed] [Google Scholar]
  • 16.Panjabi MM, Oxland TR, Yamamoto I, Crisco JJ. Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J Bone Joint Surg Am. 1994 Mar;76(3):413–424. doi: 10.2106/00004623-199403000-00012. [DOI] [PubMed] [Google Scholar]
  • 17.Wilke HJ, Rohlmann A, Neller S, et al. Is it possible to simulate physiologic loading conditions by applying pure moments? A comparison of in vivo and in vitro load components in an internal fixator. Spine (Phila Pa 1976) 2001 Mar 15;26(6):636–642. doi: 10.1097/00007632-200103150-00014. [DOI] [PubMed] [Google Scholar]
  • 18.Demetropoulos CK, Sengupta DK, Knaub MA, et al. Biomechanical evaluation of the kinematics of the cadaver lumbar spine following disc replacement with the ProDisc-L prosthesis. Spine (Phila Pa 1976) 2010 Jan 1;35(1):26–31. doi: 10.1097/BRS.0b013e3181c4eb9a. [DOI] [PubMed] [Google Scholar]
  • 19.Meyers KN, Campbell DA, Lipman JD, et al. Dynamics of an intervertebral disc prosthesis in human cadaveric spines. HSS J. 2007 Sep;3(2):164–168. doi: 10.1007/s11420-007-9049-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Goel VK, Park H, Kong W. Investigation of vibration characteristics of the ligamentous lumbar spine using the finite element approach. J Biomech Eng. 1994 Nov;116(4):377–383. doi: 10.1115/1.2895787. [DOI] [PubMed] [Google Scholar]
  • 21.Schmidt H, Galbusera F, Rohlmann A, Zander T, Wilke HJ. Effect of multilevel lumbar disc arthroplasty on spine kinematics and facet joint loads in flexion and extension: a finite element analysis. Eur Spine J. 2010 Apr 2; doi: 10.1007/s00586-010-1382-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Rohlmann A, Mann A, Zander T, Bergmann G. Effect of an artificial disc on lumbar spine biomechanics: a probabilistic finite element study. Eur Spine J. 2009 Jan;18(1):89–97. doi: 10.1007/s00586-008-0836-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Goel VK, Grauer JN, Patel T, et al. Effects of charite artificial disc on the implanted and adjacent spinal segments mechanics using a hybrid testing protocol. Spine (Phila Pa 1976) 2005 Dec 15;30(24):2755–2764. doi: 10.1097/01.brs.0000195897.17277.67. [DOI] [PubMed] [Google Scholar]
  • 24.Tang S, Rebholz BJ. Does anterior lumbar interbody fusion promote adjacent degeneration in degenerative disc disease? A finite element study. J Orthop Sci. 2011 Mar;16(2):221–228. doi: 10.1007/s00776-011-0037-3. [DOI] [PubMed] [Google Scholar]
  • 25.Crisco JJ, Fujita L, Spenciner DB. The dynamic flexion/extension properties of the lumbar spine in vitro using a novel pendulum system. J Biomech. 2007;40(12):2767–2773. doi: 10.1016/j.jbiomech.2006.12.013. [DOI] [PubMed] [Google Scholar]
  • 26.Panjabi MMWA. Clinical biomechanics of the spine. Philadelphia, PA: J.B. Lippincott; 1990. [Google Scholar]
  • 27.Spenciner D, Greene D, Paiva J, Palumbo M, Crisco J. The multidirectional bending properties of the human lumbar intervertebral disc. Spine J. 2006 May-Jun;6(3):248–257. doi: 10.1016/j.spinee.2005.08.020. [DOI] [PubMed] [Google Scholar]
  • 28.Rawlinson JJ, Punga KP, Gunsallus KL, Bartel DL, Wright TM. Wear simulation of the ProDisc-L disc replacement using adaptive finite element analysis. J Neurosurg Spine. 2007 Aug;7(2):165–173. doi: 10.3171/SPI-07/08/166. [DOI] [PubMed] [Google Scholar]
  • 29.Chen WM, Park C, Lee K, Lee S. In situ contact analysis of the prosthesis components of Prodisc-L in lumbar spine following total disc replacement. Spine (Phila Pa 1976) 2009 Sep 15;34(20):E716–723. doi: 10.1097/BRS.0b013e3181ae23d1. [DOI] [PubMed] [Google Scholar]
  • 30.Rousseau MA, Bradford DS, Bertagnoli R, Hu SS, Lotz JC. Disc arthroplasty design influences intervertebral kinematics and facet forces. Spine J. 2006 May-Jun;6(3):258–266. doi: 10.1016/j.spinee.2005.07.004. [DOI] [PubMed] [Google Scholar]
  • 31.Harrop JS, Youssef JA, Maltenfort M, et al. Lumbar adjacent segment degeneration and disease after arthrodesis and total disc arthroplasty. Spine (Phila Pa 1976) 2008 Jul 1;33(15):1701–1707. doi: 10.1097/BRS.0b013e31817bb956. [DOI] [PubMed] [Google Scholar]
  • 32.Guyer RD, McAfee PC, Banco RJ, et al. Prospective, randomized, multicenter Food and Drug Administration investigational device exemption study of lumbar total disc replacement with the CHARITE artificial disc versus lumbar fusion: five-year follow-up. Spine J. 2009 May;9(5):374–386. doi: 10.1016/j.spinee.2008.08.007. [DOI] [PubMed] [Google Scholar]
  • 33.Holm S, Ekstrom L, Kaigle Holm A, Hansson T. Intradiscal pressure in the degenerated porcine intervertebral disc. Vet Comp Orthop Traumatol. 2007;20(1):29–33. [PubMed] [Google Scholar]
  • 34.Kosmopoulos V, Keller TS, Schizas C. Early stage disc degeneration does not have an appreciable affect on stiffness and load transfer following vertebroplasty and kyphoplasty. Eur Spine J. 2009 Jan;18(1):59–68. doi: 10.1007/s00586-008-0828-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Rohlmann A, Zander T, Bergmann G, Boustani HN. Optimal stiffness of a pedicle-screw-based motion preservation implant for the lumbar spine. Eur Spine J. 2011 Oct 20; doi: 10.1007/s00586-011-2047-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Panjabi M, Henderson G, Abjornson C, Yue J. Multidirectional testing of one- and two-level ProDisc-L versus simulated fusions. Spine (Phila Pa 1976) 2007 May 20;32(12):1311–1319. doi: 10.1097/BRS.0b013e318059af6f. [DOI] [PubMed] [Google Scholar]
  • 37.Schmoelz W, Huber JF, Nydegger T, Dipl I, Claes L, Wilke HJ. Dynamic stabilization of the lumbar spine and its effects on adjacent segments: an in vitro experiment. J Spinal Disord Tech. 2003 Aug;16(4):418–423. doi: 10.1097/00024720-200308000-00015. [DOI] [PubMed] [Google Scholar]

RESOURCES