Abstract
When a treadmill accelerates continuously, the walk-run transition has generally been assumed to occur at the instant when a flight phase is first observed, while the run-walk transition has been assumed to occur at the instant of the first double support period. There is no theoretical or empirical evidence to suggest that gait transitions occur at the instant of these events, nor even whether transitions are abrupt events. The purpose of this study was to determine whether the gait transitions during human locomotion occur abruptly, and if so, to determine the instant during a stride at which a transition occurs. The time history of the vertical velocity of the hip (vhip) and the angular velocity of the ankle (ωankle) were compared between constant speed strides (walking or running) and strides at and near the walk-run and run-walk transitions to determine if and when the transition strides resemble the stride of the corresponding constant speed strides. For both the walk-run and run-walk transitions, the stride prior to the transition resembled the original gait pattern, while the stride following the transition resembled the new gait pattern. The transition stride, however, did not resemble either a walking or a running stride during either of the transition directions. It was concluded that gait transitions are initiated at about midstance of the transition stride, but the transition is not completed until after an adjustment period of between one step and one stride. Thus, gait transitions are not abrupt events during human locomotion.
Key points.
Gait transitions are not abrupt events.
Initiation of a gait transitions occur at about midstance of the transition stride.
Gait transitions are completed approximately at the next heelstrike of the ipsilateral foot.
Time period between initiation and completion of transition does not resemble either a walk or a run.
Key words: Gait changes, walking, running, treadmill locomotion
Introduction
A gait has been defined as “a pattern of locomotion characteristic of a limited range of speeds described by quantities of which one or more change discontinuously at transitions to other gaits ”(Alexander, 1989). Several researchers (Abernethy et al., 2002; Beuter and Lefebvre, 1988; Biewener and Taylor, 1986; Collins and Stewart, 1993; Diedrich and Warren, 1998; Hreljac, 1995; Raynor et al., 2002) have based conclusions related to gait transitions on the assumption that gait transitions are abrupt events, as suggested by this definition. There is, however, some evidence which suggests that gait transitions are not abrupt events. Argue and Clayton, 1993 noted that the walk-trot and trot-walk gait transitions of highly trained dressage horses generally occurred abruptly, but intermediate steps were usually detected in the transitions of novice dressage horses. Gatesy and Biewener, 1991 observed that the gait transitions of ground dwelling birds were difficult to discern since they occurred over a number of steps. For humans, Li and Hamill, 2002 reported differences in the ground reaction forces of the steps leading up to the walk-run gait transition, suggesting that this transition occurs gradually. Other researchers (Segers et al., 2006) reached a similar conclusion based upon the observation of differences in spatialtemporal characteristics in the steps leading to both the walk-run and run-walk transitions.
When studying gait transitions, researchers have primarily relied upon two different protocols to determine the preferred transition speed (PTS). In the “incremental ”protocol (Hreljac et al., 2001; Prilutsky and Gregor, 2001; Raynor et al., 2002), researchers who control the treadmill speed, increase or decrease speed incrementally, with a decision period (usually about 30 s) given to subjects to determine whether walking or running is the preferred gait at the selected speed. Because constant speeds are utilized, and subjects are allowed a fairly lengthy decision period when using this protocol, the PTS is able to be assessed accurately and easily. When using this protocol, however, an actual spontaneous transition does not occur, and an analysis of the steps leading up to a spontaneous transition is not possible (Li and Hamill, 2002). This problem is overcome by utilizing a “continuous ”protocol, in which a constantly accelerating treadmill is used to determine the transition speed. With this protocol, a spontaneous gait transition occurs, but the determination of the exact instant of the transition is not always obvious.
When using the continuous protocol, many researchers (Beuter and Lefebvre, 1988; Diedrich and Warren, 1995; 1998; Li, 2000; Li and Hamill, 2002; Segers et al., 2006; Thorstensson and Roberthson, 1987; Turvey et al., 1999) have defined the time of the walk-run transition (WR) as the instant at which a flight phase first occurs as treadmill speed increases, and the time of the run-walk transition (RW) as the instant at which double support is first observed as speed decreases. These definitions imply that WR occurs at a toeoff, and RW occurs at a heelstrike. There is no theoretical or empirical evidence to suggest that gait transitions occur at the instant of these events, nor even whether gait transitions are abrupt events. In addition, defining walking and running by the presence or absence of a double support phase is not always correct. As examples of situations in which these classical definitions of walking and running do not apply, McMahon et al., 1987 pointed out that when running in tight circles, running on very compliant surfaces, and running with exaggerated knee flexion (Groucho running), subjects do not have a flight phase. It has also been demonstrated that during slow speed running, subjects may have a short period of double support (Hreljac, 1995; Hreljac et al., 2002). Since running at speeds near the PTS could be defined as slow speed running, it is possible that the true transition time determined when using the continuous protocol may occur one or more steps prior to the first flight phase for WR, or after the emergence of double support during RW.
A more robust and unambiguous means of distinguishing walking from running is the use of two different simple models. Walking has been characterized by an inverted pendulum model (Alexander, 1984; 1989; McGreer, 1990), while running could be described by a bouncing ball model (Alexander, 1984; McMahon, 1985). In the inverted pendulum model, the pivot point of the pendulum is the stance foot, while a kneeless lower extremity represents the arm of the pendulum, with the hip or body's center of mass (CM) as the endpoint. In this model, the maximum height of the hip or CM during the stance phase occurs at approximately midstance. In the bouncing ball model of running, the minimum height of the hip or CM during the stance phase occurs at approxi-mately midstance. Using these two models as a guide, a more accurate estimate of the instant of gait transitions may be formulated from observations of the body's position at midstance. In the current study, lower extremity segment positions at midstance of the transition step were used as criteria for determining whether a subject was walking or running.
The primary purpose of this study was to determine whether gait transitions observed while using the continuous protocol occur abruptly, or over a number of steps. If the gait transitions were found to occur abruptly, then an attempt would be made to determine the relative timing of the transitions, which would be compared between WR and RW. Determination of the timing of gait transitions would allow future researchers to more confidently assess gait transition speeds when using a continuous protocol. Because of the obvious kinematic differences between walking and running, a kinematic analysis was considered to be the most appropriate means of making these assessments.
Methods
Subjects
Participants in this study were 11 (six males, five females) young, healthy college students (height = 1.70 ± 0.08 m; mass = 71.9 ± 11. 9 kg; lower extremity length = 88.0 ± 5.2 cm), who were free from musculoskeletal injury or disease at the time of the study. Prior to participation, subjects signed informed consent forms, reiterating the basic procedures and intent of the study, as well as warning of any potential risks involved. All subjects wore their own running footwear during each testing session. Subjects who were inexperienced in treadmill locomotion were habituated by walking and running at a variety of speeds on the treadmill for a period of at least 15 minutes prior to the initiation of data collection. This time period has been shown to be sufficient to allow for accommodation to treadmill locomotion (Charteris and Taves, 1978; Schieb, 1986; Wall and Charteris, 1980).
Gait transition protocols
The PTS of each subject was determined with two protocols; incremental and continuous. For all trials, an ex-perimenter controlled the speed of the treadmill, and the treadmill controller panel was not visible to the subject. The PTS found using the incremental protocol was subse-quently used as the speed for the constant speed walking and running trials.
To determine WR using the incremental protocol, the treadmill was initially set to a speed at which subjects would walk comfortably (approximately 1.2 m·s-1). Subjects were instructed to mount the treadmill and utilize the gait which felt most natural. After a decision period of approximately 30 s, the treadmill was stopped and subjects dismounted. If subjects indicated that walking was the preferred gait at that speed (as was the case for all subjects at the initial speed), the treadmill speed was increased by approximately 0.1 m·s-1 before the subject remounted. Again, after a 30 s decision period, subjects were instructed to indicate the gait which felt most natural at the new speed. This process continued until a speed was reached at which subjects indicated that running was the most natural gait at that particular speed. That speed was defined as the speed of WR. By starting the treadmill at a high enough speed to ensure that subjects ran (> 3.0 m·s-1), then decreasing the treadmill speed incrementally (in a similar manner as done when finding WR), the speed of RW was determined. The entire process was repeated three times in random order. The PTS was defined as the average of the speeds at WR and RW.
For the continuous protocol WR trials, the tread-mill was initially set to a slow walking speed (approxi-mately 1.0 m·s-1). After subjects were comfortably walk-ing at this speed, the treadmill was continuously acceler-ated by applying constant pressure to the “increase speed ”button of the treadmill controls until after the subject began running. The instant of WR was determined from observation of a sagittal plane video recording (see be-low), and defined to occur at midstance of the step during which the subject switched from an inverted pendulum to a bouncing ball model. Since the vertical position of the hip at midstance is largely determined by the amount of hip and knee flexion at midstance, and the amount of knee flexion at midstance is quite easy to observe, this was the criterion used to determine whether a subject was walking or running. When walking, the knee is close to the anatomical position at midstance (Öberg et al., 1994). During running, however, there is approximately 50° of knee flexion at midstance (Milliron and Cavanagh, 1990). Because these differences are quite large, and easily distinguishable by an observer, no measurements of knee angles (or hip heights) were used to determine the step during which a transition occurred. To make this assessment, frame by frame observations of knee angles at mid- stance were independently made by two researchers. If there would have been disagreement between observers for any trial (which did not happen), then the trial would not have been accepted. Treadmill speed at WR was determined by averaging the subject's heel marker speed while the foot was completely in contact with the treadmill. Heel position was determined from the digitized records, as described below. In the RW trials, the process was repeated in reverse, with the treadmill initially set to a speed at which subjects could run comfortably (about 3.5 m·s-1). The treadmill speed was then continuously decreased until the subject began walking. Transition direction conditions were randomly ordered, and repeated twice, with rest periods provided between trials to avoid fatigue.
Kinematic data collection and processing
Kinematic data were collected during all continuous protocol trials for each subject, and two constant speed walking and running trials. The speed of the constant speed trials was the PTS determined when using the incremental protocol. All kinematic data were collected with a single JVC GR-DVL 9800u digital video camera positioned approximately seven meters from the treadmill. Data were recorded in the sagittal plane (from the right side) at a frequency of 240 Hz. Two-dimensional position coordinates were obtained by digitizing markers placed on appropriate anatomical landmarks, including the hip (greater trochanter), knee (estimated knee joint center), ankle (lateral malleolus), heel (calcaneus), and toe (head of fifth metatarsal). Before processing, all coordinate data were smoothed using a fourth order zero-lag Butterworth filter with cutoff frequencies uniquely chosen for both coordinates of each marker. The choice of a cutoff frequency was based on the residual method (Wells and Winter, 1980).
Data were collected for three strides during each trial, with an additional 10 to 20 frames digitized prior to the first heelstrike, and after the fourth heelstrike to help avoid endpoint smoothing errors (Vint and Hinrichs, 1996). During constant speed trials, the three consecutive strides chosen for analysis always occurred after subjects had been walking or running for at least 30 s. For the continuous protocol trials, the strides analyzed included the transition stride (WRTS or RWTS), one stride before the transition stride (WRTS-1 or RWTS-1), and one stride after the transition stride (WRTS+1 or RWTS+1).
Prior to analysis, all strides were normalized in time, so that all time variables were expressed as a percentage of stride time, with consecutive heelstrikes marking the beginning and ending of a stride. Heelstrike timing was determined using previously developed algorithms (Hreljac and Marshall, 2000; Hreljac and Stergiou, 2000).
Data analysis
In an initial analysis, the two variables that had the greatest average root mean square (RMS) difference between walking and running, and thus distinguished walking from running better than all other variables, were the vertical velocity of the hip (vhip) and ankle angular velocity (ωankle). Differences were compared throughout the curves for an entire stride at one percent intervals, giving a total of 101 points of comparison. Since the vertical velocity of the hip is a fairly good representation of the vertical velocity of the body's CM, this variable, vhip, was considered to be a global variable that could distinguish between walking and running. Ankle angular velocity has been demonstrated to be associated with the walk- run gait transition (Hreljac, 1995), so this variable, ωankle, was considered to be an appropriate localized variable. Representative graphs of vhip and ωankle during constant speed walking and running are illustrated for a single stride in Figures 1a and 1b.
Figure 1.
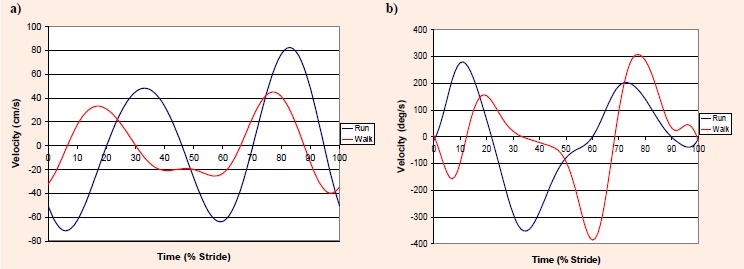
Representative graphs of a single constant speed walking and running trial for (a) vhip and (b) ωankle.
For both of the selected dependent variables (DVs), the average RMS difference between each unique pair of the three constant speed walking strides (WS1, WS2, and WS3) and running strides (RS1, RS2, and RS3) were calculated for each subject. The mean of the three average RMS differences for each gait (W-RMSavg and R-RMSavg) was determined and used in subsequent comparisons.
The RMS difference between WRTS-1 and WS1, WS2, and WS3 was then calculated for each DV. The minimum RMS difference found between WRTS-1 and the constant speed walking trials (WR1-RMSmin) was compared to W-RMSavg to determine whether this stride could fit the profile of a constant speed walking stride. Similarly, the RMS difference between WRTS+1 and RS1, RS2, and RS3 was calculated for each DV. The minimum RMS difference found between WRTS+1 and the constant speed running trials (WR3-RMSmin) was compared to R-RMSavg to determine whether this stride could fit the profile of a constant speed running stride. The RMS difference between WRTS and WS1, WS2, WS3, RS1, RS2, and RS3 was also calculated. The minimum RMS difference between WRTS and the constant speed walking trials (WR2W-RMSmin) was compared to W-RMSavg, and the minimum RMS difference between WRTS and the constant speed running trials (WR2R-RMSmin) was compared to R-RMSavg. These comparisons were made to determine whether the transition stride fit the profile of either a constant speed walking trial or a constant speed running trial.
For the run-walk transition trials, similar compari-sons were made. The minimum RMS difference found between RWTS-1 and the constant speed running trials (RW1-RMSmin) was compared to R-RMSavg to determine whether this stride fit the profile of a constant speed running stride. The minimum RMS difference found between RWTS+1 and the constant speed walking trials (RW3- RMSmin) was compared to W-RMSavg to determine whether this stride fit the profile of a constant speed walk-ing stride. The minimum RMS difference between RWTS and the constant speed running trials (RW2R-RMSmin) was compared to R-RMSavg, and the minimum RMS difference between RWTS and the constant speed walking trials (RW2W-RMSmin) was compared to W-RMSavg to determine whether the run- walk transition stride fit the profile of either a constant speed running trial or a constant speed walking trial.
If any of the comparisons showed that a specific stride during the transition trials did not fit one of the constant speed profiles for either DV, then a further analysis of this stride was conducted by breaking the stride down into 20% increments. Since the stance phase of a slow running is approximately 40% of the stride time, and the stance phase of a walking stride is approximately 60% of the stride time, 20% increments were considered appropriate. The minimum RMS difference between each of these 20% increments and the average RMS difference found within the corresponding increment of the constant speed walking and/or running were compared to determine whether the specified increment fit the profile of the corresponding increment of either a constant speed walking or running stride. In this way, the time of the actual transition could be determined more specifically. All RMS stride comparisons were made using a repeated measures ANOVA with the level of significance set at p = 0.05.
Because the data were collected on the right side of the body in this two-dimensional analysis, only trials in which the transition was determined to occur with the right side of the body were analyzed. Since the determination of transition foot was made after data were collected, trials in which the transition was determined to occur with the left foot were subsequently excluded from the analysis. Due to the exclusion of trials, the analysis of RW trials included nine subjects, while the analysis of WR trials included eight subjects.
Results
The average rate of treadmill acceleration for the WR trials was 0.18 ± 0.02 m·s-2, while the average rate of-treadmill acceleration for the RW trials was -0.20 ± 0.03 m·s-2. The average PTS found using the incremental protocol was 1.88 ± 0.11 m·s-1. This was the speed selected for all constant speed trials. Using the continuous protocol, the average speed of WR was 1.93 ± 0.14 m·s-1, and the average speed of RW was 1.85 ± 0.10 m·s-1.
For both DVs analyzed, WR1-RMSmin was significantly less than W-RMSavg (Table 1), indicating that WRTS-1 fit the profile of a constant speed walking stride. Similarly, WR3-RMSmin was not significantly different than R-RMSavg for either of the variables (Table 1), indicating that WRTS+1 fit the profile of a constant speed running trial. For both DVs, WR2R-RMSmin was significantly greater than R-RMSavg, and WR2W-RMSmin was significantly greater than W-RMSavg (Table 1). This indi-cates that WRTS did not fit the profile of either a constant speed walking or running trial (Figures 2a and 2b). Fur-ther analyses were conducted on this stride to determine whether differences occurred at any sections of the stride.
Table 1.
Relevant RMS differences for complete strides of the WR trials (n = 8). Data are means (±1 SD)
| RMS Comparison | vhip (cm·s-1) | ωankle (°·s-1) |
|---|---|---|
| W-RMSavg | 5.0 (1.2) | 40.4 (16.1) |
| R-RMSavg | 5.9 (1.7) | 34.2 (8.9) |
| WR1-RMSmin | 5.1 (2.4) | 31.3 (9.3) |
| WR3-RMSmin | 6.8 (2.4) | 38.2 (9.7) |
| WR2W-RMSmin | 9.4 (7.2) * | 33.8 (9.8) |
| WR2R-RMSmin | 33.6 (4.3) † | 119.5 (35.2) † |
* Value is significantly greater than W-RMSavg (p < 0.05).
† Value is significantly greater than R-RMSavg (p < 0.05).
Figure 2.
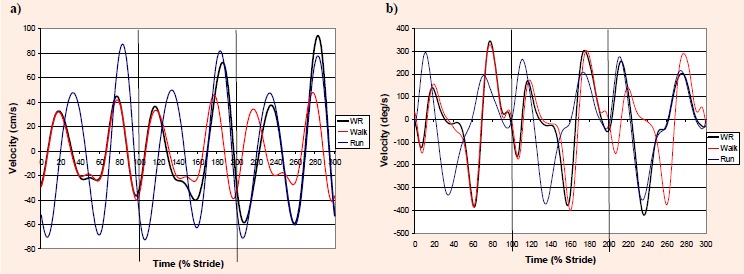
Comparison of representative graphs of the WRTS-1, WRTS, and WRTS+1 strides, and representative graphs of three constant speed walking and running strides for (a) vhip and (b) ωankle. The time of the first stride is represented as 0 to 100%, the second stride as 100% to 200%, and the third stride from 200% to 300%. Vertical lines mark the beginning and end of strides (heelstrikes).
For both vhip and ωankle, RW1-RMSmin was significantly less than R-RMSavg, indicating that RWTS-1 fit the profile of a constant speed running stride (Table 2). Also for both DVs, RW3-RMSmin was not significantly different than W-RMSavg, indicating that RWTS+1 fit the pro-file of a constant speed walking trial. For both variables, RW2W-RMSmin was significantly greater than W-RMSavg, and RW2R-RMSmin was significantly greater than R-RMSavg (Table 2). This indicates that the run-walk transition stride did not fit the profile of either a constant speed walking trial or a constant speed running trial (Figures 3a and 3b). Further analyses were conducted on this stride to determine whether differences occurred at any sections of the stride.
Table 2.
Relevant RMS differences for complete strides of the RW trials (n = 9). Data are means (±1 SD).
| RMS Comparison | vhip (cm·s-1) | ωankle (°·s-1) |
|---|---|---|
| W-RMSavg | 5.0 (1.2) | 40.4 (16.1) |
| R-RMSavg | 5.9 (1.7) | 34.2 (8.9) |
| RW1-RMSmin | 5.0 (2.4) | 36.3 (8.9) |
| RW3-RMSmin | 6.7 (2.9) | 36.7 (13.2) |
| RW2R-RMSmin | 11.0 (7.3) † | 50.7 (19.8) † |
| RW2W-RMSmin | 29.1 (8.0) * | 124.6 (45.9) * |
* Value is significantly greater than W-RMSavg (p < 0.05).
† Value is significantly greater than R-RMSavg (p < 0.05).
Figure 3.
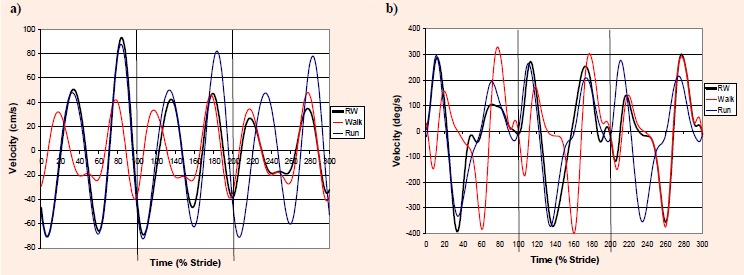
Comparison of representative graphs of the RWTS-1, RWTS, and RWTS+1 strides, and representative graphs of three constant speed walking and running strides for (a) vhip and (b) ωankle. The time of the first stride is represented as 0 to 100%, the second stride as 100% to 200%, and the third stride from 200% to 300%. Vertical lines mark the beginning and end of strides (heelstrikes).
When the transition stride was subdivided into 20% increments, it was found that WRTS resembled a walking stride for vhip until the last 20% increment, and ωankle, resembled a constant speed walking stride for the entire stride. The WRTS, however, never did resemble a running stride for either variable (Table 3).
Table 3.
Potential for the two- and three-condition experimental design to detect relationships between placebo and experimental conditions, and true baseline values. Data are means (±1 SD).
| RMS Comparison | Time Period | vhip (cm·s-1) | ωankle (°·s-1) |
|---|---|---|---|
| WR2W-RMSmin | 1-20 | 6.0 (1.8) | 37.0 (12.0) |
| 20-40 | 6.1 (3.0) | 22.5 (7.7) | |
| 40-60 | 3.3 (1.4) | 30.3 (12.6) | |
| 60-80 | 5.0 (1.7) | 41.5 (24.4) | |
| 80-100 | 4.5 (1.4) | 26.1 (21.5) | |
| WR2R-RMSmin | 1-20 | 5.0 (2.5) | 21.2 (11.1) |
| 20-40 | 5.6 (2.4) | 31.3 (9.8) | |
| 40-60 | 6.0 (2.5) | 27.5 (10.5) | |
| 60-80 | 7.6 (3.8) | 28.3 (7.8) | |
| 80-100 | 4.9 (2.5) | 19.6 (8.4) | |
| WR2W-RMSmin | 1-20 | 3.1 (1.9) | 19.5 (11.3) |
| 20-40 | 3.2 (1.7) | 12.3 (9.4) | |
| 40-60 | 3.9 (2.2) | 22.4 (12.3) | |
| 60-80 | 6.7 (4.9) | 44.0 (20.6) | |
| 80-100 | 8.7 (4.2) * | 30.5 (14.1) | |
| WR2R-RMSmin | 1-20 | 44.6 (11.1) † | 76.1 (40.5) † |
| 20-40 | 33.3 (7.6) † | 153.9 (45.8) † | |
| 40-60 | 31.4 (8.6) † | 148.2 (43.8) † | |
| 60-80 | 19.7 (7.7) † | 123.8 (56.5) † | |
| 80-100 | 15.1 (12.3) † | 45.0 (9.2) † |
* Value is significantly greater than W-RMSavg (p < 0.05).
† Value is significantly greater than R-RMSavg (p < 0.05).
For RW trials, ωankle for RWTS resembled a constant speed running stride until the last 40% of the stride, while vhip did not differ from a running stride until the last 20% increment. It was only for vhip that RWTS ever resembled a walking stride. This occurred during the last 20% increment of the stride (Table 4).
Table 4.
Relevant RMS differences for Stride 2 intervals of the RW trials (n = 9). Data are means (±1 SD).
| RMS Comparison | Time Period | vhip (cm·s-1) | ωankle (°·s-1) |
|---|---|---|---|
| W-RMSavg | 1-20 | 6.0 (1.8) | 37.0 (12.0) |
| 20-40 | 6.1 (3.0) | 22.5 (7.7) | |
| 40-60 | 3.3 (1.4) | 30.3 (12.6) | |
| 60-80 | 5.0 (1.7) | 41.5 (24.4) | |
| 80-100 | 4.5 (1.4) | 26.1 (21.5) | |
| R-RMSavg | 1-20 | 5.0 (2.5) | 21.2 (11.1) |
| 20-40 | 5.6 (2.4) | 31.3 (9.8) | |
| 40-60 | 6.0 (2.5) | 27.5 (10.5) | |
| 60-80 | 7.6 (3.8) | 28.3 (7.8) | |
| 80-100 | 4.9 (2.5) | 19.6 (8.4) | |
| RW2R-RMSmin | 1-20 | 5.3 (4.0) | 29.7 (16.1) |
| 20-40 | 8.2 (5.0) | 42.5 (23.9) | |
| 40-60 | 8.1 (5.1) | 41.0 (20.3) | |
| 60-80 | 7.1 (5.2) | 59.4 (31.6) † | |
| 80-100 | 13.6 (9.0) † | 39.2 (17.8) † | |
| RW2W-RMSmin | 1-20 | 39.0 (15.9) * | 78.8 (44.8) * |
| 20-40 | 20.8 (12.9) * | 119.9 (47.3) * | |
| 40-60 | 18.2 (12.2) * | 163.6 (60.3) * | |
| 60-80 | 8.7 (5.8)* | 162.3 (27.7) * | |
| 80-100 | 4.8 (1.7) | 47.5 (17.0) * |
* Value is significantly greater than W-RMSavg (p < 0.05).
† Value is significantly greater than R-RMSavg (p < 0.05).
Discussion
Although only three strides were analyzed in the constant speed walking and running trials, the amount of variability found within both vhip and ωankle between these strides was similar to that reported in other studies in which a greater number of strides were analyzed (Milliron and Cavanagh, 1990; Winter, 1983). In addition, the time histories of vhip and ωankle (Figures 1a and 1b) are similar to those shown by others (Winter, 1989). Thus, using the constant speed walking and running trials as a basis for determining whether the strides of the transition trials fit the profile of a walk or a run appears to be justified.
The results of the stride by stride analysis suggest that it is possible to identify the stride during which a gait transition occurs, although WRTS is not as obvious as RWTS. The exact instant of the transition, however, is not necessarily apparent. Since the criterion used to determine the transition stride occurred at midstance of the transition stride, it was expected that WR would become apparent after approximately 40% of WRTS since mid stance of a walking stride occurs at approximately 30% of stride time. It was also expected that RW would become apparent after approximately 20% of RWTS since midstance for a running stride occurs at approximately 20% of stride time. In actual fact, WR did not become apparent until the heelstrike of WRTS+1, and RW did not become apparent until the last 20% to 40% of RWTS. There are several possible explanations for these observations.
From Figures 1a and 1b, it could be seen that a large amount of the difference between walking and running for both variables lies in the relative timing of the maxima and minima. When a gait transition occurs, the relative timing may actually shift during the stride. If the gait transitions occurred prior to the swing phase, as expected, this would decrease the duty factor (ratio of time between stance and swing phases) for WR and increase the duty factor for RW. For WR, decreasing the duty factor would effectively shift the swing phase portion of the curve for both variables to the right. For RW, increasing the duty factor would effectively shift the swing phase portion of each curve to the left. This would mean that for vhip, the difference between walking and running would increase during WR, and would decrease during RW. The opposite would be true for ωankle. This may partially explain why vhip displays a difference between WRTS and walking, while ωankle did not.
The walk-run transition does not appear to be completed until the heelstrike of WRTS+1. During the latter part of the swing phase of WRTS, stride kinematics begin to differ from the kinematics of a walking stride (Table 3), but these kinematics do not resemble the kine matic pattern of a run until the heelstrike of the following stride. This would actually be about 1½ steps after the instant that many previous authors (Beuter and Lefebvre, 1988; Diedrich and Warren, 1995, 1998; Li, 2000; Li and Hamill, 2002; Segers et al., 2006; Thorstensson and Roberthson, 1987; Turvey et al., 1999) have estimated the transition to occur (instant of first flight phase), and approximately 1¾ steps after the transition was expected to occur in the current study. Thus, WR does appear to be a gradual transition, as suggested by previous researchers (Li and Hamill, 2002; Segers et al., 2006), rather than an abrupt transition, as suggested by Alexander, 1989.
The run-walk transition also does not appear to be an abrupt event. The evidence from this study suggests that RWTS begins to deviate from the kinematic pattern of a run early in the swing phase (Table 4). The stride begins to partially resemble a walking stride in the latter stages of the swing phase, but the transition is not completed until the heelstrike of RWTS+1 (Table 4). This transition would therefore take place about one step after the instant that previous authors have estimated the transition to occur (instant of first double support), and approximately 1¼ steps after the time predicted in the current study.
It was believed that vhip would be more likely to exhibit an abrupt change at the transition since this variable is a good representation of the movement of the body's CM, and thus should provide a good representation of the walking and running models. It is possible that even after a decision is made by a subject to change gaits, that the body requires some finite time period to adjust or recalibrate in terms of position, velocity, and acceleration coordination patterns. The results of this study suggest that a period of between one step and one stride may be required for these adjustments to fully take effect. This supports the hypothesis of researchers (Diedrich and Warren, 1995; 1998) who have used dynamical systems theory to explain gait transitions, since this theory suggests that there would be increased variability in variables such as relative phase angles at speeds near the gait transition speed.
Conclusion
It appears that for a continuously accelerating treadmill, the initiation of a gait transition (walk-run and run-walk) occurs at about midstance of the transition stride, but the transition is not complete until the next heelstrike of the ipsilateral foot. The time period between the initiation of the gait transition and the completion of the transition exhibits some aspects of kinematic behavior that could not be classified as being either a walk or a run.
Biographies
Alan Hreljac
Employment
Associate Professor of Biomechanics, Department of Kinesiology and Health Science, California State University, Sacramento.
Degree
PhD
Research interests
Gait transitions, running injuries.
E-mail: ahreljac@csus.edu
Rodney T. Imamura
Employment
Assistant Professor of Biomechanics, Department of Kinesiology and Health Science, California State University, Sacramento.
Degree
PhD
Research interests
Biomechanics of judo, gait, and weight lifting.
E-mail: rimamura@csus.edu
Rafael F. Escamilla
Employment
Associate Professor of Physical Therapy, Department of Physical Therapy, California State University, Sacramento.
Degree
PhD
Research interests
Exercise rehabilitation, throwing mechanics, squat lifting.
E-mail: rescamil@csus.edu
W. Brent Edwards
Employment
PhD Student, Iowa State University.
Degree
MS
Research interests
Impact force, mechanical loading and bone adaptation, signal processing and wavelet analysis in biomechanics.
E-mail: edwards9@iastate.edu
References
- Abernethy B., Hanna A., Plooy A. (2002) The attentional demands of preferred and non-preferred gait patterns. Gait & Posture 15, 256-265 [DOI] [PubMed] [Google Scholar]
- Alexander R.M. (1984) Walking and running. American Scientist 72, 348-354 [Google Scholar]
- Alexander R.M. (1989) Optimization and gaits in the locomotion of vertebrates. Physiological Reviews 69, 1199-1227 [DOI] [PubMed] [Google Scholar]
- Argue C.K., Clayton H.M. (1993) A preliminary study of transitions between the walk and trot in dressage horses. Acta Anatomica 146, 179-182 [DOI] [PubMed] [Google Scholar]
- Beuter A., Lefebvre R. (1988) Un modèle théorique de transition de phase dans la locomotion humaine. Canadian Journal of Applied Sport Science 13, 247-253 [PubMed] [Google Scholar]
- Biewener A.A., Taylor C.R. (1986) Bone strain: A determinant of gait and speed? Journal of Experimental Biology 123, 383-400 [DOI] [PubMed] [Google Scholar]
- Charteris J., Taves C. (1978) The process of habituation to treadmill walking. Perceptual and Motor Skills 47, 659-666 [DOI] [PubMed] [Google Scholar]
- Collins J.J., Stewart I.N. (1993) Coupled nonlinear oscillators and the symmetries of animal gaits. Nonlinear Science 3, 349-392 [Google Scholar]
- Diedrich F.J., Warren W.H. (1995) Why change gaits? Dynamics of the walk-run transition. Journal of Experimental Psychology: Human Perception and Performance 21, 183-202 [DOI] [PubMed] [Google Scholar]
- Diedrich F.J., Warren W.H. (1998) The dynamics of gait transitions: Effects of grade and load. Journal of Motor Behavior 30, 60-78 [DOI] [PubMed] [Google Scholar]
- Gatesy S.M., Biewener A.A. (1991) Bipedal locomotion: effects of speed, size and limb posture in birds and humans. Journal of Zoology (London) 224, 127-147 [Google Scholar]
- Hreljac A. (1995) Determinants of the gait transition speed during human locomotion: Kinematic factors. Journal of Biomechanics 28, 669-677 [DOI] [PubMed] [Google Scholar]
- Hreljac A., Marshall R.N. (2000) Algorithms to determine event timing during normal walking using kinematic data. Journal of Biomechanics 33, 783-786 [DOI] [PubMed] [Google Scholar]
- Hreljac A., Stergiou N. (2000) Phase determination during normal running using kinematic data. Medical and Biological Engineering and Computing 38, 503-506 [DOI] [PubMed] [Google Scholar]
- Hreljac A., Arata A., Ferber R., Mercer J.A., Row B.S. (2001) An electromyographical analysis of the role of dorsiflexors on the gait transition during human locomotion. Journal of Applied Biomechanics 17, 287-296 [Google Scholar]
- Hreljac A., Parker D., Quintana R., Abdala E., Patterson K., Sison M. (2002) Energetics and perceived exertion of low speed running and high speed walking. Facta Universitatis Series: Physical Education and Sport 1(9), 27-35 [Google Scholar]
- Li L. (2000) Stability landscapes of walking and running near gait transition speed. Journal of Applied Biomechanics 16, 428-435 [Google Scholar]
- Li L., Hamill J. (2002) Characteristics of the vertical ground reaction force component prior to gait transition. Research Quarterly for Sport and Exercise 73, 229-237 [DOI] [PubMed] [Google Scholar]
- McGreer T. (1990) Passive dynamic walking. International Journal of Robotics Research 9, 62-82 [Google Scholar]
- McMahon T.A. (1985) The role of compliance in mammalian running gaits. Journal of Experimental Biology 115, 263-282 [DOI] [PubMed] [Google Scholar]
- McMahon T.A., Valiant G., Frederick E.C. (1987) Groucho running. Journal of Applied Physiology 62, 2326-2337 [DOI] [PubMed] [Google Scholar]
- Milliron M.J., Cavanagh P.R. (1990) Sagittal plane kinematics of the lower extremity during distance running. In: Biomechanics of Distance Running. Ed: Cavanagh P.R. Champaign, IL: Human Kinetics; 65-105 [Google Scholar]
- Öberg T., Karsznia A., Öberg K. (1994) Joint angle parameters in gait: Reference data for normal subjects 10-79 years old. Journal of Rehabilitation Research and Development 31, 199-213 [PubMed] [Google Scholar]
- Prilutsky B.I., Gregor R.J. (2001) Swing- and support -related muscle actions differentially trigger human walk-run and run-walk transitions. Journal of Experimental Biology 204, 2277-2287 [DOI] [PubMed] [Google Scholar]
- Raynor A.J., Yi C.J., Abernethy B., Jong Q.J. (2002) Are transitions in human gait determined by mechanical, kinetic, or energetic factors? Human Movement Science 21, 785-805 [DOI] [PubMed] [Google Scholar]
- Schieb D.A. (1986) Kinematic accommodation of novice treadmill runners. Research Quarterly for Exercise and Sport 57, 1-7 [Google Scholar]
- Segers V., Aerts P., Lenoir M., De Clercq D. (2005) Differential effect of m. tibialis anterior fatigue on walk-to-run and run-to-walk transition speed in unsteady state locomotion conditions. Proceedings of the 29th Annual Meeting of the American Society of Biomechanics (ASB), Cleveland, OH [Google Scholar]
- Segers V., Aerts P., Lenoir M., De Clercq D. (2006) Spatiotemporal characteristics of the walk-to-run and run-to-walk transition when gradually changing speed. Gait & Posture 24, 247-254 [DOI] [PubMed] [Google Scholar]
- Thorstensson A., Roberthson H. (1987) Adaptations to changing speed in human locomotion: Speed of transition between walking and running. Acta Physiologica Scandinavia 131, 211-214 [DOI] [PubMed] [Google Scholar]
- Turvey M.T., Holt K.G., LaFiandra M.E., Fonseca S.T. (1999) Can the transitions to and from running and the metabolic cost of running be determined from the kinetic energy of running? Journal of Motor Behavior 31, 265-278 [DOI] [PubMed] [Google Scholar]
- Vint P.F., Hinrichs R.N. (1996) Endpoint error in smoothing and differentiating raw kinematic data: an evaluation of four popular methods. Journal of Biomechanics 29, 1637-1642 [PubMed] [Google Scholar]
- Wall J.C., Charteris J. (1980) The process of habituation to treadmill walking at different velocities. Ergonomics 23, 425-435 [DOI] [PubMed] [Google Scholar]
- Wall J.C., Charteris J. (1981) A kinematic study of long-term habituation to treadmill walking. Ergonomics 24, 531-542 [DOI] [PubMed] [Google Scholar]
- Winter D.A. (1983) Biomechanical motor patterns in normal walking. Journal of Motor Behavior 4, 302-330 [DOI] [PubMed] [Google Scholar]
- Winter D.A. (1989) Biomechanics of normal and pathological gait: Implications for understanding human locomotor control. Journal of Motor Behavior 10, 337-355 [DOI] [PubMed] [Google Scholar]
- Wells R.P., Winter D.A. (1980) Assessment of signal and noise in the kinematics of normal, pathological, and sporting gaits. : Human locomotion I: Pathological gait to the elite athlete. Proceedings of the special conference of the Canadian Society for Biomechanics. London, Ontario; 92-93 [Google Scholar]


