Regulation of ClC-2 gating by intracellular ATP

Abstract

ClC-2 is a voltage-dependent chloride channel that activates slowly at voltages negative to the chloride reversal potential. Adenosine triphosphate (ATP) and other nucleotides have been shown to bind to carboxy-terminal cystathionine-ß-synthase (CBS) domains of ClC-2, but the functional consequences of binding are not sufficiently understood. We here studied the effect of nucleotides on channel gating using single-channel and whole-cell patch clamp recordings on transfected mammalian cells. ATP slowed down macroscopic activation and deactivation time courses in a dose-dependent manner. Removal of the complete carboxy-terminus abolishes the effect of ATP, suggesting that CBS domains are necessary for ATP regulation of ClC-2 gating. Single-channel recordings identified long-lasting closed states of ATP-bound channels as basis of this gating deceleration. ClC-2 channel dimers exhibit two largely independent protopores that are opened and closed individually as well as by a common gating process. A seven-state model of common gating with altered voltage dependencies of opening and closing transitions for ATP-bound states correctly describes the effects of ATP on macroscopic and microscopic ClC-2 currents. To test for a potential pathophysiological impact of ClC-2 regulation by ATP, we studied ClC-2 channels carrying naturally occurring sequence variants found in patients with idiopathic generalized epilepsy, G715E, R577Q, and R653T. All naturally occurring sequence variants accelerate common gating in the presence but not in the absence of ATP. We propose that ClC-2 uses ATP as a co-factor to slow down common gating for sufficient electrical stability of neurons under physiological conditions.

Electronic supplementary material

The online version of this article (doi:10.1007/s00424-013-1286-0) contains supplementary material, which is available to authorized users.

Introduction

ClC-2 is a member of the CLC family of anion channels and transporters broadly expressed in neuronal and non-neuronal tissues [37]. It is an anion channel with two separate conductance pathways, the so-called protopores [12, 26]. This double-barreled architecture is the basis of two different gating mechanisms, one acting on individual protopores and another common process jointly acting on both protopores. Protopore as well as common gating is stimulated by membrane hyperpolarization resulting in ClC-2 being closed at positive potentials and slowly activating upon hyperpolarizing voltage steps [10, 46].

Each ClC-2 monomer contains 18 α-helices and a long carboxy-terminus containing two cystathionine-ß-synthase (CBS) domains [12, 14, 32]. Adenosine triphosphate (ATP) was shown to bind to CBS-domains of various ClC channels and transporters [23, 25, 36] and to modify their functional properties. The effects of ATP on ClC-1 are pH-dependent, resulting in ClC-1 inhibition by intracellular ATP at acidic pH [2, 3, 39, 40]. ClC-4 undergoes rapid downregulation in cells dialyzed with ATP-free solution [1, 41], indicating that ClC-4 requires intracellular ATP to be active. Experiments with ClC-5 demonstrated that AMP, ADP, and ATP increase the probability of ClC-5 to be in an active state [45]. For ClC-2, ATP depletion was reported to change sub-cellular trafficking [11] and to modify gating [19]. Furthermore, several sequence variants were identified in association with idiopathic generalized epilepsies (IGE) [21, 22, 33] that were localized within the putative ATP binding region at the carboxy-terminus of ClC-2.

We hypothesized that naturally occurring CLCN2 mutations might modify ATP-dependent gating processes and decided to perform a detailed investigation of ClC-2 gating at various internal ATP concentrations. We observed significant effects on gating kinetics but only slight changes in steady-state open probabilities. The effects of ATP on gating can be described by a kinetic model in which protopore gating is unaffected by ATP while common gating transitions are distinct for ATP-bound channels. In addition, we investigated three sequence variants associated with IGE and found that these mutations alter channel function in response to ATP.

Methods

Heterologous expression of WT and mutant hClC-2

IGE-associated sequence variants R577Q, R653T, and G715E were introduced into the plasmid pcDNA5/FRT/TO hClC-2 [16] using QuikChange (Agilent Technologies). Polymorphisms R688Q and E718D were inserted into the plasmid pSVL hClC-2 [16]. All mutations were verified by DNA sequencing, and two independent mutant clones were tested by transient expression in HEK293T cells or by stable expression in Flp-In T-Rex 293 cells. Stable inducible cell lines expressing wild-type (WT) or mutant ClC-2 channels were generated by selection of Flp-In T-Rex 293 cells (Invitrogen) transfected with pcDNA5/FRT/TO-hClC-2 [16] and used either with or without induction with tetracycline.

Electrophysiology and data analysis

Standard whole-cell or single-channel patch clamp recordings were performed using an EPC10 amplifier (HEKA, Lambrecht/Pfalz, Germany) as described [18]. Pipettes were pulled from borosilicate glass and had resistances between 1.3 and 2.5 MΩ for whole-cell recordings and 7–50 MΩ for single-channel recordings. For noise analyses and single-channel experiments, pipettes were covered with SigmaCote (Sigma-Aldrich Chemie, Munich, Germany) for capacitance reduction. More than 85 % of the series resistance was compensated by an analog procedure, resulting in calculated voltage errors <5 mV. Cells/patches were clamped to 0 mV for at least 45 s between test sweeps. The extracellular solution for whole-cell recordings contained (in millimolars): NaCl or NMDG·Cl (140), KCl (4, not in NMDG containing solutions), CaCl₂ (2), MgCl₂ (1), HEPES (5), pH 7.4; the intracellular solution contained (in millimolars): NaCl or NMDG·Cl (95), MgCl₂ (5), EGTA (5), HEPES (10), pH 7.4. ATP, ADP, AMP, or AMP-PNP was added to the final solutions at given concentrations followed by pH readjustment. Solutions containing ATP were stored at −20 °C for a maximum of 24 h or at −80 °C for a maximum of 3 days before use. To prevent osmotic gradients, we included mannitol in the extracellular solution at internal nucleotide concentrations higher than 1 mM. Liquid potentials were calculated and subtracted a priori. To permit equilibration between the patch pipette and the cytoplasm, we normally recorded currents starting 5 min after breaking into the whole-cell mode.

Inside-out patch recordings were made in symmetrical solutions containing (in millimolars): NMDG·Cl (130), MgCl₂ (5), EGTA (5), HEPES (5), pH 7.4. Only few patches contained channels with two equally spaced conductance levels and common closures and conductances around 2 pS. Channels that did not show these characteristics were discarded. We usually observed background noise levels around 55–65 fA RMS in single-channel experiments before applying software filtering. Single-channel recordings were sampled at 50 kHz and filtered with a 1-kHz Bessel filter. Traces were digitally filtered at 200 Hz prior to dwell time analysis.

Data were analyzed by PatchMaster (HEKA, Lambrecht/Pfalz, Germany), QuB (SUNY; Buffalo, NY; USA) and Origin 8 (OriginLab; Northampton, MA, USA). To obtain the voltage dependence of the relative open probability, instantaneous current amplitudes were determined 200 μs after a voltage step to 60 mV following prepulses to various voltages, normalized by their maximum value and plotted against the preceding potential. Prepulse durations were adjusted to allow steady-state activation. For the voltage dependences of absolute open probabilities (P _abs), relative open probabilities at different voltages were normalized to the absolute open probability at −160 mV obtained by noise analysis and single-channel analysis at −100 mV. Noise analysis was performed as recently described [16]. Dead time (T _d) for dwell time analysis was initially calculated according to [8] (T _d = 0.179/f _c with f _c being the cut-off frequency of 200 Hz) to be 0.9 ms and later increased to 1 ms after careful inspection of recordings. Single-channel amplitudes were determined from amplitude histograms and averaged over several recordings. Dwell times were measured by accumulating all recordings while omitting first and last events.

Unpaired two-sided student’s t test was used for statistical analysis unless stated otherwise. Statistical significance is either denoted in figures with a single asterisk for p < 0.05 and double asterisk for p < 0.01 or explicitly stated in the text or corresponding tables.

Computational modeling of ClC-2 gating

Modeling was based on Q-Matrix theories by Colquhoun and Hawkes ([7]) and implemented using custom-written Python scripts incorporating Q-Matrix implementations (C. Schmidt-Hieber; version 2010-08-23; http://code.google.com/p/pyqmatrix), a directed evolution Algorithm (P. Sederberg; https://github.com/compmem/desolver) running on ParallelPython (Vitalii Vanovschi; http://www.parallelpython.com).

Rate constants (k) were constructed from Eq. 1, with k ₁ or k ₋₁ being the voltage-independent component, zδ the apparent gating charge, v the voltage, F the Faraday constant, R the gas constant, and T the assumed constant temperature of 296 k.

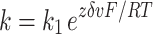Starting values of rate constants were manually adjusted and compared with experimentally obtained data by eye. Detailed values composing rate constants were obtained using directed evolution on a least-square deviation from 100–250 logarithmically spaced data points from normalized recorded currents. Time-dependent open probabilities for fast and slow gating were calculated from the rate constant Q-Matrix as described [7]. Finally, open probabilities were calculated as product of probabilities of the fast gate being open and the sum of all open slow gate probabilities (Fig. 4b). Rate constants from the Q-Matrix were used to simulate single-channel behavior of the common gating process in QuB Express (SUNY; Buffalo, NY, USA) to check for the occurrence of a long-lasting closed state.

Fig. 4.

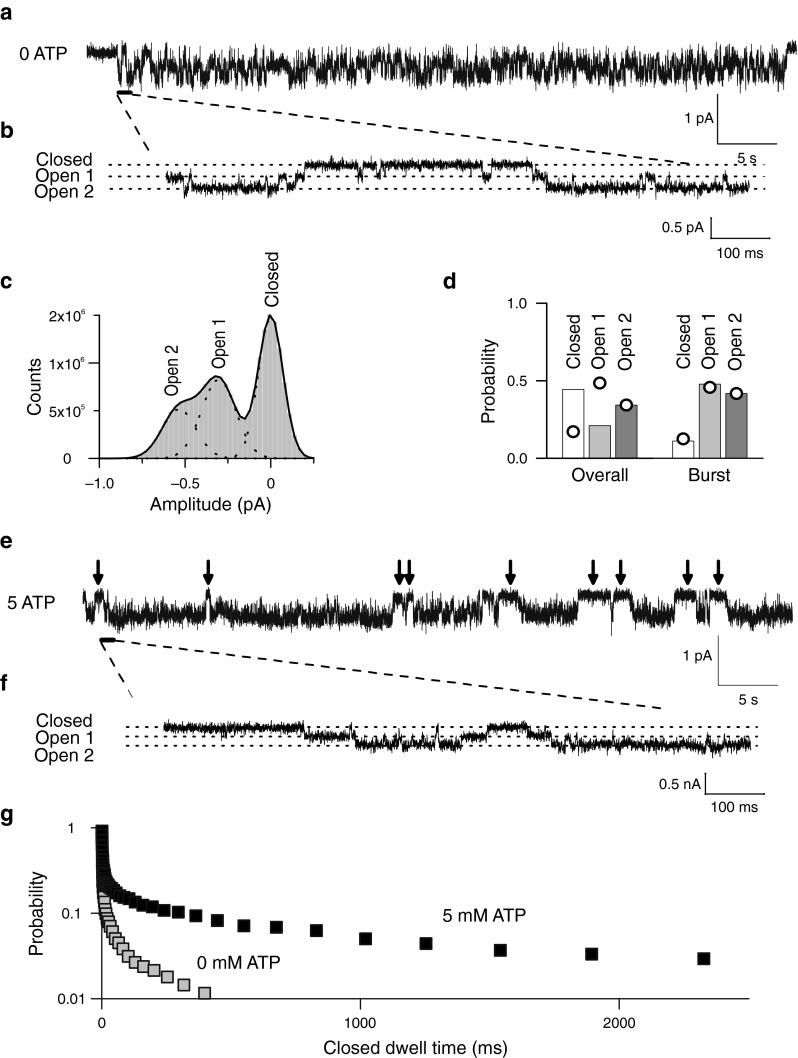
ATP modifies common gating of ClC-2. a Representative single-channel recording of WT ClC-2 at −100 mV and an internal ATP concentration of 0 mM. b Segment of a showing three separate conductance levels (closed, open 1, and open 2). c Histogram plot from the WT ClC-2 single-channel recordings shown in a. Solid line shows fit with a sum (black line) of three Gaussian (dotted lines) functions corresponding to the three separate conductance levels at approximately 0, 0.24, and 0.48 pA. d Probabilities of the three conductance states during bursts or from complete recordings. Values expected from binomial distributions were calculated assuming that the probability of the conductance state open 2 is the square of the protopore open probability and are shown as superimposed circles. e Representative recordings of WT ClC-2 channels at −100 mV and an internal ATP concentration of 5 mM. Arrows indicate long closed durations absent from the recording in a. f Segment of e showing three separate conductance levels (closed, open 1, and open 2). g Cumulative closed time distribution for WT ClC-2 at 0 mM (grey squares) or at 5 mM (black squares) of cytosolic ATP. For each abscissa value, the probability of encountering longer closed dwell times were taken from binned dwell time distributions

Fitting was repeated until the least-square deviation did not change by more than 0.1 % over more than 50 cycles. Rate constants obtained by this algorithm were then used to plot the ATP concentrations and the voltage dependences of time constants (Fig. 4c and d). Data sets that differed greatly from experimentally obtained values were discarded. Finally, a ranking of multiple runs of the fitting algorithm by the least-squares criterion was used to select the data presented in Table 3.

Table 3.

Rate constant components of whole-cell current models

Fast gate	Forward		Backward (´)
Transition	k 1 (s−1)	zδ	k −1 (s−1)	zδ
α	0.3	−0.9	1.9	0.1
Slow gate	Forward		Backward (´)
Transition	k 1 (s−1)	zδ	k −1 (s−1)	zδ
α	7	–	11	–
αATP	0.3	–	0.6	–
β	0.46	−0.5	3	0.37
Wild-type: βATP	0.34	−0.35	1.94	0.35
G715E: βATP		−0.44		0.58
R577Q: βATP		−0.36		0.54
R653T: βATP		−0.38		0.63
μ	165,000 mol−1	–	13.7	–
Wild-type: γ	2.5	–	0.5	–
G715E: γ	4.2
R577Q: γ	3.3
R653T: γ	3.5

Patients and gene screening

We analyzed a cohort of 95 multiplex families, each including at least (1) one proband with a defined IGE phenotype, (2) one additional individual with IGE, and (3) a third one with generalized epileptic discharges on electroencephalography. Families and normal controls were recruited through the EPICURE consortium (http://www.epicureproject.eu/home.aspx) (Supplementary Text 2; Supplementary Table 1). All analyzed family members gave written informed consent, and all procedures were in accordance with the declaration of Helsinki and approved by the local Ethical Committees.

The entire coding region of the CLCN2 gene was analyzed by direct Sanger sequencing. Polymerase chain reaction (PCR) products were purified by Exo/SAP digestion with Exonuclease I (New England Biolabs, Beverly, MA) and shrimp alkaline phosphatase (Promega, San Diego, USA) and directly sequenced using the ABI PRISM BigDye® Terminator v1.1 Cycle Sequencing Kit (Applied Biosystems, CA, USA), and the ABI 3730 sequencing instrument, as described by the manufacturer. All primer sequences are given in Supplementary Material (Supplementary Tables 2 and 3). Ninety-five Caucasian controls were sequenced using the PSQ HS96A pyrosequencing system (Qiagen, Hilden, Germany), according to manufacturers’ instructions using the PSQ 96 SNP Reagent Kit (Biotage AB) on a PSQ HS96A instrument (Qiagen, Hilden, Germany) and analyzed by pyrosequencing software (PSQ HS96A1.2). Segregation analysis was done by Sanger sequencing. Further genotyping was performed in a control cohort consisting of 751 individuals of European descent (94 Spanish, 94 Finnish, 94 Turkish, 94 Dutch, 188 Italian, and 188 German) using the ABI TaqMan® 7900 Real-Time PCR System. TaqMan probes and primers were obtained from the custom TaqMan SNP genotyping products provided by Applied Biosystems (Applied Biosystems, Foster City, CA, USA). Data were analyzed with the TaqMan ® Genotyper Software 1.0.1 and SDS 2.1 provided by ABI.

Results

ATP slows ClC-2 channel kinetics

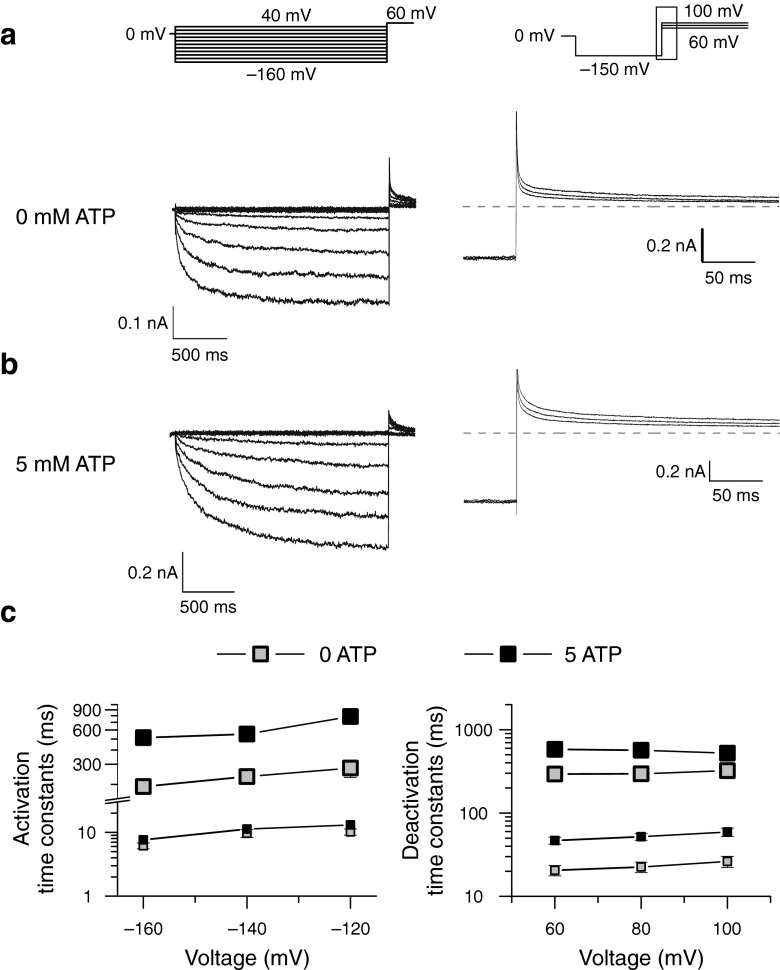
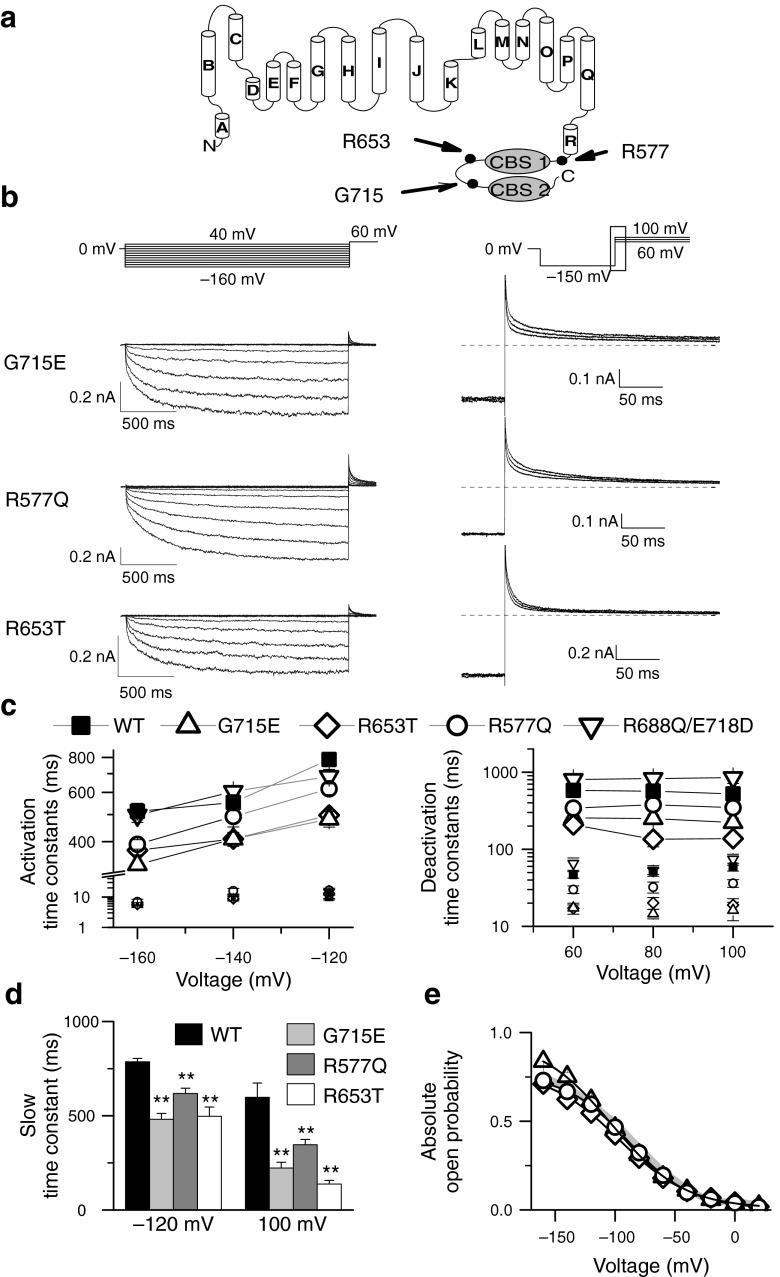
Figure 1 shows representative whole-cell patch clamp recordings from Flp-In T-Rex cells expressing WT human ClC-2 channels. Cells were bathed in physiological external solutions and dialyzed internally with pipette solutions containing either 0 (Fig. 1a) or 5 mM ATP (Fig. 1b). For both ATP concentrations, WT channels were closed at positive potentials and activated on a bi-exponential time course upon hyperpolarizing voltages. Consecutive membrane depolarization resulted in a slow bi-exponential channel deactivation. Internal dialysis with 5 mM ATP resulted in ClC-2 currents with slower activation and deactivation time courses than under ATP-free conditions.

Fig. 1.

ATP slows ClC-2 activation and deactivation at physiological concentrations. a, b Representative whole-cell current responses of cells expressing WT ClC-2 to the indicated voltage steps at 0 or 5 mM intracellular ATP. Cells were held at 0 mV, and voltage steps from −160 to 40 mV were applied to study activation kinetics (left side). Steps from 60 to 100 mV following a preconditioning pulse to −150 mV were used to analyze channel deactivation (right side). For improved illustration, only a section of the deactivation current responses are shown (depicted as black box in voltage protocol). Dashed lines indicate 0 nA. c Voltage dependence of fast and slow activation (left side) or deactivation (right side) time constants at zero (grey squares) or physiological ATP (black squares). Slow time constants are given by large symbols and connected for easier identification

ClC currents usually activate and deactivate on bi-exponential time courses [10, 13, 15, 18, 30, 31], and two time constants are also sufficient to describe macroscopic gating of ClC-2 [10, 42]. To quantify ATP-dependent alterations of ClC-2 gating, we determined fast and slow activation/deactivation time constants from cells dialyzed with ATP-free or ATP-containing solutions. Fast time constants for activation were determined by using a separate short (<250 ms) protocol using P/4 leak subtraction to remove linear capacitative artifacts (Supplemental Fig. 1a). Afterward, bi-exponential functions were fitted to long recordings such as in Fig. 1a with the fast time constant fixed to this value. Relative contributions of fast and slow time constants to the observed currents were not different at low or high concentrations of ATP and similar to values previously reported for mouse ClC-2 (Supplemental Fig. 1c) [10].

Whereas fast activation time constants were identical for both conditions (Supplemental Fig 1b), we observed a significant increase of slow activation time constants in the presence of ATP (Fig. 1c, Table 1). Deactivation time constants showed a twofold increase for both—fast and slow—time constants with intracellular ATP (Fig. 1c, Table 1).

Table 1.

Fast and slow time constants of wild type ClC-2 at various voltages

Voltage (mV)		0 mM ATP		5 mM ATP		P value
		n	(ms)	n	(ms)
100	τ fast	5	26.23 ± 3.96	6	65.97 ± 8.89	0.027
	τ slow		322.58 ± 28.42		597.88 ± 75.68	0.044
80	τ fast	6	22.53 ± 3.25	11	55.58 ± 5.69	0.004
	τ slow		296.00 ± 34.52		599.15 ± 46.08	0.009
60	τ fast	6	20.55 ± 2.93	10	49.40 ± 4.92	0.007
	τ slow		294.23 ± 35.09		620.08 ± 44.90	0.006
−120	τ fast	5	13.09 ± 1.62	5	10.18 ± 1.14	0.178
	τ slow		278.26 ± 48.14		786.50 ± 17.35	< 0.001
−140	τ fast	5	11.26 ± 1.21	5	9.67 ± 1.37	0.409
	τ slow		233.98 ± 7.25		552.14 ± 36.38	0.001
−160	τ fast	5	7.62 ± 0.74	5	6.16 ± 0.65	0.178
	τ slow		191.32 ± 8.64		513.38 ± 34.72	0.002

ATP does not alter maximal open probability of ClC-2

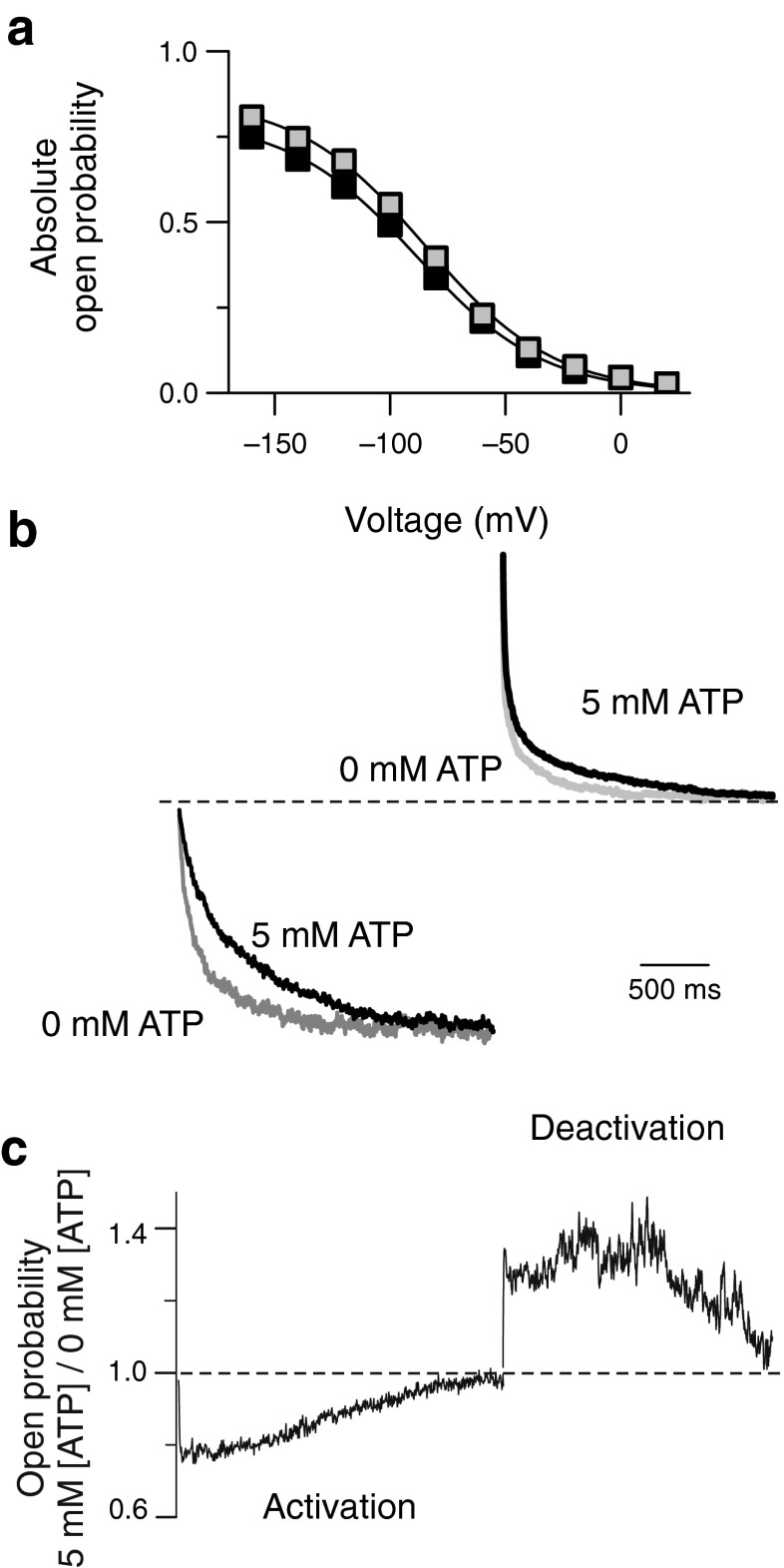
To test for a possible ATP dependence of steady-state open probabilities, we determined relative open probabilities by plotting the normalized instantaneous current amplitudes at a fixed tail pulse of +60 mV versus the preceding voltage. The voltage dependence of ClC-2 open probabilities could be well described by a single Boltzmann distribution with half-maximal activation (V _1/2) at −81.1 ± 2.2 mV (n = 7; Fig. 2a, grey squares) in the absence of ATP. Increasing the concentration of cytosolic ATP to 5 mM caused a shift of the V _1/2 to −89.8 ± 3.2 mV (n = 5; p = 0.03; Fig. 2a, black squares). Absolute open probabilities were determined at −160 mV by noise analysis yielding only insignificant differences in the maximum absolute open probability between ATP-free conditions and 5 mM ATP (0 mM ATP, 0.81 ± 0.03; 5 mM ATP, 0.75 ± 0.07; p = 0.35). The voltage dependence of absolute open probabilities was then calculated by normalizing relative open probabilities to these values (Fig. 2a).

Fig. 2.

ATP modifies the time-dependent of ClC-2 open probabilities. a Voltage dependence of absolute open probabilities at 0 mM (grey squares) or 5 mM ATP (black squares) b, Superimposed current traces at −160 or at +100 mV to illustrate ATP-dependent changes in activation and deactivation. Recordings at 5 mM ATP are given as black lines whereas grey lines indicate ATP-free conditions. Mean current amplitudes for the last 50 ms of each voltage step were normalized to the steady-state absolute open probability at −160 or +100 mV. c, Ratio of current amplitudes at 5 versus 0 mM of internal ATP from the recordings shown in b to quantify the differences in open probabilities during hyper- and depolarizing voltage steps

Figure 2b illustrates the consequences of ATP-dependent gating alterations on the time dependence of ClC-2 currents. We compared activation and deactivation time courses upon a voltage step to −160 mV followed by a depolarization to +100 mV for two representative cells dialyzed with ATP-containing or ATP-free solutions. To correct for differences in expression levels of the two cells, currents were normalized to the steady-state absolute open probability at −160 mV (Fig. 2a). This comparison demonstrates that deceleration of slow activation by ATP together with almost unaltered steady-state open probabilities results in about 20 % smaller ClC-2 currents at the begin of the hyperpolarizing voltage step (Fig. 2c). The opposite effect was observed during deactivation, where ATP increased currents by about 30 % very soon after the voltage step (Fig. 2c). These robust changes in time-dependent open probabilities during activation or deactivation gradually disappeared after several hundreds of milliseconds and finally reached similar values for both ATP concentrations at steady-state conditions.

ATP modifies ClC-2 gating in a dose-dependent manner

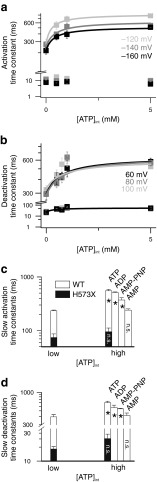
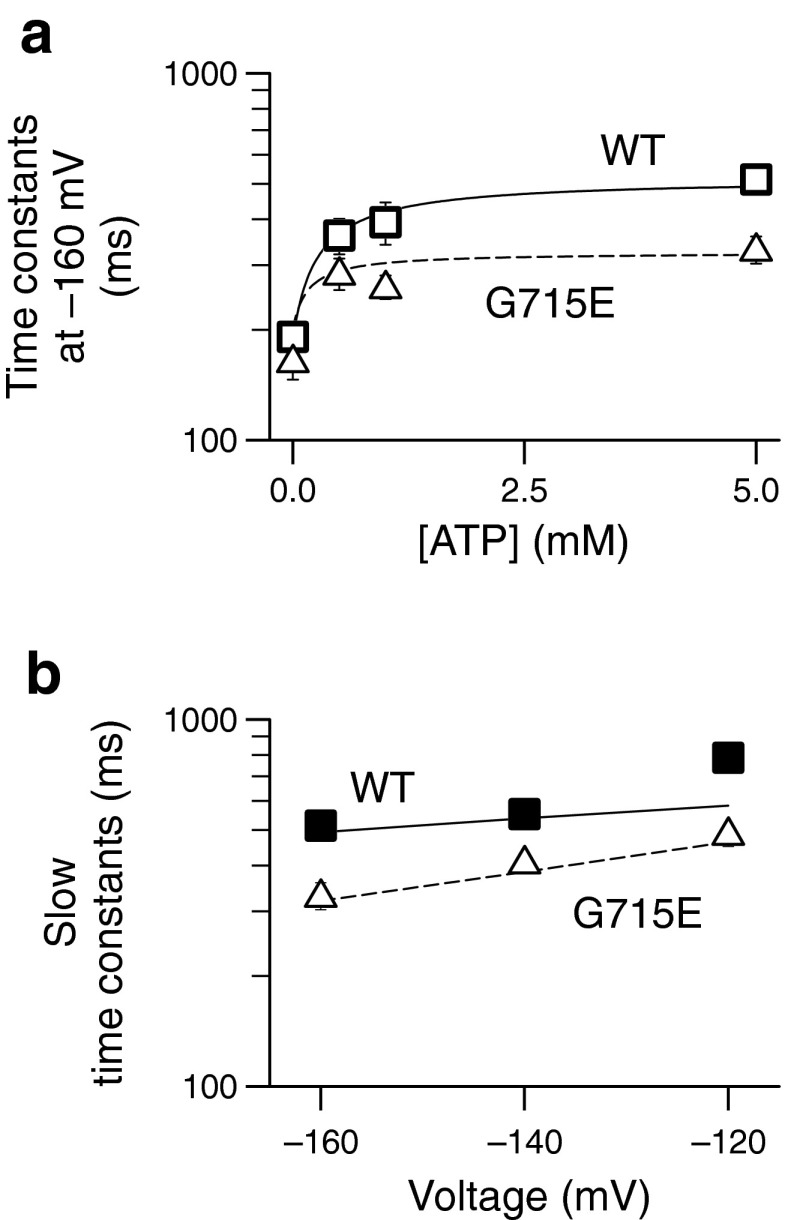
Figure 3 shows the ATP concentration dependence of fast and slow activation and deactivation time constants. Whereas fast activation constants were independent of the ATP concentration, fast deactivation as well as slow activation and deactivation time constants increased in a concentration-dependent manner. Concentration dependences could be well fit with Michaelis–Menten relationships (lines in Fig 3a and b), providing apparent Michaelis–Menten constants (K _M) in the low millimolar range (Table 2). K _M values are only slightly voltage-dependent but differed for activation and deactivation.

Fig. 3.

ATP causes concentration-dependent changes in activation and deactivation time constants. a, b ATP concentration dependences of fast and slow activation (a) or deactivation (b) time constants for WT ClC-2 at indicated voltages. Solid lines provide fits with a Michaelis–Menten equation. c, d Comparison of activation time constants at −140 mV (c) or deactivation time constants at 80 mV (d). Cells expressing WT ClC-2 (open bars) were studied without (low) or with 5 mM (high) of the indicated nucleotide inside the patch pipette. Recordings from the H573X mutant were done without (low) or with 10 mM (high) of intracellular ATP. Values for ATP, ADP, and AMP-PNP were significantly slower at high concentrations (asterisk denotes p < 0.05, n = 3–6) while AMP and the H573X mutant did not show concentration dependence (n.s.)

Table 2.

Michaelis–Menten constants (K _m) for ATP on ClC-2

Voltage [mV]	Fast [mM]		Slow [mM]
	Wild-type	G715E	Wild-type	G715E
100	0.456	–	0.87	0.71
80			2.04
60			1.74
−120	–	–	0.44	0.37
−140	–	–	0.67	0.57
−160	–	–	0.55	0.44

Under metabolic stress, ATP is degraded to ADP so that the ADP concentration rises quickly at the expense of ATP maintaining a stable [ATP]/[ADP] ratio. ATP regulation will thus only modify ClC-2 function under metabolic stress if the binding site can separate between ATP and its metabolites. We additionally tested the ADP dependence (Supplemental Fig. 2) and observed similar effects on gating and comparable apparent Michaelis–Menten constants for ADP and ATP. Obviously, ClC-2 is not capable of distinguishing between these two compounds.

We did not find any evidence for a deceleration of gating kinetics in the presence of 5 mM AMP (Fig. 3c and d). This might be due to greatly impaired binding of AMP as compared with ATP or to an absent effect of AMP binding on ClC-2 gating. We reasoned that AMP—if it can bind with high affinity to the ATP binding site without modifying gating—would shift the concentration dependence of the ATP effects on gating—resembling a competitive blocker. We therefore performed experiments with 1 mM of ATP and 5 mM AMP combined in the intracellular solution. Under these conditions, fast and slow time constants were similar to 1 mM ATP alone (at −140 mV—τ _slow = 552.0 ± 87.0 ms, n = 6, p = 0.99; at +80 mV—τ _slow = 510.4 ± 33.0 ms, p = 0.89; τ _fast = 51.6 ± 8.4 ms, n = 3, p = 0.64). We conclude that AMP binds only with low affinity and does not act as competitive inhibitor of the ATP effect.

ATP might exert its effect on gating via direct association to ClC-2, by stimulating direct phosphorylation of ClC-2 or by interaction with—yet unknown—phosphorylation-dependent proteins. To test whether nucleotide binding alone is necessary to change gating kinetics of ClC-2, we used the non-hydrolyzable ATP analog adenosine 5′-(β,γ-imido)triphosphate (AMP-PNP) that has been used to study ATP-dependent gating of ClC-4 [41]. Cells containing 5 mM of AMP-PNP indeed showed a significant deceleration compared with cells without nucleotides (Fig. 3c and d). The degree of deceleration was found to be slightly smaller than for ATP (p < 0.05 for slow activation as well as fast and slow deactivation; n = 3–7). This small difference to ATP suggests that the conformational change of the ClC-2 carboxy-termini depends on the molecular identity of the nucleotide used. However, we cannot exclude additional minor effects of ATP hydrolysis on ClC-2 gating.

ATP has been shown to bind to isolated ClC-2 carboxy-termini via CBS domains [36]. To test whether the observed effects on ClC-2 gating are mediated by association of nucleotides with the CBS domains, we tested the effects of ATP on gating of H573X ClC-2 [16]. H573X ClC-2 lacks the complete carboxy-terminus, including both CBS-domains, and exhibits faster activation and deactivation kinetics [16]. We observed activation and deactivation time constants that were independent on ATP concentrations even at concentrations as high as 1 mM (Fig. 3c and d), indicating binding of nucleotides to carboxy-terminal CBS domains as the basis of kinetic changes.

Single-channel analysis of ClC-2 reveals long-lasting closed states in the presence of ATP

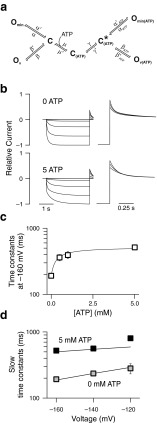
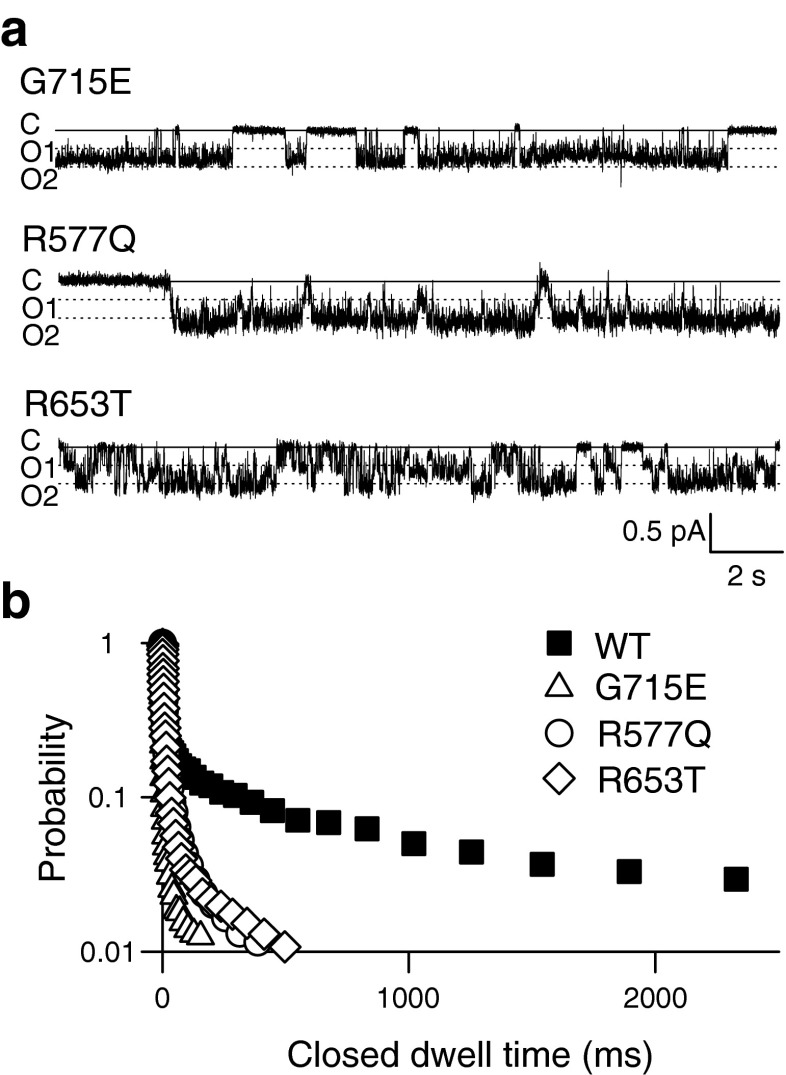
To test whether ATP modifies individual or common gating processes, we performed single-channel recordings with and without ATP at the cytoplasmic membrane side. Figure 4a shows a representative recording from an inside-out patch containing a single ClC-2 channel subjected to 0 mM ATP at the cytoplasmic side at −100 mV. ClC-2-mediated single channel currents showed two equally spaced conductance states (Fig. 4b, c; unitary current amplitude—0.23 ± 0.02 pA; n = 6). Bursts of activity with transitions between closed and both conductance states were interrupted by longer closed states (Fig. 4b), similar to previously published single channel recordings of ClC-2 [38] or of other CLC channels [15, 26, 35]. This characteristic gating arises from the dimeric double-barreled architecture of CLC channels [12, 26] that permits individual opening and closing transitions of the protopores, as well as common gating of both protopores together.

Figure 4c depicts a representative amplitude histogram from which the probability to assume the closed or one of the two conducting states (open 1: one open and one closed protopore, open 2: both protopores open) could be calculated [26, 38]. Amplitude histograms (Fig. 4c) obtained only during bursts of activity were binomially distributed (open circles, Fig. 4d, right). Such a behavior was expected if the two conduction pathways open and close independently of each other. When amplitude histograms were constructed from recording intervals that also included long closed states, open probabilities deviated from a binomial distribution (Fig. 4d, left) as expected if slow gating acts on both protopores together. These findings suggests slow common gating processes that jointly open and close both protopores as well as fast protopore gating that occurs independently of the adjacent protopore.

Five millimolar ATP neither modified single-channel amplitudes nor binomial bursting behavior (Fig. 4e and f). However, under these conditions, long closed states could be frequently observed (arrows in Fig. 4e). To quantify the kinetics of single-channel gating, we collected large numbers of transitions between closed and open states from multiple patches. Time intervals spent in one state were then plotted as dwell time histograms for the closed as well as for the two open states (Supplementary Fig. 3). This analysis could only be performed at −100 mV since less negative voltages resulted in unitary currents too small for a reliable analysis whereas more negative potentials did not allow sufficiently long recordings. Plotting the probability of finding a closed event longer than a certain value at either 0 or 5 mM cytosolic ATP (Fig. 4f) showed a significant increase of long-lasting closed states with 16.2 ± 7.4 % (n = 5) of closed events being longer than 100 ms in the presence of ATP versus only 4.4 ± 5.0 % (n = 3; p = 0.05) for ATP-free conditions. The closed dwell time distribution at high ATP could be described by at least one additional exponential function with a time constant of more than 1.6 s (Supplemental Fig. 3, Supplemental Table 4). Longer closed times without significant changes in open dwell times (Supplemental Fig. 3) predict lower open probabilities at this potential (−100 mV)—in good agreement with our experimental results. The slight shift of the activation curves (Fig. 2a) and the insignificant reduction of the maximum absolute open probability indeed resulted in a slight reduction of the absolute open probability at −100 mV by ATP. We observed similar absolute open probabilities by single channel analysis (0 mM ATP—0.59; 5 mM ATP—0.43) and by noise analysis (Fig. 2a; 0 mM ATP—0.56 ± 0.02, n = 7; 5 mM ATP—0.49 ± 0.01, n = 5; p = 0.02).

ATP-dependent time constants determined in macroscopic and microscopic current recordings are very different. This is not surprising since changes in single-channel dwell times result only in comparable changes of whole-cell current time constants for very simple microscopic schemes. Time constants from single-channel dwell time distributions directly relate to one rate constant leaving one particular state, whereas macroscopic relaxations result from gating transition of multiple channels that will—individually—shift through various states and thus depends on the majority of rate constants within a kinetic scheme of an ion channel [7].

ATP association changes the voltage dependence of common gating

To develop a kinetic scheme of voltage- and ATP-dependent gating of ClC-2, we assumed that the two structurally distinct gating processes, protopore and common gating, occur independently of each other. This assumption has been successfully used to describe gating mechanisms of various ClC channels, including ClC-2 [10, 16, 46]. We developed independent schemes for fast and slow gating and calculated the apparent open probability as the product of fast and slow gate open probabilities.

Since the fast gate is fully closed at positive potentials [16], we described fast gating by a two-state model with one voltage-dependent transition (α). The common gate of ClC-2 does not close completely at positive potentials [16]. We therefore inserted another open state (O _min; Fig. 5a) with voltage-independent opening and closing rate constants to account for this feature. The balance between closed and the voltage-independent open state (transitions α) determines the minimum open probability of the slow gate at very positive potentials while transitions (transitions β) to another open state (O _v) account for voltage-dependent activation and deactivation. A linear model separating the two open states by the closed states (O–C–O) was necessary to correctly predict the effects of ATP on current kinetics. A model with direct connection of the two open states (C–O–O) resulted in pronounced ATP-dependent changes of the minimal open probability of the common gate, in clear contrast to the experimental results.

Fig. 5.

A seven-state kinetic scheme describes the voltage and ATP dependence of ClC-2 common gating. a Seven-state diagram representing slow gating of ClC-2. In the absence of ATP (left half), the slow gate cycle consists only of one closed (C) and two open (O _min, O _v) states with voltage-dependent opening transitions to O _v and voltage-independent transitions to O _min. ATP binding causes transition into a cycle with altered rate constants that result in slower gating kinetics. b Predicted current responses to the voltage steps seen in Fig. 1. c Predicted ATP dependence for wild type channels (solid line) follow measured values (open squares). d Predicted voltage dependence of time constants of WT (continuous lines, either at 0 or 5 mM ATP internally) correspond to measured values (grey and black squares)

Since activation and deactivation time constants exhibited distinct ATP dependencies (Fig. 1c), addition of a single ATP-bound closed state corresponding to the long-lasting closed state was not sufficient to describe ATP-dependent gating of ClC-2. We thus assumed that all steps could occur in ATP-bound and –unbound conditions leading to a duplication of all states. From our experimental data, it was impossible to deduce in which state ATP binding occurs. However, ClC-0 carboxy-termini have been shown to come closer during opening and to move away from each other during closing of the common gate [5]. Moreover, ATP association leads to a conformational change within isolated ClC-5 carboxy-termini [43]. ATP also binds to isolated ClC-2 carboxy-termini [36], and we thus assumed that ATP association occurred in the closed, spaced apart conformation of the carboxy-termini and inserted a transition (μ) between an ATP-unbound and ATP-bound closed state. A conformational change following the association of ATP (transition γ) to the state C^* _ATP then allows for opening of the ATP-bound channel.

The rate constants within this kinetic scheme were initially estimated by fitting the model simultaneously to experimentally determined time courses of WT hClC-2 in response to voltage steps between −160 and +40 mV and to the absolute open probabilities at these voltages for ATP concentrations of 0 as well as for 5 mM. Repeated global fitting of current amplitudes at exponentially distributed time points yielded several sets of parameters that well reproduced the time and voltage dependences of ClC-2 currents (Fig. 5b). We then chose the final parameter set (Table 3) by testing the ability to reproduce the experimentally observed ATP-dependence of slow activation time constants (Fig. 5c). The thus obtained kinetic model predicts that ATP slightly reduces the apparent gating charge zδ of the voltage-dependent rate constants leading to O _v(ATP) (ß _ATP), and reduces the backward rate constant (δ´) by ∼75 % compared with the value of the equivalent rate constant (ß´) without bound ATP. This modification results in longer closed states of the common gate in the presence of ATP and thus accounts well for the experimentally observed ATP-dependent (Fig. 5c, d) and voltage-dependent deceleration of the slow gate (Fig. 5d). The predictions for the deactivation time courses were unexpected. Common gating was shown to have faster gating kinetics than protopore gating in the absence of ATP but to be similar in the presence of ATP. It was therefore not easily possible to attribute the fast and slow time constants of macroscopic deactivation to fast and slow time constants obtained for activation. This finding might explain why ATP-binding changes both, fast and slow macroscopic deactivation time constants, but only the slow activation time constant even though only the common gate is changed.

In qualitative agreement with experimental data (Supplemental Fig. 3), dwell time analysis of simulated single channels revealed an additional ATP-dependent closed dwell time of the common gate longer than 1 s. However, very long closed states are rare, and microscopic time constants are therefore not well defined. We hence decided not to use single-channel data for setting quantitative constraints on the fitting procedure, but to exclusively use whole-cell ensemble currents for determination of rate constants within this kinetic scheme.

Sequence variants found in patients with idiopathic generalized epilepsies accelerate ATP-dependent slow gating of ClC-2

In recent years, several CLCN2 sequence variants have been described in patients suffering from IGE [21, 22, 33]. One cluster of such mutations is localized in the carboxy-terminus of the protein. Since it is already known that ATP binds to the CBS domains of ClC proteins [36], we investigated whether variants in the carboxy-terminus might affect ATP-dependent gating of ClC-2. We decided to re-evaluate known missense mutations in CLCN2 using identical and improved experimental techniques. We studied two variants that have already been reported, G715E [22] and R577Q [33], and characterized a novel sequence variant R653T that we discovered in a genetic screening of 95 families with members suffering from IGE (Fig. 6a and b; Supplemental Fig 4 and Supplemental Text 1). As a control, we included a combination of sequence variants, R688Q and E718D, that was first found in a patient suffering from epilepsy [9] but later found to rather represent a common polymorphism[4, 22].

Fig. 6.

Disease-associated sequence variants accelerate ClC-2 under physiological ATP concentrations. a Position of tested disease-associated sequence variations in a topology model of ClC-2. 18 transmembrane helices are shown, followed by a cytoplasmic carboxy-terminus with two cystathionine-ß-synthase (CBS) domains. b Representative whole-cell current responses to indicated voltage steps. Cells were held at 0 mV, and voltage steps from −160 to 40 mV were applied to study activation kinetics (left side). Steps from 60 to 100 mV following a preconditioning pulse to −150 mV were used to analyze channel deactivation (right side). For improved illustration, only a section of the deactivation current responses are shown (depicted as black box in voltage protocol). Dashed grey lines are added to indicate a level of 0 nA. Cells either express indicated variants, and all cells were dialyzed with solution containing 5 mM ATP. c Voltage dependence of fast and slow activation (left side) or deactivation (right side) time constants for WT and ClC-2 variants at physiological ATP. Slow time constants are shown as larger symbols and connected for easier identification. d Exemplary statistical analysis of activation and deactivation time constants at indicated voltages. Asterisks denote p < 0.01 (**). e Absolute open probabilities are given as the instantaneous current at the tail-pulse of 60 mV versus the preceding voltage and normalized to the value at −160 mV obtained by stationary noise analysis or single channel recordings. A fit to a Boltzmann function is shown as solid lines. WT values are shown by a gray line

None of the sequence variants changed the general characteristics of ClC-2 gating (Fig. 6). However, at 5 mM cytosolic ATP, slow gating time constants were significantly faster than WT for all tested disease-associated sequence variants (Fig. 6c and d) across all observed voltages. The acceleration was most pronounced for R653T and G715E, both being accelerated to values similar as the wild type in the absence of ATP. R688Q/E718D ClC-2 showed kinetics that is not significantly different from WT values. The change in kinetics for all three disease associated sequence variants did not significantly change steady-state open probabilities (Fig. 6e; G715E (n = 5)—V _1/2 = −101.6 ± 4.6 mV p = 0.1; P _{open(−160 mV)} = 0.84 ± 0.06; p = 0.14; R577Q (n = 5)—V _1/2 = −89.7 ± 3.3 mV; p = 0.85; P _{open(−160 mV)} = 0.73 ± 0.03; p = 0.92; R653T (n = 5)—V _1/2 = −94.5 ± 7.0 mV; p = 0.58; P _{open(−160 mV)} = 0.71 ± 0.06; p = 0.71).

Single-channel recordings from G715E, R577Q, and R653T ClC-2 revealed one closed and two open states with amplitudes similar to WT ClC-2 (Fig. 7a). However, the long-lasting closed states present in WT channels upon exposure to 5 mM ATP at the cytoplasmic side were missing for all three mutant channels. G715E, R577Q, and R653T ClC-2 displayed significantly reduced numbers of closed dwell times longer than 100 ms (Figs. 7b and 4f, WT—16.2 ± 7.4 %; n = 5; G715E—1.9 ± 0.86 %; n = 3; p = 0.02; R577Q—4.2 ± 0.6; n = 5; p = 0.02; R653T—3.05 ± 1.7 %; n = 4; p = 0.03).

Fig. 7.

ATP modification of common gating is changed by IGE-associated sequence variants. a Representative recordings of mutant ClC-2 channels at −100 mV and an internal ATP concentration of 5 mM. b Cumulative closed time distribution for G715E (open triangles), R577Q (open circles), and R653T (open diamonds) compared with WT channels (filled squares) at 5 mM ATP

To test which rates within the kinetic scheme developed for WT ClC-2 (Fig. 5) are affected by the disease-associated sequence variants, we performed global fitting of the scheme developed for WT ClC-2 (Fig. 5) to the time and voltage dependence of G715E ClC-2. This procedure revealed changed voltage dependencies of opening and closing rates for ATP-bound channels (ß_ATP). Apparent gating charges zδ for opening (ß_ATP) and closing (ß_ATP´) of ATP-bound channels were increased in comparison to WT channels resulting in faster activation and slower deactivation kinetics (Table 3). The resulting parameters were used to simulate the ATP-dependence (dashed line in Fig. 8a) as well as the voltage dependence of activation (dashed line in Fig. 8b). Both simulations were in good agreement with experimentally determined WT and the G715E values (symbols in Fig. 8a and b). The modifications determined by global fitting were sufficient to explain all observed G715E-mediated changes of ClC-2 gating without changing ATP association and dissociation. Similar results could be obtained for R577Q and R653T by varying the degree to which the apparent gating charges in transitions ß_ATP, ß_ATP´, and γ were altered (Table 3).

Fig. 8.

Modification of voltage-dependent opening and closing of the common gate is sufficient to describe functional alterations by disease-associated sequence variants. a Dependence of slow activation time constants at −160 mV for WT and G715E channels. Experimental values are plotted as open squares or triangles, respectively. Lines are computed following the scheme with values stated in Table 3. b Slow time constants of activation across all voltages analyzed are well described by the seven-state model used and can be modified to represent the G715E mutant

Discussion

In native cells as well as in heterologous expression systems, ClC-2 is closed at positive potentials and slowly opens upon membrane hyperpolarization resulting in a strong rectification of chloride currents [6, 16, 27, 34, 37]. We here show that the kinetics of ClC-2 activation and deactivation are significantly altered by intracellular ATP (Figs. 1 and 3). Using single-channel analysis, we were able to link the ATP dependence of ClC-2 gating to the common gate (Fig. 4). Kinetic modeling identified changes in ATP-dependent rate constants that lead to the observed alterations in gating (Fig. 5).

Mammalian neurons contain ATP at concentrations between 1 and 5 mM [24, 28]. At these concentrations, ClC-2 assumes saturating values in activation and deactivation time constants indicating that under physiological conditions activation and deactivation time constants reach maximum values. Intracellular ATP concentrations vary under metabolic stress [44], and ATP regulation of ClC-2 might be part of the response to this condition. ATP degradation results in increasing ADP concentrations which modifies ClC-2 gating to a similar degree as ATP (Fig 3c and d, Supplemental Fig. 2). Only further degradation to AMP would change the kinetics of ClC-2 currents as AMP-bound channels lack the slow gating kinetics found with higher energy nucleotides. However, ClC-2 seems to have a much lower affinity toward AMP as indicated by experiments combining high concentrations of AMP with low concentrations of ATP. Nucleotide regulation thus most likely does not serve adaptation to metabolic stress but is rather necessary for the normal function of ClC-2.

When expressed in Xenopus laevis oocytes and studied by two-microelectrode voltage clamp, ClC-2 activates on a slower time course [37] than in patch-clamp transfected mammalian cells [10, 16, 42]. Since intact oocytes contain higher ATP concentrations than internally dialyzed cells, the here reported regulation by ATP provides a likely explanation for this difference.

ATP regulation has been studied in detail for the muscle-specific isoform ClC-1 [2, 3, 39, 40]. ATP binds to the cytoplasmic CBS domains and acts on the common gate of ClC-1. Its action is pH-dependent, resulting in ClC-1 inhibition by intracellular ATP at acidic pH. ATP thus exerts different effects on gating of ClC-1 and ClC-2 resulting in distinct alterations of electrical properties of muscle fibers and neuron. ClC-1 contributes to the resting conductance of skeletal muscle and regulates muscle excitability by changing threshold currents necessary for action potential formation. Downregulation of ClC-1 by pH and ATP reduces muscle excitability under metabolic stress [29]. The activation of ClC-2 at voltages negative to the chloride equilibrium potential leads to the efflux of negative charges conferring a depolarizing effect on the cell. ATP regulation of ClC-2 thus modifies the time course of a potential excitatory anion outward current.

Genetic studies linked sequence variants in CLCN2 to IGE. One cluster of sequence variants found in patients with these diseases is located within the region of the carboxy-terminus of ClC-2 that comprises parts of the ATP binding site in ClC-2. As there is an ongoing controversy about the role of CLCN2 variants in the pathophysiology of IGE [21, 22, 33], we decided to investigate the effects of some of these variants, G715E, R577Q, and R653T, on ATP-dependent gating. Whereas the polymorphism combination R688Q/E718D did not change ATP-dependent kinetics, all three point mutations accelerated ClC-2 gating under physiological, high ATP conditions. These results suggest that ATP regulation might be physiologically important for excitability in central neurons. This notion is supported by another sequence variation associated to IGE, W570X [21]. W570X causes a significant acceleration of ClC-2 activation and deactivation with only slight changes to steady-state open probabilities even in the absence of ATP (our own unpublished observation), closely similar to H573X ClC-2 that also removes the entire carboxy-terminus (Fig 3c and d) [16]. Accelerated ClC-2 gating is thus a common functional consequence of IGE-associated sequence variants. IGE sequence variants do not alter steady-state parameters and cause only modest changes in time constants; however, these alterations can lead to a 20–40 % difference to wild-type channels in time-dependent open probability after few tens of milliseconds (Supplemental Fig. 5). However, the complex inheritance pattern suggests that changes in ClC-2 gating are only a contributing factor among others, yet unknown changes to cell excitability [21].

Our present findings are in contrast to an earlier study by Niemeyer et al. [27] who did not find differences in gating kinetics between WT and G715E ClC-2. A possible explanation for these differences might be the larger macroscopic current amplitudes in the earlier study. The slow activation time course makes ClC-2 very vulnerable for incorrect determination of activation time constants because of chloride depletion. Chloride efflux during long hyperpolarizing voltage steps reduces the driving force and thus reduces chloride currents. This reduction of chloride currents leads to incorrectly fast apparent activation time constants (Supplemental Fig. 6) [17]. Moreover, test pulses were often shortened to prevent significant chloride depletion in these early studies on ClC-2 gating [46]. Chloride depletion as well as different prepulse duration might have masked gating differences between WT and mutant ClC-2 in that earlier study. We used only cells with very low expression of ClC-2 to avoid these artifacts and are thus confident that our data represent accurate values for gating kinetics. Furthermore, the single-channel recordings strongly support the results from macroscopic recordings. Open probabilities and amplitudes of single-channel recordings (Fig. 2a) perfectly matched those obtained from stationary noise analysis (Fig. 4c and d) at −100 mV. The strong shift in closed dwell times to longer durations (Fig. 4g) implies an involvement of a common ATP-dependent process that—within the context of CLC gating—we could fully attribute to the slow, common gate of ClC-2 (Fig. 5a).

A recent publication reported the identification of the accessory subunit GlialCAM that causes profound alterations of ClC-2 gating [20]. However, whereas ClC-2 is broadly expressed in various cells of the central nervous systems, GlialCAM and ClC-2 colocalize only in Bergmann glia, in astrocyte–astrocyte junctions at astrocytic endfeet around blood vessels, and in myelinated fiber tracts. We here expressed ClC-2 without GlialCAM to create conditions that resemble the most likely situation in neurons. Our work does not provide information about the small fraction of glial ClC-2 channels interacting with GlialCAM.

In conclusion, we have characterized the regulation of ClC-2 by intracellular ATP. Association of ATP decelerates the kinetics of activation and deactivation via changing voltage-dependent transitions within the common gating cycle. Certain disease-associated sequence variants modify ClC-2 regulation by ATP, suggesting that ATP-dependent deceleration might be important for the electrical stability of certain neurons.

Electronic supplementary material

Below is the link to the electronic supplementary material.