Abstract
Electronic medical record (EMR) systems have enabled healthcare providers to collect detailed patient information from the primary care domain. At the same time, longitudinal data from EMRs are increasingly combined with biorepositories to generate personalized clinical decision support protocols. Emerging policies encourage investigators to disseminate such data in a deidentified form for reuse and collaboration, but organizations are hesitant to do so because they fear such actions will jeopardize patient privacy. In particular, there are concerns that residual demographic and clinical features could be exploited for reidentification purposes. Various approaches have been developed to anonymize clinical data, but they neglect temporal information and are, thus, insufficient for emerging biomedical research paradigms. This paper proposes a novel approach to share patient-specific longitudinal data that offers robust privacy guarantees, while preserving data utility for many biomedical investigations. Our approach aggregates temporal and diagnostic information using heuristics inspired from sequence alignment and clustering methods. We demonstrate that the proposed approach can generate anonymized data that permit effective biomedical analysis using several patient cohorts derived from the EMR system of the Vanderbilt University Medical Center.
Index Terms: Anonymization, data privacy, electronic medical records (EMRs), longitudinal data
I. Introduction
Advances in health information technology have facilitated the collection of detailed, patient-level clinical data to enable efficiency, effectiveness, and safety in healthcare operations [1]. Such data are often stored in electronic medical record (EMR) systems [2], [3] and are increasingly repurposed to support clinical research (see, e.g., [4]–[7]). Recently, EMRs have been combined with biorepositories to enable genome-wide association studies (GWAS) with clinical phenomena in the hopes of tailoring healthcare to genetic variants [8]. To demonstrate feasibility, EMR-based GWAS have focused on static phenotypes; i.e., where a patient is designated as disease positive or negative (see, e.g., [9]–[11]). As these studies mature, they will support personalized clinical decision support tools [12] and will require longitudinal data to understand how treatment influences a phenotype [13], [14].
Meanwhile, there are challenges to conducting GWAS on a scale necessary to institute changes in healthcare. First, to generate appropriate statistical power, scientists may require access to populations larger than those available in local EMR systems [15]. Second, the cost of a GWAS—incurred in the setup and application of software to process medical records as well as in genome sequencing—is nontrivial [16]. Thus, it can be difficult for scientists to generate novel, or validate published, associations. To mitigate this problem, the U.S. National Institutes of Health (NIH) encourages investigators to share data from NIH-supported GWAS [17] into the Database of Genotypes and Phenotypes (dbGaP) [18].
This, however, may lead to privacy breaches if patients’ clinical or genomic information is associated with their identities. As a first line of defense against this threat, the NIH recommends investigators deidentify data by removing an enumerated list of attributes that could identify patients (e.g., personal names and residential addresses) prior to dbGaP submission [19]. However, a patients’ DNA may still be reidentified via residual demographics [20] and clinical information (e.g., standardized International Classification of Diseases (ICD) codes) [21], as illustrated in the following example.
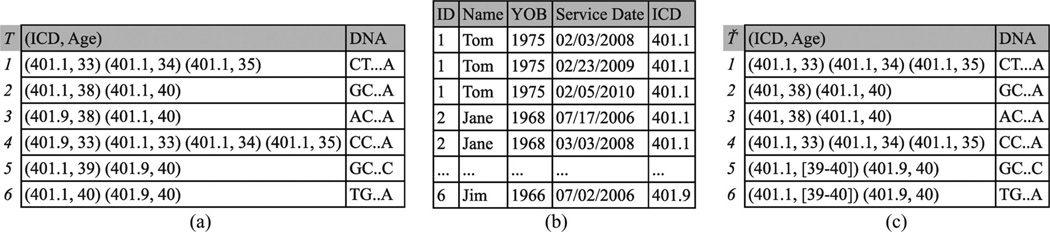
Example 1: Each record in Fig. 1(a) corresponds to a fictional deidentified patient and is comprised of ICD codes, patient’s age when a code was received, and a DNA sequence. For instance, the second record denotes that a patient was diagnosed with benign essential hypertension (code 401.1) at ages 38 and 40 and has the DNA sequence GC … A. The clinical and genomic data are derived from an EMR system and a research project beyond primary care, respectively. Publishing the data of Fig. 1(a) could allow a hospital employee with access to the EMR to associate Jane with her DNA sequence. This is because the identified record, shown in Fig. 1(b), can only be linked to the second record in Fig. 1(a) based on the ICD code 401.1 and ages 38 and 40.
Fig. 1.
Longitudinal data privacy problem. (a) Longitudinal research data. (b) Identified EMR. (c) 2-anonymization based on the proposed approach.
Methods to mitigate reidentification via demographic and clinical features [22], [23] have been proposed, but they are not applicable to the longitudinal scenario. These methods assume the clinical profile is devoid of temporal or replicated diagnosis information. Consequently, these methods produce data that are unlikely to permit meaningful longitudinal investigations.
In this paper, we propose the first approach to formally anonymize longitudinal patient records. Our work makes the following specific contributions.
We propose a framework to transform each longitudinal patient record into a form that is indistinguishable from at least k – 1 other records. This is achieved by iteratively clustering records and applying generalization, which replaces ICD codes and age values with more general values, and suppression, which removes ICD codes and age values. For example, applying our approach with k = 2 to the data of Fig. 1(a) will generate the anonymized data of Fig. 1(c). Observe that Jane’s record is now linked to two DNA sequences because the diagnosis code 401.1 in the first pair of this record has been replaced by the more general code 401.
We evaluate our approach with several cohorts of patient records from the Vanderbilt University Medical Center (VUMC) EMR system. Our results demonstrate that the anonymized data produced allow many studies focusing on clinical case counts to be performed accurately.
The remainder of this paper is organized as follows. In Section II, we review related research on anonymization and its application to biomedical data. In Section III, we formalize the notions of privacy and utility and the anonymization problem addressed in this paper. We present our anonymization framework and discuss its extensions and limitations in Sections IV and VI, respectively. Finally, Section V reports the experimental results and Section VII concludes the paper.
II. Related Research
Reidentification concerns for clinical data via seemingly innocuous attributes were first raised in [24]. Specifically, it was shown that patients could be uniquely reidentified by linking publicly available voter registration lists to hospital discharge summaries via demographics, such as date of birth, gender, and five-digit residential zip code. The reidentification phenomenon has since attracted interest in domains beyond healthcare, and numerous techniques to guard against attacks have emerged (see [25] and [26] for surveys). In this section, we survey research related to privacy-preserving data publishing, with a focus on biomedical data. We note that the reidentification problem is not addressed by access control and encryption-based methods [27]–[29] because data need to be shared beyond a small number of authorized recipients.
A. Relational Data
We first review methods for preventing reidentification in relational data (e.g., demographics), where records have a fixed number of attributes and one value per attribute.
The first category of protection methods transforms attribute values so that they no longer correspond to real individuals. Popular approaches in this category are noise addition, data swapping, and synthetic data generation (see [30]–[32] for surveys). While such methods generate data that preserve aggregate statistics (e.g., the average age), they do not guarantee data that can be analyzed at the record level. This is a significant limitation that hampers the ability to use these data in various biomedical studies, including epidemiological studies [33] and GWAS [22].
In contrast, methods based on generalization and suppression preserve data truthfulness [34]–[36]. Many of these methods are based on a principle called k-anonymity [24], [34], which states that each record of the published data must be equivalent to at least k – 1 other records with respect to quasi-identifiers (QI) (i.e., attributes that can be linked with external resources for reidentification purposes) [37]. To enhance the utility of the anonymized data, these methods employ various search strategies, including binary search [34], [35], clustering [38], [39], evolutionary search [40], and partitioning [36]. There are methods that have been successfully applied to biomedical data [35], [41].
B. Transactional Data
Next, we turn our attention to approaches that deal with more complex data. Specifically, we consider transactional data, in which records have a large and variable number of values per attribute (e.g., diagnosis codes assigned to a patient during a hospital visit). Transactional data can also facilitate reidentification in the biomedical domain. For instance, deidentified clinical records can be linked to patients based on combinations of diagnosis codes that are additionally contained in publicly available hospital discharge summaries and EMR systems from which the records have been derived [21]. As it was shown in [21], more than 96% of 2700 patient records, collected in the context of a GWAS, would be susceptible to reidentification based on diagnosis codes if shared without additional controls.
From the protection perspective, there are several approaches that have been developed to anonymize transactional data. For instance, Terrovitis et al. [42] proposed km-anonymity, a principle, and several heuristic algorithms to prevent attackers from linking an individual to less than k records. This model assumes that the adversary knows at most m attribute values of any transaction. To anonymize patient records in transactional form, Loukides et al. [22] introduced a privacy principle to ensure that sets of potentially identifying diagnosis codes are protected from reidentification, while remaining useful for GWAS validations. To enforce this principle, they proposed an algorithm that employs generalization and suppression to group semantically close diagnosis codes together in a way that enhances data utility [22], [23]. Additionally, Tamersoy et al. [43] considered protecting data in which a certain diagnosis code may occur multiple times in a patient record. They designed an algorithm which preserves patients’ privacy through suppressing a subset of the replications of a diagnosis code.
Our work differs from the aforementioned research along two principal dimensions. First, we address reidentification in longitudinal data publishing. Second, contrary to the approaches in [22] and [23] which group diagnosis codes together, our framework is based on grouping of records, which has been shown to be highly effective in retaining data utility due to the direct identification of records being anonymized [38], [39], [44].
C. Spatiotemporal Data
Spatiotemporal data are related to the problem studied in this paper. They are time and location dependent, and these unique characteristics make them challenging to protect against reidentification. Such data are typically produced as a result of queries issued by mobile subscribers to location-based service providers, who, in turn, supply information services based on specific physical locations.
The principle of k-anonymity has been extended to anonymize spatiotemporal data. Abul et al. [45] proposed a technique to group at least k objects that correspond to different subscribers and appear within a certain radius of the path of every object in the same time period. In addition to generalization and suppression, Abul et al. [45] considered adding noise to the original paths so that objects appear at the same time and spatial trajectory volume. Assuming that the locations of subscribers constitute sensitive information, Terrovitis and Mamoulis [46] proposed a suppression-based methodology to prevent attackers from inferring these locations. Finally, Nergiz et al. [44] proposed an approach that employs k-anonymity, enforced using generalization, together with reconstruction to protect data against boundary-based attacks. Our heuristics are inspired from [44]; however, we employ both generalization and suppression to further enhance data utility, and we do not use reconstruction, so as to preserve data truthfulness.
The aforementioned approaches are developed for anonymizing spatiotemporal data and cannot be applied to longitudinal data due to different semantics. Specifically, the data we consider record patients’ diagnoses and not their locations. Consequently, the objective of our approach is not to hide the locations of patients, but to prevent reidentification based on their diagnosis and time information.
III. Background and Problem Formulation
This section begins with a high-level overview of the proposed approach. Next, we present the notation and the definitions for the privacy and adversarial models, the data transformation strategies, and the information loss metrics. We conclude the section with a formal problem description.
A. Architectural Overview
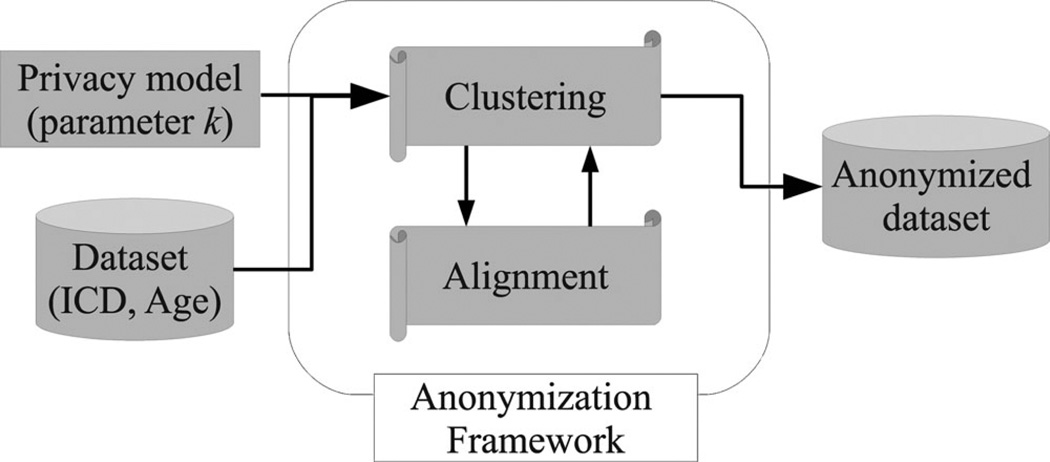
Fig. 2 provides an overview of the data anonymization process. The process is initiated when the data owner supplies the following information: 1) a dataset of longitudinal patient records, each of which consists of (ICD, Age) pairs and a DNA sequence, and 2) a parameter k that expresses the desired level of privacy. Given this information, the process invokes our anonymization framework. To satisfy the k-anonymity principle, our framework forms clusters of at least k records of the original dataset, which are modified using generalization and suppression.
Fig. 2.
General architecture of the longitudinal data anonymization process.
B. Notation
A dataset D consists of longitudinal records of the form 〈T, DN AT〉, where T is a trajectory1 and DN AT is a genomic sequence. Each trajectory corresponds to a distinct patient in D and is a multiset2 of pairs (i.e., T = {t1,…, tm}) drawn from two attributes, namely ICD and Age [i.e., ti = (u ∈ ICD, υ ∈ Age)], which contain the diagnosis codes assigned to a patient and their age, respectively. |D| denotes the number of records in D and |T| the length of T, defined as the number of pairs in T. We use the “.” operator to refer to a specific attribute value in a pair (e.g., ti.icd or ti.age). To study the data temporally, we order the pairs in T with respect to Age, such that ti − 1.age ≤ ti.age.
C. Adversarial Model
We assume that an adversary has access to the original dataset D, such as in Fig. 1(a). An adversary may perform a reidentification attack in several ways.
Using identified EMR data: The adversary links D with the identified EMR data, such as those of Fig. 1(b), based on (ICD, Age) pairs. This scenario requires the adversary to have access to the identified EMR data, which is the case of an employee of the institution from which the longitudinal data were derived.
Using publicly available hospital discharge summaries and identified resources: The adversary first links D with hospital discharge summaries based on (ICD, Age) pairs to associate patients with certain demographics. In turn, these demographics are exploited in another linkage with public records, such as voter registration lists, which contain identity information.
Note that in both cases, an adversary is able to link patients to their DNA sequences, which suggests that a formal approach to longitudinal data anonymization is desirable.
D. Privacy Model
The formal definition of k-anonymity in the longitudinal data context is provided in Definition 1. Since each trajectory often contains multiple (ICD, Age) pairs, it is difficult to know which can be used by an adversary to perform reidentification attacks. Thus, we consider the worst-case scenario in which any combination of (ICD, Age) pairs can be exploited. Regardless, k-anonymity limits an adversary’s ability to perform reidentification based on (ICD, Age) pairs, because each trajectory is associated with no less than k patients.
Definition 1 (k-Anonymity): An anonymized dataset D̃, produced from D, is k-anonymous if each trajectory in D̃, projected over QI, appears at least k times for any QI in D.
E. Data Transformation Strategies
Generalization and suppression are typically guided by a domain generalization hierarchy (DGH) (Definition 2) [47].
Definition 2 (DGH): A DGH for attribute 𝒜, referred to as H𝒜, is a partially ordered tree structure which defines valid mappings between specific and generalized values of 𝒜. The root of H𝒜 is the most generalized value of 𝒜 and is returned by a function root.
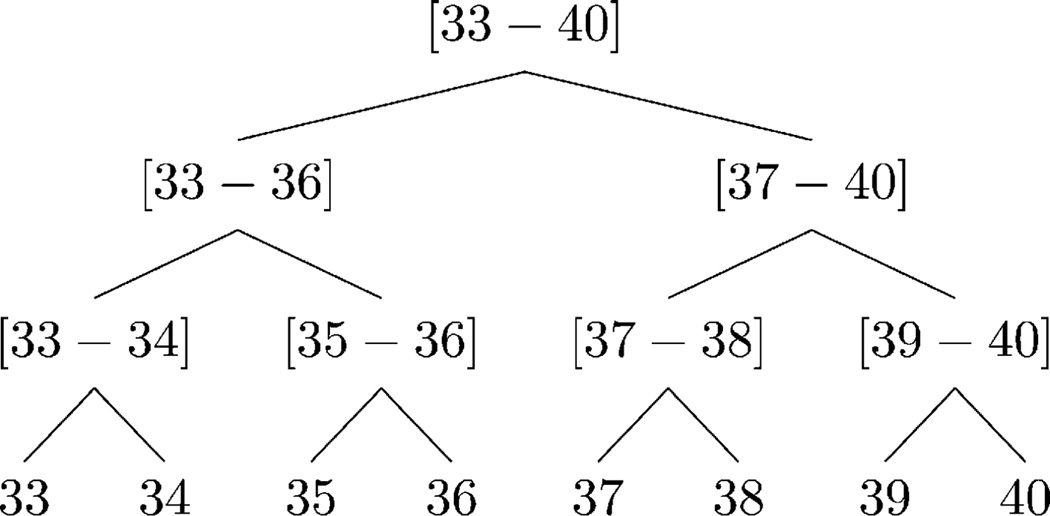
Example 2: Consider HAge in Fig. 3. The values in the domain of Age (i.e., 33, 34,…, 40) form the leaves of HAge. These values are then mapped to two, to four, and eventually to eight-year intervals. The root of HAge is returned by root(HAge) as [33 – 40].
Fig. 3.
Example of the DGH structure for Age.
Our approach does not impose any constraints on the structure of an attribute’s DGH, such that the data owners have complete freedom in its design. For instance, for ICD codes, data owners can use the standard ICD-9-CM hierarchy.3 For ages, data owners can use a predefined hierarchy (e.g., the age hierarchy in the HIPAA Safe Harbor Policy4) or design a DGH manually.5
According to Definition 3, each specific value of an attribute generalizes to its direct ancestor in a DGH. However, a specific value can be projected up multiple levels in a DGH via a sequence of generalizations. As a result, a generalized value 𝒜i is interpreted as any one of the leaf nodes in the subtree rooted by 𝒜i in H𝒜.
Definition 3 (Generalization and Suppression): Given a node 𝒜i ≠ root (H𝒜) in H𝒜, generalization is performed using a function f:𝒜i → 𝒜j which replaces 𝒜i with its direct ancestor 𝒜j. Suppression is a special case of generalization and is performed using a function g:𝒜i → 𝒜r which replaces 𝒜i with root(H𝒜).
Example 3: Consider the last trajectory in Fig. 1(c). The first pair (401.1, [39 – 40]) is interpreted as either (401.1,39) or (401.1,40).
F. Information Loss
Generalization and suppression incur information loss because values are replaced by more general ones or eliminated. To capture the amount of information loss incurred by these operations, we quantify the normalized loss for each ICD code and Age value in a pair based on the Loss Metric (LM) (Definition 4) [40].
Definition 4 (LM): The information loss incurred by replacing a node 𝒜i with its ancestor 𝒜j in H𝒜 is
| (1) |
where and denote the number of leaf nodes in the subtree rooted by 𝒜i and 𝒜j in H𝒜, respectively, and |𝒜| denotes the domain size of attribute 𝒜.
Example 4: Consider HAge in Fig. 3. The information loss incurred by generalizing [33 – 34] to [33 – 36] is because the leaf-level descendants of [33 – 34] are 33 and 34, those of [33 – 36] are 33, 34, 35, and 36, and the domain of Age consists of the values 33–40.
To introduce the combined LM, which captures the total LM of replacing two nodes with their ancestor, provided in Definition 6, we use the notation of lowest common ancestor (LCA), provided in Definition 5.
Definition 5 (LCA): The LCA 𝒜ℓ of nodes 𝒜i and 𝒜j in H𝒜 is the farthest node (in terms of height) from root(H𝒜) such that (1) 𝒜i = 𝒜ℓ or fn(𝒜i) = 𝒜ℓ and (2) 𝒜j = 𝒜ℓ or fm (𝒜j) = 𝒜ℓ, and is returned by a function lca.
Definition 6 (Combined LM): The combined LM of replacing nodes 𝒜i and 𝒜j with their LCA 𝒜ℓ is
| (2) |
Next, we define the LM for an anonymized trajectory (Definition 7) and dataset (Definition 8), which we keep separate for each attribute.
Definition 7 (LM for an Anonymized Trajectory): Given an anonymized trajectory T̃ and an attribute 𝒜, the LM with respect to 𝒜 is computed as
| (3) |
where denotes the value t̃i.𝒜 is replaced with.
Definition 8 (LM for an Anonymized Dataset): Given an anonymized dataset D̃ and an attribute 𝒜, the LM with respect to attribute 𝒜 is computed as
| (4) |
For clarity, we refer to an LM related to ICD and Age by ILM and ALM, respectively (e.g., we use ILM(D̃) instead of LM(D̃, ICD)).
G. Problem Statement
The longitudinal data anonymization problem is formally defined as follows.
Problem: Given a longitudinal dataset D, a privacy parameter k, and DGHs for attributes ICD and Age, construct an anonymized dataset D̃, such that 1) D̃ is k-anonymous, 2) the order of the pairs in each trajectory of D is preserved in D̃, and 3) ILM(D̃) + ALM(D̃) is minimized.
IV. Anonymization Framework
In this section, we present our framework for longitudinal data anonymization.
Many clustering algorithms can be applied to produce k-anonymous data [48], [49]. This involves organizing records into clusters of size at least k, which are anonymized together. In the context of longitudinal data, the challenge is to define a distance metric for trajectories such that a clustering algorithm groups similar trajectories. We define the distance between two trajectories as the cost (i.e., incurred information loss) of their anonymization as defined by the LM. The problem then reduces to finding an anonymized version T̃ of two given trajectories such that ILM(T̃) + ALM(T̃) is minimized.
Finding an anonymization of two trajectories can be achieved by finding a matching between the pairs of trajectories that minimizes their cost of anonymization. This problem, which is commonly referred to as sequence alignment, has been extensively studied in various domains, notably for the alignment of DNA sequences to identify regions of similarity in a way that the total pairwise edit distance between the sequences is minimized [50], [51].
To solve the longitudinal data anonymization problem, we propose Longitudinal Data Anonymizer, a framework that incorporates alignment and clustering as separate components, as shown in Fig. 2. The objective of each component is summarized as follows.
Algorithm 1.
Baseline(X, Y)
|
Require: Trajectories X = {x1, …, xm} and Y = {y1, …, yn}, ILM(X) and ALM(X), DGHs HICD and HAge | |
| Return: Anonymized trajectory T̃, ILM(T̃) and ALM(T̃) | |
| 1: | T̃ ← Ø |
| 2: | i ← ILM(X); a ←- ALM(X) |
| 3: | s ← the length of the shorter of X and Y |
| 4: |
for all
j ∈ [1, s] do ▷Construct a pair containing the LCAs of xj and yj |
| 5: | p ← (lca(xj.icd, yj.icd, HICD), lca(xj.age,yj.age, HAge)) ▷Append the constructed pair to T̃ |
| 6: | T̃ ← T̃ ∪ p ▷Inf. loss incurred by generalizing xj with yj |
| 7: | i ← i + ILM(xj + yj, p.icd) |
| 8: | 𝒜 ← 𝒜 + ALM(xj + yj, p.age) |
| 9: | end for |
| 10: | Z ← the longer of X and Y |
| 11: |
for all
j ∈ [(s + 1), |Z|] do ▷Information loss incurred by suppressing zj |
| 12: | i ← i + ILM(zj, root(HICD)) |
| 13: | a ← a + ALM(zj, root(HAge)) |
| 14: | end for |
| 15: | return {T̃, i, a} |
Alignment attempts to find a minimal cost pair matching between two trajectories.
Clustering interacts with the Alignment component to create clusters of at least k records.
Next, we examine each component in detail and develop methodologies to achieve their objectives.
A. Alignment
There are no directly comparable approaches to the method we developed in this study. So, we introduce a simple heuristic, called Baseline, for comparison purposes. Given trajectories X = {x1,…, xm} and Y = {y1,…, yn}, ILM(X) and ALM(X), and DGHs HICD and HAge, Baseline aligns X and Y by matching their pairs on the same index.6
The pseudocode for Baseline is provided in Algorithm 1. This algorithm initializes an empty trajectory T̃ to hold the output of the alignment and then assigns ILM(X) and ALM(X) to variables i and a, respectively (steps 1 and 2). Then, it determines the length of the shorter trajectory (step 3) and performs pair matching (steps 4–9). Specifically, for the pairs of the trajectories that have the same index, Baseline constructs a pair containing the LCAs of the ICD codes and Age values in these pairs (step 5), appends the constructed pair to T̃ (step 6), and updates i and a with the information loss incurred by the generalizations (steps 7–8). Next, Baseline updates i and a with the amount of information loss incurred by suppressing the ICD codes and Age values from the unmatched pairs in the longer trajectory (steps 10–14). Finally, this algorithm returns T̃ along with i and a, which correspond to ILM(T̃) and ALM(T̃), respectively (step 15).
To help preserve data utility, we provide Alignment using Generalization and Suppression (A-GS), an algorithm that uses dynamic programming to construct an anonymized trajectory that incurs minimal cost.
Before discussing A-GS, we briefly discuss the application of dynamic programming. The latter technique can be used to solve problems based on combining the solutions to subproblems which are not independent and share subsubproblems [52]. A dynamic programming algorithm stores the solution of a sub-subproblem in a table to which it refers every time the sub-subproblem is encountered. To give an example, for trajectories X = {x1,…, xm} and Y = {y1,…, yn}, a subproblem may be to find a minimal cost pair matching between the first to the jth pairs. A solution to this subproblem can be determined using solutions for the following subsubproblems and applying the respective operations:
Align X = {x1,…, xj−1} and Y = {y1,…, yj−1}, and generalize xj with yj;
Align X = {x1,…, xj−1} and Y = {y1,…,yj}, and suppress xj;
Align X = {x1,…, xj} and Y = {y1,…, yj−1}, and suppress yj.
Each case is associated with a cost. Our objective is to find an anonymized trajectory T̃, such that ILM(T̃) + ALM(T̃) is minimized, so we examine each possible solution and select the one with minimum information loss.
A-GS uses a similar approach to align trajectories. The algorithm accepts the same inputs as Baseline as well as weights wICD and wAge. The latter allow A-GS to control the information loss incurred by anonymizing the values of each attribute. The data owners specify the attribute weights such that wICD ≥ 0, wAge ≥ 0, and wICD + wAge = 1. The pseudocode for A-GS is provided in Algorithm 2.
In step 1, A-GS initializes three matrices: i, a, and r. The first row (indexed 0) of each of these matrices corresponds to a null value, and starting from index 1, each row corresponds to a value in X. Similarly, the first column (indexed 0) of each of these matrices corresponds to a null value, and starting from index 1, each column corresponds to a value in Y. Specifically, for indices h and j, rh,j records which of the following operations incurs minimum information loss: 1) generalizing xh and yj (denoted with <↖>), 2) suppressing xh (denoted with <↑>), and 3) suppressing yj (denoted with <←>). The entries in ih,j and ah,j keep the total ILM and ALM for aligning the subtrajectories Xsub = {x1,…, xh} and Ysub = {y1,…, yj}, respectively.
In step 2, A-GS assigns ILM(X) and ALM(X) to i0,0 and a0,0, respectively. We include null values in the rows and columns of i, a, and r because at some point during alignment A-GS may need to suppress some portion of the trajectories. Therefore, in steps 3–7 and 8–12, A-GS initializes i, a, and r for the values in X and Y, respectively. Specifically, for indices h and j, ih,0 and i0,j keep the ILM for suppressing every pair in the subtrajectories Xsub = {x1,…, xh} and Ysub = {y1,…,yj}, respectively. Similar reasoning applies to matrix a. The first row and column of r holds <↑> and <←> for suppressing values from X and Y, respectively.
Algorithm 2.
A-GS(X, ILM(X), ALM(X), Y)
|
Require: Trajectories X = {x1,…,xm} and Y = {y1,…, yn}, ILM(X) and ALM(X), DGHs HICD and HAge, weights wICD and wAge | |
| Return: Anonymized trajectory T̃, ILM(T̃) and ALM(T̃) | |
| 1: | {i, a, r} ← generate (m + 1) × (n + 1) matrices |
| 2: |
i0,0 ← ILM(X); a0,0 ← ALM(X) ▷Initialize i, a and r with respect to X |
| 3: | for all h ∈ [1, m] do |
| 4: | ih,0 ← ih−1,0 + ILM(xh, root(HICD)) × wICD |
| 5: | ah,0 ← ah−1,0 + ALM(xh, root(HAge)) × wAge |
| 6: | rh,0← <↑> |
| 7: |
end for ▷Initialize i, a and r with respect to Y |
| 8: | for all j ∈ [1, n] do |
| 9: | i0,j ← i0,j−1 + ILM(yj, root(HICD)) × wICD |
| 10: | a0,j ← a0,j−1 + ALM(yj, root(HAge)) × wAge |
| 11: | r0,j ← <←> |
| 12: | end for |
| 13: | for all h ∈ [l, m] do |
| 14: | for all j ∈ [1, n] do |
| 15: | {c, g} ← generate arrays with indices <↖>, <←>, <↑> ▷Compute the ILM for the possible solutions |
| 16: | c<↖> ← ih−1,j−1 + ILM(xh + yj, lca(xh.icd,yj.icd HICD)) × wICD |
| 17: | c<←> ← ih, j−1 + ILM(yj, root(HICD)) × wICD |
| 18: | c<↑> ← ih−1,j + ILM(xh, root(HICD)) × wICD ▷Compute the ALM for the possible solutions |
| 19: | g <↖> ← ah−1, j−1 + ALM(xh + yj, lca(xh.age, yj.age HAge)) × wAge |
| 20: | g<←> ← ah,j−1 + ALM(yj, root(HAge)) × wAge |
| 21: | g<↑> ← ah−1,j + ALM(xh, root(HAge)) × wAge ▷Solution with the minimum overall LM |
| 22: | w ← argminu∈{<↖>,<←>,<↑>} {cu + gu} |
| 23: | ih,j ← cw; ah,j ← gw; ← w |
| 24: | end for |
| 25: | end for |
| 26: | T̃ ← Ø |
| 27: |
h ← m; j ← n ▷Construct the anonymized trajectory T̃ |
| 28: | while h ≥ 1 or j ≥ 1 do |
| 29: | if rh,j = <↖> then |
| 30: | p ← (lca(xh.icd,yj.icd,HICD), lca(xh.age,yj.age,HAge)) |
| 31: | T̃ ← T̃ ∪ p |
| 32: | h ← h − 1; j ← j – 1 |
| 33: | end if |
| 34: | ifrh,j = <←> then j ← j – 1 end if |
| 35: | if rh,j = <↑> then h ← h – 1 end if |
| 36: | end while |
| 37: | return {T̃, im,n, am,n} |
In steps 13–25, A-GS performs dynamic programming. Specifically, for indices h and j, A-GS determines a minimal cost pair matching of the subtrajectories Xsub = {x1,…, xh} and Ysub = {y1,…, yj} based on the three cases listed previously. Specifically, in steps 15–21, A-GS constructs two temporary arrays, c and g, to store the ILM and ALM for each possible solution, respectively. Next, in steps 22 and 23, A-GS determines the solution with the minimum information loss and assigns the ILM, ALM, and operation associated with the solution to ih,j, ah,j, and rh,j, respectively. If there is a tie between the solutions, A-GS selects generalization as the operation for the sake of retaining more information.
In steps 26–36, A-GS constructs the anonymized trajectory T̃ by traversing the matrix r. Specifically, for two pairs in the trajectories, if generalization incurs minimum information loss, A-GS appends to T̃ a pair containing the LCAs of the ICD codes and Age values in these pairs. The unmatched pairs in the trajectories are ignored during this process because A-GS suppresses these pairs. Finally, in step 37, Baseline returns T̃ along with im,n and am,n, which correspond to ILM(T̃) and ALM(T̃), respectively.
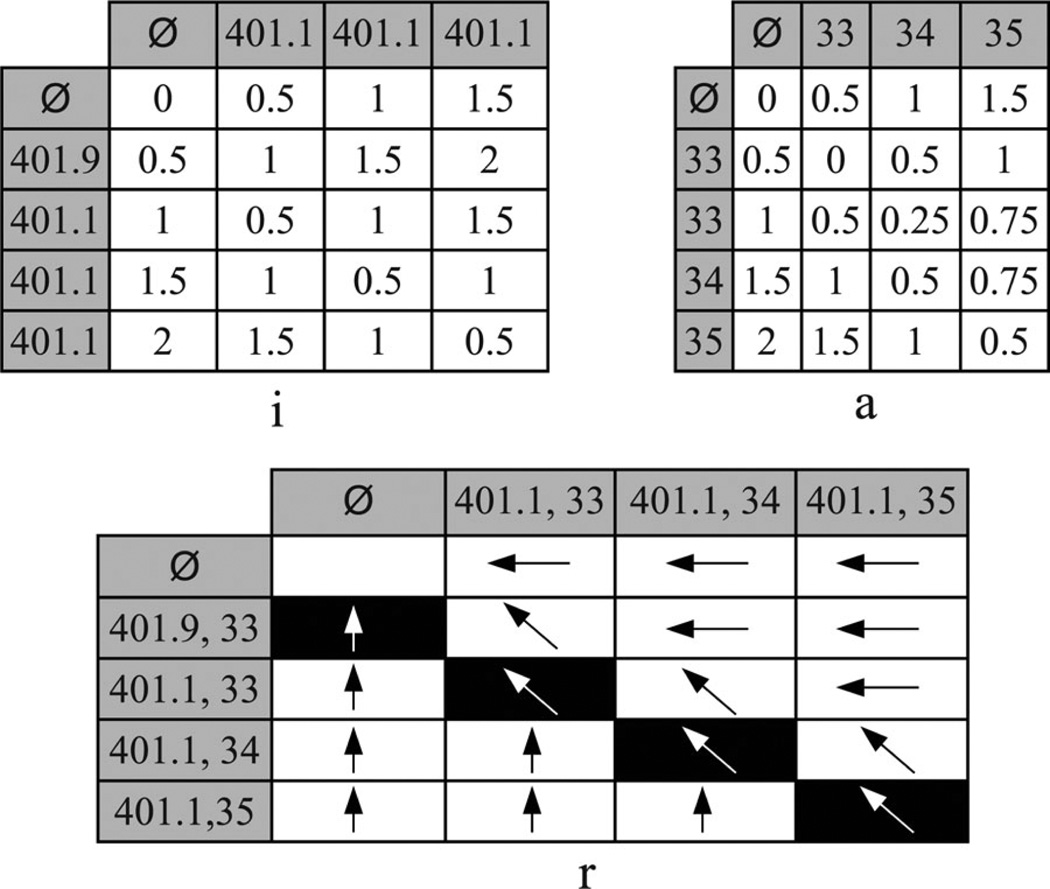
Example 5: Consider applying A-GS to T1 and T4 in Fig. 1(a) using the DGHs shown in Figs. 3 and 4 and assuming that wICD = wAge = 0.5. The matrices i, a, and r are illustrated in Fig. 5. As T1 and T4 are not anonymized, we initialize i0,0 = a0,0 = 0. Subsequently, A-GS computes the values for the entries in the first row and column of the matrices. For instance, i0,3 keeps the ILM for suppressing all ICD codes from T1 and has a value of 1 + (1 * 0.5) = 1.5. This is computed by summing the ILM for suppressing the first two ICD codes (i.e., the value stored in i0,2) with the weight-adjusted ILM for suppressing the third ICD code. Then, A-GS performs dynamic programming. The process starts with aligning T1,sub = {(401.1, 33)} and T4,sub = {(401.9, 33)}. The possible solutions for this sub-problem are as follows.
Align T1,sub = {Ø} and T4,sub = {Ø}, and generalize 401.1 with 401.9 and 33 with 33.
Align T1,sub = {(401.1,33)} and T4,sub = {Ø}, and suppress 401.9 and 33.
Align T1,sub = {Ø} and T4,sub = {(401.9, 33)}, and suppress 401.1 and 33.
Algorithm 3.
MDAV′(D)
|
Require: Original dataset D, privacy parameter k, weights wICD and wAge | |
| Return: Anonymized dataset D̃, ILM(D̃) and ALM(D̃) | |
| 1: | D̃ ← Ø; ĩ ← 0; ã ← 0; p ← ∑T∈D |T| |
| 2: | while |D| ≥ 3* k do |
| 3: | F ← the most frequent trajectory in D ▷Find the most distant trajectory to F |
| 4: | X ← argmaxT∈D{(i + a)|i, a ∈ A-GS(F, 0, 0, T)} |
| 5: | {C, i′, a′} ← formCluster(X, k) |
| 6: | D̃ ← D̃ ∪ C; ĩ ← ĩ + i′; ã ← ã + a′ |
| 7: | Y ← argmaxT∈D{(i + a)|i, a ∈ A-GS(X, 0, 0, T)} |
| 8: | {C, i′, a′} ← formCluster(Y, k) |
| 9: | D̃ ← D̃ ∪ C; ĩ ← ĩ + i′; ã ← ã + a′ |
| 10: | end while |
| 11: | while |D| ≥ 2 * k do |
| 12: | F ← the most frequent trajectory in D |
| 13: | X ← argmaxT∈D{(i + a)|i, a ∈ A-GS(F, 0,0, T)} |
| 14: | {C, i′, a′} ← formCluster(X, k) |
| 15: | D̃ ← D̃ ∪ C; ĩ ← ĩ + i′; ã ← ã + a′ |
| 16: | end while |
| 17: | R ← select a trajectory from D uniformly at random |
| 18: | {C, i′, a′} ← formCluster(R, |D|) |
| 19: | D̃ ← D̃ ∪ C; ĩ ← ĩ + i′; ã ← ã + a′ |
| 20: | return {D̃, ĩ/(p * wICD), ã/(p*wAge)} |
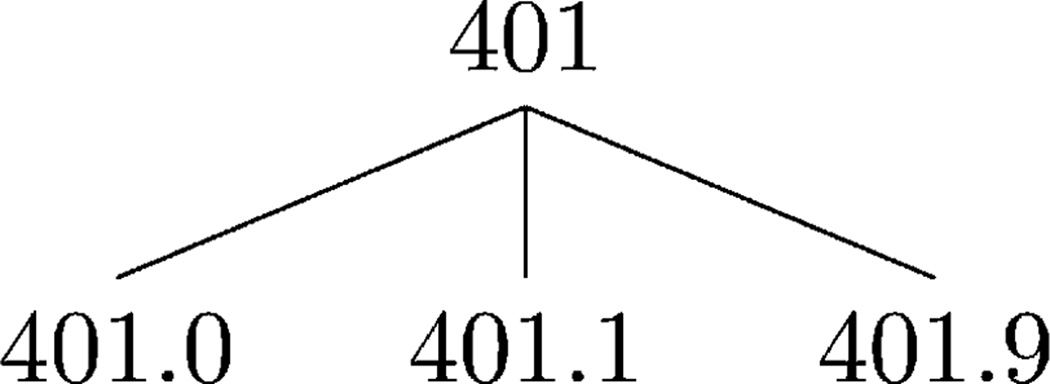
Fig. 4.
Example of the hypertension subtree in the ICD DGH.
Fig. 5.
Matrices i, a, and r for the subset of records from Fig. 1. This alignment uses the DGHs in Figs. 3 and 4 and assumes that wICD = wAge = 0.5.
The ILM and ALM for the subsubproblem in the first solution are stored in i0,0 and a0,0, respectively. Generalizing 401.1 with 401.9 has an ILM of (1 + 1) * 0.5 = 1, and generalizing 33 with 33 has an ALM of 0. Therefore, the first solution has a total LM of 1. The ILM and ALM for the subsubproblem in the second solution are stored in i0,1 and a0,1 , respectively. The suppression of 401.9 and 33 has an ILM and ALM of 1 * 0.5 = 0.5. It can be seen that the second and third solutions each have a total LM of 2. The solution with the minimum information loss is the first one; hence, A-GS stores 1, 0 and <↖> in i1,1, a1,1 and r1,1, respectively. After the values for the remaining entries are computed, A-GS uses r to construct the anonymized trajectory T̃. The process starts with examining the bottom-right entry, which denotes a generalization. As a result, A-GS appends (401.1, 35) to T̃. The process continues by following the symbols, such that A-GS returns T̃ = {(401.1, 33), (401.1, 34), (401.1, 35)} along with i4,3 and a4,3, which correspond to ILM(T̃) and ALM(T̃), respectively.
B. Clustering
We base our methodology for the clustering component on the maximum distance to average vector (MDAV) algorithm [53], [54], an efficient heuristic for k-anonymity. The pseudocode for MDAV′7 and its helper function, formCluster, are provided in Algorithms 3 and 4, respectively. MDAV′ iteratively selects the most frequent trajectory in a longitudinal dataset (steps 3 and 12), finds its most distant trajectory X (steps 4 and 13), and forms a cluster of k trajectories around the latter trajectory (steps 5 and 6 and 14 and 15). Cluster formation is performed by formCluster, a function that constructs a cluster C by aligning n trajectories in a consecutive manner and returns C, along with ILM(C) and ALM(C) which are the ILM and ALM for the anonymized trajectory resulting from the alignment, respectively. MDAV′ minimizes intercluster similarity by constructing a cluster around a trajectory Y that is most distant to X (steps 7–9). We define the distance between two trajectories as the cost of their anonymization. As such, the most distant trajectory is the one that maximizes the sum of ILM and ALM returned from A-GS.
Algorithm 4.
formCluster(W, n)
|
Require: Original dataset D, trajectory W, integer n specifying the number of trajectories to be included in the cluster | |
| Return: Cluster C, ILM(C) and ALM(C) | |
| 1: | D ← D \ {W}; W̃ ← W; i′ ← 0; a′ ← 0 |
| 2: | for all j ∈ [1, (n − 1)] do |
| 3: | Z ← argminT∈D {(i + a)|i, a ∈ A-GS(W̃, i′, a′, T)} ▷Align W̃ with Z, the closest trajectory to W̃ |
| 4: | {T̃, i, a} ← A-GS(W̃, i′, a′, Z) |
| 5: | D ← D \ {Z}; W̃ ← T; i′ ← i; a′ ← a |
| 6: |
end for ▷Form a cluster of anonymized trajectories |
| 7: | C ← the set containing n copies of W̃ |
| 8: | return {C, i′, a′} |
A similar reasoning applies when we form a cluster. We add the trajectory that minimizes the sum of ILM and ALM returned from A-GS. MDAV′ forms a final cluster of size at least k using the remaining trajectories in the dataset (steps 17–19) and returns D̃, a k-anonymized version of the longitudinal dataset, along with ILM(D̃) and ALM(D̃) (step 20).
V. Experimental Evaluation
This section presents an experimental evaluation of the anonymization framework. We compare the anonymization methods on data utility, as indicated by the LM measure (see Section V-B) and aggregate query answering accuracy (see Section V-C). Furthermore, we show that our method allows balancing the level of information loss incurred by anonymizing ICD codes and Age values (see Section V-D). This is important to support different types of biomedical studies, such as geriatric and epidemiology studies that are supported “well” when the information contained in Age and ICD attributes, respectively, is preserved in the anonymized data.
A. Experimental Setup
We worked with three datasets derived from the Synthetic Derivative (SD), a collection of deidentified information extracted from the EMR system of the VUMC [55]. We issued a query to retrieve the records of patients whose DNA samples were genotyped and stored in BioVU, VUMC’s DNA repository linked to the SD. Then, using the phenotype specification in [56], we identified the patients eligible to participate in a GWAS on native electrical conduction within the ventricles of the heart. Subsequently, we created a dataset called by restricting our query to the 50 most frequent ICD codes that occur in at least 5% of the records in BioVU. Next, we created a dataset called , which is a subset of , containing the following comorbid ICD codes selected for [43]: 250 (diabetes mellitus), 272 (disorders of lipoid metabolism), 401 (essential hypertension), and 724 (other and unspecified disorders of the back). Finally, we created a dataset called , which is a subset of , containing the records of patients who actually participated in the aforementioned GWAS [57]. is expected to be deposited into the dbGaP repository and has been used in [43] with no temporal information. The characteristics of our datasets are summarized in Table I.
TABLE I.
Descriptive Summary Statistics of the Datasets
| D | |D| | |ICD| | |Age| | Avg. ICD per T | Avg. Age per T | |
|---|---|---|---|---|---|---|
| 27639 | 50 | 102 | 5.88 | 3.10 | ||
| 16052 | 4 | 97 | 1.65 | 2.78 | ||
| 1896 | 4 | 90 | 1.96 | 4.04 |
Throughout our experiments, we varied k between 2 and 15, noting that k = 5 tends to be applied in practice [41]. Initially, we set wICD = wAge = 0.5. We implemented all algorithms in Java and conducted our experiments on an Intel 2.8 GHz powered system with 4-GB RAM.
B. Capturing Data Utility Using LM
We first compared the algorithms with respect to the LM.
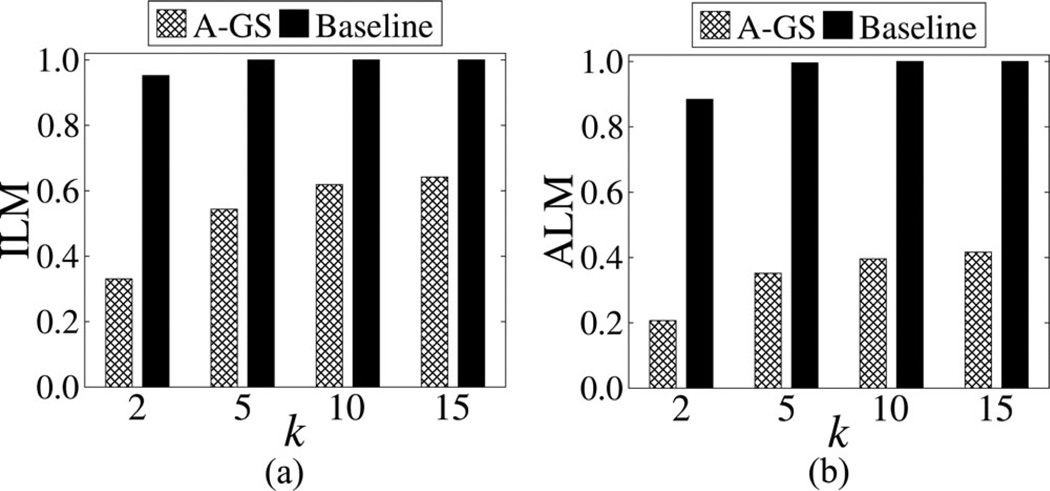
Fig. 6 depicts the results with . The ILM and ALM increase with k for both algorithms, which is expected because as k increases, a larger amount of distortion is needed to satisfy a stricter privacy requirement. Note that Baseline incurred substantially more information loss than A-GS for all k. In fact, Baseline failed to construct a practically useful result when k > 2, as it suppressed all values from the dataset. Similar trends were observed between A-GS and Baseline for and (omitted for brevity).
Fig. 6.
Comparison of information loss for using various k values.
Interestingly, A-GS, on average, incurred 48% less information loss on than . This is important because a relatively small number of ICD codes may suffice to study a range of different diseases [11], [43]. It is also worthwhile to note that the information loss incurred by our approach remains relatively low (i.e., below 0.5) for , even though it is, on average, 55% more than that for . This is attributed to the fact that is more sparse than , which implies it is more difficult to anonymize [58]. The ILM and ALM for different k values and datasets, which correspond to the aforementioned results, can be found in Appendix A.
C. Capturing Data Utility Using Average Relative Error
We next analyzed the effectiveness of our approach for supporting general biomedical analysis. We assumed a scenario in which a scientist issues queries on anonymized data to retrieve the number of trajectories that harbor a combination of (ICD, Age) pairs that appear in at least 1% of the original trajectories. Such queries are typical in many biomedical data mining applications [59]. To quantify the accuracy of answering such a workload of queries, we used the Average Relative Error (AvgRE) measure [36], which reflects the average number of trajectories that are incorrectly included as part of the query answers. Details about this measure are in Appendix B.
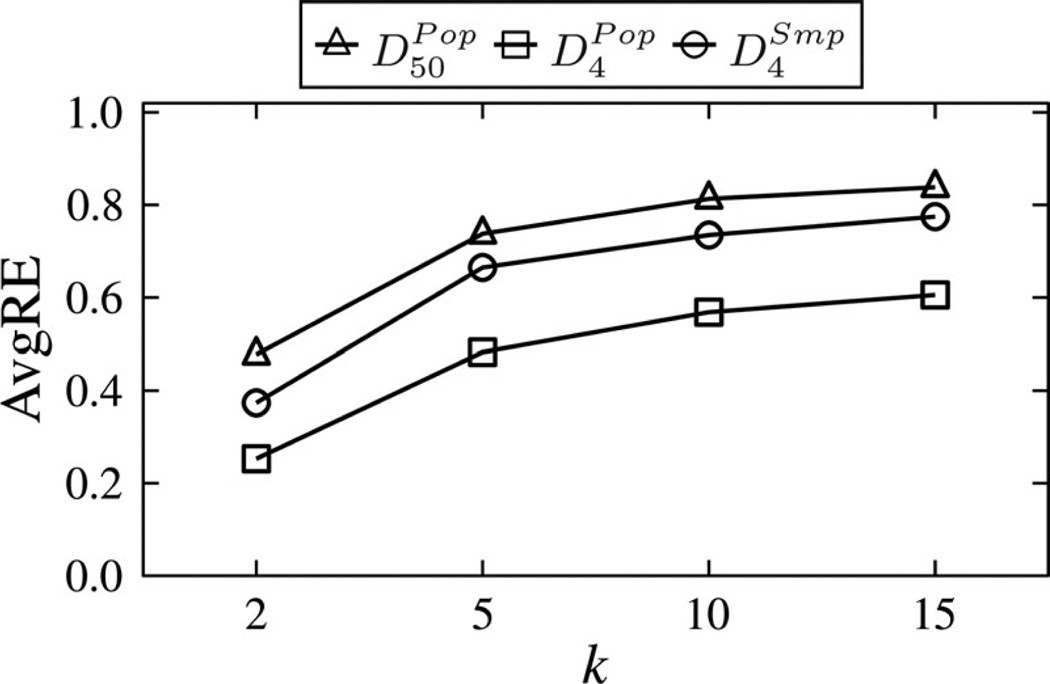
Fig. 7 shows the AvgRE scores of running A-GS on the datasets. The results for Baseline are not reported because they were more than 6 times worse than our approach for k = 2, and the worst possible for k > 2. This is because Baseline suppressed all values. As expected, we find an increase in AvgRE scores as k increases, which is due to the privacy/utility tradeoff. Nonetheless, A-GS allows fairly accurate query answering on each dataset by having an AvgRE score of less than 1 for all k. The results suggest our approach can be effective, even when a high level of privacy is required. Furthermore, we observe that the AvgRE scores for are lower than those of , which are in turn lower than those of . This implies that query answers are more accurate for small domain sizes and large datasets.
Fig. 7.
Comparison of query answering accuracy for , and using various k values.
D. Prioritizing Attributes
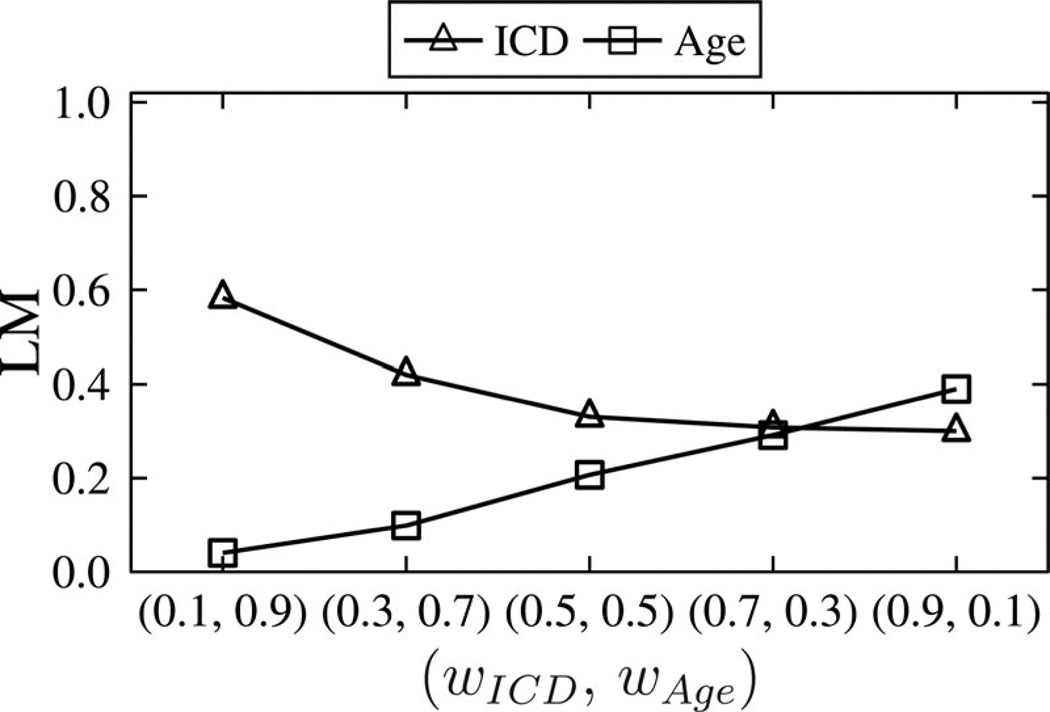
Finally, we investigated how configurations of attribute weighting affect information loss. Fig. 8 reports the results for and k = 2 when our algorithm is configured with weights ranging from 0.1 to 0.9. Observe that when wICD = 0.1 and wAge = 0.9, A-GS distorted Age values much less than ICD values. Similarly, A-GS incurred less information loss for ICD than Age when we specified wICD = 0.9 and wAge = 0.1. This result implies that data managers can use weights to achieve desired utility for either attribute.
Fig. 8.
A comparison of information loss for using various wICD and wAge values.
VI. Discussion
In this section, we discuss how our approach can be extended to prevent a privacy threat in addition to reidentification and its limitations.
A. Attacks Beyond Reidentification
Beyond reidentification is the threat of sensitive itemset disclosure, in which a patient is associated with a set of diagnosis codes that reveal some sensitive information (e.g., HIV status). k-Anonymity does not guarantee prevention of sensitive itemset disclosure, since a large number of records that are indistinguishable with respect to the potentially identifying diagnosis codes can still contain the same sensitive itemset [59]. We note that our approach can be extended to prevent this attack by controlling generalization and suppression to ensure that an additional principle is satisfied, such as ℓ-diversity [60], which dictates how sensitive information is grouped. This extension, however, is beyond the scope of this paper.
B. Limitations
The proposed approach is limited in certain aspects, which we highlight to suggest opportunities for further research. First, our algorithm induces minimal distortion to the data in practice, but it does not limit the amount of information loss incurred by generalization and suppression. Designing algorithms that provide this type of guarantee is important to enhance the quality of anonymized GWAS-related datasets, but is also computationally challenging due to the large search spaces involved, particularly for longitudinal data. Second, the approach we propose does not guarantee that the released data remain useful for scenarios in which prespecified analytic tasks, such as the validation of known GWAS [22], are known to data owners a priori. To address such scenarios, we plan to design algorithms that take the tasks for which data are anonymized into account during anonymization.
VII. Conclusion and Future Work
This study was motivated by the growing need to disseminate patient-specific longitudinal data in a privacy-preserving manner. To the best of our knowledge, we introduced the first approach to sharing such data while providing computational privacy guarantees. Our approach uses sequence alignment and clustering-based heuristics to anonymize longitudinal patient records. Our investigations suggest that it can generate longitudinal data with a low level of information loss and remain useful for biomedical analysis. This was illustrated through extensive experiments with data derived from the EMRs of thousands of patients. The approach is not guided by specific utility (e.g., satisfaction of GWAS validation), but we are confident it can be extended to support such endeavors.
Acknowledgment
The authors would like to thank A. Gkoulalas-Divanis (IBM Research) for helpful discussions on the formulation of this problem.
This work was supported by the National Institutes of Health under Grant U01HG006378, Grant U01HG006385, and Grant R01LM009989, and by a Fellowship from the Royal Academy of Engineering Research.
Appendix A
Information Loss Incurred by Anonymizing the Datasets Using A-GS
| ILM | ALM | ILM | ALM | ILM | ALM | ||||
|---|---|---|---|---|---|---|---|---|---|
| k = 2 | 0.33 | 0.21 | 0.11 | 0.10 | 0.17 | 0.16 | |||
| k = 5 | 0.54 | 0.35 | 0.21 | 0.22 | 0.33 | 0.34 | |||
| k = 10 | 0.62 | 0.40 | 0.25 | 0.30 | 0.40 | 0.46 | |||
| k = 15 | 0.64 | 0.42 | 0.28 | 0.34 | 0.44 | 0.51 | |||
Appendix B
Measuring Data Utility Using Query Workloads
The AvgRE measure captures the accuracy of answering queries on an anonymized dataset. The queries we consider can be modeled as follows:
Q: SELECT COUNT(*)
FROM dataset
WHERE (u ∈ ICD, v ∈ Age) ∈ dataset, …
Let 𝒜(Q) be the answer of a COUNT() query Q when it is issued on the original dataset. The value of 𝒜(Q) can be easily obtained by counting the number of trajectories in the original dataset that contain the (ICD, Age) pairs in Q.
Let e(Q) be the answer of Q when it is issued on the anonymized dataset. This is an estimate because a generalized value is interpreted as any leaf node in the subtree rooted by that value in the DGH. Therefore, an anonymized pair may correspond to any pair of possible ICD codes and Age values, assuming each pair is equally likely. The value of e(Q) can be obtained by computing the probability that a trajectory in the anonymized dataset satisfies Q, and then summing these probabilities across all trajectories.
To illustrate how an estimate can be computed, assume that a data recipient issues a query for the number of patients diagnosed with ICD code 401.1 at age 39 using the anonymized dataset in Fig. 1(c). Referring to the DGHs in Figs. 3 and 4, it can be seen that the only trajectories that may contain (401.1, 39) are the last two since they contain the generalized pair (401.1, [39 – 40]). Furthermore, observe that 401.1 is a leaf node in Fig. 4; hence, the set of possible ICD codes is {401.1}. Similarly, the subtree rooted by [39 – 40] in Fig. 3 consists of two leaf nodes, hence the set of possible Age values is {39,40}. Therefore, there are two possible pairs: {(401.1, 39), (401.1,40)}, and the probability that one of the trajectories was originally harboring (401.1, 39) is . Then, an approximate answer for the query is computed as .
The Relative Error (RE) for an arbitrary query Q is computed as RE(Q) = |a(Q)−e(Q)|/a(Q). For instance, the RE for the previous example query is |1 − 1|/1 = 0 since the original dataset in Fig. 1(a) contains one trajectory with (401.1, 39).
The AvgRE for a workload of queries is the mean RE of all issued queries. It reflects the mean error in answering the query workload.
Footnotes
We use the term trajectory since the diagnosis codes at different ages can be seen as a route for the patient throughout his/her life.
Contrary to a set, a multiset can contain an element more than once.
More information is available at http://www.cdc.gov/nchs/icd.htm
HIPAA Safe Harbor states all ages under 89 can be retained intact, while 90 or greater must be grouped together.
We further note that our approach is extendible to other categorical attributes, such as SNOMED-CT and Date, provided that a DGH can be specified for each of the attributes. Such extensions, however, are beyond the scope of this paper.
ILM(X) and ALM(X) are provided as input because X may already be an anonymized version of two other trajectories.
We refer to our algorithm as MDAV′ to avoid confusion.
Contributor Information
Acar Tamersoy, Email: acar.tamersoy@vanderbilt.edu, Department of Biomedical Informatics, Vanderbilt University, Nashville, TN 37232 USA.
Grigorios Loukides, Email: g.loukides@cs.cf.ac.uk, School of Computer Science and Informatics, Cardiff University, Cardiff, CF24 3AA, U.K..
Mehmet Ercan Nergiz, Email: mehmet.nergiz@zirve.edu.tr, Department of Computer Engineering, Zirve University, Gaziantep 27260, Turkey.
Yucel Saygin, Email: ysaygin@sabanciuniv.edu, Department of Computer Science and Engineering, Sabanci University, Istanbul 34956, Turkey.
Bradley Malin, Email: b.malin@vanderbilt.edu, Department of Biomedical Informatics, Vanderbilt University, Nashville, TN 37232 USA.
References
- 1.Blumenthal D. Stimulating the adoption of health information technology. New Engl. J. Med. 2009;vol. 360(no. 15):1477–1479. doi: 10.1056/NEJMp0901592. [DOI] [PubMed] [Google Scholar]
- 2.Ludwick DA, Doucette J. Adopting electronic medical records in primary care: Lessons learned from health information systems implementation experience in seven countries. Int. J. Med. Informat. 2009;vol. 78:22–31. doi: 10.1016/j.ijmedinf.2008.06.005. [DOI] [PubMed] [Google Scholar]
- 3.Jha AK, DesRoches CM, Campbell EG, Donelan K, Rao SR, Ferris TG, Shields A, Rosenbaum S, Blumenthal D. Use of electronic health records in U.S. hospitals. New Engl. J. Med. 2009;vol. 360:1628–1638. doi: 10.1056/NEJMsa0900592. [DOI] [PubMed] [Google Scholar]
- 4.Dean BB, Lam J, Natoli JL, Butler Q, Aguilar D, Nordyke RJ. Review: Use of electronic medical records for health outcomes research: A literature review. Med. Care Res. Rev. 2009;vol. 66:611–638. doi: 10.1177/1077558709332440. [DOI] [PubMed] [Google Scholar]
- 5.Holzer K, Gall W. Utilizing IHE-based electronic health record systems for secondary use. Methods Inf. Med. 2011;vol. 50(no. 4):319–325. doi: 10.3414/ME10-01-0060. [DOI] [PubMed] [Google Scholar]
- 6.Safran C, Bloomrosen M, Hammond W, Labkoff S, Markel-Fox S, Tang P, Detmer DE. Toward a national framework for the secondary use of health data: An American medical informatics association white paper. J. Amer. Med. Informat. Assoc. 2007;vol. 14:1–9. doi: 10.1197/jamia.M2273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tu K, Mitiku T, Guo H, Lee DS, Tu JV. Myocardial infarction and the validation of physician billing and hospitalization data using electronic medical records. Chron. Diseases Canada. 2010;vol. 30:141–146. [PubMed] [Google Scholar]
- 8.McCarty CA, Chisholm RL, Chute CG, Kullo IJ, Jarvik GP, Larson EB, Li R, Masys DR, Ritchie MD, Roden DM, Struewing JP, Wolf WA. The eMERGE network: A consortium of biorepositories linked to electronic medical records data for conducting genomic studies. BMC Med. Genomics. 2011;vol. 4:13–23. doi: 10.1186/1755-8794-4-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kullo IJ, Ding K, Jouni H, Smith CY, Chute CG. A genome-wide association study of red blood cell traits using the electronic medical record. Public Library Sci. ONE. 2010;vol. 5:e13011. doi: 10.1371/journal.pone.0013011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pacheco JA, Avila PC, Thompson JA, Law M, Quraishi JA, Greiman AK, Just EM, Kho A. A highly specific algorithm for identifying asthma cases and controls for genome-wide association studies. Proc Amer. Med. Informat. Assoc. Annu. Symp. 2009:497–501. [PMC free article] [PubMed] [Google Scholar]
- 11.Ritchie MD, Denny JC, Crawford DC, Ramirez AH, Weiner JB, Pulley JM, Basford MA, Brown-Gentry K, Balser JR, Masys DR, Haines JL, Roden DM. Robust replication of genotype-phenotype associations across multiple diseases in an electronic medical record. Amer. J. Human Genet. 2010;vol. 86(no. 4):560–572. doi: 10.1016/j.ajhg.2010.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liebman MN. Personalized medicine: A perspective on the patient disease and causal diagnostics. Personal. Med. 2007;vol. 4(no. 2):171–174. doi: 10.2217/17410541.4.2.171. [DOI] [PubMed] [Google Scholar]
- 13.Tucker A, Garway-Heath D. The pseudotemporal bootstrap for predicting glaucoma from cross-sectional visual field data. IEEE Trans. Inf. Technol. Biomed. 2010 Jan;vol. 14(no. 1):79–85. doi: 10.1109/TITB.2009.2023319. [DOI] [PubMed] [Google Scholar]
- 14.Jensen S. Mining medical data for predictive and sequential patterns; Proc. 5th Eur. Conf. Principles Pract. Knowl. Discov. Databases; 2001. pp. 1–10. [Google Scholar]
- 15.Burton PR, Hansell AL, Fortier I, Manolio TA, Khoury MJ, Little J, Elliott P. Size matters: Just how big is big? Quantifying realistic sample size requirements for human genome epidemiology. Int. J. Epidemiol. 2009;vol. 38:263–273. doi: 10.1093/ije/dyn147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Spencer CC, Su Z, Donnelly P, Marchini J. Designing genome-wide association studies: Sample size, power, imputation, and the choice of genotyping chip. Public Library Sci. Genet. 2009;vol. 5(no. 5):e1000477. doi: 10.1371/journal.pgen.1000477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nat. Inst. Health. Bethesda, MD: 2007. Policy for Sharing of Data Obtained in NIH Supported or Conducted Genome-Wide Association Studies (GWAS) NOT-OD-07-088. [Google Scholar]
- 18.Mailman MD, Feolo M, Jin Y, Kimura M, Tryka K, Bagoutdinov R, Hao L, Kiang A, Paschall J, Phan L, Popova N, Pretel S, Ziyabari L, Lee M, Shao Y, Wang ZY, Sirotkin K, Ward M, Kholodov M, Zbicz K, Beck J, Kimelman M, Shevelev S, Preuss D, Yaschenko E, Graeff A, Ostell J, Sherry ST. The NCBI dbgap database of genotypes and phenotypes. Nature genet. 2007;vol. 39(no. 10):1181–1186. doi: 10.1038/ng1007-1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Standards for Protection of Electronic Health Information. Washington, DC: Federal Register, Dept. Health, Human Services; 2003. p. 45. CFR Pt. 164. [Google Scholar]
- 20.Benitez K, Malin B. Evaluating re-identification risks with respect to the HIPAA privacy rule. J. Amer. Med. Informat. Assoc. 2010;vol. 17(no. 2):169–177. doi: 10.1136/jamia.2009.000026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Loukides G, Denny JC, Malin B. The disclosure of diagnosis codes can breach research participants’ privacy. J. Amer. Med. Informat. Assoc. 2010;vol. 17(no. 3):322–327. doi: 10.1136/jamia.2009.002725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Loukides G, Gkoulalas-Divanis A, Malin B. Anonymization of electronic medical records for validating genome-wide association studies. Proc. Nat. Acad. Sci. 2010;vol. 107(no. 17):7898–7903. doi: 10.1073/pnas.0911686107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Loukides G, Gkoulalas-Divanis A, Malin B. Privacy-preserving publication of diagnosis codes for effective biomedical analysis; Proc. 10th IEEE Int. Conf. Inf. Technol. Appl. Biomed; 2010. pp. 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Sweeney L. k-anonymity: A model for protecting privacy. Int. J. Uncertainty, Fuzz. Knowl.-Based Syst. 2002;vol. 10(no. 5):557–570. [Google Scholar]
- 25.Fung BCM, Wang K, Chen R, Yu PS. Privacy-preserving data publishing: A survey of recent developments. ACM Comput. Surv. 2010;vol. 42(no. 4):1–53. [Google Scholar]
- 26.Chen B-C, Kifer D, LeFevre K, Machanavajjhala A. Privacy-preserving data publishing. Found. Trends Databases. 2009;vol. 2(no. 1–2):1–167. [Google Scholar]
- 27.Sandhu RS, Coyne EJ, Feinstein HL, Youman CE. Role-based access control models. IEEE Comput. 1996 Feb;vol. 29(no. 2):38–47. [Google Scholar]
- 28.Pinkas B. Cryptographic techniques for privacy-preserving data mining. ACM Spec. Interest Group Knowl. Discov. Data Mining Explorat. 2002;vol. 4(no. 2):12–19. [Google Scholar]
- 29.Diesburg SM, Wang A-IA. A survey of confidential data storage and deletion methods. ACM Comput. Surv. 2010;vol. 43(no. 1):1–37. [Google Scholar]
- 30.Adam NR, Wortmann JC. Security-control methods for statistical databases: A comparative study. ACM Comput. Surv. 1989;vol. 21(no. 4):515–556. [Google Scholar]
- 31.Aggarwal CC, Yu PS. Privacy-Preserving Data Mining: Models and Algorithms (ser. Advances in Database Systems) vol. 34. New York: Springer-Verlag; 2008. A survey of randomization methods for privacy-preserving data mining; pp. 137–156. [Google Scholar]
- 32.Willenborg L, De Waal T. Statistical Disclosure Control in Practice (ser. Lecture Notes in Statistics) vol. 111. New York: Springer-Verlag; 1996. pp. 1–152. [Google Scholar]
- 33.Marsden-Haug N, Foster V, Gould P, Elbert E, Wang H, Pavlin J. Code-based syndromic surveillance for influenzalike illness by international classification of diseases, ninth revision. Emerg. Infect. Diseases. 2007;vol. 13:207–216. doi: 10.3201/eid1302.060557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Samarati P. Protecting respondents’ identities in microdata release. IEEE Trans. Knowl. Data Eng. 2001 Nov-Dec;vol. 13(no. 6):1010–1027. [Google Scholar]
- 35.El Emam K, Dankar FK, Issa R, Jonker E, Amyot D, Cogo E, Corriveau JP, Walker M, Chowdhury S, Vaillancourt R, Roffey T, Bottomley J. A globally optimal k-anonymity method for the de-identification of health data. J. Amer. Med. Informat. Assoc. 2009;vol. 16(no. 5):670–682. doi: 10.1197/jamia.M3144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.LeFevre K, DeWitt DJ, Ramakrishnan R. Mondrian multidimensional k-anonymity,” in; Proc. 22nd IEEE Int. Conf. Data Eng; 2006. pp. 25–35. [Google Scholar]
- 37.Dalenius T. Finding a needle in a haystack—or identifying anonymous census record. J. Offic. Statist. 1986;vol. 2(no. 3):329–336. [Google Scholar]
- 38.Nergiz ME, Clifton C. Thoughts on k-anonymization. Data Knowl. Eng. 2007;vol. 63(no. 3):622–645. [Google Scholar]
- 39.Loukides G, Shao J. Capturing data usefulness and privacy protection in k-anonymisation; Proc. 22nd ACM Symp. Appl. Comput; 2007. pp. 370–374. [Google Scholar]
- 40.Iyengar VS. Transforming data to satisfy privacy constraints; Proc. 8th ACM Int. Conf. Knowl. Discov. Data Mining; 2002. pp. 279–288. [Google Scholar]
- 41.El Emam K, Dankar FK. Protecting privacy using k-anonymity. J. Amer. Med. Informat. Assoc. 2008;vol. 15(no. 5):627–637. doi: 10.1197/jamia.M2716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Terrovitis M, Mamoulis N, Kalnis P. Privacy-preserving anonymization of set-valued data. Proc. Very Large Data Bases Endowment. 2008;vol. 1(no. 1):115–125. [Google Scholar]
- 43.Tamersoy A, Loukides G, Denny JC, Malin B. Anonymization of administrative billing codes with repeated diagnoses through censoring. Proc. Amer. Med. Informat. Assoc. Annu. Symp. 2010:782–786. [PMC free article] [PubMed] [Google Scholar]
- 44.Nergiz ME, Atzori M, Saygin Y, Guc B. Towards trajectory anonymization: A generalization-based approach. Trans. Data Privacy. 2009;vol. 2(no. 1):47–75. [Google Scholar]
- 45.Abul O, F Bonchi, Nanni M. Never walk alone: Uncertainty for anonymity in moving objects databases; Proc. 24nd IEEE Int. Conf. Data Eng; 2008. pp. 376–385. [Google Scholar]
- 46.Terrovitis M, Mamoulis N. Privacy preservation in the publication of trajectories; Proc. 9th Int. Conf. Mobile Data Manag; 2008. pp. 65–72. [Google Scholar]
- 47.Sweeney L. Achieving k-anonymity privacy protection using generalization and suppression. Int. J. Uncertainty, Fuzz. Knowl.-Based Syst. 2002;vol. 10(no. 5):571–588. [Google Scholar]
- 48.Aggarwal CC, Yu PS. A condensation approach to privacy preserving data mining; Proc. 9th Int. Conf. Extend. Database Technol; 2004. pp. 183–199. [Google Scholar]
- 49.Aggarwal G, Feder T, Kenthapadi K, Khuller S, Panigrahy R, Thomas D, Zhu A. Achieving anonymity via clustering; Proc. 25th ACM Symp. Principles Database Syst; 2006. pp. 153–162. [Google Scholar]
- 50.Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Molecular Biol. 1970;vol. 48(no. 3):443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- 51.F Smith T, Waterman MS. Identification of common molecular subsequences. J. Molecular Biol. 1981;vol. 147(no. 1):195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- 52.Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to Algorithms. 2nd ed. Cambridge, MA: MIT Press; 2001. [Google Scholar]
- 53.Domingo-Ferrer J, Mateo-Sanz JM. Practical data-oriented microaggregation for statistical disclosure control. IEEE Trans. Knowl. Data Eng. 2002 Jan-Feb;vol. 14(no. 1):189–201. [Google Scholar]
- 54.Domingo-Ferrer J, Torra V. Ordinal, continuous and heterogeneous k-anonymity through microaggregation. Data Mining Knowl. Discov. 2005;vol. 11(no. 2):195–212. [Google Scholar]
- 55.Roden DM, Pulley JM, Basford MA, Bernard GR, Clayton EW, Balser JR, Masys DR. Development of a large-scale de-identified DNA biobank to enable personalized medicine. Clin. Pharmacol. Ther-apeut. 2008;vol. 84(no. 3):362–369. doi: 10.1038/clpt.2008.89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ramirez AH, Schildcrout JS, Blakemore DL, Masys DR, Pulley JM, Basford MA, Roden DM, Denny JC. Modulators of normal electrocardiographic intervals identified in a large electronic medical record. Heart Rhythm. 2011;vol. 8(no. 2):271–277. doi: 10.1016/j.hrthm.2010.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Denny JC, Ritchie MD, Crawford DC, Schildcrout JS, Ramirez AH, Pulley JM, Basford MA, Masys DR, Haines JL, Roden DM. Identification of genomic predictors of atrioventricular conduction: Using electronic medical records as a tool for genome science. Circulation. 2010;vol. 122:2016–2021. doi: 10.1161/CIRCULATIONAHA.110.948828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Aggarwal CC. On k-anonymity and the curse of dimensionality; Proc. 31st Int. Conf. Very Large Data Bases; 2005. pp. 901–909. [Google Scholar]
- 59.Y Xu, Wang K, Fu AW-C, Yu PS. Anonymizing transaction databases for publication; Proc. 14th ACM Int. Conf. Knowl. Discov. Data Mining; 2008. pp. 767–775. [Google Scholar]
- 60.Machanavajjhala A, Gehrke J, Kifer D, Venkitasubramaniam M. ℓ-diversity: Privacy beyond k-anonymity; Proc. 22ndIEEE Int. Conf. Data Eng; 2006. pp. 24–35. [Google Scholar]