A Novel Kernel for Correcting Size Bias in the Logistic Kernel Machine Test with an Application to Rheumatoid Arthritis

Abstract

Objectives

The logistic kernel machine test (LKMT) is a testing procedure tailored towards high-dimensional genetic data. Its use in pathway analyses of GWA case-control studies results from its computational efficiency and flexibility of incorporating additional information via the kernel. The kernel can be any positive definite function; unfortunately its form strongly influences the power and bias. Most authors have recommended the use of the simple linear kernel. We demonstrate via a simulation that the probability of rejecting the null hypothesis of no association just by chance increases with the number of SNPs or genes in the pathway when applying this kernel.

Methods

We propose a novel kernel that includes an appropriate standardization, in order to protect against any inflation of false positive results. Moreover, our novel kernel contains information on gene membership of SNPs in the pathway.

Results

In an application to data from the NARAC Rheumatoid Arthritis Consortium, we find that even this basic genomic structure can improve the ability of the LKMT to identify meaningful associations. We also demonstrate that the standardization effectively eliminates problems with size bias.

Conclusion

We recommend the use of our standardized kernel and urge caution when using non-adjusted kernels in the LKMT to conduct pathway analysis.

1 Introduction

Conventional genome-wide searches for associations between a single SNP and a complex disease have recently been complemented by pathway-based association analysis [1]. Pathway-based analysis aims to identify associations between networks of genes and the investigated disease. Growing experimental evidence suggests that common diseases are caused by many genes organized in highly interconnected networks rather than individual genes. Such networks typically represent key functions of the biological processes involved in building and sustaining an organism. Thus, pathway-based analyses can help to provide biologically meaningful interpretations [2] and may even highlight promising candidates for therapeutic intervention. They take full advantage of the wide opportunities provided by genome-wide association (GWA) studies, while helping to overcome the main challenges of GWA studies. Grouping SNPs in biologically meaningful sets improves otherwise low power. Firstly, the number of tests conducted is reduced, allowing a less stringent significance threshold. Secondly, joint activity of multiple moderately associated SNPs in the same pathway will be detected with a higher probability than in the single marker setting [3]. Finally, pathways might account for genetic heterogeneity, as most SNPs in the same pathway contribute towards one particular biological function.

The field of pathway analysis has seen a marked increase in progress, instigated by sustained methodological research. In this paper, we focus on one of these pathway-based methods - the logistic kernel machine test (LKMT), a semiparametric kernel-based testing procedure [4]. This procedure belongs to a branch of machine learning tools known as kernel methods, which have proven extremely valuable in the analysis of high dimensional data. Furthermore, they perform well without the need to specify correctly the functional relationship between the effects of SNPs in a pathway and the disease status. It is well known that genes, and therefore SNPs, in the same pathway do not convey disease risk independently of each other; instead they are often involved in disease susceptibility and progression through complex networks. Such interactions between SNPs are difficult to accommodate in alternative regression-based methods without incurring sizeable power losses. In the LKMT, such relationships can be easily allowed for through the specification of an appropriate kernel function. Additionally, the LKMT is computationally efficient and permits the seamless integration of covariate effects. Its validity and good performance have been demonstrated in various genetic scenarios [4, 5, 6].

In this framework, the kernel acts as the core of the LKMT. We demonstrate here that the commonly used kernels introduce bias. This bias, which manifests itself in an inflation of the type I error, results from differently sized pathways. Size refers to either the number of SNPs or the number of genes that belong to a pathway. This particular type of bias has long been known to exist for many alternative pathway-based methods [1]. It is usually accounted for by computationally costly permutations. Here, we propose a different strategy that requires considerably less computational time than permutation strategies by using novel kernels with a correction for the expected size bias.

We applied the LKMT to real GWA data from the North American Rheumatoid Arthritis Consortium (NARAC) [7]. Rheumatoid arthritis (RA) is one of the few complex diseases in which GWA studies have been able to identify many susceptibility genes [8]. However, only a limited number of links between genes and RA, apart from the pivotal human leukocyte antigen (HLA) region, have been demonstrated convincingly. Furthermore, immune response, which involves multiple positive and negative genetic regulators, critically determines development and progression of inflammatory diseases such as RA [2]. This makes RA data an interesting data set in the development of pathway-based methods. Our analysis with the LKMT identifies many pathways that include already known susceptibility genes. This does not merely confirm previously established results, but has the potential of revealing compelling functional connections through the network structure. Moreover, we identified novel associations with pathways for ATP binding cassette (ABC) transporters and extracellular matrix (ECM) receptor interaction. We found these associations particularly intriguing, as these pathways are known to be involved in many inflammatory diseases.

The remainder is organized as follows. In the next Section (2), we give a brief description of the LKMT and outline the proposed new kernel functions. Then we present simulation results confirming the existence of size bias for p-values obtained by the LKMT with existing kernel functions. We conducted simulation studies focusing exclusively on the scenario of no real genetic effect, since simulating scenarios with comparable true genetic effect for different pathway length is extremely challenging. Furthermore, there exists little knowledge concerning the exact interaction structures causing disease. Size bias is also demonstrated for the LKMT with some kernel functions based on our real RA data. Moreover, we compare results from the LKMT to results from two other pathway-based methods. Finally, we discuss our findings and their implications for RA research.

2 Methods

2.1 Logistic Kernel Machine Test

Liu et al. [4] in 2008 were the first to apply the kernel machine framework to genetic pathways in GWA studies. In 2010, Wu et al.[5] demonstrated via a gene-based simulation study that this framework indeed allows for powerful and flexible analysis.

One of the appeals of the kernel machine framework is its ability to deal with high dimensionality - the number of explanatory variables is much greater than the number of samples. High dimensionality is usually addressed through penalization, i.e. by minimizing a loss function plus a positive, increasing penalty function. In the kernel machine framework, this penalty is selected according to the scalar product of the reproducing kernel Hilbert space (RKHS), H_K. Such a minimization problem has a solution of the form $f\left(x\right)={\stackrel{\sim }{\alpha }}^{T}K\left(x\right)$, where $\stackrel{\sim }{\alpha }$ represents a vector of unknown parameters and K(x) is a vector of functions produced by the kernel function K (representer theorem) [9]. Here we consider the function space H_K as being generated by the kernel function K in the sense that H_K is the closure of all linear combinations $f\left(x\right)={\stackrel{\sim }{\alpha }}^{T}K\left(x\right)$. Any positive definite function K is allowed, thus a wide range of statistical models is subsumed without the need to specify correctly their functional forms. Furthermore, such a penalization with a maximum likelihood loss function can be shown to be equivalent to generalized linear mixed models and thus allows the use of the rapidly computed score test. In the following, we will briefly explain how this reasoning yields the LKMT in the specific scenario of genetic pathway analysis.

We assume that a population-based case-control GWA study with n individuals was conducted. Let the pathway p contain l_p SNPs with genotype values z_i1, …, z_ilp for the i^th subject, which are coded in a ternary fashion corresponding to the number of minor alleles. The case-control status for the i^th individual is denoted by y_i. Furthermore, for every individual, an additional set of m informative covariates x_i1, …, x_im was collected. The LKMT assumes a semiparametric model given by logit (P(y_i = 1)) = β₀ + β₁x_i1 + ⋯ +β_mx_im+h(z_i1, z_ilp), where β₀, β₁,…, β_m are intercept and regression coefficient terms, also summarised as the vector β. The function h∈H_k describes the influence of the SNPs on the logit of the probability of being a case. Omitting mathematical details, the above model can be shown to be equivalent to a hierarchically expressed generalized linear mixed model (GLMM) of the following form [4];

$$\begin{array}{l}\text{logit }\left(P\right(y_i=1\left)\right)={\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_m{x}_{im}+b_i\\ b~N(0,{\sigma }_K^2\text{K}).\end{array}$$ (1)

The random regression coefficient vector b has a multivariate normal distribution with mean vector 0 and variance matrix ${\sigma }_K^{2}K$. The matrix K results from applying the kernel function K to every combination of individual pairs in the data set. This hierarchical expression, common in the Bayesian perspective, allows the kernel matrix to be interpreted as a prior covariance structure [9].

In the context of genetic epidemiology, we are interested as to whether or not there is an overall genetic pathway effect, i.e. H₀: h(z_p)= 0, where z_p is the genotype matrix for pathway p. Taking advantage of the connection to generalized linear mixed models, such a null hypothesis is equivalent to testing no variance component, i.e. $H_0:{\sigma }_K^2=0$. This can proceed via a score test, which has been demonstrated as being quite powerful in such situations [4]. Moreover, we only need to estimate β under the null hypothesis, saving considerable computational effort. The test statistics can be expressed by

$$Q=\frac{1}{2}{(y-\widehat{\mu })}^T\text{K}(y-\widehat{\mu })$$ (2)

where y is the vector of the n responses, y = (y₁, …, y_n), and $\widehat{\mu }$ is a vector with elements ${\widehat{\mu }}_i={\text{logit }}^{-1}({\beta }_0+{\beta }_1{x}_{i1}+\cdots +{\beta }_m{x}_{im})$, the maximum likelihood estimate under the null for the i^th individual. The distribution ofQ is a complicated mixture of distributions. Fortunately, it can be well approximated using a Satterthwaite procedure, which allows the approximate calculation of the effective degrees of freedom of a linear combination of ${\chi }_1^2$ distributions (for more details see Wu et al.[5]).

2.2 Existing Kernels for Genomic Information in Pathways

In genetic epidemiology, kernel functions are constructed to convert genomic information from two individuals to a quantitative value reflecting their genetic similarity or dissimilarity [10]. Beside the requirement that the kernel must be a positive definite function, no mathematical guidelines for the creation of kernels exist. This immense flexibility makes the construction of meaningful kernels challenging. Since the kernel defines the whole set of correlation coefficients between individuals, its choice strongly influences the power of the method [9, p. 118]. So a kernel function that does not anticipate the nature of the true effect will lose efficiency.

Authors implementing the LKMT for GWA studies have advocated the use of either the linear (LIN) or identity-by-state (IBS) kernels [4, 5]. The LIN kernel is given by $K(z_i,z_j)={\displaystyle {\sum }_{k=1}^{l_p}{z}_{ik}{z}_{jk}}$ for subject i and j. The function space H defined by this kernel implies the usual multiple marker logistic regression model. The IBS kernel uses the numbers of alleles shared between two individuals as a similarity metric, $K(z_i,z_j)={\displaystyle {\sum }_{k=1}^{l_p}\frac{2I(z_{ik}=z_{jk})+I\left(\right|z_{ik}-z_{jk}|=1)}{2l_p}}$. Although the set of corresponding functions for this kernel is unknown, Wu et al. [5] demonstrated in their simulation study that this kernel has adequate power for more complex genetic relationships.

Despite their frequent use, both kernels suffer from deflation of p-values due to size bias. The bias results from the tendency of larger pathways to have more variability among their kernel matrix entries. When calculated by either the IBS or LIN kernel, the probability of two values of the similarity metric differing, increases with the dimension l_p. Since SNPs cumulatively add to the value of the metric, two similarity metrics are more likely to be different when more SNPs contribute. Thus, using both the LIN and IBS kernel the probability that we reject the null hypothesis by chance increases. Note that the numerical constraint of the IBS kernel does not serve as a correction because it represents a constant scale factor. Since a constant scale factor would be subsumed ${\sigma }_K^2$, it has no effect on the magnitude of the resulting p-value. Schaid et al. [11] further noted that ”[t]he magnitude of this bias depends not only on the number of SNPs in a [pathway] but also on the correlations between the SNPs”.

Moreover, neither of the two kernel functions considers all available knowledge of the genetic architecture of pathways. Up to now, the prior genomic information is confined to pure SNP membership in pathways. However, it is conceivable that the incorporation of even the simplest genomic structure could improve power significantly.

2.3 Construction of Novel Kernels for Genomic Information in Pathways

The construction of a novel kernel allows to simultaneously address all shortcomings mentioned in the previous section. In particular, we aim to construct kernels that produce p-values invariant to the size of the pathway. We also decided to account for membership of SNPs in genes. To obtain kernels with these properties, we build on the experience with positive definite functions in the field of spatial statistics. In recent years, methods originating from this field, such as kriging, have already been successfully applied in animal genetics [12].

We suggest the variogram value between two individuals i and j given by ${\gamma }_{i,j}^g={\left(\frac{{\Vert z_i^g-z_j^g\Vert }^2}{s_g}\right)}^{{\delta }_g}$ as a measure for the genetic distance between individuals; for a particular gene g. The vectors $z_i^g$ and $z_j^g$ in the squared norm denote the vectors of genotype values of SNPs contained in gene g;δ_g and s_g are parameters with restrictions 0 < δ_g ≤ 1 and s_g> 0. Schoenberg’s relation [13] now nicely suggests a kernel, which enables us to correct for the number of SNPs in the gene: The kernel related to the variogram ${\gamma }_{i,j}^g$ is $C\left({\gamma }_{i,j}^g\right)=\text{exp}\left(-{\gamma }_{i,j}^g\right)$, which is called the stable kernel or the powered exponential kernel. Choosing

$${\delta }_g=\sqrt{\frac{k_g}{{\max }_{g\in p}{k}_g}}\in [0,1]$$ (3)

and

$$s_g={\widehat{\mu }}_g{k}_g$$ (4)

for each gene g, we can keep the mean and variance of $C\left({\gamma }_{i,j}^g\right)$ pretty much constant across all genes in a pathway (see Section A of the supplementary material). Here, the scalar k_g equals to the number of SNPs contained in gene g; ${\widehat{\mu }}_g$ denotes the empirical expectation of the squared norm calculated from two genotype vectors of size one SNP.

Using the principle that the set of positive definite functions is closed under addition and multiplication, we obtain the kernels

$$K(z_i^g,z_j^g)={\displaystyle \sum _{g\in p}C({\gamma }_{i,j}^g)={\displaystyle \sum _{g\in p}\text{exp}(-{\gamma }_{i,j}^g)}}$$ (5)

and

$$K(z_i^g,z_j^g)=\prod _{g\in p}C\left({\gamma }_{i,j}^g\right)=\prod _{g\in p}\text{exp}(-{\gamma }_{i,j}^g)$$ (6)

which we call the additive powered exponential (ADD) and multiplicative powered exponential (MULT) kernels. The addition over the genes in the same pathway implicitly assumes a linear influence of the genes on the phe-notype of interest. The multiplication over genes, on the other hand, assumes interactions.

Despite correcting for size bias on the gene level, neither the ADD nor the MULT kernel account for the number of genes in the pathway. Again this is a potential source of type I error inflation. Using the relationship between bounded variograms and kernels [14], we can find a kernel function for additive gene effects that includes a correction regarding the number of contributing genes. The resulting standardized additive powered exponential kernel (STAND.ADD) is defined as

$$K(z_i^g,z_j^g)=1-{\left[\frac{{\displaystyle {\sum }_{g\in p}\{1-C({\gamma }_{i,j}^g)\}}}{r_p{\widehat{\mu }}_p}\right]}^{{\delta }_p}$$ (7)

, where r_p denotes the number of genes in pathway p and ${\widehat{\mu }}_p=\widehat{E}\{C({\gamma }_{i,j})\}$. Similar to the standardization within a gene, we choose ${\delta }_p=\sqrt{\frac{r_p}{{\max }_p{r}_p}}\in [0,1]$. Details on this standardization approach can be found in Section B of the supplementary material. We correct the MULT kernel by recognizing that equation 6 can easily be rewritten. Without changing the positive definite nature of this function, we can then introduce a correction factor $\sqrt{\frac{1}{r_p}}$ and obtain the standardized multiplicative powered exponential kernel (STAND.MULT):

$$K(z_i^g,z_j^g)=\text{exp}\left(-\sqrt{\frac{1}{r_p}}\sum _{g\in p}{\gamma }_{i,j}^g\right)$$ (8)

Details on this standardization approach can be found in Section C of the supplementary material.

We know that a large percentage of SNPs located in genes is in strong pairwise LD. Consequently, our assumption of independence is violated. Depending on the kernel, this could result in an increase in false positives or an increase in false negatives. We use the concept of effective number of independent SNPs in a region, introduced by Cheverud [15], to account for such dependencies in our standardization. He suggested measuring the total amount of correlation between SNPs by the variance of the eigenvalues obtained from their correlation matrix. If the SNPs are perfectly correlated, the variance of the eigenvalues will be maximised. When there is no correlation, the variance will equal 1. This means one can calculate the proportional reduction in the number of independent elements and thus an effective number of SNPs, k_g^eff. The LD-scaled versions of the standardized multiplicative (LD.STAND.MULT) and additive (LD.STAND.ADD) powered exponential kernels use this k_g^eff instead of k_g.

2.4 NARAC Rheumatoid Arthritis Data

We applied the LKMT with our novel kernel functions to real GWA data and compared our results with those achieved when using either the LIN or the IBS kernel. To demonstrate consistency and robustness of our method, we compared our results to those obtained by Sohns et al. [16] on the same data with two different pathway analysis methods.

The North American Rheumatoid Arthritis Consortium (NARAC) conducted a GWA study in 868 independent cases and 1,194 independent controls to identify genetic markers associated with RA risk [7]. All participants in this study gave IRB-approved informed consent to evaluate genetic predictors of risk for RA. All samples were genotyped at 545,080 loci with the HumanHap500v1 array. After stringent quality control, 866 cases, 1,189 controls and 492,209 additively coded SNPs on chromosomes 1 to 22 remained. Missing genotypes in loci with a genotype missing rate below 10% (other loci were previously excluded) were imputed using the software BEAGLE [17]. Imputed genotype dosages make the calculation of genomic similarities possible. Imputed genotype dosage can take any value between 0 and 2 reflecting the uncertainty of imputation.

The study design hints at some level of population stratification. Cases were predominately of Northern European ancestry. Controls were sampled in the New York Metropolitan area. Therefore in accordance with the New York ethnicity mix, controls were somewhat enriched for Southern European or Ashkenazi Jewish ancestry compared to the cases. Population stratification can introduce confounding and should therefore be accounted for in the analysis. Despite this, we did not specifically correct for population stratification, assuming instead that all analysed pathways included a sufficient number of null markers, i.e. those without true genetic effect. Setakis [18] demonstrated in a simulation study that the inclusion of such markers in a logistic regression model provides good protection against possible ramifications of population stratification; and stated ”…each of the [null markers] soaks up some of the effect of population stratification, but because this effect is shared across many markers, none of them is individually significant.” Since the logistic regression model with a random effect can be shown to be equivalent to the LKMT with the LIN kernel, we argue that population stratification is inherently taken care of.

We considered all pathways in the Kyoto Encyclopaedia of Genes and Genomes (KEGG) [19]. A SNP is mapped to a pathway only when it is located within one or more genes that belong to this particular pathway. Under these criteria, we were able to assemble 62,892 SNPs in 244 pathways. Summary statistics concerning this particular annotation can be found in Table 1. (We also tried more liberal assignments, but chose not to illustrate the results as they were qualitatively similar.) We tested each of the pathways under the LIN, IBS, STAND.MULT, STAND.ADD, LD.STAND.MULT and LD.STAND.ADD kernel. (The MULT and ADD kernels were not analysed, as they are clearly inferior.)

Table 1.

Summary statistics for all pathways in the analysis, when assignment of SNPs to pathways is strict (i.e. SNPs located in gene).

	# of SNPs in pathway	# of genes in pathway	# of genes with more than 10 SNPs in pathway
1st Quantile	199	21	6
Median	487	40	13
Mean	900	54.3	20.6
3rd Quantile	1227	68	31
Maximum	10,850	839	272

2.5 Comparing Different Pathway-Based Approaches Using the NARAC Data

To evaluate the performance of the LKMT with our novel kernels, we followed the analysis protocol by Sohns et al. [16] for the same data. They restricted the number of pathways to 100 candidate pathways. These were selected to include all top associations from a previously conducted single marker analysis. SNPs were assigned to genes when located either inside the gene or in a 500kbp window around transcription start or end. Sohns et al. [16] applied Hierarchical Bayes Prioritization (HBP) [20] and Gene-Set Enrichment Analysis (GSEA) [21] to the data. HBP is an empirical Bayes approach aiming to re-rank markers using prior covariates. GSEA assesses whether associated genes in a pathway are overrepresented. The approaches are conceptually as well as methodically different, thus serving as diverse benchmarks. Since the HLA complex has an unusually strong association with RA, the authors reanalysed the data, excluding all genes in the region between MOG and KIFC1. This allows for an assessment of performance beyond the implication of HLA. We analysed the 100 candidate pathways once when the HLA complex was included and once when it was excluded under the LD.STAND.MULT kernel function (as this turned out to be the most size-invariant kernel). In particular, we were interested in how similar the ranked lists obtained by the different methods are. In order to visualize similarities, we used a method introduced by Antosh et al. [22] in 2011. First, we ranked the results from each method from most significant to least significant. We then plotted the fraction of overlap between the lists produced by GSEA and LKMT as well as HBP and LKMT against the proportion of selected entries in these lists. Furthermore, we evaluated whether or not these overlaps are statistically significant.

2.6 Simulations to Assess Size Bias

In order to verify our theoretical ideas regarding size bias and the LIN kernel, we studied the LKMT by considering its empirical type I error for pathways of different sizes. For feasibility of implementation, we did not simulate a real pathway, considering instead the region between 239000 kbp and 247200 kbp on chromosome 1. Genotype data at 3500 loci (all with MAF > 5%) as well as case control status were simulated using HAPGEN2 [23] and the CEU sample of the International HapMap Project. Since HAPGEN2 simulates haplotypes based on reference data and fine-scale recombination rates, it preserves LD structures from the reference population. Thus, it closely mimics real genetic studies.

We considered 1,000 simulations with 1,000 cases and 1,000 controls. For each simulation, we applied the LKMT with the LIN kernel for different numbers of SNPs. We started with the first 250 SNPs and then increased this number at each turn by 250 until reaching 3,500 SNPs. For each configuration, we found the proportion of Bonferroni-adjusted p-values less than α = 0.01,0.05 and 0.1.

We also investigated the impact different pathway sizes have on the size of p-values calculated by the LKMT under all described kernels. Doing this via a simulation study would have proved to be computationally infeasi-ble. Therefore, we randomly formed ”pseudo-pathways” including different numbers of SNPs or genes from the real NARAC RA data. We executed this 50 times for each pathway size. We varied the number of randomly selected SNPs to be a member of our ”pseudo-pathways” from 100 to 800 (step size=100). In the gene-based analysis, we examined ”pseudo-pathways” containing between 10 and 50 genes (step size=10). In order to be able to separate gene size and SNP size, we excluded genes of size bigger than 200 SNPs in this scenario. For the sake of computational ease, we used the STAND kernels as a proxy for their LD-scaled versions.

3 Results

3.1 Inflation of Empirical Type I Error with Pathway Size

The empirical type I errors for the LKMT with the LIN kernel are presented in Figure 1. On the basis of our simulation the test has correct size for. The test appears to be too liberal for smaller values of α, such as α = 0.01. As suspected, we can observe inflation of the empirical size with an increasing number of SNPs located in the considered region. This phenomenon exists for all investigated type I error rates. Considering the frequently used level of 0.05, the type I error rate is not protected as soon as more than 1,250 SNPs are considered. For significantly fewer SNPs, the test even appears conservative. Note that this means that unless one does pathway analysis, where the number of SNPs in pathways easily exceeds 1,000 SNPs, the LIN kernel produces valid results. Thus, the application of the LKMT with the LIN or IBS kernel as a method of single gene analysis poses no problem.

Figure 1.

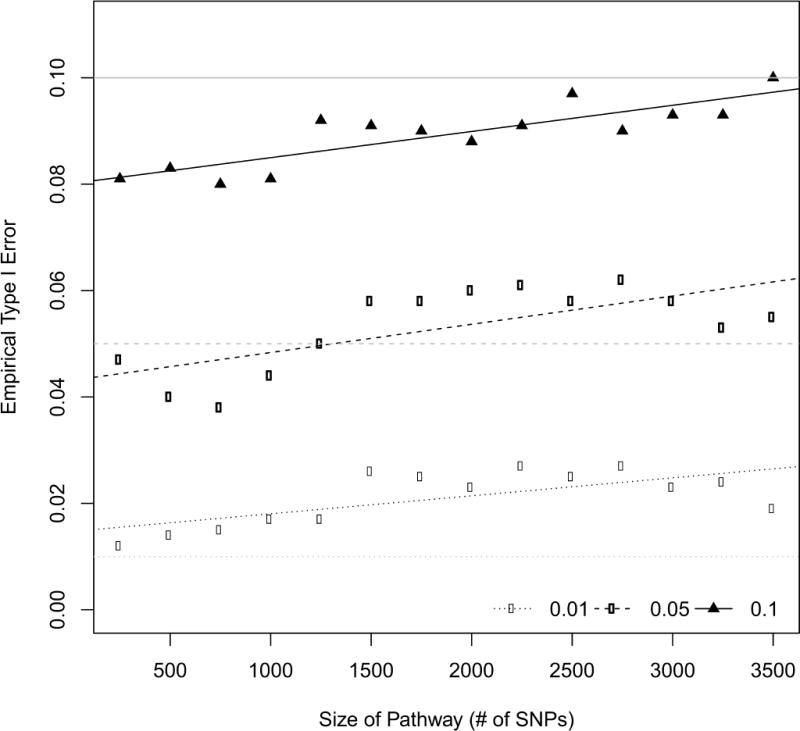
Empirical type I error rates at α = 0.01,0.05,0.1 for the LKMT with the linear kernel function when applied to regions of varying sizes based on 1000 simulations. Grey lines represent 0.01, 0.05 and 0.1, while the black lines are the regression lines estimated on the points.

3.2 Assessment of Size Bias Based on Randomly Sampled “Pseudo-Pathways”

The results from resampling ”pseudo-pathways” are summarized in Figure 2. If the number of SNPs is increased, the magnitude of the p-values for all investigated kernels decreases. However, the different kernel functions are not affected equally. The trend is most profound for the IBS kernel, while the ADD kernel seems to be the least affected. For all kernels, we observed an increase in the variability of the p-values when the number of SNPs in the ”pseudo pathway” rises. Since we did not remove SNPs that have any genuine influence on an individual’s RA risk, such an effect is to be expected. On the one hand, increasing the number of contributing SNPs increases the probability that a causal SNP will be sampled. On the other hand, many null markers are capable of diluting genuine genetic effects, as observed in simple linear regression. For linear regression, the p-value associated with the coefficient of a genuinely correlated variable increases when further un-informative variables are added to the model. Overall, these results suggest that accounting for the number of SNPs in a pathway does not offer sufficient protection against size bias. The right-hand panel of Figure 2 verifies this statement. P-values obtained from the LKMT with the ADD kernel decrease with an increasing number of genes. We do want to note that the scale of this effect is small compared to that observed, owing to an increase in the number of SNPs. For the STAND.ADD kernel, such an increase can also be observed when there are more than 30 genes in the pathways. In fact, when there are a large number of genes in the pathway, the STAND.ADD kernel seems to perform worse than the ADD kernel. The STAND.MULT kernel displays the opposite trend. The standardization works well up to 30 genes and then becomes overly conservative. For the strict SNP pathway assignment chosen here, around 25% of pathways have more than 30 genes and are thus affected (compare Table 1). If the assignment were chosen differently though, this could render the LKMT with this particular kernel structure ineffective. The multiplicative nature of the STAND.MULT kernel implies that genuine effects are diluted with a greater probability whenever more genes are added. Furthermore, it is possible that these trends can be explained partly by LD patterns that we fail to account for in this permutation study.

Figure 2.

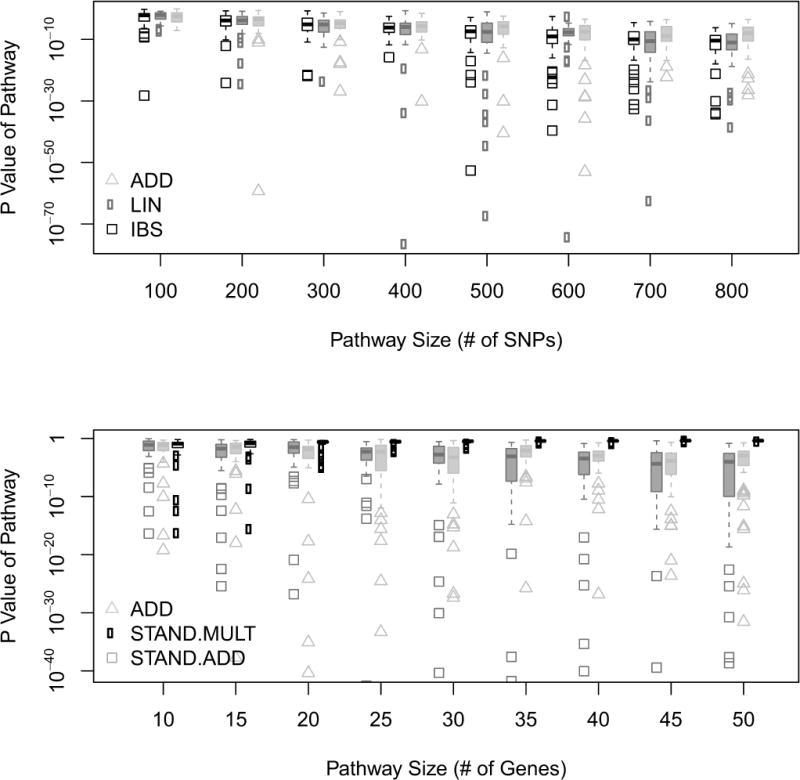
The upper panel illustrates boxplots of p-values obtained by the LKMT with LIN, IBS and modified ADD kernel function against size of respective ”pseudo-pathways” as measured by number of SNPs. The lower panel illustrates boxplots of p-values obtained by the LKMT with the ADD, STAND.ADD and STAND.MULT kernel function against size of ”pseudo-pathway” as measured by number of genes. For each investigated size, ”pseudo-pathways” were randomly put together 50 times.

3.3 NARAC Rheumatoid Arthritis Data Analysis Results

3.3.1 Empirical Evidence for Size Bias

In Figure 3, we plotted the p-values of pathways failing to reach the Bonferroni-corrected significance threshold of 0.05 against their respective size as represented by number of SNPs. We excluded significant pathways from our analysis, in order to prevent distortion due to genuine associations. We observed obvious correlations between size and magnitude of p-value for the LIN and IBS kernel. Since these observations are in agreement with the previously discussed results, this is further confirmation of the existence of size bias. Unfortunately, there is also some evidence for such a trend in the STAND.ADD and LD.STAND.ADD kernels. This is in accordance with the previously discussed permutation results. The STAND.MULT kernel, on the other hand, seems to overcompensate for large pathways. There is no evidence of bias in any direction for the LD.STAND.MULT kernel. A simple linear regression modelling the p-value of a pathway with this kernel by its respective size (measured by the number of SNPs in the pathways), reveals a regression coefficient close to 0. Furthermore, the explained variation of the model amounts to no more than 7%. Thus, we decided to carry out further analysis primarily with this kernel.

Figure 3.

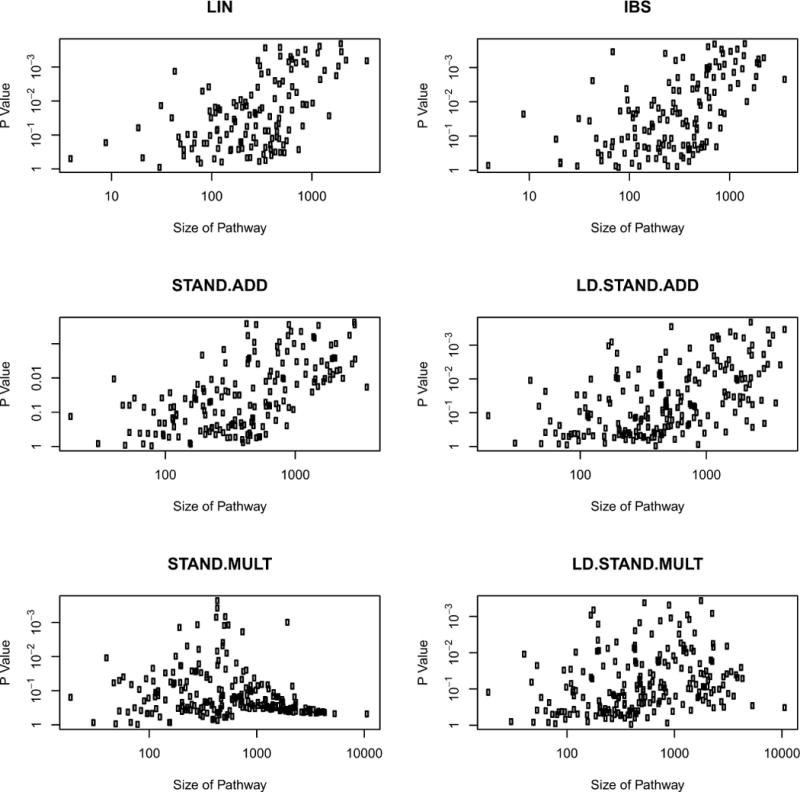
Plot of non-significant p-values against respective size of pathway as represented by number of SNPs. The different panels correspond to different kernel functions used in the LKMT to calculate the p-values. Note that both axes are logarithmic and the y-axis is reversed.

3.3.2 Pathway Association Results from LKMT

Table 2 summarises the number of significant results from the analysis with the LKMT using different kernels. The significance thresholds 0.05 and 0.1 in the table are both Bonferroni-corrected. As expected, the LIN and IBS kernels identify the most pathways as associated with RA. Furthermore, almost all previously identified susceptibility pathways are replicated. Previously identified susceptibility pathways refer to pathways which include at least one gene with more than 10 SNPs genotyped in the NARAC data that has also been significantly associated with RA in at least one scientific publication. (For a complete list of all these susceptibility genes, please refer to Section D of the supplementary material.) However, we obtained the greatest ratio of significant previously identified susceptibility pathways to all significant pathways for the LD.STAND.MULT kernel. This yet again confirms the robustness of this kernel. In the following, all further analysis will therefore be focused on this kernel.

Table 2.

Number of significant pathways identified by the LKMT with different kernel functions at Bonferroni-corrected threshold 0.05 and 0.1. Also given is the number of previously implicated pathways that were identified by the LKMT with different kernel functions. Previously implicated pathways refer to pathways including at least one gene shown to be significantly associated with RA in a scientific publication (compare Table 1).

LKMT	All KEGG Pathway (Total 244)		Previously Identified Susceptibility Pathways (Total 55)
	0.05	0.10	0.05	0.10
LIN	112	120	48	50
IBS	103	112	46	46
STAND.MULT	26	27	20	20
LD.STAND.MULT	32	33	22	22
STAND.ADD	64	70	32	33
LD.STAND.ADD	41	45	27	28

The Venn diagram in Figure 4 indicates that 10 novel pathways are detected using the LD.STAND.MULT kernel. Interestingly, three of these would have been missed using the LIN kernel. This leads us to believe that we do indeed add valuable information by incorporating information on gene membership. Table 3 lists all significant findings. As expected, pathways for inflammatory diseases such as systemic lupus are detected as being associated. Owing to the strong influence of the HLA region, these have highly significant p-values. Newly implicated pathways for RA include pathways for ABC transporters, ECM-receptor, nicotinate and nicotinamide metabolism, and focal adhesion. It is interesting to note that of these novel identifications the pathways for ABC transporters and ECM-receptor have the smallest p-values. The pathway for vitamin B6 metabolism, despite being known to be involved in RA pathogenesis, is counted as a novel finding. Susceptibility genes, which had been previously identified as being associated with RA and are located in this particular pathway, are not included in our analysis. This once more illustrates the power of pathway-based approaches.

Figure 4.

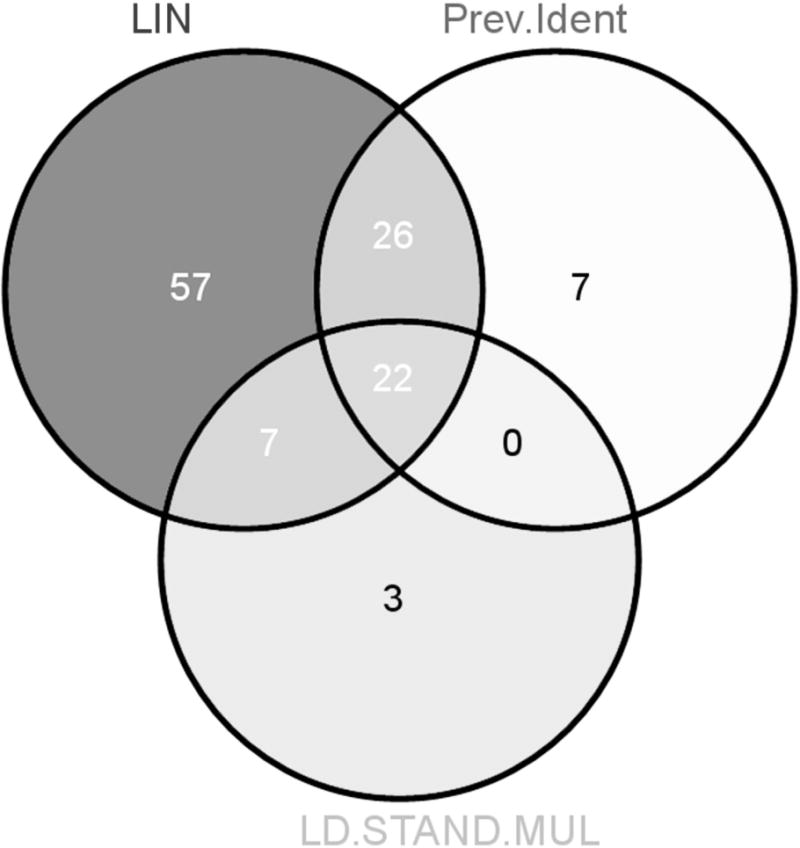
Venn diagram of results obtained by different kernels and previous studies of RA Legend: Venn diagram demonstrating the overlap between significant results obtained by LKMT with LIN and LD.STAND.MULT version. We do not include results from any of the alternative kernel functions, to keep the Venn diagram clear. Also shown is the overlap with the previously implicated pathways (Prev.Ident).

Table 3.

Significant pathways associated with RA as discovered by the LKMT with function; highlighted in grey are all pathways that did not include previously implicated genes for which more than 10 SNPs were genotyped in the data set. Also included is the pathway classification as found in the KEGG database.

KEGG Pathway Identifier	Description	P-Value of Association	KEGG Pathway Classification
path:hsa00240	Anaemia due to disorders of nucleotide metabolism	7.539 × 10−6	Metabolism
path:hsa00250	Alanine, aspartate and glutamate metabolism, Cana-van disease	9.614 × 10−5	Metabolism
path:hsa00280	Disorder of fatty-acid oxidation	2.296 × 10−5	Metabolism
path:hsa00512	Mucin type O-Glycan biosynthesis	5.282 × 10−5	Metabolism
path:hsa00750	Vitamin B6 metabolism	2.281 × 10−5	Metabolism
path:hsa00760	Nicotinate and nicotinamide metabolism	4.778 × 10−7	Metabolism
path:hsa04145	Phagosome	1.075 × 10−296	Cellular Processes
path:hsa04510	Focal adhesion	1.991 × 10−4	Cellular Processes
path:hsa02010	ABC transporter	3.546 × 10−31	Environmental Information Processing
path:hsa04512	EMC-receptor interaction	8.194 × 10−17	Environmental Information Processing
path:hsa04514	Cell adhesion molecules	1.076 × 10−99	Environmental Information Processing
path:hsa04612	Antigen processing and presentation	1.046 × 10−171	Organismal Systems
path:hsa04640	Haematopoietic cell lineage	4.191 × 10−230	Organismal Systems
path:hsa04650	Natural killer cell mediated cytotoxic-ity	5.982 × 10−5	Organismal Systems
path:hsa04672	Intestinal immune network for IgA production	6.634 × 10−154	Organismal Systems
path:hsa04974	Protein digestion and absorption	7.865 × 10−8	Organismal Systems
path:hsa04940	Type I diabetes mellitus, Antigen-activated Th1 cells produce IL-2 and IFNgamma	2.319 × 10−295	Human Diseases
path:hsa05140	Leishmaniasis	4.874 × 10−250	Human Diseases
path:has05145	Toxoplasmosis	4.351 × 10−179	Human Diseases
path:hsa05150	Staphylococcus au-reus infection	6.474 × 10−182	Human Diseases
path:hsa05152	Tuberculosis	1.532 × 10−164	Human Diseases
path:hsa05164	Influenza A	1.017 × 10−168	Human Diseases
path:hsa05166	HTLV-I infection	1.230 × 10−96	Human Diseases
path:hsa05168	Herpes simplex infection	2.782 × 10−286	Human Diseases
path:hsa05310	Asthma	7.002 × 10−104	Human Diseases
path:hsa05320	Autoimmune thyroid disease	1.408 × 10−180	Human Diseases
path:hsa05322	Systemic lupus ery-thematosus	8.970 × 10−237	Human Diseases
path:hsa05323	Rheumatoid arthritis	5.337 × 10−224	Human Diseases
path:hsa05330	Allograft rejection	1.634 × 10−103	Human Diseases
path:hsa05332	Graft-versus-host disease	2.138 × 10−103	Human Diseases
path:hsa05340	Primary immunodeficiency	2.125 × 10−44	Human Diseases
path:hsa05416	Viral myocarditis	< 10−300	Human Diseases

3.4 Comparison of Results from LKMT and Other Pathway-Based Approaches

In Figure 5, we compare results from the pathway-based approaches used by Sohns et al. [16] with results obtained by the LKMT with the LD.STAND.MULT kernel. For the data including SNPs in the HLA region, there is considerable significant overlap between the LKMT and GSEA. On the contrary, we did not find any significant overlap between the LKMT and HBP. Sohns et al. [16] demonstrated that results from GSEA and HBP indeed usually differ. Interestingly, once the HLA region was removed from the data, both HBP and GSEA show some significant overlap.

Figure 5.

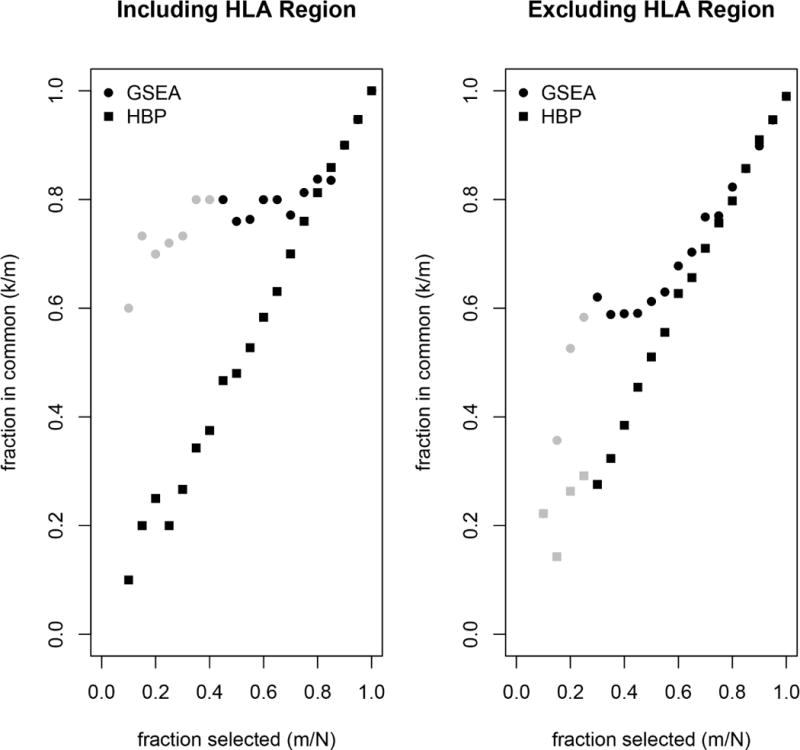
Proportion of selected pathways from total number in ranked lists against proportion of pathways in common of the selection between LKMT with the LD.STAND.MULT kernel function and GSEA/HBP. Left panel illustrates results obtained analysing unmodified pathways, while the right shows results obtained when SNPs in the HLA region were excluded. Overlaps that are statistically significant are in light grey.

The LKMT identifies 31 pathways using a Bonferroni-corrected threshold, while GSEA finds 47 significant pathways at a false discovery rate of 0.05. (HBP does not allow significances to be determined for individual pathways.) However, when we excluded SNPs located in the HLA region, the results changed dramatically. No pathways can reach significance in GSEA, although the LKMT identifies 6 susceptibility pathways. This indicates that the LKMT is more powerful and at the same time more robust than GSEA. We think that the difference in robustness stems from the ability of the LKMT to consider all markers in the pathway, whereas GSEA relies on the most significant marker in the genes located in the pathway. Therefore, the p-value determined by the LKMT is not solely driven by the strongest association in every gene.

Even though this is not a thorough performance analysis, the results indicate that the LKMT is superior to both methods. Unlike GSEA it does not rely on permutations. Other than for the HBP, it has the advantage of producing significance values, while retaining the flexibility of HBP.

4 Discussion

For the conventional kernels in logistic kernel machine-based pathway analysis, we demonstrate deflation of p-values with increasing pathway size in terms of number of genes as well as number of SNPs. In order to expunge this bias, we propose a novel pathway-size-invariant kernel. Application to a case-control study for rheumatoid arthritis empirically illustrates the effectiveness of our novel kernel compared with the linear or IBS kernel. Furthermore, this application reveals new functional connections between biological pathways and RA progression and development.

The main idea behind the construction of the new invariant kernel is to standardize the similarity metric by its empirical expectation and variance across all individuals. The chosen standardization parameters are rather unusual in order to fulfil the requirement that a kernel must be positive definite. Although these are not easily interpreted, they have several advantages compared to other corrections. Most importantly unlike permutations, the required additional computational cost is minimal. Another approach, suggested by Schaid et al. [11], capitalizes on the multivariate normal distribution of the score statistics from logistic regression to avoid permutations. However, their approach requires many separate standardization and scoring steps, whereas our new kernel integrates all necessary corrections in an elegant fashion.

Our kernel emphasizes the concept of a pathway. Conventional kernels can borrow information between SNPs in the same pathway to improve power. However, these kernels fail to harness the rich network structure of pathways, as they do not incorporate information beyond the pathway membership. In our novel kernel, we attempt to utilize this concept additionally. We integrate information on gene membership and model all possible interactions between the genes by choosing a multiplicative kernel function. Still, such information comprises only a small fraction of that available. In particular, we fail to include prior information on known direct connections between genes in the same pathway. Chen et al. [24] revealed that associated genes in the same pathway tended to be neighbours as defined by the topology of the network graph in an example considering Crohn’s disease. Explicitly specifying direct interactions of genes in the kernel function may prove a good starting point for the LKMT to exploit the vast information provided by pathway databases.

We recommend the kernel machine approach with a size-invariant kernel owing to its clear benefits and superior results compared to GSEA and HBP. The LKMT with a size-invariant kernel is more robust than other tested pathway approaches and adequate for many different scenarios. Furthermore, unlike GSEA and HBP it is fast to compute for moderate sample sizes. We advise against using kernels that offer no adjustment for the number of SNPs in a pathway. Although, we see no reason to discourage the use of these kernels for gene analysis with much fewer SNPs. For small significance levels, the LKMT with such kernels fails to control the type I error rate adequately. Generally, this effect can be compared to multiple testing, in which appropriate adjustment is required for the number of tests conducted. Multiple testing corrections are either known to be conservative or liberal, depending on the adjustment and dependencies between the tests. It seems likely that our novel kernel produces conservative results in the case of large pathways. However, more research is needed to establish the effects of dependencies between SNPs, such as LD, or interaction of genes in the same pathways.

Finally, our application to the NARAC data provides us with promising unknown associations between pathways and RA. In particular, we believe that associations with pathways for ECM molecules and cellular receptors as well as ABC transporters are of interest in the pursuit of the genetic causes of RA. Of course, future research is necessary to study these connections more thoroughly as well as replicate these association results. ECM molecules assemble cartilage proteins. In animal models, antibodies binding to these proteins have been shown to precede arthritis induction [25]. P-glycoprotein, a member of the superfamily of ABC transporters, is thought to play a major role in mechanisms of resistance to systemic administration of disease modifying anti-rheumatic drugs and low-dose glucocorticoids [26]. This type of drug resistance is common in RA patients, who rely on these drugs for prevention and control of joint damage. Thus, our results could shed more light onto effective treatments of systemic inflammation in RA patients.

5 Software

Software in the form of R code, together with a sample input data set and complete documentation is available on request from the corresponding author (saskia.freytag@med.uni-goettingen.de).

6 Appendices

Appendix 1: Additive and Multiplicative Powered Exponential Kernels

Let ${\psi }_{i,j}^g=\parallel z_i^g-z_j^g{\parallel }^2.$ Assuming that the minor allele count at an arbitrary SNP in gene g is an independent and identically distributed random quantity, then ${\psi }^g\sim D(k_g{\mu }_g,k_g{\sigma }_g^2)$ has mean k_gμ_g and variance $k_g{\sigma }_g^2.$ The variables μ_g and ${\sigma }_g^2$ refer to the expectation and variance of this distribution based on one SNP. Simulation studies (not shown) revealed that a minimum of 10 SNPs per gene is needed in order for this standardization to work appropriately.

For the standardization, let ${\gamma }^g={\left(\frac{{\psi }^g}{s_g}\right)}^{{\delta }_g}.$ The scaling factor s_g and the exponent δ_g denote the standardization parameters for gene g. As long as δ_g≤ 1 and s_g> 0, the kernel function exp(−γ^g) is positive definite. Now using the Taylor expansion with respect to ψ_g around k_gμ_g, we obtain

$${\gamma }^g\approx {\left(\frac{{\psi }^g}{s_g}\right)}^{{\delta }_g}{|}_{{\gamma }^g=k_g{\mu }_g}+{\delta }_g\frac{1}{s_g}{\left(\frac{{\psi }^g}{s_g}\right)}^{{\delta }_g-1}{|}_{{\gamma }^g=k_g{\mu }_g}({\psi }^g-k_g{\mu }_g).$$ (9)

The expectation and variance of γ_g become approximately:

$$\begin{array}{l}E\left({\gamma }_g\right)={\left(\frac{k_g{\mu }_g}{s_g}\right)}^{{\delta }_g}=1,\\ \text{Var}({\gamma }_g)={\delta }_g^2\frac{1}{s_g^2}{\left(\frac{k_g{\mu }_g}{s_g}\right)}^{2{\delta }_g-2}{k}_g{\sigma }_g^2={\delta }_g^2\frac{1}{k_g}\frac{{\sigma }_g^2}{{\mu }_g^2}\end{array}$$ (10)

Consequently, we get expressions for s_g and δ_g, that ensure invariance with regards to number of SNPs in the pathway. Since we also require δ_g ≤ 1 for all genes in the pathway, we choose δ_g = 1 for k_g = max_g∈pk_g. This automatically yields ${\delta }_g=\sqrt{\frac{k_g}{{\text{max}}_{g}p\in k_g}}$ and s_g = μ_gk_g. Furthermore, we also tested whether our results were independent with regard to the length of the largest gene in the pathway (results not shown). This seemed to be the case for moderate increase in pathways size. Results should therefore remain consistent even when a new larger non-significant gene is added to the pathway.

Appendix 2: Standardized Additive Powered Exponential Kernel

If one assumes that the central limit theorem holds, ${\displaystyle {\sum }_{g\in p}(-{\gamma }_g)}$ has mean r_pμ₀ and variance $r_p{\sigma }_p^2.$ Here r_p denotes the number of genes in the pathways, while μ_p= E(C(γ_ij)) and ${\sigma }_p^2=\text{Var}\left(C\left({\gamma }_{i,j}\right)\right)$. Similar to the standardization for the gene, one can now apply a Taylor expansion and find the appropriate standardization parameters.

Appendix 3: Standardized Multiplicative Powered Exponential Kernel

Let ${\omega }_p={\varsigma }_p{\displaystyle {\sum }_{g\in p}{\gamma }_g}$ be random variable for any arbitrary pair of individuals, where ζ_p> 0 is the additional scaling factor regarding the number of genes in the pathway. Let r_p be the number of genes in pathways p. Assuming that the genes in this pathway are independent we approximately have

$$\begin{array}{c}E\left({\omega }_p\right)={\zeta }_p{r}_{p}E\left({\gamma }_g\right)\text{ and }\\ \text{Var}\left({\omega }_p\right)={\varsigma }_p^2{r}_p\text{Var}\left({\gamma }_g\right),\end{array}$$ (11)

where E(γ_g) and Var(γ_g) are defined as given in the previous section (see Equation 10). One can easily see that ζ_p has to be selected proportionally $\sqrt{\frac{1}{r_p}}$ in order to achieve constant variance with regards to the number of genes in the pathway. Further standardization with regards to the expectation, like $K(z_i,z_j)=\exp (-\sqrt{\frac{1}{r_p}}{\displaystyle {\sum }_{g\in p}\left\{{\gamma }_{i,j}^g-1\right\}}),$ are not necessary. Such standardization represents nothing more than a constant scale factor, and it would therefore merge with ${\sigma }_K^2.$