A unified model for de novo design of elastin-like polypeptides with tunable inverse transition temperatures

Abstract

Elastin-like polypeptides (ELPs) are stimulus responsive peptide polymers that exhibit inverse temperature phase transition behavior, causing an ELP to aggregate above its inverse transition temperature (T_t). Although this property has been exploited in a variety of biotechnological applications, de novo design of ELPs that display a specific T_t is not trivial because the T_t of an ELP is a complex function of several variables, including its sequence, chain length, polypeptide concentration, and the type and concentration of cosolutes in solution. This paper provides a quantitative model that predicts the T_t of a family of ELPs (Val-Pro-Gly-Xaa-Gly, where Xaa = Ala and/or Val) from their composition, chain length, and concentration in phosphate buffered saline. This model will enable de novo prediction of the amino acid sequence and chain length of ELPs that will display a predetermined T_t in physiological buffer within a specified concentration regime, thereby greatly facilitating the design of new ELPs for applications in medicine and biotechnology.

1. INTRODUCTION

Elastin-like polypeptides (ELPs) are stimulus responsive peptide polymers derived from tropoelastin,¹ that consist of repeats of Val-Pro-Gly-Xaa-Gly (where the guest residue position ‘Xaa’ can be any amino acid except Pro). ELPs exhibit lower critical solution temperature (LCST) phase behavior, which is often called inverse transition behavior in the ELP literature. Below their LCST – also called the inverse transition temperature (T_t) – an ELP is soluble in aqueous solution, and above this temperature the ELP forms insoluble, micron-sized aggregates that ultimately coalesce into an ELP rich, coacervate phase. The T_t is a function of several factors, including the amino acid composition of the fourth “guest” residue position, the chain length, the polypeptide concentration, and the concentration of other solutes in the buffer.^2–4 The ability to tune the phase transition behavior of ELPs in response to different stimuli such as temperature and pH have led to many applications of ELPs in biotechnology,^5–7 drug delivery,^8–17 biointerface science,^18–20 and tissue engineering.^21–23

Many applications of ELPs require the T_t to occupy a narrow temperature window.^{5,8–10,17,18,23} Theoretically, an ELP can be “forced” to exhibit a T_t within a given window by using highly concentrated or very dilute polymer solutions, adding kosmotropic or chaotropic salts,²⁴ or by using high or low molecular weight ELPs. From a practical perspective, however, this strategy is not typically feasible because the ELP molecular weight (MW) or concentration is often set by the application, while the addition of other cosolutes may be impractical in many applications or simply impossible if the intended application of the ELP is in vivo. These constraints on modulating the T_t of an ELP require an alternative strategy to tune the transition temperature for most applications.

Clearly, what is needed is an algorithm that quantitatively relates the T_t to ELP composition, MW, and concentration. A unified model that does so would allow users to design ELPs de novo for a range of applications by constraining one or more of the operating parameters for a given application (ELP MW or concentration) to yield one or more ELP sequences that will exhibit the desired T_t. In response to this need, we have developed a quantitative model that predicts the T_t of a family of ELPs (Val-Pro-Gly-Xaa-Gly, where Xaa = Ala and/or Val) from their composition, chain length, and concentration in phosphate buffered saline. We term this a unified model because it “unifies” the effect of ELP composition, MW and concentration on the T_t of the ELP within a single analytical equation.

This model builds upon, but departs significantly from previous studies that quantified the ELP phase transition behavior as a function of guest residue composition. Urry used chemically synthesized ELPs to demonstrate that their T_t correlated with the mean hydrophobicity of the guest residue.^3,25,26 That study did not, however, examine the effect of ELP MW and concentration on its T_t, two variables that we know have a large impact on the experimentally observed T_t in solution (see Equation 1). In response to this limitation, Meyer and Chilkoti developed a quantitative model describing the effects of ELP chain length and concentration on the T_t of three different ELP libraries comprised of a mixture of Val, Ala, and Gly residues at the 4^th guest residue position for a range of ELP chain lengths.² MacKay then modified that model to incorporate the effects of pH on the T_t for ELPs that contain ionizable residues at the guest residue position.²⁷ These models, though valuable, only predict the T_t as a function of MW and concentration within a single ELP sequence, and only once at least three members of that sequence with different MWs have been synthesized and characterized with respect to their T_t. Because these models did not explicitly include a term that accounts for the effect of composition on the T_t, their utility as a design tool is limited because the composition is the most useful experimental parameter to modulate the T_t. In contrast, by incorporating ELP composition, MW, and concentration within a single equation that predicts the T_t, the model developed herein will enable de novo selection of ELP sequence and molecular weight combinations that will display a T_t of interest within a specific range of concentration.

2. EXPERIMENTAL SECTION

Materials

Restriction enzymes, calf intestinal phosphatase (CIP), and T4 DNA ligase were purchased from New England Biolabs (Ipswich, MA). The pET-24a+ cloning vector was purchased from Novagen Inc. (Madison, WI), and all custom oligonucleotides were synthesized by Integrated DNA Technologies Inc. (Coralville, IA). The DNA miniprep, gel purification, and PCR purification kits were purchased from Qiagen Inc. (Germantown, MD). EB5α™ and BL21™ E. coli cells were obtained from Edge BioSystems (Gaithersburg, MD) and were grown in TBDry™ media (MO BIO Laboratories, Inc; Carlsbad, CA). Chemicals used for the purification of ELPs include: IPTG (Gold Biotechnology; St. Louis, MO) and Kanamycin (CalBioChem; San Diego, CA).

ELP Synthesis and nomenclature

The synthetic genes for ELPs were assembled from chemically synthesized oligomers (IDT Inc.) by plasmid reconstruction recursive directional ligation (PRe-RDL) as described elsewhere.²⁸ The oligomers used to construct each compositional library are described in Supplemental Figure 1. The ELP nomenclature used throughout this paper is A[X]-Y, where X represents the fraction of alanine (A) in the guest residue composition (rest, valine (V)), and Y represents the length of the ELP in pentamers.

ELP Expression

BL21(DE3) cells transformed with an ELP-containing plasmid were used to inoculate a 250 mL flask containing 50 mL TBDry media supplemented with 45 μg/mL kanamycin. This flask was incubated on a shaker overnight at 200 RPM and 37°C before being used to inoculate six 4-L flasks containing 1 L of TBDry media, supplemented with 45 μg/mL kanamycin. These cultures were incubated on a shaker at 200 RPM at 37°C for six hours, treated with 0.2 mM IPTG, and grown overnight.

ELP Purification

E. coli expression cultures were centrifuged in 1 L bottles at 4°C for 10 min and 3,000 g to concentrate the cells. The supernatant was discarded and the cell pellet was resuspended in 10 mL PBS. The cells were placed on ice and were lysed via sonication for 3 min (10 s on, 40 s off) (S-4000 Misonix Sonicator; Farmingdale, NY). Polyethyleneamine (PEI; 0.7% w/v) was added to the lysate to precipitate nucleic acid contaminants, and the remaining cell debris was removed from the solution following centrifugation at 14,000 g for 10 min at 4°C. The ELP was then purified by two cycles of inverse transition cycling with minor modifications. The supernatant was heated to 60°C for 10 min, thereby inducing the ELP phase transition and precipitation of contaminant proteins, then immediately placed on ice to redissolve the ELP. Protein debris was removed by another centrifugation step (14,000 g, 10 min, 4°C). The supernatant (containing soluble ELP) was heated to 37°C, and NaCl crystals were added to a final concentration of 1–3 M to induce the ELP phase transition. ELP aggregates were precipitated by centrifugation (14,000 g, 10 min, 25°C), and the supernatant was discarded. The ELP was then resuspended in PBS, cooled, and centrifuged (14,000 g, 10 min, 4°C) to remove any remaining insoluble contaminants. This cycle (starting at the 60°C incubation) was repeated once more to yield the final product. The product was then dialyzed overnight in ddH₂O and lyophilized.

ELP Analysis

The purity of the ELPs was visually determined by SDS-PAGE, using 4–20% Tris-HCl Ready Gels (Bio-Rad, Hercules, CA) stained with copper chloride (0.5 M). MALDI-MS was performed with a PE Biosystems Voyager-DE instrument, equipped with a nitrogen laser (337 nm). Samples were prepared in a 50% (v/v) aqueous acetonitrile solution that contained 0.1% trifluoroacetic acid. The samples were analyzed in a sinapinic acid matrix, and all measured ELP masses were within a 0.5% margin of error (Supplemental Table 1).

Thermal Turbidimetry

The optical density at 350 nm (OD₃₅₀) of each ELP was measured as a function of temperature on a UV-vis spectrophotometer equipped with a multicell thermoelectric temperature controller (Cary 300, Varian Instruments; Walnut Creek, CA). ELP solutions in PBS ranging in concentration from 2 to 100 μM were heated at a rate of 1°C/min. The T_t was defined as the inflection point of the turbidity plot. To measure transition temperatures above 80°C, the ELPs were diluted into known quantities of NaCl in PBS (0.25, 0.5, 0.75, 1.0, 1.5, 2.0, or 2.5 M NaCl) to lower the T_t. A linear extrapolation of the T_t as a function of NaCl concentration for each ELP concentration was then used to estimate the transition temperatures in PBS. ^24,29,30

Data Analysis

Non-linear regression analysis was performed with IBM SPSS Statistics 19.0 (SPSS, Chicago, IL). MATLAB (MathWorks; Natick, MA) was used to generate the 3-dimensional plot of the predicted T_t as a function of composition and chain length.

3. Results

3.1 Design Considerations

To develop this model, we first limited the sequence space, as the number of unique ELP sequences that will exhibit a desired T_t are enormous, even if one of two parameters such as MW or solution concentration are fixed. This is given the fact that 19 natural amino acids (and many more unnatural amino acids) are available to tune the T_t by incorporation at the guest residue position ‘X’ in the VPGXG repeat unit. The number of such sequences expands enormously when using a combination of three or more guest residues. We also restricted the choice of guest residues to a binary combination of amino acids to minimize the sequence order related complexity in phase behavior because the complexity that sequence order creates can unpredictably alter the T_t.² Choosing a binary composition also has the benefit that it can be easily numerically encoded for modeling purposes.

We hence narrowed the composition of the two guest residues to alanine (Ala) or valine (Val) at the guest residue position. We selected Ala and Val as the specific guest residues for two reasons: (1) because a major focus of our efforts is to design ELPs that would exhibit T_t’s in the physiological temperature range, we surmised that copolymer ELPs ranging from 100% Ala to 100% Val at the guest residue position would yield multiple copolymers that exhibit T_t’s between 30–45°C for a range of MWs and ELP concentrations, given that the T_t of their homopolymers span this range;³ and (2) Ala and Val are aliphatic and thus will not display a sensitivity to pH. Although the ability to tune the T_t by pH is potentially valuable,³¹ it adds a unnecessary degree of complexity to model development at this stage.

With these parameters fixed, we recombinantly synthesized eight ELP libraries in E. coli (the gene sequence is shown in Supplemental Figure 1 and the gene libraries are shown in Supplemental Figure 2). Each ELP library consists of a set of ELPs of constant composition as defined by the fraction of Ala at the guest residue (reminder is Val) with members in that library only differing in their MW, which ranged from 15 to 60 kDa (Supplementary Table 1). The guest residue composition defined by the fraction of Ala steps across from 0 (solely Val guest residue) to 1 (solely Ala guest residue) in increments of 0.1 or 0.2 across the eight ELP libraries. After expression in E. coli, the 24 unique ELPs were purified to homogeneity; details of their physical characterization (SDS-PAGE and MALDI-MS) are contained in Supplemental Figure 3 and Supplemental Table 1, respectively.

We next fixed the solution conditions that the model was developed for by choosing phosphate buffered saline (PBS) as the solvent, as most applications of ELP are likely to be in biotechnology or medicine wherein PBS is the buffer of choice. We then measured the T_t of all 24 members of these 8 ELP libraries in PBS for a range of ELP concentrations (Supplemental Figure 4). The experimentally measured T_t’s of these ELPs were used to develop a quantitative model that incorporates the effects of ELP concentration, MW, and guest residue composition within a single equation.

3.2 Building the Model

The first step in building the model was to quantify the effect of composition on the T_t of ELPs. Each ELP composition library followed the relationship previously developed by Meyer and Chilkoti² to describe the transition behavior of ELPs (average r² = 0.987 ± 0.018):

$$T_t=T_{tc}+\frac{k}{\mathit{Length}}ln\frac{C_c}{\mathit{Conc}}$$ (1)

where the T_t depends on the chain length (Length, pentapeptides) and polymer concentration (Conc, μM), as well as three parameters specific to each ELP composition: the critical transition temperature T_tc (°C), the proportionality constant k (°C·pentapeptides), and the critical concentration C_c (μM) (Equation 1). The T_tc represents the critical transition temperature for a given composition at a critical limit –high ELP concentration and chain length– at which point these two parameters no longer affect the T_t. The parameter C_c is the corresponding theoretical polypeptide concentration that would be required to achieve T_tc. Finally, the parameter k indicates the concentration and length dependence of the T_t: larger values signify that the transition temperature is more sensitive to concentration fluctuations or changes in chain length.

These three parameters were simultaneously determined for each compositional library using a multivariate regression fit to Equation 1. The fits, summarized in Table 1, were based on a range of MWs (15 kDa, 30 kDa, 60 kDa) and five ELP concentrations (100 to 5 μM). The ELP libraries are labeled according to their composition, which is defined by the fractional alanine content (fAlanine). For example, a value of 1.0 indicates that the guest residue composition consists exclusively of alanine, and a value of 0.2 indicates that the compositional ratio is 2 alanine to 8 valine. We found that the parameters could be calculated with reasonable certainty with the exception of C_c, which showed a high level of variation that is likely due to its derivation from a logarithmic ratio.

Table 1.

Summary of multivariate fits to Equation 1 for eight ELP compositions^a

f Alanine	Ttc (°C)	k (°C·pentapeptides)	Cc (μM)	r2	n
1	54.3 (1.4)	623.0 (36.1)	843.9 (209.1)	0.975	30
0.9	44.7 (2.0)	507.0 (53.1)	2412.1 (1310.5)	0.946	30
0.8	39.3 (0.8)	484.7 (21.3)	2005.3 (442.0)	0.995	15
0.7	33.8 (0.6)	433.7 (16.3)	2748.4 (546.6)	0.997	15
0.6	29.9 (0.6)	387.0 (16.1)	3684.3 (851.4)	0.997	15
0.5	27.7 (0.6)	316.9 (15.3)	6218.9 (1822.2)	0.991	30
0.2	22.9 (0.2)	201.2 (5.0)	13573.3 (2306.7)	0.998	30
0	20.2 (0.1)	144.1 (3.4)	22130.2 (3786.0)	0.999	30

^aData fit to Equation 1 and reported as estimate (standard error). ‘n’ refers to the number of individual measurements.

To elucidate the relationship between the ELP composition and the three parameters (T_tc, k, and C_c), each parameter was plotted as a function of f Alanine (Figure 1). These plots revealed that the empirical relationship between the composition and T_tc (r² = 0.947), k (r² = 0.989), and C_c (r² = 0.959) fit the exponential form Ae^b·fAlanine, where A and b are constants.

Figure 1.

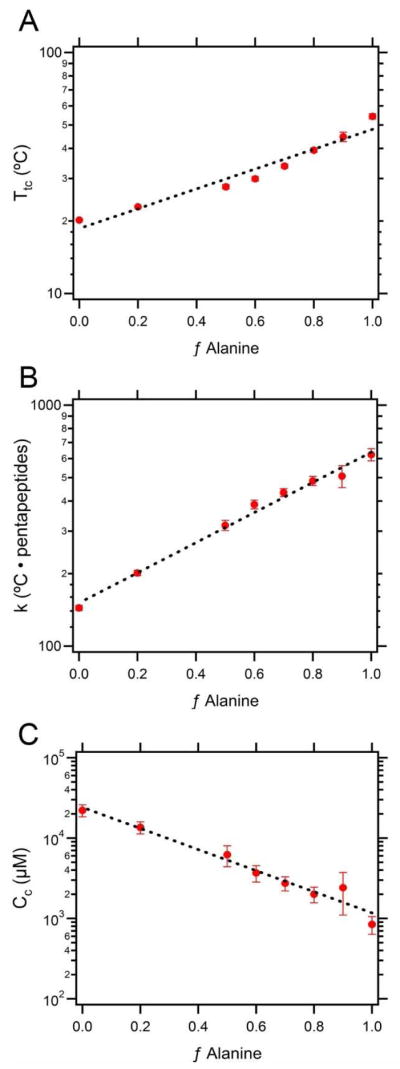
Relationship between the composition and the three parameters defined in Eq. 1. A) T_tc, B) k, and C) C_c as a function of f Alanine. Data are reported as estimates ± standard error. The dashed lines represent the best fit of the form Ae^b·fAlanine.

It is not entirely surprising that these parameters show a quantitative correlation with the ELP composition. Urry demonstrated that the critical transition temperature (T_tc) was influenced by the mean hydrophobicity of the guest residue composition.³² We have also observed that the T_t’s of hydrophobic ELPs are less dependent on the concentration (hence smaller k values) than the T_t’s of hydrophilic ELPs. Meyer and Chilkoti consolidated these observations by demonstrating that the parameters were related across three ELP libraries; they observed that k varied linearly with T_tc, whereas C_c varied as a power function with T_tc.² Although only three compositions were sampled and the ELP hydrophobicity was approximated by the T_tc (instead of the sequence, as demonstrated here), the postulated relationships are supported by this data set. As T_tc and k follow the form e^fAlanine, k as a function of T_tc generates a near-linear correlation (Supplemental Figure 5; r²=0.929). C_c, on the other hand, is approximated by e^−fAlanine, which signifies that C_c as a function of T_tc (e^fAlanine) yields a power function (C_c ≈ T_tc⁻¹) (r²=0.938).

With these relationships validated, this exponential form was substituted for each parameter in Eq. 1 to yield Eq. 2:

$$T_t={Ae}^{b\ast \mathit{fAlanine}}+\frac{{Ce}^{D\ast \mathit{fAlanine}}}{\mathit{Length}}ln(\frac{E{e}^{F\ast \mathit{fAlanine}}}{\mathit{Conc}})$$ (2)

where the variables A-F are non-zero constants and fAlanine represents the ratio of alanines to the total number of guest residue positions. For fitting purposes, Eq. 2 was then simplified with logarithmic identities to yield Eq. 3:

$$T_t={Ae}^{b\ast \mathit{fAlanine}}+\frac{{Ce}^{D\ast \mathit{fAlaine}}}{\mathit{Length}}[ln(E)+F\ast \mathit{fAlanine}-ln(\mathit{Conc})]$$ (3)

Eq. 3 was used to perform a global multivariate regression analysis (n = 120) on the data to yield the empirical relationship between the T_t, chain length, concentration, and composition for all synthesized guest residue combinations of Ala and Val (Equation 4):

$$T_t=16.8e^{1.1\ast \mathit{fAlanine}}+\frac{181.5e^{1.2\ast \mathit{fAlanine}}}{\mathit{Length}}[ln(12881.2)-2.3\ast \mathit{fAlanine}-ln(\mathit{Conc})]$$ (4)

A 3-dimensional surface plot of this model, holding the ELP concentration constant (Figure 2A) illustrates the wide range of T_t’s available to ELPs of varying length and composition. This model describes 99.4% of the observed variability in the T_t over all 24 unique ELP constructs (Figure 2B). Also evident from these data is the inverse relationship of T_t with chain length (Eq. 4); higher molecular weight ELPs exhibit lower T_t’s than smaller ELPs at the same composition and concentration. This graph also indicates that there are several ELPs with a T_t above 100°C. Each T_t > 80°C in PBS (the temperature limit of our UV-Vis spectrophotometer) was linearly extrapolated from the T_t of the ELP at three different NaCl concentrations, which is known to quantitatively depress the T_t of ELPs as a function of NaCl concentration.²⁴

Figure 2.

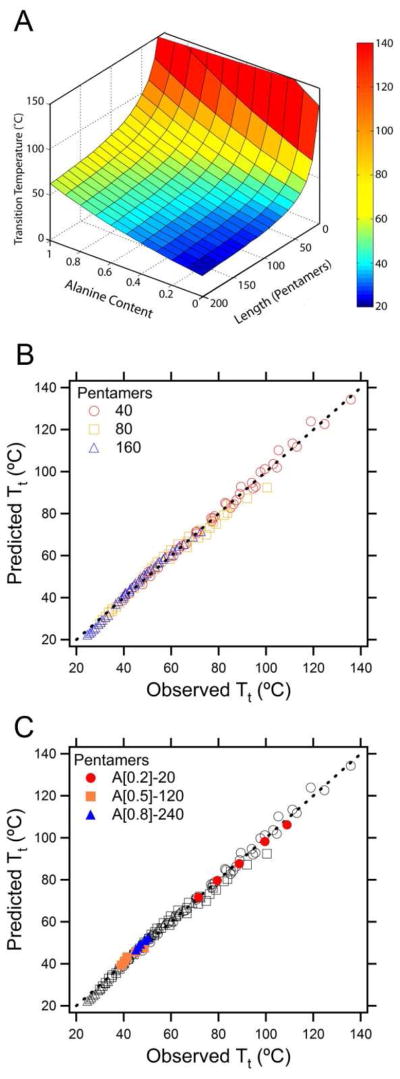
A) A 3-dimensional plot of the predicted T_t landscape for the Ala and Val superfamily of ELPs at 25 μM in PBS. B) Predicted versus observed T_t for a global fit of eight ELP sequences across 3 molecular weights and 5 concentrations in PBS (r²=0.993; n=120). C) Predicted versus observed T_t for 3 additional sequences (A[0.2]-20, A[0.5]-140, and A[0.8]-240) not included in the original data set. These three ELPs showed a high fidelity to the model (r²=0.999, slope = 0.95).

To test the robustness of the model, three ELPs were synthesized with molecular weights that were not included in the original data set (shown in Supplemental Table 1). Figure 2C shows that the model accurately predicts (r²=0.999; n=15) the transition temperatures for ELPs with MWs that are larger (240 pentamers), smaller (20 pentamers), and in-between (120 pentamers) the molecular weights used to construct the model. Finally, this model was used to develop Supplemental Table 2, which provides possible combinations of sequence (fAlanine = 0 to 1 with a 10% Ala step size) and length (pentamers = 20 to 200 with a 10 pentamer step size) to achieve a specific T_t at a specified concentrations (1 to 1000 μM) in PBS. This resource provides a clear starting point for designing ELPs for specific thermoresponsive applications.

4. DISCUSSION

The selection of ELPs that exhibit a T_t within a specific temperature window has historically relied upon trial-and-error. The Meyer and Chilkoti model² was the first to quantitatively model the T_t of ELPs as a function of ELP chain length and concentration. However, the model incorporated 3 parameters that could only be determined once the ELP was synthesized and its inverse transition behavior characterized. While the resulting relationship proved very useful in predicting the transition behavior of ELPs with different MWs within the same family, the absence of a defined “sequence” variable did not allow the a priori prediction of the T_t of new ELP sequences. The MacKay and Chilkoti model²⁷ expanded upon the Meyer and Chilkoti model by incorporating the Henderson-Hasselbalch equation to predict the relative quantities of protonated and nonprotonated residues. By splitting each of the 3 parameters into protonated and nonprotonated parameters (for a total of 6 parameters), the MacKay model is able to predict the T_t of ELPs within a specific sequence family at a specific pH. While the third design parameter is useful in exploiting the pH behavior of charged ELPs, like the Meyer model it remains limited to a single ELP family at a time.

The Meyer model can be applied in situations where the ELP library has already been generated and the user wants to know how changing the length or concentration will influence the T_t of a construct within that particular ELP library. The MacKay model also requires that the ELP library be constructed and characterized, and can be used to predict how length, concentration, or pH will influence the transition temperature of new constructs within that library. Because the model presented here is constructed from multiple separate ELP libraries, the user is able to predict how the length, concentration, and sequence will influence the transition temperature of entirely new libraries as long as the sequence is contained within that ELP superfamily (X=Ala and/or Val). This greatly increases the sequence space that can be screened for ELPs with the desired thermal behavior.

The most important finding of this study is that each of the three parameters defined in the Meyer model can be described as an analytical function of the sequence, represented by the fraction of alanines in the guest residue position. This new feature of the model eliminates the need to express and characterize ELPs prior to predicting their T_t and thereby provides an a priori predictive tool for the design of ELPs in the superfamily of constructs containing Val or Ala guest residues. While this compositional limitation restricts the compositions available for designing new ELPs, we purposely selected Ala and Val because they exhibit transition temperatures that are far removed from each other, maximizing the coverage over the physiologically relevant temperature range that is of greatest interest to us. This is evident when observing the predicted range of T_t for ELPs of different MW at a specific concentration (100 μM): 40 pentamers (38.8 – 89.4°C); 80 pentamers (27.8 – 69.9°C); and 160 pentamers (22.3 – 60.2°C).

However, if this model does not provide sufficient coverage of ELP MW or concentration over a certain temperature range, we hypothesize that this method could easily be applied to other binary systems with even wider expected ranges, such as serine (high T_t) and leucine (low T_t). It could also be combined with the MacKay model to explore the pH sensitivity of the superfamily of ELPs constructed with glycine and histidine, for example. Finally, it should be noted that a similar model developed for other binary systems would not require 8 families of ELPs prior to constructing the T_t landscape of the superfamily. In fact, this model can be recreated with little to no loss of information with only 3 ELP families (the two endpoints and the midpoint: 0%, 50%, and 100% Ala) across 3 molecular weights and 5 concentrations (n=45). The resultant model predicts the T_t’s of all eight families with high accuracy (r² = 0.992; slope of predicted T_t versus observed T_t = 1.002; n=120).

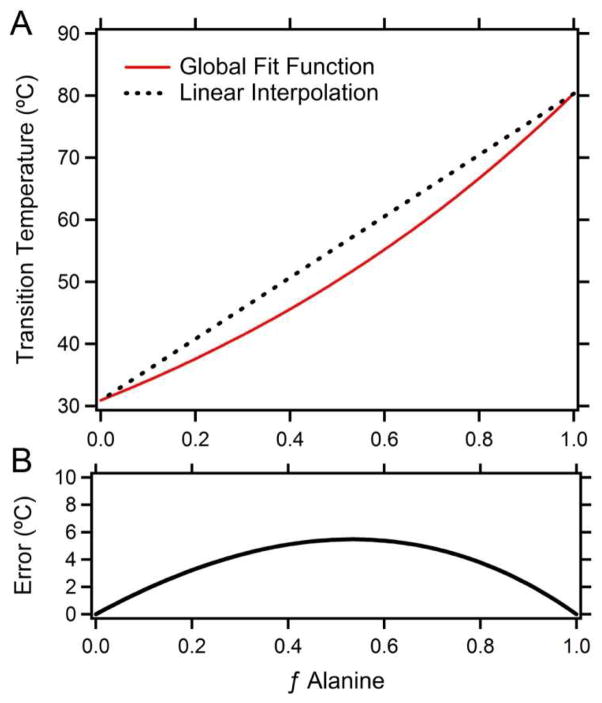
This study also sheds light on the limitations of previous models that investigated whether the T_t’s of heterogeneous ELPs (heteropolymers composed of two or more different guest residues with a pseudorandom distribution of guest residues across the ELP’s primary amino acid sequence) could be calculated by linearly interpolating between the T_t of two or more homogeneous ELPs (homopolymers), and then weighing each homopolymer ELP T_t by the mole fraction of the guest residue composition in the heteropolymer. The implementation of this method, however, has been met with conflicting results.^2,32 This study conclusively demonstrates that the T_t of heteropolymer ELPs cannot be calculated in this manner. Figure 3 illustrates that the T_t for any combination of Ala and Val is clearly depressed from the linear interpolation between the T_t of the two homopolymer ELPs. While this particular set of conditions (80 pentamers at 25 μM) yields a maximum departure of ~5 °C from the linear interpolation, the departure is inversely proportional to concentration and length. This study only examined the combination of two specific amino acids; it remains unknown to what degree other guest residue combinations will be affected, although it is our opinion that this error will be greatest when mixing guest residues of vastly different hydrophobicities. We hypothesize that the T_t is not simply dependent upon the mean hydrophobicity of the guest residue composition as previously proposed,³² but is actually determined by the specific sequence of the guest residues³³ and the difference in hydrophobicity between the guest residues. This hypothesis is currently under investigation.

Figure 3.

A) The global fit of the ELP T_t’s for ELP constructs with a chain length of 80 pentapeptides and at 25 μM ELP concentration (red line) as a function of composition. The black dashed line represents a linear interpolation between the T_t’s of two homopolymer ELPs composed with 100% Ala or Val as their guest residue. B) Error, defined as the departure of the linear interpolation from the global curve of best fit in degrees Celsius as a function of the fractional Ala content of the ELP.

Although this model is a useful step forward in the design of ELPs, more remains to be done. Examination of Supplemental Table 2 shows that although regions of the matrix of T_t as a function of ELP concentration is populated by ELPs with a range of MWs, there are regions in that matrix that are sparse in terms of available ELPs. In particular, constructs that display low T_t’s at small MW and dilute conditions and constructs that display high T_t’s at large MW and concentrated conditions are absent from the matrix. This is because at the extremes of MW and ELP concentration, this model is fundamentally limited by the properties of the Val (low T_t’s) and Ala (high T_t’s) homopolymers. Future studies will address this limitation by expanding this model by the synthesis and characterization of ELPs with other combinations of hydrophobic and hydrophilic amino acids that will provide additional ELPs to populate these regions of the matrix.

5. CONCLUSION

The model presented in this paper is the first to quantitatively correlate the T_t of a set of Ala and Val containing ELPs with an explicit compositional variable, its MW, and concentration. This allows the a priori prediction of the T_t of any ELP consisting of a combination of Ala and Val at the guest residue position across a range of ELP MWs and concentrations. This simple analytical model provides researchers with an easy tool that can be implemented as an Excel™ (Microsoft Inc.) macro for the design of ELPs. The model will enable de novo design of ELPs wherein given a desired T_t in physiological buffer, the model will provide a set of ELPs (sequence and length combinations) that will exhibit that T_t across a specific concentration regime, thereby greatly facilitating the design of new ELPs. One of its most useful applications is likely to be in the design of ELPs that exhibit a T_t in aqueous solution under physiologically relevant conditions, thereby greatly facilitating their use in medicine and biotechnology.