Abstract
There is currently no reliable way of predicting the optimal implantable cardioverter-defibrillator (ICD) placement in paediatric and congenital heart defect (CHD) patients. This study aimed to: (1) develop a new image processing pipeline for constructing patient-specific heart–torso models from clinical magnetic resonance images (MRIs); (2) use the pipeline to determine the optimal ICD configuration in a paediatric tricuspid valve atresia patient; (3) establish whether the widely used criterion of shock-induced extracellular potential (Φe) gradients ≥5 V cm−1 in ≥95% of ventricular volume predicts defibrillation success. A biophysically detailed heart–torso model was generated from patient MRIs. Because transvenous access was impossible, three subcutaneous and three epicardial lead placement sites were identified along with five ICD scan locations. Ventricular fibrillation was induced, and defibrillation shocks were applied from 11 ICD configurations to determine defibrillation thresholds (DFTs). Two configurations with epicardial leads resulted in the lowest DFTs overall and were thus considered optimal. Three configurations shared the lowest DFT among subcutaneous lead ICDs. The Φe gradient criterion was an inadequate predictor of defibrillation success, as defibrillation failed in numerous instances even when 100% of the myocardium experienced such gradients. In conclusion, we have developed a new image processing pipeline and applied it to a CHD patient to construct the first active heart–torso model from clinical MRIs.
Key points
Implantable cardioverter-defibrillators (ICDs) with transvenous leads often cannot be implanted in a standard manner in paediatric and congenital heart defect (CHD) patients. Currently, there is no reliable approach to predict the optimal ICD placement in these patients.
A pipeline for constructing personalized, electrophysiological heart–torso models from clinical magnetic resonance imaging scans was developed and applied to a paediatric CHD patient.
Optimal ICD placement was determined using patient-specific simulations of the defibrillation process. In a patient with tricuspid valve atresia, two configurations with epicardial leads were found to have the lowest defibrillation threshold.
We demonstrated that determining extracellular potential (Φe) gradients during the shock – without actually simulating defibrillation – was not sufficient to predict defibrillation success or failure.
Using the proposed methodology, the optimal ICD placement in paediatric/CHD patients can be predicted computationally, which could reduce defibrillation energy if the pipeline is used as part of ICD implantation planning.
Introduction
Defibrillation by strong electric shock is the only known procedure that reliably terminates ventricular fibrillation (VF). Implantable cardioverter-defibrillators (ICDs) have recently been implanted with increasing frequency in the paediatric population and in patients with congenital heart defects (CHDs) (Berul et al. 2008). In these patients, it is often not indicated or even impossible to implant a transvenous lead ICD because of the patient's small heart size and congenitally altered anatomy, so non-standard ICD configurations have to be used (Silka et al. 1993; Stephenson et al. 2006). Such ICD configurations commonly involve individualized epicardial or subcutaneous lead placement (Berul et al. 2001; Gradaus et al. 2001; Thogersen et al. 2001; Stephenson et al. 2006). However, there is currently no reliable, personalized way of predicting which ICD configuration would have the lowest defibrillation and cardioverstion thresholds (DFT and CVT) in a patient. In this study, we consider the configuration that exhibited the lowest DFT and CVT among tested ICD placement options as the optimal configuration. A low DFT is desirable because strong electric shocks damage cardiac myocytes (Walcott et al. 2003), increase mortality (Larsen et al. 2011), and can cause pain and psychological trauma (Maisel, 2006). Thus, it is important to be able to predict the optimal ICD configuration for a specific patient, especially in the case of a paediatric and/or CHD patient if a transvenous lead ICD configuration cannot be used.
A previous study has endeavoured to determine computationally the DFTs associated with different ICD configurations in an attempt to predict the optimal ICD configurations in paediatric and CHD patients (Jolley et al. 2008). While patient-specific torso models have been developed for this purpose from high-resolution computed tomography (CT) scans (the latter being a concern for radiation overexposure; Brenner & Hall, 2007), the models did not simulate the process of defibrillation, but rather used the criterion of static extracellular potential (Φe) gradient values above 5 V cm−1 in more than 95% of the volume of the passive ventricles during the shock as a surrogate for the DFT (Jolley et al. 2008). This criterion is based on the critical mass hypothesis, which postulates that a defibrillation shock is successful if it produces a strong Φe gradient over a large amount of ventricular tissue mass (Zipes et al. 1975; Zhou et al. 1993). This surrogate DFT criterion has been used in a number of computational defibrillation studies (Eason et al. 1998; de Jongh et al. 1999; Hunt & de Jongh Curry, 2004, 2006; Russomanno et al. 2008; Jolley et al. 2010). While Φe gradients are a determinant of post-shock activity in the heart, other mechanisms are at play as well (Knisley et al. 1999; Trayanova, 2001): not only Φe gradients but also cardiac tissue structure is responsible for virtual electrode polarizations (VEPs; depolarizing and hyperpolarizing changes in membrane potential in response to an electric field) that can generate or abolish wavefronts (Sobie et al. 1997; Efimov et al. 1998; Trayanova et al. 1998; Efimov & Ripplinger, 2006). In addition, not only what happens during the shock but events after the shock determine defibrillation outcome, as in the case of graded responses (Trayanova et al. 2003; Bourn et al. 2006) or tunnel propagation (Ashihara et al. 2008; Constantino et al. 2010). Thus, it remains questionable if any measure that accounts only for static Φe gradients could be a valid surrogate measure of defibrillation outcome, and whether such a criterion could be applied in determining the optimal ICD configurations in paediatric and CHD patients.
The aims of this study were: (1) to develop a new image processing pipeline for the construction of patient-specific heart–torso models from low-resolution clinical magnetic resonance imaging (MRI) data; (2) using this pipeline, to develop the first electrophysiological active heart–torso defibrillation model of a paediatric CHD patient, and to determine the optimal ICD configuration in that patient based on simulations of defibrillation outcome and DFT; and (3) to investigate if a measure of Φe gradients during the shock in a given volume of the ventricles can be used to predict defibrillation outcome and the DFT.
Methods
A brief presentation of the methods is given here; additional detail is provided in the Supplemental methods section.
Ethical approval
This study analysed de-identified, existing human MRI scans and was thus not considered human subject research according to Johns Hopkins Medicine Institutional Review Board guidelines.
Data acquisition
A clinical MRI (1.5 T) dataset had previously been acquired from a 14-year-old male paediatric patient with tricuspid valve atresia. The patient had a previous modified Blalock–Taussig shunt followed by bilateral bidirectional Glenn shunts. Finally, the patient had a Fontan procedure using a 12 mm extracardiac conduit. This patient was chosen for the anatomical complexity of his congenital condition and for MRI data quality; the patient did not receive an implanted defibrillator. The dataset had been de-identified before the study. Because of the tricuspid valve atresia, the right ventricle (RV) was hypoplastic and could not be delineated from the clinical low-resolution MRIs. This dataset included axial torso scans, and short-axis (SA) and long-axis (LA) cardiac cine scans. The axial image (27 slices, 384 × 300 pixels each) had a resolution of 1 × 1 × 6 mm3, and the SA cine scans (11 slices, 144 × 192 pixels each) had a resolution of 2 × 2 × 10 mm3 (Fig. 1A).
Figure 1. Model construction.
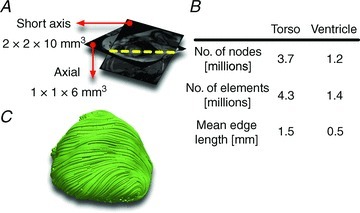
A, axial torso scans and short-axis cine scans of the paediatric CHD patient. B, the number of nodes, number of elements and mean edge length of the resulting torso mesh, and of the ventricular portion of the mesh. C, streamlined image of the fibre orientations in the ventricular mesh.
Image processing pipeline for heart–torso model construction from clinical MRI data
A novel pipeline was developed for constructing smooth and locally refined active heart–torso models with ventricular fibre architecture from low-resolution clinical MRI scans, using advanced image processing techniques. The heart–torso model of the paediatric patient with tricuspid valve atresia was used as the proof-of-principle example. The methodology described here can be applied to any clinical MRI dataset of similar (or higher) resolution.
In each slice in the axial torso image (27 slices in this dataset), tissue regions (six regions here: lungs, fat, bones, blood, muscles, torso outline) were manually labelled, creating several sets of binary image slices, each set corresponding to one tissue type. Each set was then interpolated into 1 mm isotropic resolution using the variational implicit functions method (Turk & O’Brien, 1999), and the interpolated data merged to form one image. The outer three pixels of the torso outline were then labelled as skin, and the remainder of the torso outline tissue type was labelled as conductive medium. By labelling the above tissue types, a segmented three-dimensional (3D) image of the torso labelled with tissue types (seven tissue types here, not yet including the heart) was generated. This labelled 3D image had a significantly smaller voxel size than the acquired clinical MRI, as interpolation estimated a large amount of missing data.
From the low-resolution SA cine image of the patient heart, a binary image of the ventricular geometry in diastole was built at a 1 mm isotropic voxel size (only the left ventricle in this patient as the RV could not be delineated). In this process, the breathing motion errors in the SA data were first eliminated based on horizontal and vertical LA scans, as described elsewhere (Elen et al. 2010). Epi- and endocardial contours were manually drawn on the motion-corrected SA slices, with papillary muscles included as part of the ventricular wall. The contours were interpolated to create a 1 mm isotropic 3D image of the ventricular geometry with separate labels for ventricular tissue and blood, as reported previously (Vadakkumpadan et al. 2012). This image was then merged with the segmented image of the torso by means of coordinate transformations calculated from acquired image header data, to create the final image of the torso and heart, labelled with different tissue types (eight tissue types here).
An unstructured mesh was automatically generated from the final image using the methodology developed by Prassl et al. (2009). This methodology employs an efficient octree-based algorithm to produce boundary-fitted, locally refined, smooth conformal meshes directly from segmented images. The ventricular region of the mesh was locally refined, and the rest of the torso coarsened, to reduce the mesh size without compromising important geometric detail. Mean edge length, number of nodes and number of elements of the tricuspid valve atresia heart–torso mesh in this study are given in Fig. 1B. Fibre and sheet orientations were assigned to the ventricular elements using a recently developed and validated rule-based technique (Bayer et al. 2012). Figure 1C presents a streamlined visualization of the fibre orientations. Additional details about the model construction pipeline can be found in the Supplemental methods section.
Model formulation and parameters
The finite element mesh constructed with the above pipeline was parameterized as described below to construct the first human heart–torso defibrillation model with an active, multi-scale model of the heart. The mathematical description of current flow in cardiac tissue was based on the bidomain and monodomain representations. The bidomain formulation was used when shocks were applied, and for computation of the electrocardiogram (ECG), whereas the computationally less demanding monodomain formulation was used to simulate propagation in the absence of externally applied electric fields. The bidomain and monodomain equations were solved with the Cardiac Arrhythmia Research Package (CARP) (Vigmond et al. 2002, 2003).
Ionic properties of cardiac myocytes were modelled with the ten Tusscher model of the human ventricular myocyte (ten Tusscher & Panfilov, 2006). Realistic apico-basal (Szentadrassy et al. 2005; Okada et al. 2011) and transmural (Glukhov et al. 2010; Moreno et al. 2011) electrophysiological heterogeneities were incorporated into the model, and longitudinal, transverse and sheet-normal conductivities (Poelzing et al. 2004; Caldwell et al. 2009) were chosen to achieve realistic propagation patterns as described in the Supplemental methods section. The conductivities of the non-ventricular tissue types (bones, lungs, skin, blood, muscles, fat, remaining conductive medium) were the same as in Jolley et al. (2008), with conductivity values of the skin assumed equal to that of the torso conductive medium (Jolley et al. 2008).
ICD placement
Due to the tricuspid valve atresia, there was no transvenous access to the RV and thus placement of a transvenous lead ICD was not possible. Hence, a non-standard ICD configuration had to be used. Several ICD configurations were tested using various locations of the ICD can and of the ICD lead (or leads in the case of configurations with multiple leads). Five realistic placement options for the ICD can were identified. Two of these ICD can locations were on the upper chest, two on the lower chest, and one was a sub-axillary location (Fig. 2). The dimensions of the ICD can were 6 × 5 × 1.5 cm3, roughly the size of most ICD cans used today. Next, six locations for the placement of the ICD lead were identified, three on the epicardium and three subcutaneous (Fig. 2). The choice of lead placement options was based on Stephenson et al. (2006), and enabled the exploration of both epicardial and subcutaneous lead locations and multiple electric field vectors. ICD lead dimensions were 5 × 0.2 × 0.2 cm3, roughly the size of the RV coil of a typical transvenous ICD lead, as this type of lead is commonly used ‘off-label’ for non-transvenous lead placement in the paediatric and CHD populations (Stephenson et al. 2006; Radbill et al. 2012). From the chosen ICD can and lead locations, 11 ICD configurations were assembled so that the shock vector would be across the ventricles for each configuration, and so that configurations with epicardial leads and with single and multiple subcutaneous leads could be tested. Thus, each ICD configuration consisted of one ICD can and between one and three ICD leads. Three of the 11 ICD configurations had epicardial leads, five had single subcutaneous leads and three had multiple subcutaneous leads (Fig. 2).
Figure 2. Implantable cardioverter–defibrillator placement.
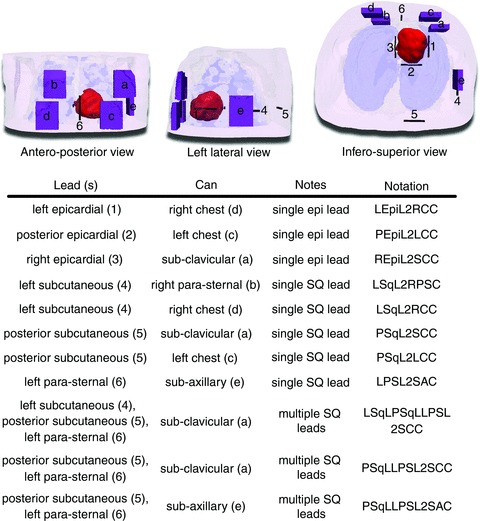
A, the finite element heart–torso mesh and ICD can (purple; a–e) and ICD lead (black; 1–6) placement locations. The ventricles are shown in red, skin in transparent pink, bones in transparent white and lungs in transparent blue. Segmented and modelled, but not shown here, were fat, blood, muscles and remaining conductive medium. B, the 11 ICD configurations that were tested in this study (characters and numbers in parentheses refer to A). Three configurations used epicardial (epi) leads, five used single subcutaneous (SQ) leads and three used multiple subcutaneous leads.
Study protocol
The ECGs were computed as described in the Supplemental methods section. As the heart model lacked a representation of the atria, the P wave was absent from the simulated ECGs. Sinus rhythm was simulated using a cable-based representation of the Purkinje system, where Purkinje activation in response to His bundle stimulation was simulated and junctional activation times were used as pacing timing offsets for sinus rhythm simulation (see Supplemental Fig. S2). Additional detail on the Purkinje cable formulation is given in the Supplemental methods section.
Defibrillation shocks were delivered to the constructed human heart–torso model, which incorporated the ionic processes in ventricular myocytes. VT and VF were induced as described in the Supplemental methods. To ensure shock delivery during different ‘phases’ of VF and VT, three different instants (or phases) during VF and three different instants during VT – i.e. different pre-shock transmembrane potential (Vm) distributions in the ventricles during VT and VF – were chosen to apply electric shocks to. Exponentially truncated, biphasic defibrillation or cardioversion shocks of 7 ms duration (3.5 ms duration and 50% tilt in each phase, positive polarity in first phase) as used in our previous study (Rantner et al. 2012), and based on experimental findings about effective defibrillation waveforms (Efimov et al. 1998), were applied from the ICD leads of the 11 ICD configurations, with the ICD can used as ground. A DFT grid – a 2D grid representing defibrillation outcomes for the 11 ICD configurations – for the three VF instants, and for a range of shock strengths, was assembled for shocks applied to the fibrillating heart, and a CVT grid – an analogue to the DFT grid, but representing the outcomes of VT cardioversion shocks – was constructed for shocks applied during VT. The DFT and CVT were defined as the lowest energy shocks that terminated the arrhythmia for all VF and VT phases, respectively. Arrhythmia was considered terminated if no propagation was present 1 s after shock onset. Further details on how the DFT and CVT grids were constructed are provided in the Supplemental methods.
The rationale for constructing both a DFT and a CVT grid to be used in choosing the optimal ICD configuration in the paediatric CHD patient was as follows. To prevent sudden cardiac death, an ICD must be capable of terminating VF. An ICD also needs to be able to terminate VT, as cardioversion by electric shock might have to be applied if anti-tachycardia pacing (ATP) fails (Kalra et al. 2012) or if ATP is not possible due to the absence of a pace–sense lead in certain ICD configurations. The occurrence of VT in CHD patients, specifically in patients with repaired tetralogy of Fallot, is well documented (Walsh, 2002; Nakazawa et al. 2004). ICD configurations that led to both low DFT and low CVT were considered favourable here.
Results
Heart–torso model and ECG
The tricuspid valve atresia heart–torso model is presented in Fig. 2; different tissue regions throughout the torso are clearly visible (shown are ventricle, bones, lungs and skin; not shown are blood, muscles, fat and remaining conductive medium). Select clinically recorded ECG traces from the tricuspid valve atresia patient as well as simulated ECGs are shown in Fig. 3. The simulated ECG traces match the clinical recordings very well, especially for the limb leads and augmented limb leads, showing that the heart–torso model is an appropriate representation of the patient's overall electrophysiology. Additional simulation results regarding the ECGs are provided in the Supplemental results section.
Figure 3. The electrocardiogram.
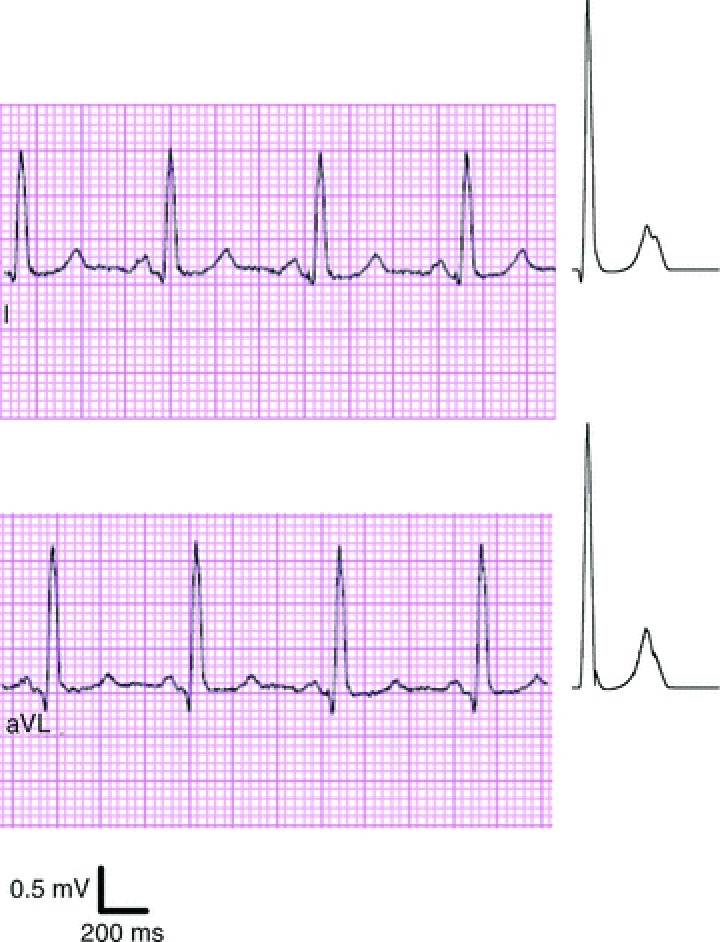
Sample clinically observed ECG traces (left panels) and simulated ECG traces (right panels) of the paediatric CHD patient with tricuspid valve atresia.
Defibrillation and cardioversion thresholds
Figure 4 shows Vm maps of the three VF and three VT pre-shock phases, along with 2 s excerpts of limb lead ECG recordings during VF and VT. Figure 5 presents the DFT grid for the 11 ICD configurations. DFTs were lowest for ICD configurations with an epicardial lead. Even the lowest DFT among ICD configurations with subcutaneous leads was four times the highest DFT for configurations with an epicardial lead. There was a four-fold difference between the highest and lowest DFTs among ICD configurations with a single subcutaneous lead. There was an eight-fold difference between the highest and lowest DFTs among ICD configurations with multiple subcutaneous. The highest DFT among all 11 ICD configurations was 64 times the lowest DFT.
Figure 4. Ventricular fibrillation and tachycardia.
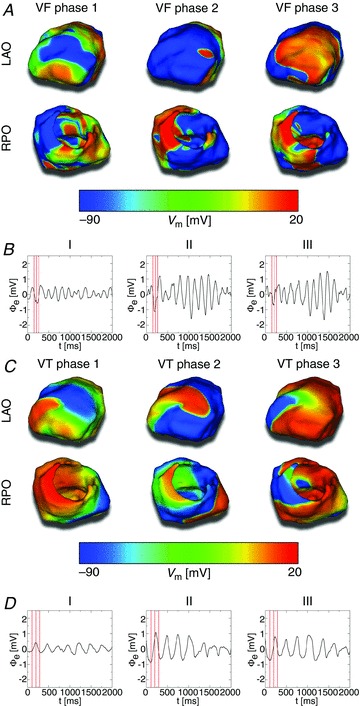
A, left anterior oblique (LAO; top row) and right posterior oblique (RPO; bottom row) Vm maps of the three VF phases to which defibrillation shocks were applied. B, limb lead ECG traces of VF. Red lines mark the three VF phases from A. C, LAO and RPO Vm maps of the three VT phases to which cardioversion shocks were applied. D, limb lead ECG traces of VT. Red lines mark the three VT phases from C.
Figure 5. Defibrillation threshold grid.
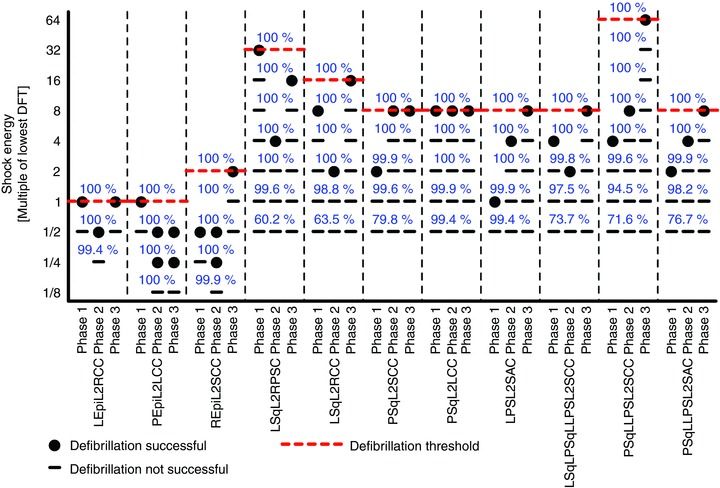
DFTs for the 11 tested ICD configurations. Red dashed lines mark the DFTs, and blue numbers show the percentage of ventricular volume experiencing Φe gradients ≥5 V cm−1 1 ms after shock onset. ICD configuration notation as in Fig. 2, and VF phases as in Fig. 4.
Figure 6 shows the CVT grid. Not only DFTs, but also CVTs were lowest for ICD configurations with epicardial leads. The lowest CVT for ICD configurations with subcutaneous leads was twice the highest CVT among any configuration with an epicardial lead. There was a four-fold difference between the highest and lowest CVTs among single subcutaneous lead ICD configurations. Likewise, the highest CVT of an ICD configuration with multiple subcutaneous leads was four times the lowest CVT among multiple subcutaneous lead configurations. Of all 11 ICD configurations, there was a 16-fold difference between the highest and lowest CVTs.
Figure 6. Cardioversion threshold grid.
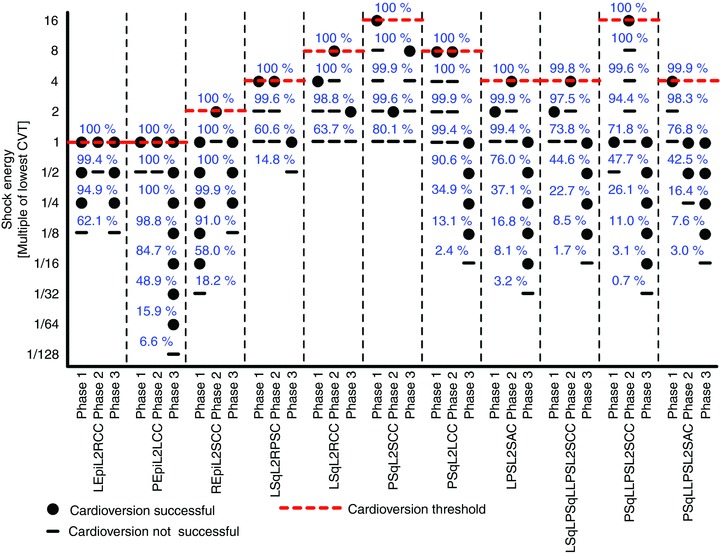
CVTs for the 11 tested ICD configurations. Red dashed lines mark the CVTs, VT phases are as in Fig. 4, and other annotations are as in Fig. 5.
The ICD configuration with a left epicardial lead and a right chest can (LEpiL2RCC in Figs 5 and 6) as well as the configuration with a posterior epicardial lead and a left chest can (PEpiL2LCC in Figs 5 and 6) had both the lowest DFT and CVT overall. Among the configurations with a single subcutaneous lead, a left para-sternal lead and sub-axillary can (LPSL2SAC in Figs 5 and 6) resulted in the lowest DFT and CVT. The same DFT and CVT was shared by two configurations with multiple subcutaneous leads: the ICD configuration with a left subcutaneous lead, a posterior subcutaneous lead, a left para-sternal lead and a sub-clavicular can (LSqLPSqLLPSL2SCC in Figs 5 and 6); and the configuration with a posterior subcutaneous lead, a left para-sternal lead and a sub-clavicular can (PSqLLPSL2SCC in Figs 5 and 6).
Extracellular potentials and the criterion for successful defibrillation
To determine whether a criterion using only Φe gradients can be used to predict defibrillation outcome and the DFT, as stated in the Introduction, we calculated Φe gradients during all defibrillation and cardioversion shocks. Figure 7 presents maps of Φe gradient distributions 1 ms after the onset of 80 J shocks. Data on the Φe gradients from Fig. 7 are also presented in Supplemental Table S3. Supplemental Figure S7 presents a plot of the Φe gradients from Fig. 7 against the corresponding DFTs and CVTs. The Φe gradients were largest during shocks from ICD configurations with epicardial leads, having a mean Φe gradient of 25.82 ± 6.21 V cm−1 in the ventricular volume. ICD configurations with multiple subcutaneous leads had a mean ventricular Φe gradient of 7.96 ± 0.26 V cm−1. Single subcutaneous lead ICD configurations had a mean Φe gradient of 7.80 ± 2.50 V cm−1 in the ventricle.
Figure 7. Extracellular potentials.
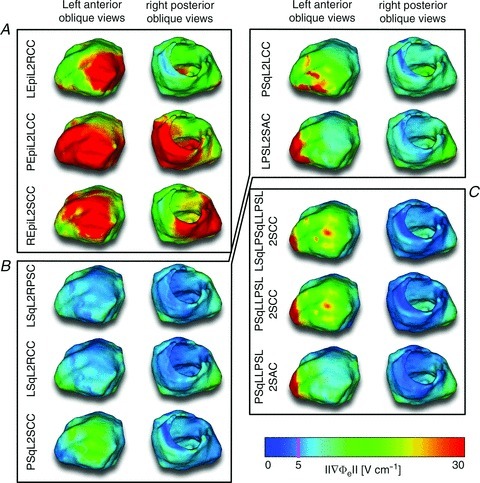
Left anterior oblique (left columns) and right posterior oblique (right columns) views of Φe gradient distributions 1 ms after shock onset of 80 J shocks. A, ICD configurations with epicardial leads. B, ICD configurations with single subcutaneous leads. C, ICD configurations with multiple subcutaneous leads. Note that 5 V cm−1 is marked by the magenta line in the colour bar.
While the Φe gradient distributions of two configurations with multiple subcutaneous leads (LSqLPSqLLPSL2SCC and PSqLLPSL2SCC in Fig. 7) looked virtually identical, one configuration had an eight times higher DFT (Fig. 5) and a four times higher CVT (Fig. 6) than the other. This indicated that Φe gradients alone were not determinants of defibrillation outcome.
To determine if a criterion used in many simulation studies – namely declaring defibrillation success if ≥95 % of ventricular tissue experienced Φe gradients ≥5 V cm−1 during the shock – is a valid surrogate measure for defibrillation success and the DFT, the amount of ventricular tissue experiencing Φe gradients ≥5 V cm−1 was determined for all defibrillation and cardioversion shocks. The blue numbers in Figs 5 and 6 show the percentage of ventricular volume that experienced Φe gradients ≥5 V cm−1 during the shocks (for reference, the threshold value of 5 V cm−1 is also marked in the colour bar of Fig. 7 with the magenta line). For a given shock energy, this percentage was generally higher for ICD configurations with epicardial leads than for subcutaneous leads. All DFT shocks resulted in Φe gradients ≥5 V cm−1 in 100% of ventricular tissue, and CVT shocks caused Φe gradients ≥5 V cm−1 in at least 99.5% of the ventricle. On the other hand, even a large number of shocks below the DFT and CVT resulted in Φe gradients ≥5 V cm−1 in 100% of ventricular tissue. For certain ICD configurations, shocks of only 6.25% of DFT strength experienced such Φe gradients in the entire ventricle, demonstrating that Φe gradients ≥5 V cm−1 in a certain fraction of the heart – or even in the entire heart – were not sufficient to predict defibrillation success or failure.
Discussion
In accordance with our aims, as stated in the Introduction, we developed a new image processing pipeline for building patient-specific heart–torso models from low-resolution, clinical MRIs. Using this pipeline, we constructed the first electrophysiological, active, multi-scale heart–torso model of a paediatric patient with CHD. We then conducted simulations to determine the optimal ICD configuration for this patient. Two configurations with epicardial leads exhibited the lowest DFTs and CVTs here and were thus the optimal choices. Finally, we endeavoured to establish whether the widely used criterion of shock-induced Φe gradients ≥5 V cm−1 in ≥95 % of ventricular volume predicts defibrillation success. Our study demonstrated that this criterion could not reliably predict defibrillation outcome; the predictions based on that criterion were very different from the predictions made with the detailed multiscale simulations used here.
While previous studies have also attempted to predict DFTs in computational torso models, most recently by Jolley et al. (2008) in CT-based models of paediatric and CHD patients, the current study provides three major advancements over these efforts: (1) our model was developed from readily available, clinical MRI scans instead of high-resolution CT scans; (2) we incorporated fibre architecture instead of using an isotropic ventricular model; and (3) our study used an electrophysiological, active ventricular model to simulate actual VF and defibrillation, as opposed to modelling only the applied electric field without the myocardial response to the field. To translate any computer model-based prediction of optimal ICD placement to the clinic, it would be desirable to use MRI instead of CT scans for model construction, circumventing concerns about radiation exposure; our model presents a major step in this direction. While the model presented here is, to the best of our knowledge, the first MRI-derived heart–torso model of a CHD patient reconstructed from MRI scans, attempts to construct heart–torso models from MRI datasets have been made in the past, but only for patients with structurally normal hearts. Such models have been employed in the study of defibrillation (Eason et al. 1998; de Jongh et al. 1999; Russomanno et al. 2008) as well as for other uses (Tilg et al. 2002; Berger et al. 2006; Vanheusden et al. 2012). None of these models, however, included an active ventricular model, and they were of much coarser resolution than our model – especially in the ventricular. The resolution of the finite element mesh of our model was fine enough to simulate electric propagation in detail, yet the overall number of nodes and elements was small enough for the model to be computationally tractable; in addition to ventricular tissue, the model also included representations of bones, lungs, blood, muscles, fat, skin and conductive medium with realistic conductivities in order to be able to accurately model the shock-induced electric fields in the torso. Our model overcomes the limitations of previous heart–torso models such as the use of a canine heart model instead of human (Eason et al. 1998), not accounting for fibre architecture and tissue anisotropy (de Jongh et al. 1999; Tilg et al. 2002; Berger et al. 2006; Russomanno et al. 2008; Vanheusden et al. 2012), or only estimating the myocardial surfaces based on a certain distance from ventricular blood masses, but not detecting and modelling the myocardial volume itself (Tilg et al. 2002; Berger et al. 2006). The model construction pipeline proposed here uses advanced image processing and meshing techniques to combine axial MRI and cine MRI scans to build a detailed heart–torso model with a high resolution and with smooth surfaces in the ventricles, and assigns fibre orientation based on chamber geometry. The pipeline can specifically be applied to construct models of paediatric and CHD patients.
Previous numerical defibrillation studies using torso models did not determine the actual DFT, but due to the lack of an active ventricular model, relied on a ‘pseudo-DFT’ criterion (lowest shock strength to result in Φe gradients ≥5 V cm−1 in ≥95 % of the passive ventricles) instead (Eason et al. 1998; de Jongh et al. 1999; Jolley et al. 2008, 2010; Russomanno et al. 2008). The current study used an active ventricular model, and enabled us not only to calculate Φe gradients but also to simulate the defibrillation process and determine the actual DFT for the tested ICD configurations. Simulating defibrillation is computationally much more demanding than only applying an electric field and computing Φe gradients in the passive heart model, so it would be beneficial if a pseudo-DFT criterion could be used instead of the actual DFT in attempts to optimize ICD placement. Our study demonstrated, however, that the pseudo-DFT criterion used in previous studies was not an appropriate predictor of the success or failure of defibrillation, as determined here: while all shocks at and above DFT fulfilled the pseudo-DFT criterion, many shocks below the DFT fulfilled that criterion as well. For some of the ICD configurations tested, there were Φe gradients ≥5 V cm−1 in the entire ventricles for shock strengths as low as 6.25% of DFT. Furthermore, we observed Φe gradient distributions that were virtually identical, where one configuration had an eight times higher DFT than the other. Thus, a criterion using the Φe gradient in a critical mass of tissue was not found to be reliable in predicting the optimal placement of ICDs. Mechanistically, Φe gradients cannot be used to predict the DFT because they do not relate to the specific processes responsible for defibrillation failure, such as propagated graded responses (Trayanova et al. 2003; Bourn et al. 2006) and tunnel propagation (Ashihara et al. 2008; Constantino et al. 2010). Following the shock, a VEP distribution is established in the tissue, from which the post-shock activations emanate (Trayanova, 2001; Trayanova et al. 2011). It is now well understood that not only Φe gradients but also ventricular tissue structures and tissue anisotropy shape the VEP distribution in the ventricles (Arevalo et al. 2007; Trayanova et al. 2011), which in turn can create or abolish propagating re-entrant waves (Trayanova et al. 1998; Efimov & Ripplinger, 2006). A possible compromise to decrease the computational load would be a two-stage approach in which the epicardial potentials are calculated from a passive torso model and then used as boundary conditions for the active simulation of defibrillation in the ventricles.
Our simulations demonstrated that ICD configurations incorporating epicardial leads had lower DFTs and CVTs than configurations with subcutaneous leads in the tricuspid valve atresia patient in this study. Specifically, two configurations with epicardial leads – one with a left epicardial lead and a right chest can, and the other a posterior epicardial lead and a left chest can – exhibited the lowest DFT and CVT and were thus the optimal ICD configurations tested. Three configurations with subcutaneous leads (one with a single lead and two with multiple leads) were electrically most favourable among subcutaneous lead ICD configurations. The single subcutaneous lead option among these three configurations had a left para-sternal lead and sub-axillary can and corresponded to the commercially available subcutaneous ICD (S-ICD®; Cameron Health Inc., San Clemente, CA, USA; Bardy et al. 2010). Our findings regarding the optimal ICD configuration are clearly specific to this patient, and may not be generalizable to the entire paediatric or CHD population. The depth of the ICD can placement may also play a role in determining how electrically favourable an ICD configuration is. As an example of such placement, we also calculated the DFT for a deeper sub-axillary ICD can location; the results are shown in Supplemental Fig. S8.
In addition to choosing an electrically favourable ICD configuration, the physician may also take additional considerations into account when deciding on which placement option to use. First, the invasiveness of the implant procedure could play a role in decision making, especially when taking into consideration the possibility of multiple ICD and lead exchanges over the CHD or paediatric patient's lifetime (Alexander et al. 2004; Cecchin et al. 2010). Second, complications associated with a particular placement option is an important consideration (Griksaitis et al. 2013). Non-transvenous shock coil failure has been shown to be of particular concern in the paediatric and CHD populations (Radbill et al. 2010). It has been reported that epicardial defibrillation leads are more vulnerable to lead break and physical damage than the thinner pace–sense leads commonly associated with subcutaneous lead placement (with the exception of the S-ICD®, which does not include a pace–sense lead and does not have pacing capacity; Griksaitis et al. 2013). Third, the patient might require pacing, which would rule out ICD configurations that lack pacing capacity. These three issues could be taken together with the predictions of our pipeline to make a decision regarding the best treatment option for the specific patient.
Large DFT and CVT differences were observed between ICD configurations, underlining the importance of choosing the optimal ICD configuration. Furthermore, clinical data evaluating the DFTs of different ICD configurations in paediatric and CHD patients are scarce (Radbill et al. 2012), so physicians cannot currently rely on published reports when deciding which ICD configuration to use in a patient of this cohort. The pipeline and methodology developed in this study presents a novel approach to predicting the optimal ICD configurations before device implantation, a tool particularly important for paediatric and CHD patients who often have contraindications for transvenous lead ICD implantation.
Limitations
There are several limitations in the modelling methodology presented here. (1) Fibre orientations in skeletal muscles were not represented, and thus the skeletal muscles were modelled as isotropic tissue. Seitz et al. (2008) showed that skeletal tissue anisotropy had a much smaller effect on the electric fields of transthoracic defibrillation shocks than myocardial tissue anisotropy. As ICD shocks have to traverse less muscle tissue than transthoracic shocks, the influence of skeletal muscle anisotropy would be even smaller here than in the case of transthoracic shocks, so we do not expect our findings to be affected by this limitation. (2) Abdominal MRI scans of this patient were not available, so no abdominal ICD locations could be modelled. However, the modelling pipeline enables the modelling of abdominal configurations if abdominal scans are available. (3) Our model lacked a patient-specific representation of the Purkinje system, but featured a generic, cable-based Purkinje representation to simulate sinus rhythm. Since Dosdall et al. (2010) demonstrated that the Purkinje system was not involved in defibrillation mechanisms after short-duration VT or VF, the lack of a patient-specific Purkinje representation does not affect the validity of our findings. (4) It is unknown whether fibre orientations have the same relationship to chamber geometry in the CHD ventricles as in the normal ventricles. In the absence of such knowledge, the methodology used previously in structurally normal hearts was employed in the modelling pipeline to assign the fibre orientations based on the ventricular geometry of paediatric and/or CHD hearts. (5) If paediatric or CHD patients have previous devices implanted, they might not be able to undergo MRI scans, unless the prior devices are MRI compatible. In this case, CT scans could be used instead of MRI scans in our modelling pipeline. (6) The prediction of optimal ICD configurations using the modelling pipeline could not be validated against patient outcomes in this study.
Translational perspective
ICDs with transvenous leads often cannot be deployed in a standard manner in paediatric and CHD patients. Currently, there is no reliable approach to predict the optimal ICD placement in these patients. A pipeline for constructing personalized, biophysically detailed active heart–torso models from clinical MRI scans was developed and applied to a paediatric CHD patient. Optimal ICD placement was determined by conducting patient-specific simulations of shock delivery from different ICD configurations and determining the corresponding defibrillation thresholds. In a patient with tricuspid valve atresia, two ICD configurations with epicardial leads were found to have the lowest defibrillation threshold. We demonstrated that determining extracellular potential (Φe) gradients during the shock – without actually simulating defibrillation – was not sufficient to predict defibrillation success or failure. Using the proposed methodology, the optimal ICD placement in paediatric/CHD patients can be predicted computationally, which could reduce defibrillation energy if the pipeline is used as part of ICD implantation planning.
Acknowledgments
We are very grateful for the help of Dr Patrick M. Boyle, who created the cable-based representation of the Purkinje system for this model (see Supplemental methods).
Glossary
- 3D
three-dimensional
- ATP
anti-tachycardia pacing
- CHD
congenital heart defect
- CT
computed tomography
- CVT
cardioversion threshold
- DFT
defibrillation threshold
- ECG
electrocardiogram
- ICD
implantable cardioverter-defibrillator
- LA
long axis
- MRI
magnetic resonance imaging/image
- RV
right ventricle
- S-ICD®
subcutaneous implantable cardioverter-defibrillator
- SA
short axis
- VEP
virtual electrode polarization
- VF
ventricular fibrillation
- Vm
transmembrane potential
- VT
ventricular tachycardia
- Φe
extracellular potential
Additional information
Competing interest
N.A.T. has partial ownership of CardioSolv, LLC. CardioSolv, LLC was not involved in this research.
Author contributions
Conception and design of the experiments: L.J.R. and N.A.T. conceptualized and designed the study, with significant contributions from J.E.C. F.V., L.J.R. and N.A.T. conceptualized and designed the model creation pipeline, with significant contributions from P.J.S. (at Johns Hopkins University, Baltimore). Collection, analysis and interpretation of data: P.J.S. collected and provided the MRI scans. F.V. and L.J.R. constructed the model, with critical input from P.J.S. L.J.R. performed the computer simulations. L.J.R. and N.A.T. analysed the data, with important contributions from J.E.C. (at Johns Hopkins University, Baltimore). Drafting the article or revising it critically for important intellectual content: L.J.R. drafted the overall manuscript, F.V. drafted the model creation sections in Methods, and N.A.T. critically revised the manuscript (at Johns Hopkins University, Baltimore).
Funding
This study was supported by National Institutes of Health (NIH) grant R01-HL103428 to N.A.T., and by National Science Foundation (NSF) grant CDI-1124804 to N.A.T.
Supplementary material
Supplemental methods section
Supplemental Fig. S2
Supplemental Table S3
Supplemental Figure S7
Supplemental Fig. S8
Supplemental results section
Supplemental methods
References
- Alexander ME, Cecchin F, Walsh EP, Triedman JK, Bevilacqua LM, Berul CI. Implications of implantable cardioverter defibrillator therapy in congenital heart disease and pediatrics. J Cardiovasc Electrophysiol. 2004;15:72–76. doi: 10.1046/j.1540-8167.2004.03388.x. [DOI] [PubMed] [Google Scholar]
- Arevalo H, Rodriguez B, Trayanova N. Arrhythmogenesis in the heart: multiscale modelling of the effects of defibrillation shocks and the role of electrophysiological heterogeneity. Chaos. 2007;17:015103. doi: 10.1063/1.2430637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashihara T, Constantino J, Trayanova NA. Tunnel propagation of postshock activations as a hypothesis for fibrillation induction and isoelectric window. Circ Res. 2008;102:737–745. doi: 10.1161/CIRCRESAHA.107.168112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bardy GH, Smith WM, Hood MA, Crozier IG, Melton IC, Jordaens L, Theuns D, Park RE, Wright DJ, Connelly DT, Fynn SP, Murgatroyd FD, Sperzel J, Neuzner J, Spitzer SG, Ardashev AV, Oduro A, Boersma L, Maass AH, Van Gelder IC, Wilde AA, van Dessel PF, Knops RE, Barr CS, Lupo P, Cappato R, Grace AA. An entirely subcutaneous implantable cardioverter-defibrillator. N Engl J Med. 2010;363:36–44. doi: 10.1056/NEJMoa0909545. [DOI] [PubMed] [Google Scholar]
- Bayer JD, Blake RC, Plank G, Trayanova NA. A novel rule-based algorithm for assigning myocardial fibre orientation to computational heart models. Ann Biomed Eng. 2012;40:2243–2254. doi: 10.1007/s10439-012-0593-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger T, Fischer G, Pfeifer B, Modre R, Hanser F, Trieb T, Roithinger FX, Stuehlinger M, Pachinger O, Tilg B, Hintringer F. Single-beat noninvasive imaging of cardiac electrophysiology of ventricular pre-excitation. J Am Coll Cardiol. 2006;48:2045–2052. doi: 10.1016/j.jacc.2006.08.019. [DOI] [PubMed] [Google Scholar]
- Berul CI, Triedman JK, Forbess J, Bevilacqua LM, Alexander ME, Dahlby D, Gilkerson JO, Walsh EP. Minimally invasive cardioverter defibrillator implantation for children: an animal model and pediatric case report. Pacing Clin Electrophysiol. 2001;24:1789–1794. doi: 10.1046/j.1460-9592.2001.01789.x. [DOI] [PubMed] [Google Scholar]
- Berul CI, Van Hare GF, Kertesz NJ, Dubin AM, Cecchin F, Collins KK, Cannon BC, Alexander ME, Triedman JK, Walsh EP, Friedman RA. Results of a multicenter retrospective implantable cardioverter-defibrillator registry of pediatric and congenital heart disease patients. J Am Coll Cardiol. 2008;51:1685–1691. doi: 10.1016/j.jacc.2008.01.033. [DOI] [PubMed] [Google Scholar]
- Bourn DW, Gray RA, Trayanova NA. Characterization of the relationship between preshock state and virtual electrode polarization-induced propagated graded responses resulting in arrhythmia induction. Heart Rhythm. 2006;3:583–595. doi: 10.1016/j.hrthm.2006.01.024. [DOI] [PubMed] [Google Scholar]
- Brenner DJ, Hall EJ. Computed tomography–an increasing source of radiation exposure. N Engl J Med. 2007;357:2277–2284. doi: 10.1056/NEJMra072149. [DOI] [PubMed] [Google Scholar]
- Caldwell BJ, Trew ML, Sands GB, Hooks DA, LeGrice IJ, Smaill BH. Three distinct directions of intramural activation reveal nonuniform side-to-side electrical coupling of ventricular myocytes. Circ Arrhythm Electrophysiol. 2009;2:433–440. doi: 10.1161/CIRCEP.108.830133. [DOI] [PubMed] [Google Scholar]
- Cecchin F, Atallah J, Walsh EP, Triedman JK, Alexander ME, Berul CI. Lead extraction in pediatric and congenital heart disease patients. Circ Arrhythm Electrophysiol. 2010;3:437–444. doi: 10.1161/CIRCEP.110.957324. [DOI] [PubMed] [Google Scholar]
- Constantino J, Long Y, Ashihara T, Trayanova NA. Tunnel propagation following defibrillation with ICD shocks: hidden postshock activations in the left ventricular wall underlie isoelectric window. Heart Rhythm. 2010;7:953–961. doi: 10.1016/j.hrthm.2010.03.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Jongh AL, Entcheva EG, Replogle JA, Booker RS, 3rd, Kenknight BH, Claydon FJ. Defibrillation efficacy of different electrode placements in a human thorax model. Pacing Clin Electrophysiol. 1999;22:152–157. doi: 10.1111/j.1540-8159.1999.tb00323.x. [DOI] [PubMed] [Google Scholar]
- Dosdall DJ, Osorio J, Robichaux RP, Huang J, Li L, Ideker RE. Purkinje activation precedes myocardial activation following defibrillation after long-duration ventricular fibrillation. Heart Rhythm. 2010;7:405–412. doi: 10.1016/j.hrthm.2009.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eason J, Schmidt J, Dabasinskas A, Siekas G, Aguel F, Trayanova N. Influence of anisotropy on local and global measures of potential gradient in computer models of defibrillation. Ann Biomed Eng. 1998;26:840–849. doi: 10.1114/1.68. [DOI] [PubMed] [Google Scholar]
- Efimov I, Ripplinger CM. Virtual electrode hypothesis of defibrillation. Heart Rhythm. 2006;3:1100–1102. doi: 10.1016/j.hrthm.2006.03.005. [DOI] [PubMed] [Google Scholar]
- Efimov IR, Cheng Y, Van Wagoner DR, Mazgalev T, Tchou PJ. Virtual electrode-induced phase singularity: a basic mechanism of defibrillation failure. Circ Res. 1998;82:918–925. doi: 10.1161/01.res.82.8.918. [DOI] [PubMed] [Google Scholar]
- Elen A, Hermans J, Ganame J, Loeckx D, Bogaert J, Maes F, Suetens P. Automatic 3-D breath-hold related motion correction of dynamic multislice MRI. IEEE Trans Med Imaging. 2010;29:868–878. doi: 10.1109/TMI.2009.2039145. [DOI] [PubMed] [Google Scholar]
- Glukhov AV, Fedorov VV, Lou Q, Ravikumar VK, Kalish PW, Schuessler RB, Moazami N, Efimov IR. Transmural dispersion of repolarization in failing and nonfailing human ventricle. Circ Res. 2010;106:981–991. doi: 10.1161/CIRCRESAHA.109.204891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gradaus R, Hammel D, Kotthoff S, Bocker D. Nonthoracotomy implantable cardioverter defibrillator placement in children: use of subcutaneous array leads and abdominally placed implantable cardioverter defibrillators in children. J Cardiovasc Electrophysiol. 2001;12:356–360. doi: 10.1046/j.1540-8167.2001.00356.x. [DOI] [PubMed] [Google Scholar]
- Griksaitis MJ, Rosengarten JA, Gnanapragasam JP, Haw MP, Morgan JM. Implantable cardioverter defibrillator therapy in paediatric practice: a single-centre UK experience with focus on subcutaneous defibrillation. Europace. 2013;15:523–530. doi: 10.1093/europace/eus388. [DOI] [PubMed] [Google Scholar]
- Hunt LC, de Jongh Curry AL. Finite element computer modelling of transthoracic atrial defibrillation. Conf Proc IEEE Eng Med Biol Soc. 2004;6:3964–3967. doi: 10.1109/IEMBS.2004.1404107. [DOI] [PubMed] [Google Scholar]
- Hunt LC, de Jongh Curry AL. Transthoracic atrial defibrillation energy thresholds are correlated to uniformity of current density distributions. Conf Proc IEEE Eng Med Biol Soc. 2006;1:4374–4377. doi: 10.1109/IEMBS.2006.259490. [DOI] [PubMed] [Google Scholar]
- Jolley M, Stinstra J, Pieper S, Macleod R, Brooks DH, Cecchin F, Triedman JK. A computer modelling tool for comparing novel ICD electrode orientations in children and adults. Heart Rhythm. 2008;5:565–572. doi: 10.1016/j.hrthm.2008.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolley M, Stinstra J, Tate J, Pieper S, Macleod R, Chu L, Wang P, Triedman JK. Finite element modelling of subcutaneous implantable defibrillator electrodes in an adult torso. Heart Rhythm. 2010;7:692–698. doi: 10.1016/j.hrthm.2010.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalra Y, Radbill AE, Johns JA, Fish FA, Kannankeril PJ. Antitachycardia pacing reduces appropriate and inappropriate shocks in children and congenital heart disease patients. Heart Rhythm. 2012;9:1829–1834. doi: 10.1016/j.hrthm.2012.06.042. [DOI] [PubMed] [Google Scholar]
- Knisley SB, Trayanova N, Aguel F. Roles of electric field and fibre structure in cardiac electric stimulation. Biophys J. 1999;77:1404–1417. doi: 10.1016/S0006-3495(99)76989-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen GK, Evans J, Lambert WE, Chen Y, Raitt MH. Shocks burden and increased mortality in implantable cardioverter-defibrillator patients. Heart Rhythm. 2011;8:1881–1886. doi: 10.1016/j.hrthm.2011.07.036. [DOI] [PubMed] [Google Scholar]
- Maisel WH. Pacemaker and ICD generator reliability: meta-analysis of device registries. JAMA. 2006;295:1929–1934. doi: 10.1001/jama.295.16.1929. [DOI] [PubMed] [Google Scholar]
- Moreno JD, Zhu ZI, Yang PC, Bankston JR, Jeng MT, Kang C, Wang L, Bayer JD, Christini DJ, Trayanova NA, Ripplinger CM, Kass RS, Clancy CE. A computational model to predict the effects of class I anti-arrhythmic drugs on ventricular rhythms. Sci Transl Med. 2011;3:98ra83. doi: 10.1126/scitranslmed.3002588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakazawa M, Shinohara T, Sasaki A, Echigo S, Kado H, Niwa K, Oyama K, Yokota M, Iwamoto M, Fukushima N, Nagashima M, Nakamura Y. Arrhythmias late after repair of tetralogy of fallot: a Japanese Multicenter Study. Circ J. 2004;68:126–130. doi: 10.1253/circj.68.126. [DOI] [PubMed] [Google Scholar]
- Okada J, Washio T, Maehara A, Momomura S, Sugiura S, Hisada T. Transmural and apicobasal gradients in repolarization contribute to T-wave genesis in human surface ECG. Am J Physiol Heart Circ Physiol. 2011;301:H200–208. doi: 10.1152/ajpheart.01241.2010. [DOI] [PubMed] [Google Scholar]
- Poelzing S, Akar FG, Baron E, Rosenbaum DS. Heterogeneous connexin43 expression produces electrophysiological heterogeneities across ventricular wall. Am J Physiol Heart Circ Physiol. 2004;286:H2001–2009. doi: 10.1152/ajpheart.00987.2003. [DOI] [PubMed] [Google Scholar]
- Prassl AJ, Kickinger F, Ahammer H, Grau V, Schneider JE, Hofer E, Vigmond EJ, Trayanova NA, Plank G. Automatically generated, anatomically accurate meshes for cardiac electrophysiology problems. IEEE Trans Biomed Eng. 2009;56:1318–1330. doi: 10.1109/TBME.2009.2014243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radbill AE, Triedman JK, Berul CI, Fynn-Thompson F, Atallah J, Alexander ME, Walsh EP, Cecchin F. System survival of nontransvenous implantable cardioverter-defibrillators compared to transvenous implantable cardioverter-defibrillators in pediatric and congenital heart disease patients. Heart Rhythm. 2010;7:193–198. doi: 10.1016/j.hrthm.2009.10.014. [DOI] [PubMed] [Google Scholar]
- Radbill AE, Triedman JK, Berul CI, Walsh EP, Alexander ME, Webster G, Cecchin F. Prospective evaluation of defibrillation threshold and postshock rhythm in young ICD recipients. Pacing Clin Electrophysiol. 2012;35:1487–1493. doi: 10.1111/j.1540-8159.2012.03519.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rantner LJ, Arevalo HJ, Constantino JL, Efimov IR, Plank G, Trayanova NA. Three-dimensional mechanisms of increased vulnerability to electric shocks in myocardial infarction: altered virtual electrode polarizations and conduction delay in the peri-infarct zone. J Physiol. 2012;590:4537–4551. doi: 10.1113/jphysiol.2012.229088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russomanno DJ, de Jongh Curry AL, Atanasova GS, Hunt LC, Caleb Goodwin JC. DefibViz: a visualization tool for the assessment of electrode parameters on transthoracic defibrillation thresholds. IEEE Trans Inf Technol Biomed. 2008;12:76–86. doi: 10.1109/TITB.2007.899511. [DOI] [PubMed] [Google Scholar]
- Seitz SA, Seemann G, Dossel O. Influence of tissue anisotropy on the distribution of defibrillation fields. Computing in Cardiology (CinC) 2008;35:489–492. Conf Proc. [Google Scholar]
- Silka MJ, Kron J, Dunnigan A, Dick M., 2nd Sudden cardiac death and the use of implantable cardioverter-defibrillators in pediatric patients. The Pediatric Electrophysiology Society. Circulation. 1993;87:800–807. doi: 10.1161/01.cir.87.3.800. [DOI] [PubMed] [Google Scholar]
- Sobie EA, Susil RC, Tung L. A generalized activating function for predicting virtual electrodes in cardiac tissue. Biophys J. 1997;73:1410–1423. doi: 10.1016/S0006-3495(97)78173-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephenson EA, Batra AS, Knilans TK, Gow RM, Gradaus R, Balaji S, Dubin AM, Rhee EK, Ro PS, Thogersen AM, Cecchin F, Triedman JK, Walsh EP, Berul CI. A multicenter experience with novel implantable cardioverter defibrillator configurations in the pediatric and congenital heart disease population. J Cardiovasc Electrophysiol. 2006;17:41–46. doi: 10.1111/j.1540-8167.2005.00271.x. [DOI] [PubMed] [Google Scholar]
- Szentadrassy N, Banyasz T, Biro T, Szabo G, Toth BI, Magyar J, Lazar J, Varro A, Kovacs L, Nanasi PP. Apico-basal inhomogeneity in distribution of ion channels in canine and human ventricular myocardium. Cardiovasc Res. 2005;65:851–860. doi: 10.1016/j.cardiores.2004.11.022. [DOI] [PubMed] [Google Scholar]
- ten Tusscher KH, Panfilov AV. Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol Heart Circ Physiol. 2006;291:H1088–1100. doi: 10.1152/ajpheart.00109.2006. [DOI] [PubMed] [Google Scholar]
- Thogersen AM, Helvind M, Jensen T, Andersen JH, Jacobsen JR, Chen X. Implantable cardioverter defibrillator in a 4-month-old infant with cardiac arrest associated with a vascular heart tumor. Pacing Clin Electrophysiol. 2001;24:1699–1700. doi: 10.1046/j.1460-9592.2001.01699.x. [DOI] [PubMed] [Google Scholar]
- Tilg B, Fischer G, Modre R, Hanser F, Messnarz B, Schocke M, Kremser C, Berger T, Hintringer F, Roithinger FX. Model-based imaging of cardiac electrical excitation in humans. IEEE Trans Med Imaging. 2002;21:1031–1039. doi: 10.1109/TMI.2002.804438. [DOI] [PubMed] [Google Scholar]
- Trayanova N. Concepts of ventricular defibrillation. Phil Trans R Soc Lond A. 2001;359:1327–1337. [Google Scholar]
- Trayanova N, Constantino J, Ashihara T, Plank G. Modeling defibrillation of the heart: approaches and insights. IEEE Rev Biomed Eng. 2011;4:89–102. doi: 10.1109/RBME.2011.2173761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trayanova N, Skouibine K, Moore P. Virtual electrode effects in defibrillation. Prog Biophys Mol Biol. 1998;69:387–403. doi: 10.1016/s0079-6107(98)00016-9. [DOI] [PubMed] [Google Scholar]
- Trayanova NA, Gray RA, Bourn DW, Eason JC. Virtual electrode-induced positive and negative graded responses: new insights into fibrillation induction and defibrillation. J Cardiovasc Electrophysiol. 2003;14:756–763. doi: 10.1046/j.1540-8167.2003.03042.x. [DOI] [PubMed] [Google Scholar]
- Turk G, O’Brien JF. Shape transformation using variational implicit functions. SIGGRAPH 99. 1999:335–342. Conf Proc ACM. [Google Scholar]
- Vadakkumpadan F, Trayanova N, Younes L, Wu KC. Left-ventricular shape analysis for predicting sudden cardiac death risk. Conf Proc IEEE Engineering in Medicine and Biology Society. 2012;2012:4067–4070. doi: 10.1109/EMBC.2012.6346860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanheusden F, Loures Salinet J, Nicolson WB, McCann GP, Ng GA, Schlindwein FS. Patient-specific three-dimensional torso models for analysing cardiac activity. Computing in Cardiology (CinC) 2012:973–976. Conf Proc. [Google Scholar]
- Vigmond EJ, Aguel F, Trayanova NA. Computational techniques for solving the bidomain equations in three dimensions. IEEE Trans Biomed Eng. 2002;49:1260–1269. doi: 10.1109/TBME.2002.804597. [DOI] [PubMed] [Google Scholar]
- Vigmond EJ, Hughes M, Plank G, Leon LJ. Computational tools for modelling electrical activity in cardiac tissue. J Electrocardiol. 2003;36(Suppl):69–74. doi: 10.1016/j.jelectrocard.2003.09.017. [DOI] [PubMed] [Google Scholar]
- Walcott GP, Killingsworth CR, Ideker RE. Do clinically relevant transthoracic defibrillation energies cause myocardial damage and dysfunction. Resuscitation. 2003;59:59–70. doi: 10.1016/s0300-9572(03)00161-8. [DOI] [PubMed] [Google Scholar]
- Walsh EP. Arrhythmias in patients with congenital heart disease. Card Electrophysiol Rev. 2002;6:422–430. doi: 10.1023/a:1021192526642. [DOI] [PubMed] [Google Scholar]
- Zhou X, Daubert JP, Wolf PD, Smith WM, Ideker RE. Epicardial mapping of ventricular defibrillation with monophasic and biphasic shocks in dogs. Circ Res. 1993;72:145–160. doi: 10.1161/01.res.72.1.145. [DOI] [PubMed] [Google Scholar]
- Zipes DP, Fischer J, King RM, Nicoll Ad, Jolly WW. Termination of ventricular fibrillation in dogs by depolarizing a critical amount of myocardium. Am J Cardiol. 1975;36:37–44. doi: 10.1016/0002-9149(75)90865-6. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


