The compression of deaths above the mode

Abstract

Kannisto (2001) has shown that as the frequency distribution of ages at death has shifted to the right, the age distribution of deaths above the modal age has become more compressed. In order to further investigate this old-age mortality compression, we adopt the simple logistic model with two parameters, which is known to fit data on old-age mortality well (Thatcher 1999). Based on the model, we show that three key measures of old-age mortality (the modal age of adult deaths, the life expectancy at the modal age, and the standard deviation of ages at death above the mode) can be estimated fairly accurately from death rates at only two suitably chosen high ages (70 and 90 in this study). The distribution of deaths above the modal age becomes compressed when the logits of death rates fall more at the lower age than at the higher age. Our analysis of mortality time series in six countries, using the logistic model, endorsed Kannisto’s conclusion. Some possible reasons for the compression are discussed.

1. Background

The substantial decline of overall mortality since the nineteenth century made it possible for a larger proportion of people to survive to old ages, thereby concentrating deaths into a relatively narrow range of old age. This has made the survival curve (the life-table l(x) function) more rectangular and the age distribution of deaths (the life-table d(x) function) more compressed (Comfort 1956; Fries 1980; Wilmoth and Horiuchi 1999).

The considerable decline of death rates in childhood and young adult ages during the first half of the twentieth century was the major driving force of the mortality compression. Then, significant declines in old-age mortality started in economically developed countries during the second half of the twentieth century (Kannisto et al. 1984). In this period, the compression of the overall death distribution was slow, and even almost stagnant in some populations (Wilmoth and Horiuchi 1999; Yashin et al. 2001). Thus, changes in the distribution of adult deaths during the last few decades is shown to be approximated well by models in which the distribution is assumed to shift to the right without changing its shape (Bongaarts 2005; Canudas-Romo 2010, forthcoming).

However, in the context of the longevity extension, it has become increasingly important to distinguish old-age mortality compression from overall mortality compression, and to analyze changes in the shape of age distribution of deaths at very old ages separately from changes in the age distribution of deaths over the entire lifespan (or over a broad range of adult ages). Based on the model of death distribution by Lexis (1878), Kannisto (2000, 2001) focused on the modal age of adult deaths as an important central tendency measure of longevity, and examined the dispersion of deaths above the mode. He presented extensive evidence to show that the distribution of deaths at old ages was not simply sliding to the right. Instead, the right hand downward slope was being flattened vertically, so that the distribution became more compressed, as if (in his words) it was meeting an invisible wall. He contended that the ascending trajectory of mortality at high ages formed such a barrier but only in a relative sense, offering increasing resistance to further progress without setting any definite limit to it.

Kannisto’s method of analysing this old-age mortality compression was to calculate the modal age of adult deaths M, the expectation of life at the mode, denoted by e(M), and the standard deviation (root mean square) of those individual life deviations from M for those who live up to age M or longer. This upward standard deviation is denoted as SD(M+). A formal definition is given in the next section. He found that in cases where M had risen, there had generally been a fall in both e(M) and SD(M+). Since these are measures of dispersion, their fall showed that the distribution of ages at death above the mode had become more compressed. Kannisto’s approach with focus on M has been elaborated further in recent studies by Cheung and her collaborators (Cheung et al. 2005, 2008, 2009; Cheung and Robine 2007; Robine et al. 2006) and Canudas-Romo (2010, forthcoming).

The mortality compression can be analyzed with respect to the age pattern of mortality (life-table m(x) or q(x) function) as well, because the q(x), d(x), and l(x) functions uniquely determine each other. In general, a faster mortality reduction at younger ages leads to a steeper age-associated increase in mortality, thereby concentrating deaths in older ages. Previous research on age patterns of adult mortality by Strehler and Mildvan (1960) and Gavrilov and Gavrilova (1991) are closely related to mortality compression. Using the international data, Strehler and Mildvan have shown that two parameters of the Gompertz model are negatively correlated, indicating the following tendency: as the level of adult mortality declines, the mortality curve rises more steeply upward. Gavrilov and Gavrilova use the Makeham model to show that the Strehler-Mildvan correlation is largely due to the substantial reduction of background mortality (premature mortality unrelated to senescence). However, even after the effect of background mortality has been removed, the two parameters of the Gompertz term of the Makeham model remain negatively associated, suggesting that the reduction of senescence-related mortality may produce some compression in the senescent death distribution.

The study by Strehler and Mildvan and that by Gavrilov and Gavrilova are based on the Gompertz model and Makeham model, respectively, and the data analyzed in those studies are mainly for periods before the onset of considerable decline in old-age mortality. However, an extensive analysis of old-age mortality data (Kannisto-Thatcher database) has revealed that the age-related mortality increase tends to slow down at very old ages, which cannot be captured by the Gompertz or Makeham model, and age patterns of old-age mortality are well represented by logistic models (Thatcher 1999; Thatcher et al. 1998).

In this paper, we will investigate the compression of old-age mortality by combining a simple version of logistic model with Kannisto’s analytical tools. In what follows, we present our methodology, show results of its application to time series of official life tables for England and Wales and life tables for six selected countries in the Human Mortality Database, compare our approach and results with those based on the shifting mortality model, and discuss possible reasons for the old-age mortality compression.

2. Methodology

2.1 Definition and estimation of e(M) and SD(M+)

e(M) is defined as the expectation of life of those who have just reached the modal age of adult deaths. The upward standard deviation from the mode, SD(M+), is the root-mean-square of the lengths of life lived beyond the modal age. Note that e(M) can be considered a dispersion measure, because it is the upward mean deviation from the mode. If the age at death in the life table is considered a continuous random variable, then the mode M is the age with the highest density of adult deaths, while e(M) and SD(M+) are given by integrals of deviation and squared deviation, respectively, from the mode as shown in the Appendix, section 1.

Alternatively, if we are working from a complete life table which shows the number of persons out of 100,000 who die at age x, then there are various ways to estimate the mode M of a continuous age distribution. By shifting the origin to the mode, e(M) and SD(M+) can then be calculated from first principles by the method of moments. However, there are also short cuts, described in the Appendix, section 2.

2.2 Choice of model

With only one exception (males in England and Wales for 1900–04), all the modes in the data analyzed in this paper are above the age of 70. These modal ages are therefore determined by the distribution of the relative frequencies of deaths at each age over 70. Death rates below age 70 will determine the numbers of survivors who reach age 70, but they will not affect the relative frequencies for the ages at death above age 70. At least in a standard life table, these relative frequencies above age 70 are determined solely by the death rates at ages 70 and over. From the life table entries we can estimate not only M but also e(M) and SD(M+), so all three are determined by the death rates at ages 70 and over. In these circumstances, what are the conditions in which compression will occur?

In order to study this question, we need a model which will fit the data at high ages reasonably well and which will be simple enough to provide the answer to our question. Kannisto’s approach to old-age mortality compression is based on the model originally proposed by Lexis, under which adult deaths are regarded as either “normal” (reflecting the “natural lifetime”) or premature. The normal deaths, which may be interpreted as senescence-related deaths, are presumed to produce the upper half of a normal distribution of the ages of death above the mode. Despite having only two parameters, this normal-distribution model fits the data on deaths above the mode very well, except perhaps at extreme ages in some populations (Cheung and Robine 2007).

In this paper, we combine Kannisto’s approach, which is based on the Lexis model, with the logistic model, which is known to fit empirical age patterns of old-age mortality well. We adopt a special case of the logistic model of mortality, which also has a long history and literature (see Thatcher 1999). This special case has only two parameters as does the Lexis model, and it is usually written in the form

$$\mu (x)=a{e}^{bx}/(1+a{e}^{bx})$$ (1)

Here μ_x is the force of mortality at age x, while a and b are parameters which are constant in any given period (or in any cohort, if the model is applied to cohort mortality data).

Theoretical derivations of the logistic model are given in the Appendix, section 3. The simple logistic model has only two parameters, whereas the general logistic model has four. One of these four (Makeham’s constant) becomes significant at some stage below age 70, while another allows for alternative limits of mortality at extremely high ages, such as supercentenarians. For the present paper, however, we are not concerned with ages below 70 or with the most extreme high ages. Within the range to which we shall confine ourselves, the simple 2-parameter version seems to be adequate.

The model (1) can be written in a simplified form, if we make use of the mathematical function known as the logit function, which is only the difference between two logarithms. The logit function is defined by

$$\mathit{logit}(z)=ln(z/(1-z))=lnz-ln(1-z)$$ (2)

With this notation it is easily seen that (1) can be written as

$$\mathit{logit}(\mu (x))=a^{\ast }+bx$$ (3)

where a* = ln a. If we calculate y = logit (μ_x) then the points (x, y) will lie on a straight line represented by equation (3). We shall call this the “logit line”.

The fact that this very special case of the logistic model holds, approximately, at least for modern data at high ages, was first noted by Kannisto (1992), and shown with a large set of international data by Thatcher et al. (1998). The model (1) has a very important property, crucial to the study of compression. Although the death rates at individual ages depend on both of the parameters a and b, the compression (as measured by the decrease in e(M) or SD(M+)) depends only on the single parameter b. It is shown in the Appendix, section 4, that if μ_x follows (1) then the modal age of death will occur at the age M which satisfies

$${ae}^{bM}=b,$$ (4)

which is equivalent to equation (20) in Robine et al. (2006) and equation (11) in Canudas-Romo (2008). It then follows that (1) can be written as

$$\mu (M+y)={be}^{by}/(1+{be}^{by}),\text{for}\text{any}y\ge 0.$$ (5)

The significance of this is that if we measure ages from the mode, then the whole shape of the distribution of both death rates and of ages at death depends only on the single parameter b, which summarises the age distribution of deaths above the modal age.

When b is known, equation (5) makes it possible to construct a theoretical life table with its origin at the mode. This life table will give the death rate at age y=x−M for y≥0, and this death rate will depend only on b and y. Thus the death rate at age y above the mode can be calculated without actually knowing the value of the mode. Since e(M) and SD(M+) can be calculated from the death rates above the mode, they too can be calculated from b, without knowing the mode. This is shown in a more formal manner in section 5 of the Appendix.

The numerical relationship is shown in Table 1. As expected, higher b values are associated with smaller e(M) and SD(M+) values, i.e., greater extents of compression.

Table 1.

Value of b, e(M), SD(M+), and ratio SD(M+)/e(M) derived from the two-parameter logistic model

b	e(M)	SD(M+)	Ratio SD(M+)/e(M)
0.090	7.34	9.04	1.2307
0.092	7.20	8.86	1.2309
0.094	7.06	8.69	1.2310
0.096	6.93	8.53	1.2312
0.098	6.80	8.38	1.2314
0.100	6.68	8.23	1.2315
0.102	6.57	8.09	1.2317
0.104	6.45	7.95	1.2318
0.106	6.35	7.82	1.2320
0.108	6.24	7.69	1.2322
0.110	6.14	7.57	1.2323
0.112	6.05	7.45	1.2325
0.114	5.95	7.34	1.2326
0.116	5.86	7.23	1.2328
0.118	5.78	7.12	1.2330
0.120	5.69	7.02	1.2331
0.122	5.61	6.92	1.2333
0.124	5.53	6.82	1.2334
0.126	5.46	6.73	1.2336
0.128	5.38	6.64	1.2338
0.130	5.31	6.55	1.2339
0.132	5.24	6.47	1.2341
0.134	5.18	6.39	1.2342
0.136	5.11	6.31	1.2344
0.138	5.05	6.23	1.2345
0.140	4.99	6.16	1.2347
0.142	4.93	6.08	1.2349
0.144	4.87	6.01	1.2350
0.146	4.81	5.94	1.2352
0.148	4.76	5.88	1.2353
0.150	4.70	5.81	1.2355

If we know b, then we can simply read off the values of e(M) and SD(M+). Since 1900, with only one exception, all the estimated value of parameter b has been between 0.09 and 0.15, and the ratio of SD(M+) to e(M) has fallen in a very narrow band, between 1.231 and 1.235. (This parallels a fixed ratio of 1.253 in the Lexis model). In view of this proportionality, results for e(M) will always imply results for SD(M+), and vice versa.

A further important feature of the model is that while b determines the compression, as measured by e(M) and SD(M+), the two values a and b in conjunction enable us to calculate the mode M. From equation (4) it follows that

$$M=ln(b/a)/b=(lnb)/b-(lna)/b.$$ (6)

Thus the compression is determined by the change in the slope of the line (3), while the location of the mode depends on the level as well as the slope.

Our plan to combine Kannisto’s tools based on the Lexis model with the logistic model seems reasonable, because the two models produce almost the same distribution of d(x) in a wide range of ages above the mode (Robine et al. 2006). This is despite the fact that the usual explanations of these two models are so different. As described in the Appendix, section 7, the logistic equation of mortality can be derived from at least two sets of completely different assumptions: the frailty model of selective survival and the Le Bras model of stochastic ageing processes (Le Bras 1976). The Lexis model uses the normal distribution, which is approximated by the sum of a large number of independent and identically distributed random variables. The fact that these totally different assumptions produce almost the same results over a wide range of ages above the mode is therefore surprising, but also reassuring.

2.3 Estimating b and predicting M, e(M), and SD(M+)

In order to apply the simple logistic model, we need to be able to estimate the parameter b. Since b is the slope of the straight line (3), it is sufficient to know the value of μ_x at any two ages, say x₁ and x₂, where x₂ > x₁. The slope of the line between these ages is then given by

$$b=[\mathit{logit}\mu (x_2)-\mathit{logit}\mu (x_1)]/(x_2-x_1)$$ (7)

However, since the central death rate m(x) at age x satisfies the approximation

$$m(x)\approx \mu (x+1/2)$$ (8)

we can use

$$b\approx [\mathit{logit}m(x_2)-\mathit{logit}m(x_1)]/(x_2-x_1)$$ (9)

to calculate b readily from life tables.

There is a wide choice for the ages x₁ and x₂. In theory, in a range where the data fit the simple logistic model precisely, we could choose any pair of ages whatever and they would all produce exactly the same value for b. However, x₁ and x₂ need to be chosen with consideration for several opposing criteria. First, x₁ should be high enough for the two-parameter logistic model to fit data well, because premature mortality (often modeled as the Makeham parameter) may have notable effects on the age pattern of mortality at younger old ages. Secondly, it is desirable for x₁ to be under or around the modal age of adult deaths, as the focus of our study is on mortality above the mode. Thirdly, it is desirable for x₁ and x₂ to be widely separated, because a wider difference will make the standard error of b (estimated by equation 9) smaller. Lastly, however, the difference should not be so wide as to make x₂ an extremely old age, at which the small number of deaths may notably increase the standard error of logit m(x₂), and in turn, that of b.

In consideration of these issues, we chose age 70 and age 90 for x₁ and x₂, respectively. Age 70 seems appropriate because in the 80 life tables from the Human Mortality Database that we analyzed, the estimated M was above age 70 in all cases except males in England and Wales, 1900–1904, for which M was 69.85. As described later, we compared our results among three sets, ages 70–90, 70–80, and 80–90, and found parameter trends were less erratic for ages 70–90 than for ages 70–80 and 80–90.

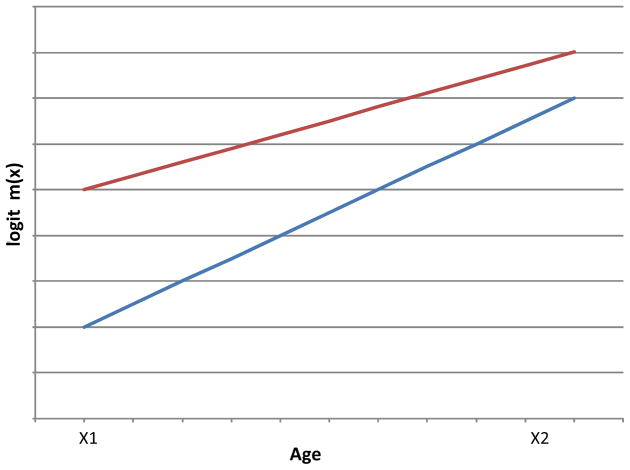
By comparing the estimates of b at two different dates, we can see whether b is increasing, and hence whether compression is occurring. The situation is illustrated in the schematic diagram (Figure 1), in which the vertical axis is taken as logit m(x). It can be seen that if logit m(x) falls faster at age 70 than at age 90, then the slope b will increase and compression will occur.

Figure 1.

Schematic diagram for the compression of mortality in the simple logistic model

Of course, in the simple logistic model it is not possible for the death rates at ages 70 and 90 to change in isolation. Death rates at all the other ages have to change as well, if the model is to be maintained. It would be more accurate to say that compression will occur if the death rates at ages 70 and over follow the simple logistic model, and change in such a way that logit m(x) falls faster at age 70 than at age 90.

Once the value of b has been obtained by applying equation (9) to death rates at ages 70 and 90, the modal age of adult deaths M can be predicted by

$$M=(lnb)/b-[\mathit{logit}m(x_1)]/b+x_1+1/2$$ (10)

where x₁=70 in this study. Equation (10) is an approximated version of equation (6), as shown in section 6 of the Appendix. e(M) and SD(M+) can be obtained by numerical integration based on equations (A.13) and (A.14) in section 5 of the Appendix, or simply by interpolation of values in Table 1.

3. Illustrations for England and Wales

The illustrations which follow use data for England and Wales, obtained from the English Life Tables and Interim Life Tables.

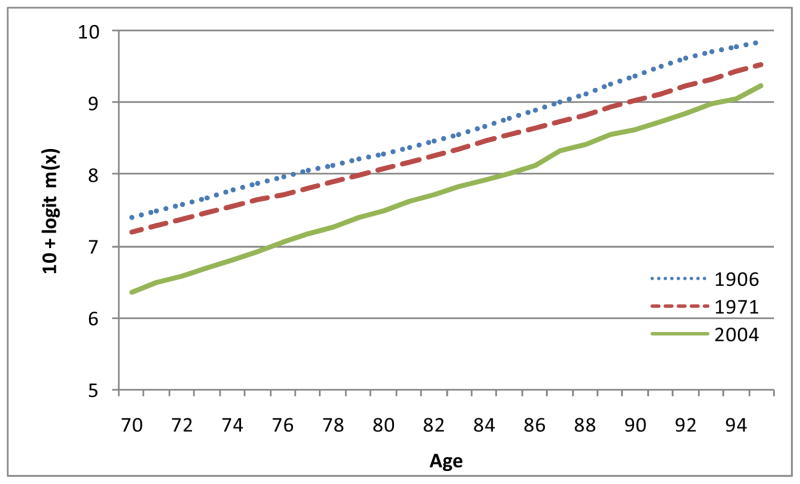
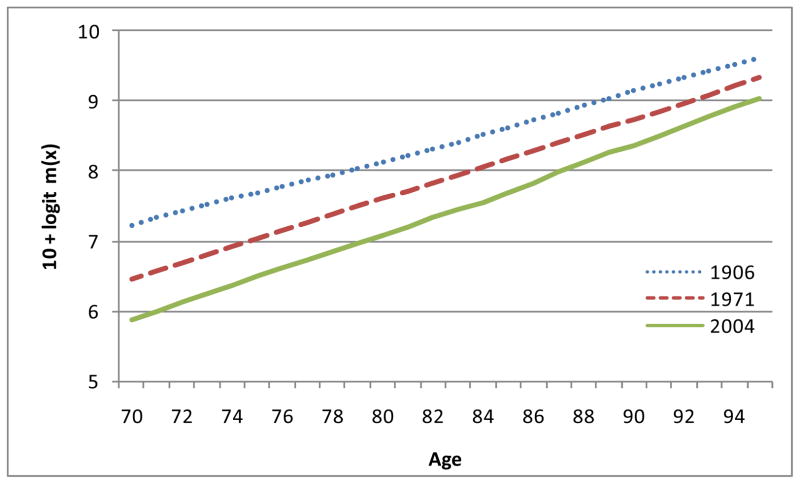
Figures 2 and 3 show logit m(x) for males and females in England and Wales for 1906, 1971 and 2004. It can readily be seen that the observed points look fairly straight. These are the logit m(x) curves. It must be remembered that we are not formally fitting straight lines. We are only seeking confirmation that the observed points of logit m(x) are close enough to straight lines to justify the choice of the logistic equation as a simple working model. As can be seen at a glance, the lines do not all have quite the same slopes. The model therefore indicates that there were changes over time in the parameter b and hence in e(M) and SD(M+).

Figure 2.

Logit m(x) for males in England and Wales: 1906, 1971 and 2004

Figure 3.

Logit m(x) for females in England and Wales: 1906, 1971 and 2004

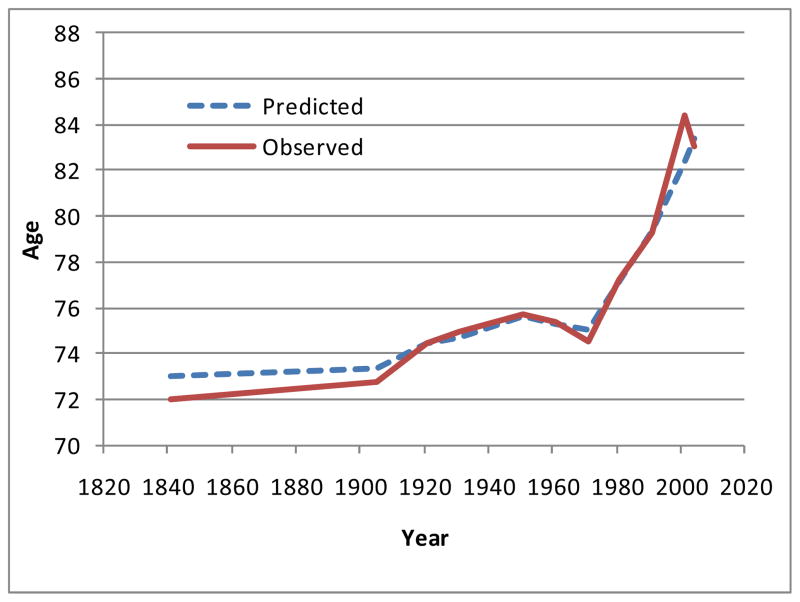
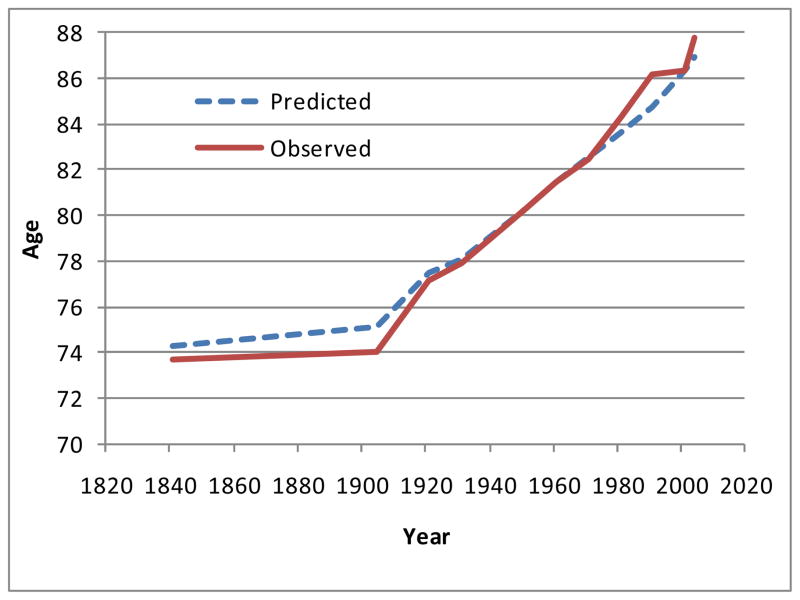
Figures 4 and 5 show how the modal ages of death have varied, using both observed values (full lines) and the predicted modes given by the simple logistic model (dashed lines). All the data which are plotted in these figures are given in Table 2, which also shows, for interest, the values for e(M) and SD(M+) predicted by the model. There are footnotes giving the sources and methods.

Figure 4.

Modal age of death for males in England and Wales, 1841–2004

Figure 5.

Modal age of death for females in England and Wales, 1841–2004

Table 2.

Modal age at death, b and predicted e(M) and SD(M+) for England and Wales by sex

	ENGLAND AND WALES
MALES
Year	MODAL AGE OF DEATH		b	Predicted e(M)	Predicted SD(M+)
	Predicted	Observed
1841	73.00	72.00	0.094307	7.04	8.68
1906	73.35	72.79	0.098928	6.75	8.32
1921	74.43	74.46	0.096267	6.91	8.52
1931	74.70	74.93	0.101799	6.58	8.11
1951	75.65	75.70	0.107409	6.27	7.73
1961	75.30	75.36	0.096639	6.89	8.50
1971	75.05	74.54	0.091890	7.21	8.89
1981	77.18	77.23	0.096200	6.92	8.53
1991	79.34	79.22	0.099906	6.89	8.50
2001	82.39	84.38	0.109159	6.18	7.62
2004	83.40	83.07	0.113777	5.96	7.35

FEMALES
Year	MODAL AGE OF DEATH		b	Predicted e(M)	Predicted SD(M+)
	Predicted	Observed
1841	74.31	73.67	0.095701	6.95	8.57
1906	75.14	74.00	0.096494	6.90	8.51
1921	77.46	77.15	0.100735	6.64	8.19
1931	78.05	77.86	0.107003	6.29	7.76
1951	80.28	80.25	0.116308	5.85	7.21
1961	81.45	81.42	0.116333	5.85	7.21
1971	82.50	82.42	0.113851	5.96	7.35
1981	83.62	84.33	0.115700	5.88	7.25
1991	84.75	86.17	0.112585	6.02	7.42
2001	86.36	86.30	0.120560	5.67	6.99
2004	86.93	87.76	0.124741	5.50	6.78

Sources: English Life Tables no 1, 1841; no 7, 1901–10; no 9, 1920–22; no 10, 1930–32; no 11, 1950–52; no 12, 1960–62; no 13, 1970–72; no 14, 1980–82; no 15, 1990–92. Interim Life Tables for England and Wales 2000–2002; 2003–5. These life tables were prepared successively by the Registrar General, the Government Actuary and now the Office for National Statistics.

Methods: The parameter b was estimated from (9), taking the x’s as 70 and 90. The predicted mode was then given by (10). The observed mode was estimated by (A.3) in the Appendix. The predicted values of e(M) and SD(M+) were found from b by interpolation in Table 1.

The predictions in Figures 4 and 5 were all made independently of each other, using only the observed death rates (and hence their logits) at ages 70 and 90. The predictions are reasonably close to the observed values.

For males there was little change between 1841 and 1906, but the mode then started to rise, rather falteringly. A strong rise did not start until 1971, but then it was faster than the rise for females, and has continued at a rapid pace for thirty years. The picture for females in Figure 5 is notably different. Again there was little change between 1841 and 1906, but the mode then started to rise and has risen ever since.

The data are given in Table 2, which gives a conspectus of the changes in England and Wales over the whole period from 1841 to 2004, as derived from the national life tables. The mode M rose for both males and females. For males, e(M) and SD(M+) both rose and fell. For females, we see only falls and this is the progression observed by Kannisto (2001). The changes were not monotonic.

4. Results for six countries

4.1 Trends in the parameter b

A further study on age patterns of mortality at high ages has been conducted using international mortality data in the HMD (Human Mortality Database 2007), not only for England and Wales but also for France, Japan, Italy, Sweden and Switzerland. Curves of logit m(x) between ages 70 and 90 have been drawn for each of these countries for every single year for which data are given in the HMD (Figures of these many lines are available on line at www.demographic-research.org/Volumes/Vol22/17/default.htm).

Visual inspection of those curves suggested that patterns and trends for those 12 (six countries times two sexes) sets of HMD life tables were similar to those in Figures 2 and 3 for English life tables: the curves were nearly or fairly straight (with some exceptions in early years and war/epidemic periods) but their slope appears to be increasingly steeper over decades.

We then examined this visual impression by estimating the parameter b from the slope of the logit line between ages 70 and 90. These ages were chosen with one below the mode and one above it, and with a span of 20 years in order to make the standard errors of the estimate of b small. If the data on deaths followed the simple logistic model exactly, any pair of ages in the range 70 and over would give the same estimate of b, but it is natural to wonder whether this holds in practice.

Accordingly, the slopes of the 80 logit lines described above were found from the pairs of ages 70–80, 80–90 and 70–90. Comparison showed that the differences among those slopes were mostly negligible. Any larger differences could only be due to the occasional “wobbles” in the logit lines. It was noticeable, however, that trends of the estimates based on 70–80 and 80–90 were more erratic, suggesting that they have more “noise” than the estimates based on 70–90.

In all cases, the b at the latest date was higher than the b at the earliest date, so the predicted standard deviation SD(M+) was lower at the later date. Thus over the period as a whole there had been compression above the mode in all six countries, for both males and females.

This work used b as calculated by equation (9), using the pair of ages 70 and 90. This choice worked well for the present paper. However, the distribution of ages at death continues to shift to the right, and the logistic pattern of mortality may be shifting with it. For any future work, it might be advisable to look at the slope based on ages 80–100 as well, at least in cases when the number of deaths at age 100 is accurate and large enough to make the death rate reliable.

4.2 Mode and SD(M+)

Time series giving the data for the six countries are assembled in Table 3. This shows for each country the observed value of the mode M, the observed value of the standard deviation above the mode SD(M+), the value of the parameter b found from the logit functions of the death rates at ages 70 and 90, and the prediction of SD(M+) given by b. Trends in the observed and predicted SD(M+) are also displayed in Figure 6. The table and figure enable us to see the differences between countries and to examine whether rises in the mode have always been accompanied by falls in the standard deviation. Comparisons between the observed and predicted values of SD(M+) also show whether the data support the theoretical deduction from the simple logistic model, that the standard deviation is related to the death rates at the high ages such as 70 and 90, so that it is the factors which affect these death rates differently which may be regarded as the ultimate causes of compression or decompression.

Table 3.

Modal age of death and the standard deviations above the mode for six countries

SWEDEN	From 1900–04 to 2000–04
	MALES				FEMALES
Period	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b
1900–04	77.54	7.45	7.15	0.1174	78.13	7.74	7.43	0.1125
1905–09	77.51	7.74	7.14	0.1177	78.96	7.56	7.24	0.1159
1910–14	79.57	6.84	7.28	0.1151	80.01	7.03	7.42	0.1126
1915–19	76.83	8.01	7.32	0.1143	79.35	7.34	7.48	0.1115
1920–24	77.75	7.92	7.24	0.1158	79.05	7.61	7.19	0.1168
1925–29	79.04	7.18	7.31	0.1145	78.77	7.65	7.27	0.1153
1930–34	78.57	7.44	7.24	0.1159	79.88	7.13	7.36	0.1137
1935–39	77.73	7.64	7.16	0.1174	79.44	7.09	7.17	0.1171
1940–44	78.13	7.81	7.30	0.1147	80.88	6.80	7.29	0.1149
1945–49	79.59	7.04	7.15	0.1175	79.39	7.49	6.93	0.1219
1950–54	79.22	7.28	7.29	0.1149	80.89	6.84	7.18	0.1169
1955–59	79.64	7.31	7.36	0.1136	80.88	7.24	7.05	0.1194
1960–64	79.84	7.24	7.29	0.1148	82.03	6.82	6.87	0.1231
1965–69	79.46	7.59	7.65	0.1086	82.86	6.76	6.74	0.1258
1970–74	78.72	8.23	7.80	0.1063	84.18	6.77	6.81	0.1244
1975–79	79.91	7.59	7.75	0.1071	84.80	6.68	6.72	0.1264
1980–84	80.04	7.75	7.61	0.1094	85.34	6.71	6.70	0.1266
1985–89	80.77	7.55	7.41	0.1128	85.96	6.55	6.59	0.1291
1990–94	81.58	7.43	7.33	0.1141	87.26	6.10	6.46	0.1321
1995–99	82.66	7.11	7.03	0.1198	87.89	6.02	6.42	0.1332
2000–04	84.05	6.69	6.89	0.1226	88.73	5.67	6.41	0.1334

SWITZERLAND	From 1900–04 to 2000–04
	MALES				FEMALES
Period	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b
1900–04	71.37	8.95	8.07	0.1022	74.83	7.49	8.16	0.1010
1905–09	70.54	9.27	8.14	0.1013	73.60	8.20	8.15	0.1011
1910–14	71.49	8.91	8.31	0.0990	73.08	8.81	8.16	0.1009
1915–19	72.61	8.30	8.13	0.1014	73.79	8.39	8.13	0.1015
1920–24	72.02	9.00	8.22	0.1002	73.11	9.03	7.98	0.1036
1925–29	74.56	7.90	8.06	0.1025	75.71	7.94	7.76	0.1069
1930–34	74.12	8.45	7.97	0.1038	76.14	8.10	7.75	0.1070
1935–39	75.15	7.84	7.71	0.1078	76.50	8.02	7.53	0.1106
1940–44	75.69	7.74	7.56	0.1102	78.73	7.22	7.21	0.1164
1945–49	76.04	7.94	7.81	0.1062	79.59	6.95	7.34	0.1140
1950–54	77.54	7.58	7.64	0.1089	79.87	7.26	7.18	0.1169
1955–59	77.51	7.74	7.69	0.1080	80.48	7.19	7.06	0.1193
1960–64	77.95	7.70	7.67	0.1084	82.02	6.65	6.73	0.1260
1965–69	78.86	7.47	7.77	0.1067	82.03	6.90	6.76	0.1254
1970–74	78.71	7.88	7.66	0.1085	83.80	6.47	6.62	0.1286
1975–79	79.60	7.79	7.94	0.1042	84.76	6.59	6.48	0.1318
1980–84	81.38	7.15	7.72	0.1075	85.67	6.41	6.37	0.1344
1985–89	82.10	7.17	7.18	0.1169	87.22	6.06	6.36	0.1348
1990–94	82.60	7.12	7.44	0.1123	87.48	6.07	6.34	0.1352
1995–99	83.20	7.09	7.12	0.1181	88.61	5.65	6.16	0.1398
2000–04	83.14	7.63	7.09	0.1187	89.55	5.50	6.14	0.1404

ENGLAND & WALES	From 1900–04 to 2000–04
	MALES				FEMALES
Period	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b
1900–04	69.85	10.36	9.58	0.0844	74.09	9.16	9.33	0.0868
1905–09	72.31	9.08	8.77	0.0931	74.87	8.79	8.65	0.0945
1910–14	73.29	8.74	8.89	0.0917	74.04	9.56	8.86	0.0920
1915–19	74.04	7.91	8.32	0.0988	77.05	7.78	8.17	0.1009
1920–24	73.89	8.67	8.41	0.0977	76.49	8.57	8.17	0.1009
1925–29	75.37	7.67	8.20	0.1004	76.53	8.32	7.96	0.1039
1930–34	73.93	8.53	8.08	0.1021	78.12	7.81	7.89	0.1049
1935–39	75.05	7.97	7.86	0.1054	77.31	8.36	7.73	0.1073
1940–44	76.28	7.68	7.89	0.1049	78.80	7.83	7.59	0.1097
1945–49	76.55	7.97	7.91	0.1046	78.78	8.30	7.57	0.1101
1950–54	74.77	8.57	7.84	0.1056	79.26	7.92	7.35	0.1138
1955–59	74.69	8.75	8.08	0.1022	80.42	7.64	7.27	0.1152
1960–64	75.14	8.69	8.34	0.0985	81.04	7.55	7.34	0.1139
1965–69	74.49	9.24	8.62	0.0949	82.47	7.25	7.35	0.1138
1970–74	74.14	9.48	8.71	0.0938	82.98	7.13	7.32	0.1144
1975–79	76.02	8.63	8.38	0.0980	83.59	6.99	7.19	0.1167
1980–84	77.52	8.27	8.37	0.0982	83.70	7.34	7.31	0.1145
1985–89	78.58	8.10	8.17	0.1009	84.99	6.97	7.28	0.1151
1990–94	79.32	8.19	8.07	0.1022	86.07	6.79	7.45	0.1120
1995–99	79.64	8.41	7.75	0.1071	86.00	6.89	7.25	0.1156
2000–04	82.20	7.77	7.44	0.1122	86.87	6.70	6.91	0.1222

FRANCE	From 1900–04 to 2000–04
	MALES				FEMALES
Period	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b
1900–04	73.06	8.16	7.91	0.1047	76.33	7.42	8.16	0.1010
1905–09	72.61	8.27	7.66	0.1085	73.93	8.53	7.90	0.1048
1910–14	73.22	8.19	7.76	0.1070	76.20	7.68	7.85	0.1055
1915–19	73.72	7.82	7.68	0.1082	74.99	8.11	7.65	0.1086
1920–24	73.79	8.29	7.74	0.1073	77.73	7.31	7.62	0.1092
1925–29	74.55	7.66	7.46	0.1118	77.83	7.11	7.40	0.1129
1930–34	74.55	8.03	7.85	0.1055	78.02	7.55	7.57	0.1100
1935–39	73.39	8.61	7.96	0.1039	77.83	7.75	7.51	0.1109
1940–44	74.29	7.50	7.35	0.1138	77.67	7.13	7.01	0.1196
1945–49	76.98	7.51	7.80	0.1062	79.79	7.27	7.27	0.1153
1950–54	76.32	7.85	7.60	0.1096	80.80	7.00	7.11	0.1183
1955–59	77.33	7.66	7.77	0.1068	81.84	6.83	6.91	0.1223
1960–64	77.70	7.73	7.80	0.1063	83.01	6.55	6.86	0.1233
1965–69	77.04	8.29	8.12	0.1015	83.00	6.86	6.88	0.1230
1970–74	76.62	8.80	8.18	0.1007	83.75	6.76	6.74	0.1258
1975–79	78.42	8.11	7.95	0.1041	84.27	6.85	6.63	0.1283
1980–84	80.53	7.33	7.74	0.1072	85.70	6.39	6.41	0.1336
1985–89	81.10	7.46	7.54	0.1106	86.73	6.32	6.33	0.1356
1990–94	83.00	7.05	7.56	0.1102	87.87	6.22	6.37	0.1346
1995–99	82.70	7.48	7.54	0.1106	88.76	6.01	6.34	0.1352
2000–04	85.49	6.55	7.36	0.1136	88.77	6.25	6.31	0.1360

ITALY	From 1900–04 to 2000–04
	MALES				FEMALES
Period	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b
1900–04	72.84	8.59	7.69	0.1080	74.12	7.91	8.60	0.0952
1905–09	73.28	8.22	8.23	0.1000	73.25	8.39	9.17	0.0886
1910–14	74.55	7.90	8.23	0.1001	74.31	8.22	8.99	0.0905
1915–19	73.64	7.84	7.64	0.1088	73.40	8.12	8.41	0.0976
1920–24	75.23	7.63	7.66	0.1085	76.48	7.28	8.15	0.1011
1925–29	76.00	7.17	7.46	0.1181	78.23	6.64	7.09	0.1186
1930–34	76.79	7.42	7.88	0.1050	77.58	7.63	8.27	0.0985
1935–39	76.57	7.30	7.46	0.1118	77.14	7.63	7.58	0.1099
1940–44	76.78	6.70	6.96	0.1212	78.15	6.65	7.00	0.1204
1945–49	77.55	7.47	7.31	0.1145	79.45	7.02	7.29	0.1149
1950–54	78.18	7.29	7.20	0.1165	79.44	7.35	7.16	0.1173
1955–59	78.71	7.29	7.47	0.1116	80.43	7.21	7.17	0.1171
1960–64	80.02	6.83	7.48	0.1116	81.38	6.98	6.96	0.1213
1965–69	77.93	8.04	8.06	0.1024	81.60	7.12	6.98	0.1208
1970–74	77.25	8.51	7.87	0.1052	82.78	6.85	6.77	0.1253
1975–79	78.79	7.68	7.95	0.1041	83.73	6.55	6.62	0.1284
1980–84	79.35	7.71	7.85	0.1055	84.72	6.44	6.55	0.1302
1985–89	79.89	7.94	7.81	0.1062	85.54	6.57	6.54	0.1303
1990–94	81.76	7.48	7.67	0.1083	86.97	6.26	6.56	0.1300
1995–99	81.10	8.23	7.67	0.1084	87.86	6.20	6.47	0.1319
2000–04	82.46	7.94	7.36	0.1136	88.44	6.23	6.36	0.1348

JAPAN	From 1950–54 to 2000–04
	MALES				FEMALES
Period	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b	Observed M	Observed SD(M+)	Predicted SD(M+)	Parameter b
1950–54	74.16	8.54	8.10	0.1019	78.57	7.70	7.69	0.1081
1955–59	74.93	8.27	8.04	0.1027	79.87	7.26	7.56	0.1102
1960–64	76.04	7.72	7.79	0.1064	80.14	7.13	7.07	0.1190
1965–69	77.00	7.64	7.69	0.1080	81.26	6.94	6.96	0.1212
1970–74	78.24	7.54	7.62	0.1092	82.32	6.85	6.72	0.1262
1975–79	79.20	7.72	7.44	0.1123	83.93	6.56	6.57	0.1296
1980–84	81.33	7.19	7.25	0.1155	85.34	6.44	6.39	0.1339
1985–89	81.74	7.50	7.17	0.1170	86.69	6.38	6.28	0.1369
1990–94	83.51	6.89	7.18	0.1169	87.72	6.30	6.24	0.1378
1995–99	84.30	6.97	7.40	0.1130	89.52	6.15	6.38	0.1342
2000–04	85.32	7.14	7.77	0.1068	91.22	6.10	6.57	0.1296

Source: Human Mortality Database (2007) University of California, Berkeley (U.S.A.) and Max Planck Institute for Demographic Research (Germany). Available online at www.mortality.org.

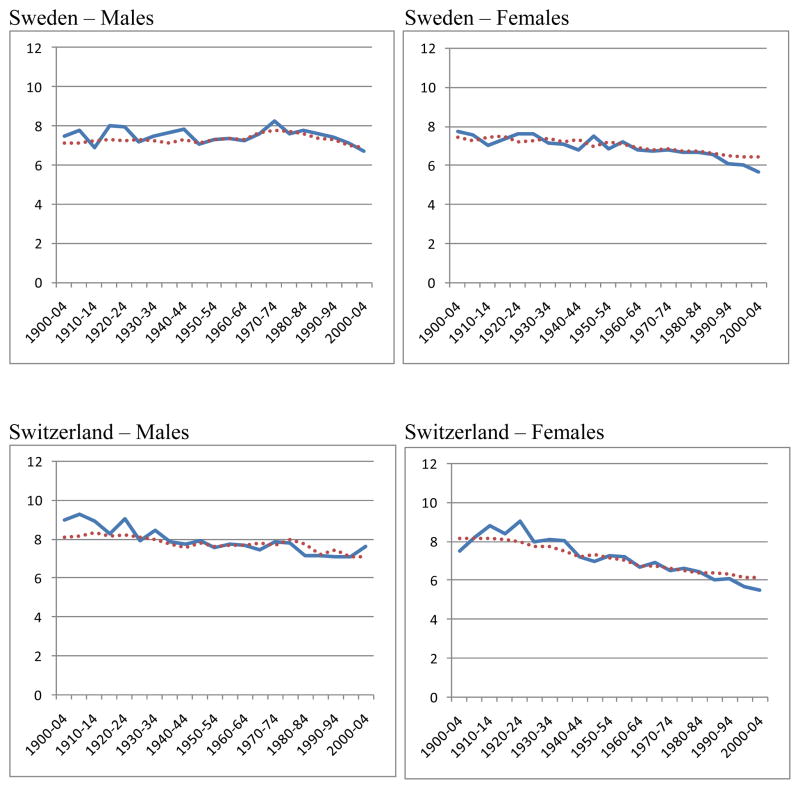
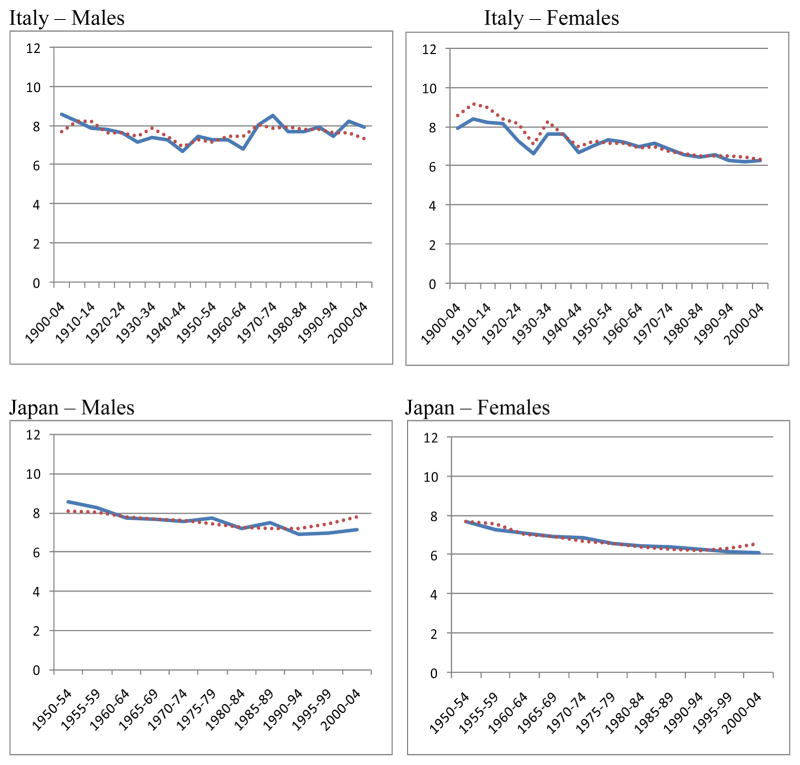
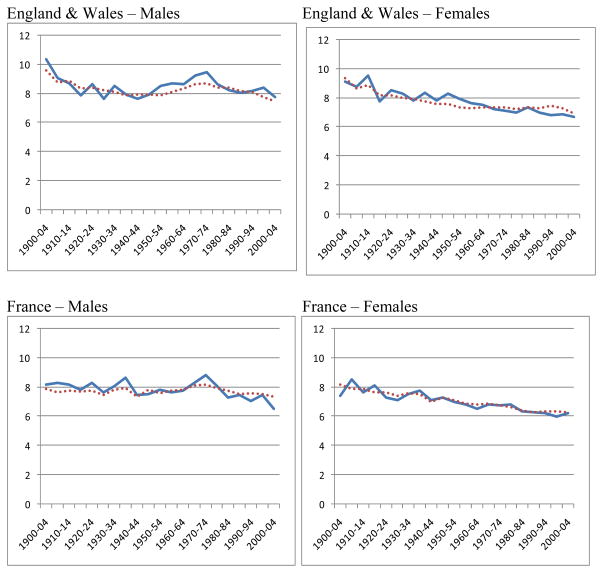
Figure 6.

Observed and predicted standard deviations above the mode

Table 3 gives the series for 5-year periods from 1900–1904 to 2000–2004 for Sweden, Switzerland, Italy, England and Wales and France, and from 1950–1954 to 2000–2004 for Japan. The methods by which the table was constructed are given in the Appendix, section 3.

The average changes can be summarised briefly as follows: for males in the five countries excluding Japan, the observed mode rose from 72.9 to 77.2 in the first fifty years, and from 77.2 to 83.5 in the second fifty years. The observed standard deviation SD(M+) fell from 8.7 to 7.7 in the first fifty years, and from 7.7 to 7.3 in the second. Thus, the rise in the mode sped up, but the fall in the standard deviation slowed down.

For females in these same countries, the average mode rose from 75.5 to 80.1 in the first 50 years, and from 80.1 to 88.5 in the second. The observed standard deviation fell from 7.9 to 7.3 in the first fifty years, and from 7.3 to 6.1 in the second. Again, the rise in the mode sped up, but for females the fall in the observed standard deviation accelerated.

The changes for individual countries were not always so steady. For example, for males in Italy between 1950–54 and 2000–04 the mode rose but the standard deviation rose too. A rise in the mode is not necessarily accompanied by a fall in SD(M+). In another case, the observed SD(M+) fell, then levelled off and stayed virtually steady for 30 years, then rose to a higher level for 25 years and finally fell again (males in England and Wales). In Japan, observed and predicted SD(M+) decreased only slightly or even increased between 1990–94 and 2000–04, which is consistent of the finding of Cheung and Robine (2007) using a different method that SD(M+) had levelled off in Japan in the 1990s Thus, overall, SD(M+) tend to decrease over time and negatively associated with M, but the trend is not highly consistent and the association is not very strong.

4.3 Accuracy of the predictions of SD(M+)

Predictions of SD(M+) from m(70) and m(90) are subject to errors because mortality between 70 and 90 may not exactly follow the simple logistic model, but so are the observed values, because the mode of age at death as a continuous variable has to be estimated based on some assumption. There can also be errors in the data due to the use of provisional figures, or errors in the stated ages at death. When a prediction is different from the observed value, the fault does not always lie in the prediction.

The series for the observed and predicted values of SD(M+) are illustrated in Figure 6. Considering that these two series are derived so differently, and that all the points are independent, the agreement between the two series is very close.

Figure 6 clearly supports the basic conclusion that the prediction method works well enough to confirm the theoretical deduction from the model: that e(M) and SD(M+) can be predicted from the death rates at just two high ages, such as 70 and 90. In order fully to understand the changes in e(M) and SD(M+), we need to understand the factors which affect the death rates at these ages.

The highest values of the difference (Observed minus Predicted) for individual countries, regardless of sign, were 1.1 in the 50 years before 1950–1954 and 0.8 in the 50 years from 1950–1954 onwards. However, these were extreme values in six countries over a century. In 80 per cent of all the cases the difference was less than 0.6, both before and after 1950 and for both males and females. To put this in perspective, a difference of 0.6 year in a standard deviation SD(M+) implies a difference of 6 months in the expectation of life at the mode (see Table 1). Thus one might say that e(M) predicted from the death rates at just the two ages 70 and 90 had an 80 per cent chance of being within six months of the observed e(M). For females since 1950, the agreement was much closer, with a 98 per cent chance of being within six months.

5. Discussion

The previous section concluded that in the six countries studied, there had been mortality compression above the mode in the period from 1950–1954 to 2000–2004. The fall in the observed SD(M+) for females was an average of 1.3 years, but 1.8 in Sweden and 1.6 in Japan. This differs from one of the conclusions found by Bongaarts (2005). He used the 3-parameter logistic model, which includes Makeham’s constant taken as a measure of “background mortality”. When this model was fitted to ages 25–109, he found that in many countries the parameter b had remained almost constant from 1950 to 2000. He therefore decided that it was reasonable to assume that in future the parameter b would remain constant over time for any given country. This means that the frequency distribution of ages at death will shift to the right without any change of shape or compression above the mode. This is the shifting logistic model.

A key reason for the difference between these two conclusions is the fact that Bongaarts fitted his model to the very wide range of ages from 25 to 109, whereas we only used data at ages 70 and over. Bongaarts (2008) has since found that if his model is fitted over shorter age ranges, the estimates of the slope b are not all the same. In particular, if the model is fitted to ages 30–109 then b appears almost constant over time, whereas if the same model is fitted to ages 70–90 and 70–109 there is a marked increase in b over time. This is fully consistent with Kannisto’s finding, and ours, about the mortality compression above the mode. A further factor may be that the slope b which fits the ages below 70 has not remained the same as the slope which fits ages 70 and over. In this paper, we have confined ourselves to ages 70 and over.

Kannisto (2001) has shown that that SD(M+) fell for some female populations in recent decades. In order to study this mortality compression further, we combined Kannisto’s measures with the simple two-parameter logistic model. Our results support Kannisto’s extended to cover males as well as females and also the most recent periods.

Kannisto contended that the compression he observed was due to the resistance caused by the ascending trajectory of mortality. In our analysis, the resistance is reflected in the fact that the death rates at very high ages did not fall fast enough to prevent compression. This is a distinction without much of a difference.

The long-term average tendency for the logit function of the death rates to fall more at younger old ages may perhaps reflect age-related changes in society, such as arrangements for the care of the very old, which vary from country to country and may change over time. Also, it is presumably possible that some medical advances and lifesaving technologies may be more effective at lower old ages than at higher old ages, when there is less resilience. In order to account for a tendency towards compression it does not seem necessary to invoke any fundamental biological changes in the ageing process itself.

The compression above the mode, however, has been fairly slow, and it is an open question how far SD(M+) may continue to fall. Nevertheless, if medical advances do not have quite the same effect around age 90 as around age 70, the compression may continue to hold for some time yet. For the future, there is also the uncertainty that there may not be enough caregivers to look after the expected enormous numbers of old people. This may eventually affect the mortality rates of the very old.

Appendix

Note: In this Appendix the symbols typed as μ_x and μ(x) are interchangeable, and similarly for other suffixes.

A1. M, e(M), and SD(M+) for a continuous distribution

Consider the case in which the ages at death have a continuous frequency distribution, with a density function d(x) which is estimated from data or which has been assumed to follow a mathematical equation that has been fitted to data by some suitable method. The adult modal age of death M is the age at which d(x) has its maximum in the age range defined as “adult age” (e.g., 15 and over). The remaining expectation of life for those who have just reached the mode is

$$e(M)=\frac{\underset{M}{\overset{\infty }{\int }}(x-M)d(x)dx}{\underset{M}{\overset{\infty }{\int }}d(x)dx}$$ (A.1)

The standard deviation SD(M+) of the ages at death above the mode, measured from the mode, is

$$SD(M+)=\sqrt{\frac{\underset{M}{\overset{\infty }{\int }}{(x+M)}^{2}d(x)dx}{\underset{M}{\overset{\infty }{\int }}d(x)dx}}$$ (A.2)

A2. Approximations when the distribution is discrete

Alternatively, we may be working with an observed frequency distribution of the ages at death which are discrete. For example, in a standard complete life table there is a column d(x) which shows the number (out of 100,000) of individuals who die between exact age x and x+1, where x is a non-negative integer. The mode M can be estimated either by an approximate formula, or more elaborately by fitting a short segment of a smooth curve to a few of the observed frequencies at the tip of the distribution.

In order to use the approximate formula, we must find in the life table the age X which has the highest number of deaths. We then extract the values of d(X), d(X−1) and d(X+1) as given in the life table. The approximate value of the mode is then given by

$$M=X+\frac{d(X)-d(X-1)}{[d(X)-d(X-1)]+[d(X)-d(X+1)]}$$ (A.3)

This is the formula used by Kannisto (2001). It can be derived by the method of differences (see Yule and Kendall, 1950, page 582). It has also been derived from first principles by Canudas-Romo (2008). The tip of the continuous curve is approximated in the range (X−1, X+1) by the parabola which has the right areas below it to produce the observed values d(X−1), d(X) and d(X+1). The resulting estimate M always lies between X and X+1.

Having found an estimate of M, either by using (A.3) or in some other way, the expectation of life at the mode can be found by interpolating between the life table values e(X) and e(X+1). This gives

$$e(M)=e{(X)}^{\ast }(X+1-M)+e{(X+1)}^{\ast }(M-X).$$ (A.4)

We now use the fact that the ratio of SD(M+) to e(M) is practically constant. In a Lexis model the ratio is always exactly 1.253. In the simple logistic model it is very slightly less, but in a very narrow band. Table 1 shows that the ratio lies between 1.231 and 1.235 when the parameter b lies anywhere from 0.09 to 0.15. For practical purposes we estimate SD(M+) by

$$SD(M+)={1.233}^{\ast }e(M).$$ (A.5)

A3. Different versions and derivations of the logistic model

The logistic model of mortality has been published in several different forms and notations, but all can be converted to the expression

$$\mu (\text{x})=\text{c}+\text{kz}/(1+\text{z})\text{where}\text{z}={\text{ae}}^{\text{bx}}$$ (A.6)

This has four parameters: a, b, c and k. If it was not for the denominator (1+z), we should recognise b from Gompertz’s law and c as the constant in Makeham’s law, sometimes described as background mortality, a simple way of representing deaths at adult ages from causes which are not related to age. However, the presence of the denominator bends the curve downwards at high ages.

A very common explanation of this downward bend is that it can be caused by heterogeneity (selective survival). Because less healthy individuals are more likely to die at younger ages, survivors to older ages tend to have favourable health endowments and/or healthy life styles. This selection process could slow down the age-related mortality increase at the population level.

Specific assumptions about the nature of heterogeneity which lead to the expression (A.6) were first proposed by Beard (1971) and later discovered independently by Vaupel et al. (1979). Individual differences are assumed to remain essentially unchanged throughout their lifetimes, so the models are called the “fixed frailty” models, and the individual differences are assumed to follow the gamma distribution. However, it was also shown by Le Bras (1976) that the same expression (A.6) can be produced in a completely differently way, in which ageing is modelled as a stochastic process. Individuals progress by jumps at random times through a succession of steadily deteriorating states of health. Even a cohort which starts as homogeneous will become increasingly heterogeneous. Thus, completely different underlying mechanisms could produce the logistic pattern of mortality (Yashin et al. 1994).

The model (A.6) was among those fitted by Thatcher et al. (1998), though in a different notation, to all officially published data on deaths at ages 80 and over for males and females in 13 countries with reliable data for the ten-year periods from 1960–1990 and also for some cohorts in those countries. They found that at these ages c was negligible, of the order of 0.00001. This was surprising, as one would expect background mortality to extend to all ages. Presumably at ages 80 and over risks of death from most causes, even accidents, may be correlated with age. The parameters which they fitted showed that k was close to unity. This would also have been surprising, except for the fact that the combination c=0 and k=1 leads immediately to the logit relationship (3), which was already known to fit the data at high ages.

However, Thatcher (1999) realised that it was not possible to fit the two-parameter version of (A.6), with c=0 and k=1, to data extending down to age 30. He therefore tried the three-parameter version, taking k=1 but with no constraint on c. For the data from age 30 upwards the fitted value of c was of the order of 0.01, which is far from negligible as a component of an age-specific death rate. This shows that the 2-parameter model breaks down at some stage below age 80, when c ceases to be negligible. Moreover, Bongaarts (2008) has found that the slope b which fits the ages below 70 has not remained the same as the slope which fits ages 70 and over.

In the present paper we have steered clear of these problems by using only data for ages 70 and over. At these ages the 2-parameter version with c = 0 and k = 1 fits well. The fact that this very simple model fits the data at these ages is accepted as a fact of observation, which fortunately enables us to make the predictions of M and SD(M+) which are the subject of the paper.

A4. Proof of equation (4)

The force of mortality is defined as

$$\mu (x)=-\frac{1}{l(x)}\frac{dl(x)}{dx}$$ (A.7)

where l(x) is the life table survival function at age x.

The density of deaths at age x is given by

$$d(x)=l(x)\mu (x)$$ (A.8)

The mode of the distribution of deaths is therefore found by differentiating (A.8) and equating to zero. Substituting from (A.7) then produces

$$(d{\mu }_x/dx)/{\mu }_x={\mu }_x\text{at}\text{the}\text{mode},\text{i}.\text{e}.,\text{for}x=M.$$ (A.9)

This is a standard result which applies to all continuous laws of mortality. Note that the left hand side of the above equation is the life table aging rate (LAR). Thus, at the modal age, the force of mortality is equal to the LAR. This important fact was previously shown by Pollard (1991) for the Gompertz model and by Robine et al. (2006) in a general form.

The simple logistic model is defined by equation (1) in the text. Differentiating μ_x with respect to x gives (dμ_x/dx) as a function of a and b. On substituting (A.9) the equation simplifies to produce

$${ae}^{bx}=b\text{at}\text{the}\text{mode},$$ (A.10)

which proves equation (4).

A5. Proof that in the simple logistic model, e(M) and SD(M+) are determined solely by b, independently of M

In the simple logistic model, mortality above M is given by

$${\mu }_{M+y}=\frac{{ae}^{b(M+y)}}{1+{ae}^{b(M+y)}}=\frac{{ae}^{bM}{e}^{by}}{1+{ae}^{bM}{e}^{by}}\text{for}\text{any}y\ge 0$$

Substituting ae^bM = b from (A.10) into the above, we get

$$\mu (M+y)=\frac{{be}^{by}}{1+{be}^{by}}=\frac{d}{dx}ln{(1+{be}^{by})}^{1/b}$$ (A.11)

Thus,

$$\frac{l(M+x)}{l(M)}=exp\left(-\underset{0}{\overset{x}{\int }}\mu (M+y)dy\right)=exp\left\{{\left[-(ln{(1+{be}^{by})}^{1/b}\right]}_{y=0}^{y=x}\right\}={\left(\frac{1+b}{1+{be}^{bx}}\right)}^{\frac{1}{b}}.$$ (A.12)

Therefore, the expectation of life at M, which is also the upward mean deviation of age at death from M, is given by

$$\begin{array}{l}e(M)=\frac{{\int }_0^{\infty }xd(M+x)dx}{{\int }_0^{\infty }d(M+x)dx}=\frac{{\int }_0^{\infty }xd(M+x)dx}{l(M)}=\underset{0}{\overset{\infty }{\int }}x\frac{l(M+x)}{l(M)}\mu (M+x)dx\\ =\underset{0}{\overset{\infty }{\int }}x{\left(\frac{1+b}{1+{be}^{bx}}\right)}^{\frac{1}{b}}\frac{{be}^{by}}{1+{be}^{by}}dx=\underset{0}{\overset{\infty }{\int }}{\left(\frac{1+b}{1+{be}^{bx}}\right)}^{\frac{1}{b}}dx.\end{array}$$ (A.13)

by integration by parts. This clearly indicates that e(M) is solely determined by b, regardless of a and M.

Similarly,

$$SD(M+)=\sqrt{\underset{0}{\overset{\infty }{\int }}{x}^2\frac{l(M+x)}{l(M)}{\mu }_{M+x}dx}=\sqrt{\underset{0}{\overset{\infty }{\int }}{x}^2{\left(\frac{1+b}{1+{be}^{bx}}\right)}^{\frac{1}{b}}\frac{{be}^{bx}}{1+{be}^{bx}}dx},$$ (A.14)

which indicates that SD(M+) is also solely determined by b, independently of a and M.

A6. Proof of equation (10)

From equation (4) we have

$$lna+bM=lnb$$

and hence, as in equation (6),

$$M=(lnb)/b-(lna)/b$$ (A.15)

In the simple logistic model, if μ(x₁) is the force of mortality at any given age x₁, then by equation (3) we have

$$a^{\ast }=lna=\mathit{logit}\mu (x_1)-{bx}_1$$ (A.16)

Thus from (A.15)

$$M=(lnb)/b-[\mathit{logit}\mu (x_1)]/b+x_1$$ (A.17)

Since m(x)’s, but not μ(x)’s, are given in empirical life tables, we can make use of the fact that m(x) is approximately equal to μ(x + ½). Hence, using equation (3), we find

$$\mathit{logit}m(x)=\mathit{logit}\mu (x+1/2)=\mathit{logit}\mu (x)+b/2$$ (A.18)

Substituting (A.18) into (A.17) gives

$$M=(lnb)/b-[\mathit{logit}m(x_l)]/b+x_1+1/2$$ (A.19)

which is equation (10).

A7. Construction of Table 3

Table 3 was constructed from the life tables for the six countries in the Human Mortality Database from 1900 to 2004. The observed values of M were found by using equation (A.3), taking X from the life tables. This formula worked satisfactorily in all except seven special cases where there were double modes or adjacent modes, which needed special treatment. The observed values of e(M) and hence SD(M+) were then estimated from equations (A.4) and (A.5), taking e(X) and e(X+1) from the life tables. The parameter b was estimated from equation (9). The predicted value of SD(M+) was then found by interpolation on values listed in a more detailed version of Table 1.