Electrostatic forces in the Poisson-Boltzmann systems

Abstract

Continuum modeling of electrostatic interactions based upon numerical solutions of the Poisson-Boltzmann equation has been widely used in structural and functional analyses of biomolecules. A limitation of the numerical strategies is that it is conceptually difficult to incorporate these types of models into molecular mechanics simulations, mainly because of the issue in assigning atomic forces. In this theoretical study, we first derived the Maxwell stress tensor for molecular systems obeying the full nonlinear Poisson-Boltzmann equation. We further derived formulations of analytical electrostatic forces given the Maxwell stress tensor and discussed the relations of the formulations with those published in the literature. We showed that the formulations derived from the Maxwell stress tensor require a weaker condition for its validity, applicable to nonlinear Poisson-Boltzmann systems with a finite number of singularities such as atomic point charges and the existence of discontinuous dielectric as in the widely used classical piece-wise constant dielectric models.

INTRODUCTION

Solvation interaction is one of the essential determinants of the structures and functions in proteins and nucleic acids, and is crucial in their accurate modeling.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} Due to the high computational overhead in the explicit treatments of solvent molecules, continuum models of solvation interactions, specifically the electrostatic solvation modeling that is based upon the Poisson-Boltzmann equation (PBE), are widely used in the studies of biomolecules.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} Indeed continuum electrostatics represents an effective and physically sound approach that makes it possible to account for a number of phenomena involving solvent electrostatic effects on the functional analyses of biomolecules.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15} These efforts have been facilitated by numerical solutions of the PBE that can be obtained routinely for biomolecules and their complexes.^{3, 16, 17, 18, 19, 20, 21} Among the numerical solution methods, finite-difference method (FDM),^{22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34} finite-element method (FEM),^{35, 36, 37, 38, 39, 40, 41, 42, 43} and boundary-element method (BEM)^{44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59} are mostly used.

A disadvantage of the numerical continuum electrostatics methods is that it is conceptually difficult to incorporate them into molecular mechanics programs, mainly because of the problem of assigning forces related to the dielectric boundary (“dielectric stress”) to individual atoms.^{30, 35, 60, 61, 62, 63, 64, 65, 66, 67, 68} Other problems are the convergence of the energy and forces with respect to the resolution of the solute-solvent boundary and charge representation.^{69, 70, 71} Thus in most practical applications, the PBE is only solved for a few fixed conformations of a solute or solute complex. This limits the application of PBE in more elaborative modeling of biomolecules.

Many efforts have been invested to develop methods to compute electrostatic forces.^{30, 35, 49, 60, 61, 62, 63, 64, 65, 66, 67, 68, 72, 73, 74, 75, 76, 77, 78, 79} The “virtual work” method is apparently the defining benchmark for all analytical methods. In the “virtual work” method the electrostatic energy G is recalculated for a small displacement d of each atom in the x, y, and z directions, respectively. The numerical force is then −ΔG/d for each direction. The limitation of this approach, however, is that at least four full numerical calculations are required in order to calculate each force vector. Apparently, this is only realistic for molecules treated as rigid bodies. In addition, the numerical forces, defined as the negative finite-difference derivatives, are very difficult to converge when the electrostatic energies are computed numerically due to the cancellation of significant digits in the subtraction of two large numbers. Thus analytical calculation of solvation forces is necessary for practical applications.

For the classical abrupt-transitioned two-dielectric models, multiple strategies have been proposed by Davis and McCammon,⁶⁰ Che et al.,⁶⁵ Li et al.,⁶⁷ and most recently Cai et al.⁶⁸ These formulations were derived following different strategies and were found to be consistent as to be discussed below. For the smooth-transitioned dielectric models, we have the ground-breaking strategy by Gilson et al.⁶⁴ Subsequent works by Im et al.³⁰ and Cai et al.⁶⁶ were shown to be consistent with that of Gilson et al.,⁶⁴ though different strategies were proposed to enhance numerical stability and convergence in the later works. The numerical methods derived from these formulations are mostly adapted for the numerical solutions by the FDM. Another promising approach to incorporate the PBE electrostatics into molecular mechanics is the BEM. The force calculation in a BEM calculation was first described by Zauhar.⁶² Cortis et al.³⁵ also tried to compute the solvation force for their FEM calculations, leading to the same formulation as that of Zauhar.⁶²

These pioneer efforts in calculating the solvation forces for the numerical PBE methods laid the foundation to develop more robust methods that eventually will lead to routine application of the numerical PBE methods to biomolecular simulations. Interestingly, there is yet no theoretical analysis on how to derive the Maxwell stress tensor, a crucial step in formulating the analytical solvation forces, even if the concept has been used in the solvation force derivations in the past. This study presents a theoretical framework of deriving the Maxwell stress tensor based on the full nonlinear PBE. In addition, it offers a systematic derivation of the formulations of electrostatic forces for systems with and without singularities that exist as point charges, abrupt-transitioned dielectric interface, and ionic interface. The theoretical study further discusses the relations between the Maxwell stress tensor-based formulations and the existing methods in the literature, and highlights the benefits of various numerical strategies proposed in the literature.

DERIVATION OF MAXWELL STRESS TENSOR FOR THE FULL POISSON-BOLTZMANN SYSTEMS

In the following we focus on the full PBE for systems with continuum mobile ions

$$\begin{array}{c}\hfill \nabla •\left(\varepsilon \nabla \phi \right)=-4\pi {\rho }^f-4\pi \sum _i{q}_i{c}_i{e}^{-q_i\phi /k_{B}T}\lambda ,\end{array}$$ (1)

where ɛ is the dielectric constant, φ is the potential, ρ^f is the fixed charge distribution, q_i is the charge of ion type i, c_i is the bulk number density of ion type i, λ is the ion exclusion function, k_B is the Boltzmann constant, and T is the absolute temperature. Introducing the electric displacement vector D = −ɛ∇φ, we can rewrite Eq. 1 as

$$\nabla •\mathbf{D}=4\pi {\rho }^f+4\pi \sum _i{q}_i{c}_i{e}^{-q_i\phi /k_{B}T}\lambda .$$ (2)

The total electrostatic free energy of a Poisson-Boltzmann system can then be formulated as⁷⁶

$$\begin{array}{ccc}\hfill G& =& \int \left({\rho }^f\phi -\frac{1}{8\pi }\mathbf{D}•\mathbf{E}-\Delta \Pi \lambda \right)dv,\hfill \\ \\ \hfill \Delta \Pi & =& k_{B}T\sum _i{c}_i(e^{-q_i\phi /k_{B}T}-1),\hfill \end{array}$$ (3)

where E is the electric field.

In classical electrostatics, electrostatic forces can be computed via the variational approach, for example, as in Ref. 64, or via the stress tensor approach.⁸⁰ Though both strategies are not trivial to follow, here we follow the strategy based on the Maxwell stress tensor. The advantage of this strategy is that it is straightforward once the Maxwell stress tensor is defined for the problem at hand. As will be shown below, no matter what strategy is followed, the general formulation for total electrostatic forces is the same, at least for solution systems without any singularity.

Given the Maxwell stress tensor in the form of a rank-two tensor

$$\mathbf{P}=\left[\begin{array}{ccc}\hfill T_{xx}& \hfill T_{xy}& \hfill T_{xz}\\ \hfill T_{yx}& \hfill T_{yy}& \hfill T_{yz}\\ \hfill T_{zx}& \hfill T_{zy}& \hfill T_{zz}\end{array}\right],$$ (4)

we first proceed to compute the nine components T_ij from the electrostatic free energy for the ionic solution system obeying the full PBE (Eq. 1).

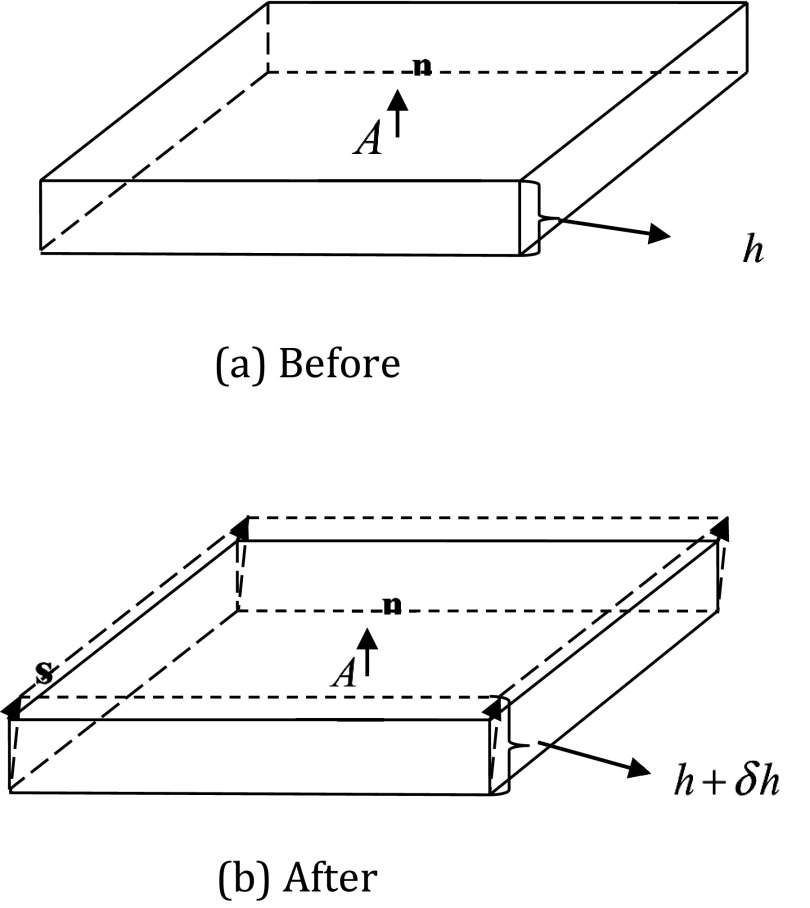
Following Landau's notation,⁸⁰ with no loss of generality, we consider a thin and small disk of dielectric with small area A and thickness h. Here $h\ll \sqrt{A}.$ Given the small dimension of the volume element, we can assume its uniform composition, density, temperature, and electrostatic properties, such as ɛ and λ. Furthermore, charge density ρ^f, potential φ, and electric field E can all be assumed to be smooth variables within the volume element so that the electrostatic free energy density g is also smoothly changed.

Consider the upper surface of the disk with area A and normal vector n. The definition of stress tensor shows that force acting upon the upper surface (by the volume element) can be written as −∫P • ndA, where −P • n = −(T_xjn_j, T_yjn_j, T_zjn_j)^T is simply the pressure acts upon the upper surface. Here Einstein's summation convention is used, i.e., $T_{ij}{n}_j=\sum _j{T}_{ij}{n}_j$. Our goal is to impose a virtual deformation of the thin disk along a small virtual displacement s (s ≪ h) whose direction is arbitrary to compute the associated pressure via the virtual displacement method. Suppose the deformation of the disk is homogeneous so that the surface area of the deformed thin disk remains the same, A. Homogeneity also means that if a disk layer is located at z from the bottom surface, its displacement is $\frac{z}{h}\mathbf{s}$ after the deformation. See Fig. 1 before and after the deformation.

Figure 1.

Deformation of the disk volume element in deriving the Maxwell stress tensor.

We further assume that the virtual deformation process is isothermal to focus on the electrostatic properties. Upon the virtual deformation the volume element does work −T_ijn_jAs_i towards its environment. Again the Einstein's summation convention is used here: $T_{ij}{n}_{j}A{s}_i=\sum _i\sum _j{T}_{ij}{n}_{j}A{s}_i.$ On the other hand, the work done by the volume element is equal to the decrease in electrostatic free energy contained in the volume element. Introducing $\overline{g}$ to denote the average electrostatic free energy density (g), we can write the total electrostatic free energy within the volume element as $\overline{g}Ah.$ Thus

$$-T_{ij}{n}_{j}A{s}_i=-\delta \left(\overline{g}Ah\right)=-A\delta \left(\overline{g}\right)h-A\overline{g}\delta h.$$ (5)

Removing identical terms from both sides,

$$T_{ij}{n}_j{s}_i=h\delta \left(\overline{g}\right)+\overline{g}\delta h.$$ (6)

According to Eq. 3, $g={\rho }^f\phi -\frac{\mathbf{D}•\mathbf{E}}{8\pi }-\Delta \Pi \lambda$,⁷⁶ variation of the electrostatic free energy density anywhere within the volume element gives

$$\begin{array}{ccc}\hfill \delta g& =& \phi \delta {\rho }^f-\frac{1}{8\pi }{E}^2\delta \varepsilon -k_{B}T\sum _i^N\left[(e^{-\frac{q_i\phi }{k_{B}T}}-1)c_i\right]\delta \lambda +{\rho }^f\delta \phi \hfill \\ & & -\frac{1}{4\pi }\mathbf{D}•\delta \mathbf{E}+\lambda \sum _i^N{q}_i{c}_i{e}^{-\frac{q_i\phi }{k_{B}T}}\delta \phi .\hfill \end{array}$$ (7)

The change of ρ^f is related to the change in the thickness of the thin disk by $\delta {\rho }^f=-\frac{{\rho }^f\delta h}{h}$ due to the assumption of the homogeneous deformation.

The variation in E is computed based on the following approximation on the potential distribution. The homogenous deformation process implies that the potential distribution in each disk layer remains the same. This is only true in a charge-free parallel capacity field⁸⁰ and is an approximation since the change in the charge density apparently leads to a change in potential if the PBE is satisfied. However, as shown in the Appendix, Subsections A1, A2, A3, the change in potential is a higher order small value compared with other changes if the PBE is preserved.

Thus at a given point (r) within a disk layer there appears to be a point originally at r − u within another disk layer. Here u is the vector of the displacement of the disk layer. This observation leads to the following relation between the potential and field as δφ = φ(r − u) − φ(r) = −u•∇φ = u•E, where E is the electric field in the undeformed volume element.⁸⁰ Given E ≠ 0 and $\mathbf{u}=\frac{z\mathbf{s}}{h}$ due to the uniform deformation, we have

$$\delta \phi =\frac{z\left(\mathbf{s}•\mathbf{E}\right)}{h},$$ (8)

where z is the distance of the layer from the lower disk surface. Taking the derivative of δϕ over z gives

$$\delta \mathbf{E}=\frac{\mathbf{n}\left(\mathbf{s}•\mathbf{E}\right)}{h}.$$ (9)

Finally ɛ and λ are the variables that only depend on the position and do not change upon the variation of ρ^f and E so that they do not cause any change in the free energy g at any given position within the volume element.

With all above preparations and also given that δφ is a higher order small value compared to δE and δρ^f as shown in the Appendix, Subsections A2, A3, Eq. 7 can be simplified as

$$\delta g=\phi \delta {\rho }^f-\frac{1}{4\pi }\mathbf{D}•\delta \mathbf{E},$$ (10)

after eliminating all the terms with δɛ, δλ, and δφ because they either do not or only make higher order small changes when comparing with the variations in δρ^f and δE. Note too that ρ^f is the free-charge density. In contrast, variation of the classical electrostatics free energy density, with the same assumptions, leads to $\delta g=\frac{1}{2}\phi \delta \rho =\frac{1}{4\pi }\mathbf{D}•\delta \mathbf{E}=\phi \delta \rho -\frac{1}{4\pi }\mathbf{D}•\delta \mathbf{E}$, with ρ being the total charge density. Hence, if the classical electrostatics is used to model the full PBE solution system, ρ should include both the free (atomic) charges and the mobile ion charges. Thus the variation of energy of Eq. 10 is different from the standard statement in the classical electrostatics. The extra term is responsible for the entropy change from the ionic concentration change upon polarization.⁸¹

Substituting 9 in 10, we have

$$\delta g=\phi \delta {\rho }^f-\frac{1}{4\pi }\frac{(\mathbf{D}•\mathbf{n})\left(\mathbf{s}•\mathbf{E}\right)}{h}.$$ (11)

Given $\overline{g}\to g$ and $\delta \left(\overline{g}\right)\to \delta g$ in the limit for the dimension of the volume element going to zero, and $\delta {\rho }^f=-\frac{{\rho }^f\delta h}{h}$, the Maxwell stress tensor element in Eq. 6 can be computed as

$$\begin{array}{ccc}\hfill T_{ij}{n}_j{s}_i& =& \frac{1}{4\pi }(\mathbf{D}•\mathbf{n})(\mathbf{E}•\mathbf{s})-{\rho }^f\phi \left(\mathbf{s}•\mathbf{n}\right)+g\left(\mathbf{s}•\mathbf{n}\right)\hfill \\ & =& \left(\frac{\varepsilon E_i{E}_j}{4\pi }-\frac{1}{8\pi }\varepsilon E^2{\delta }_{ij}-\Delta \Pi \lambda {\delta }_{ij}\right)n_j{s}_i.\hfill \end{array}$$ (12)

Here we have also used the fact that δh = s•n. In summary

$$T_{ij}=\frac{1}{4\pi }\varepsilon E_i{E}_j-\frac{1}{8\pi }\varepsilon E^2{\delta }_{ij}-\Delta \Pi \lambda {\delta }_{ij},$$ (13)

where $\Delta \Pi =k_{B}T\sum _i{c}_i(e^{-q_i\phi /k_{B}T}-1)$. Note also that the tensor is symmetric, i.e., T_ij = T_ji.

COMPUTATION OF ELECTROSTATIC FORCES—GENERAL METHOD

The force can be computed as P•nda for any area element da with a normal direction of n. Since we are dealing with an ideal classical fluid, the natural first step is the computation of force density fdv for a volume element dv. This is readily available as ∮P•nda once P is known, namely, the net force felt by the volume element is the total force acting upon it on its enclosing surface. This procedure suggests that the concept of divergence of the stress tensor can be introduced, which is $\underset{dv\to 0}{lim}\frac{\oint \mathbf{P}•\mathbf{n}da}{dv}$, as is the case for the divergence of a vector field. It is straightforward to show that the divergence theorem also holds for the stress tensor⁸⁰

$$\int \nabla •\mathbf{P}dv=\oint \mathbf{P}•\mathbf{n}da.$$ (14)

There are two consequences in Eq. 14 concerning us here. (1) The force density is simply the divergence of the stress tensor, i.e.,

$$\mathbf{f}=\nabla •\mathbf{P}.$$ (15)

(2) Total force can be computed either by the differential form, i.e., through the computation of force density [Eq. 15] followed by volume integration, or by the integral form, i.e., through the surface integral of the stress tensor, and they are consistent according to Eq. 14, i.e., when the divergence theorem holds. Since the divergence is undefined in regions with discontinuity, the differential form can only be used in regions without singularity, i.e., without jump of dielectric constant and without singular charge sources (for example, the point charges represented as delta functions in the PB equation). However, for systems/regions with singularity, only the integral form can be applied. As a side note, the variational approach is also limited because it only holds in regions without singularity.⁶⁴ In the following, we shall first start our derivation on systems without any singularity.

TOTAL ELECTROSTATIC FORCES FOR SYSTEMS WITHOUT SINGULARITY

Based on the general discussion in Sec. 3, the force density is simply the divergence of the Maxwell stress tensor.⁸⁰ The electrostatic force density f can then be expressed as

$$\mathbf{f}={\rho }^f\mathbf{E}-\frac{1}{8\pi }{\mathbf{E}}^2\nabla \varepsilon -\Delta \Pi \nabla \lambda ,$$ (16)

with a simple derivation shown in the Appendix, Subsection A4. The first term represents the free-charge force, the second term represents the bound-charge force due to the variation in dielectric constant, and the third term represents the pressure due to the presence of mobile ions. This is formally consistent with the formulation derived from the variational strategy by Gilson et al. from the total electrostatic free energy (Eq. 3).⁶⁴ However, it is worth noting the different condition from the variational approach by Gilson et al. that requires the smoothness in charge density, potential, and electric field throughout the solvated system of interest: the differential approach based on the stress tensor only requires the smoothness in charge density, potential, and electric field within a local region where the divergence operator is to be applied.

Cai et al. showed that the second term, termed dielectric boundary force, can be reformulated with the explicit presence of the bound polarization charge⁶⁶

$${\mathbf{f}}_{bnd}^{diel}=-\frac{1}{8\pi }{\left|\mathbf{E}\right|}^2\nabla \varepsilon =\frac{1}{2}{\rho }^{pol}\frac{{\left|\mathbf{D}\right|}^2}{\mathbf{D}•\mathbf{n}}\mathbf{n},$$ (17)

where ρ^pol is the polarized charge density, n is the normal direction of the boundary surface, and D is the electric displacement within the polarized area. Their numerical tests on realistic biomolecules show that the atomic solvation forces are more stable and converge faster using the so-called charge-based method. Of course both formulations are consistent with the “virtual work” principle as they demonstrated in the tested systems.

TOTAL ELECTROSTATIC FORCES IN SYSTEMS WITH SINGULARITY

If singularity exists in a solution system, Eq. 16 cannot be used to compute electrostatic forces. We shall turn to the integral form, which is more fundamental and does not require the divergence of a singular Maxwell stress tensor. In general, we consider four situations, i.e., the solute region without singularity, the solute region with singularity, the dielectric interface region, and finally the mobile ion term at the Stern layer.

Solute region with and without singularity

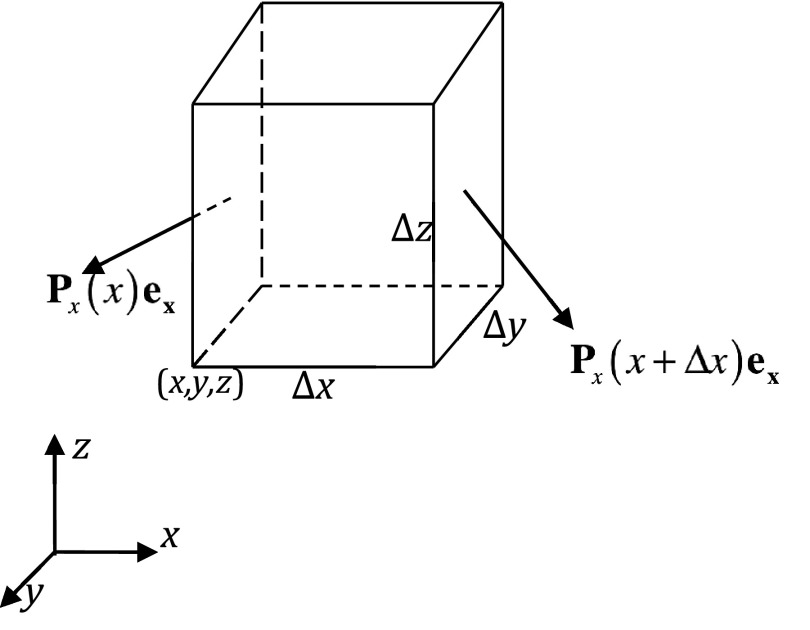
To obtain a detailed force distribution on each atom of the solute molecule, we first divide the solute volume into small rectangular elements, Δv (see Fig. 2). Apparently any rectangular volume element is much smaller than each atom, but it is still an order-of-magnitude larger than the disk-like element shown in Fig. 1 utilized to derive the expression of the Maxwell stress tensor. As shown in the Appendix, Subsections A5, for a solute region without singularity, the electrostatic force for each volume element Δv is

$$\mathbf{F}={\rho }^f\mathbf{E}.$$ (18)

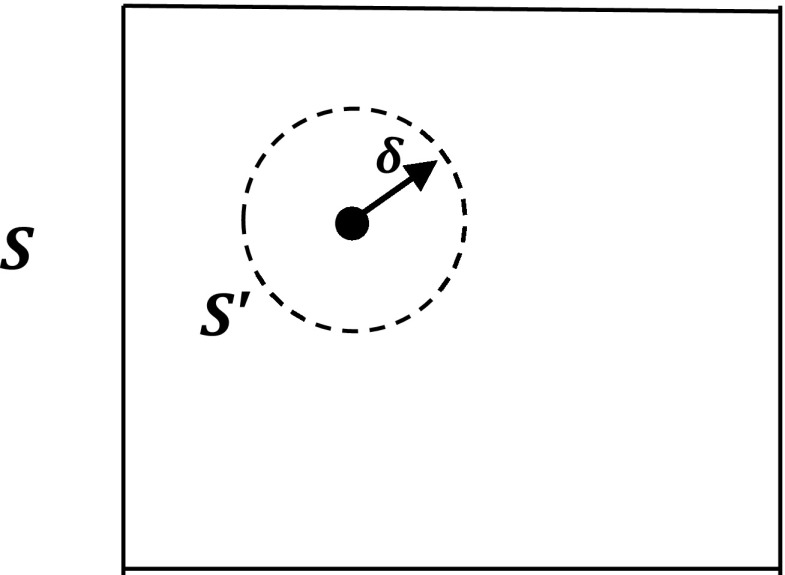
For a solute volume element with singularity, we further divide the volume element into a smaller spherical region containing the singular charge and the rest where there is no singular charge (see Fig. 3). We can then obtain the analytical expression for the electrostatic force in the small rectangular volume element based on the Maxwell stress tensor. As shown and summarized in the Appendix, Subsections A6, the force density can then be universally written as

$$\mathbf{f}={\rho }^f\mathbf{E}$$ (19)

in the solute region whether the charge density is singular or not.

Figure 2.

The force on a small volume in the continuum solute.

Figure 3.

Singular charge enclosed by an infinitely small spherical volume S′ with radius δ.

The dielectric interface region

Cai et al. utilized the integral formulation based on the Maxwell stress to compute the force in the dielectric interface region for the piece-wise constant classical dielectric models of biomolecules.⁶⁸ Their derivation shows that

$$\begin{array}{ccc}\hfill {\mathbf{f}}_{bnd}^{diel}& =& ({\mathbf{P}}_o-{\mathbf{P}}_i)•\mathbf{n}=\frac{1}{4\pi }[\left({\varepsilon }_o{E}_{o\mathbf{n}}^2-\frac{1}{2}{\varepsilon }_o{\mathbf{E}}_o^2\right)\hfill \\ & & -\left({\varepsilon }_i{E}_{i\mathbf{n}}^2-\frac{1}{2}{\varepsilon }_i{\mathbf{E}}_i^2\right)]\mathbf{n},\hfill \end{array}$$ (20)

where n is the outward-directed normal unit vector of the molecular surface, and P_i and P_o are the stress tensors on the surfaces parallel to the dielectric interface inside and outside of the solute. E_o, E_i, respectively, are the electric fields on the two sides of the solute-solvent interface; and E_in, E_on, respectively, are the electric field components on the n directions of E_o, E_i.

They further pointed out that a charge-based strategy could also be proposed for the piece-wise constant dielectric treatment. Briefly the dielectric boundary force can be written as

$${\mathbf{f}}_{bnd}^{diel}=\frac{1}{2}{\sigma }^{pol}\frac{{\varepsilon }_i{\mathbf{E}}_i•{\mathbf{E}}_o}{E_{o\mathbf{n}}}\mathbf{n}=\frac{1}{2}{\sigma }^{pol}\frac{{\mathbf{D}}_i•{\mathbf{D}}_o}{D_{o\mathbf{n}}}\mathbf{n},$$ (21)

where σ^pol is the bound polarized surface charge density, and D_o and D_i are the corresponding electric displacements of the solvent and solute side, respectively.

An interesting observation is the similarity of Eq. 21 and the charge-based approach for the smooth-transition dielectric treatment Eq. 17.⁶⁶ Of course, volume density and integration should be used in the smooth-transition dielectric model because there is no longer a sharp interface between the solvent and solute. However, the basic operation is still the same where the polarization charges and electric displacements are needed in the region of non-uniform dielectric constant.

The numerical tests show that the charge-based formulation offers much better consistency between the results at all grid spacings, as demonstrated by the fact that the slope is always very close to 1 and the deviation from analytical values is smaller than the method as in Eq. 20. Furthermore, the numerical uncertainties of the atomic forces by the charge-based method are also smaller, suggesting less significant grid dependence. The mean total electrostatic force by the charge-based formulation is also closer to zero, but its fluctuation is on the same order as that by the method as in Eq. 20.

The ionic interface region

At the Stern Layer, mobile ions exist only on one side though the dielectric constants on both sides are the same. The classical method models the Stern layer with a step function of λ that changes from 0 to 1. Given the availability of Maxwell stress tension, the boundary force caused by the excess osmotic pressure is the same as that caused by the jump of dielectric constant. We have

$$f_{bnd}^{ion}=({\mathbf{P}}_o-{\mathbf{P}}_i)•\mathbf{n}=-\nabla \Pi ,$$ (22)

where P_o, P_i are the corresponding stress tensors on outside and inside of the Stern layer from Eq. 13. Here we have used the notation that λ is 1 or 0 on the two sides of the layer. The simplicity of the derivation demonstrates the clean physics in the Maxwell stress tensor approach.

CONNECTION AND COMPARISON WITH THE STRATEGY OF GILSON ET AL.

As discussed above, the field-based methods and the charge-based methods in the computation of dielectric boundary forces are mathematically consistent with the original method proposed by Gilson et al. Furthermore, by taking the limit of infinite thin transition zone in the smooth-transitioned dielectric model, the smooth-transitioned and abrupt-transitioned formulations can be shown to be consistent with each other mathematically, implying a high level of internal consistency between the integral and differential approaches based on the Maxwell stress tensor.

We expect all algorithms become numerically indistinguishable in the limit of zero grid spacing in the finite-difference method when the harmonic averaging method is used to smooth the transition between the solute and solvent dielectrics (chosen to be 1 and 80, respectively, in this test). Here we used a poly-alanine alpha-helix (eight residues) as an example to demonstrate their consistency numerically at the tested fine grid spacing of 1/16 Å. The finite difference box was set to be 1.5 times the dimension of the model helix due to the extremely large memory usage requirement of the finite-grid spacing. No electrostatic focusing was applied to maintain the highest possible quality in the numerical solution. The convergence of the numerical solver is reached when the relative residue is less than 10⁻⁹. The default Amber charges and continuum radii were used in the numerical calculations.⁸²

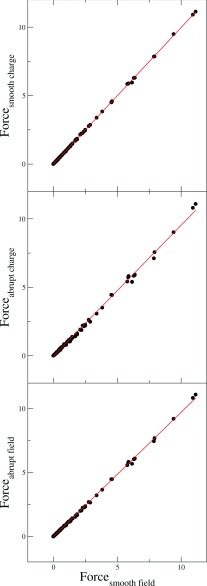
The correlations among the four methods are shown in Fig. 4. It can be seen that the linear correlation coefficients between the other three methods and the method of Gilson et al. are very high. Worth noting is the much higher agreement between the two methods based on the same smooth-transitioned dielectric treatment, i.e., the method of Gilson et al. (labeled as “Smooth Field” in the figure) and the charge-based method (labeled as “Smooth Charge”). The numerical test demonstrates that the four methods are numerically consistent, in agreement with our theoretical discussion above.

Figure 4.

Correlations between the atomic dielectric boundary forces for a model helix computed by the smooth field method (i.e., the method of Gilson et al.) and those computed by the smooth charge view method, the abrupt charge view method, and abrupt field method, respectively. Top: correlation between the smooth charge view method and the smooth field method; regression line y = −0.005 + 0.999x, r² = 0.9999. Middle: correlation between the abrupt charge view method and the smooth field method; regression line y = −0.036 + 0.957x, r² = 0.9989. Bottom: correlation between the abrupt field method and the smooth field method; regression line y = −0.022 + 0.974x, r² = 0.9996. All computations were at the grid spacing of 1/16 Å. Unit: kcal/(mol Å).

DISCUSSION

Much community-wide effort has been devoted to the calculation of the solvation forces in the numerical PBE methods.^{1, 30, 35, 49, 60, 61, 62, 63, 64, 65, 66, 67, 68, 72, 73, 74, 75, 76, 77, 78, 79, 80} Due to the difficulty in computation of dielectric boundary forces, most of the previous reports were focused on this aspect of the force calculation.

For the abrupt-transitioned dielectric models, Davis and McCammon proposed a formulation by examining the integration of the Maxwell stress tensor of a Poisson system, the dielectric boundary forces surface density was shown as⁶⁰

$${\mathbf{f}}_{DBF}=-\frac{1}{8\pi }\left({\varepsilon }_o-{\varepsilon }_i\right)\left({\mathbf{E}}_o·{\mathbf{E}}_i\right)\widehat{\mathbf{n}}.$$ (23)

Integration of this quantity over the surface yields the total dielectric boundary force for the molecule. The dielectric boundary forces formulation of Cai et al.⁶⁸ on the abrupt-transitioned dielectric models is also derived from the Maxwell stress tensor. It can be shown that their method is consistent with the Davis and McCammon method: Eq. 20 can be transformed into Eq. 23 by Davis and McCammon⁶⁰ given the jump conditions.⁶⁸

Che et al. revisited the dielectric boundary forces calculation through a variational strategy in the classical abrupt-transitioned dielectric models.⁶⁵ Given the assumption that the normal surface field contributes predominantly to dielectric boundary force, they showed that the dielectric boundary force can be formulated as

$${\mathbf{f}}_{DBF}=-\frac{1}{8\pi }\left(\frac{1}{{\varepsilon }_i}-\frac{1}{{\varepsilon }_o}\right){\left|\varepsilon \nabla \phi \right|}^2\widehat{\mathbf{n}},$$ (24)

where ɛ∇φ represents the continuous normal dielectric displacement vector on the solute/solvent dielectric interface. This formulation was later updated by Li et al. in their second paper on deriving the dielectric boundary forces from the variation of the electrostatic free energy with respect to the location change of the dielectric boundary to⁶⁷

$$\begin{array}{ccc}\hfill {\mathbf{f}}_{DBF}& =& \frac{1}{4\pi }[{\varepsilon }_o{\left|\nabla {\phi }_o·\mathbf{n}\right|}^2-\frac{1}{2}{\varepsilon }_o{\left|\nabla {\phi }_o\right|}^2\hfill \\ & & -{\varepsilon }_i{\left|\nabla {\phi }_i·\mathbf{n}\right|}^2+\frac{1}{2}{\varepsilon }_i{\left|\nabla {\phi }_i\right|}^2].\hfill \end{array}$$ (25)

This formulation can be shown as consistent with Eq. 23 and Eq. 20.

For the smooth-transitioned dielectric models, Gilson et al. presented a ground-breaking variational approach for the dielectric boundary forces,⁶⁴ and it was further tailored into a numerical algorithm for the FDM. Their expression for the dielectric boundary forces can be expressed as

$${\mathbf{f}}_{DBF}=-\frac{1}{8\pi }{\left|\mathbf{E}\right|}^2\nabla \varepsilon .$$ (26)

Note this is consistent with Eq. 17 as derived by Cai et al. based on the Maxwell stress tensor discussed above.⁶⁶ Im et al. proposed a method equivalent to Eq. 26 as

$${\mathbf{f}}_{DBF}=\left[\frac{1}{8\pi }\phi \nabla ·\left(\frac{\partial \varepsilon }{\partial r}\nabla \phi \right)\right]\widehat{\mathbf{n}},$$ (27)

where r represents the atomic coordinates.³⁰ Apparently both Eqs. 26, 27 require smoothly varying dielectric models since ∇ɛ has to be finite, i.e., ɛ has to be designed to change from ɛ_i to ɛ_o sufficient smoothly for stable numerical performance.⁸³ This would exclude the abrupt-transitioned dielectric models where ∇ɛ is infinite.

The BEM is another promising approach to incorporate the continuum electrostatics into molecular mechanics simulations.^{49, 72, 73, 74, 75, 84, 85} The dielectric boundary forces calculation in the BEM using a polarization charge method was first described by Zauhar,⁶² who showed that the dielectric boundary forces can be calculated as

$${\mathbf{f}}_{DBF}=-\left[2\pi {\sigma }^2{\varepsilon }_i+\frac{1}{8\pi }\left({\varepsilon }_o-{\varepsilon }_i\right){\left|{\mathbf{E}}_o\right|}^2\right]\widehat{\mathbf{n}}.$$ (28)

This expression was derived from Eq. 23. The use of surface polarization charge density makes it straightforward in the BEM, where the Poisson's equation can be solved through the iteration of the surface polarization charge density. Cortis et al. also tried to compute the dielectric boundary forces via the Maxwell stress tensor for their FEM, leading to the same formulation as that of Zauhar.³⁵ Of course, it is also consistent with Eq. 21 as proposed by Cai et al.⁶⁸

CONCLUSION

In this study, we addressed the theoretical issue in using the Maxwell stress tensor to derive the electrostatic solvation forces in systems obeying the nonlinear Poisson-Boltzmann equation and further using the stress-tensor based methods in formulating electrostatic solvation forces. Different from the widely used variational approach that requires the smoothness in charge density, potential, and electric field throughout the solvated system of interest, the integral approach based on the stress tensor only requires the smoothness in charge density, potential, and electric field within a local region. This is because that the variational approach requires the variation of the total free energy of the whole system that has to be smooth everywhere. In contrast, the integral approach based on the Maxwell stress tensor allows the existence of a finite number of singularities as presented as atomic point charge sources. It is also straightforward to handle both piece-wise constant dielectric models. Of course the simple step-function model of the ionic interface can also be addressed.

It is worth noting that a charge-based strategy can be proposed to enhance the numerical behavior of numerical forces for the FDM calculations.^{66, 68} An interesting observation is the similarity of the charge-based approaches between the smooth-transitioned and the abrupt-transitioned dielectric treatments.^{66, 68} Indeed, by taking the limit of infinite thin transition zone in the smooth-transitioned dielectric model, the two formulations can be shown to be consistent with each other mathematically, implying a high level of internal consistency between the integral and differential approaches based on the Maxwell stress tensor. The numerical tests for both types of dielectric models show that the charge-based formulation offers much better consistency between the numerical forces at all grid spacings.^{66, 68} Furthermore, the numerical uncertainties of the atomic forces by the charge-based method are also smaller, suggesting less significant grid dependence. The mean total electrostatic force by the charge-based formulation is also closer to zero.^{66, 68} These are all important for future applications to molecular mechanics applications.

Given the summary of both the theoretical analyses and algorithm developments, it is instructive to address the future direction to be taken to reach the goal of routine applications of the numerical PBE methods for molecular mechanics simulations. To further improve the numerical PBE methods, it is important to work on both its efficiency and accuracy. Regarding to the accuracy of the numerical PBE methods, more advanced numerical solvers are certainly necessary to achieve higher accuracy than the widely used classical methods to improve the convergence of numerical forces. To improve the scalability of force calculations on more complex biomolecular systems, the particle-particle particle-mesh method can certainly be explored to achieve a good scalability of the proposed algorithms.

APPENDIX: MATHEMATICAL DETAILS

Derivation of δE upon the variation of the volume element

As shown in Eq. 8

$$\delta \phi =\frac{z\left(\mathbf{s}•\mathbf{E}\right)}{h}.$$ (A1)

Taking the derivative, we obtain

$$\delta \mathbf{E}=-\delta \nabla \phi =-\frac{\mathbf{n}\left(\mathbf{s}•\mathbf{E}\right)}{h}-\frac{\nabla \left(\mathbf{s}•\mathbf{E}\right)}{h}z.$$ (A2)

Given that E is a smooth variable, ∇(s•E) in Eq. A2 is well defined and bounded. Define $k=\frac{\left|\nabla \left(\mathbf{s}•\mathbf{E}\right)\right|}{\left|\mathbf{s}•\mathbf{E}\right|}.$ Then we have

$$\left|\nabla \left(\mathbf{s}•\mathbf{E}\right)\right|=\left|k\left(\mathbf{s}•\mathbf{E}\right)\right|.$$ (A3)

Since h can be arbitrarily small, it is always possible to choose h so that $k\ll \frac{1}{h}$ and

$$\left|k\left(\mathbf{s}•\mathbf{E}\right)\right|\ll \left|\frac{\left(\mathbf{s}•\mathbf{E}\right)}{h}\right|=\left|\frac{\left(\mathbf{s}•\mathbf{E}\right)\mathbf{n}}{h}\right|.$$ (A4)

The condition of z < h leads to

$$\left|\frac{\nabla \left(\mathbf{s}•\mathbf{E}\right)}{h}z\right|<\left|\nabla \left(\mathbf{s}•\mathbf{E}\right)\right|.$$ (A5)

Combining Eqs. A3, A4, A5, we have

$$\left|\frac{\nabla \left(\mathbf{s}•\mathbf{E}\right)}{h}z\right|\ll \left|\frac{\left(\mathbf{s}•\mathbf{E}\right)\mathbf{n}}{h}\right|,$$ (A6)

which is denoted as $|\frac{\nabla \left(\mathbf{s}•\mathbf{E}\right)}{h}z|\sim |o\left[\frac{\left(\mathbf{s}•\mathbf{E}\right)\mathbf{n}}{h}\right]|,\mathrm{as}h\to 0.$ Here the little o notation means $\underset{h\to 0}{lim}|o\left[\frac{\left(\mathbf{s}•\mathbf{E}\right)\mathbf{n}}{h}\right]|/|\frac{\left(\mathbf{s}•\mathbf{E}\right)\mathbf{n}}{h}|=0.$ Thus Eq. A2 can be written as

$$\delta \mathbf{E}=-\frac{\mathbf{n}\left(\mathbf{s}•\mathbf{E}\right)}{h}+o\left[\frac{\mathbf{n}\left(\mathbf{s}•\mathbf{E}\right)}{h}\right].$$ (A7)

Relative orders among δφ, δE, and δρ^f upon the variation of the volume element

We are now ready to prove that δφ is a higher order small value than δE, and δρ^f is the same order small value as δE. Dot production by n on both side of Eq. A7 gives

$$\mathbf{n}•\delta \mathbf{E}=-\frac{\left(\mathbf{s}•\mathbf{E}\right)}{h}+o\left[\frac{\left(\mathbf{s}•\mathbf{E}\right)}{h}\right].$$ (A8)

Comparing A8 and $\delta \phi =\frac{z\left(\mathbf{s}•\mathbf{E}\right)}{h}$, A1 and also noting z < h, we have

$$\left|\delta \phi \right|<\left|h\mathbf{n}•\delta \mathbf{E}\right|\sim \left|o(\mathbf{n}•\delta \mathbf{E})\right|,\mathrm{as}h\to 0.$$ (A9)

Here the little o notation means $\underset{h\to 0}{lim}\left|o\left[\mathbf{n}•\delta \mathbf{E}\right]\right|/\left|\mathbf{n}•\delta \mathbf{E}\right|=0.$ Thus δφ is a higher order small value than δE.

Next given δh = s•n, we have

$$\left|\delta {\rho }^f\right|=\left|\frac{{\rho }^f\delta h}{h}\right|=\left|\frac{{\rho }^f(\mathbf{s}•\mathbf{n})}{h}\right|.$$ (A10)

Comparison of Eqs. A10 with A8 shows that δρ^f is a same order small value as δE since they both contains small value s in the numerator and small value h in the denominator while both ρ^f and E are finite.

Similarly from A1 we have

$$\left|\delta \phi \right|=\left|\frac{\left(\mathbf{s}•\mathbf{E}\right)z}{h}\right|.$$ (A11)

Since z is a small value but both ρ^f and E are finite, δφ is one order smaller than δρ^f as given in A10.

Preservation of nonlinear-PB equation upon the variation of the volume element

We have shown in A7 that the leading term of δE is

$$\delta \mathbf{E}=-\frac{\mathbf{n}\left(\mathbf{s}•\mathbf{E}\right)}{h}.$$ (A12)

Apparently any change in the field must also satisfy the governing PB equation

$$\nabla ·\varepsilon \mathbf{E}=-4\pi {\rho }^f-4\pi {\rho }^m,$$ (A13)

where ${\rho }^m=\sum _i{q}_i{c}_i{e}^{-q_i\phi /k_{B}T}\lambda$ is the charge distribution of the mobile ions. Indeed a potential violation of the PB equation is possible during the deformation process as discussed in the following. However, any deviations from the PB equation are only higher order small variations than that in A12 and its comparable variations.

Given that ɛ and λ do not change at the same position, δλ = 0 and δɛ = 0 during the deformation process. The PB equation

$$\nabla ·\varepsilon \mathbf{E}=-4\pi {\rho }^f-4\pi \sum _i{q}_i{c}_i{e}^{-q_i\phi /k_{B}T}\lambda$$ (A14)

can be varied as

$$\nabla ·\varepsilon \delta \mathbf{E}=-4\pi \delta {\rho }^f+4\pi \sum _i{q}_i^2{c}_i/k_{B}T{e}^{-q_i\phi /k_{B}T}\lambda \delta \phi$$ (A15)

after dropping the zero variations. Since we only consider a very small volume element with infinite small changes in all smooth variables in the variational analysis, only the lowest order small terms need to be retained. All higher order small terms can be eliminated during the derivation.

After eliminating δφ in Eq. A15, we have

$$\nabla ·\left(\varepsilon \delta \mathbf{E}\right)=4\pi {\rho }^f\frac{\delta h}{h}.$$ (A16)

Substitution of Eq. A12, we have

$$\nabla ·\left(\varepsilon \delta \mathbf{E}\right)=-\frac{\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}}{h}.$$ (A17)

Next we show that Eq. A16 can be satisfied by making an infinitely small adjustment of δE. Introducing $\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}$ to denote the average value of the gradient within the volume element, we change δE to $\delta \mathbf{E}+\frac{\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}}{\varepsilon h}z+4\pi {\rho }^f\frac{\delta h}{\varepsilon h}z$, so that

$$\delta \mathbf{E}=-\frac{\mathbf{n}\left(\mathbf{s}•\mathbf{E}\right)}{h}+\frac{\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}}{\varepsilon h}z+4\pi {\rho }^f\frac{\delta h}{\varepsilon h}z.$$ (A18)

And then

$$\nabla ·\varepsilon \delta \mathbf{E}=-\frac{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}{h}+\frac{\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}}{h}+4\pi {\rho }^f\frac{\delta h}{h}.$$ (A19)

Notice that ɛ, E are both smoothly changed and hence we can expect that there is only a very small difference between $\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]$ and $\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}.$ Also given δh = s • n, so that

$$\begin{array}{ccc}\hfill \left|4\pi {\rho }^f\frac{\delta h}{h}\right|& \sim & \left|4\pi {\rho }^f\frac{\mathbf{s}•\mathbf{n}}{h}\right|\sim \left|\frac{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}{h}\right|\hfill \\ & \gg & \left|-\frac{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}{h}+\frac{\overline{\frac{\partial }{\partial n}\left[\varepsilon (\mathbf{s}•\mathbf{E})\right]}}{h}\right|.\hfill \end{array}$$ (A20)

Thus we can eliminate the first two terms on the right side of Eq. A19 and Eq. A16 is satisfied.

Finally z < h is a very small value, so that the second term and the third term on the right hand side of Eq. A19 are one order smaller compare to the first term. In summary we only need to modify the original variation of E with a higher order small value to preserve the PB equation. The same argument can also be applied for derivation with δφ as the leading small value.

Derivation of the electrostatic force density

Based on the general discussion in Sec. 3, the force density is simply the divergence of the Maxwell stress tensor.⁸⁰

$$\mathbf{f}=\nabla •\mathbf{P}=\frac{\partial }{\partial x}({\mathbf{e}}_x•\mathbf{P})+\frac{\partial }{\partial y}({\mathbf{e}}_y•\mathbf{P})+\frac{\partial }{\partial z}({\mathbf{e}}_z•\mathit{P}).$$ (A21)

We rewrite Eq. 13 into the following form:

$$T_{ij}=\frac{1}{4\pi }{E}_i{D}_j-\frac{1}{8\pi }\varepsilon E^2{\delta }_{ij}-\Delta \Pi \lambda {\delta }_{ij},$$ (A22)

where $\Delta \Pi =k_{B}T\sum _i{c}_i(e^{-q_i\phi /k_{B}T}-1)$. So along the direction of e_x, the force component is

$$\begin{array}{ccc}\hfill f_x& =& \frac{\partial T_{xx}}{\partial x}+\frac{\partial T_{xy}}{\partial y}+\frac{\partial T_{xz}}{\partial z}\hfill \\ & =& \frac{1}{4\pi }\left[-\frac{1}{2}\varepsilon \frac{\partial }{\partial x}{E}^2+\sum _i\frac{\partial \left(E_x{D}_i\right)}{\partial i}\right]-\frac{E^2}{8\pi }\frac{\partial \varepsilon }{\partial x}-\Delta \Pi \frac{\partial \lambda }{\partial x}\hfill \\ & & +\sum _j{q}_j{c}_j{e}^{-q_i\phi /k_{B}T}\lambda \frac{\partial \varphi }{\partial x}\hfill \\ & =& \frac{1}{4\pi }\left[-\sum _i\varepsilon E_i\frac{\partial E_i}{\partial x}+\sum _i{D}_i\frac{\partial E_x}{\partial i}+E_x\sum _i\frac{\partial D_i}{\partial i}\right]\hfill \\ & & -\frac{E^2}{8\pi }\frac{\partial \varepsilon }{\partial x}-\Delta \Pi \frac{\partial \lambda }{\partial x}-\sum _j{q}_j{c}_j{e}^{-q_i\phi /k_{B}T}\lambda E_x\hfill \\ & =& \frac{1}{4\pi }\sum _i{D}_i\left(\frac{\partial E_x}{\partial i}-\frac{\partial E_i}{\partial x}\right)-\frac{E^2}{8\pi }\frac{\partial \varepsilon }{\partial x}-\Delta \Pi \frac{\partial \lambda }{\partial x}\hfill \\ & & +\frac{1}{4\pi }\left(-4\pi \sum _j{q}_j{c}_j{e}^{-q_i\phi /k_{B}T}\lambda +\nabla •\mathbf{D}\right)E_x,\hfill \end{array}$$ (A23)

where i = x, y, z. Since there is no changing magnetic field, we have ∇ × E = 0. Thus the first term on the right side of Eq. A23 equals to zero. Given the notation in Eq. 2, we obtain

$$f_x={\rho }^f{E}_x-\frac{E^2}{8\pi }\frac{\partial \varepsilon }{\partial x}-\Delta \Pi \frac{\partial \lambda }{\partial x}.$$ (A24)

Following the same way, we obtain

$$\begin{array}{ccc}\hfill f_y& =& {\rho }^f{E}_y-\frac{E^2}{8\pi }\frac{\partial \varepsilon }{\partial y}-\Delta \Pi \frac{\partial \lambda }{\partial y},\hfill \\ \\ \hfill f_z& =& {\rho }^f{E}_z-\frac{E^2}{8\pi }\frac{\partial \varepsilon }{\partial z}-\Delta \Pi \frac{\partial \lambda }{\partial z}.\hfill \end{array}$$ (A25)

Thus the force density f is

$$\mathbf{f}={\rho }^f\mathbf{E}-\frac{1}{8\pi }{\mathbf{E}}^2\nabla \varepsilon -\Delta \Pi \nabla \lambda .$$ (A26)

Solute region without singularity

For a volume element in the solute region, shown in Fig. 2, the force acting on the left surface perpendicular to the x axis is written as

$$\begin{array}{ccc}\hfill F_x\left(x\right)& =& P\left(x\right)\Delta y\Delta z\hfill \\ & =& \left[\frac{1}{4\pi }\left({\varepsilon }_i{E}_x^2-\frac{1}{2}{\varepsilon }_i{E}^2\right){\mathbf{e}}_{\mathbf{x}}+\frac{1}{4\pi }\left({\varepsilon }_i{E}_y{E}_x\right){\mathbf{e}}_{\mathbf{y}}\right.\hfill \\ & & +\left.\frac{1}{4\pi }\left({\varepsilon }_i{E}_z{E}_x\right){\mathbf{e}}_{\mathbf{z}}\right]\Delta y\Delta z\hfill \\ & =& \left[\frac{1}{8\pi }({\varepsilon }_i{E}_x^2-{\varepsilon }_i{E}_y^2-{\varepsilon }_i{E}_z^2){\mathbf{e}}_{\mathbf{x}}+\frac{1}{4\pi }\left({\varepsilon }_i{E}_y{E}_x\right){\mathbf{e}}_{\mathbf{y}}\right.\hfill \\ & & \left.+\frac{1}{4\pi }\left({\varepsilon }_i{E}_z{E}_x\right){\mathbf{e}}_{\mathbf{z}}\right]\Delta y\Delta z.\hfill \end{array}$$ (A27)

Similarly the force acting on the right surface perpendicular to the x axis is

$$\begin{array}{ccc}& & F_x(x+\Delta x)\hfill \\ & & =\left[\frac{1}{8\pi }[{\varepsilon }_i{E}_x^2(x+\Delta x)-{\varepsilon }_i{E}_y^2(x+\Delta x)-{\varepsilon }_i{E}_z^2(x+\Delta x)]{\mathbf{e}}_{\mathbf{x}}\right.\hfill \\ & & +\frac{1}{4\pi }\left[{\varepsilon }_i{E}_y(x+\Delta x)E_x(x+\Delta x)\right]{\mathbf{e}}_{\mathbf{y}}\hfill \\ & & \left.+\frac{1}{4\pi }\left[{\varepsilon }_i{E}_z(x+\Delta x)E_x(x+\Delta x)\right]{\mathbf{e}}_{\mathbf{z}}\right]\Delta y\Delta z\hfill \\ & & =\left[\frac{1}{8\pi }{\varepsilon }_i\left[{\left(E_x+\frac{\partial E_x}{\partial x}\Delta x\right)}^2-{\left(E_y+\frac{\partial E_y}{\partial x}\Delta x\right)}^2\right.\right.\hfill \\ & & \left.-{\left(E_z+\frac{\partial E_z}{\partial x}\Delta x\right)}^2\right]{\mathbf{e}}_{\mathbf{x}}\hfill \\ & & +\frac{1}{4\pi }{\varepsilon }_i\left[\left(E_y+\frac{\partial E_y}{\partial x}\Delta x\right)\left(E_x+\frac{\partial E_x}{\partial x}\Delta x\right)\right]{\mathbf{e}}_{\mathbf{y}}\hfill \\ & & +\left.\frac{1}{4\pi }{\varepsilon }_i\left[\left(E_z+\frac{\partial E_z}{\partial x}\Delta x\right)\left(E_x+\frac{\partial E_x}{\partial x}\Delta x\right)\right]{\mathbf{e}}_{\mathbf{z}}\right]\Delta y\Delta z.\hfill \end{array}$$ (A28)

Due to the absence of singularity, the Taylor expansion can be used. The difference of F_x(x) and F_x(x + Δx) is the force acting on the surface perpendicular to the x direction. With ΔxΔyΔz = dv, we have

$$\begin{array}{ccc}& & F_x\left(x\right)-F_x(x+\Delta x)\hfill \\ & & =\frac{1}{4\pi }{\varepsilon }_i\left[\left(\frac{\partial E_x}{\partial x}{E}_x-\frac{\partial E_y}{\partial x}{E}_y-\frac{\partial E_z}{\partial x}{E}_z\right){\mathbf{e}}_{\mathbf{x}}\right.\hfill \\ & & +\left(\frac{\partial E_x}{\partial x}{E}_y+\frac{\partial E_y}{\partial x}{E}_x\right){\mathbf{e}}_{\mathbf{y}}\hfill \\ & & +\left.\left(\frac{\partial E_x}{\partial x}{E}_z+\frac{\partial E_z}{\partial x}{E}_x\right){\mathbf{e}}_{\mathbf{z}}\right]dv.\hfill \end{array}$$ (A29)

Similarly, the force acting on the surfaces perpendicular to the y direction and the z direction is

$$\begin{array}{ccc}& & F_y\left(y\right)-F_y(y+\Delta y)\hfill \\ & & =\frac{1}{4\pi }{\varepsilon }_i\left[\left(\frac{\partial E_x}{\partial y}{E}_y+\frac{\partial E_y}{\partial y}{E}_x\right){\mathbf{e}}_{\mathbf{x}}\right.\hfill \\ & & +\left(\frac{\partial E_y}{\partial y}{E}_y-\frac{\partial E_x}{\partial y}{E}_x-\frac{\partial E_z}{\partial y}{E}_z\right){\mathbf{e}}_{\mathbf{y}}\hfill \\ & & +\left.\left(\frac{\partial E_y}{\partial y}{E}_z+\frac{\partial E_z}{\partial y}{E}_y\right){\mathbf{e}}_{\mathbf{z}}\right]dv.\hfill \end{array}$$ (A30)

$$\begin{array}{ccc}& & F_z\left(z\right)-F_z(z+\Delta z)\hfill \\ & & =\frac{1}{4\pi }{\varepsilon }_i\left[\left(\frac{\partial E_x}{\partial z}{E}_z+\frac{\partial E_z}{\partial z}{E}_x\right){\mathbf{e}}_{\mathbf{x}}\right.\hfill \\ & & +\left(\frac{\partial E_y}{\partial z}{E}_z+\frac{\partial E_z}{\partial z}{E}_y\right){\mathbf{e}}_{\mathbf{y}}\hfill \\ & & +\left.\left(\frac{\partial E_z}{\partial z}{E}_z-\frac{\partial E_x}{\partial z}{E}_x-\frac{\partial E_y}{\partial z}{E}_y\right){\mathbf{e}}_{\mathbf{z}}\right]dv.\hfill \end{array}$$ (A31)

Summation of the e_x components of F_x(x) − F_x(x + Δx), F_y(y) − F_y(y + Δy), and F_z(z) − F_z(z + Δz) gives us the force acting on the volume element in the x direction

$$\begin{array}{ccc}\hfill F_x& =& \frac{1}{4\pi }{\varepsilon }_i\left(\frac{\partial E_x}{\partial x}{E}_x-\frac{\partial E_y}{\partial x}{E}_y-\frac{\partial E_z}{\partial x}{E}_z+\frac{\partial E_x}{\partial y}{E}_y\right.\hfill \\ & & \left.+\frac{\partial E_y}{\partial y}{E}_x+\frac{\partial E_x}{\partial z}{E}_z+\frac{\partial E_z}{\partial z}{E}_x\right)dv.\hfill \end{array}$$ (A32)

Due to ∇ × E = 0, we have

$$\left\{\begin{array}{c}\frac{\partial E_y}{\partial x}{E}_y=\frac{\partial E_x}{\partial y}{E}_y\\ \frac{\partial E_z}{\partial x}{E}_z=\frac{\partial E_x}{\partial z}{E}_z,\end{array}\right.$$ (A33)

With Eq. A33, Eq. A32 can be simplified as

$$F_x=\frac{1}{4\pi }{\varepsilon }_i\left(\frac{\partial E_x}{\partial x}{E}_x+\frac{\partial E_y}{\partial y}{E}_x+\frac{\partial E_z}{\partial z}{E}_x\right)dv.$$ (A34)

Similarly it can be shown that

$$F_y=\frac{1}{4\pi }{\varepsilon }_i\left(\frac{\partial E_x}{\partial x}{E}_y+\frac{\partial E_y}{\partial y}{E}_y+\frac{\partial E_z}{\partial z}{E}_y\right)dv$$ (A35)

$$F_z=\frac{1}{4\pi }{\varepsilon }_i\left(\frac{\partial E_x}{\partial x}{E}_z+\frac{\partial E_y}{\partial y}{E}_z+\frac{\partial E_z}{\partial z}{E}_z\right)dv.$$ (A36)

With Eqs. A34, A35, A36, the total force acting the volume element can be written as

$$\begin{array}{ccc}\hfill \mathbf{F}& =& F_x{\mathbf{e}}_{\mathbf{x}}+F_y{\mathbf{e}}_{\mathbf{y}}+F_z{\mathbf{e}}_{\mathbf{z}}\hfill \\ & =& \frac{1}{4\pi }{\varepsilon }_i\left(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}\right)(E_x{\mathbf{e}}_{\mathbf{x}}+E_y{\mathbf{e}}_{\mathbf{y}}+E_z{\mathbf{e}}_{\mathbf{z}})dv\hfill \\ & =& \frac{1}{4\pi }{\varepsilon }_i\nabla ·\mathbf{EE}dv\hfill \\ & =& {\rho }^f\mathbf{E}dv.\hfill \end{array}$$ (A37)

Solute region with singularity

In elementary physics the total electrostatic force is presented as qE given a singular charge of qδ(x − x′) in an external field. Apparently the electric field here does not include the singular self field, i.e., it is the field from all other fixed/mobile charges and polarized bound charges. This expression can be obtained with the force formulation based on the Maxwell stress tensor though it is not trivial. The difficulty exists because the stress tensor is a function of total electric field that contains the singular self field.

To start we note that for any singular charge source in an arbitrary solute region enclosed by S, we can always isolate the singular charge in a small spherical volume element enclosed by S′ with the charge in the center, as shown in Fig. 3. Since there is no more singularity in the region enclosed by surface S and S′, we know the total force acting on the S and S′ surfaces is∫ρ^fEdv from Eq. A37. Here, we have assumed that a smooth charge source, ρ^f, still exists in the region. Now the question is the total force acting upon the small spherical volume element enclosed by S′. We cannot follow the previous strategy based on the Taylor expansion to compute the total force because the total electric field is singular at the center of S′.

We proceed by separating the total electric field into two parts, E = E^s + E^r. Here E^s is the singular self field, the Coulombic field of the singular charge source; and E^r is the regular interaction field, including the Coulombic field of all other charge sources and the reaction field. We further exploit the fact that the singular Coulombic field E^s is spherically symmetrical to make the derivation manageable within a few pages. Indeed, the small spherical volume element was also chosen to exploit the symmetry. Since E^s only has the normal component on S′, the force on S′ is also spherically symmetrical if there is no other field in the system. Thus self Coulombic force is zero, as expected.

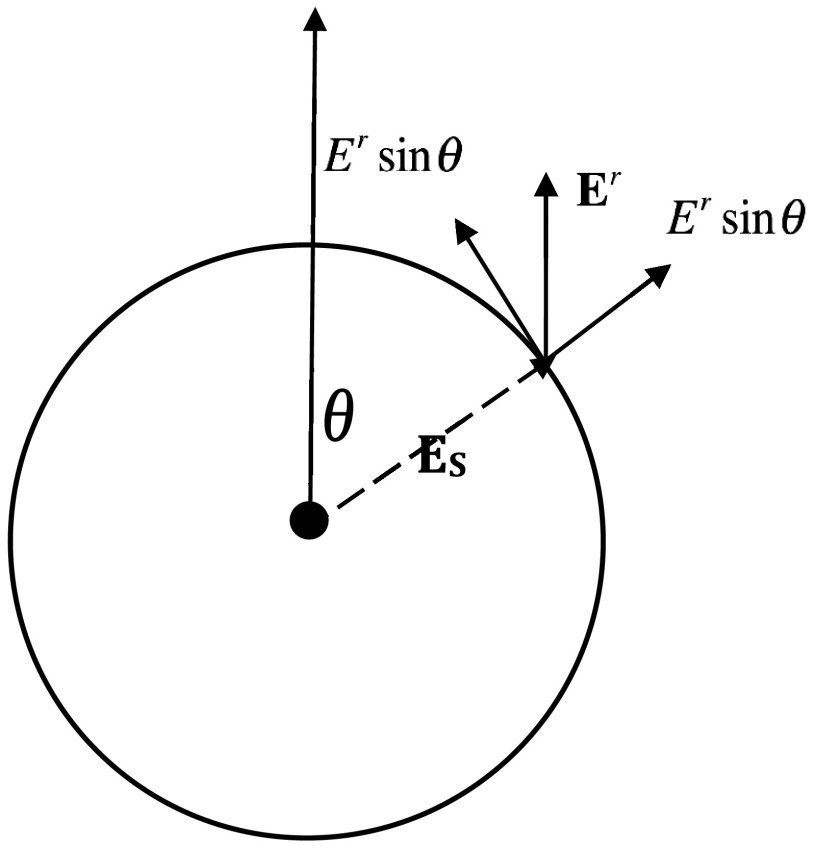
Next we first assume that E^r is a constant within S′ to obtain the 0th order approximation for the total force. It will become clear later that this is already a very good approximation because the charge density [qδ(x − x′)] is infinitely large at x′. Without loss of generality, we set E^r to be along the z-axis (Fig. 5). And since the charge density ρ^f, potential φ, and electric field E is smooth on the surface of S′, the Maxwell stress tensor in the local coordinate system of (n, t), is

$$\left[\begin{array}{cc}{E}_n^2-\frac{1}{2}(E_n^2+E_t^2)& E_n{E}_t\\ E_t{E}_n& E_t^2-\frac{1}{2}(E_n^2+E_t^2)\end{array}\right].$$ (A38)

Note that the contribution from the tangential force density is zero. And the force density on the surface element is

$$\mathbf{P}·\mathbf{n}=\left[\frac{1}{2}\left(E_n^2-E_t^2\right),E_t{E}_n\right].$$ (A39)

In general both the normal and tangential force density components are nonzero as follows:

$$\begin{array}{ccc}\hfill F_n& =& \frac{1}{2}{(E_S+E^r\cos \theta )}^2-\frac{1}{2}{\left(E^r\right)}^2\sin \theta ,\hfill \\ \\ \hfill F_t& =& E^r\sin \theta (E_S+E^r\cos \theta ),\hfill \end{array}$$ (A40)

with E_n = E_s + E^rsin θ and E_t = E^rcos θ, where E_s is the electric filed induced by the singularity, and E^r is the mode of the approximated constant field E^r.

Figure 5.

Decomposition of E^r on the surface of the chosen small spherical volume S′ in Fig. 3.

The force from F_n in the z-direction is

$$\begin{array}{ccc}\hfill F_n^Z& =& F_n\cos \theta \hfill \\ & =& r^2{\int }_0^{2\pi }d\phi {\int }_0^{\pi }\sin \theta \cos \theta \left[E_S^2+\frac{1}{2}{\left(E^r\right)}^2({\cos }^2\theta \right.\hfill \\ & & \left.-{\sin }^2\theta )+E_S{E}^r\cos \theta \right]d\theta \hfill \\ & =& \frac{4}{3}\pi r^2{E}_S{E}^r.\hfill \end{array}$$ (A41)

And similarly we can obtain the force from F_t in the z-direction

$$\begin{array}{ccc}\hfill F_t^Z& =& F_t\sin \theta \hfill \\ & =& r^2{\int }_0^{2\pi }d\phi {\int }_0^{\pi }{E}^r{\sin }^3\theta (E_s+E^r\cos \theta )d\theta \hfill \\ & =& \frac{8}{3}\pi r^2{E}_S{E}^r.\hfill \end{array}$$ (A42)

Finally the total force from F_n and F_t in the z-direction are

$$\begin{array}{ccc}\hfill F^Z& =& F_n^Z+F_t^Z\hfill \\ & =& 4\pi r^2{E}_S{E}^r\hfill \\ & =& q{E}^r.\hfill \end{array}$$ (A43)

Here the Gauss law for the singular point charge is used. Similarly we can obtain the total forces in the x- and y-direction and these are identically zero, apparently due to symmetry. Thus the total force is qE^r that is along the direction of E^r. This result holds regardless of the radius of the spherical volume element due to the existence of the singular charge source.

With variable E^r, the derivation is more complicated when the Taylor expansion of E^r at the center has to be used to represent E^r on S′. Nevertheless, if we represent E^r as

$${\mathbf{E}}^r={\mathbf{E}}^r\left(x^{\prime }\right)+O(\delta ,\theta ,\varphi ),$$ (A44)

where $\underset{\delta \to 0}{lim}O(\delta ,\theta ,\varphi )=0$ collectively represents the first-order variations (as in Taylor expansions) of E^r on S′ with respect to E^r at center x′. It is straightforward to show that substitution of Eq. A44 into Eq. A43 does not make the finite term qE go away even if all terms containing O(δ, θ, φ) go to 0 in the limit of δ → 0. This is because of the singular charge density of qδ(x − x′). In summary, our discussion shows that the total force of the spherical volume element can still be expressed as ∫ρ^fEdv with the understanding that ρ^f can be singular and E does not contain the singular self field. Thus the force density can be universally written as

$$\int {\rho }^f\mathbf{E}dv$$ (A45)

in the solute region whether the charge density is singular or not.