A Free Energy Study of the Catalytic Mechanism of Trypanosoma cruzi Trans-Sialidase. From the Michaelis Complex to the Covalent Intermediate

Abstract

Trypanosoma cruzi trans -sialidase (TcTS) is a crucial enzyme for the infection of Trypanosoma cruzi, the protozoa responsible for Chagas’ disease in humans. It catalyzes the transfer of sialic acids from the host’s glycoconjugates to the parasite’s glycoconjugates. Based on kinetic isotope effect (KIE) studies, a strong nucleophilic participation at the transition state could be determined and; recently, elaborate experiments used 2-deoxy-2,3-difluorosialic acid as substrate and were able to trap a long-lived covalent intermediate (CI) during the catalytic mechanism. In this paper, we compute the KIE and address the entire mechanistic pathway of the CI formation step in TcTS using computational tools. Particularly, the free energy results indicate that in the transition state there is a strong nucleophilic participation of Tyr342 and after this, the system collapsed into a stable CI. We find that there is no carbocation intermediate for this reaction. By means of the energy decomposition method, we identify the residues that have the biggest influence on catalysis. This study facilitates the understanding of the catalytic mechanism of TcTS and can serve as a guide for future inhibitor design studies.

Chagas’ disease (American trypanosomiasis) is a lethal, chronic disease of humans and other mammals. It is widely found in Central and South America with 17 million people currently infected according to World Health Organization’s estimates. It has a death toll of 50,000 people each year (1). Chagas’ disease is caused by the protozoan parasite Trypanosoma cruzi and no effective drug or vaccine exists although it has been a century since the disease was discovered.

T. cruzi’s infectivity in the human body depends on the enzyme trans-sialidase (TcTS) (2–6). Unable to synthesize sialic acid (7), which is used for human cell recognition (8, 9), T. cruzi would be vulnerable in the host body (4, 5). However, sialic acids transferred to its surface glycoconjugates by TcTS provide T. cruzi the ability to evade the immune system of the host and to adhere to and invade the host cells (10). The parasite invasion is found to be significantly reduced when sialylated epitopes are neutralized with antibodies (11), when TcTS is neutralized by various other protocols (12–14) or when sialic acids are present in neither the host cells nor the external medium (10). The direct involvement of this enzyme in animal pathogenesis (15) and thymocyte apoptosis (16) has also been shown. The genome of T. cruzi is found to have many copies of the genes encoding for TcTS and its isoforms (constituting ~15% of the entire genome) (17). Having such an important role in Chagas’ disease infection, TcTS has been the focus of many studies. The lack of this enzyme or analogs in humans presents the enzyme as a potential and appealing therapeutic target for the disease.

TcTS catalyzes the transfer of α-(2→3) sialic acid from sialoglycoconjugates to β-galactosyl glycoconjugates, with retention of configuration (3). TcTS is a member of the CAZY GH33 (18) family (www.cazy.org) (19), which is part of the superfamily of sialidase enzymes. This family features a sixfold β-propeller structure, and members feature an active site tyrosine residue as the putative nucleophile. An overview of various GH33 mechanisms has been reported (20). Interestingly, TcTS is unlike most family members, in that TcTS is not a committed hydrolase. It acts through a ping-pong mechanism (i.e. double displacement mechanism) in which binding of the first substrate leads to a modified enzyme form with the sugar glycon, which then binds to the second acceptor substrate and forms the final product (21–23). In the initial stages of the mechanism, the sialic acid is scavenged from the donor glycoconjugate with evidence suggesting nucleophilic participation of the enzyme at the transition state (24). A historical question for glycosidases is whether there is nucleophilic participation, requiring collapse into a covalent intermediate (CI); or if the bound substrate remains as an oxocarbenium ion. This has been long discussed for enzymes of similar families, even for the very well-studied lysozyme (25–28). In the case of sialic acids, the question is especially interesting given the somewhat enhanced stability its oxocarbenium ion has in solution, relative to conventional sugars such as glucose (29).

For TcTS catalyzed reaction of sialic acid glycosides, kinetic isotope effect (KIE) studies revealed strong nucleophilic participation in the transition state (TS) and these results together with the fact that this enzyme retains the stereochemistry around the reaction center pointed towards subsequent CI formation (30). In a separate effort, the TcTS CI was trapped and Tyr342 was identified -unprecedented among retaining glycosidases (31)- as the nucleophile that attack the anomeric C atom of the sialic acid (23). The identification of a tyrosine acting as a nucleophile for TcTS catalysis was first deemed unlikely (31) because glycosidases (e.g. lysozyme) usually use a pair of protein carboxylates (Asp or Glu residues) as the nucleophile and the acid/base catalyst (32, 33). It was suggested that as both the sialic acid and a Glu (or Asp) residue posses a carboxylate group, a carboxylate residue acting as a direct nucleophile would generate unfavorable interactions. However, by using a Tyr/Glu couple, TcTS would achieve appreciable negative character on the phenolic oxygen only at the TS (23). This change in the nucleophilic character of Tyr342 after the proton transfer to Glu230, which is enhanced upon substrate binding, has been recently examined by us (34).

In the rest of the article we will use the IUPAC nomenclature for substitution transformation (35) where the reactions are written in terms of associative (A) and dissociative (D) processes. Thus a concerted bimolecular “S_N2” displacement will be written as A_ND_N. D_N + A_N and D_N*A_Nint denote stepwise “S_N1” mechanisms. The “+” symbol indicates that the intermediate carbocation can diffuse away before it reaches the nucleophilic reagent, while “*” represents a short living intermediate formed faster than diffusing away. A_ND_N reactions may also be divided into dissociative or associative classifications depending on the relation between the nucleophilic approach and the departure of the leaving group. An A_ND_N (dissociative) mechanism indicates that in the TS the loss of bonding has progressed further than bond formation. When these characteristics are inverted, the mechanism is considered associative.

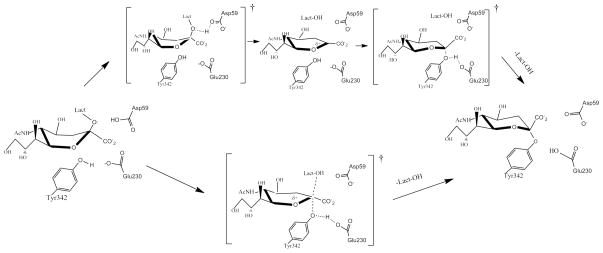
The detailed way in which the CI is reached in the mechanism of TcTS is still being investigated. In Fig. 1 the two extreme cases for reaching the CI from the Michaelis complex in TcTS are depicted. Traditional physical organic chemistry arguments would suggest that the formation could not happen through an A_ND_N mechanism due to the highly hindered reaction site, arguing for a dissociative path with little or no nucleophilic participation from Tyr342 (upper path in Fig. 1). However, the architecture of the active site can plausibly change the mechanism to an A_ND_N route where bond breaking and making are concerted to some degree (lower path in Fig 1). In this manuscript, we investigate the conversion from the Michaelis complex (MC) to the CI in the mechanism of TcTS with sialyl-lactose using the umbrella sampling technique. The stabilization pattern of the active site residues on the transition state (TS) in relation to the MC is examined by means of the energy decomposition method. KIE calculations considering a model of the enzyme active site are also depicted.

Figure 1.

Two possible paths (considering or not an oxocarbenium intermediate) to reach the covalent intermediate in the catalytic mechanism of TcTS.

The rest of the article is organized as follows. In the next section we briefly describe the methodologies employed in the calculations. Then, we present the results and discuss them. Finally, the conclusions of this work are outlined.

Methods

General aspects

The crystal structure of TcTS in complex with sialyl-lactose was used as the starting geometry (PDB entry code 1S0I (21)). In what follows, the numbers of residues and the names of the atoms correspond to this crystallographic structure. Asp59 acts as an acid/base catalyst during the enzyme mechanism, so it was experimentally mutated to Ala59 prior to crystallization to protect the ligand from hydrolysis (31). In our simulations, in order to model the wild-type form, Ala59 was mutated in silico back to Asp59. The resulting structure was fed into the leap module of the AMBER10 molecular dynamics package (36) where the necessary hydrogen atoms were added. The system was solvated in a truncated octahedral cell of TIP3P (37) explicit water molecules. The ff99SB (38, 39) force field was used to construct the topology files. In all quantum mechanics/molecular mechanics (QM/MM) simulations, the self consistent charge Density Functional Tight Binding (scc-DFTB) (40), as implemented in AMBER10 (41), was the level of theory selected to describe the potential energy of the QM subsystem. The Particle Mesh Ewald method was used to calculate the long-range Coulomb force. The initial structure was minimized at constant volume and, in a second stage; the system was heated, at constant volume, from 0 K to a target temperature of 300 K during 55.0 ps using the weak-coupling algorithm with a τ_tp value of 2.8 ps. After this, we switched to constant-temperature and pressure conditions, using a value of 2.0 ps for both τ_tp and τ_p. Finally a 300 ps molecular dynamics (MD) simulation was practiced in order to equilibrate the system. This MD simulation, as well as all the others carried out in this work, was performed using periodic boundary conditions with a cutoff distance of 12.0 Å and a time step of 1.0 fs. The equilibrated structure was used as the initial point for the umbrella sampling analysis.

Umbrella sampling calculations

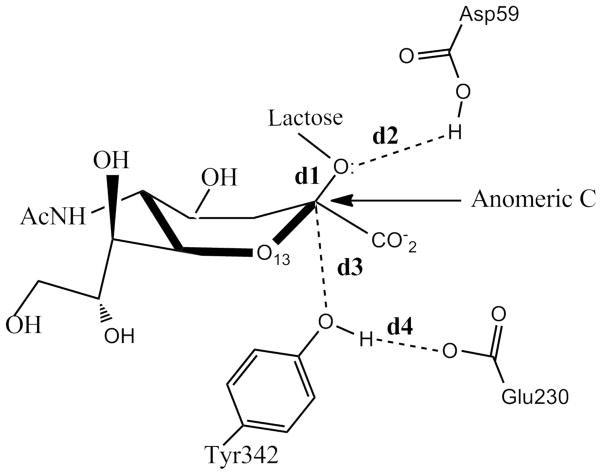
The distances involved in the reaction coordinate definitions are depicted in Fig. 2: d1 refers to the distance between the anomeric C atom of sialic acid and the glycosidic O of lactose and d2 accounts for that between the glycosidic O of lactose and the H atom of the carboxylic group of Asp59. d3 defines the distance between the anomeric C of the sialic acid and the hydroxyl O atom of Tyr342 while d4 describes the distance between one carboxyl O atom of Glu230 and the hydroxyl H atom of Tyr342. A 2-D free energy profile was evaluated to explore the formation of the CI in the mechanism of TcTS, defining two coordinates: RC1 = d1 − d2 and RC2 = d3 + d4. RC1 was sampled from −0.61 Å to 2.91 Å while RC2 was scanned from 5.24 Å to 2.36 Å. The scans were done in steps of 0.08 Å. In each point of the grid, a 25 ps. QM/MM MD simulation was performed constraining the value of the 2-D reaction coordinate with a harmonic potential using a force constant of 450.0 kcal/mol. The last structure of an umbrella window run, was used as the starting point for the next one. Structures and the value for the reaction coordinate were dumped every 200 fs and 2.0 fs respectively. Before each production MD run, a 10 ps equilibration phase was carried out. The 2-D weighted histogram analysis method (WHAM-2D) (42) implemented in the package written by Alan Grossfield, was used to analyze the probability density and to obtain the free energy profiles for the unbiased system along the reaction coordinate. Statistical uncertainties for each point were calculated with a Monte Carlo bootstrap error analysis (43) as implemented within the WHAM program. To evaluate if the free energy results were time converged, we scanned RC1 from −0.61 Å to 2.91 Å fixing RC2 equal to 5.0. Another 1-D sampling was carried out fixing RC1 equal to 2.5 and scanning RC2 from 5.24 Å to 2.36 Å. These two 1-D analyses were done in exactly the same conditions as those for the 2-D examination except that each MD simulation lasted 50 ps.

Figure 2.

Distances used to scan the 2-D reaction coordinate. d1 refers to the distance between the anomeric C atom of sialic acid and and the glycosidic O of lactose. d2 is the distance between the glucosidic O of lactose and the H atom of the carboxylic group of Asp59, d3 the one between the anomeric C of the sialic acid and the hydroxyl O atom of Tyr342 and d4 described that that involves one carboxyl O atom of Glu230 and the hydroxyl H atom of Tyr342.

Interaction energy decomposition

We used the energy decomposition method to analyze how the active site residues stabilize/destabilize the TS in the catalyzed reaction of TcTS with sialyl-lactose. This method has been extensively applied to enzymes (44–51) and was recently employed by us to understand how the presence of the substrate modifies the $\mathrm{\Delta }{G}_r^0$ for the proton transfer from Tyr342 to Glu230 in the catalytic mechanism of this reaction (34). The influence of an individual residue on the energy of a particular structure is measured taking into account the difference of energies when a particular residue is present (denoted by (I) in eq. (1)) or when it is replaced by Gly ((I-1) in eq. (1)) (50, 51)

$$\mathrm{\Delta }{E}_i=[E_i^{QM}+E_i^{\mathit{QMMM}}]-[E_{i-1}^{QM}+E_{i-1}^{\mathit{QMMM}}]$$ (1)

where each term in brackets represents the energy of the QM subsystem influenced by the classical environment. Then, the differences between the stabilization effects in going from MC to TS, for each residue, were estimated by:

$$\mathrm{\Delta }\mathrm{\Delta }{E}_i=\mathrm{\Delta }{E}_i^{TS}-\mathrm{\Delta }{E}_i^{MC}$$ (2)

In the present analysis, the QM subsystem was composed by the substrate and Asp59. To calculate the average values for the interaction energy and stabilization effects (〈ΔΔE_i〉) of each residue in a particular configuration, 125 snapshots from MD simulations were considered taken from the umbrella sampling calculation with reaction coordinates corresponding to the MC and TS. The method was applied for residues in which the distance between their center of mass and the center of mass of the QM subsystem was < 10.0 Å in the crystallographic structure. This includes 75 residues for the active site of TcTS.

DFTB validation

Full QM calculations were performed in order to validate the semi-empirical level of theory implemented in QMMM calculations. For this purpose, we used a model system containing residues Asp59, Tyr342, Glu230 and sialyl-lactose. To construct this model, we started from the crystallographic structure of the enzyme, cut the bonds linking the Cα atoms to the rest of the protein backbone, and then filled the free valence of each Cα with hydrogen atoms. From the one side and using the Sander module implemented in AMBER10, we scanned the DFTB minimum energy path (MEP) sampling RC1 vs. RC2 considering the same conditions as the one mentioned for umbrella sampling study. During these computations, the Cα atoms of the three residues of the model were fixed at their initial positions so as to mimic the distances in the protein environment. By the other side and using the GAUSSIAN09 (52) program, optimizations for reactants (MC like-configurations), transition states and products (CI like-configurations) were performed using Hartree Fock (HF) and Density Functional Theory (with a B3LYP functional). The initial structures employed were taken from the DFTB MEP surface and the same kind of restraints was also applied for these computations. MP2 methodology was also employed to perform single point calculation on the structures minimized at the DFTB level of theory. The basis set 6-31G(d) was implemented for HF, B3LYP and MP2 calculations.

KIE calculations

Two distinct systems were taken into account for these computations. One of them was the one mentioned above for the DFTB validation composed by Asp59, Tyr342, Glu230 and sialyl-lactose. The other system consisted in sialyl-lactose and H₃O⁺ and was considered in order to investigate the KIE for the A_N+D_N acid solvolysis of sialyl-lactose. For both systems, the reactants and TS structure were obtained by means of the B3LYP/6-31G(d) methodology and the frequencies were computed at the same level of theory. These calculations were performed using GAUSSIAN09 (52). For the sialyl-lactose acid solvolysis case, water was considered an implicit solvent and the polarizable Continuum Model (53) was implemented for this fact.

Frequencies results were employed to estimate the KIEs at 299 K considering eq. 3 (54)

$$\mathit{KIE}=\frac{k_L}{k_H}=\frac{{\nu }_L^{\#}}{{\nu }_H^{\#}}\prod _i^{3n^R-6}\frac{{\mu }_{iH}^R}{{\mu }_{iL}^R}\frac{sinh({\mu }_{iL}^R/2)}{sinh({\mu }_{iH}^R/2)}\prod _i^{3n^{\#}-7}\frac{{\mu }_{iL}^{\#}}{{\mu }_{iH}^{\#}}\frac{sinh({\mu }_{iH}^{\#}/2)}{sinh({\mu }_{iL}^{\#}/2)}$$ (3)

where L and H denote the light and heavy isotopes, respectively. R denotes reactants while the symbol “#” does it for the transition state; n is the number of atoms, ν are the frequencies and ν^#, particularly, is the imaginary frequency of crossing the barrier. μ is equal to hν/kT where T is the temperature and h and k are Planck’s and Boltzmann’s constants, respectively. These calculations were performed by means of the Isoeff98 program (55).

Results and Discussion

The DFTB method not only has been shown to be an accurate level of theory for describing the energetics of chemical reactions (56), but it was also demonstrated for biological systems, that MEP results are also in good agreement with higher levels of theory like MP2 (57). Recently, it was also shown that DFTB provides the best semiempirical description of six-membered carbohydrate ring deformation (58). For the model system containing Asp59, Tyr342, Glu230 and sialyl-lactose, RMSD results of the minimized reactants and products structures obtained with DFTB, HF and B3LYP are similar indicating that the geometries are being well reproduced by the semi-empirical method. Nevertheless, although, DFTB and B3LYP ΔEs are close each other (difference < 3.0kcal/mol), HF produces a significant overestimation of this value (See Table 1). Regarding the barriers, DFTB and HF results overestimate the B3LYP values. However, it should be remarked that, although the MP2 level of theory was implemented for single point calculations of DFTB optimized structures, this semi-empirical methodology closely mimics its ΔE and ΔE^# indicating that DFTB reproduce suitably MP2 barriers and energy changes.

Table 1.

Comparison of the ΔE, ΔE^# and root-mean-square deviations between the different levels of theory used to study the model system which includes Asp59, Glu230, Tyr342 and the substrate.

Parameter	DFTB	Hartree Fock	B3LYP	MP2
Reactants rmsd(Å)	-	0.26	0.20	-
Products rmsd(Å)	-	0.19	0.18	-
ΔE(kcal/mol)	−0.62	12.11	2.32	0.88
ΔE#(kcal/mol)	30.43	26.73	23.75	28.11

The nature of transition states and intermediates in the catalytic mechanism of glycosidases is a controversial subject due to the complexity of these nucleophilic substitution reactions (59). Particularly, for TcTS, several aspects of its mechanism have been the subject of discussion. For instance, it has been questioned whether a CI or an oxocarbenium ion is the stable intermediate formed during the course of the reaction which would subsequently react with the target lactose. Yang et al., based on KIE analysis, gave evidence supporting CI formation (30) and then Tyr342 was proposed as the nucleophile residue (24). Later, Watts et al. captured a CI using deoxy-2,3-difluorosialic acid as substrate and obtained the X-ray crystal structures (23). These results together with KIE experiments are highly suggestive that a CI is present during the catalyzed mechanism. Nevertheless, there is still an important mechanistic question to be answered: is the putative carbocation that must occur from the MC to CI an intermediate or a transition state?

Knowledge of the TS for this reaction, for instance, would be very important because it can provide information to design stable analogs as TS inhibitors (60). Experimentally, the determination of KIEs is the only currently available method that can offer information about this species. Computational studies are a powerful instrument in these scenarios because they can provide a detailed picture of the TS and of the entire mechanistic pathway.

Fig. 3a shows the contour plot of the free energy surface that describes the path from the MC towards the CI in the reaction catalyzed by TcTS. The minimum free energy path is highlighted with a white line. For this path, the changes in the distances involved in the reaction coordinate definition are depicted in Fig. 3b. As predicted in KIE experimental analysis (30), results indicate that the most probable pathway corresponds to an A_ND_N mechanism. This type of mechanism was also predicted for other enzymatic O- and N-glycoside reactions (61–72). Regarding the energetics, the observed $\mathrm{\Delta }{G}_r^{\#}$ is 20.80 ± 0.7 kcal/mol and once the TS is reached, the path is downhill towards the CI formation which implies a proton transfer from Tyr342 to Glu230 and a covalent bond formation between Tyr342 and the sialic acid. The computed $\mathrm{\Delta }{G}_r^0$ for the reaction is −0.89 ± 0.43 kcal/mol making the CI roughly equienergetic with the MC. This is a very direct evidence of the formation of this species in the TcTS reaction mechanism. An analogous free energy analysis was recently done on a related enzyme (hen egg white lysozyme) in which the presence of the CI was also predicted and a similar energy barrier was found (73). When the 1-D free energy profiles performed at RC1=2.5 Å and RC2=5.0 Å were compared with the correspondent ones of the 2-D profile to test the convergence of the length of the MD simulation, the differences in $\mathrm{\Delta }{G}_r^{\#}$ and $\mathrm{\Delta }{G}_r^0$ were < 1.0 kcal/mol, indicating that the sampling on the 2-D surface was adequate.

Figure 3.

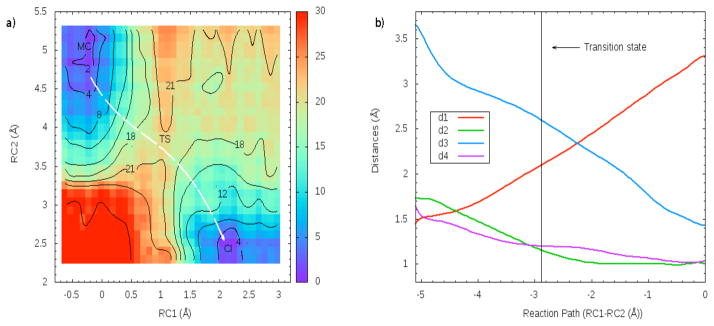
a) Free energy contour plot of the CI formation in TcTS using sialyl-lactose as substrate. Results are in kcal/mol. The white line illustrates the minimum path. For this path, the distances involved in the reaction coordinate definition are depicted in b)

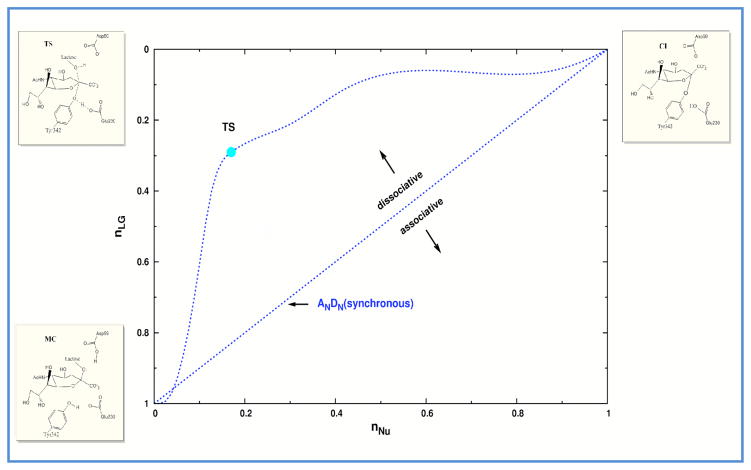
In order to better describe the mechanism, a “reaction space” plot, based on a More O’Ferral-Jenk style diagram (74), is presented in Fig. 4. The characteristic parameters of the MC, TS and CI are presented in Table 2. The commonly used Pauling bond orders (75) of the structures along the minimum free energy path to the leaving group (n_LG) and the nucleophile (n_Nu) were determined using eq. 3 (76):

$$N_x=N_0\ast exp((R_0-R_x)/c)$$ (3)

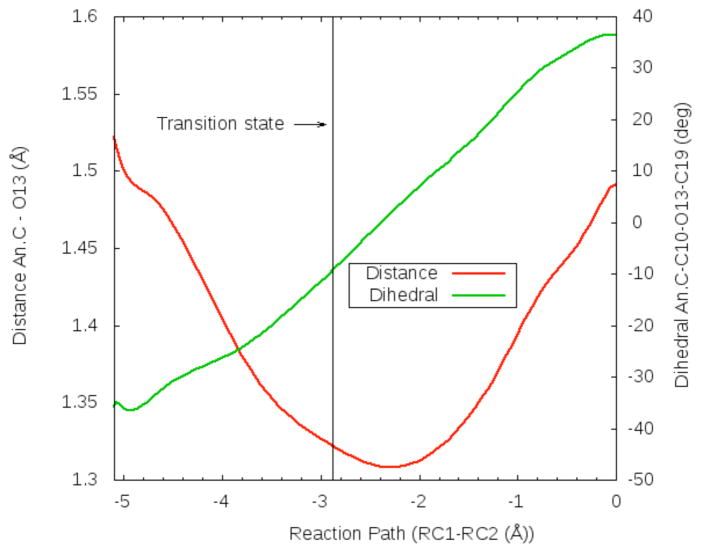
where R_x denotes the average distance between the leaving-group/nucleophile and the anomeric C. N₀ =1, c=0.6 and R₀=1.4 were the values used for the parameters. The reaction path depicted in Fig. 4 shows that the leaving group departs well before the TS is reached. This indicates that the A_ND_N mechanism is a dissociative one. The values of d2 and d3 in Table 2 also show that the Asp59 proton is almost transferred at the TS and that the hydroxyl oxygen of Tyr342 is ~1.0 Å closer to the anomeric C when the TS is reached. In this configuration the hydroxyl oxygen of Tyr342 has become more negative, measured as a (Mulliken) partial charge of −0.47 in the MC and −0.61 at the TS. The enhanced charge would render Tyr342 a better nucleophile. This nucleophilic participation was suggested by Yang et al on the basis of KIE experiments (30). Later, it was proposed that Tyr342 was a good choice for the nucleophile because unlike traditional carboxylate nucleophiles, it might have an easier electrostatic approach to the anomeric carbon in the neighborhood of the negatively charged anomeric carboxylate (23). From KIE experimental results it was also inferred there was little charge development on the anomeric C when the system goes from the MC to the TS. Table 2 results illustrate that the partial charge of the anomeric C is practically constant during the whole path and that its neighboring O13 (See Fig 2) is instead the atom which suffers a considerable change of its partial charge when the TS is reached. In Fig. 5 the anomeric C-O13 distance and the dihedral anomeric C-C10-O13-C19 along the minimum free energy reaction path is shown. As it can be seen, the anomeric C-O13 bond shortens in going from MC to TS gaining partial double character, and at the TS the carbocation is almost planar. Once the CI is reached, the sialic acid ring inverts its configuration and the anomeric C-O13 bond returns to single bond character.

Figure 4.

Reaction space for the CI formation in TcTS mechanism. The axes are the Pauling bond orders from the anomeric C to the leaving group (n_LG) and the nucleophile (n_NU). The reactant, TS and product configuration are shown in the bottom left, top left and top right, respectively.

Table 2.

Parameters selected to illustrate the characteristics of the MC, TS and CI. Definition of d1, d2, d3 and d4 are depicted in Fig. 2. The values correspond to averages considering the structures sampled on MD simulations related to those configurations. Distances are in Å

Parameter	MC	TS	CI
d1	1.512 ± 0.044	2.190 ± 0.042	3.30 ± 0.036
d2	1.800 ± 0.046	1.158 ± 0.056	1.023 ± 0.043
d3	3.512 ± 0.102	2.524 ± 0.105	1.441 ± 0.026
d4	1.580 ± 0.113	1.289 ± 0.089	0.962 ± 0.030
Dist (An. C-O13)	1.454 ± 0.035	1.298 ± 0.029	1.485 ± 0.032
OH partial charge	−0.472 ± 0.02	−0.608 ± 0.028	−0.407 ± 0.004
An. C partial charge	0.399 ± 0.006	0.414 ± 0.006	0.4231 ± 0.006
O13 partial charge	−0.414 ± 0.012	−0.182 ± 0.013	−0.4502 ± 0.007

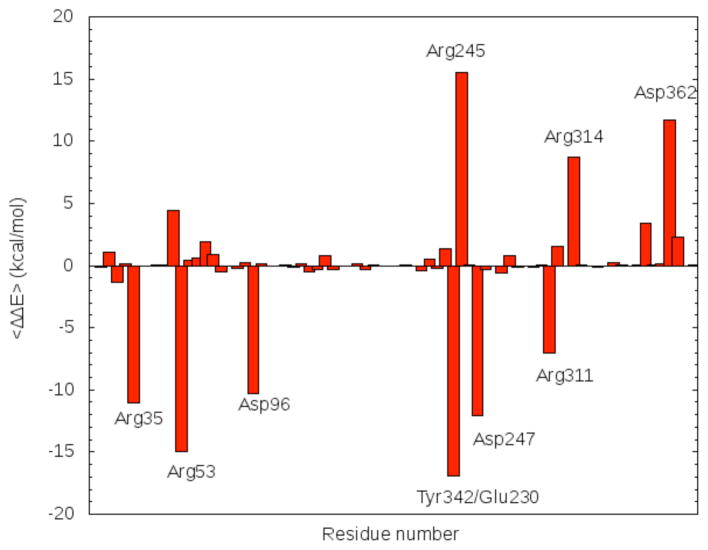
Figure 5.

Relative stabilization pattern (eq. (2)) of the active site residues on the TS considering the MC as reference.

In order to describe the changes in the sialic acid ring during the reaction, we followed IUPAC nomenclature (77). In the MC, the ring has a B_2,5 boat conformation. To precisely quantify the puckering coordinates we calculated the average of the Cremer-Pople parameters (78) over the umbrella coordinates at the relevant states state. For the MC configurations, the values for Q, ϕ and θ were 0.66 ± 0.05, −14.80° ± 7.52° and 101.58° ± 5.65° respectively. The structures sampled at the TS, adopt a ⁴H₅ half-chair conformation where atoms O5, C1, C4 and C5 form the reference plane. In this case the puckering values were Q= 0.54 ± 0.06, ϕ = −60.12° ± 4.82° and θ = 148.91° ± 4.01°. Finally, when the CI is reached, the sialic acid ring conformation migrates to a ²C₅ chair considering the same reference plane as for the Michaelis complex. For this chair conformation, the Cremer-Pople parameters obtained were Q= 0.55 ± 0.02, ϕ = −14.19° ± 11.80° and θ = 162.94° ± 4.93°.

Most glycoside hydrolases and transferases proceed through highly oxocarbenium ion (carbocation)-like TS and therefore stabilizing the charged ion is a potential strategy to catalyze the reaction (79). The energy decomposition method was applied to analyze the stabilization pattern of the active site residues on the TS with respect to the MC. Results are presented in Fig. 6. The addition over all the ΔΔE values for each residue represents an indication of the degree of the stabilization of the TS from the enzyme environment on the QM subsystem. The resultant value was −21.09 kcal/mol indicating a strong stabilizing effect on the TS. Particularly, Asp362 and two arginines (Arg245 and Arg314) out the three of the arginine triad, exert a destabilizing effect on the TS. However this effect does not counteract the stabilizing effect mainly produced by the residues: Arg35, Arg53, Asp96, Glu247, Arg311, and the Glu230-Tyr342 couple. Tyr342-Glu230 is considered as a couple because a proton is transferred from Tyr342 to Glu230 and then the former residues makes a covalent bond with the anomeric C of the sialic acid to reach the CI. The stabilization effect of this couple is large (−16.0 kcal/mol), and it mainly due to the Tyr342 nucleophilic participation in the TS configuration. Arg35 and Asp96 are two residues that directly interact with the substrate and have also a large stabilizing effect on the TS, with their ΔΔE values being −11.0 kcal/mol and −10.3 kcal/mol, respectively. Arg53 forms a hydrogen bond with the carboxylic group of Asp59 which changes its electronic distribution after transferring its proton to the substrate. Lastly, Arg311 interacts with the lactose part of the substrate and Glu247, and although being close to the active site, does not interact directly with the substrate or with Asp59.

Figure 6.

Distance anomeric C-O13 (red) and dihedral angle C9 (anomeric C)-C10-O13-C19 (green) along the minimum free energy path (characterized as RC1-RC2). Atom names correspond to those in the pdb file.

The strict hydrolase Trypanosoma rangeli sialidase (TrSA) is an enzyme related to TcTS which, although having a 70% sequence identity and an overall Cα rmsd of 0.78 Å, possesses only hydrolase activity (ie. it cannot catalyze the transfer of sialic acid). All stabilizing and destabilizing residues mentioned above are conserved in both TcTS and TrSA. Although, due to a small changes in the relative orientation, there exists the possibility that the stabilization pattern of these residues would not be the same in TrSA and TcTS; it can be inferred that they would produce the same stabilizing effect on the TS structure of the reaction catalyzed by TrSA and thus, both enzymes would use the same strategy to reach the CI. Besides this, single point mutations in any of the residues that exert a big stabilization effect on the TS, would make any of these two enzymes lose their ability to catalyze the reaction.

In Table 3 the results for the estimations and the experimental values of the β dideuterium ²H and ¹³C KIEs are presented. Regarding the β ²H KIEs, both the estimated and the experimental results indicate that the value for solvolysis is larger than the correspondent value for the enzymatic reaction. Considering the ¹³C KIEs, B3LYP/6-31G(d) results not only exhibit the same trend that the experimental ones, but also the values are in good agreement. Solvolysis estimations indicate that for this system B3LYP/6-31G(d) frequencies are appropriate to analyze KIEs, being better for the primary ¹³C case than for secondary β dideuterium ²H one. On the other hand, the correspondence that exists between the computed and the experimental KIE for the enzyme reaction is a clear indication that the TS structure found is appropriate.

Table 3.

Results for β dideuterium ²H and ¹³C KIE calculations using the B3LYP/6-31G(d) level of theory. Experimental values taken from reference (30) are also shown.

Type of KIE	Sialyl-lactose acid solvolysis		Enzyme reaction
	Calculated	Experimental	Calculated	Experimental
β dideuterium 2H	1.161	1.113 ± 0.012	1.065	1.053 ± 0.010
13C primary	1.008	1.016 ± 0.011	1.018	1.021 ± 0.014

Conclusions

We computed the free energy surface that describes the CI formation in the catalytic mechanism of TcTS with sialyl-lactose. In accordance with experiments, our results indicate that the most probable path corresponds to a highly dissociative A_ND_N reaction and that there exist a strong nucleophilic participation in the TS and very little charge development at the anomeric C. Although experimental data were suggestive about the formation of the CI for non-fluorinated substrates, our results strongly support this suggestion and provide atomic-level detail for the mechanism. The estimated reaction barrier was 20.8 kcal/mol and the bond orders at the TS to the leaving group and the nucleophile were 0.26 and 0.16, respectively. The analysis of the Mulliken charges at the TS shows significant charge load for the hydroxyl oxygen of the nucleophile and the O13 atom of the sialic acid. By means of the energy decomposition method, it was determined that the enzyme active site highly stabilizes the TS. Particularly, the couple Tyr342-Glu230, Arg35, Arg53, Glu247, Arg311 and Asp96 are mainly responsible for this effect. ¹³C and β dideuterium ²H KIEs could also be estimated for a model system calculating the frequencies at the B3LYP 6-31G(d) level of theory and the results were in accordance with experimental measurements.

Summarizing, even though there are many aspects of this catalyzed reaction that require further clarification, the results presented in this article provide relevant information regarding the mechanistic scenario for the CI formation in TcTS. We hope it can contribute to future studies of this important system and could eventually facilitate development of potent TcTS inhibitors for treatment of Chagas’ disease.

Abbreviations

TcTS

Trypanosoma cruzi trans-sialidase

MD

Molecular dynamics

MM

Molecular mechanics

QM

Quantum mechanics

WHAM

weighted histogram analysis method

KIE

Kinetic isotope effect

MC

Michaelis complex

TS

Transition state

CI

covalent intermediate

DFTB

density-functional tight-binding

HF

Hartree Fock

RMSD

root-mean-square deviations

MEP

minimum energy surface