Versatile multi-wavelength ultrafast fiber laser mode-locked by carbon nanotubes

Abstract

Multi-wavelength lasers have widespread applications (e.g. fiber telecommunications, pump-probe measurements, terahertz generation). Here, we report a nanotube-mode-locked all-fiber ultrafast oscillator emitting three wavelengths at the central wavelengths of about 1540, 1550, and 1560 nm, which are tunable by stretching fiber Bragg gratings. The output pulse duration is around 6 ps with a spectral width of ~0.5 nm, agreeing well with the numerical simulations. The triple-laser system is controlled precisely and insensitive to environmental perturbations with <0.04% amplitude fluctuation. Our method provides a simple, stable, low-cost, multi-wavelength ultrafast-pulsed source for spectroscopy, biomedical research and telecommunications.

Ultrafast mode-locked fiber lasers have widespread applications (e.g. fiber telecommunications, pump-probe measurements, terahertz generation), due to their various advantages (e.g. small footprint, high stability, efficient heat dissipation, low-cost¹,²,³,⁴,⁵,⁶). Thus far, single-wavelength ultrafast fiber lasers have been investigated theoretically and demonstrated experimentally⁷,⁸,⁹,¹⁰,¹¹. However, there are few papers reporting multi-wavelength ultrafast fiber lasers¹²,¹³,¹⁴,¹⁵,¹⁶, which mainly use the naturally formed birefringence of single-mode fiber (SMF) for lasing wavelength selection. In such fiber lasers, the output wavelengths cannot be controlled precisely due to the difficulty of accurately adjusting the birefringence in SMF. Therefore, these multi-wavelength pulsed fiber lasers are not very stable, and output central wavelengths are not selectable to meet the requirements of various applications. To address this issue, a simple way is to use fiber Bragg gratings for the wavelength selection, which can offer all-fiber based alignment-free structure¹⁷,¹⁸,¹⁹. Furthermore, fast development in the chirped fiber Bragg grating (CFBG) fabrication technology has been achieved to provide changeable dispersion, broad bandwidth, and tunable transmittance wavelength covering all major laser wavelengths (e.g. 1, 1.55, and 2 μm). These make CFBG an ideal wavelength selection component for ultrafast broadband fiber lasers.

To achieve multi-wavelength pulsed lasers, another key element is the saturable absorber, which can operate at multi-wavelengths (i.e. broad operation bandwidth²⁰). Currently, various saturable absorbers, such as nonlinear loop mirrors²¹,²², nonlinear polarization rotation²³,²⁴, semiconductor saturable absorber mirrors (SESAMs)²⁰,²⁵,²⁶, carbon nanotubes⁷,¹⁰,¹¹,²⁷,²⁸,²⁹,³⁰, and graphene⁸,³¹,³²,³³,³⁴, have been employed for ultrafast pulse generation. Among these saturable absorbers, nanotube and graphene are particularly interesting for multi-wavelength pulsed lasers as they both exhibit extraordinarily broad operation bandwidth for multi-wavelength pulse generation. Indeed, such unique broadband property has been experimentally confirmed for nanotube²⁹,³⁵ and graphene³³ by wavelength tunable³²,³⁵ and dual-wavelength³⁰,³⁴ pulsed lasers. However, triple-wavelength mode-locking laser has not been demonstrated with carbon nanotubes.

In this article, we report a compact nanotube-mode-locked all-fiber laser system based on CFBGs, delivering three lasing wavelengths simultaneously. The output central wavelengths are 1539.5, 1549.5, and 1559.5 nm, respectively, which can be accurately selected by CFBGs. The output wavelengths are tunable by stretching CFBGs. The pulse durations of three wavelengths are 6.3, 6.7, and 5.9 ps, respectively. Our laser is insensitive to environmental perturbation with near-transform-limited pulses, and thus is viable for various practical applications, such as fiber telecommunications, pump-probe measurements, and terahertz generation. The proposed method of precisely selecting output wavelengths by fiber gratings and using nanotubes with broad operation bandwidth can be readily adopted for other fiber lasers from 1 to 2 μm.

Results

Nanotube-based compact all-fiber triple-wavelength laser system

The schematic diagram of our nanotube-based compact all-fiber triple-laser system is shown in Fig. 1(a). The laser system consists of a wavelength-division multiplexer (WDM), a fused coupler with 10% output ratio, two polarization controllers (PCs), three CFBGs, a 5-m-long erbium-doped fiber (EDF) with 6 dB/m absorption at 980 nm, a single-wall carbon nanotube (SWNT) saturable absorber, and a circulator. The EDF and SMF have dispersion parameters of about 11.6 and −22 ps²/km at 1550 nm, respectively. CFBGs, written on a standard SMF, have a super-Gaussian reflection profile with a bandwidth of ~1 nm (Fig. 1(b)). The dispersion parameter of these three CFBGs is ~2.2 ps²/cm with the length of ~10 mm, and the corresponding central transmittance wavelengths λ_1–3 are 1539.5, 1549.5, and 1559.5 nm, respectively. The wavelengths of our laser output are separated by another three CFBGs for characterization of individual wavelengths.

Figure 1.

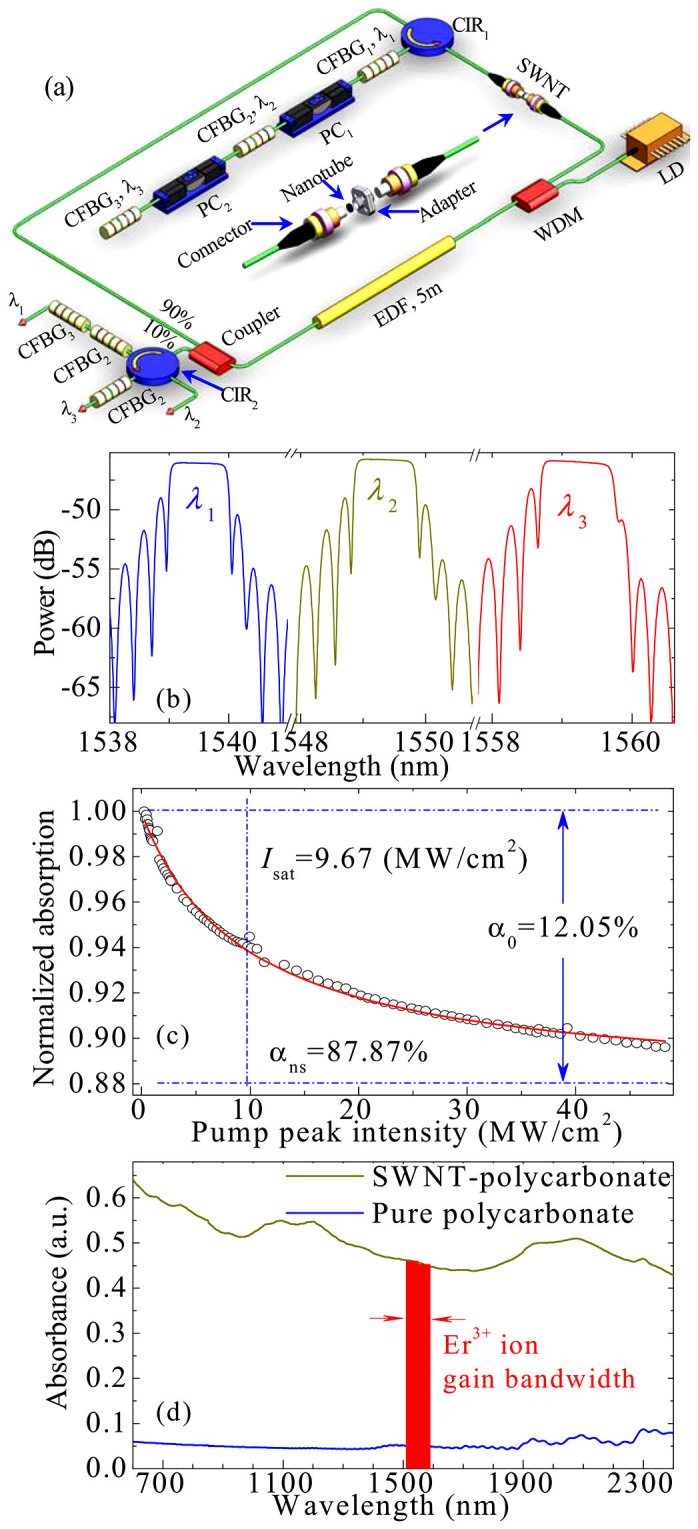
(a) Laser setup. Inset: the assembly of SWNT saturable absorber. EDF, erbium-doped fiber; WDM, wavelength-division multiplexer; PC, polarization controller; LD, laser diode; CIR, circulator; CFBG, chirped fiber Bragg grating; SWNT, single wall carbon nanotube. (b) Reflection spectra of three CFBG_1–3. (c) Nonlinear absorption characterization of the SWNT saturable absorber. The solid curve is fitted from the experimental data (circle symbols). (d) Absorption spectrum of the SWNT–polycarbonate composite and pure polycarbonate. The red stripe illustrates the spectral gain region of the Er³⁺-doped fiber.

The integrated SWNT-based fiber device is realized by sandwiching a ~2 mm² sample between two fiber connectors (see Methods), as shown in inset of Fig. 1(a). The normalized nonlinear absorption of our integrated SWNT absorber is experimentally measured with a homemade ultrafast laser at 1550 nm, as shown in Fig. 1(c). According to a simplified two-level saturable absorber model³⁵,³⁶, the experimental data are fitted as the solid curve of Fig. 1(c). Figure 1(d) shows the absorption spectrum of the SWNT–polycarbonate composite in comparison with pure polycarbonate, which is measured by a spectrometer (JASCO V-570 UV-vis-NIR).

Experimental observations

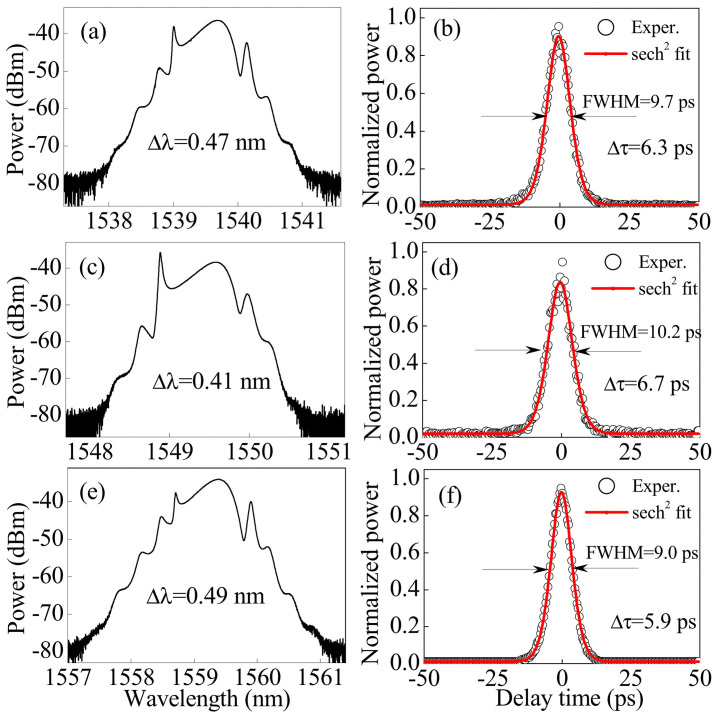
Continuous wave (CW) operation starts at the pump power of P ≈ 9 mW, and self-starting mode-locking is observed at P ≈ 15 mW. With the appropriate setting of two PCs, output at three wavelengths is generated from the oscillator. The typical output spectra of three lasers λ_1–3 at P ≈ 45 mW are shown in Figs. 2(a), 2(c), and 2(e) with the central wavelengths at 1539.5, 1549.5, and 1559.5 nm, respectively. The corresponding autocorrelation traces of the experimental data and the sech²–shaped fit for λ_1–3 are shown in Figs. 2(b), 2(d), and 2(f). It is found that the optical spectra have sidebands, which are the typically spectral characteristics of standard solitons¹,³⁷,³⁸. The full width at half maximum (FWHM) spectral widths at different wavelengths are about 0.47, 0.41, and 0.49 nm, respectively. The output pulse durations (Δτ) are about 6.3, 6.7, and 5.9 ps. The calculated time-bandwidth products at three different wavelengths are about 0.37, 0.35, and 0.36, respectively, which are slightly larger than the value of 0.315 for the transform-limited sech²-shaped pulses. It is worth noting that here the output spectral width and pulse duration are limited by the bandwidth (i.e. 1 nm) of CFBGs used in the cavity. Broader bandwidth CFBGs in principle can offer broader spectral width, and thus shorter pulse duration.

Figure 2.

Optical spectra of the experimental observations for three lasers (a) λ₁, (c) λ₂, and (e) λ₃. Autocorrelation traces of the experimental data (circle symbols) and sech²–shaped fit (solid curves) for (b) λ₁, (d) λ₂, and (f) λ₃.

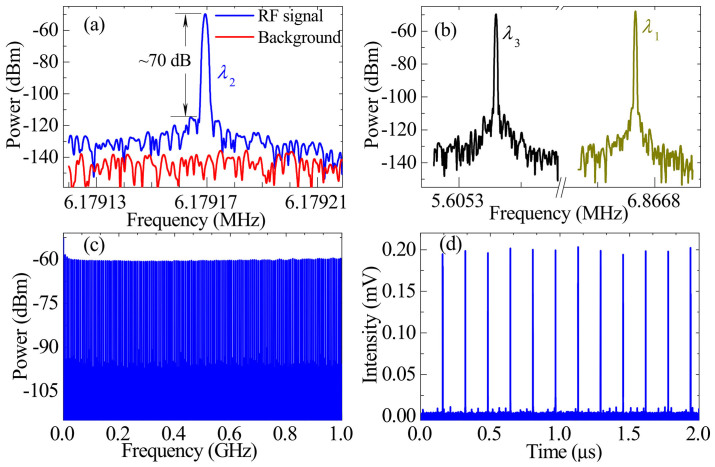
Figures 3(a–d) show the RF spectra and oscilloscope traces of lasers, respectively. Figures 3(a–b) are the fundamental RF spectra with the 1 Hz resolution and the 100 Hz span for three lasers λ_1–3. Figures 3(c) and 3(d) are the wideband RF spectrum up to 1 GHz and the oscilloscope traces up to 2 μs for the laser λ₂, respectively. Figure 3(a) exhibits that the repetition rate of the fundamental harmonic frequency is 6.17917 MHz, corresponding to ~161.8 ns round-trip time, as shown in Fig. 3(d). No spectrum modulation is observed over 1 GHz (Fig. 3(c)), indicating no Q-switching instabilities.

Figure 3.

Typically experimental results: the fundamental RF spectra with the resolution of 1 Hz and the span of 100 Hz for three lasers (a) λ₂ and (b) λ₁ and λ₃. The fundamental repetition rates of λ_1–3 are 6.86678, 6.17917, and 5.60533 MHz, respectively. (c) Wideband RF spectrum up to 1 GHz and (d) oscilloscope traces up to 2 μs for the laser λ₂.

The RF spectrum in Fig. 3(a) gives a signal-to-noise ratio ~ 70 dB (10⁷ contrast), showing low-amplitude fluctuations and good mode-locking stability¹⁰,³⁹. With the power ratio of ΔP ≈ 10⁻⁷, the frequency resolution Δf_res = 1 Hz, and the frequency width (FWHM) of Δf_A ≈ 1.3 Hz (Fig. 3(a)), we estimate an amplitude fluctuation ΔE/E ≈ 3.6 × 10⁻⁴ from the equation ΔE/E = (ΔPΔf_A/Δf_res)^1/2 39. Note that no pulse is observed in the experimental observations if SWNT is removed.

Numerical results

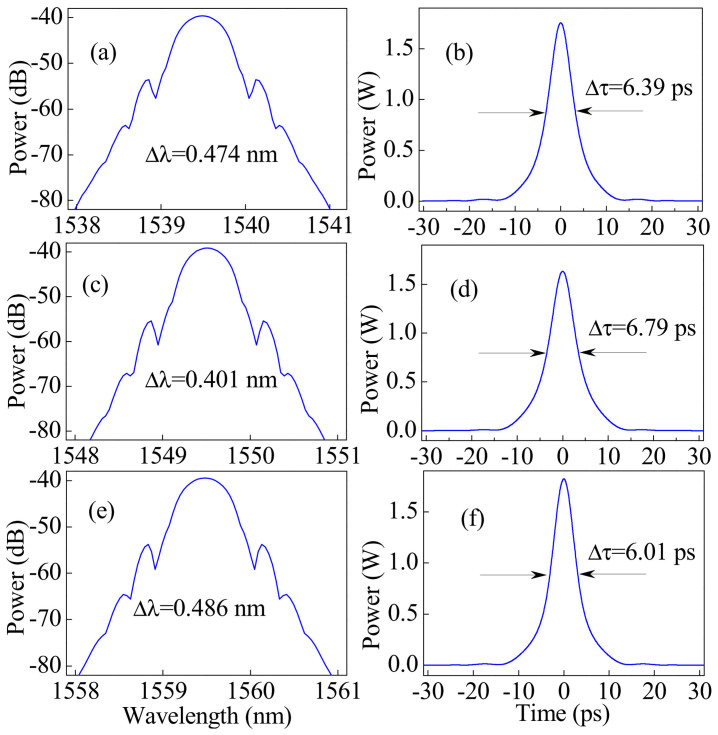
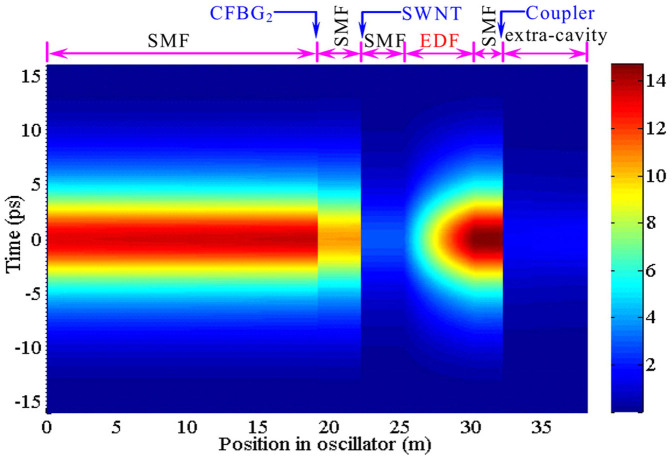
The typical results of numerical simulations for three lasers λ_1–3 in the mode-locking regime are demonstrated in Fig. 4. Parameters are chosen to match the experimental values (see Methods). We can see from Fig. 4 that the spectral width and pulse duration of λ_1–3 are 0.474, 0.401, 0.486 nm, and 6.39, 6.79, 6.01 ps, respectively. So the time-bandwidth products of λ_1–3 are about 0.38, 0.34, and 0.36, respectively, showing that they are sech²-shaped pulses rather than Gaussian-shaped pulses. The numerical results (Fig. 4) are in good agreement with the experimental observations, as shown in Fig. 2. Figure 5 shows the evolution of pulse along the oscillator for the laser λ₂. Obviously, it is dynamic rather than static. The evolution of pulse profile in a round trip is demonstrated in the supplemental material.

Figure 4. Optical spectra and pulse profiles of the numerical simulations for three lasers (a) and (b) λ₁, (c) and (d) λ₂, (e) and (f) λ₃.

Figure 5. Pulse evolution of laser λ₂ along the intra- and extra-cavity position.

The supplemental material demonstrates the evolution of pulse profile along the oscillator in detail.

Discussion

In the experiments, the proposed oscillator (Fig. 1) fails to simultaneously delivering three wavelengths if SWNT is replaced by such saturable absorbers as nonlinear loop mirror, nonlinear polarization rotation, SESAM, and graphene. It attributes to the inherent characteristic of SWNT, which has highly environmental stability and is independent of the polarization of pulses evolving in the laser cavity¹⁰,³⁵,⁴⁰,⁴¹.

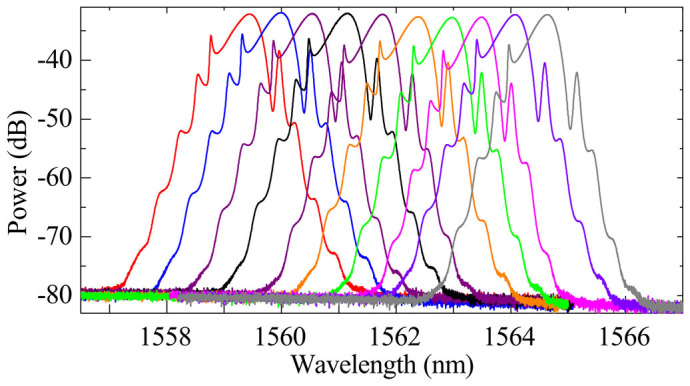
Based on the cascade of CFBGs, the laser system with more than three wavelengths (e.g. four and five wavelengths) can be achieved in principle. By stretching CFBGs in our experiments, its central wavelength is tunable. Figure 6 demonstrates the output spectra at ten wavelengths within the tuning range from ~1560 to 1565 nm. The experimental results show that the spectral width and pulse duration are almost unchanged, indicating the stability of our output pulses. Note that other two wavelengths also can be tuned but with limited wavelength range. For example, the λ₁ can be tuned from 1540 to 1546 nm, and the λ₂ can be tuned from 1550 to 1556 nm. The tuning range is determined by the CFBGs.

Figure 6. Output spectra at ten different wavelengths by stretching CFBG₃ in the cavity.

Methods

SWNT film

SWNT with the tube diameter <2 nm is grown with the catalytic chemical vapor decomposition method using CH₄ as the carbon source and Co as the catalyst. 0.5 mg·mL⁻¹ SWNT solution is prepared by dispersing SWNT powder in de-ionized water with sodium dodecyl benzenesulfonate (SDBS) using a sonicator system operating at 20 kHz with 180 W power for 5 hours. To avoid unwanted scattering losses from aggregates and bubbles, the resulting dispersion is centrifuged at 12000 g for an hour, and the upper 90% of the supernatant is then collected. 10 wt% aqueous polyvinyl alcohol (PVA) solution and 0.5 mg·mL⁻¹ SWNT solution are mixed at the volume ratio of 1:2 overnight by a magnetic stirrer. Slow evaporation under ambient temperature and pressure results in a ~30-μm-thick freestanding SWNT-PVA composite film.

Measurement method

An optical spectrum analyzer (Yokogawa AQ-6370), an autocorrelator, a 6-GHz oscilloscope, a radio-frequency (RF) analyzer, and a 10-GHz photodetector are used to measure the laser output performances.

Numerical simulation

To confirm the experimental observations, we numerically simulate the pulse formation at three wavelengths in the oscillator. The modeling includes such the physics terms as the group velocity dispersion of fiber, the self-phase modulation, the dispersion of CFBGs, and the saturated gain with a finite bandwidth. Thus the extended nonlinear Schrödinger equation is used to describe the pulse propagation in the laser oscillator⁴²,

Here A, β₂, and γ denote the electric filed envelop of the pulse, the fiber dispersion, and the cubic refractive nonlinearity of the fiber, respectively. The variables t and z represent the time and the propagation distance, respectively. Ω_g is the bandwidth of the gain spectrum. g describes the gain function for the EDF and is expressed by⁴³

where g₀, E_p, and E_s are the small-signal gain coefficient related to the doping concentration, the pulse energy, and gain saturation energy that relies on pump power, respectively. The normalized absorption is fitted according to a simple two-level saturable absorber model³⁵,³⁶

Here α(I) is the intensity-dependent absorption coefficient, and α₀, α_ns and I_sat are the linear limit of saturable absorption, nonsaturable absorption, and saturation intensity, respectively.

Eq. (1) is solved with a predictor–corrector split-step Fourier method⁴⁴. To numerically simulate the feature and behavior of this laser system, the simulation has started from an arbitrary signal and converged into a stable solution after approximately 200 round trips. In the simulation, we use the following parameters to match the experimental conditions: g₀ = 6 dB/m, Ω_g = 25 nm, E_s = 55 pJ, γ = 4.5 W⁻¹km⁻¹ for EDF, γ = 1.3 W⁻¹km⁻¹ for SMF. The parameters for SWNT saturable absorber are set with the values measured (Fig. 1 (c)), i.e. α₀ = 12.05%, α_ns = 87.87%, and I_sat = 9.67 MW/cm².

Author Contributions

X.L. proposed the laser system, completed the numerical simulation, and wrote the main manuscript text. D.H. performed the main experimental results and discussed the numerical simulation. Z.S. discussed the design of the system and considerably improved the manuscript presentation. C.Z. performed the sample preparation of carbon nanotubes. H.L. carried out the data analysis and performed the video. D.M. and Y.C. provided technical support and prepared part figures. F.W. contributed to the scientific discussion and discussed the nanotube sample. All authors discussed the results and substantially contributed to the manuscript.

Supplementary Material

Supplementary Information

A supplemental material of Fig. 5