Moment Adjusted Imputation for Multivariate Measurement Error Data with Applications to Logistic Regression

Abstract

In clinical studies, covariates are often measured with error due to biological fluctuations, device error and other sources. Summary statistics and regression models that are based on mismeasured data will differ from the corresponding analysis based on the “true” covariate. Statistical analysis can be adjusted for measurement error, however various methods exhibit a tradeo between convenience and performance. Moment Adjusted Imputation (MAI) is method for measurement error in a scalar latent variable that is easy to implement and performs well in a variety of settings. In practice, multiple covariates may be similarly influenced by biological fluctuastions, inducing correlated multivariate measurement error. The extension of MAI to the setting of multivariate latent variables involves unique challenges. Alternative strategies are described, including a computationally feasible option that is shown to perform well.

1. Introduction

The problem of measurement error arises whenever data are measured with greater variability than the true quantities of interest, X. It can be attributed to sources like device error, assay error, and biological fluctuations. Summary statistics and regression models based on mis-measured data, W, may have biased parameter estimators, reduced power and insu cient confidence interval coverage (Fuller, 1987; Armstrong, 2003; Carroll et al., 2006).

Many strategies to adjust for measurement error have been proposed. Correction for measurement error in covariates, X, in linear and generalized linear models is commonly achieved by regression calibration (RC), which substitutes an estimate of the conditional mean E(X|W) for the unknown X (Carroll and Stefanski, 1990; Gleser, 1990). When estimation of the density of X is of interest, this is not particularly useful, as E(X|W) is over-corrected in terms of having reduced spread (Eddington, 1940; Tukey, 1974). However, the linear regression based on this substitution estimates the underlying parameters of interest. RC is also implemented in non-linear models because of its simplicity, but is typically most effective for general linear models when the measurement error is not large (Rosner, Spiegelman and Willett, 1989; Carroll et al., 2006). Alternatives for non-linear models are thoroughly reviewed by Carroll et al. (2006) and include maximum likelihood, conditional score, SIMEX and Bayesian methods. Density estimation is addressed in a separate literature, where deconvolution methods are a prominent approach for scalar variables (Carroll and Hall, 1988; Stefanski and Carroll, 1990). Recent papers add to the theoretical basis for deconvolution estimators and offer extension to heteroscadastic measurement error (Carroll and Hall, 2004; Delaigle, 2008; Delaigle, Hall and Meister, 2008; Delaigle and Meister, 2008).

Despite the variety of available methodology, measurement error correction is rarely implemented (Jurek, 2004), and when it is, RC remains popular. Convenience may be a priority for a method to achieve widespread use. The preceding methods target estimation of parameters in a specific regression context; a different method must be implemented for every type of regression model in which X is used, and density estimation is treated separately. An alternative approach is to focus on re-creating the true X from the observed W, at least approximately, as the primary quantity of interest or as a means to improving parameter estimation (Louis, 1984; Bay, 1997; Shen and Louis, 1998; Freedman et al., 2004). Most recently, Thomas, Stefanski, and Davidian (2011) introduce a Moment Adjusted Imputation (MAI) method that aims to replace scalar, mis-measured data, W, with estimators, $\widehat{X}$, that have asymptotically the same joint distribution with a response, Y, and potentially error-free covariates Z, as does the latent variable, X, up to some number of moments. Originally developed in an unpublished dissertation, (Bay, 1997), MAI extends the idea of moment reconstruction (MR), which focuses on the first two moments of the joint distribution (Freedman et al., 2004, 2008). Thomas, Stefanski, and Davidian (2011) investigate the performance of MAI in logistic regression and demonstrate superior results to RC and MR when the distribution of X is non-normal. Moreover, the $\widehat{X}$ can be used for density estimation, with a guarantee of matching the latent variable mean, variance and potentially higher moments.

Thomas, Stefanski, and Davidian (2011) discuss an important application where measurement error is likely present in multiple covariates and a scalar adjustment method would not be adequate. In this example, Gheorgiade et al. (2006) studied blood pressure at admission in patients hospitalized with acute heart failure using data from the Organized Program to Initiate Lifesaving Treatment in Hospitalized Patients with Heart Failure (OPTIMIZE-HF) registry. Logistic regression was used to describe the relationship in-hospital mortality and both systolic and diastolic blood pressure. These variables, when measured at the same time, are likely to have correlated measurement error due to common biological fluctuations and measurement facilities. The original analysis by Gheorgiade et al. (2006) regards both variables as error free. Thomas, Stefanski, and Davidian (2011) revise the analysis to account for measurement error in systolic blood pressure, which is of primary interest, but not diastolic blood pressure. Adjustment of both variables could be important. When multiple covariates are measured with error, one could apply a univariate adjustment separately. However, this would not account for correlation between the latent variable measurement errors.

Here, we introduce the extension of MAI to multivariate mis-measured data and provide a computationally convenient approach to implementation. The result is quite similar to univariate MAI, but unique challenges are addressed. In Section 2, we define a set of moments that are feasible for matching with multivariate measurement error and introduce the natural extension of the MAI algorithm, used to obtain adjusted data with appropriate moments. In Section 3, a numerically convenient method for the implementation of multivariate MAI is proposed. In Section 4, the alternative implementations of multivariate MAI are evaluated and MAI is compared to other imputation methods via simulation in applications to density estimation and logistic regression. In Section 5, we revise the OPTIMIZE-HF analysis to account for measurement error and obtain estimates that describe the features of “true” diastolic and systolic blood pressure.

2. The Method

Here we introduce notation for the current problem that is similar to Thomas, Stefanski, and Davidian (2011) but not identical. Let X_i = (X_i1, …, X_iG)^T be a (G × 1) vector of latent variables for i = 1, …, n. The observed data are W_i = X_i + U_i where U_i ~ MVN(0, Σ_ui), MVN(μ, Σ) is the multivariate normal distribution with mean μ and covariance matrix Σ, 0 is a G × 1 vector of zeros, U_i is independent of X_i, and U_i are mutually independent. We assume that Σ_ui is known. The latent variables X_i may be of particular interest, as in density estimation or as predictors in a regression model. In the latter case, we also have a response Y_i and potentially a vector of (K − 1) error-free covariates Z_i. These additional variables are collected to create ${\mathbf{V}}_i=(Y_i,{\mathbf{Z}}_i^T)$, with components V_ik for k = 1, …, K. We make the usual surrogacy assumption that Y_i and Z_i are not related to the measurement error in X_i, so that V_i is conditionally independent of W_i given X_i (Carroll et al., 2006).

The goal is to obtain adjusted versions of the W_i, ${\widehat{\mathbf{X}}}_i$, whose distribution closely resembles that of X_i and possibly the joint distribution of X_i and other variables. In terms of moments, we require that $E\left(n^{-1}{\sum }_{i=1}^n{\widehat{\mathbf{X}}}_i\right)=E\left({\mathbf{X}}_i\right)$, $E\left(n^{-1}{\sum }_{i=1}^n{\widehat{\mathbf{X}}}_i{\widehat{\mathbf{X}}}_i^T\right)=E({\mathbf{X}}_i,{\mathbf{X}}_i^T)$, $E\left(n^{-1}{\sum }_{i=1}^n{\widehat{\mathbf{X}}}_i{V}_{ik}\right)=E\left({\mathbf{X}}_i{V}_{ik}\right)$ for k = 1, …, K, and $E\left(n^{-1}{\sum }_{i=1}^n{\widehat{X}}_i^r\right)=E\left({\mathbf{X}}_i^r\right)$ for r = 3, …, M, and the r^th power is applied component-wise. This differs from Thomas, Stefanski, and Davidian (2011) in that only first order cross products between X_i and error free covariates are matched. Additional moment constraints can be added, but unlike the case of univariate MAI, estimators for higher order cross products are not straightforward. They are complex functions of many parameters that each have to be estimated. We therefore favor a reduced set cross products for parsimony and good performance in simulations.

2.1. Implementation

The first step is to define unbiased estimators for the unknown quantities ${\mathbf{m}}_r=E\left({\mathbf{X}}_i^r\right)$, (G × 1) and r = 1, …, M, ${\mathbf{m}}^{\ast }=E\left({\mathbf{X}}_i{\mathbf{X}}_i^T\right)$, (G × G), ${\mathit{m}}_k^V=E\left({\mathit{X}}_i{V}_{ik}\right)$, (G × 1). Because W_i|X_i ~ MVN(X_i, Σ_ui), we know that E(W_i) = E{E(W_i|X_i)} = E(X_i) so ${\widehat{\mathit{m}}}_1=n^{-1}{\sum }_{i=1}^n{\mathbf{W}}_i$. Unbiased estimators for the higher-order moments are defined using the recursion formula H₀(z) = 1, H₁(z) = z, H_r(z) = zH_r−1(z) − (r − 1)H_r−2(z) for r = 2, 3, … (Cramer, 1957). Stulajter (1978) proved that if W ~ N(μ, σ²), then E{σ^rH_r(W/σ) = μ^r (Stefanski, 1989; Cheng and Van Ness, 1999). Let W_ig and X_ig denote the g^th component of W_i and X_i, respectively, and let Σ_ui,gg′ denote the element of Σ_ui in the g^th row and g′^th column. Marginally, W_ig|X_ig ~ N(X_ig, Σ_ui,gg). Letting P_r(w, σ) = σ^rH_r(w/σ), we have $E\left\{P_r\right(W_{ig},{\sum }_{ui,gg}\left)\right\}=E\left[E\right\{P_r(W_{ig},{\sum }_{ui,gg})\mid X_{ig}\left\}\right]=E\left(X_{ig}^r\right)$. The g^th component of ${\widehat{\mathbf{m}}}_r$ is ${\widehat{m}}_{rg}=n^{-1}{\sum }_{i=1}^n{P}_r(W_{ig},{\sum }_{ui,gg})$ for r = 1, …, M. In addition, $E({\mathbf{W}}_i{\mathbf{W}}_i^T\mid {\mathbf{X}}_i)={\mathbf{X}}_i{\mathbf{X}}_i^T+{\sum }_{ui}$, so ${\widehat{\mathbf{m}}}^{\ast }=n^{-1}{\sum }_{i=1}^n({\mathbf{W}}_i{\mathbf{W}}_i^T-{\sum }_{ui})$ is unbiased for m*. In some cases the estimate ${\widehat{\mathbf{m}}}^{\ast }$ may be non-positive definite, corresponding to an invalid moment sequence. We only perform adjustment for a valid sequence of moments estimates, as defined in Section 2.2. Under the surrogacy assumption, E(W_iV_ik) = E{E(W_iV_ik|X_i, V_ik)} = E{V_ikE(W_i|X_i)} = E(X_iV_ik). Therefore, the estimators ${\widehat{\mathbf{m}}}_k^V=n^{-1}{\sum }_{i=1}^n{\mathbf{W}}_i{V}_{ik}$ are unbiased for ${\mathbf{m}}_k^V$.

The adjusted ${\widehat{\mathbf{X}}}_i$ are obtained by minimizing

$$\sum _{i=1}^n{({\mathbf{W}}_i-{\mathbf{X}}_i)}^T\sum _{ui}^{-1}({\mathbf{W}}_i-{\mathbf{X}}_i),$$ (1)

subject to the following constraints on sample moments and cross products: $n^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i^r={\widehat{\mathbf{m}}}_r$, $n^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^T={\widehat{\mathbf{m}}}^{\ast }$, and $n^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{V}_{ik}={\widehat{\mathbf{m}}}_k^V$. This is minimized by taking the derivative with respect to X_i, and constraints are imposed by Lagrange multipliers.

For example, in the case where there are no error-free covariates, so V_i = Y_i, and we are only interested in matching two moments of X_i, the following objective function is required:

$$n^{-1}\sum _{i=1}^n{({\mathbf{W}}_i-{\mathbf{X}}_i)}^T\sum _{ui}^{-1}({\mathbf{W}}_i-{\mathbf{X}}_i)+{\lambda }_1^T(n^{-1}\sum _{i=1}^n{\mathbf{X}}_i-{\mathbf{W}}_i)+{\lambda }_2^T\mathrm{vech}(n^{-1}\sum _{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^T-{\mathbf{W}}_i{\mathbf{W}}_i^T+\sum _{ui})+{\lambda }_3^T(n^{-1}\sum _{i=1}^n{\mathbf{X}}_i{\mathbf{Y}}_i-{\mathbf{W}}_i{\mathbf{Y}}_i),$$ (2)

where ${\lambda }_1^T$ and ${\lambda }_3^T$ are (G × 1) vectors of Lagrange multipliers and ${\lambda }_2^T$ is a vector of length G + G!/2!(G − 2)!}. Let I_G denote the identity matrix of dimension G. Taking the derivative with respect to X_i gives (X_i − W_i)+ λ₁ +({vech⁻¹(λ₂)+I_G}X_i + λ₃Y_i = 0, and the solution for X_i is X_i = A(W_i − λ₁ − λ₃Y_i) where A = {2I_Gvech⁻¹(λ₂) + I_G}⁻¹, and vech⁻¹ re-creates a symmetric matrix from its vech half so that if A = vech(B) for symmetric matrix B, then vech⁻¹(A) = B. The solution for X_i depends on the unknown $\Lambda ={({\lambda }_1^T,{\lambda }_3^T,{\lambda }_2^T)}^T$, which must be estimated to obtain ${\widehat{\mathbf{X}}}_i$. Taking the derivative of Equation 2 with respect to Λ provides additional equations that we can solve to obtain $\widehat{\Lambda }$. In this simple case, a solution can be obtained analytically, as described in Web Appendix A. More generally, we obtain the derivatives analytically, set them equal to 0 and solve numerically using the R function multiroot().

The adjusted data, ${\widehat{\mathbf{X}}}_i$, depend on estimated moments and are therefore not independent. In applications where ${\widehat{\mathbf{X}}}_i$ is substituted for X_i, the usual data, standard errors, which assume independent should not be used. We recommend that standard errors for analyses involving ${\widehat{\mathbf{X}}}_i$ be obtained by bootstrapping.

2.2. Practical Considerations

The estimators ${\widehat{\mathbf{m}}}_r$, ${\widehat{\mathbf{m}}}^{\ast }$ and ${\widehat{\mathbf{m}}}_k^V$ are not always a valid set of moments in finite samples. This is primarily a problem if the sample size n is small or the measurement error in W_i is very large. Before adjusting data, we first check that our estimators represent a valid sample variance-covariance matrix. When M = 2, our adjustment corresponds to matching the variance-covariance matrix of ${(1,{\mathbf{X}}_i^T,{\mathbf{V}}_i^T)}^T$. For simplicity, let X_i be (2 × 1) (G = 2), and let V_i include only the response Y_i and a single error free covariate Z_i. We check that the following matrix is positive definite to verify that we are targeting a valid set of moments:

$$\left[\begin{array}{cccc}\hfill 1\hfill & \hfill {\widehat{\mathbf{m}}}_1^T\hfill & \hfill n^{-1}\sum _{i=1}^n{Y}_i\hfill & \hfill n^{-1}\sum _{i=1}^n{Z}_i\hfill \\ \hfill {\widehat{\mathbf{m}}}_1\hfill & \hfill {\widehat{\mathbf{m}}}^{\ast }\hfill & \multicolumn{2}{c}{{\left({\widehat{\mathbf{m}}}_k^V\right)}^T}\\ \hfill n^{-1}\sum _{i=1}^n{Y}_i\hfill & \hfill {\widehat{\mathbf{m}}}_k^V\hfill & \hfill n^{-1}\sum _{i=1}^n{Y}_i^2\hfill & \hfill n^{-1}\sum _{i=1}^n{Y}_i{Z}_i\hfill \\ \hfill n^{-1}\sum _{i=1}^n{Z}_i\hfill & \hfill n^{-1}\sum _{i=1}^n{Y}_i{Z}_i\hfill & \hfill n^{-1}\sum _{i=1}^n{Z}_i^2\hfill \end{array}\right].$$

For M = 4, we match higher-order moments for the G components of X_i. In this case, additionally check the following determinants

$$\mid \begin{array}{ccc}\hfill 1\hfill & \hfill {\widehat{\mathbf{m}}}_{1g}\hfill & \hfill {\widehat{\mathbf{m}}}_{2g}\hfill \\ \hfill {\widehat{\mathbf{m}}}_{1g}\hfill & \hfill {\widehat{\mathbf{m}}}_{2g}\hfill & \hfill {\widehat{\mathbf{m}}}_{3g}\hfill \\ \hfill {\widehat{\mathbf{m}}}_{2g}\hfill & \hfill {\widehat{\mathbf{m}}}_{3g}\hfill & \hfill {\widehat{\mathbf{m}}}_{4g}\hfill \end{array}\mid \ge 0,$$

for all g = 1, …, G. The problem of invalid moments is rare under many practical conditions. However, we expect that an invalid set of estimated moments may occur more frequently as sources of error in the moment estimation increase, including smaller samples sizes and larger measurement error. The reliability ratio (RR), defined as Var(X)/Var(W), is frequently used to quantify the amount of measurement error. In simulations studies, below, with sample sizes of at least n = 1000 and reliability ratios as low as 0.5, we rarely encountered an invalid set of estimated moments. In those cases, we reduced the order to M = 2, and would recommend the same in practice. This always solved the problem.

In general, we do not have an analytical solution for the ${\widehat{\mathbf{X}}}_i$, and we solve for these numerically, as described in Section 2.1. Even for a valid sequence of moments, numerical problems occur for some data sets, and a solution is not obtained. In our simulations this happens for about 10% of data sets, even when X_i is 2 dimensional. In the following section, we suggest an alternative method of obtaining adjusted data that generally avoids numerical problems.

3. Alternative Implementation of Adjustment

Our goal is to obtain adjusted data ${\widehat{\mathbf{X}}}_i$ that have unbiased moments for the corresponding moments of X_i. In Section 2.1, we do this by imposing constraints on the moments and minimizing the “distance” between our observed data W_i and the adjusted data ${\widehat{\mathbf{X}}}_i$, as measured by Equation (1). This measure simultaneously incorporates the G components of ${\widehat{\mathbf{X}}}_i$ and their cross products and weights the components inversely according to their measurement error. Equation (1) can be difficult to minimize numerically, since nG adjusted data points are obtained, and many constraints may be involved. This approach can be approximated by performing a univariate adjustment sequentially; adjusting (W_1g, …, W_ng) for each g = 1, …, G. The estimators ${\widehat{\mathbf{m}}}_r$, ${\widehat{\mathbf{m}}}^{\ast }$, and ${\widehat{\mathbf{m}}}_k^V$ are obtained exactly as in Section 2.1, based on the distribution W_i|X_i ~ MVN(X_i, Σ_ui). For each g, beginning with g = 1, we obtain (${\widehat{X}}_{1g},\dots ,{\widehat{X}}_{ng}$) by minimizing ${\sum }_{i=1}^n{(W_{ig}-X_{ig})}^2∕{\sum }_{ui,gg}$ with the following constraints imposed by Lagrange multipliers: $n^{-1}{\sum }_{i=1}^n{X}_{ig}^r={\widehat{m}}_{rg}$, $n^{-1}{\sum }_{i=1}^n{X}_{ig}{V}_{ik}={\widehat{m}}_{kg}^V$ and $n^{-1}{\sum }_{i=1}^n{X}_{ig}{X}_{i{g}^{\prime }}={\widehat{m}}_{g{g}^{\prime }}^{\ast }$ fog g′ < g.

At each step, a separate objective function is defined, and Newton Raphson is used to solve for (${\widehat{X}}_{1g},\dots ,{\widehat{X}}_{ng}$). At the first step, adjusted data are not available, so we can not impose constraints to match ${\widehat{m}}_{1g^{\prime }}^{\ast }$. The second objective function,

$$n^{-1}\sum _{i=1}^n\frac{1}{2\sum _{ui,11}}{(W_{i1}-X_{i1})}^2+\sum _{r=1}^M\frac{{\lambda }_r}{r}\left(n^{-1}\sum _{i=1}^n{X}_{i1}^r-{\widehat{m}}_{r1}\right)+\sum _{k=1}^K{\lambda }_k^V\left(n^{-1}\sum _{i=1}^n{X}_{i1}{V}_{ik}-{\widehat{m}}_{k1}^V\right),$$

where λ_r and ${\lambda }_k^V$ are Lagrange multipliers. The adjusted data, (${\widehat{X}}_{11},\dots ,{\widehat{X}}_{n1}$), can be used to adjust W_i2 so that (${\widehat{X}}_{12},\dots ,{\widehat{X}}_{n2}$) have $E\left(n^{-1}{\sum }_{i=1}^n{\widehat{X}}_{i1}{\widehat{X}}_{i2}\right)=E\left(X_{i1}{X}_{i2}\right)$. The second objective function, which incorporates this additional constraint, is

$$n^{-1}\sum _{i=1}^n\frac{1}{2\sum _{ui,22}}{(W_{i2}-X_{i2})}^2+\sum _{r=1}^M\frac{{\lambda }_r}{r}\left(n^{-1}\sum _{i=1}^n{X}_{i2}^r-{\widehat{m}}_{r2}\right)+\sum _{k=1}^K{\lambda }_k^V\left(n^{-1}\sum _{i=1}^n{X}_{i2}{V}_{ik}-{\widehat{m}}_{k2}^V\right)+{\lambda }_1^{\ast }\left(n^{-1}\sum _{i=1}^n{\widehat{X}}_{i1}{X}_{i2}-{\widehat{m}}_{12}^{\ast }\right),$$

where λ_r, ${\lambda }_k^V$ and ${\lambda }_1^{\ast }$ are Lagrange multipliers. This process is continued at each step using the previously adjusted data. So (${\widehat{X}}_{1G},\dots ,{\widehat{X}}_{nG}$) have $E\left(n^{-1}{\sum }_{i=1}^n{\widehat{X}}_{ig}{\widehat{X}}_{iG}\right)=E\left(X_{ig}{X}_{iG}\right)$, for g = 1, …, (G − 1). The final objective function is

$$n^{-1}\sum _{i=1}^n\frac{1}{2\sum _{ui,gg}}{(W_{ig}-X_{ig})}^2+\sum _{r=1}^M\frac{{\lambda }_r}{r}\left(n^{-1}\sum _{i=1}^n{X}_{ig}^r-{\widehat{m}}_{rg}\right)+\sum _{k=1}^K{\lambda }_k^V\left(n^{-1}\sum _{i=1}^n{X}_{ig}{V}_{ik}-{\widehat{m}}_{kg}^V\right)+\sum _{g=1}^{G-1}{\lambda }_g^{\ast }\left(n^{-1}\sum _{i=1}^n{\widehat{X}}_{ig}{X}_{iG}-{\widehat{m}}_{gG}^{\ast }\right),$$

where, λ_r, ${\lambda }_k^V$ and ${\lambda }_g^{\ast }$ are Lagrange multipliers.

Multiple considerations suggest that the order of sequential adjustment may be important. Firstly, the joint distance measure, defined by Equation 1, puts greater weight on adjusting the elements with largest measurement error. This is not possible where the g elements of X_i are adjusted separately, although sequential minimization does incorporate weighting to account for unique measurement error on individual subjects. An additional feature of the sequential approach, is that the full set of constraints is not implemented simultaneously, but more constraints are added at each step. We recommend that W_ig be adjusted in the order of least measurement error to greatest measurement error. This may achieve a similar end to joint minimization, in that variables with greatest measurement error are subject to the most constraints and adjusted most. This topic is explored by simulation below.

The sequential approach imposes the same moment constraints defined in Section 2. Both minimization strategies use an unbiased estimator of cross products between two mis-measured variables, that appropriately accounts for correlation in the measurement errors. The adjusted data are constrained to have the same unbiased moments and to stay “close” to the original data. A primary difference is in the definition of “close”. Joint minimization has a distance measure based on the weighted cross product between multiple mis-measured variables. Adjusted data points are encouraged to stay close to their original value and products of adjusted variables are encouraged to stay close to the corresponding multiple of raw data. The sequential minimization measures only the distance between adjusted data and their original value. The simpler measure may be su cient, for as long as the adjusted data stay close to their original value, other relationships may also be preserved. Moreover, to the extent that certain analyses, such as regression, depend on the moments of the data, results may be insensitive to the particular value of each data point. These considerations led us to expect that the computationally simpler, sequential approach, might still perform well.

4. Simulations

In this section we address two distinct objectives. First, we verify that the sequential approach to adjustment, described in Section 3, performs similarly to the full joint minimization of Equation (1). Joint minimization is excessively slow for simulation and prone to numerical problems so we evaluate results in individual simulated data sets. Fortunately, this seems adequate, as we observe nearly identical results for the two approaches. Subsequently, we focus on the sequential approach and implement a full simulation study to evaluate its performance relative to other methods. We address the dual objectives of density estimation and logistic regression.

Variations of the following basic scenario are considered. The latent data, X = (X₁, X₂), are either standard multivariate normal or each element has a chi-square distribution with four degrees of freedom, standardized to have mean zero and variance one, with Corr(X₁, X₂) ≈ ρ. A response Y is observed with probability P(Y = 1|X₁, X₂) = F(β₀ + β₁X₁ + β₂X₂), where F(v) = 1 + exp(−v)⁻¹. Thomas, Stefanski, and Davidian (2011) considered two sets of coefficients for this model, representing stronger and weaker associations of the covariates with Y. In preliminary simulations MAI performed more favorably compared to RC and MR with larger coefficients and a more non-linear model. Here, we compromise between the two and select moderate values. The coefficients β =(β₀, β₁, β₂) are (1.5, 0.5, 0.5). In place of X_i, we observe ${\mathbf{W}}_i={\mathbf{X}}_i+(1∕r_i){\sum }_{j=1}^{r_i}{\mathbf{U}}_{ij}$, U = (U₁, U₂)^T ~ MVN(0, Σ_u), Σ_u = vech{1, ρ(0.3)^1/2, 0.3 with ρ representing the measurement error correlation, and two levels of replication: r_i = r = 1 or r_i = 1, 2, 3, 4 or 5 with equal probability. The off-diagonal of Σ_u includes a positive correlation in measurement errors of ρ, as would likely be induced by common sources of error in the measurement process, such as biological fluctuations. The measurement error in X₁ is large and, without replication, corresponds to a reliability ratio of 0.5. The measurement error in X₂ is smaller with a reliability ratio of 0.76. When the amount of replication is varied, some subjects have substantially reduced measurement error where others do not. The observed data are Y_i, W_i, for i = 1, …, n.

4.1. Comparison of sequential and joint minimization

We compare sequential and joint minimization in single data sets, and emphasize a case most likely to favor joint minimization, where the latent variables are correlated chi-square (ρ = 0.5) with heteroskedastic measurement error between the g elements of X, as above.

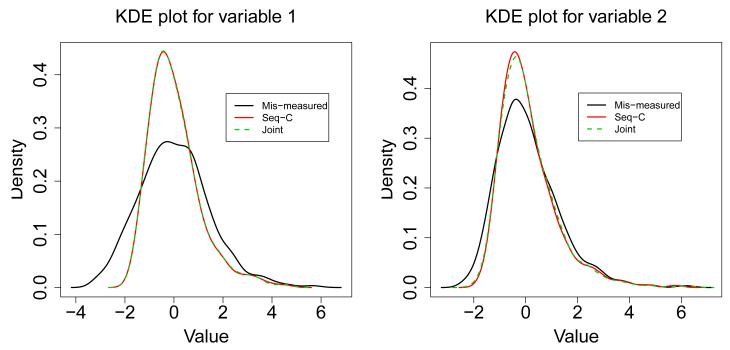
In Figure 1 we illustrate the results of marginal density estimation on X₁ and X₂. Both approaches match a single cross product with response in addition to marginal moments. Although this is not required for marginal density estimation, we subsequently find that there is no harm in doing so. There is virtually no difference in the densities depending on whether the sequential or joint minimization was performed. Additional examples in Web Appendix B show similar results.

Figure 1.

Kernel density estimation (KDE) for the marginal densities of X₁ and X₂ from a single simulated data set. Reliability ratios for X₁ and X₂ are 0.50 and 0.75, respectively, ρ = 0.5 and n = 1000: solid-dark line: KDE of $\widehat{X}$ for sequential MAI matching 4 moments, solid-light line: KDE of $\widehat{X}$ for joint minimization, Equation (1), matching 4 moments.

In the same data set we compare the logistic parameter estimates corresponding to each analytical method. Our goal is obtain a coefficient estimate that is close to the estimate based on the latent variable, shown in the first row. There is substantial improvement, in the first decimal place, when any adjustment strategy is used (Table 1). The difference is less, but still noticeable, when two or four moments are matched. However, a difference between joint and sequential minimization strategies is only present in the second or third decimal place. This is consistent with every data set that we have observed (Web Appendix B). The gains from joint minimization are not promising, in light of substantial numerical challenges. It appears that the impact of adjustment on logistic model parameter estimation comes primarily from the moment constraints rather than from differences in these minimization strategies.

Table 1.

Coefficient estimates from a single simulated data set. Reliability ratios for X₁ and X₂ are 0.50 and 0.75, respectively, ρ = 0.5 and n = 1000. Methods: X, true covariates; W, mis-measured covariates; M2 and M4, multivariate MAI with M=2 and 4; J-2 and J-4, joint minimization, Equation (1), with M=2 and 4.

Method	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$
X	1.175	0.371	0.743
W	1.050	0.076	0.516
M2	1.074	0.243	0.611
J-2	1.076	0.247	0.614
M4	1.102	0.283	0.688
J-4	1.108	0.318	0.688

In these comparisons, we implement sequential adjustment in order of least to greatest measurement error. In Web Appendix B, we address the impact of adjustment order. In the cases that we considered, the order of adjustment had a negligible impact on density estimation and logistic regression parameter estimation. The sequential approach, as opposed to joint minimization runs more quickly and encounters fewer numerical problems. We favor this approach and further investigate its performance in subsequent simulations under the title multivariate MAI.

4.2. Histogram and Kernel Density Estimation

Thomas, Stefanski, and Davidian (2011) show that MAI can improve histogram and kernel density estimation (KDE) for a scalar latent variable, relative to the naive approach that uses mis-measured data and relative to other imputation methods such as RC and MR. Even when multiple variables are measured with error, researchers typically focus on the marginal distributions, which are easier to visualize. For this purpose we can apply the method of Thomas, Stefanski, and Davidian (2011) to each variable separately and ignore the multivariate nature of the mis-measured data. We will refer to this approach as univariate adjustment. Some additional gains in precision may be achieved by matching cross products, with all correlated variables, mismeasured and error-free. Via simulation we evaluate whether there are any practical differences in the two approaches to density estimation; univariate and multivariate adjustment. Additionally, we compare to the multivariate versions of RC and MR. For RC, ${\widehat{X}}_{RC}$ is the best estimated linear unbiased estimator of E(X|W). We use the multivariate version of MR described by Freedman et al. (2004) so that ${\widehat{\mathbf{X}}}_{MR}=\widehat{E}(\mathbf{W}\mid Y)(1-\widehat{\mathbf{G}})+\mathbf{W}\widehat{\mathbf{G}}$, where $\widehat{G}=\widehat{Cov}{(\mathbf{W}\mid Y)}^{-1∕2}\widehat{Cov}{(\mathbf{X}\mid Y)}^{1∕2}$. MAI refers to the sequential approach, matching either 2 or 4 marginal moments: E(X₁), E(X₂), $E\left(X_1^2\right)$, $E\left(X_2^2\right)$, E(X₁Y), E(X₂Y), E(X₁X₂) or additionally $E\left(X_1^3\right)$, $E\left(X_1^4\right)$, $E\left(X_2^3\right)$ and $E\left(X_2^4\right)$.

The data were generated as described previously, under a range of scenarios:

1. Distribution of X: multivariate normal, standardized chi-square df=4.

2. Level of correlation between the latent variables: ρ = 0.5, 0.7.

3. Sample size: n = 1000, 2000.

4. Replication: r_i = 1 or varies between 1 and 5.

5. Two levels of measurement error: X₁ and X₂ have reliability ratios of 0.5 and 0.76.

The sample sizes 1000 and 2000 are typical for measurement error applications (Stefanski and Carroll, 1985; Freedman et al., 2004). Though the OPTIMZE-HF data is even larger, simulations for this application were too slow for large n.

Each ${\widehat{X}}_g$, is evaluated according to closeness to the underlying X_g as measured by $\mathrm{MSE}\left(\widehat{X}\right)=B^{-1}{\sum }_{b=1}^B{n}^{-1}{\sum }_{i=1}^n{({\widehat{X}}_{i,b}-{\mathbf{X}}_{i,b})}^2$ over B simulated data sets and additionally, by computing the integrated squared error between the empirical distribution functions, given by $\mathrm{ISE}\left(G_{\widehat{X}}\right)=B^{-1}{\sum }_{b=1}^B\int {\left\{G_{\widehat{X},b}\right(t)-G_{X,b}(t\left)\right\}}^{2}dt$, where $G_X\left(t\right)=n^{-1}{\sum }_{i=1}^n{I}_{(X_i\le t)}$, −∞ < t < 1. $\mathrm{ISE}\left(G_{\widehat{X}}\right)$ measures the proximity between the distribution of mis-measured or adjusted data and the latent distribution of interest. $\mathrm{MSE}\left(\widehat{X}\right)$ measures the average distance between individual mis-measured or adjusted data points and their corresponding true value. We report an MSE ratio, $\mathrm{MSE}\left(W\right)∕\mathrm{MSE}\left(\widehat{X}\right)$, and an ISE ratio, $\mathrm{ISE}\left(G_w\right)∕\mathrm{ISE}\left(G_{\widehat{X}}\right)$ so that larger ratios indicate a greater reduction in error. Standard errors for these ratios are obtained by the delta method and are reported as a “coefficient of variation,” which is the ratio standard error divided by the ratio itself.

Table 2 includes results for the case of chi-square latent variables with no replication, r_i = 1. Other results are presented in Web Appendix C. We see that the reduction in MSE provided by multivariate MAI is markedly better than univariate MAI when the measurement error is large. In fact, when four moments are matched, multivariate MAI is nearly as good as RC in terms of MSE for the variable measured with large error, and slightly better for the variable measured with less error. Consistent with Thomas, Stefanski, and Davidian (2011) we see that MAI can be far superior to RC and MR at estimating the latent variable density, reflected in large ISE ratios. Its superiority increases with larger sample size, presumably because the precision in estimation of higher-order moments improves. In terms of ISE ratios, we see little difference between multivariate and univariate MAI. Clearly, when multivariate adjustment is preferred, the adjusted data can also be used for marginal density estimation. Additional simulations in Web Appendix C are consistent with these conclusions.

Table 2.

Density estimation for X₁ and X₂ from B=250 simulated data sets. Reliability ratios for X₁ and X₂ are 0.50 and 0.75, respectively. Statistics reported: (a) $MSE\left(W\right)∕MSE\left(\widehat{X}\right)$, where $MSE\left(\widehat{X}\right)=B^{-1}{\sum }_{b=1}^B{n}^{-1}{\sum }_{i=1}^n{({\widehat{X}}_{i,b}-X_{i,b})}^2$ (coefficient of variation ≈ 0.001), and (b) $ISE\left(G_W\right)∕ISE\left(G_{\widehat{X}}\right)$, where $ISE\left(G_{\widehat{X}}\right)=B^{-1}{\sum }_{b=1}^B\int {\left\{G_{\widehat{X},b}\right(t)-G_{X,b}(t\left)\right\}}^{2}dt$, for $G_X\left(t\right)=n^{-1}{\sum }_{i=1}^n{I}_{X_i\le t}$, −∞ < t < ∞ (coefficient of variation ≈ 0.02). Adjusted data $\widehat{X}$: RC, regression calibration; MR, moment reconstruction; M2 and M4, multivariate MAI with M=2 and 4, respectively; U2 and U4, univariate MAI with M=2 and 4, respectively.

					$\left(a\right)\frac{MSE\left(W\right)}{MSE\left(\widehat{X}\right)}$
Variable	ρ	n	RC	MR	M2	M4	U2	U4
X 1	0.5	1000	2.04	1.79	1.74	1.94	1.71	1.85
		2000	2.04	1.79	1.74	1.89	1.71	1.82
	0.7	1000	2.43	2.01	2.04	2.24	1.71	1.88
		2000	2.45	2.01	2.04	2.21	1.71	1.86
X 2	0.5	1000	1.33	1.26	1.23	1.36	1.22	1.35
		2000	1.33	1.27	1.23	1.36	1.22	1.35
	0.7	1000	1.30	1.20	1.23	1.37	1.22	1.35
		2000	1.30	1.23	1.23	1.37	1.22	1.35
					$\left(b\right)\frac{ISE\left(W\right)}{ISE\left(\widehat{X}\right)}$
Variable	ρ	n	RC	MR	M2	M4	U2	U4
X 1	0.5	1000	1.86	5.49	4.35	10.51	4.34	10.48
		2000	1.88	5.85	4.66	18.25	4.65	18.13
	0.7	1000	2.65	6.55	5.30	10.57	4.34	10.40
		2000	2.79	7.07	5.67	16.97	4.61	16.61
X 2	0.5	1000	1.36	2.73	2.27	6.48	2.27	6.43
		2000	1.44	2.93	2.42	8.48	2.43	8.36
	0.7	1000	1.37	2.78	2.29	7.10	2.32	7.05
		2000	1.37	2.98	2.38	8.73	2.41	8.62

4.3. Simulations in Logistic Regression

Thomas, Stefanski, and Davidian (2011) observed less bias in logistic regression parameter estimation when MAI was compared to RC or MR for the case of non-normal latent variables, but nearly equivalent performance for normal latent variables. We confirm these results in the multivariate case using the range of conditions outlined in Section 4.2, and the additional sample size, n = 9000.

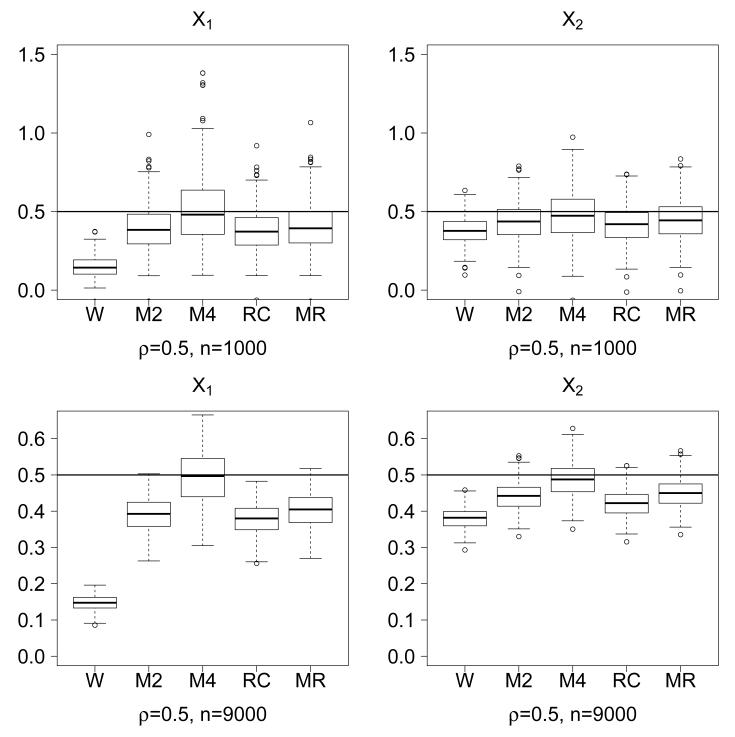
Boxplots of the estimated coefficients ${\widehat{\beta }}_X$ from B = 250 simulations are displayed in Figure 2 for the case where X has chi-square elements, r_i = 1 and ρ = 0.5. The naive estimator for ₁ is more biased than for ₂, as this corresponds to the variable measured with greatest error. RC and MR substantially reduce the bias in both coefficients, though MAI, matching 4 moments, virtually eliminates the bias. There is some tradeo in variability, with the latter approach having greatest variance. The variance in MAI decreases when the sample size is increased so that even the most outlying values are a great improvement over the naive method and are generally better than other approaches.

Figure 2.

Boxplots of ${\widehat{\beta }}_X$ from B = 250 simulated data sets, for chi-square X₁ and X₂ and P(Y = 1|X₁, X₂) = F(β₀ + β₁X₁ + β₂X₂), with true values β=(β₀, β₁, β₂) =(1.5, 0.5, 0.5) denoted by a horizontal line. Reliability ratios for X₁ and X₂ are 0.50 and 0.75, respectively, ρ = 0.50 and n = 1000 or n = 9000. Method: W, naive; M2 and M4, multivariate MAI with M=2 and 4, respectively; RC, regression calibration; MR, moment reconstruction.

Results for multivariate normal latent variables, reported in Web Appendix D, are consistent with scalar case (Thomas, Stefanski, and Davidian, 2011). All three adjustment methods nearly eliminate bias and have similar variance. RC appears to have slightly lower variability and small bias. There is clear benefit to matching 4 moments rather than 2. The results are consistent across the various latent variable correlations and samples sizes considered.

MAI appears to be an attractive strategy for measurement error adjustment in logistic regression, with the computationally feasible multivariate extension performing very well. As we observed in the scalar case, matching four moments is important when the distribution of X is not multivariate normal.

5. Application to OPTIMIZE-HF

We carry out the OPTIMIZE-HF analyses performed by Gheorgiade et al. (2006) accounting for measurement error in various measures of blood pressure. The data set consists of n = 48, 612 subjects, aged 18 or older, with heart failure. We focus on the logistic regression model for in-hospital mortality reported by Gheorgiade et al. (2006), which includes linear splines and truncation that account for non-linearity in continuous covariates. Their model can be written as

$$P(Y=1\mid \mathbf{Z},X)={\{1-\exp ({\beta }_0+{\beta }_Z^T\mathbf{W}+{\beta }_{1}S+{\beta }_{2}D\left)\right\}}^1,$$ (3)

where Z includes error-free covariates listed in Web Appendix E, Table 7; S is a truncated version of true systolic blood pressure at baseline, X₁, in 10-mm Hg units, i.e. S = −{X₁I(X₁ < 160) + 160I(X₁ ≥ 160)}; D is a truncated version of true diastolic blood pressure at baseline, X₂, i.e. D=−{X₂I(X₂ < 100) + 100I(X₂ ≥ 100). Gheorgiade et al. (2006) fit these models using observed blood pressure measurements, W=(W₁, W₂) in place of X=(X₁, X₂). We adjust the mismeasured W by matching four moments, cross-products with response and baseline history of hypertension, and impute $\widehat{X}$ in place of X.

This analysis differs from Thomas, Stefanski, and Davidian (2011), in that we address measurement error in multiple related measures of blood pressure, beyond the primary measure of interest, systolic blood pressure (SBP). The measurement error due to biological fluctuations, or device error in these variables is likely correlated, suggesting the need for multivariable adjustment. Any adjustment requires that the measurement error variance-covariance matrix, _u, be known. In practice, it would be best to estimate _u from replicate measures of systolic and diastolic blood pressure. Replicate measures were not available in the OPTIMIZE-HF data set; however, variability in blood pressure has been extensively studied. One source is the Framingham data set (Carroll et al., 2006), which includes four measurements of blood pressure, two taken at the first exam and two taken at a second exam. The average standard deviation in four measurements is 9 mm Hg, which corresponds to a reliability ratio of about 0.75. Based on the information from other external studies, the measurement error may actually be larger (Marshall, 2008). Here, we conservatively assume a reliability ratio of 0.75 for both systolic and diastolic blood pressure and postulate a correlation of .50 between the measurement errors in these variables. In practice it is very important to obtain replicate data or consider a range of possible values for Σ_u in a sensitivity analysis.

In Table 3 we compare the MAI odds ratios to those obtained by Gheorgiade et al. (2006) and Thomas, Stefanski, and Davidian (2011). We report odds and hazard ratios per 10-mm Hg units. Ninety-five percent Wald confidence intervals for the odds ratios are based on standard errors obtained from 1000 bootstrap samples. The adjusted estimates indicate a stronger effect of SBP. Univariate MAI, applied to SBP only, results in larger coefficients for SBP and the effect of DBP is completely attenuated. Multivariate MAI, applied to both variables, has a relatively modest impact on the coefficient for SBP and DBP remains important. Conclusions about the importance of blood pressure differ when we take into account the variability in measurement of each.

Table 3.

Odds ratios for the OPTIMIZE-HF data analysis. Confidence intervals, based on bootstrap standard errors, are given in parenthesis. Method: Unadjusted; U2 and U4, univariate MAI adjusting only systolic blood pressure (SBP) with M=2 and 4, respectively; M2 and M4, multivariate MAI adjusting both systolic and diastolic blood pressure (DBP) with M=2 and 4, respectively.

Variable	Unadjusted	U2	U4	M2	M4
SBP	1.21 (1.17, 1.25)	1.36 (1.30, 1.44)	1.43 (1.35, 1.51)	1.31 (1.24, 1.38)	1.34 (1.27, 1.42)
DBP	1.10 (1.04, 1.16)	1.01 (0.95, 1.07)	0.99 (0.93, 1.05)	1.11 (1.02, 1.20)	1.15 (1.04, 1.26)

6. Discussion

The OPTIMIZE-HF study of systolic blood pressure of Gheorgiade et al. (2006) is illustrative of a typical data analysis. The mis-measured variable is included in descriptive analyses and in complex models involving splines to account for non-linearity. Interest is focused on a particular covariate and measurement error in this variable is likely correlated with that of related variables. Multivariate MAI can address such measurement error and is particularly attractive for moderate to large data sets such as OPTIMIZE-HF. The adjusted data are useful for univariate descriptive purposes like density estimation and as predictors in a logistic regression model and therefore provides a more comprehensive solution than other approaches. Similar to Thomas, Stefanski, and Davidian (2011), we find that MAI performs well under the general recommendation of matching four moments. This recommendation may be limited to moderately large samples, such as those considered here, where higher order moments can be estimated with good precision. For density estimation, the multivariate adjusted data are potentially better than univariate adjusted data and MAI is superior to convenient alternatives. In simulations of logistic regression, the method is similar to MR and RC when the latent variable is normally distributed, but is a superior imputation method when the latent variable is chi-square.

Thomas, Stefanski, and Davidian (2011) noted that MAI was not generally superior to RC when accounting for measurement error in a predictor of time-to-event outcomes, modeled by Cox proportional hazards regression. We observed similar results in preliminary simulations involving multivariate measurement error data. MAI typically provided substantial improvement over the naive method, but RC was frequently superior. This is not entirely surprising, since MAI is based on recreating the joint distribution of latent covariates and response. In the presence of censoring for time-to-event data the appropriate definition of “response” is unclear. More effort is needed to explore various options. Presently, we would recommend other approaches for survival analysis.

We observe relatively little difference between the sequential and joint minimization approaches to calculating adjusted data. The various implementations of MAI could differ in situations that we did not consider. Joint minimization has the benefit of accounting for differential measurement error between the latent variables and could be explored in future research using alternative software or programming methods. We have developed MAI for the case of multivariate normal measurement error. We find many applications where this is a reasonable assumption. However, the method depends on correct specification of the measurement error distribution. Extensions to other measurement error distributions are reported elsewhere.