Characterization of Anomalous Diffusion in Porous Biological Tissues Using Fractional Order Derivatives and Entropy

Abstract

In this high-resolution magnetic resonance imaging (MRI) study at 17.6 Tesla of a fixed rat brain, we used the continuous time random walk theory (CTRW) for Brownian motion to characterize anomalous diffusion. The complex mesoporus structure of biological tissues (membranes, organelles, and cells) perturbs the motion of the random walker (water molecules in proton MRI) introducing halts between steps (waiting times) and restrictions on step sizes (jump lengths). When such waiting times and jump lengths are scaled with probability distributions that follow simple inverse power laws (t^−(1+α), |x|^−(1+β)) non-Gaussian motion gives rise to sub- and super- diffusion. In the CTRW approach, the Fourier transform yields a solution to the generalized diffusion equation that can be expressed by the Mittag-Leffler function (MLF), E_α (− D_{α, β}|q|^βΔ^α). We interrogated both white and gray matter regions in a 1 mm slice of a fixed rat brain (190 μm in plane resolution) with diffusion weighted MRI experiments using b-values up to 25,000 s/mm², by independently varying q and Δ. When fitting these data to our model, the fractional order parameters, α and β, and the entropy measure, $H(q,\stackrel{‒}{\Delta })$, were found to provide excellent contrast between white and gray matter and to give results that were sensitive to the type of diffusion experiment performed.

1. Introduction

The diagnostic capability of magnetic resonance imaging (MRI) is principally dependent on the performance of both system hardware (RF coil arrays, faster gradients, and higher static fields) and software (constrained reconstruction, compressed sampling and fiber tracing). Often overlooked, however, are the underlying mathematical models of MRI phenomena that are the basis of tissue contrast. While the fundamental processes of precession and relaxation encoded in the Bloch equation are the basis for imaging, there is additional contrast available through modulating factors such as chemical exchange, local magnetic field inhomogeneity, and diffusion [1]. In the case of diffusion, where the simplest model predicts a single exponential signal decay, exp[−(bD)], (where D is the diffusion coefficient (mm²/sec) and b is a pulse sequence controlled parameter), the restrictions introduced by cell membranes, extracellular matrix and tissue heterogeneity provide a rich mix of phenomena that are both anisotropic and complex [2]. Diffusion tensor imaging (DTI), for example, provides new biomarkers (mean diffusivity and fractional anisotropy) that capture additional anatomical features in the brain (e.g., white matter connectivity and fiber density) [3]. Diffusion kurtosis imaging (DKI) is an another example of a diffusion based technique that is able to characterize the complexity of multiscale neural tissue [4]. Here, we wish to present a third method – fractional order anomalous diffusion – that describes underlying tissue complexity through measurements of diffusion signal attenuation at high b-values.

In this paper we consider a probabilistic approach to modeling diffusion attenuation in fixed brain tissue by generalizing the underlying random walk statistics [5, 6]. The generalization relaxes the constraint that the diffusing particle (undergoing Browning motion) must take equal length jumps at regular intervals, by allowing variable increments in both the jump distance and the waiting times between jumps. We retain the statistical properties of independent and identical particle behavior to have a stable process, but one that characterizes the jump lengths and waiting times by probability distributions that fall off separately in distance and time as inverse power laws (|x|^−(1+β), t^−(1+α)). In essence, we are assuming that it is less likely for the particles to take large jumps or for them to experience long waiting times. This generalization is formally incorporated into the analysis of MRI diffusion data as the Continuous Time Random Walk (CTRW) model [7]. We will show below, that this approach provides new biomarkers that encode tissue complexity in the fractional order of the power law decays, which pass directly over to the fractional order of the governing partial differential equation for the CTRW statistical process.

2. Theory

In random walk (RW) theory, the Brownian motion of diffusing particles, P(x, t), in homogeneous and isotropic geometries can be described by the second order partial differential equation,

$$\frac{\partial P(x,t)}{\partial t}=D\frac{{\partial }^{2}P(x,t)}{\partial {\mid x\mid }^2}$$ (1)

where D is the diffusion coefficient. The solution to Eq. (1) follows as the familiar Gaussian form of the probability distribution function (pdf),

$$P(x,t)=\frac{1}{\sqrt{4\pi Dt}}exp\left(-\frac{x^2}{4Dt}\right).$$ (2)

However, the motion of diffusing particles is said to be anomalous (non-Gaussian) for heterogeneous materials with tortuous and porous geometries. As such, the RW formalism can be extended to the CTRW to account for this anomalous diffusion, and, P(x, t), can be described with a fractional partial differential equation,

$${}_0{}^C\mathcal{D}_t^{\alpha }P(x,t)=D_{\alpha ,\beta }\frac{{\partial }^{\beta }P(x,t)}{\partial {\mid x\mid }^{\beta }}$$ (3)

where ${}_0{}^c\mathcal{D}_t^{\alpha }$ is the α^th (0 < α ≤ 1) fractional order time derivative in the Caputo form, ∂^β/∂|x|^β is the β^th (0 < α ≤ 2) fractional order space derivative in the Riesz form, and D_{α, β} is the effective diffusion coefficient (e.g. mm^β/s^β).

The solution to Eq. (3) can be expressed in terms of the characteristic function, p(k, t), of the distribution by taking the Fourier transform of Eq. (3) and solving the resultant fractional order differential equation in time [5, 6]. The result can be written as,

$$p(k,t)=E_{\alpha }(-D_{\alpha ,\beta }{\mid k\mid }^{\beta }{t}^{\alpha })$$ (4)

where E_α is the single-parameter MLF (defined in [8]). This decay function interpolates between a stretched exponential and a power law for small and large values of its argument, respectively, with the conventional single exponential arising for the nominal choice of parameters: α = 1 and β = 2 (see Fig. 7.3, page 253 in [9]).

A phase diagram of α and β can be constructed from the MLF for p(k, t) to visualize the regions of sub-, super-, and normal diffusion, as shown in Fig. 1 [7]. Moving left from the point of Gaussian diffusion (α = 1, β = 2) by fixing α = 1 and decreasing β, the characteristic form of super-diffusion (Lévy stable process) is given by a stretched exponential function. Moving down from the point of Gaussian diffusion (α = 1; β = 2) by fixing β = 2 and decreasing α, the characteristic form of sub-diffusion is given by as a stretched MLF (fractional Brownian motion). For all other points inside the area bounded by the α = 1 horizontal and β = 2 vertical lines, the characteristic form of anomalous diffusion is given by Eq. (4).

Figure 1.

Diffusion phase diagram with respect to the order of the fractional derivative in space, β, and the order of the fractional derivative in time, α (adapted from [5, 7]).

In spin-echo diffusion MRI experiments, the signal decay, S, is modeled with a mono-exponential as,

$$S∕S_0=exp(-bD)$$ (5)

where b is the product of the q-space and diffusion time terms, b = q²(Δ − δ/3). For brevity, we will define $\stackrel{‒}{\Delta }=\Delta -\delta ∕3$ as the effective diffusion time. As such, a diffusion experiment can be constructed with a particular b-value, with arbitrary weighting on the q and $\stackrel{‒}{\Delta }$ components. Fig. 2 shows iso-b-value curves plotted as a function of q² and $\stackrel{‒}{\Delta }$, such that either $\stackrel{‒}{\Delta }$ (moving vertically) or q² (moving horizontally) can be varied, to achieve an array of b-values.

Figure 2.

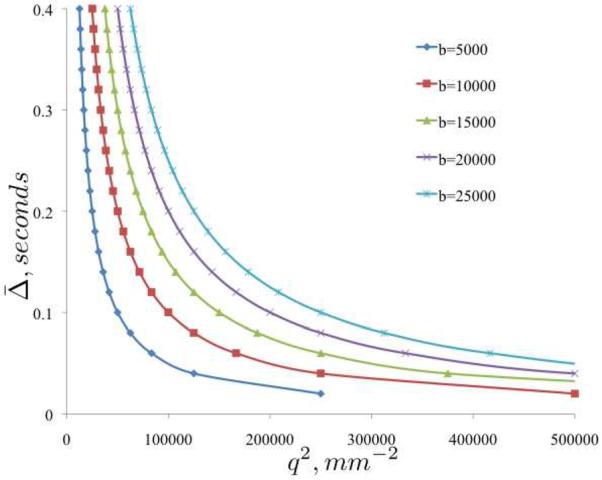
Iso-b-value phase diagram of $\stackrel{‒}{\Delta }$ vs. q² for five b-values (5, 000 – 25, 000s/mm²).

In [10], data obtained in fixed $\stackrel{‒}{\Delta }$, variable q experiments were fit with a stretched-exponential μ (analogous to our β) parameter and data obtained in fixed q, variable $\stackrel{‒}{\Delta }$ experiments were fit with a stretched-exponential α parameter as an approach to independently interrogate fractional space and fractional time diffusion features described in [5], respectively. Here we extend this approach in a diffusion MRI experiment to probe the phase diagram using the MLF to fit the data,

$$p(q,\stackrel{‒}{\Delta })=E_{\alpha }(-D_{\alpha ,\beta }{\mid q\mid }^{\beta }{\stackrel{‒}{\Delta }}^{\alpha }),$$ (6)

where β incorporates the square of the q term to operate as 0 < β ≤ 2. The resultant α and β values are expected to characterize diffusion in each tissue region.

The uncertainty, or information, in a signal can be expressed in terms of the entropy in the power spectrum of the Fourier transform [11, 12]. Likewise, we can adapt this formalism to multi-b-value diffusion data acquired as a function of q and $\stackrel{‒}{\Delta }$,

$$H(q,\stackrel{‒}{\Delta })=-\sum _{i=1}^N\frac{\widehat{p}(q_i,\stackrel{‒}{\Delta })ln\left(\widehat{p}\right(q_i,\stackrel{‒}{\Delta }\left)\right)}{ln\left(N\right)}.$$ (7)

where $\widehat{p}(q_i,\stackrel{‒}{\Delta })$, is the individual q value's contribution to a normalized power spectrum, and the term, ln(N) (i.e. discrete uniform distribution of N samples), is a normalization factor applied to the spectral entropy, $H(q,\stackrel{‒}{\Delta })$, keep its total value between 0 and 1.

Considering Eq. (6) encompasses the phase space of diffusion phenomena as shown in Fig. 1, we can evaluate the entropy, or uncertainty, in Eq. (6) by insertion into Eq. (7). Fig. 3 shows the entropy surface computed against the generalized solution to the diffusion equation for 0 < α ≤ 2 and 0 < β ≤ 4. Of particular interest is the singular case for Gaussian diffusion (α = 1, β = 2), in which the entropy settles near the global minimum of the basin. At points away from Gaussian diffusion, in the sub- (2α/β < 1), super- (2α/β > 1), and even the effective normal (2α/β = 1) diffusion regimes, the entropy is greater. For further analysis of this entropy surface, see [13].

Figure 3.

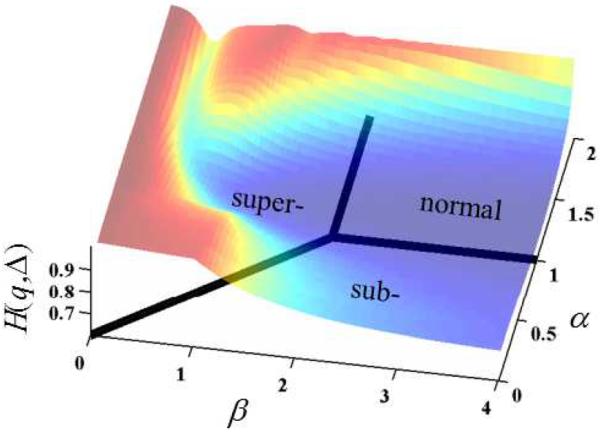
The representative entropy, H(q, $\stackrel{‒}{\Delta }$) superimposed on the phase diagram of the diffusion process as represented by the MLF as the characteristic function.

In this paper, we investigate the feasibility of using the fractional order parameters α and β in Eq. (6) and entropy, $H(q,\stackrel{‒}{\Delta })$, defined in Eq. (7) to describe tissue complexity, heterogeneity, and tortuosity, as observed in diffusion-weighted MRI experiments on a fixed rat brain.

3. Experimental

The rat brain was excised and fixed in 4% paraformaldehyde. Overnight, prior to imaging experiments, the rat brain was washed in phosphate buffered saline. During the imaging experiments the rat brain was immersed in Fluorinert and oriented such that the anterior-posterior axis of the brain was aligned ~ 30° with respect to the main B₀ field. For this orientation, a central oblique slice was selected to provide a full brain axial image. The axial slice is defined as the y − z plane with medial-lateral direction along the y-axis and the anterior-posterior direction along the z-axis. At the Advanced Magnetic Resonance Imaging and Spectroscopy (AMRIS) Facility (Gainesville, Florida), pulsed gradient stimulated echo (PGSTE) experiments were performed on a Bruker spectrometer (17.6 Tesla, 750 MHz, 89 mm bore) with the following parameters: TR=2 s, TE=28 ms, b-values up to 25,000 s/mm², δ = 3.5 ms, NA = 2, 1 diffusion weighting direction along the y-axis, slice thickness = 1 mm, FOV=27×18 mm, matrix size 142 × 94, giving an in plane resolution of 190 μm. Additionally, variable TR data were collected to correct for T1 relaxation effects in the direction of the diffusion weighting experiment. One constant $\stackrel{‒}{\Delta }$, variable q experiment was performed with Δ fixed at 17.5 ms and one constant q, variable $\stackrel{‒}{\Delta }$ experiment was performed with gradient strength fixed at 525 mT/m to achieve q-value of 78 mm⁻¹.

The raw data were fit to the MLF in Eq. (6) using a non-linear least squares fitting algorithm (Levenberg-Marquardt) in Matlab (Nantick, MA) using procedures described in [14]. The values for α and β were determined assuming starting values of α = 1 and β = 2. The convergence criteria for the fit was 10⁻⁶. To estimate the diffusion coefficient, a mono-exponential function was fit to the first 3 low b-value samples where the semi-log signal decay is assumed to be linear. After the MLF parameters were determined, the characteristic decay curve for p(q, $\stackrel{‒}{\Delta }$) was constructed using N=1,500 increments arrayed over variable q or variable $\stackrel{‒}{\Delta }$ for b-values between 0 and 25,000 s/mm². Then, the entropy (defined in Eq. (7)) in the diffusion process as modeled by the MLF was computed as H(q, $\stackrel{‒}{\Delta }$).

4. Results

An axial T2 weighted MR image of a 1 mm slice through the central region of the entire rat brain is shown in Fig. 4. Using this image we selected regions of interest (ROI) in the gray matter and in the white matter (corpus callosum). In each ROI we then fit the diffusion attenuation curves (for fixed Δ or q) to our fractional order model and estimated the parameters α and β, D, and H(q, $\stackrel{‒}{\Delta }$). In Table 1 we present the results for Δ = 17.5 ms and q = 78 mm⁻¹. These data were obtained with the diffusion gradient directed along the y-axis, which corresponds to the principal fiber direction at the center of the corpus callosum. For the selected ROI, the α and β determined in the WM were less than those values in the GM, reflecting the greater WM complexity (porosity, tortuosity). These differences were larger for the constant Δ experiment than for the constant q experiment. In addition, for the constant q experiment the fractional order parameters in GM were found to be very close to the nominal Gaussian values of α = 1 and β = 2, while for the constant Δ experiment, α < 1 and β ~ 2, which is a characteristic of fractional Brownian motion [7]. The computed values of the diffusion coefficient, D, were also sensitive to the q and Δ weighting, but differed little between WM and GM. The entropy measure, H(q, $\stackrel{‒}{\Delta }$), distinguished between both experiment and tissue, with higher values (greater microstructural complexity) in the constant Δ than the constant q experiment.

Figure 4.

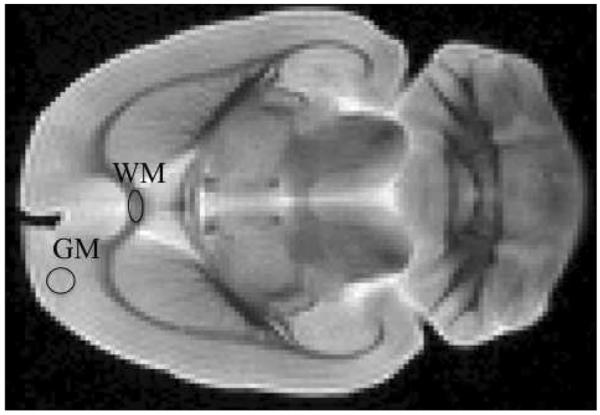
T2-weighted image of an axial slice through a fixed, whole rat brain with gray matter (GM) and white matter (WM) ROIs.

Table 1.

MLF parameter and entropy values for white and gray matter ROIs in the constant Δ = 17.5 ms and q = 78 mm⁻¹ experiments.

parameter	ROI	Δ = 17.5 ms	q = 78 mm−1
	GM	0.76 ± 0.05	0.95 ± 0.01
α	WM	0.42 ± 0.04	0.69 ± 0.05
	GM	1.95 ± 0.06	1.91 ± 0.03
β	WM	1.15 ± 0.13	1.85 ± 0.07
D(×10−3mm2/s)	GM	0.32 ± 0.01	0.29 ± 0.01
	WM	0.36 ± 0.04	0.25 ± 0.02
	GM	0.82 ± 0.01	0.78 ± 0.01
$H(q,\stackrel{‒}{\Delta })$	WM	0.93 ± 0.01	0.88 ± 0.02

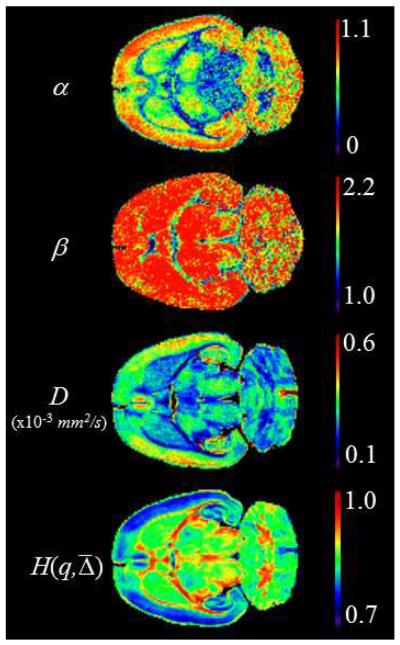
This analysis was extended to each pixel in the entire slice. The results are displayed as parameter maps for α and β, D, and H(q, $\stackrel{‒}{\Delta }$) in Fig. 5 for the constant Δ experiment, as an example. The α map shows excellent contrast between WM and GM. In addition, good contrast is visible for GM within the frontal, parietal and occipital lobes. The β map shows good contrast between WM and GM only for the region of the central corpus callosum, and within the occipital lobe of the GM. The D map displays excellent WM/GM contrast throughout the brain. H(q, $\stackrel{‒}{\Delta }$) combines all this information giving an image with excellent contrast in both the WM and the GM of the whole brain slice. In particular, the central regions of the brain slice (caudate, putamen, thalamus, etc.) are clearly differentiated from each other.

Figure 5.

MLF, diffusion coefficient and entropy parameter maps for constant Δ = 17.5 ms experiment

5. Discussion

The overall goal in our work is to develop a more thorough basis for the use of power law models in the description of NMR relaxation and diffusion phenomena. We take inspiration from the ability of fractal models to provide simple, but complete descriptions of complex geometric structures, often involving fractional powers, and from `universality' in statistical mechanics, where the overall dynamics of a complex system - in the scaling limit of a large number of interacting particles - is independent of the dynamical details, and is simply expressed as an order parameter (often with a fractional order critical exponent).

In the field of diffusion MRI, Magin et al., proposed a fractional generalization of the Bloch-Torrey equation where both the space and the time derivatives could in principle be of fractional order [14]. The solution to this model was demonstrated - under reasonable imaging conditions - to be expressed in the form of a stretched exponential function. Recently, this work was extended and applied in clinical imaging studies of normal human subjects [15, 16]. In the current paper, we have approached this problem directly from the diffusion perspective, motivated in part by the recent stretched exponential fits to packed bead phantom systems by [10] and by the higher-order moment fits to fixed rat brains by [17]. Here we notice that the dual space-time fractional order diffusion equation has an analytical solution in the form of the MLF with two fractional order parameters (α, β), where the first reflects the fractional time derivative (and the order of the single parameter MLF), and the second the fractional space derivative (and the fractional power of the q). The physical interpretation of α and β is concisely incorporated in the CTRW model - as articulated by [5] - through the assumption that the pdf for diffusion is separable into individual probability distributions of waiting times (water trapping) and distance increments (jump lengths). This solution reverts, of course, to the normal or Gaussian case for α = 1 and, β = 2. Since this solution is in the simple form of the characteristic function of the pdf, entropy can be used as an overall measure of anomalous features in the diffusion decay dynamics, which differs from the use of entropy to characterize DTI metrics in [18]. The results demonstrate the utility of the fractional order generalization as one that simplifies complex dynamical relationships, and in addition, appears to encode additional information (i.e. greater entropy) when the fits diverge from the normal or Gaussian case.

Many groups are now investigating ways to extract meaningful biomarkers from the observed decay of high b-value diffusion data [15, 19, 20]. Using a wide variety of fitting methods (and underlying mathematical models) fractional order fits are obtained that highlight significant spatial heterogeneity and directional dependence. These data, of course, are just reflecting the underlying porosity and tortuosity within the imaging voxels. In this feasibility study, we have examined diffusion in only one direction. Investigations of the directional dependence of the fractional order parameters, and of the entropy, which can in principle – like diffusion – be described by a tensor, are works in progress.

6. Conclusions

The probabilistic perspective of the continuous time random walk (CTRW) theory of Brownian motion provides a convenient framework for analyzing the variety of behaviors observed when diffusion weighted MR imaging is applied to biological tissues. Three aspects of this perspective are perhaps worthy of note. First, the underlying idea of hindered or restricted diffusion in complex, heterogeneous, and multi-scale tissue is encapsulated by α and β directly in the CTRW idea that the diffusing particle is sometimes trapped and sometimes free to jump. This idea simply links the decreasing (power law) likelihood of such events with the fractional order differential operators of the generalized diffusion equation. Second, the resulting anomalous diffusion process, as expressed though α and β in the MLF, identifies specific forms of sub- or even super-diffusion as natural simplifications of the model, not as an added complexity. Hence, one can more clearly identify the effects on image contrast of changing the direction of the applied diffusion gradients or of keeping either q or Δ fixed when spanning a selected range of b-values. Third, the estimation of the entropy as a measure of system complexity introduces a new way to view the fractional diffusion phase diagram through a surface of growing randomness (increasing complexity) as the fractional order parameters deviate from the trough near α=1 and β=2 in Fig. 3. Individual cuts of this surface describe specific features of the system behavior, and can be used to guide more efficient/effective diffusion acquisition schemes, via, what we call, “phase slice tuning”. Although this study suggests the constant $\stackrel{‒}{\Delta }$ experiment is able to identify more anomalous and directionally dependent diffusion phenomena (i.e. greater entropy) compared to the constant q experiment, each approach remains important to pursue for further investigation as they appear to encode different information about the diffusion process. As such, degeneration, plasticity, and therapeutic response in neural tissue may be probed with the method that best interrogates changes in the relevant anatomical morphology. Further work is underway to extend these techniques to an examination of fixed tissue with known pathologies, to imaging applications in vivo, and to identify the histological basis for the directional dependence of the fractional order fits.