Abstract
A three-state equilibrium unfolding of a protein can be difficult to detect if two of the states fail to differ in some easily measurable way. It has been unclear whether staphylococcal nuclease unfolds in a two-state fashion, with only the native and denatured states significantly populated at equilibrium, or in a three-state manner, with a well-populated intermediate. Since equilibrium unfolding experiments are commonly used to determine protein stability and the course of denaturation are followed by changes in the fluorescence which has difficulty in distinguishing various states, this is a potential problem for many proteins. Over the course of twenty years we have performed more than one hundred guanidine hydrochloride equilibrium denaturations of wild-type staphylococcal nuclease; to our knowledge, a number of denaturations unrivaled in any other protein system. A careful examination of the data from these experiments shows no sign of the behavior predicted by a three-state unfolding model. Specifically, a three-state unfolding should introduce a slight, but characteristic, non-linearity to the plot of stability versus denaturant concentration. The average residuals from this large number of repeated experiments do not show the predicted behavior, casting considerable doubt on the likelihood of a three-state unfolding for the wild-type protein. The methods used for analysis here could be applied to other protein systems to distinguish a two-state from a three-state denaturation.
Keywords: Folding intermediate, Linear extrapolation, Residual structure, Protein stability
1. Introduction
Staphylococcal nuclease is one of the proteins most intensively studied to examine the effects of mutation upon protein stability. Protein stability in nuclease and many other proteins is often determined by a spectroscopic measurement of the amounts of native and denatured protein at equilibrium under differing conditions of a denaturant. These spectroscopic measurements are used to determine the relative amounts of these two states and calculate an equilibrium constant. Of course, in the process of unfolding or refolding, the protein will likely pass through one or more intermediate states, but a common assumption is that these transient intermediates are unstable and such small amounts of protein are present in them that they can be ignored for purpose of thermodynamic stability calculations. Although a two state unfolding model is normally used for data analysis when determining the stabilities of wild-type staphylococcal nuclease or its mutants, there is evidence that at least some mutants of nuclease, in particular the V66W mutant, unfold during solvent denaturation in a three state process [1-13], where an unfolding intermediate is significantly populated. Note that we use the word intermediate in the strict equilibrium thermodynamic sense; a state that is stable enough to accumulate at high enough concentrations to be taken into account as significant in the calculations of equilibrium constants. In a more kinetic sense, intermediates or ‘in-between’ states must be present as the protein passes from the folded to unfolded state. If these states are only transiently passed through and not significantly populated, they are moot in terms of their effect on protein stability calculations. However, if wild-type and the many other mutants of nuclease characterized over the years do in fact denature via an intermediate state, a failure to take this into account in the analysis can lead to large errors in the apparent stabilities relative to the true free energy difference between the native state and the denatured states.
This problem is not limited to nuclease. Indeed, despite years of exhaustive study and multiple groups working with the protein, it took nearly twenty-five years before any evidence of a three-state mechanism was observed in nuclease and, now, twenty years later, while one mutant unequivocally has a three-state unfolding mechanism, there is still disagreement about whether or not wild-type staphylococcal nuclease and most mutants have a significantly populated unfolding intermediate. It is also unclear what causes at least some nuclease mutants to populate an intermediate. With such confusion evident in a rigorously observed protein, the odds are good that similar situations exist for other model proteins that have not been recognized.
A large part of the difficulty arises because the usual probe of structure is the fluorescence of the single tryptophan found in staphylococcal nuclease at position 140. Fluorescence, of course, reports only very local structure. One physical model for three state denaturation in nuclease is that the C-terminal helix, which ends with tryptophan 140, unfolds in the first transition. The resulting partially folded state has been proposed to break down cooperatively in a subsequent step. The fluorescence from tryptophan 140 is quenched in both denatured states as it is fully exposed in both, making them apparently indistinguishable in this model. This state of affairs is not unique to staphylococcal nuclease.
While there is no clear cut spectroscopic signal, a three-state unfolding event does differ in the plot of stability versus denaturant concentration in some subtle, but characteristic ways. Over the course of the past twenty years examining numerous staphylococcal nuclease mutants, we have also denatured wild-type staphylococcal nuclease many times as a control for instrumental performance, to validate different batches of guanidine hydrochloride, and to check the quality of wild-type made for other experiments. Over a hundred of these denaturations are of fine quality and this very large number of replicate experiments upon a single protein is unlikely to be duplicated in any other system soon. Therefore, a careful examination of this aggregated data to look for the thermodynamic signature of a three-state denaturation was undertaken and the results are reported here. Similar techniques should be applicable to other proteins even without such a large number of denaturations available.
2. Experimental procedures
2.1. Protein expression
Protein expression and purification was carried out as previously described [14]. Final dialysis was against a 100 mM NaCl, 25 mM sodium phosphate buffer, pH 7.00. Purity was verified by SDS-PAGE. Typical protein yields of at least 98% pure protein were in the range of 5–15 mg per 250 ml of growth media.
2.2. Titration of proteins
Wild-type staphylococcal nuclease was denatured as generally described previously [15,16]. All the results reported here were obtained at 20.0 °C, 100 mM NaCl, and a sodium phosphate buffer, 25 mM in phosphate, pH 7.00 with a protein concentration of 50 μg/ml. The denaturant was 6.00 M guanidine hydrochloride buffered at pH 7.00 with a sodium phosphate buffer, 25 mM in phosphate, with no added sodium chloride.
3. Results
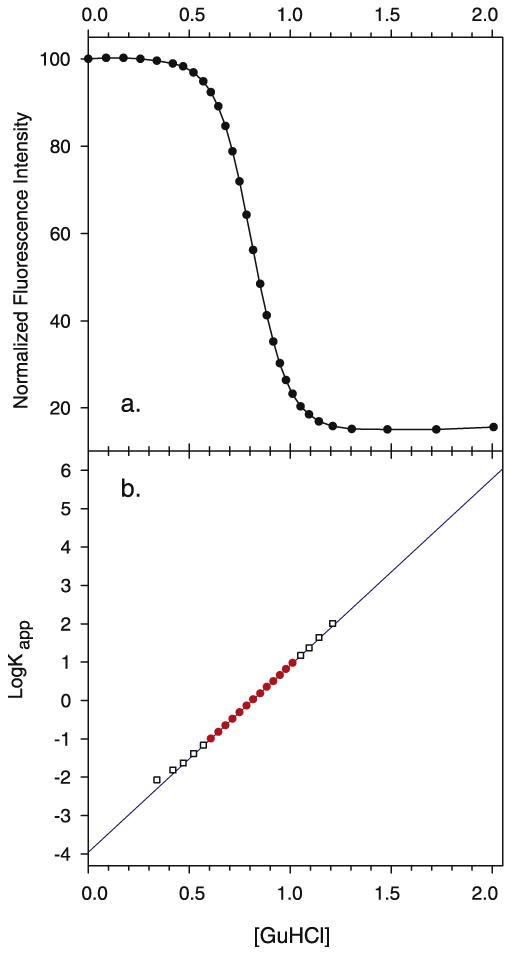
Approximately four hundred guanidine hydrochloride denaturations of wild-type staphylococcal nuclease have been performed in our laboratory using our automated titrating fluorometer [15,16]. Many denaturations were performed using unusual conditions of temperature, ionic strength, pH or some other experimental parameter. Some of these denaturations were performed in the original development of the techniques when the instrument was new, some to train new students, and many to troubleshoot instrument problems. Such data may be of lower quality. Therefore, experimental runs with known instrumental problems, with unusual discontinuities in the titration curve, or with other signs, in our judgment, of questionable experimental quality were excluded. Further, we excluded all titrations that had a denatured intensity greater than 19% of the initial native state intensity, as in our experience higher denatured intensities are primarily caused by protein preparations with high levels of nuclease fragments or other impurities, and lead to low stability values. We were left with 106 denaturation experiments deemed of very high quality. Of these, 102 were carried out using identical guanidine hydrochloride concentrations in the transition region of the sigmoidal titration curve. A representative curve is shown in Fig. 1a.
Fig. 1.
Experimental denaturation of wild-type staphylococcal nuclease followed by tryptophan fluorescence. (a) A representative sample plot of the fluorescence of tryptophan 140 versus guanidine hydrochloride concentration. The intensity at zero molar guanidine hydrochloride is assigned the arbitrary value of 100 and all subsequent fluorescence values are normalized to it. (b) Plot of log Kapp versus the concentration of guanidine hydrochloride. The solid line is the least square fit of log Kapp versus [GuHCl] in the region where 1 > log Kapp > −1. Experimental data points used in the regression are shown by filled circles. Outside this region they are hollow squares.
These curves were analyzed using a two-state model of denaturation where the apparent equilibrium constant, Kapp, for the reaction native state ℜ denatured state is calculated using the equation:
where In is the fluorescence of the native state, Id the fluorescence of the denatured state, and I is the fluorescence intensity at a given concentration of guanidine hydrochloride (GuHCl).
The apparent free energy change upon denaturation, ΔGapp, can be determined by use of the equation:
A protein’s thermodynamic stability (ΔGH2O), the rate of change of free energy with respect to GuHCl concentration (mGuHCl or d(ΔG)/d[GuHCl]), and the midpoint concentration, Cm, the concentration of GuHCl at which half of the protein molecules are unfolded are all determined by linear least squares fit of log Kapp against [GuHCl] for all values of Kapp between 0.1 and 10 (log Kapp between 1 and −1). The line thus obtained, log Kapp = mGuHCl[GuHCl] + c, is then extrapolated to zero [GuHCl] to obtain the value of log Kapp and ultimately the free energy difference between the native and denatured states in the absence of denaturant, ΔGH2O. This is shown in Fig. 1b.
One issue which has a trivial impact on ΔGH2O and mGuHCl values, but as discussed further below is of possible importance in the more painstaking analysis here, is that neither In and Id are completely unaffected by changing concentrations of GuHCl. This is true for both wild-type nuclease and most mutants. The denatured baseline usually has a very slight increase with guanidine hydro-chloride concentration. While the values of Id change from protein prep to protein prep, the change within any given denaturation experiment caused by this slope is small. Therefore, normal data analysis in this laboratory uses the lowest value of the denatured baseline as Id. The first data point at zero guanidine hydrochloride concentration is assigned the value of 100 and subsequent intensities are normalized to it. In the 106 denaturations considered here, the values of Id after normalization ranged from 12.17 to 18.79, a median of 15.42, an average of 15.58 and a standard deviation of 1.18. Again, while this changes from experiment to experiment, there is little slope to the denatured baseline in a given experiment.
On the other hand, there is typically an increase in the native baseline intensity with the first addition of guanidine hydrochloride. The usual procedure used in our laboratory is to use the maximum value of the native baseline as In. However, these changes tend to be larger than for the denatured baseline. The maximal value in the 106 denaturations considered here ranged from 100 to 101.40, with a median of 100.39, an average of 100.49 and a standard deviation of 0.34. In addition to this usual procedure, the data was analyzed by four other methods. First, In was set in every case to 100.6, a value rather higher than that found as the maximum in most denaturations. Second, the value of In was set to 100 (i.e. the intensity at zero molar guanidine hydrochloride, which is assigned the arbitrary value of 100 and to which all subsequent fluorescence values are normalized). This is a value significantly lower than the maximal value of In found for most denaturations. Third, In was set to be equal to the average of the intensity of the first four guanidine hydrochloride concentrations for each denaturation. This region of the titration curve, up to approximately 0.25 M GuHCl, is fairly flat. These averages were higher than 100, but lower than the maximum, with values in the 106 denaturations considered here ranging from 99.72 to 101.03, a median of 100.20, an average of the averages being 100.27 with a standard deviation of 0.26.
Finally, the data were fit to a two-state model using the technique of Santoro and Bolen [17]. In this method both the native and denatured baselines are presumed to be linear functions of guanidine hydrochloride concentration and they are fit simultaneously along with log Kapp in a non-linear regression. In this fitting model the value of In ranged from 99.64 to 100.74, a median of 100.17, with an average of 100.20 and a standard deviation of 0.20. The slope of In, in units of intensity per M GuHCl, ranged from −1.61 to +3.19, a median of 0.72, an average of 0.66 and a standard deviation of 1.05. The value of Id ranged from 11.92 to 20.88, a median of 15.42, with an average of 15.63 and a standard deviation of 1.59. The slope of Id, in units of intensity per M GuHCl, ranged from −2.29 to +2.02, a median of 0.13, an average of 0.04 and a standard deviation of 0.66.
In Table 1 are compiled the averages for the wild-type free energy of unfolding (ΔGH2O), midpoint (Cm), and slope values (mGuHCl) determined for each of the 106 denaturations using the five different methods of setting In and Id. The error estimates are standard deviations. Differences in the average values returned by each fitting method are significantly less than the standard deviations. All methods give very good linear fits, as shown in Table 2 for the methods using least squares regression.
Table 1.
Average thermodynamic values of various two-state fits to 106 guanidine hydrochloride denaturations of wild-type staphylococcal nuclease.
| Fit | Δ G H2O a | Cm b | m GuHCl c |
|---|---|---|---|
| Max | 5.297 ± 0.096 | 0.821 ± 0.009 | 6.449 ± 0.116 |
| 100.6 | 5.282 ± 0.106 | 0.821 ± 0.009 | 6.435 ± 0.125 |
| 100 | 5.353 ± 0.106 | 0.823 ± 0.009 | 6.506 ± 0.125 |
| Average of first 4 | 5.322 ± 0.096 | 0.822 ± 0.009 | 6.448 ± 0.117 |
| Santoro–Bolen | 5.284 ± 0.087 | 0.820 ± 0.019 | 6.444 ± 0.109 |
Average free energy difference between native and denatured states in the absence of denaturant and standard deviation in units of kcal/mol.
Average midpoint concentration (concentration of guanidine hydrochloride at which half of the protein is denatured) and standard deviation in units of molar. The Santoro–Bolen fit used here does not directly return a value of Cm for each denaturation so the overall average value is calculated from the average ΔGH2O and mGuHCl and the standard deviation is propagated from the errors in those values.
Average slope value (change in free energy with respect to change in guanidine hydrochloride concentration) and standard deviation in units of kcal mol−1 M−1.
Table 2.
Coefficient of determination for least squares fitting methods.
| Fit | Median R2 | Average R2 | Standard deviation |
High | Low |
|---|---|---|---|---|---|
| Max | 0.99992 | 0.99981 | ±0.00025 | 0.99999 | 0.99853 |
| 100.6 | 0.99992 | 0.99981 | ±0.00025 | 0.99999 | 0.99841 |
| 100 | 0.99988 | 0.99972 | ±0.00034 | 0.99999 | 0.99803 |
| Average of first 4 | 0.99978 | 0.99991 | ±0.00029 | 0.99999 | 0.99841 |
4. Discussion
There is evidence that at least some mutants of nuclease, in particular the V66W mutant, unfold during solvent denaturation in three states, rather than just two states [1-13]. Some have argued most or all nuclease mutants as well as wild-type denature via an intermediate [18,19], meaning that a three-state model should be used to analyze the data rather than the two-state model commonly used. It is important to note that there is good evidence for many proteins, including nuclease, that folding and unfolding proceeds through well-defined states, often referred to as intermediates. The question at issue here is whether or not these kinetic intermediates, whose existence is not in doubt, are stable enough to become significantly populated to become intermediates in the thermodynamic sense. If this occurs, the analysis of the thermodynamic equilibrium that ignores their existence will be flawed and will give incorrect values for the stability of the various states.
Previously, we compared the circular dichroism (CD) and fluorescence signals in thermal denaturation of wild-type and many mutant staphylococcal nuclease but found no evidence of an equilibrium three state thermal denaturation [20]. CD and fluorescence data for guanidine hydrochloride denaturation are also in good agreement for wild-type staphylococcal nuclease [21]. CD is relatively noisy and insensitive compared to fluorescence. Is there a way to distinguish a three-state equilibrium unfolding mechanism from a two-state equilibrium mechanism using fluorescence alone?
In the three state model, the main probe of structure used to follow nuclease denaturation, fluorescence of tryptophan 140, does not distinguish between the intermediate and fully denatured state. It would, therefore, at first seem that there is no way to distinguish between a two-state and three-state model using this probe. A careful examination of the predictions of each model shows that there are in fact definite differences in the expected denaturation behavior.
In the two-state model, log Kapp is a linear function of guanidine hydrochloride concentration. This is not the case for a denaturation that proceeds through an intermediate. Let us examine in more detail the denaturation behavior of nuclease assuming that it is best described by a three-state equilibrium.
Where
| (1) |
and
| (2) |
The equilibriums, and , in the absence of evidence to the contrary, will be assumed to be two-state and where [N], [D1] and [D2] are the concentrations of protein in, respectively, the N, D1 and D2 states. The first denatured state, D1, may be thought of as a folding intermediate if preferred. Let us further assume that D1 and D2 states are indistinguishable by the probe of structure used here, fluorescence of W140, which is at the end of the C-terminal helix proposed to unfold in the first transition of a putative three-state unfolding [22-24]. In this model, the remaining structure, primarily the main beta barrel, then breaks down cooperatively in the subsequent step. The overall or total apparent equilibrium, , for native state ℜ all denatured states is then described by
| (3) |
In this model the fluorescence intensity of tryptophan 140 (W140) is high in the native state and low in both the D1 and D2 states. It is shown in Supplementary material that this three-state equilibrium can be described by the following relationship:
| (4) |
where and are, respectively, the free energy differences at zero guanidine hydrochloride concentration between N and D1 and between D1 and D2 and and are the rates of change of free energy with respect to GuHCl concentration (d(ΔG)/d[GuHCl]) for the respective equilibria.
In contrast, if the overall folding reaction were a true two-state equilibrium, with a single denatured state, would be more simply described as
| (5) |
or
| (6) |
The three-state model reduces to two-state behavior under certain circumstances. In equation (4), if the term has a value much greater than 1 (in the limit ), then is closely approximated as
This is, of course, equivalent to equation (6) for a two-state equilibrium where and .On the other hand, if has a value close to zero (in the limit ), then is closely approximated as
which is, again, an equation for a two-state equilibrium. Thus, when has a value near one (in the limit deviation from two-state behavior is most pronounced.
Put in energetic terms, if the states D1 and D2 are similar in stability over a given concentration range of GuHCl, then denaturation over that range of GuHCl will exhibit the maximal deviation from two-state behavior as the slope changes from a value of to a value of . The inflection will be most pronounced when is fairly large relative to . On the other hand, if either D1 or D2 is energetically favored over a given concentration range of GuHCl, then denaturation over that range will closely approximate two-state behavior even though the underlying equilibrium is between three states. The bigger the energy difference between D1 and D2, the more closely two-state behavior is approximated.
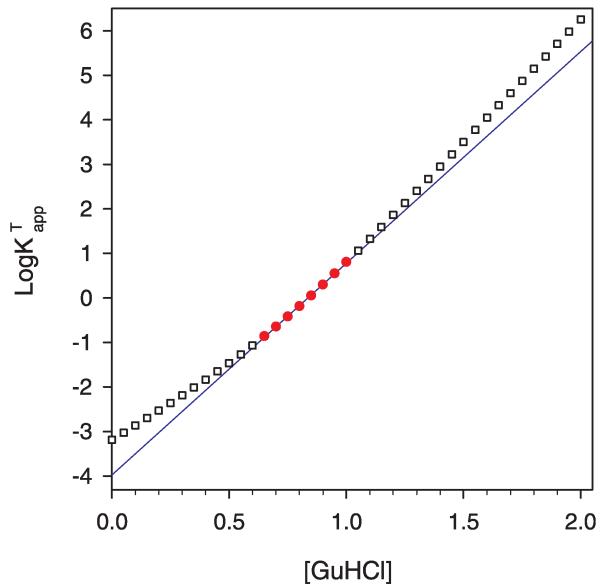
In Fig. 2 is shown the values for log calculated at intervals of 0.05 M GuHCl by using equation (4) in logarithm base 10 (i.e. taking the logarithm base 10 of equation D in the Supplementary material) and the using values for , , and given in the caption. (The logarithm base 10 rather than the natural log is used for convenience in analyzing experimental data so that approximate ratios of N/D and intensity are more easily determined without use of a calculator.) The simulated data points shown in red are the region where log as a function of guanidine hydrochloride concentration is least linear. There are two regions where the value of log is very linear. At low denaturant concentration the equilibrium is basically between N and D1 and at higher guanidine hydrochloride concentration the equilibrium is mostly between N and D2.
Fig. 2.
Simulation of three-state unfolding where the denatured states D1 and D2 are indistinguishable by the spectroscopic probe. Points are versus [GuHCl] calculated using the three-state model. The solid line is the two-state least square fit of versus [GuHCl] in the region where 1 > log Kapp > −1. Points used in the regression are shown by filled circles. Outside this region the calculated values are hollow squares. In this particular simulation of three-state unfolding behavior the first transition between N and D1 is assumed to be two-state with values for of 4.3 kcal mol−1 M−1 and of 4 kcal mol−1. The second transition between D1 and D2 was assigned values for of 2.9 kcal mol−1 M−1 and of 2 kcal mol−1 for . Using these values in equation D in Supplementary material and then taking its logarithm base 10, was calculated at 0.05 M intervals.
It is important to remember that only a limited range of GuHCl concentrations provide experimentally useful data. When fitting to the two-state model we normally use data in the range where is 0.1–10 (log is 1 to −1). As inspection of equation D in the Supplementary material shows, outside of this range very small errors in the measured experimental fluorescence intensity lead to very large errors in log . We deliberately chose values in Fig. 2 for , , and that would place this experimentally accessible region right where the two-state approximation is at its most inaccurate.
Over this experimentally accessible range, as Fig. 2 shows, the two-state model fits this simulated protein very well indeed, despite the fact that the underlying behavior is three-state. There is a very slight upward curvature in the data points calculated from the three-state model, deviating only slightly from the straight line predicted by the two-state model. The value of R2 for the linear regression is 0.9992, not dissimilar to the values in Table 2. It is only when we look over a broader (largely experimentally inaccessible) range that we see significant deviation from the behavior predicted by the two-state model.
If this three-state model is correct, our inability to distinguish three-state from two-state behavior has some potentially serious consequences. The two-state fit over the experimentally accessible region, when extrapolated back to 0 M GuHCl, gives a value for and, hence, ΔGH2O significantly different from the correct value. Our choice of values for , , and was also intended to give values of and which closely mimic observed wild-type values. For the two state fit to the simulated three-state model shown in Fig. 2, the value of ΔGH2O is 5.3 kcal/mol, Cm is 0.84 M, and mGuHCl is 6.39 kcal mol−1 M−1, in reasonable imitation of actual values for wild-type staphylococcal nuclease. There are a wide range of values that agree with experiment as well or better than the arbitrary choices shown here, but regardless of the exact values used, the key point is that fitting a three-state unfolding to a two-state model will introduce significant error. In this particular simulation, the actual free energy difference for the equilibrium at zero molar guanidine hydrochloride between the native state and both denatured states is 4.3 kcal/mol, an error of 1.0 kcal/mol.
Yet another complication could result. Suppose the protein of interest happens to be unfolding in such a way that D1 and D2 are comparable in stability in the experimentally accessible region for equilibrium measurements, as shown in Fig. 2, and a mutation is made that perturbs the stability of either the D1 or D2 state slightly more than the other. Balanced on the cusp where their stabilities are comparable, this could shift to a denaturation with even larger amounts of D1 or to one where N denatures straight to D2. Either possibility will cause the fit of the two state model to the underlying three state reality to change dramatically, giving very different values of ΔGH2O and mGuHCl, all erroneous.
It has been suggested that the changes in slope that are the hallmark of mutations in staphylococcal nuclease result from exactly this mechanism. If this argument is correct the many published stabilities measured for mutant nucleases, most of which also have experimentally significant changes in mGuHCl, are signs of a three-state denaturation in this transition region and the values of both ΔGH2O and mGuHCl are incorrect. This criticism is frequently raised by reviewers as a reason to avoid staphylococcal nuclease as a model system for understanding changes in protein stability caused by mutation.
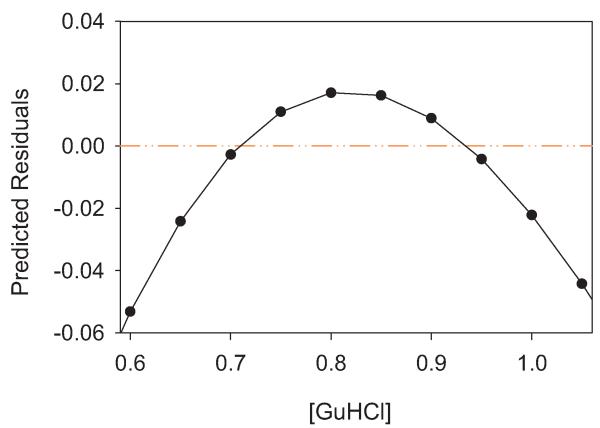
Fortunately, this model makes a testable prediction. As shown in Fig. 2, while the values of log Kapp calculated using a two-state model from the putative underlying three-state reality fit well to the linear model of the two-state model, there is a distinct upward curvature. If the experimentally derived log Kapp values are subtracted from the log Kapp values predicted by the linear two-state fit, the residuals have a downward inflection on either side of the point where the predominately denatured state shifts from D1 to D2. This “frown” is shown in Fig. 3.
Fig. 3.
Plot of residuals from a two-state fit versus a three-state model. log Kapp predicted from the two-state fit, i.e. the line in Fig. 2, minus the log values from the three-state simulation, i.e. the points in Fig. 2.
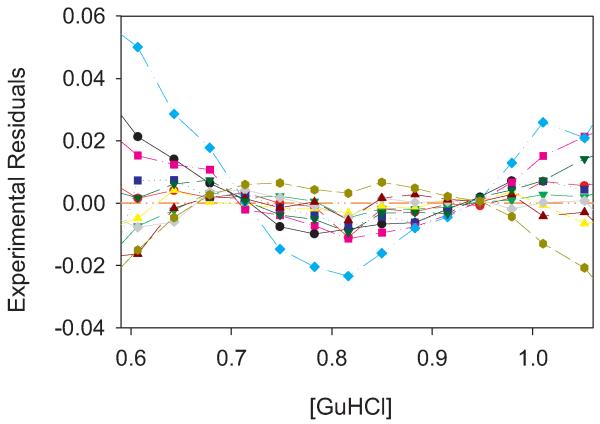
We have calculated the residuals from the 106 denaturations of wild-type staphylococcal nuclease using all five fitting methods discussed above. The fits are quite good with very low residuals. In every case, the residuals show an upward or downward curvature. Representative plots, every tenth in chronological order, of both upward and downward trending residuals are shown in Fig. 4. The lack of random scatter in the residuals indicates that there is indeed some systematic fitting error. The question is whether or not it is the fitting error discussed above. We could chose a fit with a downward curvature to argue there is an underlying three-state denaturation, or we could choose a fit with an upward curvature to make the opposite case. Clearly these small residuals are sensitive to the exact parameters of the fit and the specific of each denaturation. However, by averaging out these factors we can tease out whether there is a statistically significant overall trend.
Fig. 4.
Plot of residuals from two-state fits to experimental data. Every tenth denaturation run was selected as a representative. log Kapp predicted from the two-state fit, e.g. the line in Fig. 1b, minus the experimental log Kapp values from the three-state simulation, e.g. the points in Fig. 1b. In this particular case In was set to the maximal intensity recorded in the denaturation and Id to the minimum, but similar plots are observed for other methods of setting In and Id.
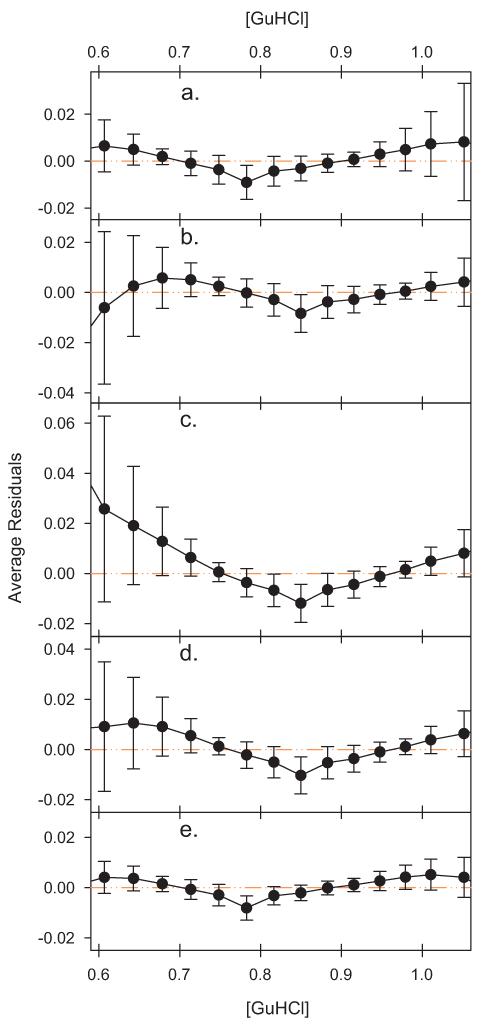
Since we habitually use standard volumes of guanidine hydrochloride addition when titrating wild-type, the residuals can be directly compared in the transition region for 102 of the denaturations. The average residual and its standard deviation at each guanidine hydrochloride concentration used in these 102 titrations are shown in Fig. 5 for each method of setting In and Id.
Fig. 5.
Plot of the average residuals. The average value of the residuals was determined for each concentration and the error bars indicate the standard deviation. Although the range of the residuals varies between Figs. 3 and 4, and the panels of this figure, in each case the scale of the y axis in terms of equilibrium units per height is constant to facilitate comparison. (a) In was set to the maximal intensity recorded in the denaturation. (b) In was set to 100.6. (c) In was set to 100. (d) In was set to the average of the intensities recorded at zero molar guanidine hydrochloride and first three guanidine hydrochloride concentrations thereafter. (e) In and Id modeled as linear functions of [GuHCl] and fit as part of a non-linear regression also fitting log Kapp versus [GuHCl].
The average residual at each concentration is fairly small in magnitude, with the highest values reached at most concentrations being in the range of 0.01 log Kapp. At the temperature of these experiments, after conversion to free energy, that corresponds to no more than and often much less than 0.01–0.02 kcal/mol difference between most experimental data points and the fitted two-state line. It should be noted that in virtually every case the average residual is within one standard deviation of zero, an absolutely perfect fit. To provide further context, a 0.1–0.2% change in fluorescence intensity is sufficient to bring most of the average experimental residuals to zero (or to double them). In terms of shape of the curves in Fig. 5 and the magnitudes of the residual, there are some differences in detail, especially for the cases were In is set unrealistically high (panel b) or low (panel c). But the general shapes of the curves are very similar.
Most importantly, as Fig. 5 shows, the average trend of the residuals is upward as one moves away from the midpoint of the denaturation, not downward, as shown in Fig. 3, and as would be expected if there were truly a three-state denaturation underlying the two-state fit. Regardless of the whether the value of In is set above the maximal level, at the maximal level, at an average value, or at the initial value the shape of the curve described by the residuals is very similar and not consistent with the predictions of the three-state model. The Santoro–Bolen fitting method adjusts the native and denatured baselines to get the overall best fit possible.
Unlike our normal fitting procedure, log Kapp is fit versus guanidine hydrochloride concentration over the entire concentration range. Despite these differences, the pattern of the residuals is very similar to the simple least squares fits. There is still an overall upward curvature for the residuals of Santoro–Bolen fitting method in the center of the plot that this fitting model cannot remove. The additional variables in the fitting model allow compensation at high and low guanidine concentrations, giving the residuals less of an upward trend. Outside the area we normally fit by least squares the residuals in two-state model fit by the Santoro–Bolen method actually trend downward. This is in line with the prediction of the three-state model, but the trend in the critical central region, where the best experimental intensity data is found, is still at odds with the predictions of the three-state model.
The magnitudes of the residuals in Fig. 5 are of interest for another reason as well. The simulation in Figs. 2 and 3 was calculated to maximize the error of the two-state fit while maintaining a correlation coefficient similar to that experimentally observed. At the lower guanidine hydrochloride concentrations shown in Fig. 3 the residuals in this simulation are not only of opposite sign, they are approximately an order of magnitude higher than the experimental residuals in Fig. 5, implying that the divergence, if any, between the fitted value of ΔGH2O and the actual value is much, much lower than the worst case scenario of one kcal/mol shown in the simulation in Fig. 2.
As noted earlier, since the residuals are not distributed as randomly one would expect from a perfect fit to the two-state model, there is clearly some systematic source of error. The question is what causes this systematic error? One source is likely something we have already explored, the fact that Id and, particularly, In are not fixed values or simple linear functions of denaturant concentration. We considered the possibility that the residuals could be affected by the value of Id. As noted earlier, higher levels of Id are generally associated with higher levels of proteolytic fragments of the protein. Comparison of the average residuals of those experiments where Id was more than a standard deviation below the average was made to those where Id was more than a standard deviation above the average. There was no significant difference in the residuals of these two populations (data not shown).
Regardless of its source, it is theoretically possible that this systematic error is obscuring the systematic error from an underlying three-state denaturation, but is it likely? It is important to remember that these residuals are very small and that the fit to the two-state model is excellent, as attested by the correlation coefficients. Regardless of the precise method used to determine Id and In, the values for ΔGH2O and mGuHCl in Table 1 are essentially identical. That two small systematic errors would interact across a wide range of guanidine hydrochloride concentrations, several variants of fitting procedure, and that the resultant would neatly cancel out the expected effect of a three-state error without any indication stretches credulity.
Previously we have shown that thermal denaturation of wildtype staphylococcal nuclease and a variety of mutants were identical within experimental error whether structural breakdown was followed by fluorescence or circular dichroism of alpha helix [20]. We concluded that this was incompatible with any model for three-state denaturation that requires significant levels of residual structure in the intermediate denatured state. Here we have shown that while there is a very slight systematic error in fitting the solvent denaturation data for wild-type staphylococcal nuclease to a two-state model, the experimental data is incompatible with the errors predicted if the protein denatured with two distinct denatured states. The analysis techniques we describe here will be applicable to other proteins as well.
5. Conclusions
The accurate calculation of a protein structure’s stability is at the heart of methods to predict structure. Development of these methods relies in part upon calibration against known structures of known stability. Staphylococcal nuclease is one of a handful of proteins with large numbers of mutations whose thermodynamic stability has been characterized. If these values were incorrect this would represent the loss of major data resource at best and a dangerously misleading set of values at worst. Fortunately, repeated experiments upon wild-type staphylococcal nuclease are not consistent with the behavior predicted by the three-state model for staphylococcal nuclease denaturation. Thus we conclude that this is not the mechanism by which wild-type staphylococcal nuclease and most mutants denature and the published stability values are reliable. A further conclusion, with wide-ranging implications, is that changes in mGuHCl values observed in staphylococcal nuclease mutants are not attributable to a three-state unfolding mechanism in most cases. In a future publication, we will show that changes in mGuHCl values upon mutation are reflected in thermal denaturation parameters.
Supplementary Material
Acknowledgments
This work was supported by NIH grant NCRR COBRE P20 RR15569. We thank Dr. Joon Song for helpful discussions regarding the statistical analysis and Bertrand García-Moreno for comments upon the manuscript. This study was completely dependent on the efforts of numerous graduate and undergraduate students who over the years produced the protein and carried out the titrations. We thank them for their careful work.
Footnotes
Appendix A. Supplementary data
Supplementary data related to this article can be found at http://dx.doi.org/10.1016/j.biochi.2013.03.003.
References
- [1].Gittis AG, Stites WE, Lattman EE. The phase transition between a compact denatured state and a random coil state in staphylococcal nuclease is first-order. J. Mol. Biol. 1993;232:718–724. doi: 10.1006/jmbi.1993.1425. [DOI] [PubMed] [Google Scholar]
- [2].Xie D, Fox R, Freire E. Thermodynamic characterization of an equilibrium folding intermediate of staphylococcal nuclease. Protein Sci. 1994;3:2175, 2184. doi: 10.1002/pro.5560031203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Carra JH, Anderson EA, Privalov PL. Three-state thermodynamic analysis of the denaturation of staphylococcal nuclease mutants. Biochemistry. 1994;33:10842–10850. doi: 10.1021/bi00201a035. [DOI] [PubMed] [Google Scholar]
- [4].Carra JH, Privalov PL. Energetics of denaturation and m values of staphylococcal nuclease mutants. Biochemistry. 1995;34:2034–2041. doi: 10.1021/bi00006a025. [DOI] [PubMed] [Google Scholar]
- [5].Eftink MR, Ionescu R, Ramsay GD, Wong CY, Wu JQ, Maki AH. Thermodynamics of the unfolding and spectroscopic properties of the V66W mutant of Staphylococcal nuclease and its 1-136 fragment. Biochemistry. 1996;35:8084–8094. doi: 10.1021/bi9530090. [DOI] [PubMed] [Google Scholar]
- [6].Wong CY, Eftink MR. Biosynthetic incorporation of tryptophan analogues into staphylococcal nuclease: effect of 5-hydroxytryptophan and 7-azatryptophan on structure and stability. Protein Sci. 1997;6:689–697. doi: 10.1002/pro.5560060318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Wong CY, Eftink MR. Incorporation of tryptophan analogues into staphylococcal nuclease: stability toward thermal and guanidine-HCl induced unfolding. Biochemistry. 1998;37:8947–8953. doi: 10.1021/bi971863g. [DOI] [PubMed] [Google Scholar]
- [8].Walkenhorst WF, Green SM, Roder H. Kinetic evidence for folding and unfolding intermediates in staphylococcal nuclease. Biochemistry. 1997;36:5795–5805. doi: 10.1021/bi9700476. [DOI] [PubMed] [Google Scholar]
- [9].Ye K, Jing G, Wang J. Interactions between subdomains in the partially folded state of staphylococcal nuclease. Biochim. Biophys. Acta. 2000;1479:123–134. doi: 10.1016/s0167-4838(00)00060-1. [DOI] [PubMed] [Google Scholar]
- [10].Maity H, Eftink MR. Perchlorate-induced conformational transition of Staphylococcal nuclease: evidence for an equilibrium unfolding intermediate. Arch. Biochem. Biophys. 2004;431:119–123. doi: 10.1016/j.abb.2004.07.023. [DOI] [PubMed] [Google Scholar]
- [11].Maki K, Cheng H, Dolgikh DA, Shastry MC, Roder H. Early events during folding of wild-type staphylococcal nuclease and a single-tryptophan variant studied by ultrarapid mixing. J. Mol. Biol. 2004;338:383–400. doi: 10.1016/j.jmb.2004.02.044. [DOI] [PubMed] [Google Scholar]
- [12].Ferreon AC, Bolen DW. Thermodynamics of denaturant-induced unfolding of a protein that exhibits variable two-state denaturation. Biochemistry. 2004;43:13357–13369. doi: 10.1021/bi048666j. [DOI] [PubMed] [Google Scholar]
- [13].Yang M, Liu D, Bolen DW. The peculiar nature of the guanidine hydrochloride-induced two-state denaturation of staphylococcal nuclease: a calorimetric study. Biochemistry. 1999;38:11216–11222. doi: 10.1021/bi9909400. [DOI] [PubMed] [Google Scholar]
- [14].Byrne MP, Manuel RL, Lowe LG, Stites WE. Energetic contribution of side chain hydrogen bonding to the stability of staphylococcal nuclease Biochemistry. 1995;34:13949–13960. doi: 10.1021/bi00042a029. [DOI] [PubMed] [Google Scholar]
- [15].Stites WE, Byrne MP, Aviv J, Kaplan M, Curtis PM. Instrumentation for automated determination of protein stability. Anal. Biochem. 1995;227:112–122. doi: 10.1006/abio.1995.1259. [DOI] [PubMed] [Google Scholar]
- [16].Schwehm JM, Stites WE. Application of automated methods for determination of protein conformational stability. Meth. Enzymol. 1998;295:150–170. doi: 10.1016/s0076-6879(98)95039-x. [DOI] [PubMed] [Google Scholar]
- [17].Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1 Unfolding of phenylmethanesulfonyl alpha-chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- [18].Carra JH, Privalov PL. Thermodynamics of denaturation of staphylococcal nuclease mutants: an intermediate state in protein folding. FASEB J. 1996;10:67–74. doi: 10.1096/fasebj.10.1.8566550. [DOI] [PubMed] [Google Scholar]
- [19].Soulages JL. Chemical denaturation: potential impact of undetected intermediates in the free energy of unfolding and m-values obtained from a two-state assumption. Biophys. J. 1998;75:484–492. doi: 10.1016/S0006-3495(98)77537-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Byrne MP, Stites WE. Thermal denaturations of staphylococcal nuclease wild-type and mutants monitored by fluorescence and circular dichroism are similar: lack of evidence for other than a two state thermal denaturation. Biophys. Chem. 2007;125:490–496. doi: 10.1016/j.bpc.2006.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Shortle D, Meeker AK. Mutant forms of staphylococcal nuclease with altered patterns of guanidine hydrochloride and urea denaturation. Proteins. 1986;1:81–89. doi: 10.1002/prot.340010113. [DOI] [PubMed] [Google Scholar]
- [22].Wrabl J, Shortle D. A model of the changes in denatured state structure underlying m value effects in staphylococcal nuclease. Nat. Struct. Biol. 1999;6:876–883. doi: 10.1038/12338. [DOI] [PubMed] [Google Scholar]
- [23].Wooll JO, Wrabl JO, Hilser VJ. Ensemble modulation as an origin of denaturant-independent hydrogen exchange in proteins. J. Mol. Biol. 2000;301:247–256. doi: 10.1006/jmbi.2000.3889. [DOI] [PubMed] [Google Scholar]
- [24].Walkenhorst WF, Edwards JA, Markley JL, Roder H. Early formation of a beta hairpin during folding of staphylococcal nuclease H124L as detected by pulsed hydrogen exchange. Protein Sci. 2002;11:82–91. doi: 10.1110/ps.28202. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.