Aβ Monomers Transiently Sample Oligomer and Fibril-like Configurations: Ensemble Characterization Using a Combined MD/NMR Approach

Abstract

Amyloid β (Aβ) peptides are a primary component of fibrils and oligomers implicated in the etiology of Alzheimer’s disease (AD). However, the intrinsic flexibility of these peptides has frustrated efforts to investigate the secondary and tertiary structure of Aβ monomers, whose conformational landscapes directly contribute to the kinetics and thermodynamics of Aβ aggregation. In this work, de novo replica exchange molecular dynamics (REMD) simulations on the μs/replica timescale are used to characterize the structural ensembles of Aβ42, Aβ40, and M35-oxidized Aβ42, three physiologically relevant isoforms with substantially different aggregation properties. J-coupling data calculated from the REMD trajectories were compared to corresponding NMR-derived values acquired through two different pulse sequences, revealing that all simulations converge on the order of hundreds of ns/replica toward ensembles that yield good agreement with experiment. Though all three Aβ species adopt highly heterogeneous ensembles, these are considerably more structured compared to simulations on shorter timescales. Prominent in the C-terminus are antiparallel β-hairpins between L17-A21, A30-L36, and V39-I41, similar to oligomer and fibril intrapeptide models, that expose these hydrophobic side chains to solvent and may serve as hotspots for self-association. Compared to reduced Aβ42, the absence of a second β-hairpin in Aβ40 and the sampling of alternate β topologies by M35-oxidized Aβ42 may explain the reduced aggregation rates of these forms. A persistent V24-K28 bend motif, observed in all three species, is stabilized by buried backbone to side chain hydrogen bonds with D23 and a cross-region salt bridge between E22 and K28, highlighting the role of the familial AD-linked E22 and D23 residues in Aβ monomer folding. These characterizations help illustrate the conformational landscapes of Aβ monomers at atomic resolution and provide insight into the early stages of Aβ aggregation pathways.

Introduction

Senile plaques are a pathological hallmark of Alzheimer’s disease (AD), a progressive, incurable neurodegenerative disease currently affecting ∼27 million people worldwide.¹ These extracellular neuritic plaques are predominantly composed of β-rich, insoluble, fibrillar deposits of amyloid β (Aβ) peptides that may be directly linked to disease symptoms by the extreme load of amyloid material they present on nearby tissues.² Aβ can also form soluble, synaptotoxic oligomers that impair memory function, now believed to be the proximate factor underlying the neurotoxic conditions of AD.^3-5

Aβ is produced by the endoproteolytic cleavage of a transmembrane protein, the amyloid precursor protein (APP), by β- and γ-secretases. Variability in the exact location of the γ-secretase cleavage site results in the production of different Aβ alloforms, ranging in length from 36 to 43 residues. The most predominant of these species are Aβ40 (∼90% of Aβ content secreted by all cells) and Aβ42 (∼10%), the latter of which is characterized by higher amyloidogenicity and toxicity.^5,6 It is the Aβ42 form that deposits first and makes up the primary component of AD senile plaques.⁷ Aβ40 and Aβ42 species demonstrate distinct mechanisms of oligomerization,^8,9 and Aβ40 inhibits the aggregation of Aβ42 monomers in a Aβ42/Aβ40 ratio-dependent manner.^10,11 The side chain of methionine 35 in both of these isoforms may be oxidized by reactive oxygen species in vivo. Oxidized Aβs have been demonstrated to comprise 10-50% of Aβ content in postmortem senile plaques.¹² The sulfoxide form of Aβ42, Aβ42-M35ox, demonstrates diminished aggregation and delayed protofibril formation compared to its reduced form¹³, with experimental aggregation kinetics ranked Aβ42 > Aβ40 > Aβ42-M35ox.¹⁴ M35-oxidation abolishes Aβ42’s characteristic paranuclei formation and results in the assembly of oligomers indistinguishable from those formed by Aβ40.^15,16 Further, oxidation of the M35 side chain to sulfoxide induces Aβ40-like changes in structure and dynamics of the V18 and C-terminal region compared to reduced Aβ42.^17,18 The processes underlying the drastic changes induced by this chemical modification are not yet fully understood at the atomic level.

The mechanisms by which the different Aβ variants form these fibrils and oligomers also remain poorly understood. In order to discern these aggregation pathways, knowledge of the biophysical properties of the various starting and intermediate conformers is crucial. These include Aβ monomers, which, despite being nontoxic themselves,^19,20 represent a building block common to the complex scheme of Aβ aggregation mechanisms, including those that yield aggregates "on pathway" to fibril assembly as well as "off pathway" conformers.²¹ Aβ monomers have been observed to interact with higher order oligomers⁸ and fibrils²² and directly form aggregation nuclei and pathogenic dimers.²³ One of the fundamental strategies among current efforts to develop AD therapeutics involves protecting nontoxic Aβ monomers from aggregation into toxic species.²⁴ A clear definition of the biophysical properties of Aβ monomers may be decisive in our efforts to understand and influence the Aβ self-assembly processes implicated in the etiology of AD. However, Aβ is part of a class of proteins known as intrinsically disordered proteins (IDPs) that fail to adopt a stable native state under physiological conditions.²⁵ IDPs like Aβ pose a significant challenge to the structural biology community because their plasticity typically precludes the use of traditional techniques for structure determination. Further, while most proteins are understood in terms of a single native state, the structural properties of IDPs must be evaluated as an ensemble composed of many states.

Although experimental knowledge about Aβ monomer structure is sparing at best, there is evidence suggesting the importance of key regions in Aβ folding and aggregation. Solution NMR reveals an ensemble that does not fold into a unique conformation in an aqueous solution and is primarily characterized by collapsed coil structure;^26,27 however, backbone Hα, Cα, and Cβ chemical shift indices indicate β-strand propensities in the central hydrophobic cluster (CHC, L17−A21), I31−V36, and V39-I41, as well as turn character in D7-E11 and F20-S26 in Aβ42.¹⁴ These secondary structure inclinations (except V39-I41) are significantly reduced upon M35 oxidation.¹⁴ Circular dichroism (CD) spectra further suggest substantial β content in Aβ40 monomers (∼24%).²⁸ When co-incubating Aβ40 fragments with the full length peptide, only the fragments containing residues 17-20 or 30-35 enhanced fibrilization rates.²⁹ Further, proline mutations of residues in these regions more thoroughly disrupt fibrilization than mutagenesis in certain positions of the 21-30 region or the N-terminus in both Aβ40 and Aβ42.^30-32 Finally, NMR relaxation data reveals that Aβ42 demonstrates more rigidity at the C-terminus than Aβ40.³³ These results suggest that the CHC and C-terminus are critical toward self-assembly.

Further studies reveal the importance of the central region in Aβ folding. The A21-A30 fragment is resistant to proteolysis, while solution NMR of this fragment reveals V24-K28 adopts a turn-like structure that is suggested to nucleate folding of the monomer.³⁴ Replacement of pairs of residues in the 24-27 region with a D-ProGly motif largely accelerated fibril self-assembly of Aβ40.³⁵ Additionally, while hydrogen/deuterium (HD) exchange data acquired with mass spectrometry on the minutes timescale suggest that Aβ monomers are almost completely solvent accessible (indicative of highly flexible dynamics),³⁶ similar data on the 100 millisecond timescale obtained through the CLEANEX-PM pulse sequence reveal that the G25-G29 region is particularly susceptible to solvent exchange in free Aβ40.^37,38 Finally, amino acid substitutions that change E22 or D23 to non-ionized or positively ionized residues have been linked to familial AD (FAD) and cerebral amyloid angiopathy (CAA), as well as increased Aβ40 oligomerization orders or fibrilization rates in vitro.³⁹ Further, the oligomerization propensity of these mutants has been correlated to both susceptibility to trypsin proteolysis and the magnitude of destabilization of the V24-K28 turn region in the Aβ(21-30) fragment.⁴⁰

Due to the experimental limitations inherent in studying these flexible, polymorphic peptides, several groups have turned to computational simulations to comprehensively investigate the biophysical properties of Aβ monomers. A number of simulation papers for these systems have been published, each using different simulation parameters and strategies. The most recent and exhaustive of these simulations include Monte Carlo simulated annealing with implicit solvent,⁴¹ 225 ns/replica all-atom REMD simulations with explicit solvent,⁴² 700-900 ns/replica HT-REMD simulations with the OPEP coarse grain force field and implicit solvent,⁴³ 100 ns multiple-reservoir replica exchange simulations with explicit solvent,⁴⁴ and 200 μs cumulative all-atom MD simulations in explicit solvent using the Folding@home platform.⁴⁵ The results for these simulations and others in the field, however, are highly divergent. For example, Mitternacht and coworkers⁴¹ report high β-sheet content, with ∼40% of the Aβ42 residues adopting significant (>40%) β-sheet probability. Sgourakis et al.^42,46 and Cote et al.⁴³ both report Aβ ensembles with mostly random coil structure, very little α-helical content, and some β-sheet content; however, the first two of these papers present structures with hairpins primarily at the CHC and C-terminus while the latter study places this β content almost exclusively at the N-terminus. (Further analysis of the simulations described by Sgourakis et al.⁴² does, however, reveal significant β character within the first 6 residues (unpublished data)). Ball et al.⁴⁴ and Lin et al.,⁴⁵ in contrast, describe mostly disordered Aβ ensembles with significant α character in residues 10-21 and little to no β content. Variation between these studies may arise from changes in force field and simulation parameters, insufficient sampling, and disparities in trajectory analysis. The dramatic differences between these studies further emphasize the need for sensitive experimental validation. Here, we will extend the MD/NMR methodology (already described in previous investigations by our lab^42,46) to optimize simulation validation and accuracy with a more comprehensive set of NMR observables.

In this study, we employed a combined MD/NMR approach toward investigating the structural ensembles of the three physiologically relevant Aβ monomer species: Aβ40, Aβ42, and Aβ42-M35ox(S), the latter of which has not, up until now, been investigated through MD simulation. Employing a REMD protocol with similar parameters to the simulations by Sgourakis and coworkers⁴⁶ that produced good correlation to experimental data, we observe that long simulation times on the order of hundreds of ns/replica are required to reach convergence. This is the first study to sample Aβ extensively on the μs/replica timescale using unbiased, all-atom, explicitly solvated REMD simulations. Our simulation data is validated by quantitative comparison of calculated three-bond J-couplings and residual dipolar couplings (RDCs) with their experimental counterparts. These NMR data are derived from a single set of resonances that almost entirely (>90%) represent the monomeric state in solution.⁴⁷ To our knowledge, we present the most complete sets of ³J_HNHA couplings for these Aβ monomers, supplemented and validated through acquisition by two different pulse sequences (HNHA⁴⁸ and J-resolved SOFAST-HMQC⁴⁹).

Although our simulations reveal that all three species share similar regional organization and secondary structure tendencies, we have identified key differences in tertiary structure and hydrogen bonding patterns that may underlie the differential aggregation rates between these Aβ isoforms. Among the diverse set of topologies sampled by Aβ, our data reveal that there is a substantial proclivity to adapt β-hairpins encompassing the CHC and 30-36 in all 3 species. Further, residues 39-41 in Aβ42 and Aβ42-M35ox(S) contribute to additional β-hairpin motifs absent in Aβ40. Contact maps and hydrogen bond populations suggest prevalent sampling of a β-meander composed of three antiparallel strands (CHC, 30-36, and 39-41) in Aβ42. Reduced sampling of this motif by Aβ42-M35ox(S) in favor of increased contact between CHC and 39-41 may be responsible for the decrease in aggregation propensity of this form. The transiently-sampled β topologies of Aβ40 and Aβ42 are comparable to hypothesized intramolecular models for fibrils and “on-pathway” intermediate oligomers;^50-53 they expose hydrophobic side chains to solvent and may serve as hotspots for self-association. These β structures are also the slowest to converge in our simulations, which may explain their absence in other computational studies that rely on characterizations made on shorter timescales. We also observe that V24-K28 forms a persistent bend motif in all three species that is directly nucleated by buried backbone to side chain hydrogen bonds with D23 and further stabilized by a long distance salt bridge between E22 and K28. This observation provides insight into the role of the side chain identities of FAD-linked E22 and D23 in Aβ monomer structure. This study has yielded rigorous, experimentally-consistent representations of three different intrinsically disordered Aβ monomer ensembles, allowing us to identify key structural features and properties that may serve as determinants of Aβ self-assembly.

Results

Validation with Experimental Results

³J_HNHA Couplings

Here, we present a comprehensive set of ³J_HNHA values for Aβ monomers, acquired using two different NMR pulse sequences, HNHA⁴⁸ and J-resolved SOFAST-HMQC⁴⁹, that are in close agreement with each other (r² > 0.8 for all three species). ³J_HNHA couplings derived from backbone ϕ dihedrals in the simulation data are compared to these experimentally determined values, as described in the Methods section, in order to validate local backbone conformations in the simulation.

Appropriate values for the Karplus equation are required for this validation. Table 1 illustrates both the correlation and RMSD between production period values and experiment using different sets of Karplus parameters, namely the sets proposed in Vuister et al.⁴⁸ and Sgourakis et al.⁴² respectively, as well as sets determined from least square minimization of the RMSD between the simulated and experimental sets over the production period. This fitting is done to account for motional averaging effects within our trajectories that may not be represented by parameter sets determined by fitting to well-ordered X-ray structures, such as Vuister et al.’s parameter set⁴⁸; this approach was taken in a number of other studies.^42,46 In general, we calculate good agreements between experiment and simulation no matter which parameter set we choose, with the Pearson correlation coefficient (PCC) ranging between 0.5-0.6 for Aβ42, 0.7-0.8 for Aβ40, and 0.4-0.5 for Aβ42-M35ox(S). Further, we observe that the RMSDs are significantly reduced by fitting, while overall PCCs are consistent among the three parameter sets, with the exception of the best fit Aβ42 set, which represents a small increase in PCC over the other unfitted sets.

TABLE 1.

PCC and RMSD between experimental and calculated J-coupling constants. For each parameter set and species, PCC and RMSD are calculated between the computational data and experimental data set 1 (derived from HNHA experiment, colored in dark blue), experimental data set 2 (derived from the J-resolved SOFAST-HMQC experiment, colored in light blue), and the weighted average of these two sets (bolded). The “Best Fit” parameters are the Karplus parameters that minimize RMSD between experimental and computational values; they are explicitly listed in the Methods section.

Parameter Set	Vuister et al.1		Sgourakis et al.2		Best Fit
	PCC	RMSD (Hz)	PCC	RMSD (Hz)	PCC	RMSD (Hz)
Species
Aβ42	0.43 0.48 0.50	1.25 1.25 1.21	0.43 0.47 0.49	0.85 0.92 0.82	0.51 0.57 0.58	0.68 0.78 0.66
Aβ40	0.79 0.71 0.76	1.37 1.23 1.29	0.79 0.71 0.75	0.91 0.83 0.83	0.75 0.72 0.75	0.58 0.60 0.54
Aβ42-M35ox(S)	0.41 0.52 0.49	1.10 1.06 1.06	0.41 0.52 0.49	0.75 0.67 0.67	0.41 0.52 0.49	0.67 0.58 0.57

Figure 1a monitors the agreement between the MD-derived J-couplings and the average of the two experimental data sets and as a function of simulation time over 20 ns/replica blocks. For all three simulations, there is an initial phase where the agreement with experiment generally increases with increased sampling, followed by a steady-state phase wherein oscillations in the agreement around an equilibrium value are maintained. This equilibrium value is estimated as the average PCC value of all of the 20 ns/replica blocks in the production time period; this is consistently smaller than the PCC obtained when the entire production period is considered for each species (such as those reported in Table 1) by ∼0.07-0.10. The duration of the initial phase described above differs for each simulation and is used as an indicator of the time required for simulations to converge, as is discussed in the Methods section.

Figure 1.

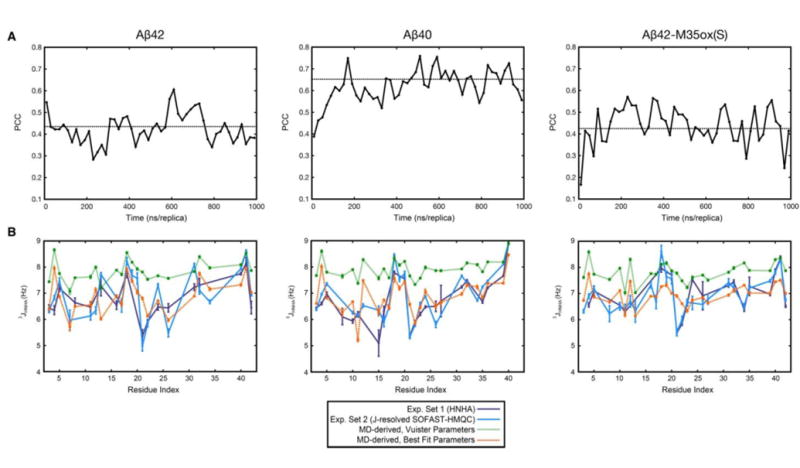
Validation with ³J_HNHA couplings. a) Pearson’s correlation coefficient between simulated ³J_HNHA couplings (using Vuister parameters⁴⁸) and the weighted average of the corresponding experimental values as a function of simulation time for all 3 species. J-couplings were calculated over 20 ns/replica blocks, as discussed in the Methods section. The broken line illustrates the average PCC value of the blocks over the production period. b) Direct comparison of simulated ³J_HNHA couplings calculated over the production period with their experimentally-determined counterparts for all 3 Aβ species, shown as a function of residue number. Best fit Karplus parameters A, B, and C are given in the Methods section. Glycines are not included due to experimental ambiguity.

Figure 1b directly superposes the J-coupling values calculated over the production period (the 400-1000 ns time segment for each of 7 replicas at temperatures 289.2-310.7 K) of the simulations onto the two experimental data sets used for the comparisons above. When using Vuister et al.’s parameter set⁴⁸, backcalculated ³J_HNHA couplings are universally too high, except in β-dominant residues (ie, V18, V39-I41), which may suggest oversampling of β-conformations in our ensemble. In contrast, with fitted parameters, for all 3 species, we observe, in general, that the average value and range of the J-couplings match. In both cases, variations along the sequence agree very well. Dramatically outlying residues – that is, locations in which the experimental average and fitted MD-derived J-coupling differ by more than 1 Hz – include: {F4, H13, A21} in Aβ42, {F4, A21} in Aβ40, and {F4, A21} in Aβ42-M35ox(S) (Supplemental Figure 1). It is interesting to note that residue A21 appears to be a consistent outlier among studies that use comparison of ³J_HNHA to validate computational ensembles for Aβ monomers^41-44,46, suggesting that there is a systematic difference in this region that has not yet been mitigated by different force field choices.

As an alternative to fitting the parameters of the Karplus equation, the contributions of centroid structures representing each of the MD ensembles were fit to produce a weighted average of ³J_HNHA couplings backcalculated with the Vuister set⁴⁸ with minimal RMSD to experimental values; however, we found that this fitting did not substantially improve agreement (Supplemental Figure 2). An extra parameter to this fit representing a “random coil centroid” (with ³J_HNHA equal to the average of all experimental ³J_HNHA for all residues, 6.8-6.92 Hz) was also considered. The results of these fits exhibited two possible behaviors: either the RMSD would be minimized to a local minimum where the resulting fit did not change appreciably from the case where “random coil” population was not considered, or the random coil population would significantly dominate the weights of all of the other natural centroids, lowering the average ³J_HNHA and reducing RMSD (toward lower minima near an ensemble of 100% random coil: {Aβ42, Aβ40, Aβ42-M35ox(S)} = {0.77 Hz, 0.80 Hz, 0.66 Hz}) at the cost of significantly reducing both the variability of the curve and the PCC to experimental values (data not shown).

The values for hitherto unpublished experimental J-couplings (Supplemental Table 1), as well as experimental validation using ³J_NHB couplings (Supplemental Figure 3) and residual dipolar couplings (RDCs) (Supplemental Figure 4) are presented in the Supporting Information.

Secondary Structure

Figure 2a illustrates the secondary structure propensity for each of the Aβ species averaged over all production period structures for all residues, as determined by the DSSP^54,55 program. All 3 ensembles possess similar overall secondary structure distributions. In terms of β propensity, the ranking is Aβ40 > Aβ42 > Aβ42-M35ox(S), with other secondary structures like coil and bend compensating for the difference between these species, though we note that the experimental ³J_HNHA couplings suggest that the content of β character should be similar for all three alloforms. These compositions, in general, compare well to values for monomeric Aβ40 as determined by a recent CD experiment (8.7% α-helix, 24.0% β-sheet, 67.3% statistical coil),²⁸ though the composition of α-helix is underestimated. As discussed in the Methods section, hundred ns/replica timescales or larger are necessary to reach steady state values for secondary structure composition. Figure 8b illustrates that the β content is the slowest to converge, which may explain why other computational studies report lower values.

Figure 2.

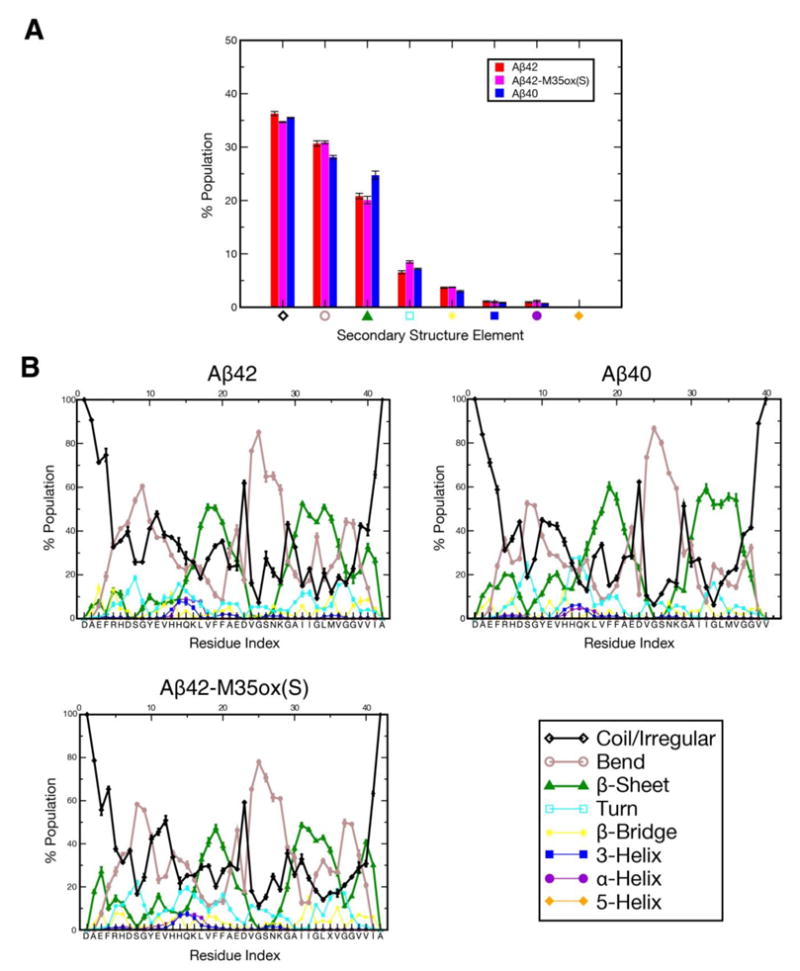
Percent composition of secondary structure as determined by DSSP^54,55 for each of the three Aβ species, averaged over the production ensemble a) over all residues and b) as a function of residue index. Of particular importance are the three dominant secondary structure elements in the ensemble, denoted with thicker lines in the graph: coil/irregular in black, bend in grey, and β-sheet in green.

Figure 8.

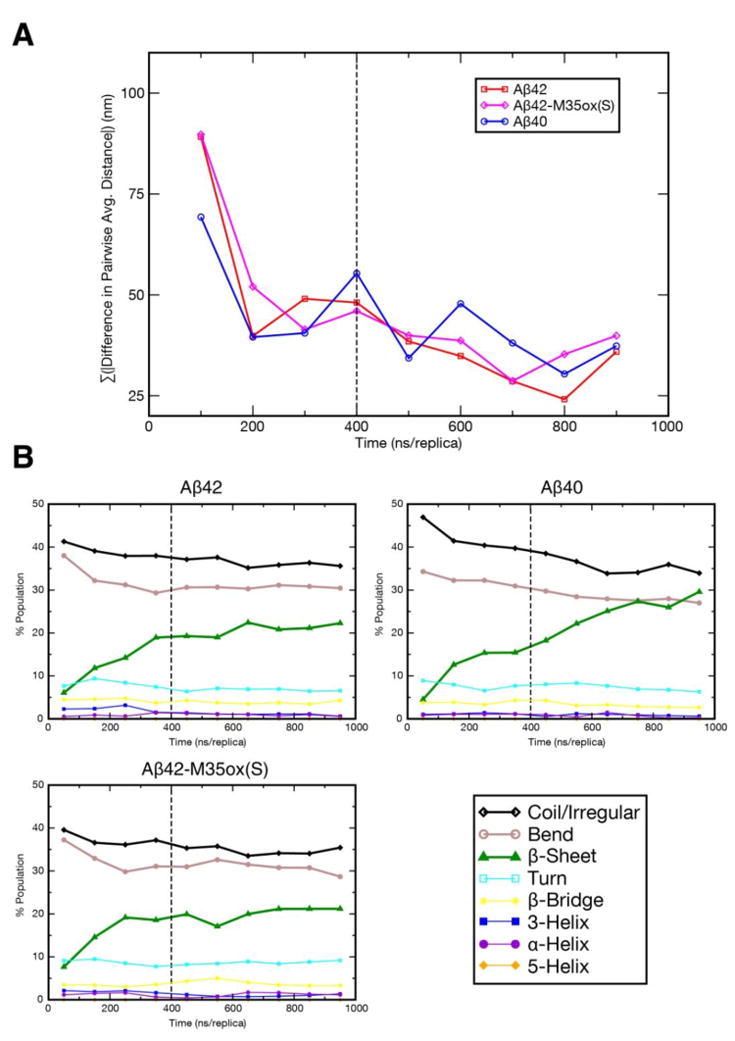
Equilibration of REMD trajectories as gauged by: a) Cα average distance maps over 100 ns/replica windows. Each point on the graph represents the difference in the sum over the absolute value of distance for all coordinates between the current 100 ns/replica interval and that of the previous interval. b) content of each secondary structure element as determined by DSSP^54,55 over 100 ns/replica windows. Coil/irregular, bend, and β-sheet denoted with thick lines.

Illustrated in Figure 2b are the ensemble-averaged secondary structure populations per residue for each Aβ isoform. Prominently, all species are similarly characterized by robust β propensity in residues 17-21 (the central hydrophobic cluster (CHC)) and 30-36, as well as very pronounced bend character in residues 24-28, indicating the sampling of a β-hairpin like motif. In terms of both β and bend character in these regions, the ordering is Aβ40 > Aβ42 > Aβ42-M35ox(S). Aβ42 and Aβ42-M35ox(S) also possess substantial β character in V39, V40, and I41 separated by a bend centered around glycines 37-38, suggesting a second β-hairpin topology between the residues 30-36 and 39-41 in these species. The N-terminus is generally disordered, but can be characterized by up to ∼30% β character in certain regions in Aβ42-M35ox(S). α-helical character is virtually non-existent, except some minor populations at residue 13-17 (with Aβ42 > Aβ42-M35ox(S) > Aβ40). Other regions of strong bend/turn character in Aβ40 include residues 6-9 and 14-16. These observations match the positions of β proclivity inferred by chemical shift indices¹⁴ and the position of the 24-28 turn region that nucleates monomer folding described by NMR.³⁴ Regions strongly characterized as bend or turn here correlate well with fast HD exchanging regions in Aβ40, while those strongly affiliated with β character in our simulations generally undergo slower exchange.^37,38 The 18-20 and 39-41 (in Aβ42/42-M35ox(S)) regions annotated as β-dominant by DSSP also coincide with regions of high experimental ³J_HNHA (> 7.5 Hz) (Figure 1b), further validating these characterizations.

Tertiary Structure

Contact Map Analysis

The Cα contact map analysis in (Figure 3, upper corner) illustrates a characteristic pattern shared by the equilibrated Aβ populations, wherein structures adopt three regions: N-terminal (residues 1-20), central (residues 21-30), and C-terminal (residues 31-40/42). Intra-region contacts are ample for all 3 regions, except the C-terminus in Aβ40. While the N-terminal and C-terminal regions have close mutual contacts, interactions between the central region and the other two regions are significantly limited, except at the very extreme N-terminus (residues 4-6). The restriction of this central region from the rest of the protein corresponds to the fact the composite residues align with a bend-dominated population bridging two β-compatible regions (as shown in Figure 2).

Figure 3.

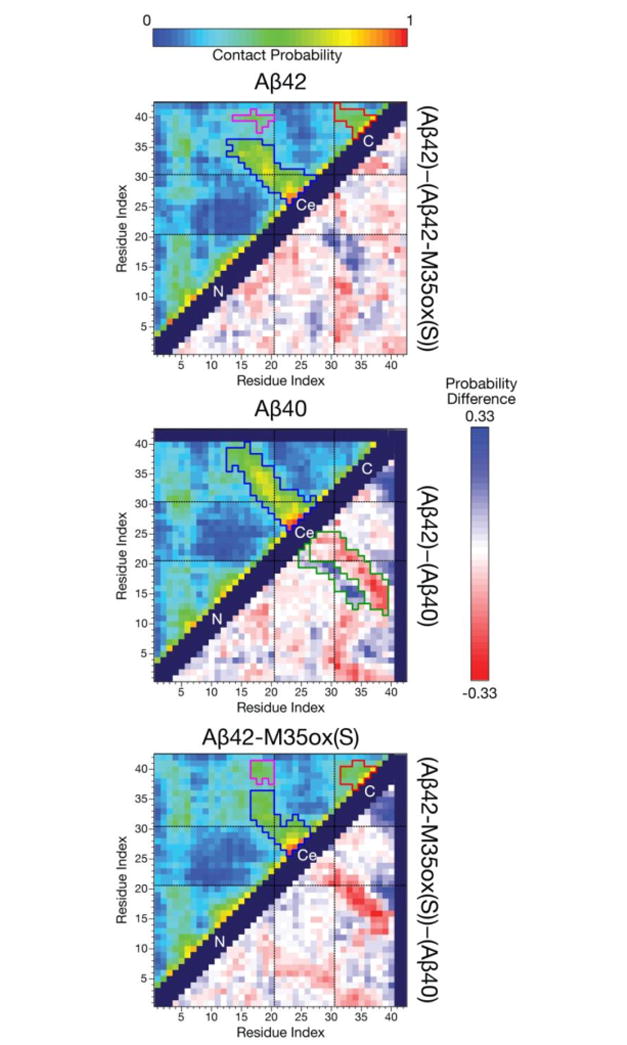
(upper corner) Maps illustrating the probability of contact over the production ensemble for each of the three Aβ species. Here, two residues are defined to be in contact if their Cα- Cα distance is ≤ 8 Å⁹³. Regions are demarcated with black dashed lines (N = N-term., Ce = central, C = C-term.), and contact blocks on the map are segmented by contact probability: blue corresponds to contacts associated with the CHC to 30-36 hairpin, red corresponds to contacts associated with the 30-36 to the 39-41 hairpin, while magenta corresponds to CHC to 39-41 contacts. (lower corner) Difference between these contact probability maps for each pair of Aβ isoforms. A red color indicates a reduced likelihood of contact while a blue value indicates increased contact probability for the minuend species compared to the subtrahend species. The register shift in contacts between Aβ40 and Aβ42 are segmented in green on that difference map. Self or sequential contacts, such as between (i,i), (i, i+1), and (i, i+2), and invalid squares on the map were not computed and are represented by the dark purple regions.

Robust anti-diagonal contacts exist between 15-25 and 27-39 for Aβ40 and are particularly well-populated between 16-20 and 30-35, indicative of antiparallel β hairpin interactions between these regions. Similar antiparallel contacts also exist in Aβ42, but occur between residues 15-25 and 27-36, representing a truncation of the C-terminal partner compared to Aβ40. Aβ42 possesses a second set of anti-diagonal contacts that occur between 31-36 and 37-41. This suggests a second β-hairpin motif between these residues. Difference contact maps (Figure 3, lower corner) further reveal a register shift in the antiparallel contacts in Aβ40 versus Aβ42 among the first β-hairpin motif, with residues in the CHC contacting residues further C-terminal in Aβ40. These two sets of Aβ42-like antiparallel contacts exist but are less robust in Aβ42-M35ox(S), and the pattern of cross-central domain contacts seems to follow the Aβ40 register in terms of contact partners. Conversely, there are greater contact probabilities observed between the CHC and the 39-41 region in Aβ42-M35ox(S) compared to Aβ42. In tandem with the secondary structure characterization of these regions, this suggests the oxidized form adopts alternate CHC to 39-41 β contacts that compete with the sampling of the aforementioned β-meander that is prevalent in the reduced form. Finally, in all simulations, residues 4-6 readily contact the rest of the protein, including the central region.

Notably, there is a much smaller difference between the ensembles in how the N-terminal half of the protein interacts with itself compared to how the C-terminus acts with itself and the rest of the protein. This matches the observation that only C-terminal residues have significant chemical shift differences when comparing the respective ¹H-¹⁵N HSQCs for each alloform.¹⁸ Further, while the dissimilarities between ensembles noted here may serve as key structural hallmarks for distinguishing Aβ species, it is important to emphasize that these differences are relatively subtle, with no average pairwise distance between Cα atoms changing by more than 0.57 nm (0.33 nm excluding residues 38-42) between any two of the ensembles, also in accordance with subtle changes in ¹H-¹⁵N HSQC patterns between the species.

Electrostatic Interactions

The most commonly populated long distance backbone hydrogen bonds between the CHC and the C-terminal regions reveal a shift in register between species (Supplemental Table 2). Prevalent in Aβ42 is a register defined by hydrogen bonds between V18/G33 and F20/I31, while Aβ40 has a dominant bonding register defined by hydrogen bonds between V18/M35 and F20/G33, yielding a shift of 2 residues for the C-terminal partner between the two species (illustrated schematically in Figure 4). Described above are the preferred registers for these systems, but other cross-hairpin bonds outside the register are possible (even substantially populated) due to the intrinsic flexibility of the system. However, these register hydrogen bonds are surprisingly well-populated for a disordered system, reaching populations up to ∼30% of the ensemble. Notably, this Aβ40 pattern exactly matches the register of the affibody-trapped monomeric Aβ40 hairpin solved with NMR by Hoyer et al.⁵⁶ (PDB: 2OTK). Further, the side chain contacts in the intramolecular model of Aβ40 fibrils proposed by Bertini et al.⁵³ are analogous to the backbone hydrogen bonding of this hairpin model; both models are related by a 90 degree rotation about the axes of both β strands. Aβ42 is also characterized by high hydrogen bond populations between residues A30/G37 and L34/V41, suggesting a second hairpin structure. This double beta hairpin structure is comparable to the intrapeptide topology for a toxic Aβ42 oligomer proposed by Ahmed et al.⁵² Consistent with reduced hairpin content, Aβ42-M35ox(S) is characterized by significantly weaker cross-region interactions. Interestingly, between the Aβ40 and Aβ42 registers, Aβ42-M35ox(S) shows a slight bias toward the Aβ40 pattern, however, this may not be significant given the meager populations of the bonds involved and frequent contradictions to the pattern. The A30/G37 and L34/V41 interactions are also depleted for this system, while long-range interactions with the C-terminus such as K16/V41 and A30/V41 are more populated. This supports the idea that Aβ42-M35ox(S) more frequently samples alternate binding patterns that compete with the Aβ42-like double hairpin. Finally, it is important to emphasize that, while the models proposed in Figure 4 are based on ensemble-based secondary structure and hydrogen populations, they also match actual representative centroid structures sampled during the simulations (discussed in the RMSD-Based Clustering subsection), such as the third and fourth centroid of Aβ40 and the eighth centroid of Aβ42.

Figure 4.

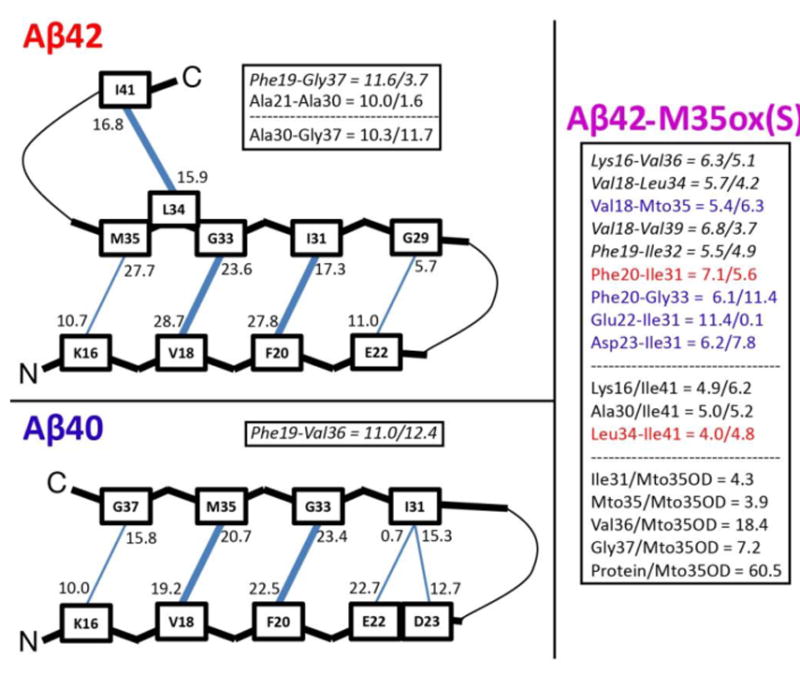
Schematics illustrating hypothetical β-hairpin backbone hydrogen bonding patterns for Aβ42 and Aβ40, based on the most populated cross-region backbone hydrogen bonds, as well as secondary structure characterizations. The donor-acceptor and acceptor-donor populations of these hydrogen bonds are listed such that the number is closest to the donor residue of that bond. If two residues are connected such that both hydrogen bonds between them are populated more than 15%, the line between them is bolded in the figure. Well-populated bonds (>10%) that don’t fit into the schematic are listed as (% donor-acceptor/acceptor-donor); those that don’t fall into register are italicized. Prominent cross-region backbone-backbone and backbone-Mto35OD hydrogen bond populations for Aβ42-M35ox(S) are also listed. Here, blue coloring indicates bonds that match the Aβ40 register, while red coloring indicates bonds that match the Aβ42 register.

Charge-altering substitutions in E22 and D23 implicated in FAD result in increased Aβ40 oligomerization order and fibrilization rates,³⁹ linked to destabilization of a turn in the Aβ(21-30) fragment.⁴⁰ Observation of the interactions involving the side chains of these residues in our monomer simulations (Table 2) indicates that D23 often forms side chain to backbone hydrogen bonds with each of the amides of residues V24 through K28, with certain populations exceeding 60% of the ensemble in Aβ40. These interactions are very prevalent in all three simulations with a general ordering Aβ40 > Aβ42 > Aβ42-M35ox(S), correlating to the DSSP-annotated bend character for this region. E22 frequently samples a salt bridge with the side chain of K28 across the bend region; this interaction is significantly more populated in Aβ40 and Aβ42-M35ox(S) (20% and 18% respectively) than Aβ42 (9%), inversely correlating with the aggregation proclivity of the species. Direct observation of V24-K28 turn in hairpin-forming centroid structures of Aβ40 (Figure 5) suggest that the amide groups of the turn point inward to form the aforementioned hydrogen bonds with a buried D23 side chain, exposing all of the negatively polarized carbonyl groups of the turn to solvent. The electrostatic interactions involving D23’s side chain are likely to be essential toward establishing bend structure in this region, while the long range salt bridge formed by E22 and K28 is also likely to be important toward both burying D23 and stabilizing this motif. These results are thus consistent with the observation that FAD mutations of these residues to nonpolar or positively ionized side chains disrupt turn structure in this region.

TABLE 2.

Central region electrostatic interactions involving side chains E22 and D23. Highly populated interactions involving the side chains of E22 and D23 in the central region are listed here. Listed populations represent average bond frequencies for equivalent atoms in the side chain (for example, “ASP23O_γ” is the average of interactions involving the ASP23O_γ1 and ASP23O_γ2 atoms).

Donor – Acceptor Atoms	% in Aβ42 Ensemble	% in Aβ40 Ensemble	% in Aβ42-M35ox Ensemble
Hydrogen Bonds
VAL24HN – ASP23Oγ	27.70	31.71	24.87
GLY25HN – ASP23Oγ	56.61	61.15	50.93
SER26HN – ASP23Oγ	58.69	65.38	53.56
SER26HOγ – ASP23Oγ	32.43	32.43	37.29
ASN27HN – ASP23Oγ	31.43	36.00	29.41
LYS28HN – ASP23Oγ	17.41	24.69	17.68
Salt Bridges
LYS28Hζ – GLU22Oδ	9.03	20.26	17.52
LYS28Hζ – ASP23Oγ	3.67	2.25	4.25

Figure 5.

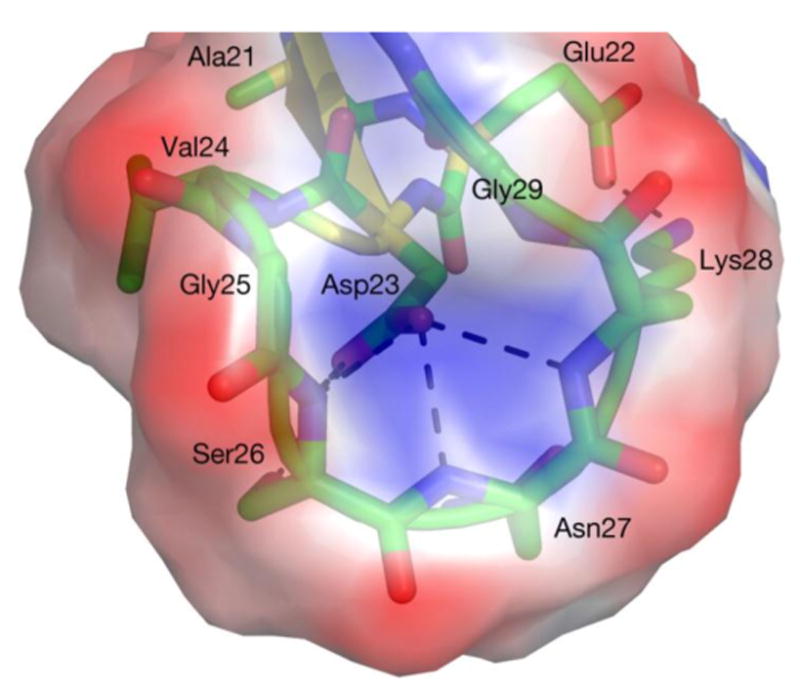
Central region (A21-G29) in Aβ40’s third most populated centroid after single linkage clustering (see Figure 6). For all three alloforms, the side chain of D23 is buried and forms hydrogen bonds with the inwardly pointing backbone amide groups of V24-K28 with very high fidelity (some bonds present in >60% of the Aβ40 ensemble), while E22 forms a persistent salt bridge with K28 (present in ∼20% of the ensemble). This motif presents a negatively charged external surface created by radially exposed backbone carbonyl groups and D23’s side chain, with a central indentation of positive charge aligning with the backbone amide groups. The electrostatic surface was calculated with ABPS⁹⁵ and PDB2PQR^96,97 using default parameters. Figure rendered in Pymol⁹⁸.

RMSD-Based Clustering

Representatives of the populations for each Aβ variant are depicted in Figure 6, revealing conformations that are topologically diverse but nonetheless share several common structural motifs. Although both mostly random coil and partially β-structured conformations are observed, all of the centroids are collapsed. The central region (residues 21-30) aligns with yellow in the rainbow spectrum coloring of the backbone ribbon; as expected from the previous analyses, this region is consistently isolated from the rest of the protein and characterized by loop structure. The C-terminal region (in orange) frequently folds back on the rest of the protein to interact with N-terminal region residues in all three species, particularly at the CHC (in green) to form an antiparallel β-hairpin. Indeed, the centroids are almost exclusively represented by a mixture of loop and β secondary structures, with α character very rare. It should be further noted that, even with single linkage clustering scheme using a relatively large 2.0 Å cutoff, only 30-50% of the structures of the production period are represented by the top 10 centroids for all 3 species, indicative of highly diverse simulated ensembles.

Figure 6.

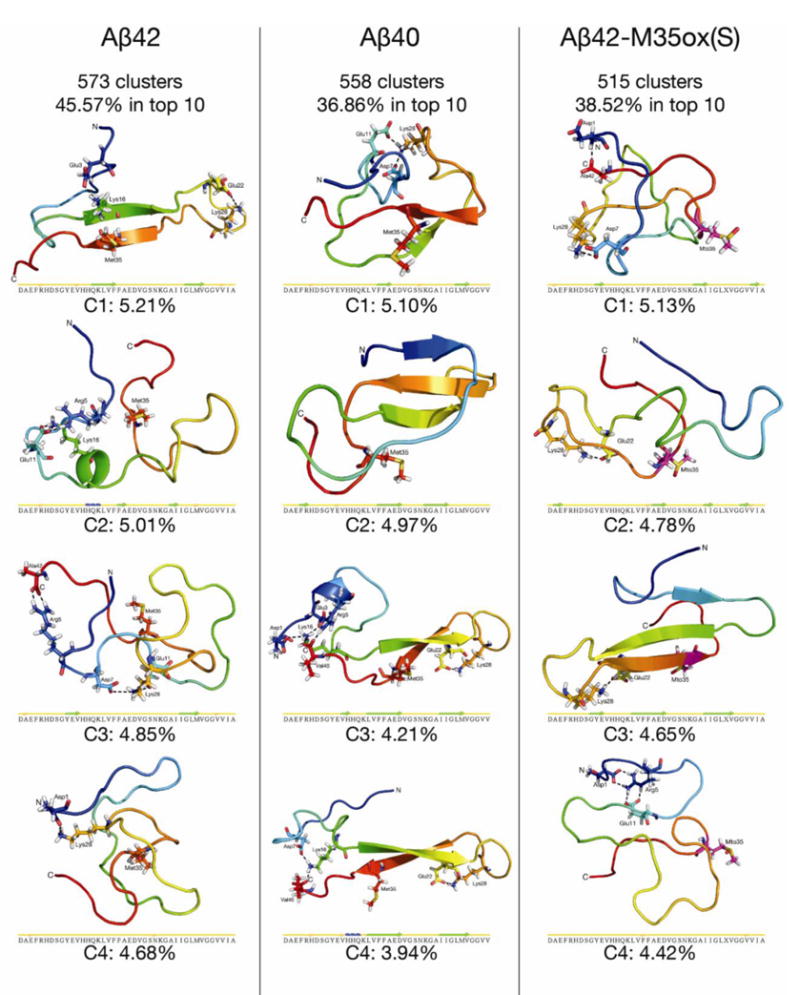
The four highest-populated centroids from single linkage cluster analysis⁹⁰ around Cα atoms with an RMSD cutoff of 2.0 Å for each Aβ isoform over the production period. Mto = L-methioinine-(S)-sulfoxide. Ribbons are colored by a blue-to-red rainbow spectrum from the N-to-C terminus. Met/Mto 35 and residues involved in long-distance ionic networks are explicitly shown, and Mto 35 is explicitly colored in magenta. Secondary structure strips for each centroid, as calculated by STRIDE,⁹⁹ are also shown. Figure rendered in Pymol⁹⁸.

Aβ40’s third and fourth centroid, together representing 8.15% of the ensemble, each possess a nearly identical extended C-terminal β hairpin topology (residues 16-35 have a Cα RMSD of 0.583 Å). This topology is similar to the affibody-trapped Aβ monomer hairpin solved by Hoyer and coworkers.⁵⁶ Cα RMSD of residues 16-35 between the third and fourth centroid structure and this NMR-derived conformation are 2.810 Å and 2.718 Å, respectively. Indeed, 13.3% of the entire Aβ40 REMD ensemble has a Cα RMSD ≤ 3Å compared to this NMR structure for this region (Supplemental Figure 5). Further, these two centroids both possess cross-region hydrogen bonds between V18/M35, F20/G33, E22/I31(donor/acceptor), and D23/I31(acceptor/donor) characteristic of the Aβ40 bonding register derived from ensemble hydrogen bond populations.

Aβ42’s most populated centroid also represents an extended β-hairpin, this time possessing long distance hydrogen bond pairs for K16/M35 and V18/G33 characteristic of the Aβ42 ensemble hydrogen bonding register. A double hairpin between the CHC, the 31-36 region, and residues 39-42 is directly observed in Aβ42’s eighth centroid (representing 4.33% of the ensemble, Supplemental Figure 6a) as well as the two Aβ42 centroids with backcalculated ³J_HNHA values that have the highest PCC and lowest RMSD, respectively, to the average experimental J couplings (Supplemental Figure 6b). In all three of these conformations, the first hairpin has similar K16/M35, V18/G33, and F20/I31 backbone hydrogen bond pairs, while the second hairpin is stabilized by a pair of L34/V41 hydrogen bonds; the bonds and secondary structure align well with our ensemble-based model.

Aβ42-M35ox(S)’s third centroid also possesses a similar CHC to C-terminal β-strand-turn-β-strand motif, but is unique from the other centroids discussed above in that the N-terminus interacts with the motif with residues G9-E11 contributing an additional β-strand. Here, the cross region hydrogen bonds are K16/G37 (acceptor/donor), V18/MTO35, and F20/G33, aligning with the Aβ40-characteristic bonding pattern. Note that the two Aβ42-M35ox(S) centroids with ³J_HNHA values that have the highest PCC and lowest RMSD compared to experiment (Supplemental Figure 6b) do not form double hairpins like Aβ42; neither 34-36 nor 39-41 form β-interactions and instead tend to interact with more N-terminal parts of the protein.

Among the top four centroids for each species, the only structures where D23’s side chain is not binding to multiple inwardly pointing amide groups of V24-K28 are Aβ42 centroid 4 and Aβ42-M35ox(S) centroid 1. Of the extended CHC to C-terminus β-hairpin structures in the top 4 discussed above (Aβ40 centroids 3 and 4, Aβ42 centroid 1, Aβ42-M35ox(S) centroid 3), all feature these interactions with D23, as well as an additional E22-K28 salt bridge. This salt bridge is a rarer feature outside this set, however, as it is only seen in one other centroid in the top 4 (Aβ42-M35ox(S) centroid 2).

Order Parameters

We want a measure that can be used to characterize the fluctuations of the ensemble given the lack of a dominant reference structure. The isotropic reorientational eigenmode dynamics (iRED) method proposed by Prompers and Brüschweiler⁵⁷ permits the calculation of modes of correlated motion and their associated order parameter without the need of an overall alignment frame, a condition that is especially unlikely to be satisfied in long timescale simulations of IDPs. Order parameters derived for backbone amide groups in this system by this method describe the angular rigidity of the internuclear vector for each group (Figure 7). The obtained order parameters for all amides fall within the range 0 to 0.6, as expected for a highly flexible system. Nevertheless, there are substantial residue-specific differences for this quantity. For all three species, the CHC, 31-36, and (in Aβ42/42-M35ox(S)) 40-41 regions possess significantly larger order parameters, correlating to the locations of β-character of the systems. The 6-8 section also demonstrates substantial rigidity; this region is weakly structured but is observed to make significant cross-region interactions in all three contact maps. Low order parameters, in contrast, are generally observed in the mostly disordered 9-15 positions as well as the 25-26, 28, and (in Aβ42/42-M35ox(S)) 37-38 regions that are dominantly characterized by DSSP as bend secondary structure. Aβ42-M35ox(S) demonstrates reduced rigidity in the CHC and 31-36 regions compared to the other alloforms; this may be attributed to weakening of hydrogen bonding interactions between these regions. Further, Aβ40 demonstrates higher order parameters for 23-24 and residue 27 compared to the other species; the former may be a consequence of Aβ40 register backbone hydrogen bonds involving D23 (Supplemental Table 2) while the latter is may be connected to the greater prevalence of D23 side chain to 27-28 backbone hydrogen bonding in Aβ40 (Table 2). Finally, it is important to note the very low Prompers-Brüschweiler separability indices of 1.3-1.4 for these ensembles, compared to a value of 5.39 for well folded ubiquitin in bulk water.⁵⁸ This is indicative of disordered dynamics where the global and internal motions are highly intertwined. Unfortunately, due to the low separability of the disordered Aβ ensembles, the standard model-free formalism proposed by Lipari and Szabo⁵⁹ cannot be used to fit order parameters from NMR relaxation data, prohibiting accurate comparison of these data to experiment.

Figure 7.

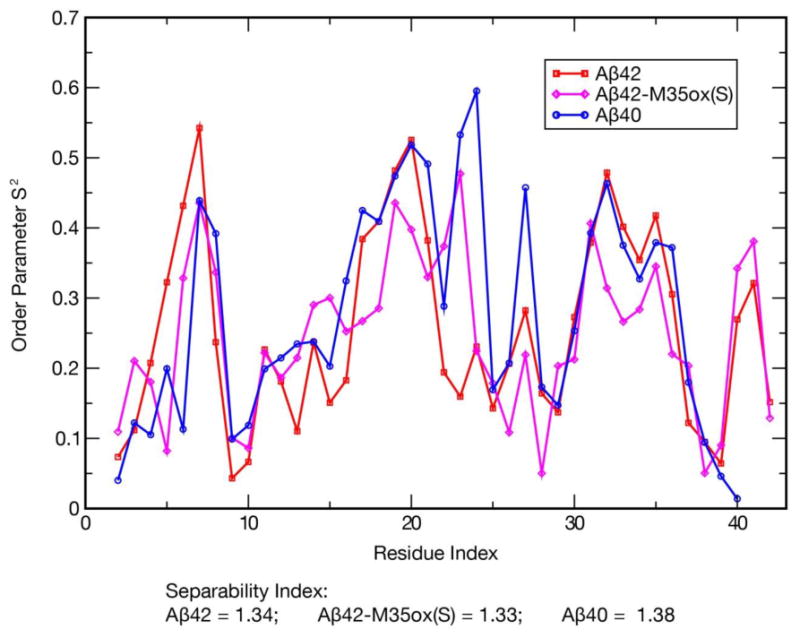
S² order parameters for all backbone N-H internuclear vectors (excluding the N-terminus), calculated with the iRED technique⁵⁷ over the production period. The Prompers-Brüschweiler separability index between the internal modes and global modes is also provided for each species; compare to an index of 5.39 for ubiquitin in bulk water.⁵⁸

Discussion

Key to understanding and manipulating the self-assembly processes that naturally yield the higher order Aβ assemblies intimately associated with Alzheimer’s disease lies in properly characterizing the Aβ monomers that comprise the building blocks of these conformers. While there have been many attempts to characterize Aβ monomers through NMR, CD, and computational simulations, the results of these studies present an overall incomplete and inconsistent depiction of the system. This is largely due to the highly disordered and aggregative nature of these peptides, which preclude the use of many traditional experiments, frustrate sample preparation, and increase the roughness of the free energy landscape, thereby complicating folding simulations of the system. To help address these issues, we have performed REMD simulations on the μs/replica timescale for each of the full length Aβ40, Aβ42, and Aβ42-M35ox(S) peptides while closely monitoring trajectory convergence and comparing calculated J-couplings and RDCs with their experimental counterparts. Further, the secondary structure character and sampled topologies of Aβ determined from analysis of these trajectories are consistent with several previously published experimental findings about the system. Here, we will summarize our results and compare them to those of previous experimental and computational investigations.

Our simulations suggest that all three Aβ species frequently sample β-hairpin topologies between the CHC (residues 17-21) and residues 30-36, with the 24-28 region composing the intermediary bend region. These secondary structure proclivities are supported by chemical shift indices,¹⁴ and it is recognized experimentally (by the effects of proline mutations as well as co-incubation with protein fragments) that the exact regions characterized as β dominant above are critical for Aβ fibrilization.^29-32 Further, the β-hairpin structure of monomeric Aβ40 in complex with a phage selected affibody determined by solution NMR⁵⁶ (PDB: 2OTK) aligns with the central β topology in the free monomer simulations presented here, with the backbone hairpin hydrogen bonding pattern of the NMR structure exactly matching the dominant bonding register of our Aβ40 simulation. This robust agreement lends support to the hypothesis presented by the investigators that this hairpin represents a transiently populated conformation accessible to Aβ monomers.

Extended hairpin structures such as these are likely to expose the dominantly hydrophobic faces of the β-sheet residues to solvent, which may permit them to act as seeds for self-association. (Note that an exception to this would occur in the environment of an oxidized methionine 35 side chain.) Hoyer and coworkers further posited an aggregation mechanism wherein Aβ stacks along these hydrophobic interfaces to form soluble oligomers, which then undergo a concerted 90° rotation about the axes of both β strands of the hairpin to form fibril seeds characterized by intermolecular parallel β-sheets.⁵⁶ This hypothesis is supported by attenuated total reflectance Fourier-transform infrared (ATR-FTIR) studies, which consistently report a peak at ∼1695 cm^-1 indicative of antiparallel β character for soluble oligomers but not for fibrils.^60,61 In agreement with this hypothesis, the generally unstructured N-terminus and the C-terminal β-strand-turn-β-strand motif we report in our simulations shares important structural characteristics with different intrapeptide models for Aβ fibrils and "on-pathway" intermediate oligomers.^50-53 In particular, the locations of secondary structure correlate well to these models, and reported side chain contacts in these intrapeptide models are often analogous to the most populated backbone hydrogen bonds in our monomer simulations. This is consistent with a putative 90° rotation in the axis of backbone hydrogen bonding from perpendicular to parallel to the fibril axis in the pathway between monomers and fibrils.

Further analysis of the Aβ42 and Aβ42-M35ox(S) simulations reveal that a second hairpin motif involving residues 39-41 is formed, with 37-38 constituting a second bend-dominated region. This is consistent with the measurement of greater C-terminal rigidity in Aβ42 compared to Aβ40³³ by NMR, as well as the observation of similar hairpin structures in simulations of Aβ42 C-terminal fragments.⁶² It is also reminiscent of the β-meander topology in the component monomer model for toxic Aβ42 pentameric, "on pathway" oligomers derived from solid state NMR data by Ahmed and coworkers.⁵² Based on the dimensions and shape of these oligomers as determined by size exclusion chromatography and atomic force microscopy, Ahmed et al. further propose a model wherein the C-terminal components of the meander associate to form a core, a structure that would be less likely to form with the less rigid C-terminus of Aβ40. This may explain the presence of paranuclei in Aβ42-like aggregation but lack thereof in Aβ40-like aggregation. If this is true, however, the inability of Aβ42-M35ox to form paranuclei would not be explained directly by the secondary structure proclivities of our simulation, which suggest strong sampling of C-terminal β character in this alloform. Nevertheless, it is observed that antiparallel contacts involved in β-meander formation (CHC to 30-36 and 30-36 to 39-41) are significantly weaker in Aβ42-M35ox(S), while there is a greater tendency to form CHC to 39-41 contacts. Likewise, hydrogen bonds across the β-meander, in general, are considerably weaker than the other alloforms, while 39-41 contacts with other parts of the protein (like K16/V41 and A30/V41) are better populated. Reduced sampling of a double hairpin topology in favor of alternate β-hairpin binding patterns may therefore account for Aβ42-M35ox’s altered aggregation properties.

Differences in the backbone hydrogen bonding patterns that form these hairpins represent another significant change between these species. The C-terminally shifted pattern of contacts between the CHC to 30-36 in Aβ40 compared to Aβ42 may be preferred in that species because it can better accommodate the interactions that form the central region. For example, the E22-K28 salt bridge is able to form with significantly higher frequency in Aβ40 and Aβ42-M35ox(S) compared to Aβ42 (Table 2). Aβ42 also uniquely features E22/G29 as a significantly populated backbone hydrogen bond (Supplemental Table 2). N-terminal shifting of cross-hairpin contacts in Aβ42 may be induced by the formation of hairpin character between 30-36 and 39-41 (in particular, the strongly populated hydrogen bonds between A30/G37 and L34/V41). If this is the case, then the weakening of these interactions in Aβ42-M35ox(S) may explain the weak preference for this species to actually adopt Aβ40-like bonds across the CHC to 30-36 motif rather than those of its reduced counterpart.

Solution NMR studies reveal that V24-K28 forms a turn that is suggested to nucleate folding of the monomer.³⁴ The very high prevalence of bend character in these simulations and the quicker equilibration of bend compared to β-sheet in our simulations seem to support this hypothesis (though it is important to note that REMD simulations will not reflect the true folding dynamics of the system). We report that this region typically forms a crown-like motif in all 3 Aβ simulations, wherein D23’s side chain is positioned in the core of the turn and interacts with the inwardly-pointed amide groups of the composite residues of the turn. The maintenance of this motif structure throughout the simulation appears to be reliant on electrostatic interactions involving the negatively charged side chains of the FAD-linked residues E22 and D23. The latter appears to position the turn residues and the former seems to position D23 itself and forms a long distance salt bridge with K28 across the region. It is very probable that the FAD mutations that disrupt the capacity of these side chains as hydrogen bond and salt bridge partners would also disrupt the turn structure, aligning with experimental observations of this phenomenon.⁴⁰ The structure of the central region and electrostatic involvement of E22 and D23 reported in our simulations nearly perfectly match the characterizations of the highest populated cluster in REMD simulations of the Aβ(21-30) fragment using a similar OPLS-AA/TIP3P combination.⁶³ This suggests that the fold of the 21-30 region is not affected appreciably by the rest of the protein, supporting the idea that it folds autonomously and nucleates the folding of the monomer. Indeed, the frequency of these interactions in the ensemble and consistency of their presence among the top centroid structures suggests that D23’s sidechain to backbone hydrogen binding may be the first step in turn nucleation in the central region, while the E22-K28 long distance salt bridge caps off the domain allowing even further long distance hydrogen bonds to form between the β-regions. The structural features of the turn region reported here are also reminiscent of other reported computational ensembles derived with different simulation parameters for both the Aβ(21-30) fragment^64-66 and the central region of full length Aβ monomers.⁶⁷ It is important to note, however, that despite a central region turn motif being common to the affibody-trapped monomer⁵⁶ and oligomer/fibril models,^50-53 the roles of E22 and D23 are observed or are hypothesized to be substantially different. In the former, E22 and D23 appear to interact with the solvent and affibody protein rather than bonding to the 24-28 region, while in the latter, it is proposed that D23 actually forms a salt bridge with the K28 side chain.

The central region crown-like motif present in our simulations exposes the carbonyl groups radially outward into the solvent, creating a negatively dominated external surface with a central, positively charged indentation (Figure 5). This distribution of charge, in tandem with the preferred geometries of the protein, may explain why this bend region is restricted from interacting with all of the other (mostly hydrophobic) segments of protein, with residues 4-6 (containing a positively charged R5) being the only exception observable in the contact maps (Figure 3) presented in this study. We speculate that this may present a link to the H6R and D7N FAD mutations, which both increase positive charge in this region. It is possible they promote the N-terminus to interact more persistently with the negative side chains and carbonyls in the region, competing with the electrostatic interactions that nucleate the turn and potentially destabilizing the motif. The negative character of the loop surface could also explain certain experimental findings for Aβ, such as the increased resistance of this region to proteolytic attack not accounted for by sequence-specific variation³⁴ and the reduced ¹H-¹⁵N HSQC chemical shift perturbation of these residues compared to the rest of the protein when titrating Aβ monomers against negatively polarized or hydrophobic dominated compounds.^68,69 While formation of the V24-K28 turn correlates with the formation of cross-region β-hairpin character that may form aggregation-prone hydrophobic interfaces, one could also speculate that the negative surface presented by this turn could also have a protective effect against this hydrophobic-dominated self-assembly. This hypothesis may explain why disruption of the turn region is associated with higher orders of oligomerization.⁴⁰

In this study, we report computationally-derived ensembles for wild type Aβ42, Aβ40, and Aβ42-M35ox(S) monomers that reproduce experimental NMR observables with reasonable fidelity and match experimental trends observed for the system by other studies. The high proclivity of Aβ monomers to establish hairpin-like conformations that resemble oligomer and fibril models hints at the importance of these motifs in Aβ self-assembly. Further, the enduring presence of a bend region nucleated by interactions with the side chain of D23 suggests a mechanism that explains the electrostatic involvement of FAD-linked residues in Aβ structure. Aβ monomers is a building block in the formation of both “on pathway” intermediate structures in fibril formation and "off pathway" oligomers. The major conformations calculated in this study may be useful for drug discovery targeting this basic form. Further, the detailed biophysical characterization of Aβ monomers presented here, if experimentally verified, is expected to provide valuable predictions for understanding and manipulating the mechanisms that yield the pathogenic assemblies involved in AD.

Methods

Details of REMD Simulations

In this study, we have investigated the structural ensembles of Aβ42, Aβ40, and Aβ42-M35ox(S) using the REMD simulation protocol coupled with the OPLS-AA/L force field⁷⁰ and the TIP3P water model,⁷¹ a combination which has been previously shown to yield good correlation to experimental observables for these systems.⁴⁶ Comparison of simulation data published in this study with OPLS-AA/TIP3P and that generated by Sgourakis et al.⁴² with AMBER99sb/TIP4P-Ew showed that the former described the experimental data better in longer simulations. REMD is a generalized ensemble method,^72,73 wherein several initially identical copies of the system (replicas) are simulated in parallel over a set of temperatures. Trials to exchange temperature between neighboring replica pairs with a probability of success governed by a Metropolis Monte Carlo criterion occur repeatedly throughout the simulation. All molecular dynamics calculations were performed with the GROMACS 4.5.3 package.⁷⁴

The Aβ42-M35ox(S) system features L-methioinine-(S)-sulfoxide (MTO) in place of L-methionine at the residue 35 position. From what is currently known, oxidation of the prochiral sulfur atom on methionine by typical reactive oxidation species is believed to occur racemically between R and S diastereomers,⁷⁵ so our choice of the S conformation here was made arbitrarily. To accommodate this new residue, we used a modified OPLS-AA/L force field for this system only. Parameters in the OPLS force field are, in general, optimized to fit experimental thermodynamic properties for pure liquids of a set of small, model compounds containing key functional groups. These parameters have therefore been designed to be highly transferable among molecules containing similar chemical groups. Given the similarities between the –CH₂- SO-CH₃ moiety in methionine sulfoxide and DMSO (CH₃-SO-CH₃) molecule already parameterized in OPLS,⁷⁶ the nonbonded and bonded parameters have been transferred from DMSO to the corresponding group in L-methioinine-(S)-sulfoxide (with a modification on the CG partial charge to preserve neutrality) to complete the definition of this residue. The modifications to the force field are further described in Supplemental Table 3, and the parameters and topologies used in this study are available upon request.

All three peptide systems were constructed from a completely extended conformation of the full length peptide with zwitterionic termini and side chain protonation states appropriate for pH 7. The sequences are:

$$\begin{array}{ll}\mathrm{A}\mathrm{\beta }42:\hfill & {}^1\mathrm{D}\mathrm{AEFRHDSG}{}^{10}\mathrm{Y}\mathrm{EVHHQKLVF}{}^{20}\mathrm{F}\mathrm{AEDVGSNKG}{}^{30}\mathrm{A}\mathrm{IIGLMVGGV}{}^{40}\mathrm{V}\mathrm{IA}\hfill \\ \mathrm{A}\mathrm{\beta }40:\hfill & {}^1\mathrm{D}\mathrm{AEFRHDSG}{}^{10}\mathrm{Y}\mathrm{EVHHQKLVF}{}^{20}\mathrm{F}\mathrm{AEDVGSNKG}{}^{30}\mathrm{A}\mathrm{IIGLMVGGV}{}^{40}\mathrm{V}\hfill \\ \mathrm{A}\mathrm{\beta }42-\mathrm{M}35\mathrm{ox}(\mathrm{S}):\hfill & {}^1\mathrm{D}\mathrm{AEFRHDSG}{}^{10}\mathrm{Y}\mathrm{EVHHQKLVF}{}^{20}\mathrm{F}\mathrm{AEDVGSNKG}{}^{30}\mathrm{A}\mathrm{IIGLXVGGV}{}^{40}\mathrm{V}\mathrm{IA}\hfill \end{array}$$

where X = L–methioinine– (S) –sulfoxide

Each of these systems were then constructed using identical protocols with identical parameters. First, a 1-ns MD simulation of the peptide was run in vacuo at a high temperature (700 K) to collapse each extended system. Each system was then energy minimized and solvated to produce a 5.4 nm cubic simulation box with 4947 TIP3P water molecules. An equilibration simulation was run for each of these solvated systems at a constant temperature (300 K) and pressure (1 atm), both coupled with the standard Berendsen method,⁷⁷ for 1 ns with an integration time step of 1 fs. For all three systems, the simulation box dimensions only changed marginally after the NPT simulation, remaining 5.4 nm in each dimension.

From the resulting configuration, 52 replicas were generated to optimally span the temperature range 270.0 K to 601.2 K with an average exchange ratio of 15%, as calculated in a previous study.⁴² Constant volume REMD simulations were run using these replicas for a total 1000 ns/replica for each of the three systems (cumulative simulation time of 52 μs per system). These extensive simulations are required to properly sample the equilibrated state, as discussed in the Convergence subsection. Exchange moves were attempted every 4 ps between all adjacent replicas in temperature space throughout the simulation. In this stage, the bond lengths were constrained with the LINCS⁷⁸ and SETTLE⁷⁹ algorithms, permitting an integration step of 2 fs. A 1 nm cutoff for Lennard-Jones interactions was imposed, while the neighbor list was updated every 10 steps. Electrostatic interactions were calculated with the particle mesh Ewald method⁸⁰ with a 54 unit cubic grid and fourth order extrapolation. Explicit ions were not added to the solvent; instead, charge neutrality of each system was established by use of the Ewald method for the computation of long-range electrostatics. These conditions closely imitate the minimal salt buffers (20 mM K₂HPO₄ with no other salt³³) used in the NMR experiments presented in this study. The system was thermalized with a Nose-Hoover heat bath⁸¹ to maintain constant temperatures between exchanges. The REMD simulations were each performed with 208 or 416 CPUs of a Linux based cluster based at Rensselaer Polytechnic Institute, using an assortment of domain decomposition schemes.

Comparison with Experimental Data

Quantitative comparison of J-coupling (³J_HNHA and ³J_NHB) and residual dipolar coupling (RDC) data calculated from the REMD trajectories with their corresponding experimental values are used to both monitor equilibration over time and assess the validity of the MD ensemble. All experimentally-derived J-couplings were measured using the sample preparation and experimental conditions as described.³³ For each species, ³J_HNHA couplings were measured as an average of two data sets at identical sample conditions, employing the HNHA pulse sequence⁴⁸ and the J-resolved SOFAST-HMQC pulse sequence⁴⁹ respectively. The ³J_HNHA coupling HNHA set for Aβ42 were obtained from Sgourakis et al.⁴² while Aβ40’s HNHA set was published by Yan and coworkers,¹⁷ both acquired on an 800 MHz spectrometer. The remaining four sets are newly published data. The Aβ42-M35ox HNHA set was measured on a 600 MHz spectrometer, while all other sets were measured on the aforementioned 800 MHz spectrometer. Both of these spectrometers are equipped with a cryoprobe and are located at the NMR core facility in the Center for Biotechnology and Interdisciplinary Studies at Rensselaer. Data sets acquired through the J-resolved SOFAST-HMQC method are based on splitting in the indirect J (ω₁) dimension only. Both glycine couplings and couplings of ambiguous assignment (due to spectral overlap) were ignored in all comparisons with simulation data. For Aβ42, Aβ40, and Aβ42-M35ox, the component HNHA sets consisted of 17, 22, and 19 unambiguous couplings and the component J-resolved SOFAST-HMQC sets consisted of 21, 24, and 27 unambiguous couplings, yielding 15, 20, and 19 couplings covered by both sets and 23, 26, and 27 unique coupling values for each of these species, respectively. The J-coupling data was highly reproducible between the two composite data sets, yielding an r² correlation of 0.82, 0.88, and 0.82 respectively and with |Δ³J_HNHA| > 0.5 Hz between the two sets for the following residues: {H13, V18, V24, S26, I31}for Aβ42, {Q15, V18, S26, M35} for Aβ40, and {V18, V24, V39} for Aβ42-M35ox. ³J_NHB couplings were measured for 28 residues in Aβ40 collected on the 600 MHz spectrometer mentioned above using the HNHB pulse sequence ⁸². The experimental RDCs studied here for amides in all 3 systems (30 in Aβ42, 29 in Aβ40, and 32 in Aβ42-M35ox) were also previously published by Yan et al.;¹⁷ these were measured in 10% polyacrylamide gel using an IPAP-HSQC technique.⁸³ All spectra were processed using nmrPipe⁸⁴ and analyzed with Sparky (T. D. Goddard and D. G. Kneller, SPARKY 3, University of California, San Francisco, CA).

Both ³J_HNHA and ³J_NHB couplings were calculated from the REMD coordinates for each system using the Karplus equation:⁸⁵

$${}^3\mathrm{J}(\mathrm{\theta })=A{cos}^2(\mathrm{\theta })+Bcos(\mathrm{\theta })+C$$

where A, B, and C are semi-empirically determined coefficients and θ = (ϕ - 60°) or θ = (χ₁ - 60°) for ³J_HNHA or ³J_NHB respectively, where ϕ and χ₁ are peptide dihedral angles. The best fit Karplus coefficients for computational J-couplings were determined by least square fitting to find the parameters that minimized RMSD between the average of experimental J-couplings and their computational counterparts based on data from the production period. This fitting accounts for motional averaging effects in the REMD trajectories. A table of the resulting Karplus parameters used for J-coupling determination is shown below:

Coupling	System	A	B	C
3JHNHA	Aβ42	6.88	-6.5	-3.53
3JHNHA	Aβ40	7.99	-5.58	-3.68
3JHNHA	Aβ42-M35ox(S)	6.92	-1.62	0.55
3JNHB	Aβ40	3.82	-1.03	1.05

Compared to empirically-derived values⁴⁸ for ³J_HNHA, the best fit Karplus parameters for Aβ42-M35ox(S) are comparable, while the B and C coefficients for Aβ42 and Aβ40 are appreciably changed by this method. These changes greatly reduce the Karplus curve for positive ϕ; however, since all couplings for this system are predicted to be >5 Hz (Figure 1), according to the Karplus curves for each of these fitted parameter sets (Supplemental Figure 7), the expectation for ϕ over the MD ensemble, <ϕ>, must lie in the negative ϕ region of Ramachandran space for all residues. The effect of the parameter changes in this region thereby exclusively make the Karplus curve steeper relative to the Vuister et al. parameters⁴⁸ while preserving the same maximum, effectively broadening the lower bound of the dynamic range of the calculated J-couplings. For ³J_NHB, the best fit coefficients are similar to the published fundamental/consensus values⁸⁶ for all three systems, with a modest increase in A being the only substantial change.

³J_HNHA was also backcalculated for all centroid structures obtained from single linkage clustering (described in the Ensemble Analysis subsection) for each species using Vuister et al. parameters⁴⁸. A second strategy to fit ³J_HNHA values for the MD-derived ensemble was investigated, wherein a weighted average of the ³J_HNHA values associated with these centroids was compared to experimental data. After initializing each centroid’s contribution to the average as equal to the population of the ensemble represented by that centroid, the set of weights was subsequently modified to minimize RMSD of the weighted average to the inclusive average of the experimental values using the Nelder-Mead downhill simplex algorithm⁸⁷. Fits for centroids top 4, top 10, and top 50 centroids for each were produced in this manner for each species, with a function tolerance of 0.00001. The maximum number of iterations and maximum number of function calls were both set to 100000, required for the 50 parameter fits to reach convergence. The objective function was modified to strongly penalize any weight sets with negative values, effectively constraining the fitting. These fits were also repeated using an extra parameter with ³J_HNHA equal to the average of all experimental ³J_HNHA for all residues, to investigate the effects of introduction of a “random coil” centroid into the ensemble.

RDCs were calculated from the REMD trajectories using the PALES program.^88,89 As the alignment tensor magnitude is a function of the extent of alignment of the particles of the media which is dependent on experimental conditions, the reported computational ensemble values were uniformly scaled to minimize the RMSD compared to experimental data. The resulting scaling factors were 0.37 for Aβ42, 0.30 for Aβ40, and 0.42 for Aβ42-M35ox(S).

Correlations of these three couplings between experiment and the REMD ensemble average are examined similarly to previous studies^42,46 by use of the Pearson’s correlation coefficient (PCC):

$$\text{PCC}=\frac{{\displaystyle {\sum }_{i=1}^n((x_i-\overline{x})(y_i-\overline{y}))}}{(n-1){\sigma }_x{\sigma }_y}$$

for data sets x and y of size n with standard deviation σ_x and σ_y, respectively.

Ensemble Analysis

Given the relative convergence of the data (see below) and good agreement with NMR observables, we proceeded to analyse the simulated conformations of Aβ42, Aβ40, and Aβ42-M35ox(S) using REMD data over the 400-1000 ns/replica time interval over 7 temperatures composing the range 289.2 K to 310.7 (this is referred to as the "production period" in the rest of the paper). Multiple temperatures were used to improve the sampling statistics. Analysis was done using the GROMACS 4.5.3 suite⁷⁴ and Python/shell scripts. Secondary structures were annotated over the ensemble using the DSSP method.^54,55 Tertiary structure was studied via clustering, contact maps, and populations for key hydrogen bonds and salt bridges. The single linkage,⁹⁰ Jarvis-Patrick,⁹¹ and Daura⁹² clustering methods implemented in GROMACS’s g_cluster tool were each employed to cluster around Cα atoms over the production period for every 100 ps-th frame, grouping 42000 conformations for each monomer. Each of these identified similar dominant centroids, but single linkage was chosen as the method best suited toward both categorizing the well separated, highly diverse set of morphologies in the Aβ ensemble with fewer, more highly representative structures and yielding output that is minimally dependent on the cutoff parameter. Given this, the clusters presented in the RMSD-Based Clustering subsection were calculated with the single linkage clustering scheme with an RMSD cutoff of 2.0 Å. Contact maps are based on the probability of contact over the production period, with two residues defined to be in contact if their Cα- Cα distance is ≤ 8 Å.⁹³ Hydrogen bonds between donor atom (D), hydrogen atom (H), and acceptor atom (A) were identified when D to A distance ≤ 3.5 Å and an H-D-A angle ≤ 60°, while salt bridges were detected using a 4.0 Å distance cutoff between any pair of oppositely charged atoms. S² order parameters for all backbone N-H internuclear vectors (excluding the N-terminus) were calculated with the iRED technique.⁵⁷ Finally, to complement this analysis, we also measured solvent accessible area⁹⁴ per residue and histograms of radius of gyration for the production period. Histograms of Cα RMSD between residues 16-35 for each frame in the production period compared to Chain C, Model 1 from an NMR structure of Aβ40 monomer trapped by an affibody protein⁵⁶ (PDB: 2OTK) were also determined.

Convergence

Simulation convergence (steady state) was assessed by three criteria: 1) The time required for the simulations to equilibrate is first determined by the convergence of computationally derived couplings to their experimentally determined values as judged by PCC. For each experimental coupling, the PCC of the block average over each 20 ns/replica period for the temperature range 289.2 K to 310.7 K compared to the corresponding experimental value for each system is reported (Figure 1a, Supplemental Figure 3a, Supplemental Figure 4a). Based on the apparent transition of this data from a phase where PCC generally improves to a phase where oscillations about a steady state occur, we judge equilibration for ³J_HNHA to occur at ∼320 ns/replica for Aβ42, ∼360 ns/replica for Aβ40, and ∼180 ns/replica for Aβ42-M35ox(S). On the other hand, while the block average PCCs for both ³J_NHB and RDCs generally appear to improve over time, it is difficult to make out distinct phases in the time progression of these values, and so we don’t consider these values in judging convergence. 2) Cα average distance maps over 100 ns/replica windows in the same temperature range throughout the simulation serve as another reporter on equilibration time. We determine distance map equilibration to occur at 100-200 ns/replica for Aβ42, 500-600 ns/replica for Aβ40, and 200-300 ns/replica for Aβ42-M35ox(S) because at these points, the sum over the absolute value of differences between the pairwise distances in the map of the current interval and that of the previous interval is no greater than 50 nm for all subsequent time windows (Figure 8a). 3) Finally, the content of secondary structure over the whole peptide as determined by DSSP over 100 ns/replica windows is used as a final check on simulation equilibration. Beginning at the following intervals – 300-400 ns/replica for Aβ42 and 200-300 ns/replica for Aβ42-M35ox(S) – each ensemble has sampled to a state where the composition of each DSSP element varies by no more than 4% and 3% respectively over all time windows, implying convergence at these junctures (Figure 8b). On the other hand, there are substantial directional changes in Aβ40’s β, bend, and coil/irregular content well into later points of the simulation. A state approaching convergence occurs beginning with the 600-700 ns/replica interval, where variation in secondary structure elements among subsequent time windows does not exceed 5%.

Overall, this evidence illustrates that the Aβ simulations are very dynamic even on the 100 ns/replica timescale, stressing the necessity for long timescales in simulations of these systems, at least using the parameters we have chosen. For Aβ42 and Aβ42-M35ox(S), these three methods reveal that our choice of the analysis period to be 400-1000 ns/replica successfully captures an equilibrated segment of the simulation. Although these methods reveal that Aβ40 converges only later in the simulation, the analysis period for Aβ40 was also chosen to be 400-1000 ns/replica so that we acquire sufficient data for statistical significance and consistently analyse the same duration of time for each simulation.

• Ensembles of Aβ42, Aβ40, and Aβ42-M35ox(S) monomers characterized with REMD.

• Validation through J-couplings acquired with two different pulse sequences.

• Observation of structures similar to intrapeptide models of oligomers and fibrils.

• Sampling of different β topologies may explain variation in aggregation propensity.

Abbreviations used

Aβ

amyloid β

AD

Alzheimer's disease

REMD

replica exchange molecular dynamics

CHC

central hydrophobic cluster

PCC

Pearson's correlation coefficient