Significance
Electrons emitted from equivalent centers in isolated molecules via the photoelectric effect interfere, providing an atomic-scale equivalent of the celebrated Young’s double-slit experiment. We have developed a theoretical and experimental framework to characterize such interference phenomena accurately, and we have applied it to the simplest hydrocarbons with different bond lengths and bonding types. We demonstrate that such fundamental observations can be related to crucial structural information, such as chemical bond lengths, molecular orbital composition, and quantitative assessment of many-body effects, with a very high accuracy. The experimental and theoretical tools we use are relatively simple and easily accessible, and our method can readily be extended to larger systems, including molecules of biological interest.
Keywords: coherent state and molecular photoemission, interference phenomena
Abstract
Interferences in coherent emission of photoelectrons from two equivalent atomic centers in a molecule are the microscopic analogies of the celebrated Young’s double-slit experiment. By considering inner-valence shell ionization in the series of simple hydrocarbons C2H2, C2H4, and C2H6, we show that double-slit interference is widespread and has built-in quantitative information on geometry, orbital composition, and many-body effects. A theoretical and experimental study is presented over the photon energy range of 70–700 eV. A strong dependence of the oscillation period on the C–C distance is observed, which can be used to determine bond lengths between selected pairs of equivalent atoms with an accuracy of at least 0.01 Å. Furthermore, we show that the observed oscillations are directly informative of the nature and atomic composition of the inner-valence molecular orbitals and that observed ratios are quantitative measures of elusive many-body effects. The technique and analysis can be immediately extended to a large class of compounds.
Wave-particle duality, nowadays considered as a milestone in the development of quantum mechanics, is the revolutionary concept that was experimentally demonstrated by Young’s double-slit experiment in 1801. In Feynman’s words, wave-particle duality is “a phenomenon which is impossible… to explain in any classical way, and which has in it the heart of quantum mechanics” (1). Once the wave nature of light was revealed in such an experiment, similar experiments were carried out with several particles, including electrons (2, 3) and even heavy species such as C60 (4), in which a beam passed through two slits separated by a distance comparable to their associated de Broglie wavelength.
In 1966, Cohen and Fano (5) interpreted the oscillatory behavior of the photoabsorption spectra of N2 and O2 molecules (6) by theorizing the possibility of realizing the double-slit experiment in the photoionization of homonuclear, diatomic molecules, where the electrons are emitted by two equivalent atomic centers. Due to coherence in the initial molecular state, the absorption of a single photon by the homonuclear molecule gives rise to two coherent electron waves, which naturally lead to interference oscillations.
Further theoretical studies were carried out on the coherent emission of electrons from the H2 molecule and the 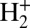 ion by photoionization (7) and by fast electron impact (8, 9). The interference in the D2 molecule was also studied using electron impact (10). Projectiles such as heavy ions have also been used to study similar phenomena in diatomic molecules (11, 12). Interference phenomena were also found and studied extensively in the K-shell ionization of diatomic molecules, such as N2 (13, 14). Recently, the cold target recoil ion momentum spectroscopy (COLTRIMS) technique has been used to study the double-slit interference effect in the double ionization of H2 induced by synchrotron radiation (15, 16).
ion by photoionization (7) and by fast electron impact (8, 9). The interference in the D2 molecule was also studied using electron impact (10). Projectiles such as heavy ions have also been used to study similar phenomena in diatomic molecules (11, 12). Interference phenomena were also found and studied extensively in the K-shell ionization of diatomic molecules, such as N2 (13, 14). Recently, the cold target recoil ion momentum spectroscopy (COLTRIMS) technique has been used to study the double-slit interference effect in the double ionization of H2 induced by synchrotron radiation (15, 16).
Direct observation of the interference pattern in photoionization is often difficult, being a small modulation superimposed on a rapidly decreasing cross-section. The cleanest observation is expected by measuring the ratio of two cross sections, corresponding to symmetrical (g) and antisymmetrical (u) combinations of 1s orbitals, which are expected to give oscillations in antiphase, thus magnifying the interference pattern. For the same reason, no oscillation is present in the unresolved g/u cross-section. Unfortunately, the g/u splitting of core orbitals is generally too small to be observable, due to the dominating natural lifetime broadening. However, in N2 (17) and C2H2 (18, 19), it is of the order of 100 meV, owing to the very short interatomic distance associated with the triple bond, and beautiful interference patterns have been observed (13, 14). Another possibility that has been exploited recently is to observe the interferences from the ratios of individual vibrational components, and clear patterns have been observed in both the valence shell and core regions (20, 21). This method has some advantages but requires vibrational resolution, which is often not achievable in more complex systems.
Beyond the fundamental interest in observing quantum interference between electron waves coherently emitted, many important questions remain to be addressed by a broader study of these interference patterns:
A strong geometrical dependence of the interference patterns is expected, as also predicted by the Cohen–Fano formula (5). This dependence may provide a means of accurate determination of molecular geometries, especially when photoemission is the primary investigation tool.
Most molecular orbitals (MOs) are complex and delocalized over several atoms. In fact, the focus in the past on analyzing core orbitals is due to the complete localization of such orbitals on the equivalent centers only, providing a clean two-slit situation. It is expected that the interference from complex MOs will survive but will be distorted. This, in turn, may give valuable information on the atomic orbital (AO) composition of the relevant MOs. In heteronuclear diatomics, it has been proposed to treat them as “unequal” slits, weighting the amplitude of emission by AO-dependent coefficients (22, 23).
The extension of the interference pattern from a two-slit situation to a many-slit situation is possible, and can provide information on, for example, the electronic structure and dynamics of longer chain hydrocarbons with two or more pairs of chemically equivalent carbon atoms, as well as linear and branched-chain isomers. This will be a natural extension of our present results. That interferences may survive in much more complex systems is shown by the long known oscillations in the highest occupied molecular orbital (HOMO)/HOMO-1 cross-section ratio in C60 (24, 25), which were originally deemed unique to this molecule but are very likely a manifestation of the same general phenomenon.
Another source of oscillatory behavior in the photoionization cross-sections is the diffraction by neighboring centers, which is well known in extended X-ray absorption fine structure (EXAFS) spectroscopy and is obviously due to the underlying photoemission channels. A beautiful observation of such structures has been reported recently for a series of gas-phase molecules (26, 27). The recognized success of EXAFS in producing structural information, coupled to the much richer information available in photoemission by means of the ability to select a specific orbital or emission center, bears great promise for the study of high-energy structures in photoemission. The interplay between interference and diffraction patterns is another uncharted territory, and it will constitute an obvious development of our present work. This interplay is expected to be prominent in outer-valence orbitals, which show similar patterns, but are generally more complex due to the extensive delocalization.
Although the spectrally unresolved splitting of core orbitals prevents the study of interferences in most systems, an interesting possibility is restored by studying the ionization of inner-valence 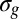 and
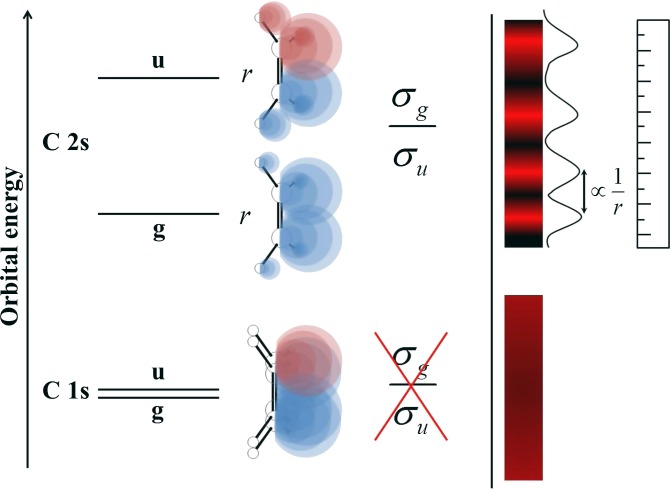
and 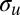 orbitals originating from the 2s AOs of the first-row atoms. They have much larger g/u splitting due to the stronger bonding interaction, and are thus easier to resolve experimentally. This opens the possibility of a direct study of interference patterns in a much broader range of molecular systems and facilitates the exploration of most of the issues previously considered. Often, ionizations of 2s-derived MOs are plagued by very strong many-body effects, which completely destroy the primary line. However, at least in many hydrocarbon molecules, such C 2s-derived orbitals are still defined well, as has been amply surveyed (28–30), and can offer a good opportunity for direct study of the above interference effects. Furthermore, the analysis of a series of related compounds can provide information on the dependence of the interference pattern on the geometrical structure as well as on the orbital composition, both of which represent parameters of great chemical interest. Moreover, even if they are partially involved in the bonding and they are mixed with AOs of neighboring atoms, such orbitals are still predominantly localized on the equivalent centers, so that well-developed and rather simple interference patterns are expected. A pictorial representation of the essence of our method is shown in Fig. 1. In this study, we have explored the feasibility of studying interference in photoemission from 2s-derived orbitals in the simple pseudo–two-center systems C2H2, C2H4, and C2H6. This already permits a neat study of the bond-length dependence of the interference pattern, together with the study of the possible weaker changes in MO composition due to the different insaturation and chemical environment.
orbitals originating from the 2s AOs of the first-row atoms. They have much larger g/u splitting due to the stronger bonding interaction, and are thus easier to resolve experimentally. This opens the possibility of a direct study of interference patterns in a much broader range of molecular systems and facilitates the exploration of most of the issues previously considered. Often, ionizations of 2s-derived MOs are plagued by very strong many-body effects, which completely destroy the primary line. However, at least in many hydrocarbon molecules, such C 2s-derived orbitals are still defined well, as has been amply surveyed (28–30), and can offer a good opportunity for direct study of the above interference effects. Furthermore, the analysis of a series of related compounds can provide information on the dependence of the interference pattern on the geometrical structure as well as on the orbital composition, both of which represent parameters of great chemical interest. Moreover, even if they are partially involved in the bonding and they are mixed with AOs of neighboring atoms, such orbitals are still predominantly localized on the equivalent centers, so that well-developed and rather simple interference patterns are expected. A pictorial representation of the essence of our method is shown in Fig. 1. In this study, we have explored the feasibility of studying interference in photoemission from 2s-derived orbitals in the simple pseudo–two-center systems C2H2, C2H4, and C2H6. This already permits a neat study of the bond-length dependence of the interference pattern, together with the study of the possible weaker changes in MO composition due to the different insaturation and chemical environment.
Fig. 1.
Schematic representation of double-slit interference in core and inner-valence photoionization of a polyatomic molecule and its relationship with the bond length. Interference cannot be observed in the C 1s core levels, where it is impossible to resolve the g/u splitting due to the large natural lifetime.
Concerning the geometrical structure, Young-type interference is directly dependent on the distance between the slits, and therefore on the interatomic distance in a diatomic molecule: The larger the distance, the smaller is the period of the oscillations. Concerning the electronic structure, even if inner-valence MOs remain basically atomic, a certain amount of delocalization is always present. In the case of simple hydrocarbons, the most important effect will be the amount of H 1s orbital participation, which will give a drift in the mean value of the g/u cross-section ratio due to the rapidly decreasing hydrogen cross section at high energy.
Results and Discussion
In this paper, we present evidence of the Cohen–Fano interferences in the C 2s photoionization of C2H2 (acetylene), C2H4 (ethylene), and C2H6 (ethane).
We obtained photoelectron spectra for the inner-valence region for all three systems in the photon energy range of 70–700 eV and derived the g/u cross-section ratios. The experimental data have been collected at the soft X-ray PLEIADES beamline at Synchrotron SOLEIL (www.synchrotron-soleil.fr/Recherche/LignesLumiere/PLEIADES) (31). The experimental results are compared with the theoretical predictions by first-principles density functional theory (DFT) calculations (32–35) (details on the experiments and theory are provided in Materials and Methods).
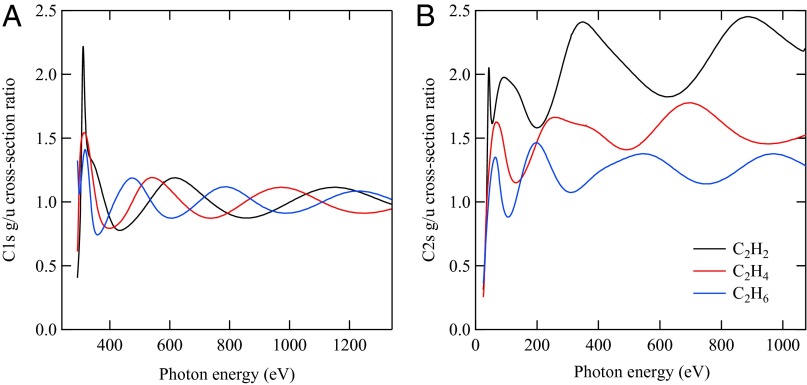
In Fig. 2, we show the calculated cross-section g/u ratios for the C 1s-derived orbitals ionization channel (Left) and the g/u ratios for the C 2s-derived orbitals (Right) in the three molecules. There are significant similarities and differences between the two panels. The main similarity is that the period of the oscillations is very sensitive to the bond length and becomes shorter as the bond length increases. The main difference is that whereas the oscillations for core orbitals are very regular around 1 as a mean value, the oscillations for the inner-valence orbitals are far from being regular around a mean value; rather, they diverge quite rapidly at high photon energies. Additionally, the observed oscillations are not symmetrical, which reflects the different degree of admixture of the H 1s orbitals in the two g/u C 2s-derived MOs and the different trend of the cross sections of H and C orbitals as a function of photon energy. Therefore, such irregularities in the oscillations are directly informative of the nature and atomic composition of the inner-valence MOs.
Fig. 2.
Theoretical cross-section ratios as a function of photon energy for the C 1s-derived orbitals ionization channel (A, Left) and for the C 2s-derived orbitals of C2H2, C2H4, and C2H6 molecules (B, Right).
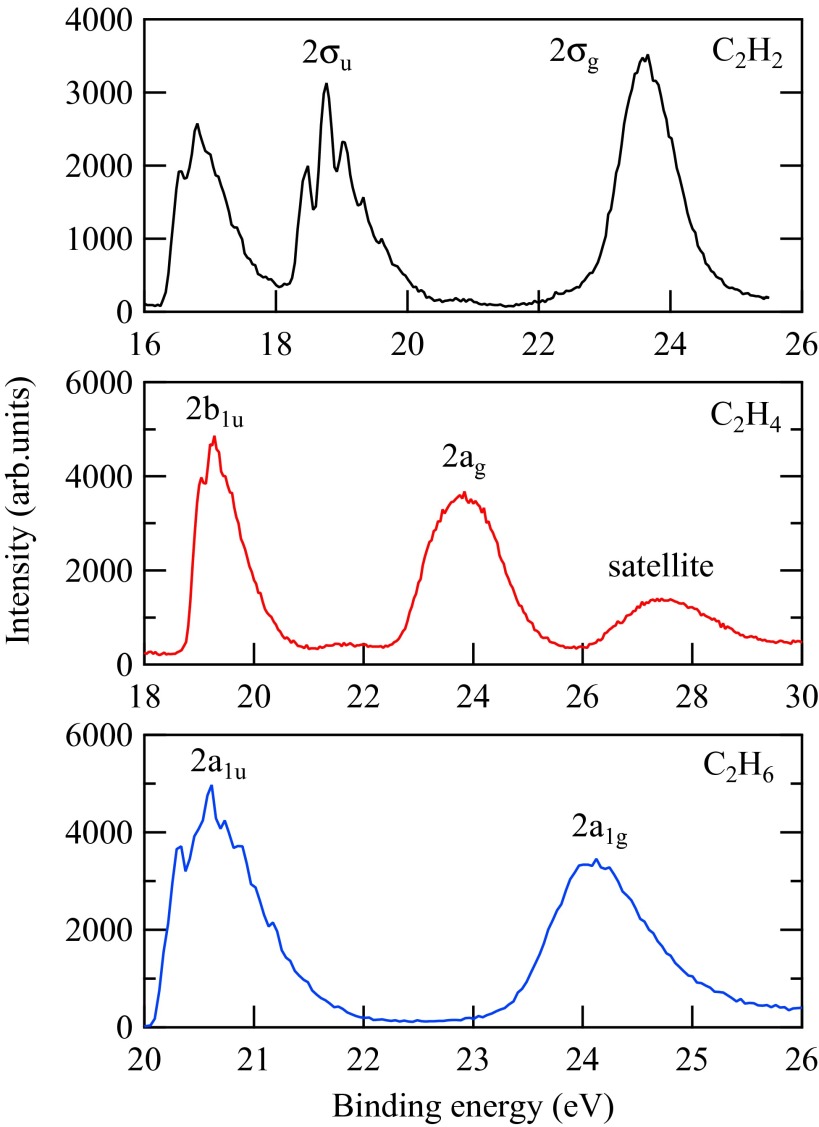
In Fig. 3, we show the inner-valence spectra taken at a representative photon energy of 100 eV for all three molecules. The main peaks labeled there are the ones whose ratios are examined in the following. The background, as well as the satellite transitions’ contributions in the spectral profiles, have been subtracted from the measured spectra during data analysis. The g/u splitting is resolved well throughout the whole photon energy range. The peak areas have been obtained, and their ratios have been derived.
Fig. 3.
Photoelectron spectra of all three molecules recorded at 100 eV of photon energy (28–30).
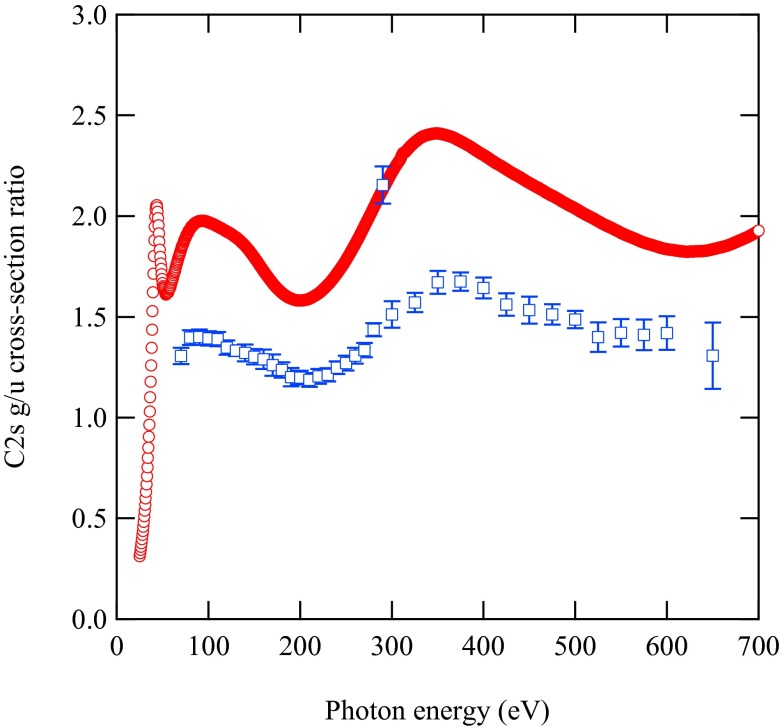
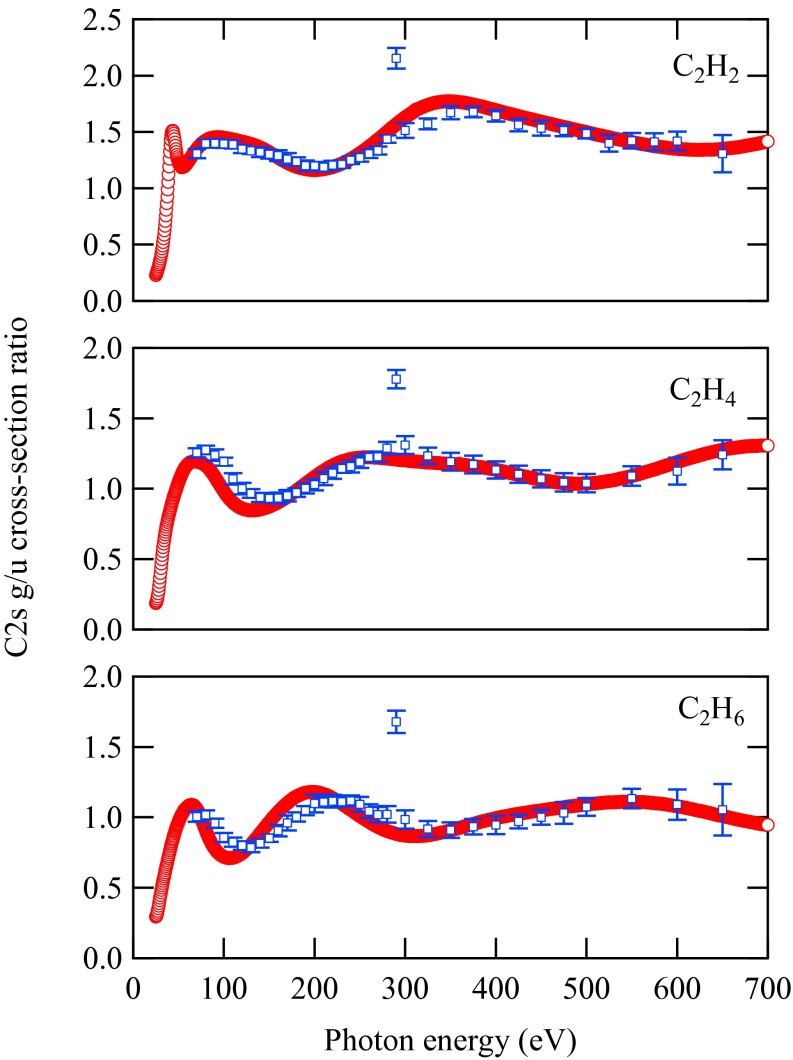
In Fig. 4, we illustrate the experimental and calculated values for one of the molecules, namely, C2H2. The points below 70 eV of photon energy have been measured in different experimental conditions (higher spectral resolution) and will be reported in a forthcoming article. One of experimental data points deviates from the oscillatory trend. This point is at the photon energy corresponding to the C 1s-lowest unoccupied molecular orbital (LUMO) resonance; thus, it is expected to show a completely different behavior because g/u ionization cross-sections can be affected by the resonance in a different fashion. We have performed time-dependent DFT calculations for explaining the trend of cross-section ratios at resonance, but this study is beyond the scope of present work and will be presented later on.
Fig. 4.
The g/u ratios as a function of photon energy in C 2s photoionization of C2H2. The error bars include only statistical contributions. The red circles are calculated points, and the blue squares with error bars are experimental results. Both theoretical and experimental results are displayed without any scaling.
Although the shape of the theoretical curve is matched extremely well by the experimental points, there is a systematic discrepancy in the absolute values. Such a discrepancy has a ready physical explanation: In the calculations, the pole strengths for the inner-valence main peaks are assumed to be equal to 1 in all cases. However, it is known that in the inner-valence region, the breakdown of the one-electron picture occurs, with part of the intensity of the inner-valence states being redistributed over several main and satellite peaks. To match the experimental and the theoretical values, we have applied scaling factors that correspond to the pole strength ratios of the main peaks and provide some additional information that we can derive with our method. Unfortunately, despite a number of theoretical studies available in the literature, widely varying ratios of pole strengths are reported, depending on basis sets and many-body approaches, so that no useful comparison is available, and this represents a challenge for further studies of this difficult topic.
Fig. 5 shows the calculated and measured g/u oscillation as a function of photon energy for all three molecules. Reduction scaling factors have been applied to the theoretical points (1.42 for C2H2, 1.36 for C2H4, and 1.24 for C2H6) to obtain a fully quantitative agreement between experiment and theory. This is in line with the increase in the contribution of many-body effects for the inner g ionization with increasing insaturation (i.e., the availability of low-lying π* valence orbitals responsible for larger correlation effects). The agreement between theory and experiment is excellent within the above-mentioned corrections regarding the pole strengths.
Fig. 5.
Cross-section ratios between the C 2s-derived orbitals photoionization channel, such as 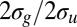 ratios in C2H2 (acetylene),
ratios in C2H2 (acetylene), 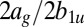 ratios in C2H4 (ethylene), and
ratios in C2H4 (ethylene), and 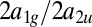 ratios in C2H6 (ethane). The error bars include only statistical contributions. The red circles are calculated points, and the blue squares with error bars are experimental results. The scaling is done for each molecule as discussed in the main text.
ratios in C2H6 (ethane). The error bars include only statistical contributions. The red circles are calculated points, and the blue squares with error bars are experimental results. The scaling is done for each molecule as discussed in the main text.
The oscillation shape and period differ for each molecule. This is expected because the C–C bond length in C2H2, C2H4, and C2H6 is different. The sensitivity of the oscillations to the bond lengths is providing a new perspective for accurate estimation of those, which is a dream of many chemists and physicists.
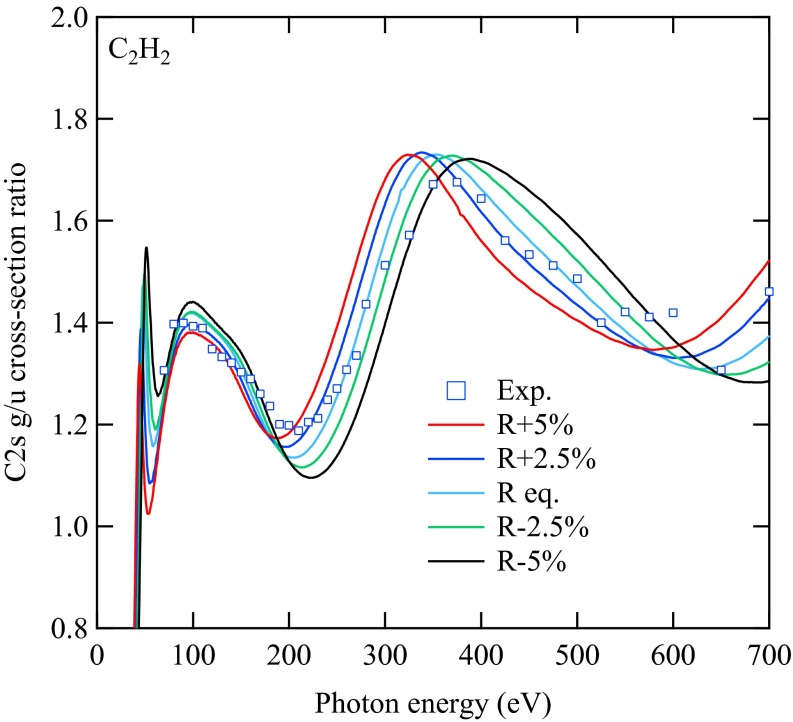
In Fig. 6, we report the ratios obtained for C2H2 computed by changing the equilibrium distance by R ± 2.5% and R ± 5.0%. A least-squares fitting is then performed, in which fitting the experimental data with the calculated profiles is scaled as 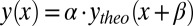 (i.e., the calculated ratio is scaled by the multiplicative factor α, and the energy is scaled by an energy shift β). From Table 1, it is apparent that the lowest
(i.e., the calculated ratio is scaled by the multiplicative factor α, and the energy is scaled by an energy shift β). From Table 1, it is apparent that the lowest 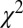 value for the fit is obtained at the experimental equilibrium value. Moreover, a parabolic fitting to the three lowest values of
value for the fit is obtained at the experimental equilibrium value. Moreover, a parabolic fitting to the three lowest values of 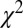 gives R(fit) = 1.2003 Å. It is clear that with the present simulation approach, it would not be difficult to reach by least-squares fitting an accuracy in the range of 0.01 Å or better in geometry determination. The number of existing methods to determine bond lengths accurately for isolated molecules is large, including, for example, gas-phase electron diffraction (GED), which has been successfully used in recent years even in a time-resolved mode to study chemical reactions, transient species, and structural modifications (e.g., ref. 37 and references therein). However, GED and other common tools are not element-specific; they are at variance with EXAFS and our newly developed method, and therefore cannot be focused on one particular pair of atoms. A strong interest in exploiting photoionization for structural determination comes from the development of ultrastrong and ultrafast new sources like free-electron laser (FEL), high-harmonic generation (HHG), and strong field ionization (ref. 38 and references therein), mostly from molecular frame photoelectron angular distribution (MFPADS). Although it is not obvious that the present approach can be extended to the ultrashort time domain, it has the advantage of not requiring difficult molecular orientation. As for absorption methods, which can be tailored to a specific absorption edge, there was a long controversy in the literature several years ago concerning the possibility of using experimental data from absorption spectra, and the energy position of continuum shape resonance features above a ionization threshold, to derive bond lengths in simple molecules, such as hydrocarbons. This method was called “bond lengths with a ruler” (39). In our opinion, although this claimed relationship could be valid only in selected cases, and did not have a general outcome, the method we propose here is founded on quantities directly related to bond distances and really can be considered as a way of deriving bond lengths with a ruler, with the “ruler” being the oscillation period. To carry on further with such a comparison, we stress that our method has significant advantages over absorption techniques because of the initial-state discrimination offered by photoelectron detection compared with total absorption, which gives the possibility of distinguishing among inequivalent sites that are summed in the absorption signal. Furthermore, our method can be applied to core, inner-valence, and outer-valence ionization processes, allowing one to choose the most suitable dataset from the standpoint of both experimental accessibility and ease of interpretation.
gives R(fit) = 1.2003 Å. It is clear that with the present simulation approach, it would not be difficult to reach by least-squares fitting an accuracy in the range of 0.01 Å or better in geometry determination. The number of existing methods to determine bond lengths accurately for isolated molecules is large, including, for example, gas-phase electron diffraction (GED), which has been successfully used in recent years even in a time-resolved mode to study chemical reactions, transient species, and structural modifications (e.g., ref. 37 and references therein). However, GED and other common tools are not element-specific; they are at variance with EXAFS and our newly developed method, and therefore cannot be focused on one particular pair of atoms. A strong interest in exploiting photoionization for structural determination comes from the development of ultrastrong and ultrafast new sources like free-electron laser (FEL), high-harmonic generation (HHG), and strong field ionization (ref. 38 and references therein), mostly from molecular frame photoelectron angular distribution (MFPADS). Although it is not obvious that the present approach can be extended to the ultrashort time domain, it has the advantage of not requiring difficult molecular orientation. As for absorption methods, which can be tailored to a specific absorption edge, there was a long controversy in the literature several years ago concerning the possibility of using experimental data from absorption spectra, and the energy position of continuum shape resonance features above a ionization threshold, to derive bond lengths in simple molecules, such as hydrocarbons. This method was called “bond lengths with a ruler” (39). In our opinion, although this claimed relationship could be valid only in selected cases, and did not have a general outcome, the method we propose here is founded on quantities directly related to bond distances and really can be considered as a way of deriving bond lengths with a ruler, with the “ruler” being the oscillation period. To carry on further with such a comparison, we stress that our method has significant advantages over absorption techniques because of the initial-state discrimination offered by photoelectron detection compared with total absorption, which gives the possibility of distinguishing among inequivalent sites that are summed in the absorption signal. Furthermore, our method can be applied to core, inner-valence, and outer-valence ionization processes, allowing one to choose the most suitable dataset from the standpoint of both experimental accessibility and ease of interpretation.
Fig. 6.
Cross-section ratios 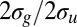 as a function of photon energy for the C2H2 molecule computed by changing the equilibrium distance.
as a function of photon energy for the C2H2 molecule computed by changing the equilibrium distance.
Table 1.
Fitting parameters of the observed spectra of C2H2 for accurate estimation of the bond length
| RCC | α | β | 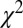 |
| 1.2027 | 0.7177 | 4.584 | 0.06973 |
| 1.2322 | 0.7500 | 9.462 | 0.10135 |
| 1.1732 | 0.6925 | −2.707 | 0.09236 |
| 1.2616 | 0.7771 | 12.500 | 0.19299 |
| 1.1438 | 0.6623 | −14.775 | 0.15578 |
The value of the fitted parameters, such as 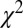 , α, and β, for various bond lengths is shown in the table. The first line is the experimental carbon-carbon bond length (RCC) value (cccbdb.nist.gov) (36).
, α, and β, for various bond lengths is shown in the table. The first line is the experimental carbon-carbon bond length (RCC) value (cccbdb.nist.gov) (36).
Moreover, chemical information, which is an input in the calculation, as the composition of the relevant MOs, is contained in the spectrum, although it is not so directly derivable from the spectral structures. However, the differential admixture of H 1s contribution, which has a fast-decreasing cross section, in the two orbitals considered can be directly monitored from the high-energy limit of the one-cycle averaged ratio. Qualitatively, this is the largest in C2H2, and it decreases rapidly in C2H4 and C2H6. Population analysis shows that although the content of C 2s in the 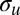 orbital is nearly constant, it is steadily decreasing from C2H2 to C2H6 in
orbital is nearly constant, it is steadily decreasing from C2H2 to C2H6 in 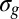 because of increasing bonding with the hydrogens, which is nicely observed in the experimental g/u ratio. It must be stressed that orbital composition is intimately related to the theoretical models chosen. In the most general formulation, this is tied to the so-called “Dyson orbital” as the initial state, which is defined perfectly well for any wave function. At the Hartree–Fock (HF) and static DFT levels, it reduces to the HF or Kohn–Sham orbital, respectively. The latter is used in the present modeling. The most obvious test of orbital composition stems from the comparison of the calculated profile with the experimental one, with different initial orbitals. This approach has been widely used, for example, in the context of MO analysis in electron momentum spectroscopy studies (e.g., refs. 40, 41). Therefore, precise orbital composition can be derived from comparison with the theoretical results using different initial orbitals. At a more qualitative level, behaviors can be directly obtained by profiles, as in the present case, for the amount of C 2s AO contribution in the initial orbitals, which is a piece of information especially valuable to obtain trends in, for example, chemically related systems, change of the bonding schemes, or amount of a specific AO in a given orbital. We speculate that it will be possible to develop simplified schemes, such as approximate multiple scattering models based on sums of atomic amplitudes, to invert experimental data in a semiquantitative way. Another very important output of our method is a precise determination of the ratio of spectroscopic factors, a number of great significance in many-body theory (the norm of the Dyson orbital), which is quite difficult to compute precisely [a look at the literature for the present molecules shows ratios differing by a factor of 2 in different calculations (42, 43)].
because of increasing bonding with the hydrogens, which is nicely observed in the experimental g/u ratio. It must be stressed that orbital composition is intimately related to the theoretical models chosen. In the most general formulation, this is tied to the so-called “Dyson orbital” as the initial state, which is defined perfectly well for any wave function. At the Hartree–Fock (HF) and static DFT levels, it reduces to the HF or Kohn–Sham orbital, respectively. The latter is used in the present modeling. The most obvious test of orbital composition stems from the comparison of the calculated profile with the experimental one, with different initial orbitals. This approach has been widely used, for example, in the context of MO analysis in electron momentum spectroscopy studies (e.g., refs. 40, 41). Therefore, precise orbital composition can be derived from comparison with the theoretical results using different initial orbitals. At a more qualitative level, behaviors can be directly obtained by profiles, as in the present case, for the amount of C 2s AO contribution in the initial orbitals, which is a piece of information especially valuable to obtain trends in, for example, chemically related systems, change of the bonding schemes, or amount of a specific AO in a given orbital. We speculate that it will be possible to develop simplified schemes, such as approximate multiple scattering models based on sums of atomic amplitudes, to invert experimental data in a semiquantitative way. Another very important output of our method is a precise determination of the ratio of spectroscopic factors, a number of great significance in many-body theory (the norm of the Dyson orbital), which is quite difficult to compute precisely [a look at the literature for the present molecules shows ratios differing by a factor of 2 in different calculations (42, 43)].
Conclusion
The present work clearly demonstrates the importance of the MO localization/delocalization for interference phenomena in photoionization. We have given a first example of a general phenomenon, namely, long-range structures in molecular photoionization. It occurs in all photoionization cross-sections: core, inner-valence, and outer-valence ones. These structures, which are easily experimentally accessible and are most evident in terms of cross-section ratios, are highly informative of geometrical structure, conformational equilibria, molecular electronic structure, and many-body effects that can often be qualitatively understood in simple structural terms and may be quantitatively reconstructed by least-squares fitting by means of accurate theoretical modeling with robust and established computational simulations.
The present results open the way to extensive investigations of such phenomena in a wide range of systems. Present DFT simulation of the spectra is very accurate and may provide an important tool for their quantitative analysis.
Materials and Methods
Sample Handling, Beamline, and Electron Spectrometer.
Experiments have been carried out at the soft X-ray PLEIADES beamline of the Synchrotron SOLEIL (31). An 80-mm period Apple II undulator was used, which covers the energy range of 35–1,000 eV, with variable polarization starting from 55 eV. The measurements were carried out using a wide-angle lens VG-Scienta R4000 electron spectrometer installed at a fixed position, with the electron detection axis perpendicular to the storage ring plane. X-ray light polarization was set at the magic angle of 54.7° with respect to the electron detection axis. The gas-phase samples C2H2, C2H4, and C2H6 (99.95% purities; Air Liquide) were introduced in a gas cell with polarized electrodes, which were adjusted to minimize the effect of plasma potentials caused by the ion density gradient created along the synchrotron beam propagating through the gas cell. The gas pressure in the spectrometer vacuum chamber was kept constant at about 6.5 × 10−6 mbar for all measurements. The contribution of the R4000 electron analyzer to the instrumental broadening was 200 meV, defined by the pass energy of 100 eV and the curved entrance slit of 0.8 mm. A platinum-coated diffraction grating with 1,600 L/mm was used to produce monochromatic radiographs, and the monochromator exit slit was adjusted to maintain the photon energy resolution at about 200 meV in the photon energy range of 70–700 eV used in this study.
Theoretical Methods.
Cross-section calculations have been performed at the static-exchange DFT level (i.e., using both bound and continuum orbitals obtained as eigenfunctions of the Kohn–Sham Hamiltonian defined by the ground-state density ρ):
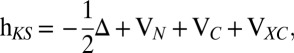 |
where VN is the nuclear attraction potential, VC(ρ) is the Coulomb potential, and VXC(ρ) is the exchange correlation potential, defined by ρ. For VXC, we have used the LB-94 potential (32). All orbitals are expanded in a multicenter basis obtained as products of radial B-spline functions (34) times spherical harmonics, fully adapted to the molecular symmetry. Asymptotic angular expansions up to a maximum L angular momentum value of 20 for C2H2 and 24 for C2H4 and C2H6, which ensure complete convergence of the calculated cross-sections up to 40 arbitrary units of electron kinetic energy, have been used. Full details of the method have been documented previously (34, 35).
Acknowledgments
The authors thank the Synchrotron SOLEIL staff for smooth operation of the facility and the personnel of the PLEIADES beamline for assistance in setting up the experiment (Project 20110691). P.D. acknowledges the generous granting of computing time from the Cineca. R.K.K. and M.N.P. thank the French Agence Nationale de la Recherche (ANR) for financial support in the framework of a “Chaire d’Excellence” grant. P.D. acknowledges support from Italian Project Programma di ricerca di Rilevante Interesse Nazionale (PRIN) 2009.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Feynman RP, Leighton R, Sands M. The Feynman Lectures on Physics. Vol III. Reading, MA: Addison–Wesley; 1965. pp. 1-1–1-9. [Google Scholar]
- 2.Jönsson C. Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Z Phys. 1961;161:454–474. German. [Google Scholar]
- 3.Jönsson C. Electron diffraction at multiple slits. Am J Phys. 1974;42:4–11. [Google Scholar]
- 4.Arndt M, et al. Wave-particle duality of C60 molecules. Nature. 1999;401(6754):680–682. doi: 10.1038/44348. [DOI] [PubMed] [Google Scholar]
- 5.Cohen HD, Fano U. Interference in the photo-ionization of molecules. Phys Rev. 1966;150:30–33. [Google Scholar]
- 6.Samson JAR, Cairns RB. Total absorption cross sections of H2, N2, and O2 in the region 550-200 Å. J Opt Soc Am. 1965;55:1035. [Google Scholar]
- 7.Walter M, Briggs J. Photo-double ionization of molecular hydrogen. J Phys B At Mol Opt Phys. 1999;32:2487–2587. [Google Scholar]
- 8.Joulakian B, Hanssen J, Rivarola R, Motassim A. Dissociative ionization of H2+ by fast-electron impact: Use of a two-center continuum wave function. Phys Rev A. 1996;54(2):1473–1479. doi: 10.1103/physreva.54.1473. [DOI] [PubMed] [Google Scholar]
- 9.Milne-Brownlie DS, Foster M, Gao J, Lohmann B, Madison DH. Young-type interference in (e, 2e) ionization of H2. Phys Rev Lett. 2006;96(23):233201. doi: 10.1103/PhysRevLett.96.233201. [DOI] [PubMed] [Google Scholar]
- 10.Kamalou O, et al. Evidence for interference effects in both slow and fast electron emission from D2 by energetic electron impact. Phys Rev A. 2005;71:010702. [Google Scholar]
- 11.Stolterfoht N, et al. Evidence for interference effects in electron emission from H2 colliding with 60 MeV/u Kr34+ ions. Phys Rev Lett. 2001;87:023201. [Google Scholar]
- 12.Misra D, et al. Interference effect in electron emission in heavy ion collisions with H2 detected by comparison with the measured electron spectrum from atomic hydrogen. Phys Rev Lett. 2004;92(15):153201. doi: 10.1103/PhysRevLett.92.153201. [DOI] [PubMed] [Google Scholar]
- 13.Rolles D, et al. Isotope-induced partial localization of core electrons in the homonuclear molecule N2. Nature. 2005;437(7059):711–715. doi: 10.1038/nature04040. [DOI] [PubMed] [Google Scholar]
- 14.Liu XJ, et al. Young’s double-slit experiment using core-level photoemission from N2: Revisiting Cohen-Fano’s two-centre interference phenomenon. J Phys B At Mol Opt Phys. 2006;39:4801–4817. [Google Scholar]
- 15.Akoury D, et al. The simplest double slit: Interference and entanglement in double photoionization of H2. Science. 2007;318(5852):949–952. doi: 10.1126/science.1144959. [DOI] [PubMed] [Google Scholar]
- 16.Kreidi K, et al. Interference in the collective electron momentum in double photoionization of H2. Phys Rev Lett. 2008;100(13):133005. doi: 10.1103/PhysRevLett.100.133005. [DOI] [PubMed] [Google Scholar]
- 17.Hergenhahn U, Kugeler O, Rüdel A, Rennie EE, Bradshaw AM. Symmetry-selective observation of the N 1s shape resonance in N2. J Phys Chem A. 2001;105:5704–5708. [Google Scholar]
- 18.Kempgens B, et al. Core level energy splitting in the C 1s photoelectron spectrum of C2H2. Phys Rev Lett. 1997;79:3617. [Google Scholar]
-
19.Thomas TD, et al. Photon energy dependence of the
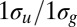 intensity ratio in carbon 1s photoelectron spectroscopy of ethyne. Phys Rev Lett. 1999;82:1120. [Google Scholar]
intensity ratio in carbon 1s photoelectron spectroscopy of ethyne. Phys Rev Lett. 1999;82:1120. [Google Scholar] - 20.Canton SE, et al. Direct observation of Young’s double-slit interferences in vibrationally resolved photoionization of diatomic molecules. Proc Natl Acad Sci USA. 2011;108:7302–7306. [Google Scholar]
- 21.Argenti L, et al. Double-slit experiment with a polyatomic molecule: Vibrationally resolved C 1s photoelectron spectra of acetylene. New J Phys. 2012;14:033012. [Google Scholar]
- 22.Tachino CA, Galassi ME, Martín F, Rivarola RD. Coherence in collisionally induced electron emission from diatomic heteronuclear molecules. J Phys B At Mol Opt Phys. 2009;42:075203. [Google Scholar]
- 23.Tachino CA, Galassi ME, Martín F, Rivarola RD. Partial localization in coherent electron emission from asymmetric diatomic molecules. J Phys B At Mol Opt Phys. 2010;43:135203. [Google Scholar]
- 24.Benning PJ, et al. Electronic states of solid C60: Symmetries and photoionization cross sections. Phys Rev B Condens Matter. 1991;44(4):1962–1965. doi: 10.1103/physrevb.44.1962. [DOI] [PubMed] [Google Scholar]
- 25.Liebsch T, et al. Angle-resolved photoelectron spectroscopy of C60. Phys Rev A. 1995;52(1):457–464. doi: 10.1103/physreva.52.457. [DOI] [PubMed] [Google Scholar]
- 26.Söderström J, et al. Nonstoichiometric intensities in core photoelectron spectroscopy. Phys Rev Lett. 2012;108(19):193005. doi: 10.1103/PhysRevLett.108.193005. [DOI] [PubMed] [Google Scholar]
- 27.Carroll TX, et al. Intensity oscillations in the carbon 1s ionization cross sections of 2-butyne. J Chem Phys. 2013;138(23):234310–234315. doi: 10.1063/1.4810870. [DOI] [PubMed] [Google Scholar]
- 28.Potts AW, Streets DG. Photoelectron spectra of inner valence shells, Part 1. Unsaturated hydrocarbons. J Chem Soc Faraday Trans 2. 1974;70:875–884. [Google Scholar]
- 29.Streets DG, Potts AW. Photoelectron spectra of inner valence shells Part 2.-unsaturated hydrocarbons. J Chem Soc Faraday Trans 2. 1974;70:1505–1515. [Google Scholar]
- 30.Pireaux JJ, et al. Core-electron relaxation energies and valence-band formation of linear alkanes studied in the gas phase by means of electron spectroscopy. Phys Rev A. 1976;14:2133–2146. [Google Scholar]
- 31.Miron C, et al. Imaging molecular potentials using ultrahigh-resolution resonant photoemission. Nat Phys. 2012;8:135–139. [Google Scholar]
- 32.van Leeuwen R, Baerends EJ. Exchange-correlation potential with correct asymptotic behavior. Phys Rev A. 1994;49(4):2421–2431. doi: 10.1103/physreva.49.2421. [DOI] [PubMed] [Google Scholar]
- 33.Bachau H, Cormier E, Decleva P, Hansen JE, Martín F. Applications of B-splines in atomic and molecular physics. Rep Prog Phys. 2001;64:1815–1943. [Google Scholar]
- 34.Toffoli D, Stener M, Fronzoni G, Decleva P. Convergence of the multicenter B-spline DFT approach for the continuum. Chem Phys. 2002;276:25–43. [Google Scholar]
- 35.Stener M, Fronzoni G, Decleva P. Time-dependent density-functional theory for molecular photoionization with noniterative algorithm and multicenter B-spline basis set: CS2 and C6H6 case studies. J Chem Phys. 2005;122(23):234301. doi: 10.1063/1.1937367. [DOI] [PubMed] [Google Scholar]
- 36.Strey G, Mills IM. Anharmonic force field of acetylene. J Mol Spectrosc. 1976;59:103–115. [Google Scholar]
- 37.Zewail AH. 4D ultrafast electron diffraction, crystallography, and microscopy. Annu Rev Phys Chem. 2006;57:65–103. doi: 10.1146/annurev.physchem.57.032905.104748. [DOI] [PubMed] [Google Scholar]
- 38.Blaga CI, et al. Imaging ultrafast molecular dynamics with laser-induced electron diffraction. Nature. 2012;483(7388):194–197. doi: 10.1038/nature10820. [DOI] [PubMed] [Google Scholar]
- 39.Piancastelli MN. The neverending story of shape resonances. J Electron Spectrosc Relat Phenomena. 1999;100:167–190. [Google Scholar]
- 40.Miao YR, Ning CG, Deng JK. Calculation of Dyson orbitals using a symmetry-adapted-cluster configuration-interaction method for electron momentum spectroscopy: N2 and H2O. Phys Rev A. 2011;83:062706–062707. doi: 10.1063/1.3593271. [DOI] [PubMed] [Google Scholar]
- 41.Tian Q, Yang J, Shi Y, Shan X, Chen X. Outer- and inner-valence satellites of carbon dioxide: Electron momentum spectroscopy compared with symmetry-adapted-cluster configuration interaction general-R calculations. J Chem Phys. 2012;136(9):094306–094310. doi: 10.1063/1.3691103. [DOI] [PubMed] [Google Scholar]
- 42.Duffy P, et al. Electron momentum spectroscopy of the valence orbitals of acetylene: Quantitative comparisons using near Hartree-Fock limit and correlated wavefunctions. Chem Phys. 1992;165:183–199. [Google Scholar]
- 43.Hasegawa J, Ehara M, Nakatsuji H. Theoretical study on the ionized states of ethylene by the SAC-CI (general-R) method. Chem Phys. 1998;230:23–30. [Google Scholar]