Joint Modeling and Estimation for Recurrent Event Processes and Failure Time Data

Abstract

Recurrent event data are commonly encountered in longitudinal follow-up studies related to biomedical science, econometrics, reliability, and demography. In many studies, recurrent events serve as important measurements for evaluating disease progression, health deterioration, or insurance risk. When analyzing recurrent event data, an independent censoring condition is typically required for the construction of statistical methods. In some situations, however, the terminating time for observing recurrent events could be correlated with the recurrent event process, thus violating the assumption of independent censoring. In this article, we consider joint modeling of a recurrent event process and a failure time in which a common subject-specific latent variable is used to model the association between the intensity of the recurrent event process and the hazard of the failure time. The proposed joint model is flexible in that no parametric assumptions on the distributions of censoring times and latent variables are made, and under the model, informative censoring is allowed for observing both the recurrent events and failure times. We propose a “borrow-strength estimation procedure” by first estimating the value of the latent variable from recurrent event data, then using the estimated value in the failure time model. Some interesting implications and trajectories of the proposed model are presented. Properties of the regression parameter estimates and the estimated baseline cumulative hazard functions are also studied.

1. INTRODUCTION

Recurrent event data are often collected in longitudinal follow-up studies. During the observation period, recurrent events, such as repeated tumor occurrences (Byar 1980), repeated hospitalizations (Eaton et al. 1992a,b), or recurrent injuries (Wassell, Wojciechowski, and Landen 1999), are recorded in the studies. The observation of recurrent events could be terminated (i.e., censored) by loss to follow-up, end of the study, or a failure event such as death. Conventional analysis usually focuses on either failure time data (Cox 1972; Cox and Oakes 1984) or recurrent event data [Prentice, Williams, and Peterson 1981; Andersen and Gill 1982; Pepe and Cai 1993; Lin, Wei, Yang, and Ying 2000; Wang, Qin, and Chiang (WQC) 2001]. In this article, the event process and the failure time are both of interest, and we consider the joint modeling of a recurrent event process and a failure time.

In analyzing recurrent event data, an independent censoring condition is usually required for the development of statistical methods under different types of models. When a failure event serves as a part of the censoring mechanism, validity of the independent censoring assumption is violated when the recurrent event process is correlated with the failure time. Lancaster and Intrator (1998) considered a joint parametric model of the recurrent event process and the failure time, and demonstrated the use of their methodology using AIDS panel data. In their work, then used a latent variable to characterize the association between the recurrent event process and the failure time, and a common baseline function is shared by the intensity of the recurrent event process and the hazard of the failure time. In non-parametric and semiparametric settings, WQC (2001) proposed estimation procedures for estimating the cumulative rate function and regression parameters under multiplicative intensity models with dependent censoring. The WQC model focused on the distributional pattern of the recurrent event process where the censoring time was treated as a nuisance and the joint modeling of recurrent event process and failure time was not considered.

To jointly model recurrent events and failure time, Ghosh and Lin (2003) studied correlated marginal models for these two outcomes. At the cost of censoring some of the originally uncensored data, they developed estimation inferences with the correlation between recurrent events and failure time unspecified. Using a general censoring pattern, Huang and Wang (2002) proposed statistical methods to study two nested joint models of a recurrent event process and a failure time, where the correlation of the two outcomes is partially specified in the conditional distribution of the recurrent event process given the failure time. Note that neither of those two articles used frailty in their joint models. In this article we consider joint modeling of the recurrent event process and the failure time via frailty. This joint model has attractive features of frailty models, especially in its interpretation of correlation, and avoids parametric assumptions on the frailty term.

The article is organized as follows. In Section 2 we introduce a joint model of recurrent event process and failure time in which a common subject-specific latent variable (frailty) is used to model the association between intensity of the recurrent event process and hazard of the failure time. The proposed joint model is flexible in that no parametric assumptions on the distributions of censoring times and latent variables are made, and under the model, informative censoring is allowed for observing both the recurrent events and failure times. In Section 3 we present theoretical implications and trajectories of the proposed model. In Section 4 we study a “borrow-strength estimation procedure” by first estimating the value of the latent variable from recurrent event data, then using the estimated values in the failure time models. We explore properties of the regression parameter estimators and the estimated baseline cumulative hazard functions. In Section 5 we report results of simulation studies, along with the application to a Denmark schizophrenia case cohort study, and we conclude with discussion in Section 6.

2. NOTATION AND THE JOINT MODEL

Let N(t) denote the number of events occurring before or at time t, and let D be the failure time and C be the potential censoring time for reasons other than the failure event. The research interest is to derive inferential results on N(·) and D within a fixed time interval [0, T₀], where the event process potentially could be observed beyond T₀. Let X be a 1 × p vector of covariates. We then make the following model assumptions:

• (M1)
  There exists a nonnegative-valued latent variable Z so that, given X = x and Z = z, the recurrent event process N(·) is a nonstationary Poisson process with intensity function

  $$\lambda \left(t\right)=z{\lambda }_0\left(t\right)\exp \left(x\alpha \right),0\le t\le T_0,$$

  where α is a p × 1 vector of parameters and the baseline intensity function λ₀(t) is a continuous function with ${\Lambda }_0\left(T_0\right)={\int }_0^{T_0}{\lambda }_0\left(u\right)du=1$. The latent variable Z satisfies E(Z|X) = E(Z).
• (M2)
  Given (x, z), the hazard function of D takes the form

  $$h\left(t\right)={\mathit{zh}}_0\left(t\right)\exp \left(x\beta \right),$$

  where β is a p × 1 vector of parameters and the baseline hazard function h₀(t) is continuous.
• (M3)Conditioning on (x, z), (N(·), D, C) are mutually independent.

The occurrence of recurrent events is modeled by a subject-specific Poisson process via a latent variable. Conditioning on z, the rate function equals the intensity function, because a Poisson process is memoryless. Under (M1), the baseline in tensity function λ₀(t) is shared by all subjects and is left unspecified. A multiplicative hazard function with the same latent variable but a different baseline function is assumed for the hazard of failure event in (M2). Clearly, a large value of z inflates both the intensity of recurrent events and the hazard of the failure event. Under assumption (M3), D, C, and N(·) are allowed to be correlated via their connection with (x, z). This model relaxes the requirement that a common baseline function be shared by the intensity of N(·) and the hazard of D assumed by Lancaster and Intrator (1998), while keeping the semiparametric model features of WQC (2001). Define Y = min(C, D, T₀), the time when the observation of the recurrent event process is terminated, and Δ_i = I(D_i ≤ Y_i), the observed censoring indicator. By further conditioning on z, the usual independent censoring condition that N(·) is independent of Y given x is relaxed for recurrent events, and, interestingly, the independent censoring condition that D be independent of C given x is also relaxed for failure time data.

Note that the rate function of event occurrence at time t in a random population, for study subjects with explanatory variable x, is μ_Zλ₀(t) exp(xα), where μ_Z = E[Z]. In many public health and biomedical studies, the rate function is preferred for analysis, especially in identifying treatment effects and risk factors, because of its marginal interpretation. For instance, the parameter α can be interpreted as the logarithm of the ratio of the rate function for every unit increase in the explanatory variable.

Under (M1)–(M3), the distribution of Z, the baseline functions λ₀(t) and h₀(t), and the distribution of C serve as nonparametric components in the model. In the next section we examine model implications with or without additional parametric assumptions on Z, yet with no parametric assumptions made on Z for our development of estimation inferences in Section 4.

3. MODEL IMPLICATIONS

Let $\mathcal{H}\left(t\right)=\left\{N\right(u):0\le u\le t\}$ be the event history up to t, and let t₁ ≤ t₂ ≤ … ≤ t_N(t) be the ordered event times before or at t. Define f_Z(·) as the probability density function of the latent variable Z, f(·) as a general probability density function, and f(·|·) as a general conditional probability density function. In this section we discuss model implications under the proposed joint model with or without additional parametric assumptions on Z. To simplify the discussion, we consider the reduced model without covariates. Similar results for regression models with covariates can be obtained with replacement (Λ₀(t), λ₀(t), H₀(t), h₀(t)) by (Λ₀(t)e^xα, λ₀(t)e^xα, H₀(t)e^xβ, h₀(t)e^xβ).

Proposition 1 (Posterior mean of Z). Given the observed recurrent event data, we show in Appendix A that the posterior mean of Z can be expressed as

$$E\left[Z\right]\mathcal{H}\left(y\right),y]=\frac{N\left(y\right)+1}{{\Lambda }_0\left(y\right)}\times \frac{f\left(N\right(y)+1\mid y)}{f\left(N\right(y)\mid y)},$$

where f(N(y)|y) is the conditional probability density function of N(Y) given Y. We can see that, given the follow-up time y, the posterior mean depends on the event history $\mathcal{H}\left(y\right)$ only through the number of observed events. The posterior mean can be used for individual-specific prediction when additional model assumptions are available for obtaining an explicit form of the formula.

Proposition 2 (Residual lifetime). Let t and s be nonnegative constants. For individuals who survive beyond time t (D ≥ t), the conditional probability for the residual life time to be longer than s units of time given $\mathcal{H}\left(t\right)$ is

$$P(D\ge t+s\mid \mathcal{H}(t),D\ge t)=\frac{E\left[e^{-Z\left\{H_0\right(t+s)+{\Lambda }_0(t\left)\right\}}{Z}^{N\left(t\right)}\right]}{E\left[e^{-Z\left\{H_0\right(t)+{\Lambda }_0(t\left)\right\}}{Z}^{N\left(t\right)}\right]}.$$

The derivation is given in Appendix A. The computation implies that

$$P(D\ge t+s\mid N(t),D\ge t)=P(D\ge t+s\mid \mathcal{H}(t),D\ge t);$$

that is, the residual life time probability depends on the event history only through the number of events occurring up to time t. Further, the median residual lifetime after time t can be obtained by solving P(D ≥ t + s|N(t), D ≥ t) = 1/2. The residual lifetime unconditional on the event history has the survival function

$$P(D\ge t+s\mid D\ge t)=\frac{E\left[e^{-{\mathit{ZH}}_0(t+s)}\right]}{E\left[e^{-{\mathit{ZH}}_0\left(t\right)}\right]}.$$

For the specific case where Z is distributed as gamma(a, b) with mean a/b, the residual lifetime probability, given the event history, has the survivor function

$$P(D\ge t+s\mid N(t),D\ge t)={\left(\frac{b+H_0\left(t\right)+{\Lambda }_0\left(t\right)}{b+H_0(t+s)+{\Lambda }_0\left(t\right)}\right)}^{N\left(t\right)+a}.$$

This conditional survival function has the following interesting interpretation. With each additional event occurrence in the time interval [0, t], the survival probability at time t + s is decreased by the constant factor, {b + H₀(t) + Λ₀(t)}/{b + H₀(t + s) + Λ₀(t)} where the constant factor has a value between 0 and 1 and depends on (H₀(t), H₀(t + s), Λ₀(t), b). In additional, with the assumption that Z is distributed as gamma(a, b), the survival function for the residual lifetime unconditional on the event history can be expressed as

$$P(D\ge t+s\mid D\ge t)={\left(\frac{b+H_0\left(t\right)}{b+H_0(t+s)}\right)}^a.$$

It is then interesting to see that P(D ≥ t + s|N(t) = 0, D ≥ t) ≥ P(D ≥ t + s|D ≥ t), where the inequality relationship becomes strict if Λ₀(t) > 0 and H₀(t + s) > H₀(t) as s > 0. That is, survivors at time t who experienced no events before t would have higher probability to live s units of residual lifetime than those population survivors at time t.

Proposition 3 (Residual lifetime for censored subjects). It is also possible to examine the residual lifetime of those who are censored at time t given the event history

$$\begin{array}{cc}\hfill P(D\ge t+s\mid Y=t,\Delta =0,& \mathcal{H}\left(t\right))\hfill \\ \hfill & =\frac{E[e^{-Z\left\{H_0\right(t+s)+{\Lambda }_0(t\left)\right\}{Z}^{N\left(t\right)}{f}_c(t\mid Z)]}}{E[e^{-Z\left\{H_0\right(t)+{\Lambda }_0(t\left)\right\}{Z}^{N\left(t\right)}{f}_c(t\mid Z)]}},\hfill \end{array}$$

where Δ = I(D ≤ C) is the censoring indicator and f_c(t|z) is the conditional probability density function of the censoring time, C, given Z. If we assume that the hazard function of C given Z is λ_c(t|z) = zg₀(t) and that Z is distributed as gamma(a, b), then we have

$$\begin{array}{cc}\hfill P(D\ge t+s\mid N(t),& Y=t,\Delta =0)\hfill \\ \hfill & ={\left(\frac{b+H_0\left(t\right)+{\Lambda }_0\left(t\right)+G_0\left(t\right)}{b+H_0(t+s)+{\Lambda }_0\left(t\right)+G_0\left(t\right)}\right)}^{a+N\left(t\right)+1},\hfill \end{array}$$

where G₀ is the cumulative distribution function of g₀. With each additional event, the probability of surviving an extra s unit of time after being censored at t is decreased by a constant factor, where the constant factor depends on (H₀(t), H₀(t + s), Λ₀(t), G₀(t), b).

Proposition 4 (Effect of failure time on recurrent events). We derive in Appendix A the mean function of the recurrent event process conditional on the failure time. For t ≥ s,

$$E\left[N\right(s)\mid D\ge t]=\frac{E\left[{\mathit{Ze}}^{-{\mathit{ZH}}_0\left(t\right)}\right]}{E\left[e^{-{\mathit{ZH}}_0\left(t\right)}\right]}{\Lambda }_0\left(s\right).$$

The mean function given failure time can be decomposed into two parts, one part depending on the baseline cumulative rate function, and the other part depending on the baseline cumulative hazard function and the frailty distribution. The function E[N(s)|D ≥ t] can be further shown to be decreasing in t, where t ≥ s. This result is intuitive, because our model implies that the subject-specific event occurrence rate is positively correlated with the risk of failure event; subjects who survive longer tend to have lower event occurrence rates.

4. ESTIMATION PROCEDURE AND ASYMPTOTIC PROPERTIES

4.1 A Brief Review

Let subscript i be the index for a subject, i = 1, 2, …, n. For subject i, let X_i denote the time-independent covariate, Z_i denote the subject-specific latent variable, Y_i denote the observed terminating time for observing the event process N_i(·), D_i denote the failure time, and Δ_i = I(D_i ≤ Y_i) denote the censoring indicator. We further let m_i denote the number of recurrent events occurring before time Y_i and t_i1, …, t_imi denote the observed event times for subject i. For ease of notation, we use m_i and t_ij, i = l,2, …, n, j = 1,2, …, m_i, to denote either random variables or realized values. Assume that {(X_i, Z_i, N_i(·), D_i, C_i)} are iid, so that the observed {(X_i, Z_i, m_i, (t_i1, …, t_imi), Y_i)} are also iid.

Under assumption (M3), Y and N(·) are independent given the values of Z and X. The estimation procedure of WQC (2001) can then be adopted to estimate Λ₀ and α. A key step of their estimation procedure is to observe that, conditional on (x_i, y_i, z_i, m_i), the observed event times, {t_i1, t_i2, …, t_imi}, are the order statistics of a set of iid random variables with the density function π_i(t), where, for z_i > 0,

$${\pi }_i\left(t\right)=\frac{z_i{\lambda }_0\left(t\right)\exp \left(\alpha {\mathbf{x}}_i\right)}{z_i{\Lambda }_0\left(y_i\right)\exp \left(\alpha {\mathbf{x}}_i\right)}=\frac{{\lambda }_0\left(t\right)}{{\Lambda }_0\left(y_i\right)},0\le t\le y_i.$$

Note that π_i(t) depends on neither z_i nor x_i, and it is a truncated density function of λ₀(t) with observations truncated from the right side of y_i. As a result, the conditional likelihood function L_c given (x_i, y_i, z_i, m_i), where

$$L_c\propto \prod _{i=1}^n\prod _{j=1}^{m_i}\frac{{\lambda }_0\left(t_{\mathit{ij}}\right)}{{\Lambda }_0\left(y_i\right)},$$

does not require information on x_i and the unobserved z_i. Although the data are correlated, computationally the conditional likelihood has the form of the nonparametric likelihood for independently right-truncated data. The nonparametric maximum likelihood estimator (MLE) of Λ₀, ${\widehat{\Lambda }}_0$, based on randomly truncated data is known to have a product-limit representation (Wang, Jewell, and Tsai 1986),

$${\widehat{\Lambda }}_0\left(t\right)=\prod _{s_{\left(l\right)}>t}\left(1-\frac{d_{\left(l\right)}}{R_{\left(l\right)}}\right),$$

where {s_(l)} are the ordered and distinct values of the event times {t_ij}, d_(l) is the number of events occurring at s_(l), and R_(l) is the total number of events with event time and observation terminating time satisfying {t_ij ≤ s_(l) ≤ y_i}.

It follows from E[m_i|X_i, Y_i, Z_i] = Z_iexp(X_iα)Λ₀(Y_i) that

$$\begin{array}{cc}\hfill E\left[m_i{\Lambda }_0^{-1}\right(Y_i)\mid {\mathbf{X}}_i,Y_i]& =E\left[E\right[m_i\mid {\mathbf{X}}_i,Y_i,Z_i\left]{\Lambda }_0^{-1}\right(Y_i)\mid {\mathbf{X}}_i,Y_i]\hfill \\ \hfill & ={\mu }_Z\exp \left({\mathbf{X}}_i\alpha \right).\hfill \end{array}$$

Thus a class of estimating equations for α is defined as

$$n^{-1}\sum _{i=1}^n{w}_i{\stackrel{‒}{X}}_i^T(m_i{\Lambda }_0{\left(Y_i\right)}^{-1}-\exp ({\stackrel{‒}{\mathbf{X}}}_i\gamma \left)\right)=0,$$ (1)

where ${\stackrel{‒}{\mathbf{X}}}_i=(1,{\mathbf{X}}_i)$, γ^T = (ln(μ_Z), α^T), and w_i is a weight function depending on (X_i, γ, Λ₀). An estimate of α, $\widehat{\alpha }$ can be obtained by solving the estimating equation with Λ₀(Y_i) replaced by ${\widehat{\Lambda }}_0\left(Y_i\right)$.

It is clearly seen that the estimation focus of WQC (2001) was placed on the recurrent event process where the occurrence of the failure event is treated as a nuisance. In Section 4.2 we consider inferential results for the failure event as well as the joint model.

4.2 A Borrow-Strength Method

Let $\widehat{\epsilon }$ and ε represent the sample empirical means and the limit of average expectation. More specifically, for any function a of (X, Y, Z, Δ), let $\widehat{\epsilon }\left\{a\right(\mathbf{X},Y,\mathbf{Z},\Delta \left)\right\}=n^{-1}{\sum }_{i=1}^{n}a({\mathbf{X}}_i,Y_i,Z_i,{\Delta }_i)$ and $\epsilon \left\{a\right(\mathbf{X},Y,Z,\Delta \left)\right\}={\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^{n}E\left[a\right({\mathbf{X}}_i,Y_i,Z_i,{\Delta }_i\left)\right]$, assuming existence of the limit.

Conditional on {(X_i, Y_i, Z_i), i = 1,…, n}, under (M2) the score function derived from the partial likelihood can be expressed as

$$\begin{array}{cc}\hfill U\left(\beta \right)=& \frac{1}{n}\sum _{i=1}^n{\Delta }_i\left\{{\mathbf{X}}_i-\frac{{\Sigma }_{j=1}^n{\mathbf{X}}_j{Z}_j\exp \left({\mathbf{X}}_j\beta \right)I(Y_j\ge Y_i)}{{\Sigma }_{j=1}^n{Z}_j\exp \left({\mathbf{X}}_j\beta \right)I(Y_j\ge Y_i)}\right\}\hfill \\ \hfill & \times I(Y_i\le T_0)\hfill \\ \hfill =& \widehat{\epsilon }\left\{\mathbf{X}\Delta I\right(Y\le T_0\left)\right\}-{\int }_0^{T_0}\frac{\widehat{\epsilon }\left\{\mathbf{X}Z\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}{\widehat{\epsilon }\left\{Z\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}\hfill \\ \hfill & \times d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}.\hfill \end{array}$$ (2)

U defines a functional of four empirical processes for each fixed β. It is known that under mild regularity conditions, U(β) converges almost surely to $\mathcal{U}\left(\beta \right)$ for each fixed β, where

$$\begin{array}{cc}\hfill \mathcal{U}\left(\beta \right)=& \epsilon \left\{\mathbf{X}\Delta I\right(Y\le T_0\left)\right\}\hfill \\ \hfill & -{\int }_0^{T_0}\frac{\epsilon \left\{\mathbf{X}Z\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}{\epsilon \left\{Z\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}.\hfill \end{array}$$

Under (M3) and minor regularity conditions, it can be proved that the two equalities

$$d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}=\epsilon \left\{Z\exp \right(\beta \mathbf{X}\left)I\right(Y\ge s\left)\right\}{h}_0\left(s\right)\mathit{ds}$$

and

$$d\epsilon \left\{\mathbf{X}\Delta I\right(Y\le s\left)\right\}=\epsilon \left\{\mathbf{X}Z\exp \right(\beta \mathbf{X}\left)I\right(Y\ge s\left)\right\}{h}_0\left(s\right)\mathit{ds}$$

hold when β satisfies (M2). It follows that $\mathcal{U}\left(\beta \right)=0$ if β is the true regression parameter. By applying the Cauchy–Schwartz inequality to the derivative of $\mathcal{U}$, it can be further shown that the true regression parameter is the unique root (zero-crossing) of $\mathcal{U}$.

In reality, we are not able to observe the value of Z, and thus cannot have the direct use of the score function U. Conditioning on (X_i, Y_i, Z_i), the expected value of m_i is Z_iexp(X_iα)Λ₀(Y_i). It is natural to estimate Z_i by

$${\widehat{Z}}_i=\frac{m_i}{{\widehat{\Lambda }}_0\left(Y_i\right)e^{{\mathbf{X}}_i\widehat{\alpha }}},$$

where ${\widehat{\Lambda }}_0(\cdot )$ and $\widehat{\alpha }$ are obtained from the estimation procedure discussed in the previous section. We propose a “borrow-strength estimation procedure” as follows. First, compute the individual frailty value ${\widehat{Z}}_i$. Next, estimate the empirical processes in the score function (2) by plugging in $({\widehat{Z}}_1,\dots ,{\widehat{Z}}_n)$, and, in the final step, use this working score function to estimate β.

Note that the estimate of Λ₀(t), and hence of Z_i, is obtained from the entire collection of recurrent event data, and that ${\widehat{Z}}_i$ captures the subject-specific characteristics under model (M1)–(M3). The proposed estimator ${\widehat{Z}}_i$ has desirable moment properties; as we show in the next section, the two processes $\widehat{\epsilon }\left\{\widehat{Z}\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}$ and $\widehat{\epsilon }\left\{\mathbf{X}\widehat{Z}\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}$ converge almost surely to the limits ε{Zexp(Xβ)I(Y ≥ s)} and ε{Zexp(Xβ)I(Y ≥ s)} for each fixed β. Therefore, this strength-borrowing method allows the working score function to attain the same limit $\mathcal{U}$ as if the latent variable were observed. The zero-crossing of the working score function serves as an estimator of the zero-crossing of $\mathcal{U}$, that is, β. To be specific, the working score function $\widehat{U}$ of U is given by

$$\begin{array}{cc}\hfill \widehat{U}\left(\beta \right)=& \widehat{\epsilon }\left\{\mathbf{X}\Delta I\right(Y\le T_0\left)\right\}\hfill \\ \hfill & -{\int }_0^{T_0}\frac{\widehat{\epsilon }\left\{\mathbf{X}\widehat{Z}\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\},\hfill \end{array}$$ (3)

with the usual convention that 0/0 = 0. We show in Section 5 that $\widehat{U}$ converges to $\mathcal{U}$ almost surely in a neighborhood of β. We then estimate β by $\widehat{\beta }$, where $\widehat{U}\left(\widehat{\beta }\right)=0$ = 0.

If Z were observed, then the Breslow estimator ${\tilde{H}}_0\left(t\right)$ of the baseline cumulative hazard function, H₀, would be

$${\tilde{H}}_0\left(t\right)={\int }_0^t\frac{d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}}{\widehat{\epsilon }\left\{Z\exp \right(\mathbf{X}\widehat{\beta }\left)I\right(Y\ge s\left)\right\}},$$

which is a functional of two empirical processes. Under the conditional independence assumption of C and D, given (X, Z), we can show that the baseline cumulative hazard function, H₀(t), is the limit of ${\tilde{H}}_0\left(t\right)$.

As with the estimation procedure for the regression parameters, we propose an estimator of H₀(t) as

$${\widehat{H}}_0\left(t\right)={\int }_0^t\frac{d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}\exp \right(\mathbf{X}\widehat{\beta }\left)I\right(Y\ge s\left)\right\}}.$$ (4)

The limit of the estimator ${\widehat{H}}_0\left(t\right)$ can be shown to be the functional of the limits of the two processes in (4), that is, ${\widehat{H}}_0\left(t\right)\to H_0\left(t\right)$ almost surely. We study the asymptotic normality of the proposed estimator ${\widehat{H}}_0\left(t\right)$ in the next section.

5. LARGE-SAMPLE PROPERTIES

To study the large-sample properties of the proposed estimators, we impose the following regularity conditions:

• (A1)Pr(Y ≥ T₀, Z > 0) > 0.
• (A2)X is uniformly bounded.
• (A3)EZ² < ∞.
• (A4)G(u) = E[ZI(Y ≥ u)] is a continuous function for u ∈ [0, T₀].

Under these regularity conditions, the large-sample properties of ${\widehat{\Lambda }}_0$ and $\widehat{\alpha }$ were established by WQC (2001). Let t_ij denote the jth event time of the ith subject, and define the functions G(t) = E[Z₁I(Y₁ ≥ t)], R(t) = G(t)Λ₀(t), $Q\left(t\right)={\int }_0^{t}G\left(u\right)d{\Lambda }_0\left(u\right)$, and, for i = 1, …, n,

$$b_i\left(t\right)=\sum _{i=1}^{m_i}\left\{{\int }_t^{T_0}\frac{I(t_{\mathit{ij}}\le u\le Y_i)\mathit{dQ}\left(u\right)}{R^2\left(u\right)}-\frac{I(t<t_{\mathit{ij}}\le T_0)}{R\left(t_{\mathit{ij}}\right)}\right\}.$$

Under regularity conditions (A1)–(A4), it has been shown that ${\widehat{\Lambda }}_0\left(t\right)-{\Lambda }_0\left(t\right)=n^{-1}{\sum }_{i=1}^n{\Lambda }_0\left(t\right)b_i\left(t\right)+o_p\left(n^{-1∕2}\right)$, for inf{y: Λ₀(y) > 0} < t < T₀, and that $\sqrt{n}\left({\widehat{\Lambda }}_0\right(t)-{\Lambda }_0(t\left)\right)$ converges weakly to a normal distribution with mean 0 and variance ${\Lambda }_0{\left(t\right)}^{2}E\left[b_1^2\right(t\left)\right]$.

Define V* to be the joint probability measure of (w, $\stackrel{‒}{\mathbf{X}}$, m, Y) and

$$\begin{array}{cc}\hfill {\mathbf{e}}_i=-\int \frac{w{\stackrel{‒}{\mathbf{x}}}^t{\mathit{mb}}_i\left(y\right)}{{\Lambda }_0\left(y\right)}{\mathit{dV}}^{\ast }(w,& \stackrel{‒}{\mathbf{x}},m,y)\hfill \\ \hfill & +w_i{\stackrel{‒}{\mathbf{x}}}_i^t\{m_i{\Lambda }_0{\left(y_i\right)}^{-1}-\exp ({\stackrel{‒}{\mathbf{x}}}_i\gamma \left)\right\}.\hfill \end{array}$$

Then the left side of the estimating function (1) can be expressed as $n^{-1}{\sum }_{i=1}^n{\mathbf{e}}_i+o_p\left(n^{-1∕2}\right)$. Assuming that E[∂e₁/∂γ] is nonsingular, we have $\sqrt{n}(\widehat{\alpha }-\alpha )=n^{-1∕2}{\sum }_{i=1}^n{\mathbf{f}}_i\left(\alpha \right)+o_p\left(1\right)$, where f_i(α) is the vector function E[−∂e₁/∂γ]⁻¹e_i without the first entry, and $\sqrt{n}(\widehat{\alpha }-\alpha )$ converges to a multivariate normal distribution with mean 0 and variance $E\left[{\mathbf{f}}_1^2\right]$.

Note that in the WQC model, the baseline cumulative intensity function was not assumed to satisfy Λ₀(T₀) = 1 as we assumed in (M1). The aforementioned asymptotic representations have been modified to accommodate the current model assumptions.

The weak convergence of $\sqrt{n}\left(\widehat{\epsilon }\right\{\mathbf{X}\Delta I(Y\le T_0)\}-\epsilon \{\mathbf{X}\times \Delta I(Y\le T_0)\left\}\right)$ and $\sqrt{n}\left(\widehat{\epsilon }\right\{\Delta I(Y\le t)\}-\epsilon \{\Delta I(Y\le t)\left\}\right)$ follow from the classical central limit theorem and example 2.11.16 of van der Vaart and Wellner (1996). The two empirical processes converge weakly to a mean-0 normal distribution, ${\mathcal{W}}_1$, and a mean-0 Gaussian process, ${\mathcal{W}}_2$.

Furthermore, letting V denote the joint probability density function of (X, Y, m) and arguing as in the proof of theorem 1 of WQC (2001), we are able to show that $\sqrt{n}\left(\widehat{\epsilon }\right\{\widehat{Z}\exp \left(\mathbf{Xb}\right)\times I(Y\ge t)\}-\epsilon \{Z\exp \left(\mathbf{Xb}\right)I(Y\ge t)\left\}\right)=n^{-1∕2}{\sum }_{i=1}^n{\psi }_{3i}(t;\mathbf{b})+o_p\left(1\right)$, where

$$\begin{array}{cc}\hfill {\psi }_{3i}(t;\mathbf{b})& \hfill \\ \hfill =& \int \left\{m{\Lambda }_0^{-1}\right(y\left)e^{\mathbf{x}(b-\alpha )}I\right(y\ge t\left)\right({\mathbf{xf}}_i\left(\alpha \right)+b_i\left(y\right)\left)\right\}\mathit{dV}(\mathbf{x},y,m)\hfill \\ \hfill & +m_i{\Lambda }_0^{-1}\left(Y_i\right)e^{{\mathbf{x}}_i(b-\alpha )}I(Y_i\ge t)-\epsilon \left\{{\mathit{Ze}}^{\mathrm{Xb}}I\right(Y\ge t\left)\right\},\hfill \end{array}$$

with the usual convention 0/0 = 0. Note that the ψ_3i’s are uncorrelated random variables, because ψ_3i(t, b) depends only on observed data from the ith individual. It follows from the law of large numbers that $\widehat{\epsilon }\left\{\widehat{Z}\exp \right(\mathbf{Xb}\left)I\right(Y\ge t\left)\right\}-\epsilon \left\{Z\exp \right(\mathbf{Xb})\times I(Y\ge t\left)\right\}\to 0$ almost surely, for each fixed b. Furthermore, by the central limit theorem, the process converges in finite dimension to a mean-0 Gaussian process ${\mathcal{W}}_3$ on the time interval [0, T₀]. The explanatory variable X is assumed to be bounded, and without loss of generality we assume that X is a semi-positive definite matrix. Because items in ψ_3i(t; b) are monotone processes for each b, the process ψ_3i(t; b) is tight and converges weakly to ${\mathcal{W}}_3$ (see example 2.11.16 of van der Vaart and Wellner 1996). Similar arguments hold for $\widehat{\epsilon }\left\{\mathbf{X}\widehat{Z}\exp \right(\mathbf{Xb}\left)I\right(Y\ge t\left)\right\}-\epsilon \left\{\mathbf{X}Z\exp \right(\mathbf{Xb})\times I(Y\ge t\left)\right\}\to 0$ almost surely, and the process $\sqrt{n}\left(\widehat{\epsilon }\right\{\mathbf{X}\widehat{Z}\exp \left(\mathbf{Xb}\right)\times I(Y\ge t)\}-\epsilon \{\mathbf{X}\widehat{Z}\exp \left(\mathbf{Xb}\right)I(Y\ge t)\left\}\right)$ has the asymptotically iid representation $n^{-1∕2}{\sum }_{i=1}^n{\psi }_{4i}(t;\mathbf{b})+o_p\left(1\right)$, where ψ_4i is defined by

$$\begin{array}{cc}\hfill {\psi }_{4i}(t;\mathbf{b})& \hfill \\ \hfill =& \int m\mathbf{x}{\Lambda }_0^{-1}\left(y\right)e^{\mathbf{x}(b-\alpha )}I(y\ge t)\left({\mathbf{xf}}_i\right(\alpha )+b_i(y\left)\right)\mathit{dV}(\mathbf{x},y,m)\hfill \\ \hfill & +m_i{\mathbf{x}}_i{\Lambda }_0^{-1}\left(Y_i\right)e^{{\mathbf{x}}_i(b-\alpha )}I(Y_i\ge t)-\epsilon \left\{\mathbf{X}{\mathit{Ze}}^{\mathrm{Xb}}I\right(Y\ge t\left)\right\}.\hfill \end{array}$$

Moreover, the process converges weakly to a mean-0 Gaussian process, denoted by ${\mathcal{W}}_4$.

We establish the consistency of $\widehat{\beta }$ as follows. Define the two functions

$$\begin{array}{cc}\hfill A_n\left(\mathbf{b}\right)=\widehat{\epsilon }& \left\{\right(\mathbf{X}\Delta I(Y\le T_0)\left\}\right(\mathbf{b}-\beta )\hfill \\ \hfill & -{\int }_0^{T_0}\ln \left(\frac{\widehat{\epsilon }\left\{\widehat{Z}\exp \right(\mathbf{Xb}\left)I\right(Y\ge s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}\right)d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill A\left(\mathbf{b}\right)=& \epsilon \left\{\right(\mathbf{X}\Delta I(Y\le T_0)\left\}\right(\mathbf{b}-\beta )\hfill \\ \hfill & -{\int }_0^{T_0}\ln \left(\frac{\epsilon \left\{Z\exp \right(\mathbf{Xb}\left)I\right(Y\ge s\left)\right\}}{\epsilon \left\{Z\exp \right(\mathbf{X}\beta \left)I\right(Y\ge s\left)\right\}}\right)d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}.\hfill \end{array}$$

We can easily verify that $\widehat{U}\left(\mathbf{b}\right)$ and $\mathcal{U}\left(\mathbf{b}\right)$ are derivatives of A_n(b) and A(b), and that β is the unique maximum of A. Furthermore, $\widehat{\beta }$ can be shown to be the unique maximum of A_n.

From the foregoing discussions, the four processes in $\widehat{U}$ has the $\sqrt{n}$-convergence rate; hence the four processes converge almost surely to their limits. Applying lemma 3 of Gill (1989) and the chain rule, we can show that the functional defined by $\widehat{U}$ is continuous with respect to the supremum norm under regularity conditions (A1)–(A4). Then, for some compact neighborhood $\mathcal{B}$ of β, as n → ∞, ${\sup }_{\mathbf{b}\in \mathcal{B}}\mid \widehat{U}\left(\mathbf{b}\right)-\mathcal{U}\left(\mathbf{b}\right)\mid \to 0$ almost surely. Applying Taylor expansion and using the fact that A_n(β) = A(β) = 0, we have that $A_n\left(\mathbf{b}\right)-A\left(\mathbf{b}\right)=\left\{\widehat{U}\right({\beta }^{\ast })-\mathcal{U}({\beta }^{\ast }\left)\right\}(\mathbf{b}-\beta )$, where β* lies between b and β. Now it is clear that as n → ∞, ${\sup }_{\mathbf{b}\in \mathcal{B}}\mid A_n\left(\mathbf{b}\right)-A\left(\mathbf{b}\right)\mid \to 0$ almost surely.

Define $\widehat{\Gamma }\left(\mathbf{b}\right)=d\widehat{U}\left(\mathbf{b}\right)∕d\mathbf{b}=d^2{A}_n\left(\mathbf{b}\right)∕d{\mathbf{b}}^2$ and $\widehat{\Gamma }\left(\mathbf{b}\right)=d\mathcal{U}\left(\mathbf{b}\right)∕d\mathbf{b}=d^{2}A\left(\mathbf{b}\right)∕d{\mathbf{b}}^2$, that is,

$$\begin{array}{cc}\hfill \widehat{\Gamma }\left(\mathbf{b}\right)={\int }_0^{T_0}& \{-\frac{\widehat{\epsilon }\left\{{\mathbf{X}}^2\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}\phantom{\}}\hfill \\ \hfill & +\phantom{\{}\frac{\widehat{\epsilon }{\left\{\mathbf{X}\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}{\widehat{\epsilon }{\left\{\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}\}d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill \Gamma \left(\mathbf{b}\right)={\int }_0^{T_0}& \{-\frac{\epsilon \left\{{\mathbf{X}}^2{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}\phantom{\}}\hfill \\ \hfill & +\phantom{\{}\frac{\epsilon {\left\{\mathbf{X}{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}{\epsilon {\left\{{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}\}d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}.\hfill \end{array}$$

We can show that $\widehat{\Gamma }\left(\mathbf{b}\right)$ and Γ(b) are both negative definite, and it follows that A_n and A are concave. By Lenglart’s theorem (appendix II in Andersen and Gill 1982), the unique maximum of A_n, $\widehat{\beta }$, converges in probability to the unique maximum of A, that is, β. Hence, we establish the consistency of $\widehat{\beta }$.

Note that $\{{\widehat{Z}}_1,\dots ,{\widehat{Z}}_n\}$ are correlated because these values are estimated from the entire collection of recurrent event data; therefore, martingale theory does not apply to the working score function, $\widehat{U}$. In this article we study the large-sample properties of $\widehat{\beta }$ and ${\widehat{H}}_0\left(t\right)$ by empirical process theories and the functional delta method. For convenience, we denote a² = aa^T for any vector a. We present asymptotic theories in Lemmas 1–3, with the proofs given in Appendix B, and summarize these results in Theorem 1.

Lemma 1. Under regularity conditions (A1)–(A4) and the assumption that Ψ = E [∂e₁/∂γ] is nonsingular, $n^{1∕2}\widehat{U}\left(\beta \right)$ is the sum of asymptotically uncorrelated random variables; $n^{1∕2}\widehat{U}\left(\beta \right)=n^{-1∕2}{\sum }_{i=1}^n{\psi }_i\left(\beta \right)+o_p\left(1\right)$, where ψ_i(β) is defined in Appendix B. Moreover, $\sqrt{n}\widehat{U}\left(\beta \right)$ converges weakly to a normal distribution with mean 0 and variance–covariance matrix Σ(β) = E[ψ_i(β)²].

Note that the variance–covariance matrix Σ can be consistently estimated by $\widehat{\Sigma }\left(\widehat{\beta }\right)$, where $\widehat{\Sigma }\left(\widehat{\beta }\right)$ is defined in Appendix B. To study the large-sample property of $\widehat{\beta }$, we further define $\Gamma \left(\beta \right)=\partial \mathcal{U}\left(\beta \right)∕\partial \beta$ and $\widehat{\Gamma }\left(\beta \right)=\partial \widehat{U}\left(\beta \right)∕\partial \beta$.

Lemma 2. Assume that Ψ and Γ = Γ (β) are both nonsingular. Then, under regularity conditions? (A1)–(A4), $\sqrt{n}(\widehat{\beta }-\beta )=n^{-1∕2}{\sum }_{i=1}^n{\Gamma }^{-1}{\psi }_i\left(\beta \right)+o_p\left(1\right)$, where ψ(β) is defined in Appendix B. Thus $\sqrt{n}(\widehat{\beta }-\beta )$ converges weakly to a normal distribution with mean 0 and variance–covariance matrix Γ⁻¹Σ(Γ⁻¹)^T, which can be consistently estimated by $\widehat{\Gamma }{\left(\widehat{\beta }\right)}^{-1}\widehat{\Sigma }\left(\widehat{\beta }\right){\left\{\widehat{\Gamma }{\left(\widehat{\beta }\right)}^{-1}\right\}}^T$.

Lemma 3. Under regularity conditions (A1)–(A4) and by assuming that Ψ and Γ are nonsingular, the cumulative hazard function, H₀(t), can be expressed as the sum of asymptotically uncorrelated random variables, $n^{1∕2}\left\{{\widehat{H}}_0\right(t)-H_0(t\left)\right\}=n^{-1∕2}{\sum }_{i=1}^n{\varphi }_i\left(t\right)+o_p\left(1\right)$, where t ∈ [0, T₀] and φ_i(t) is defined in Appendix B. Then $n^{1∕2}\left\{{\widehat{H}}_0\right(t)-H_0(t\left)\right\}$ converges weakly on [0, T₀] to a mean-0 Gaussian process with variance–covariance function E[φ₁ (t₁)φ₁ (t₂)].

Along with the results stated in Section 4.1 and following directly from Lemmas 2 and 3, we state the main asymptotic theorem.

Theorem 1. Assume that Γ and Ψ are nonsingular. Under regularity conditions (A1)–(A4), for each fixed s, inf{y: Λ₀(y) > 0} < s < T₀, and fixed t, t ∈ [0, T₀], the random vector $\sqrt{n}(\widehat{\alpha }-\alpha ,\widehat{\beta }-\beta ,{\widehat{\Lambda }}_0(s)-{\Lambda }_0(s),{\widehat{H}}_0(t)-H_0(t\left)\right)$ converges weakly to a multivariate normal distribution with mean 0 and variance–covariance matrix $E\left[{\eta }_1^2\right]$, where the η_i’s are uncorrelated random vectors defined by η_i = (f_i(α), Γ ψ_i, (β), Λ₀(s)b_i(s), φ_i(t)).

6. SIMULATIONS AND DATA ANALYSIS

6.1 Monte Carlo Simulations

We conducted studies to assess the performance of the proposed estimators. For all simulation studies, we generated 1,000 simulated dataseis, each with n = 200 and n = 500 independent subjects. The explanatory variable X was generated from a Bernoulli distribution with P(X = 0) = P(X = 1) = .5, and the subject-specific latent variable Z was generated from a discrete (poisson with mean 10) and a continuous (gamma with mean 10 and variance 50) distribution. Given X = x and Z = z, the subject’s underlying recurrent event process {N(t), t ∈ [0, 10]} is a nonstationary Poisson process with the corresponding intensity function zλ₀(t) exp(xα), and the subject’s failure time D has a hazard function zh₀(t) exp(xβ). To examine the performance of proposed estimators under different choices of (α, β) and (λ₀(·), h₀(·)), we also consider combinations corresponding to (α, β) = (0,0) and (−1, −1.5) and the following two sets of functions for λ₀(t) and h₀(t).

• Scenario I: λ₀(t) = 1/10, and h₀(t) = t/400;

• Scenario II: h₀(t) = (t + 1)/10, $\sqrt{t}∕200$.

Finally, the censoring time C is either a exponential variable with mean 10 when x = 1 or a exponential variable with mean 300/z² when x = 0. Given (x, z), the triplets (N(·), D, C) are mutually independent.

Suppose that the censoring time C is the potential dropout time. The justification for such a design for the censoring variable is as follows. Suppose that the frailty is an unobserved health indicator. In the control group (X = 0), sick patients with a high occurrence rate of recurrent events drop out early due to large values of frailty; in the treatment group (X = 1), in contrast, because the treatment has effectively reduced the event occurrence rates, the dropout is noninformative for both the recurrent event process and the failure time.

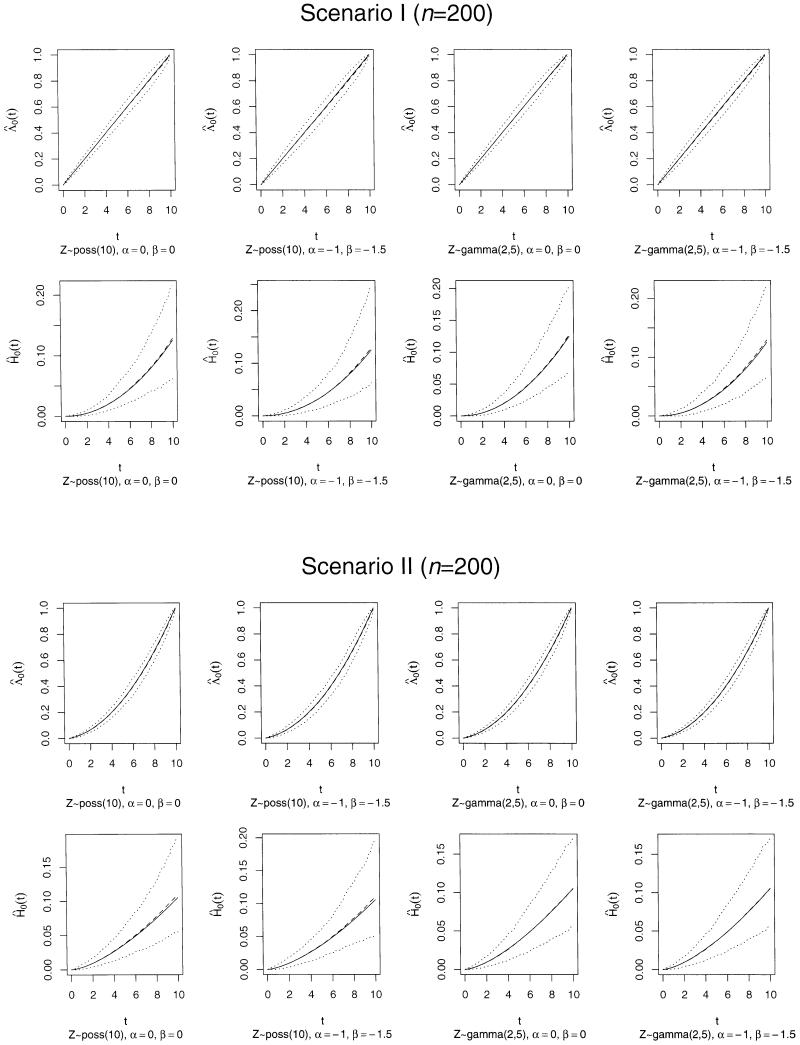
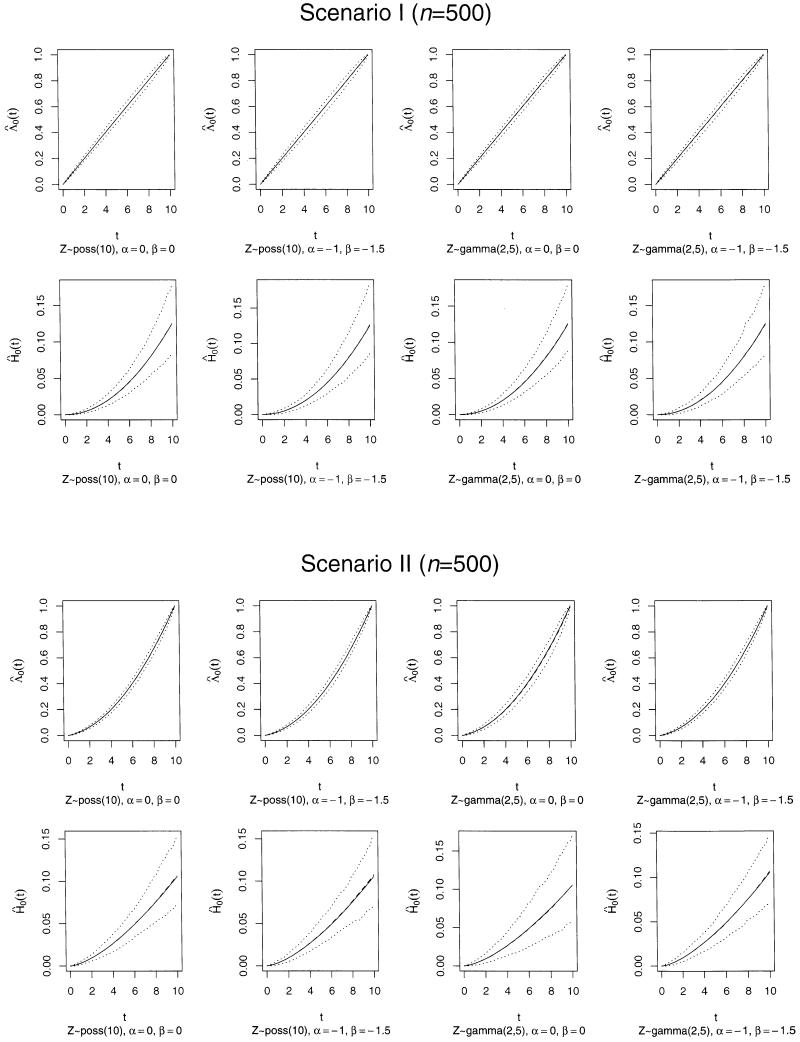
As summarized in Table 1, the average death rate ranges from 13% to 28%, the average length of follow-up period ranges from 3.9 to 4.91, and the average number of observed recurrent events ranges from 1.57 to 3.65 in the conducted simulation studies. Noted that the average follow-up time is approximately the same under different choices of (λ₀, h₀), but the average number of observed events is smaller under Scenario II. The result of simulation studies is summarized in Table 2. For each simulation study, the empirical bias, standard error, and correlation coefficient of proposed estimators were calculated based on 1,000 samples. Figures 1 and 2 show the estimates and the pointwise 95% confidence intervals of the baseline cumulative intensity function and baseline cumulative hazard function. As shown in Table 2 and Figures 1 and 2, the proposed estimator performs reasonably well; that is, the empirical bias in the estimates of regression parameters are small, and the averages of ${\widehat{\Lambda }}_0\left(t\right)$ and ${\widehat{H}}_0\left(t\right)$ are almost indistinguishable from the true curves. Note that the parameter estimates under Z ~ poisson(10) have smaller standard errors than those under Z ~ gamma(2, 5), and the empirical correlation coefficients between $\widehat{\alpha }$ and $\widehat{\beta }$ are smaller under the assumed Poisson distribution; this is because the poisson(10) distribution has smaller variability than the gamma(2, 5) distribution; that is, the defined population is more homogeneous under Z ~ poisson(10).

Table 1.

Summary of the Simulated Data

	Z ~ poisson(10)			Z ~ gamma(2, 5)
(α, β)	P(death)	Y	m	P(death)	Y	m
Scenario I: λ0(t) = 1/10, h0(t) = t/400
(0, 0)	.27	3.90	3.64	.26	4.44	3.40
(−1, −1.5)	.14	4.41	2.34	.14	4.91	2.19
Scenario II: λ0(t) = (t + 1)/60, $h_0\left(t\right)=\sqrt{t}∕200$
(0, 0)	.28	3.80	2.40	.26	4.35	2.26
(−1, −1.5)	.15	4.36	1.59	.14	4.87	1.58

NOTE: P(death) is the average death rate; Y is the average terminating time; m is the average number of recurrent events.

Table 2.

Summary Statistics of the Simulation Studies

	Z ~ poisson(10)							Z ~ gamma(2, 5)
(α, β)	Bα	Vα	Bβ	Vβ	ρ	$Avg{\widehat{\beta }}^{\ast }$	Vβ*	Bα	Vα	Bβ	Vβ	ρ	$Avg{\widehat{\beta }}^{\ast }$	Vβ*
Scenario I: λ0(t) = 1/10, h0(t) = t/400
n = 200
(0, 0)	0	181	−3	383	.43	.383	334	4	274	−4	438	.61	.584	331
(−1, −1.5)	−8	255	−25	487	.49	−1.228	406	−5	277	−25	484	.50	−.769	395
n = 500
(0, 0)	−3	151	−1	243	.58	.244	191	7	199	21	283	.67	.599	207
(−1, −1.5)	0	176	−6	307	.54	−1.211	249	−13	212	−1	324	.63	−.752	244
Scenario II: λ0(t) = (t + 1)/60, $h_0\left(t\right)=\sqrt{t}∕200$
n = 200
(0, 0)	−13	412	2	496	.75	.211	305	17	511	23	608	.83	.539	319
(−1, −1.5)	−38	422	−44	558	.64	−1.253	400	−51	553	−17	681	.78	−.846	410
n = 500
(0, 0)	10	243	15	303	.72	.208	197	4	358	16	399	.86	.538	192
(−1, −1.5)	−23	287	−16	373	.71	−1.246	246	−18	369	−15	445	.81	−.822	246

NOTE: Bα and Bβ are the empirical bias (× 1,000) of $\widehat{\alpha }$ and $\widehat{\beta }$ V_α and V_β are the empirical standard error (× 1,000) of $\widehat{\alpha }$ and $\widehat{\beta }$ ρ is the empirical correlation coefficient of $\widehat{\alpha }$ and $\widehat{\beta }$ Avg ${\widehat{\beta }}^{\ast }$ is the empirical average and V_β, is the empirical standard error (× 1,000) of the estimator based on the Cox proportional hazards model.

Figure 1.

Plots of Estimated ${\widehat{\Lambda }}_0\left(t\right)$ and ${\widehat{H}}_0\left(t\right)$ With Pointwise 95% Confidence for n = 200. Scenario I: λ₀(t)= 1/10, and h₀(t) = t/400; Scenario II: λ₀(t) (t + 1)/60, $h_0\left(t\right)=\sqrt{t}∕200$ (—-, true curve; – – – – –; empirical average;………, pointwise 95% confidence intervals).

Figure 2.

Plots of Estimated ${\widehat{\Lambda }}_0\left(t\right)$ and ${\widehat{H}}_0\left(t\right)$ With Pointwise 95% Confidence for n = 500. Scenario I: λ₀(t)= 1/10, and h₀(t) = t/400; Scenario II: λ₀(t) (t + 1)/60, $h_0\left(t\right)=\sqrt{t}∕200$ (—-, true curve; – – – – –; empirical average;………, pointwise 95% confidence intervals).

With data generated by model (M1)–(M3), it is interesting to see results from the use of a popular but incorrect model, that is, the proportional hazards model, $h\left(t\right)=h_0^{\ast }\left(t\right)\exp \left(x{\beta }^{\ast }\right)$, for the failure time data. Using the partial likelihood method (Cox 1972), Table 2 also reports the average and empirical standard error of the 1,000 estimates of β*. Note that using the Cox proportional hazards model, which incorrectly assumes the independent censoring assumption, results in biased estimation of the treatment effect. This phenomenon can be explained as follows. In the simulated control group (X = 0), sicker patients with higher hazards tend to drop out at earlier times; thus risk sets are likely to consist of healthier patients at later time points. As a result, the estimates given by the Cox proportional hazards model based on comparisons of subjects within risk sets under-estimate the treatment effect when treatment reduces the risk of death and conclude that treatment is associated with increased risk of death when the treatment does not affect the mortality rate.

6.2 Data Analysis

A Denmark registry dataset recorded the initial and recurrences of hospitalizations and associated patient information from 8,811 patients whose first schizophrenia-related hospitalization occurred between April 1, 1970 and March 25, 1988 (Eaton et al. 1992a,b). The catchment area for the register is the entire nation of Denmark. The dataset provides a large collection of repeated psychiatric measurements as well as recorded hospitalization episodes. All death records in Denmark are linked into the register.

Table 3 summarizes numbers of hospital admissions and deaths for subgroups by gender and age of onset. Comparing crude proportions seems to suggest that patients whose first hospitalization occurred after age 20 tend to have fewer hospitalizations but are more likely to die before the end of study. The hospitalizations and survival experiences do not look very different in males and females based on these summary statistics.

Table 3.

Hospital Admissions and Deaths for Different Subgroups

			No. of hospital admissions since entry
Subgroup	No. of patients	No. of deaths	0	1	2	3	4	5	≥ 6
Male	3,318	368	984	581	394	331	200	157	671
(%)	100	11.1	29.7	17.5	11.9	10	6	4.7	20.2
Female	5,493	685	1,392	945	636	470	363	279	1,408
(%)	100	12.5	25.3	17.2	11.6	8.6	6.6	5.1	25.6
Onset age ≤20	1,065	76	187	130	144	90	82	59	373
(%)	100	7.1	17.6	12.2	13.5	8.5	7.7	5.5	35.0
Onset age >20	7,746	977	2,189	1,396	886	711	481	377	1,706
(%)	100	12.6	28.3	18.0	11.4	9.2	6.2	4.9	22.0

We apply the proposed joint model to the Denmark schizophrenia cohort data and investigate the effects of gender and age of onset on the rate of hospitalization and the risk of death. The gender indicator is set to be 1 for male and 0 for female, and the indicator of age onset is set to be 1 for under 20 years of age and 0 for 20 years old and older.

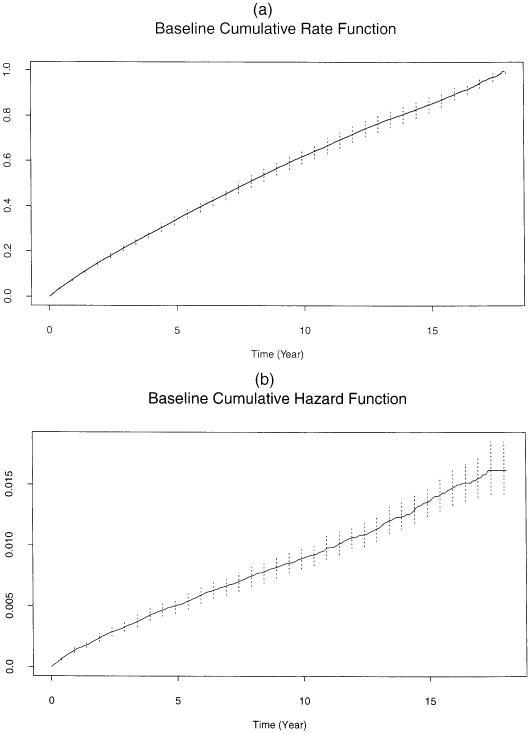
To estimate the standard errors of $\widehat{\alpha }$, $\widehat{\beta }$, ${\widehat{\Lambda }}_0\left(t\right)$, and ${\widehat{H}}_0\left(t\right)$ at selected time points, we adopted a nonparametric bootstrap method for clustered data by repeatedly sampling 8,811 subjects with replacement, using subject as the sampling unit, from the schizophrenia cohort data. The results of the data analysis are summarized in Table 4. Estimates of Λ₀(t) and H₀(t), and their pointwise 95% bootstrap confidence intervals are given in Figure 3. Table 4 shows that patients with early onset (age ≤ 20 years) are hospitalized more often (21% higher) and have a lower risk of death (57% lower) than patients with later onset. Moreover, being a male decreases one’s rate of hospitalization episodes by 16% (≈ 1 − e^−.18) and risk of death by 10% (≈ 1 − e^−.11). The estimated covariate effects are statistically significant, except for the gender effect on the risk of death, which is marginally significant. It is interesting to see that age of onset has opposite effects on hospital admissions rate and the hazard of death; this is not surprising, however, because young patients tend to have longer life expectancy. Also, the analysis confirms the theory in schizophrenia that patients with early onset age tend to be hospitalized more often than those with later onset age.

Table 4.

Summary of Denmark PCR Data Analysis

Risk factor	Estimate	SE	95% bootstrap CI
Hospital admissions
Onset age ≤ 20	.19	.04	(.10, .27)
Gender	−.18	.04	(−.26, −.09)
Death
Onset age ≤ 20	−.84	.13	(−1.10, −.62)
Gender	−.11	.07	(−.25, .01)

NOTE: SE, standard error of estimates from the 200 bootstrap samples; 95% bootstrap CI, (2.5%, 97.5%) quantiles of the 200 estimates.

Figure 3.

Plots of ${\widehat{\Lambda }}_0\left(t\right)$ and ${\widehat{H}}_0\left(t\right)$ for the Denmark Schizophrenia Cohort Data, With Pointwise 95% Bootstrap Confidence Intervals, (a) Baseline cumulative rate function; (b) baseline cumulative hazard function (—, estimates;…….., 95% pointwise CI).

In the case of a degenerate frailty, the Cox proportional hazards model gives estimates of −.74 [standard error (SE) = .12] and −.14 (SE = .06) for the effects of early onset and gender. The direction of covariate effects estimated in the Cox proportional hazards model are consistent with the estimates under the proposed model.

7. DISCUSSION

Frailty models are commonly adopted in modeling multivari ate survival time data (Clayton 1978; Oakes 1982) and in jointly modeling repeated measures and survival time data (Henderson, Diggle, and Dobson 2000; Lin, Turnbull, McCulloch, and Slate 2002). In this article, we propose a semiparametric joint model for the recurrent event process and failure time data. A latent variable (frailty) is assumed to act as a multiplicative factor in both the intensity function and the hazard function, and hence induces the correlation between the event process and the failure time. Unlike the usual setting of frailty models, where a parametric distribution is assumed for the frailty, a specific feature of our model is that the frailty distribution is treated as a nuisance parameter and no parametric assumptions were imposed. Additionally, via the use of frailty, the proposed model relaxes the independent censoring condition for observing both the recurrent event process and the failure time data.

For a semiparametric model like (M1)–(M3), model checking is expected to be a difficult task in general. In this article we do not intend to develop methods for formal model checking, we simply suggest possible approaches for validating model assumptions. A rigorous study of model checking methods will be done elsewhere. To test the assumption of a common baseline intensity function shared by all subjects, we use the fact that, under (M1) and conditioning on (m_i, x_i, y_i, z_i), t_ij are iid with the cdf F(t)I(0 ≤ t ≤ y_i)/F(y_i). Define V_ij = F(t_ij)I(0 ≤ t_ij ≤ y_i)/F(y_i); then V_ij are order statistics of iid uniform(0, 1) random variables. Let ${\widehat{V}}_{ij}=\widehat{F}\left(t_{ij}\right)I(0\le t_{ij}\le y_i)∕\widehat{F}\left(y_i\right)$; then a necessary condition to validate the assumption of sharing a common intensity function is to check whether the empirical distribution of {${\widehat{V}}_{ij}$:j = 1, …, m_i; i = 1, …, n} is approximately uniform(0, 1) distribution. To check on the proportional rate and hazards model assumption imposed by (M1) and (M2), replace Z with $\widehat{Z}$ to derive the Schoenfeld residuals (Schoenfeld 1982). If the assumption of proportional hazards holds, then the derived residuals are expected to randomly scattered around 0 and to gradually converge to 0 over time.

In this article we proposed a borrow-strength procedure by first estimating the value of the latent variable from recurrent event data, then using the estimated value in the failure time models. The central idea of estimation is to use moment properties of $\widehat{Z}$ so that the partial score functions, with Z or $\widehat{Z}$, attain the same convergence function. The proposed $\widehat{Z}$ requires no parametric assumption on Z and is easy to compute. As opposed to this approach, an alternative choice is to estimate Z by the posterior mean of Z given the observed recurrent event data; however, as discussed in Proposition 1, the posterior mean does not have an explicit form in our model setting, and thus is not a useful choice in theory or application.

The proposed estimation procedure is not without constraints. It is applicable only to time-independent covariates. In some applications, it would be desirable to develop estimation procedures that allow for both time-invariant and time-dependent covariates. Also, the propositions and trajectories described in Section 3 help understand the general relationship between the recurrent event process and the failure time. However, the probability formulas established in Section 3 cannot be made explicit unless the unknown parameters in the formulas are known or estimable, and accomplishing such a task requires more parametric modeling and alternative estimation procedures. Such work will be considered elsewhere in the future. Finally, the proposed time-to-events models assume that a common baseline intensity/rate function is shared by all subjects and that the intensity/rate function does not change after the occurrence of an event. To characterize the possible change in the risk of event occurrence after each event time, techniques for time-between-events models by, say, Prentice et al. (1981) and Chang and Wang (1999), can be adopted.

APPENDIX A: PROOFS OF PROPOSITIONS

Proposition 1

The probability density function of the event history given the value of the frailty and the termination time can be expressed as

$$\begin{array}{cc}\hfill f\left(\mathcal{H}\right(y)\mid z,y)& =f\left(\mathcal{H}\right(y)\mid N(y),z,y)f\left(N\right(y)\mid z,y)\hfill \\ \hfill & =\left(\prod _{j=1}^{N\left(y\right)}\frac{{\lambda }_0\left(t_j\right)}{{\Lambda }_0\left(y\right)}\right)f\left(N\right(y)\mid z,y),\hfill \end{array}$$

where f(N(y)|z, y) is the probability density function of the number of observed recurrent events given the value of the frailty and the termination time. Consequently,

$$f\left(\mathcal{H}\right(y)\mid y)=\int f\left(\mathcal{H}\right(y)\mid z,y)f(z\mid y)\mathit{dz}=\left(\prod _{j=1}^{N\left(y\right)}\frac{{\lambda }_0\left(t_j\right)}{{\Lambda }_0\left(y\right)}\right)f\left(N\right(y)\mid y).$$

Thus we can write the posterior mean of Z, given the observed recurrent event data, as

$$\begin{array}{cc}\hfill E& [Z\mid \mathcal{H}(y),y]\hfill \\ \hfill & =\int \mathit{zf}\left(\mathcal{H}\right(y)\mid z,y)\frac{f(z\mid y)}{f\left(\mathcal{H}\right(y)\mid y)}\mathit{dz}\hfill \\ \hfill & =\int \mathit{zf}\left(N\right(y)\mid z,y)\frac{f(z\mid y)}{f\left(N\right(y)\mid y)}\mathit{dz}\hfill \\ \hfill =& \int z\frac{\exp {(-z{\Lambda }_0(y\left)\right)\left(z{\Lambda }_0\right(y\left)\right)}^{N\left(y\right)}}{N\left(y\right)!}\frac{f(z\mid y)}{f\left(N\right(y)\mid y)}\mathit{dz}\hfill \\ \hfill & =\frac{N\left(y\right)+1}{{\Lambda }_0\left(y\right)}\int f\left(N\right(y)+1\mid z,y)\frac{f(z\mid y)}{f\left(N\right(y)\mid y)}\mathit{dz}\hfill \\ \hfill & =\frac{N\left(y\right)+1}{{\Lambda }_0\left(y\right)}\frac{f\left(N\right(y)+1\mid y)}{f\left(N\right(y)\mid y)}.\hfill \end{array}$$

Proposition 2

For 0 ≤ t ≤ t + s ≤ T₀, the survival function of the residual life time after time t, given the event history before and up to time t, can be expressed as $P(D\ge t+s\mid \mathcal{H}(t),D\ge t)=P(D\ge t+s,\mathcal{H}(t\left)\right)∕P(D\ge t,\mathcal{H}(t\left)\right)$, where

$$\begin{array}{cc}\hfill P(& D\ge t+s,\mathcal{H}\left(t\right))\hfill \\ \hfill & =\int P(D\ge t+s\mid z)f\left(\mathcal{H}\right(t)\mid z)f_Z\left(z\right)\mathit{dz}\hfill \\ \hfill & =\int P(D\ge t+s\mid z)f\left(\mathcal{H}\right(t)\mid N(t),z)f\left(N\right(t)\mid z)f_Z\left(z\right)\mathit{dz}\hfill \\ \hfill & =\int e^{-{\mathit{zH}}_0(t+s)}\left(\prod _{j=1}^{N\left(t\right)}\frac{{\lambda }_0\left(t_j\right)}{{\Lambda }_0\left(t\right)}\right)\frac{e^{-z{\Lambda }_0\left(t\right)}{\left(z{\Lambda }_0\right(t\left)\right)}^{N\left(t\right)}}{N\left(t\right)!}{f}_Z\left(z\right)\mathit{dz}\hfill \\ \hfill & =\frac{1}{N\left(t\right)!}\prod _{j=1}^{N\left(t\right)}{\lambda }_0\left(t_j\right)E\left[e^{-Z\left\{H_0\right(t+s)+{\Lambda }_0(t\left)\right\}}{Z}^{N\left(t\right)}\right],\hfill \end{array}$$

and, similarly,

$$P(D\ge t,\mathcal{H}(t\left)\right)={\left(N\right(t)!)}^{-1}\prod _{j=1}^{N\left(t\right)}{\lambda }_0\left(t_j\right)E\left[e^{-Z\left\{H_0\right(t)+{\Lambda }_0(t\left)Z^{N\left(t\right)}\right\}}\right].$$

We then simplify the formula

$$P(D\ge t+s\mid \mathcal{H}(t),D\ge t)=\frac{E\left[e^{-Z\left\{H_0\right(t+s)+{\Lambda }_0(t\left)\right\}}{Z}^{N\left(t\right)}\right]}{E\left[e^{-Z\left\{H_0\right(t)+{\Lambda }_0(t\left)\right\}}{Z}^{N\left(t\right)}\right]}.$$

Proposition 4

Following (M3), the mean function of the recurrent event conditional on the failure time can be expressed as

$$\begin{array}{cc}\hfill & E\left[N\right(s)\mid D\ge t]\hfill \\ \hfill & =\int \frac{E\left[N\right(s)\mid z]P(D\ge t\mid z)}{P(D\ge t)}{f}_Z\left(z\right)\mathit{dz}\hfill \\ \hfill & =\int \frac{z{\Lambda }_0\left(s\right)e^{-{\mathit{zH}}_0\left(t\right)}}{E\left[e^{-{\mathit{ZH}}_0\left(t\right)}\right]}{f}_z\left(z\right)\mathit{dz}=\frac{E\left[{\mathit{Ze}}^{-{\mathit{ZH}}_0\left(t\right)}\right]}{E\left[e^{-{\mathit{ZH}}_0\left(t\right)}\right]}{\Lambda }_0\left(s\right).\hfill \end{array}$$ (A.1)

The partial derivative of the right side term in (A.1) with respect to t can be derived as

$$\frac{E{\left[{\mathit{Ze}}^{-{\mathit{ZH}}_0\left(t\right)}\right]}^2-E\left[Z^2{e}^{-{\mathit{ZH}}_0\left(t\right)}\right]E\left[e^{-{\mathit{ZH}}_0\left(t\right)}\right]}{E{\left[e^{-{\mathit{ZH}}_0\left(t\right)}\right]}^2}{h}_0\left(t\right){\Lambda }_0\left(s\right).$$

The partial derivative can be shown to be nonpositive by applying the Cauchy–Schwartz inequality, and, as a result, the mean function in (A.1) is decreasing in t, t ≥ s.

APPENDIX B: PROOFS OF LEMMAS

Proof of Lemma 1

Straightforward algebra yields

$$\begin{array}{cc}\hfill n^{1∕2}\widehat{U}\left(\beta \right)=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\int }_0^{T_0}& {\mathbf{X}}_i-\frac{\widehat{\epsilon }\left\{\mathbf{X}\widehat{Z}{e}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}{e}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}\hfill \\ \hfill & \times \left\{d{\Delta }_{i}I\right(Y_i\le s)-{\widehat{Z}}_i{e}^{{\mathbf{X}}_i\beta }I(Y_i\ge s\left)h_0\right(s\left)\mathit{ds}\right\}.\hfill \end{array}$$

Because the mapping of $\widehat{U}$ from the four empirical processes, under the regularity conditions, is compactly differentiable with respect to the supremum norm and the four empirical processes converge weakly to their limits, we apply the functional delta method to $\widehat{U}$ and establish its asymptotic representation $n^{1∕2}\widehat{U}\left(\beta \right)=n^{-1∕2}{\sum }_{i=1}^n{\psi }_i\left(\beta \right)+o_p\left(1\right)$, where

$$\begin{array}{cc}\hfill {\psi }_i\left(\beta \right)=& {\mathbf{X}}_i{\Delta }_{i}I(Y_i\le T_0)-\epsilon \left\{\mathbf{X}\Delta I\right(Y\le T_0\left)\right\}\hfill \\ \hfill & +{\int }_0^{T_0}\frac{{\psi }_{3i}(s;\beta )\epsilon \left\{\mathbf{X}{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}{\epsilon {\left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}^2}d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}\hfill \\ \hfill & -{\int }_0^{T_0}\frac{{\psi }_{4i}(s;\beta )}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}\hfill \\ \hfill & -{\int }_0^{T_0}\frac{\epsilon \left\{\mathbf{X}{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}d\left({\Delta }_{i}I\right(Y_i\le s)-\epsilon \{\Delta I(Y\le s)\left\}\right).\hfill \end{array}$$

Note that the ψ_i’s are uncorrelated random variables, because ψ_i depends only on the observed data of the ith individual. Following the classical central limit theorem, $n^{1∕2}\widehat{U}\left(\beta \right)$ is asymptotically normal with mean 0 and variance–covariance matrix Σ(β) = E[ψ_i(β)²]. Define ${\widehat{\psi }}_i\left(\beta \right)$ by substituting empirical processes for their limits in ψ_i, and define $\widehat{\Sigma }\left(\beta \right)=n^{-1}{\sum }_{i=1}^n\left\{{\widehat{\psi }}_i\right(\beta )-{\psi }^{\ast }(\beta \left)\right\}{\left\{{\widehat{\psi }}_i\right(\beta )-{\psi }^{\ast }(\beta \left)\right\}}^T$, where ψ_i*(β) is the average over ${\widehat{\psi }}_1\left(\beta \right),\dots ,{\widehat{\psi }}_n\left(\beta \right)$. It can be shown that the second moment of ${\widehat{\psi }}_i\left(\beta \right)$ exists, and it follows from the strong law of large numbers that $\widehat{\Sigma }\left(\beta \right)$ converges to its limit, Σ(β), uniformly. Arguing as in the proof for the consistency of $\widehat{\beta }$, we can show that the functional defined by $\widehat{\Sigma }$ satisfies ${\sup }_{\mathbf{b}\in \mathcal{B}}\mid \widehat{\Sigma }\left(\mathbf{b}\right)-\Sigma \left(\mathbf{b}\right)\mid \to 0$ almost surely. By the consistency of $\widehat{\beta }$, as well as the continuity of Σ(b) at β, we are able to show that $\widehat{\Sigma }\left(\widehat{\beta }\right)$ is a consistent estimator of Σ(β). Moreover, in terms of the notations used before, we can rewrite the limit of $\sqrt{n}\widehat{U}\left(\beta \right)$ as

$$\begin{array}{cc}\hfill {\mathcal{W}}_1-{\int }_0^{T_0}& {\mathcal{W}}_4\left(s\right)h_0\left(s\right)\mathit{ds}\hfill \\ \hfill & -{\int }_0^{T_0}\frac{\epsilon \left\{\mathbf{X}{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}\left\{d{\mathcal{W}}_2\right(s)-{\mathcal{W}}_3(s\left)h_0\right(s\left)\mathit{ds}\right\}.\hfill \end{array}$$

Proof of Lemma 2

Define $\widehat{\Gamma }\left(\mathbf{b}\right)=d\widehat{U}\left(\mathbf{b}\right)∕d\mathbf{b}$, that is,

$$\begin{array}{cc}\hfill \widehat{\Gamma }\left(\mathbf{b}\right)={\int }_0^{T_0}& \{-\frac{\widehat{\epsilon }\left\{{\mathbf{X}}^2\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}\phantom{\}}\hfill \\ \hfill & +\phantom{\{}\frac{\widehat{\epsilon }{\left\{\mathbf{X}\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}{\widehat{\epsilon }{\left\{\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}\}d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}.\hfill \end{array}$$

It can be shown that $\widehat{\Gamma }\left(\mathbf{b}\right)$ defines a functional of four empirical processes. Arguing as in the proof of consistency of $\widehat{\beta }$, we can show that $\widehat{\Gamma }\left(\mathbf{b}\right)\to \Gamma \left(\mathbf{b}\right)$ in a neighborhood $\mathcal{B}$ of β, where Γ(b) is the derivative of $\mathcal{U}$ and

$$\begin{array}{cc}\hfill \Gamma \left(\mathbf{b}\right)={\int }_0^{T_0}& \{-\frac{\epsilon \left\{{\mathbf{X}}^2{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}\phantom{\}}\hfill \\ \hfill & +\phantom{\{}\frac{\epsilon {\left\{\mathbf{X}{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}{\epsilon {\left\{{\mathit{Ze}}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}^2}\}d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}.\hfill \end{array}$$

Applying Taylor expansion, we have $\widehat{U}\left(\widehat{\beta }\right)-\widehat{U}\left(\beta \right)=\widehat{\Gamma }\left({\beta }^{\ast }\right)(\widehat{\beta }-\beta )$, where β* lies on the segment between $\widehat{\beta }$ and β. In light of the consistency of $\widehat{\beta }$, and therefore β*, for β, as well as the continuity of Γ(β) at β, $\widehat{\Gamma }\left({\beta }^{\ast }\right)$ converges to Γ(β) almost surely. By Slutsky’s theorem, $\sqrt{n}(\widehat{\beta }-\beta )$ converges to a normal distribution with mean 0 and covariance matrix Γ(β)⁻¹Σ(β){Γ(β)⁻¹}^T, where Σ(β) = E[ψ₁(β)ψ₁ (β)^T]. Arguing as before, Γ(β) can be consistently estimated by $\widehat{\Gamma }\left(\widehat{\beta }\right)$, and, as a result, $\widehat{\Gamma }{\left(\widehat{\beta }\right)}^{-1}\widehat{\Sigma }\left(\widehat{\beta }\right){\left\{\widehat{\Gamma }{\left(\widehat{\beta }\right)}^{-1}\right\}}^T$ is a consistent variance estimator.

Proof of Lemma 3

Define the functions ${\widehat{H}}_0(t;\mathbf{b})={\int }_0^t\frac{d\widehat{\epsilon }\left\{\Delta I\right(Y\le s\left)\right\}}{\widehat{\epsilon }\left\{\widehat{Z}{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}$ and $H_0(t;\mathbf{b})={\int }_0^t\frac{d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}}{\epsilon \left\{Z{e}^{\mathbf{Xb}}I\right(Y\ge s\left)\right\}}$. ${\widehat{H}}_0(t;\mathbf{b})$ is a continuous functional of two processes because the denominator is bounded away from 0. The almost-sure convergence of the two processes can be established from the previous discussions. It can be shown that ${\sup }_{t\in [0,T_0]\mathbf{b}\in \mathcal{B}}\mid {\widehat{H}}_0(t;\mathbf{b})-H_0(t;\mathbf{b})\mid \to 0$ almost surely. Then the consistency of ${\widehat{H}}_0(t,\widehat{\beta })$ for H₀(t) follows the strong consistency of $\widehat{\beta }$ for β.

A Taylor expansion of ${\widehat{H}}_0(t;\widehat{\beta })$ about β gives

$${\widehat{H}}_0(t;\widehat{\beta })={\widehat{H}}_0(t;\beta )+{\phantom{\mid }\frac{\partial {\widehat{H}}_0(t;\mathbf{b})}{\partial \mathbf{b}}\mid }_{\mathbf{b}={\beta }_t^{\ast }}(\widehat{\beta }-\beta ),$$ (B.1)

where ${\beta }_t^{\ast }$ depends on t and lies on the line segment between $\widehat{\beta }$ and β. By a similar argument used earlier, we can show that $\partial {\widehat{H}}_0(t;\mathbf{b})∕\partial \mathbf{b}{\mid }_{\mathbf{b}={\beta }_t^{\ast }}$, converges in probability to ∂H₀(t; b)/∂b|_b=β for t ∈ [0, T₀]. Moreover, the functional delta method applied to ${\widehat{H}}_0(t,\beta )$ yields

$$\begin{array}{cc}\hfill \sqrt{n}& \left({\widehat{H}}_0\right(t;\beta )-H_0(t;\beta \left)\right)\hfill \\ \hfill & ={\int }_0^t-\frac{\sqrt{n}\left(\widehat{\epsilon }\right\{\widehat{Z}{e}^{\mathbf{X}\beta }I(Y\ge s)\}-\epsilon \{{\mathit{Ze}}^{\mathbf{X}\beta }I(Y\ge s)\left\}\right)}{\epsilon {\left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}^2}d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}\hfill \\ \hfill & +{\int }_0^t\frac{d\sqrt{n}\left(\widehat{\epsilon }\right\{\Delta I(Y\le s)\}-\epsilon \{\Delta I(Y\le s)\left\}\right)}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}+o_p\left(1\right).\hfill \end{array}$$

Following Theorem 2, $\sqrt{n}(\widehat{\beta }-\beta )=-\Gamma \left(\beta \right)\sqrt{n}\widehat{U}\left(\beta \right)+o_p\left(1\right)$, and, by definition, H₀(t,β) = H₀(t). From (B.1), the estimator of the baseline cumulative hazard function can be expressed as

$$\begin{array}{cc}\hfill \sqrt{n}& \left\{{\widehat{H}}_0\right(t;\widehat{\beta })-H_0(t\left)\right\}\hfill \\ \hfill & =\sqrt{n}\left\{{\widehat{H}}_0\right(t;\beta )-H_0(t;\beta \left)\right\}+{\phantom{\mid }\frac{\partial {\widehat{H}}_0(t;\mathbf{b})}{\partial \mathbf{b}}\mid }_{\mathbf{b}={\beta }_t^{\ast }}\sqrt{n}(\widehat{\beta }-\beta )\hfill \\ \hfill & =\frac{1}{\sqrt{n}}\sum _{i=1}^n{\varphi }_1\left(t\right)+o_p\left(1\right),\hfill \end{array}$$

where φ_i(t) is defined by

$$\begin{array}{cc}\hfill {\varphi }_i\left(t\right)=& {\int }_0^t-\frac{{\psi }_i^{\left(3\right)}(s;\beta )d\epsilon \left\{\Delta I\right(Y\le s\left)\right\}}{\epsilon {\left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}^2}\hfill \\ \hfill & +{\int }_0^t\frac{d\left({\Delta }_{i}I\right(Y_i\le s)-\epsilon \{\Delta I(Y\le s)\left\}\right)}{\epsilon \left\{{\mathit{Ze}}^{\mathbf{X}\beta }I\right(Y\ge s\left)\right\}}\hfill \\ \hfill & -\frac{\partial H_0(t;\beta )}{\partial \beta }\Gamma \left(\beta \right){\psi }_i\left(\beta \right).\hfill \end{array}$$

Because φ_i(t) is a linear combination of monotone processes with bounded second moments, the weak convergence of $\sqrt{n}\left({\widehat{H}}_0\right(t;\widehat{\beta })-H_0(t\left)\right)$ follows from example 2.11.16 of van der Vaart and Wellner (1996).