Planned Missing Data Designs in Experience Sampling Research: Monte Carlo Simulations of Efficient Designs for Assessing Within-Person Constructs

Abstract

Experience sampling research involves trade-offs between the number of questions asked per signal, the number of signals per day, and the number of days. By combining planned missing data designs and multilevel latent variable modeling, we show how to reduce items-per-signal without reducing the number of items. After illustrating different designs using real data, we present two Monte Carlo studies that explore the performance of planned missing data designs across different within-person and between-person sample sizes and across different patterns of response rates. The missing data designs yielded unbiased parameter estimates but slightly higher standard errors. With realistic sample sizes, even designs with extensive missingness performed well, so these methods are promising additions to an experience sampler's toolbox.

The idea behind experience sampling is simple: to understand what is happening in people's everyday lives, “beep” them with a device and ask them to answer questions about their current experiences (Bolger & Laurenceau, 2013; Conner, Tennen, Fleeson, & Barrett, 2009). Experience sampling methods have been increasingly used in social, clinical, and health psychology to examine topics as wide-ranging as substance use (Buckner et al., 2011), romantic relationships (Graham, 2008), psychosis (Oorschot, Kwapil, Delespaul, & Myin-Germeys, 2009), self-injury (Armey, Crowther, & Miller, 2011), and personality dynamics (Fleeson & Gallagher, 2009). But as in many things, the devil is in the details. For fixed-interval and random-interval designs, in which people are beeped at fixed or random times throughout the day, researchers must decide how many items should be asked at each beep, how many beeps should be given each day, and how many days the study should last. These three design parameters—number of items per beep, number of daily beeps, and number of total days—tug against each other and thus require compromises to avoid participant burden, fatigue, and burnout. For example, asking many items per beep usually requires using fewer beeps per day; conversely, using many beeps per day usually requires asking fewer questions per beep (Hektner, Schmidt, & Csikszentmihalyi, 2007). If the demands on participants are too high, both the quality and quantity of responses will suffer.

In this article, we describe some useful planned missing data designs (Enders, 2010; Graham, Taylor, Olchowski, & Cumsille, 2006). Although such designs have been popular in cross-sectional and longitudinal work, researchers have not yet considered their potential for experience sampling studies. Planned missing data designs allow researchers to omit some items at each beep. This reduces the time and burden needed to complete each assessment, and it enables researchers to ask more questions in total without expanding the number of questions asked per beep. We suspect that they could thus be useful for experience sampling research, in which space in the daily-life questionnaire is tight. Using real data from a study of hypomania and positive affect in daily life (Kwapil et al., 2011), we first illustrate some common planned missing data designs and describe their typical performance. We then present two Monte Carlo simulations that evaluate the performance of planned missing data across a range of within-person (Level 1) and between-person (Level 2) sample sizes and patterns of response rates.

The Basics of Planning Missing Data

During the dark ages of missing data analysis, missing observations were usually handled with some form of deletion or simple imputation (Graham, 2009; Little & Rubin, 2002). With the advent of modern methods—particularly multiple imputation and maximum likelihood—researchers have many sophisticated options for analyzing datasets with extensive missingness if certain assumptions are made (Enders, 2010). The rise of methods for analyzing missing data has brought new attention to planned missing data designs (Graham et al., 2006), which have a long history but were relatively impractical until the development of modern analytic methods. Sometimes called efficiency designs, planned missing data designs entail deliberately omitting some items for some participants via random assignment. In cross-sectional research, for example, the items might be carved into three sets, and each participant would be randomly assigned two of the sets. This method would reduce the number of items that each participant answers (from 100% to 67%) without reducing the overall number of items asked. In longitudinal research, for another example, researchers could randomly assign participants to a subset of waves instead of collecting data from everyone at each wave. Such methods save time and money, and they can “accelerate” a longitudinal project, such as in cohort sequential designs (Duncan, Duncan, & Stryker, 2006).

Planned missing data designs allow researchers to trade statistical power for time, items, and resources. Unlike unintended types of missing data, planned missing data are missing completely at random (MCAR): the observed scores are a simple random sample of the set of complete scores, so the likelihood of missingness is unrelated to the variable itself or to other variables in the dataset (Little & Rubin, 2002). As a result, maximum likelihood methods for missing data that assume MCAR or missing at random (MAR)—the likelihood of missingness is unrelated to the variable itself but is related to other variables in the dataset (Little & Rubin, 2002)—mechanisms can be applied. The body of simulation research on maximum likelihood methods, viewed broadly, shows that standard errors are somewhat higher—consistent with the higher uncertainty that stems from basing an estimate on less data—but the coefficients themselves are unbiased estimates of the population values (see Davey & Savla, 2010; Enders, 2010; McKnight, McKnight, Sidani, & Figueredo, 2007). The higher standard errors are the price researchers pay for the ability to ask more items or to reduce the time needed to administer the items. It can be a good investment if the savings in time and money enable asking more items, sampling more people, or yielding better data, such as by reducing fatigue or increasing compliance.

An Empirical Demonstration of Planned Missing Data Designs

To illustrate different missing data designs in action, we used data collected as part of a study of hypomania's role in daily emotion, cognition, and social behavior (Kwapil et al., 2011). In this study, 321 people took part in a 7-day experience sampling study. Using personal digital assistants (PDAs), we beeped the participants 8 times per day for 7 days. One beep occurred randomly within each 90 minute block between noon and midnight. Compliance was good: people completed an average of 41 daily life questionnaires (SD = 10). In the original study, each person received all items at each beep.

The key to implementing planned missing data designs for beep-level, within-person constructs is to model the Level 1 constructs as latent variables. Multilevel models with latent variables are combinations of familiar structural equation models and hierarchical linear models (Mehta & Neale, 2005; Muthén & Asparouhov, 2011; Skrondal & Rabe-Hesketh, 2004); Heck and Thomas (2009) provide a thorough didactic introduction for researchers interested in learning to run multilevel structural equation models. Instead of averaging across items—especially cases where researchers would average across three or more items—researchers can specify the items as indicators of a Level 1 latent outcome. Apart from enabling the use of planned missing designs, modeling latent Level 1 variables has the other advantages of latent variable modeling, such as the ability to model measurement error.

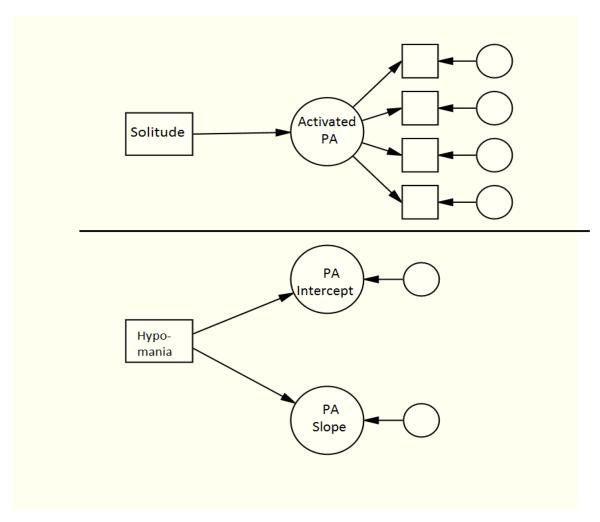
Figure 1 depicts the multilevel model used for our examples. The outcome variable is activated positive affect (PA), which is a latent variable defined by observed items enthusiastic, excited, energetic, and happy. The Level 1 predictor, solitude, is a binary variable that reflects whether people are alone or with other people. Much research shows that PA is higher when people are with others (Burgin et al., 2012; Silvia & Kwapil, 2011; Watson, 2000). Solitude was group-mean centered (i.e., within-person centered) using the observed solitude scores, and the slopes and intercepts were modeled as random. At Level 2, we estimated a main effect of hypomania, measured with the Hypomanic Personality Scale (Eckblad & Chapman, 1986), on PA (shown as the path from Hypomania to the PA Intercept) as well as a cross-level interaction between solitude and hypomania (shown as a path from Hypomania to the PA Slope). The Hypomanic Personality Scale measures a continuum of trait-like variability in bipolar spectrum psychopathology (see Kwapil et al., 2011). Hypomania was grand-mean centered using the observed scores. As is typical for experience sampling research, the data were fully complete at Level 2 but partially complete at Level 1 because not everyone responded to every beep (Silvia, Kwapil, Eddington, & Brown, in press). The models were estimated using Mplus 6.12 using maximum likelihood estimation with robust standard errors.

Figure 1.

A multilevel model with a latent outcome.

Matrix Designs for Three Within-Person Indicators

A typical experience sampling study of mood would have many affect items to capture a range of affective states. If there are three items for a construct, researchers can use a family of matrix designs. In our study, we included many Level 1 items that assessed PA. For this example, we'll consider three of them: enthusiastic, excited, and energetic.

A simple matrix design for three indicators randomly administers two of the three items at each beep. Table 1 depicts the design. In our example, people would be asked enthusiastic and excited a third of the time, enthusiastic and energetic a third of the time, and excited and energetic a third of the time—no one receives all three items at any beep. Table 2 depicts the covariance coverage for this sampling design. The diagonal of the table displays the proportion of complete data for an item. Each item is 67% complete because it is asked two-thirds of the time. The off-diagonal elements represent the proportion of complete data for a covariance between two items. All off-diagonal cells have a value of 33% because each item is paired with each other item a third of the time. This last point is a critical feature of the matrix design and planned missing designs generally: each item must be paired with every other item. If an off-diagonal cell has a value of zero—two items never co-occur—the model will fail unless advanced methods beyond the scope of this article are applied (e.g., Willse, Goodman, Allen, & Klaric, 2008).

Table 1.

Depiction of a Matrix Sampling Design for Three Indicators of Activated Positive Affect

	Enthusiastic	Excited	Energetic
Item Group 1	X	X
Item Group 2		X	X
Item Group 3	X		X

Note. X indicates that the item was administered.

Table 2.

Covariance Coverage Matrix for the Three Indicator Matrix Design

	Enthusiastic	Excited	Energetic
Enthusiastic	.67
Excited	.33	.67
Energetic	.33	.33	.67

Note. The diagonal elements indicate the percentage of complete data for an item; the off-diagonal elements indicate the percentage of complete data for a pair of items.

What are the consequences of using such a design? We estimated the multilevel model described earlier: a latent “Activated PA” variable was formed by the three items, and it served as the Level 1 outcome predicted by solitude (Level 1), hypomania (Level 2), and their interaction. The predictor variables in these models had complete scores—in these and other planned missing models, the missingness is varied only for the outcomes. We estimated two models. The first used the complete cases data file, in which everyone was asked all three items at all occasions. The second used a matrix sampling design, in which we randomly deleted observed Level 1 cases based on the matrix sampling design in Table 1, which yields a dataset with the covariance coverage displayed in Table 2. The intraclass correlations (ICCs) for the individual items—the percentage of the total variance at Level 2—ranged from .243 to .267. To estimate an ICC for the latent variable, researchers must ensure that it is invariant across the two levels, thereby placing the Level 1 and Level 2 variances on the same scale (Mehta & Neale, 2005). Equating the latent variable across Level 1 and Level 2 is a good idea regardless of missing data, and it is accomplished by constraining the factor loadings to be equal across levels (see Heck & Thomas, 2009, chap. 5; Mehta & Neale, 2005, p. 273). The ICC for the latent Activated PA variable was .353.

Table 3 displays the patterns of effects. Comparing the parameters and standard errors reveals very little difference: not much is lost when only two of three items are asked. Consistent with formal simulation research, the primary difference was in the standard errors. The estimates of regression paths and variances were at most modestly affected, but the standard errors were somewhat higher for elements of the model that hinged on the three PA items. Not surprisingly, the standard errors were most inflated for the factor loadings for the three items that served as indicators of the latent Activated PA variable.

Table 3.

Parameter Estimates for the Complete Cases Model and the Matrix Sampling Model for Three Indicators

	Complete	Matrix
L1 Solitude Effect	.263 (.032)	.263 (.033)
L2 Hypomania Effect	.039 (.006)	.038 (.006)
Cross-Level Interaction	−.003 (.004)	−.002 (.004)
L1 CFA: Enthusiastic Loading	1 (0)	1 (0)
L1 CFA: Excited Loading	1.077 (.019)	1.073 (.032)
L1 CFA: Energetic Loading	.961 (.020)	.991 (.031)
L1 Latent PA Residual Variance	1.326 (.057)	1.299 (.067)
L2 Random Slope Residual Variance	.127 (.035)	.117 (.034)
L2 Random Intercept Residual Variance	.627 (.062)	.618 (.064)

Note. The loading for Enthusiastic was fixed to 1 in each model. Numbers in parentheses are standard errors.

Matrix Designs for Four Indicators

All else equal, standard errors will increase as missingness becomes more extensive. To illustrate this, we can consider a model with four within-person indicators. Table 4 shows a balanced matrix design for four indicators. It adds another item, happy, to the within-person Activated PA latent variable. In this design, each beep asks two of the four items, and all pairs of items are asked. The covariance coverage is thus much lower than in the three-item matrix design. As Table 5 shows, 50% of the data are missing for each item, and each covariance is estimated based on about 16% of the beeps.

Table 4.

Depiction of a Matrix Sampling Design for Four Indicators of Activated Positive Affect

	Happy	Enthusiastic	Excited	Energetic
Item Group 1	X	X
Item Group 2	X		X
Item Group 3	X			X
Item Group 4		X	X
Item Group 5		X		X
Item Group 6			X	X

Note. X indicates that the item was administered.

Table 5.

Covariance Coverage Matrix for the Four Indicator Matrix Design

	Happy	Enthusiastic	Excited	Energetic
Happy	.50
Enthusiastic	.16	.50
Excited	.16	.16	.50
Energetic	.16	.16	.16	.50

Note. The diagonal elements indicate the percentage of complete data for an item; the off-diagonal elements indicate the percentage of complete data for a pair of items.

As before, we estimated two multilevel models: one using the complete cases data file, and another that randomly deleted Level 1 data to create a matrix sampling design for the four items. The ICCs for the indicators ranged from .227 to .267, and the ICC for the latent Activated PA variable was .345. Table 6 displays the effects and their standard errors. As before, and as expected, the factor loadings and regression weights are essentially the same, but the standard errors are larger, particularly for elements of the model involving the individual items.

Table 6.

Parameter Estimates for the Complete Cases Model, the Matrix Sampling Model, and the Anchor Test Model

	Complete	Matrix	Anchor Test
L1 Solitude Effect	.221 (.025)	.213 (.025)	.229 (.025)
L2 Hypomania Effect	.029 (.004)	.028 (.004)	.029 (.004)
Cross-Level Interaction	−.002 (.003)	−.002 (.003)	−.002 (.003)
L1 CFA: Happy Loading	1 (0)	1 (0)	1 (0)
L1 CFA: Enthusiastic Loading	1.285 (.031)	1.359 (.052)	1.281 (.036)
L1 CFA: Excited Loading	1.393 (.029)	1.472 (.052)	1.397 (.031)
L1 CFA: Energetic Loading	1.216 (.029)	1.297 (.049)	1.215 (.032)
L1 Latent PA Residual Variance	.808 (.039)	.734 (.048)	.806 (.040)
L2 Random Slope Residual Variance	.074 (.020)	.060 (.018)	.071 (.020)
L2 Random Intercept Residual Variance	.373 (.036)	.341 (.037)	.373 (.036)

Note. The loading for Happy was fixed to 1 in each model. Numbers in parentheses are standard errors.

Anchor Test Designs for Within-Person Indicators

In the matrix sampling designs we have discussed, no single item is always asked. Sometimes, however, a researcher may always want to ask a particular item. An item might be a “gold standard” item, an item reviewers expect to see, or a particularly reliable item. For such occasions, researchers can use anchor test designs. For example, an experience sampling study of positive affect might want to always ask happy, given its centrality to the construct, but occasionally ask the other items.

An example of an anchor test design is shown in Table 7. People are asked three of the four items at each beep. The item happy is always asked, and two of the three remaining items are occasionally asked. (This particular design is akin to Graham et al.'s (2006) three-form design with an X-set asked of everyone.) Table 8 shows the covariance coverage for the four items. Because happy is always asked, it occurs 67% of the time with the other three items. The occasional items, in contrast, are missing 33% of the time and occur 33% of the time with each other. This matrix illustrates the sense in which the item happy “anchors” the set of items. Data for the item most central to the latent construct—both the item itself and its relations with other items—are less sparse than data for the items more peripheral to the latent construct. Like the matrix design, the anchor test design requires each item to co-occur with each other item—no off-diagonal cell is zero—but the degree of co-occurrence will vary between pairs.

Table 7.

Depiction of an Anchor Test Design for Four Indicators of Activated Positive Affect

	Happy	Enthusiastic	Excited	Energetic
Item Group 1	X	X	X
Item Group 2	X		X	X
Item Group 3	X	X		X

Note. X indicates that the item was administered.

Table 8.

Covariance Coverage Matrix for the Anchor Test Design

	Happy	Enthusiastic	Excited	Energetic
Happy	1
Enthusiastic	.67	.67
Excited	.67	.33	.67
Energetic	.67	.33	.33	.67

Note. The diagonal elements indicate the percentage of complete data for an item; the off-diagonal elements indicate the percentage of complete data for a pair of items.

Table 6 depicts the results in the final column and enables a comparison with both the complete cases design and the matrix sampling design. In its coefficients and standard errors, the anchor test design is much closer to the complete cases estimates compared to the matrix sampling design. For the coefficients, neither design is especially discrepant, but the estimates for the anchor test design are particularly close to the complete cases design. For the standard errors, both the anchor test design and matrix sampling design have higher standard errors for the parts of the model involving the four indicators, but the standard errors for the anchor test design are appreciably less inflated compared to the matrix sampling design. The better performance for the anchor test design is intuitive: both designs have four indicators, but the anchor test design has less overall missingness (as shown in their covariance coverage matrices).

A Monte Carlo Study of Level 1 and Level 2 Sample Sizes

The empirical demonstrations that we presented have their strengths: they capture the coarse character of real experience sampling data, and they reflect the kinds of effects that researchers can expect when using these methods in the field. Nevertheless, formal Monte Carlo simulations, although more artificial, can illuminate the behavior of the planned missing designs across a range of factors and conditions (Mooney, 1997). One subtle but important strength of Monte Carlo designs for missing data problems is the ability to evaluate effects relative to the true population parameters. In our empirical simulations, the population values are unknown, so the planned missing designs were evaluated against the complete-cases sample. Missing data methods, however, seek to reproduce the population values, not what the observed data would look like if there were no missing values (Enders, 2010). Monte Carlo simulations specify the population values, so we can gain a more incisive look at the performance of designs with different patterns of missing within-person data.

Our first simulation examined three designs: complete cases for four indicators, an anchor test design for four indicators, and a matrix design for four indicators. We picked these because the anchor test design is relatively cautious (one item is always asked) and the matrix design is relatively risky (the covariance coverage is only 16%). To obtain population values for the Monte Carlo simulations, we used the observed values from the complete-cases analysis of our hypomania study used in the empirical simulations (Kwapil et al., 2011). Using values from actual data increases the realism and hence practicality of Monte Carlo simulations: the values of the parameters and ICCs reflect values that researchers are likely to encounter (Paxton, Curran, Bollen, Kirby, & Chen, 2001). The model we estimated was the same as in the empirical simulation: hypomania (Level 2), solitude (Level 1), and their cross-level interaction predicted Activated PA, a latent outcome with four indicators.

Our simulation focused on the role of Level 1 and Level 2 sample sizes in the performance of the various designs. These elements are important for two reasons. First, one would expect sample size to play a large role: with smaller sample sizes, especially at Level 1 (the number of beeps), one should encounter more convergence failures and higher standard errors. Second, Level 1 and Level 2 sample sizes are under a researcher's control, whereas many other aspects of a model (e.g., the ICC) are not. Our simulation used a 3 (Type of Design: Complete Cases, Anchor Test, Matrix) by 3 (Level 2 Sample Size: 50, 100, 150, 200) by 3 (Level 1 Sample Size: 15, 20, 45, 60) design. Simulation research commonly includes values that are unrealistic to illuminate a model's performance under dismal situations. In our analysis, a Level 2 sample size of 50 would strike most researchers as relatively small and a poor candidate for planned missing data designs; the remaining levels (100, 150, and 200) are more realistic and consistent with typical samples in experience-sampling work. Likewise, a Level 1 sample size of 15 is obviously too small, 30 is somewhat low for a week-long experience sampling project, and 45 and 60 represent realistic values for a typical 7 to 14 day sampling frame.

To simplify the reporting of the results, we focused on three parameters: the Level 1 main effect of solitude on PA, the Level 2 main effect of hypomania on PA, and the factor loading for one of the Level 1 PA CFA items (the item excited, chosen randomly). There were three kinds of outcomes. First, how many times did the model fail to terminate normally? Second, how biased—discrepant from the population values—were the estimates of the regression weights and factor loadings? And third, how did the missing data designs affect standard errors across the Level 1 and Level 2 sample sizes? The simulated data were generated and analyzed using Mplus 6.12 using maximum likelihood. Each condition had 1000 simulated samples.

Estimation Problems

How often did the multilevel model fail to converge? The number of times the model failed to terminate normally is shown in Table 9 and Figure 2. Not surprisingly, termination failures were most common at the lowest sample sizes (50 people responding to 15 beeps), particularly when a missing data design was used. Even in the worst case, however, the model failed to terminate normally only 2.10% of the time. As Figure 2 shows, termination failures were essentially zero for all designs once reasonable sample sizes (at least 100 people and 30 beeps) were achieved.

Table 9.

Effects of Planned Missing Design and Level 1 and Level 2 Sample Sizes on Termination Failures, Parameter Bias, and Standard Errors

		Complete Cases				Anchor Test				Matrix
		50	100	150	200	50	100	150	200	50	100	150	200
Termination Failures	15	1.70	.60	.40	.30	1.90	1.00	.70	.40	2.10	3.40	1.70	.40
	30	.50	.50	.40	.10	.80	.30	.10	.10	1.20	.00	.10	.10
	45	.80	.00	.10	.00	.20	.00	.10	.10	.20	.20	.10	.00
	60	.00	.00	.30	.10	.00	.00	.00	.10	.00	.10	.00	.00
L1 Factor Loading Bias	15	.187	−.065	.050	.043	.739	.043	.000	−.057	1.392	.057	.136	.251
	30	.151	.179	.000	.014	.194	.151	.122	−.043	.660	.215	.029	.143
	45	.258	.122	.187	−.036	.158	−.057	.093	−.029	.344	.201	.244	.086
	60	.079	.043	−.100	−.029	.022	.007	−.093	.057	−.294	.036	.029	−.108
L1 Main Effect Bias	15	1.830	−.357	−.759	−.089	.714	.446	−.491	.893	−3.214	−.893	.179	.179
	30	−.938	−.491	.804	−1.071	−2.321	−.089	.089	.848	−.268	.580	.937	−.179
	45	−.268	.491	.625	.759	−.714	.937	−.089	−.714	−1.071	−.268	.268	.402
	60	1.429	.759	.446	.446	.893	−.268	.268	−.357	.491	−.223	−.268	−.491
L2 Main Effect Bias	15	1.480	2.224	.519	.187	.458	.372	.701	.803	3.431	.501	−.143	−.330
	30	.128	−.629	−.341	.770	1.757	.055	.084	.559	−1.108	1.416	1.018	.458
	45	.801	.337	.528	.165	.105	−.325	.440	1.177	2.536	.105	−.075	.842
	60	1.713	.963	−.226	.319	−.576	.526	.033	.004	3.589	1.164	.374	−.141
L1 Factor Loading SE	15	.088	.062	.050	.044	.106	.074	.060	.052	.170	.117	.095	.083
	30	.064	.045	.036	.031	.077	.054	.044	.038	.123	.087	.070	.061
	45	.052	.037	.030	.026	.063	.045	.036	.032	.103	.072	.059	.051
	60	.045	.032	.026	.023	.055	.039	.032	.028	.090	.064	.052	.045
L1 Main Effect SE	15	.116	.080	.065	.056	.120	.084	.068	.059	.128	.089	.072	.062
	30	.081	.057	.046	.040	.084	.059	.048	.041	.089	.063	.051	.044
	45	.066	.047	.038	.033	.069	.048	.039	.034	.074	.051	.042	.036
	60	.058	.041	.033	.029	.060	.042	.034	.030	.064	.045	.036	.031
L2 Main Effect SE	15	2.147	1.479	1.194	1.034	2.147	1.495	1.215	1.046	2.260	1.543	1.242	1.082
	30	2.011	1.397	1.137	.986	2.000	1.406	1.142	.990	2.058	1.445	1.169	1.015
	45	1.969	1.370	1.118	.963	1.967	1.382	1.123	.971	2.013	1.401	1.136	.988
	60	1.915	1.361	1.101	.957	1.942	1.362	1.104	.963	1.958	1.375	1.119	.972

Note. Termination failures are the percentage of the 1000 samples that the model did not terminate normally. Bias is the percentage difference between the simulated value and the population value. SE = standard errors. Factor loading refers to the loading of an individual item on the Level 1 latent “positive affect” variable. L2 main effect refers to the effect of hypomania, the Level 2 predictor, on the latent positive affect variable.

Figure 2.

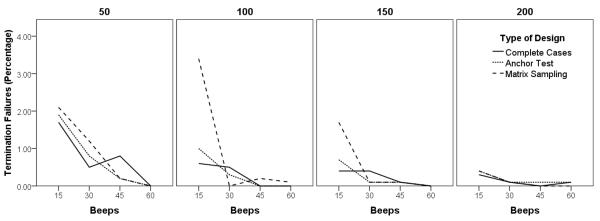
Effects of planned missing data design and sample sizes on termination failures.

Parameter Bias

How closely did the factor loadings and regression weights resemble the population values? Bias scores—differences between simulated estimates and population estimates, expressed as percentages—are shown in Table 9. As a visual example, Figure 3 illustrates the bias scores for the Level 1 CFA factor loading. Consistent with the broader missing data literature, the level of bias was small across all three planned missing data designs. Most of the bias scores (87%) were less than ±1%, and the most biased estimates were nevertheless only −3.21% and 3.59% different from the population values. The findings thus support prior simulations, albeit in a different context.

Figure 3.

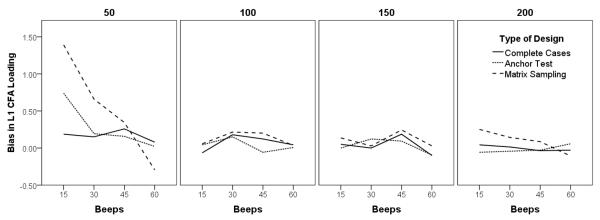
Effects of planned missing data design and sample sizes on the Level 1 CFA loading parameter bias.

Standard Errors

How did the planned missing data designs influence standard errors across different sample sizes? Table 9 displays the standard errors. First, it is apparent that the standard errors decline as both Level 1 and Level 2 sample sizes increase, consistent with the literature on power analysis in multilevel models (Bolger, Stadler, & Laurenceau, 2012; Maas & Hox, 2005; Scherbaum & Ferreter, 2009). More relevant for our purposes is how the standard errors differed across the different planned missing data designs. Overall, standard errors were lowest for the complete cases design, somewhat higher for the anchor test design, and notably higher for the matrix design—as one would expect, the standard errors increased as missingness increased. Furthermore, the influence of missing data was restricted to the within-person aspects of the model: missing data increased standard errors for the Level 1 factor loading and for the Level 1 main effect but not for the Level 2 main effect. To illustrate this pattern, Figure 4 displays the standard errors for the Level 1 CFA factor loading.

Figure 4.

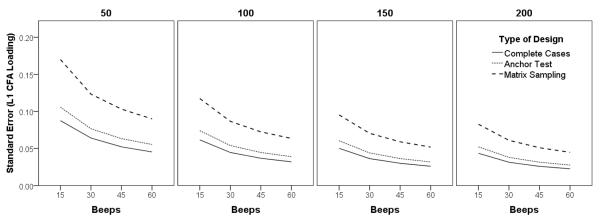
Effects of planned missing data design and sample sizes on the Level 1 CFA loading standard error.

Discussion

The Monte Carlo simulations revealed several things about the behavior of planned missing data designs. For model termination, all designs converged well once acceptable sample sizes were reached (at least 100 people and 30 beeps), so the use of planned missing data designs for within-person constructs doesn't create notable convergence problems, which were determined primarily by sample size. For parameter bias, the estimates of the factor loadings and regression weights were minimally biased. All the designs accurately recovered the parameter values, even under sparse conditions (e.g., a matrix design with 50 people and 15 beeps). Although perhaps counter-intuitive, this finding follows from the underlying statistical theory (Little & Rubin, 2002; Rubin, 1976) and replicates the broader simulation literature that supports the effectiveness of maximum likelihood methods when data are missing completely at random (MCAR), as in planned missing designs. Finally, for standard errors, the planned missing designs influenced the size of standard errors as one would expect: standard errors increased as missingness increased. The anchor test design yielded somewhat higher standard errors; the matrix design, which has covariance coverage of only 16%, yielded much higher standard errors. But in all cases standard errors declined as both Level 1 and Level 2 sample sizes increased. The increase in standard errors due to planned missing data can thus be offset by larger samples at both levels.

A Monte Carlo Simulation of Variable Response Rates

For our second Monte Carlo study, we wanted to explore the effects of variable response rates on the behavior of planned missing data designs. As experience sampling researchers know all too well, participants vary in how many surveys they complete, an irksome form of unplanned missingness. Some participants respond to every single beep, most participants respond to most beeps, and some participants respond to few beeps. Part of conducting experience sampling research is developing procedures to boost response rates, such as incentives (e.g., everyone who completes at least 70% is entered into a raffle), establishing a rapport with participants, sending reminder texts or e-mails, or having participants return to the lab once or twice during the study (Barrett & Barrett, 2001; Burgin, Silvia, Eddington, & Kwapil, in press; Conner & Lehman, 2012; Hektner et al., 2007).

In our prior simulation, response rates were fixed: each “participant” in a sample had the same number of Level 1 observations, which is akin to a study in which everyone responded to the same number of beeps. In a real study, however, researchers would observe a range of response rates, including low response rates for which planned missing designs might fare poorly. The present simulation thus varied response rates to examine their influence, if any, on the performance of different planned missing designs.

Empirical Context

As with the prior Monte Carlo simulations, we used results from real experience sampling data as population values. For these simulations, we shifted to a new context and sample dataset. The data are from a study of social anhedonia and social behavior in daily life (Kwapil et al., 2009). Social anhedonia, viewed as a continuum, represents trait-like variation in people's ability to gain pleasure from social interaction (Kwapil, Barrantes-Vidal, & Silvia, 2008). People high in social anhedonia have a diminished need to belong, spend more time alone, and are at substantially higher risk for a range of psychopathologies (Brown, Silvia, Myin-Germeys, & Kwapil, 2007; Kwapil, 1998; Silvia & Kwapil, 2011). In the original study, we measured social anhedonia as a Level 2 variable prior to the experience sampling study. People then responded to questions about mood and social engagement for several times a day across 7 days. For the present analyses, we focused on four items that people completed when they were with other people at the time of the beep: I like this person (these people); My time with this person (these people) is important to me; We are interacting together; and I feel close to this person (these people). The four questions, not surprisingly, covary highly and thus load highly on a latent social engagement variable. The ICCs for the items ranged from .155 to .254; the ICC for the latent variable was .246. These items are good examples of items that could productively be used for a planned missing data design: one would want to measure social engagement at each beep, but the four items are interchangeable.

For our simulations, we chose a simple Level 2 main effect model: social anhedonia, an observed Level 2 variable, had a main effect on the latent social engagement variable. There were no Level 1 predictors or cross-level interactions. As one would expect, as social anhedonia increased, people reported lower social engagement with other people, b = −.389, SE = .064, p < .001, which would be considered a large effect size (R² = 29%).

Monte Carlo Design

The Monte Carlo simulations explored the effects of four kinds of response rate variability. We created a hypothetical experience sampling study in which 100 people were beeped 60 times over the course of a week. Three planned missing data designs were examined, as in the prior simulations: a complete cases design, an anchor test design, and a matrix sampling design. We then created four kinds of response rate patterns. In a fixed condition, response rates were fixed at 45 out of 60, to represent a case in which everyone completed 75% of the beeps and to serve as a no-variability benchmark. In a uniform condition, response rates varied from 20 out of 60 (33%) to 60 out of 60 (100%) in increments of 5. (Twenty beeps served as a floor; experience sampling research commonly drops participants whose response rates fall under a predefined threshold.) In a high response rate condition, 70% of the sample completed at least 75% of the beeps, with some variability around 75%. And in a low response rate condition, 70% of the sample again completed at least 75% of the beeps, but 30% of the sample piled up at the floor. These conditions are easiest to understand when visualized: Figure 5 illustrates the response rates for the low, high, and uniform conditions. The simulation thus used a 3 (Type of Design: Complete Cases, Anchor Test, Matrix) by 4 (Response Rate: Fixed, Uniform, Low, High) design. As before, we used Mplus 6.12 and 1000 simulated samples in each condition.

Figure 5.

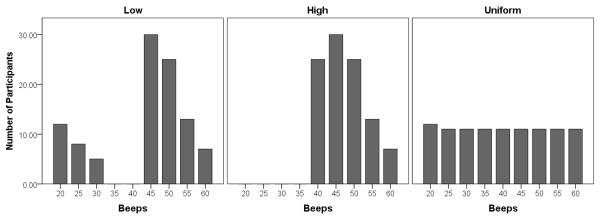
Depiction of the low, high, and uniform response rates used in the simulations.

We focused on two effects for which poor performance would be obvious: the factor loading for one of the Level 1 items (the item I feel close to this person (these people), chosen randomly) and the regression weight for the main effect of social anhedonia on the latent social engagement variable. As before, we evaluated parameter bias (how much did the simulated factor loading and regression weight diverge from the population values?) and the standard errors (how much did the standard errors change as a function of response rates and missing data designs?). We did not evaluate estimation failures because, given the simpler model and solid sample sizes at both levels, all samples terminated normally in all conditions.

Parameter Bias

For parameter bias, we again found minimal bias in the estimated Level 1 factor loading and Level 2 main effect. Table 10 displays the bias values, as percentages, for all conditions. Bias values were tiny: the most biased score was only −1.2% different from the population value. These results indicate that parameter bias is essentially unaffected by the type of planned missing data design and the types of response rates.

Table 10.

Effects of Planned Missing Design and Response Rates on Parameter Bias and Standard Errors

	Complete Cases				Anchor Test				Matrix
	Low	High	Fixed	Uniform	Low	High	Fixed	Uniform	Low	High	Fixed	Uniform
Factor Loading Bias	.049	.056	.021	−.028	−.035	.042	.070	.049	−.105	.140	.021	.049
L2 Main Effect Bias	−.823	−1.208	−.591	−.694	.925	−.129	−.334	.000	.848	.334	.977	.360
Factor Loading SE	.0154	.0148	.0151	.0160	.0188	.0183	.0187	.0199	.0309	.0296	.0303	.0322
Main Effect SE	.0650	.0643	.0640	.0650	.0652	.0643	.0650	.0655	.0654	.0646	.0648	.0655

Note. Bias is the percentage difference between the simulated value and the population value. SE = standard errors. Factor loading refers to the loading of an individual item on the Level 1 latent “social engagement” variable. L2 main effect refers to the effect of social anhedonia, the Level 2 predictor, on the latent social engagement variable.

Standard Errors

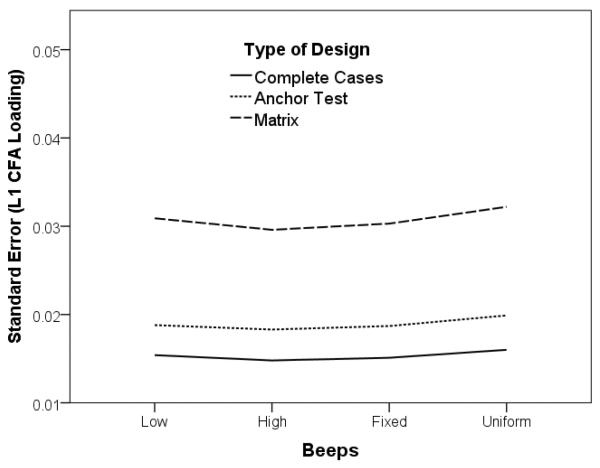
For standard errors, we again found an influence of the planned missing data design. The standard errors for the Level 2 main effect were essentially identical across all conditions, as shown in the last row in Table 10. But the standard errors for the Level 1 factor loading, not surprisingly, varied across the conditions. These values are displayed in Table 10 and Figure 6. As in our prior simulations, standard errors increased as the amount of missingness increased: they were lowest for the complete cases design, somewhat higher for the anchor test design, and notably higher for the matrix design.

Figure 6.

Effects of planned missing data design and response rates on the Level 1 CFA loading standard error.

The type of response rate had minor effects at most: standard errors were lowest for the high response rate conditions, but the variation between the types of response rates were trivial. As a result, variation in response rates appears to exert a minor influence regardless of the kind of missing data design.

Discussion

The Monte Carlo simulations replicated the general findings from the prior simulation and from the broader literature on planned missing data. As before, missing data created minimal bias in the parameter estimates (factor loadings and regression weights), but it did increase the standard errors as the amount of missingness increased. In this simulation, the increase in standard errors was restricted to the Level 1 CFA. Beyond the prior study, we evaluated the possible influences of different patterns of response rates. Overall, these patterns created at most minor differences in standard errors. The trivial influence of different response-rate patterns should be reassuring, given that experience sampling research always finds between-person variability in response rates.

General Discussion

In research, as in life, there is no free lunch, but there are occasionally good coupons. To date, experience sampling research hasn't considered the value of planned missing data designs, which have proven to be helpful in other domains in which time and resources are tight (Graham et al., 2006). Planned missing data designs offer a way for researchers to ask more Level 1 items overall without presenting more items at each beep. But nothing comes for free—as the level of missingness increases, the standard errors increase—so these designs should be applied only when the gains outweigh the somewhat reduced power.

The findings from our simulated designs resemble the findings from the broader missing-data literature (Davey & Savla, 2010; Enders, 2010; McKnight et al., 2007) and fit the underlying statistical theory (Little & Rubin, 2002; Rubin, 1976). Standard errors increased as the covariance coverage decreased. Anchoring the set of items by always asking one of the items yielded only slightly higher standard errors. For all the designs, the inflated standard errors were restricted to the parts of the multilevel structural equation model that involved the items, as one would expect, so the designs did not cause a widespread inflation of error throughout the model. Higher standard errors, of course, reduce power to detect significant effects, so researchers should weigh the virtues of a planned missing design in light of its drawbacks.

Practical Considerations

When should researchers considering using a planned missing data design in their experience sampling study? We see planned missing data designs as being particularly valuable when researchers intend to collect several items to measure a dependent variable and then average across them. This is common in experience sampling research, particularly research on affect, social behavior, and inner experience. Instead of simply averaging to form the outcome, researchers can use a matrix or anchor test design and use shorter questionnaires. But like any method, planned missing data designs should be used when their trade-offs are favorable, not because they seem novel, fancy, or interesting.

The primary payoff of these designs is space: fewer items are asked at each beep, so each daily-life survey takes less time. For example, consider a study with 20 items overall but only 15 items per beep, a savings of 5 items. The savings in space can be spent in several ways. First, it can be spent on lower burden. Asking fewer questions per beep reduces the participants' burden, which should lead to higher compliance rates. Deliberate nonresponse—ignoring the beeper, PDA, or phone—is a vexing source of missing data, and any simple methodological or procedural element that can boost response rates is worthwhile (Burgin et al., in press). Simply keeping it short is its own virtue.

Second, the saved space can be spent on asking additional constructs. Researchers could add five new items, thus asking 20 items per beep out of a 25-item protocol. The amount of time participants spend completing a survey is thus the same, but a wider range of constructs is assessed. In this case, somewhat higher standard errors are traded for the ability to measure and analyze more constructs. Our intuition is that this option capitalizes the most on the strengths of a planned missing approach.

Third, the saved space can be spent on increasing the Level 1 sample size. As noted earlier, there is a tension between the number of items per beep and the number of beeps per day. Shorter questionnaires can be administered more often. Instead of asking 20 items 6 times daily, for example, researchers might ask 15 items 8 times daily. This would increase the Level 1 sample size and thus power, all else equal (Bolger et al., 2012). In some cases, having more Level 1 units will eliminate the effect of missing data on power.

Finally, the saved space can be spent to offset other influences on administration time. There are many technologies for collecting responses (Conner & Lehman, 2012), but some take more time than others. In our lab, we have compared text surveys given via Palm Pilots to interactive voice response surveys using participants' own phones (Burgin et al., in press). It took much less time to complete the same set of items on a Palm Pilot (around 55 seconds) than on a phone (around 158 seconds). In such cases, applying a planned missing design can reduce administration time and thus presumably increase response rates.

Beyond saving space, a smaller virtue of planned missing data methods is the reduction of automatic responding. When people get the same items in the same order dozens of times, they tend to respond automatically and to “click through” the survey. Planned missing designs, by presenting different item sets at each beep, disrupt the development of response habits, which should increase data quality.

We have focused on applying these designs to within-person constructs, but experience sampling researchers could extend them to both levels of their multilevel designs. Planned missing data designs are typically seen in cross-sectional designs, such as large-scale educational assessment (e.g., Willse et al., 2008) or in psychological research where time and resources are limited (e.g., Graham et al., 2006). For example, some Level 2 constructs might lend themselves to a matrix sampling or anchor test design. We should emphasize, of course, that planned missing data designs involve a trade-off: researchers are willing to accept higher standard errors for the ability to measure more things, thus allowing more questions to be asked in the same amount of time. We doubt that the trade-off usually favors planned missing designs for Level 2 constructs of core interest to a research project, but we should note that there's nothing in theory that prevents implementing these designs at both model levels.

Planning for Power

When considering a study that would include planned missing data, researchers can estimate the influence of different designs on power by conducting small-scale Monte Carlo simulations of their own. Missingness increases standard errors and hence reduces power, but this reduction decreases when Level 1 and Level 2 sample sizes increase. Researchers can run a handful of simulations, using data from their prior work or from other research as population values, to understand how different designs and sample sizes would influence power for their particular study. Muthén and Muthén (2002) provide a user-friendly description of how to use simulations to estimate power in Mplus; several recent chapters illustrate applications specific to experience sampling designs (Bolger et al., 2012; Bolger & Laurenceau, 2013).

One virtue of using Monte Carlo methods to estimate power is that it can alleviate unrealistic fears of the effects of planned missing data. As the present simulations show, most of the influence of missing data is on standard errors, and this increase can be offset by higher Level 1 and Level 2 sample sizes. A few simulations will show researchers the sample points at which power is acceptably high.

Future Directions

An important direction for future work would be to test the effects of planned missing data methods on participant behavior, such as response rates (e.g., number of surveys completed) and data quality (e.g., time taken to complete each survey, the reliability of the within-person constructs). Based on how experience sampling researchers discuss the trade-offs between items-per-beep and beeps-perday, one would expect shorter surveys to foster higher compliance. But the methodological literature in experience sampling is surprisingly small, and only recently have studies examined factors—such as technical and design factors, personal traits of the participants, and aspects of the daily environment—that predict response rates and data quality (Burgin et al., in press; Conner & Reid, 2012; Courvoisier, Eid, & Lischetzke, 2012; Messiah, Grondin, & Encrenaz, 2011; Silvia et al., in press).

Collecting data on how planned missing designs influence compliance would also afford a look at how multiple types of missingness behave. Experience sampling research has extensive missing data at Level 1. Scores are typically missing at the beep-level—someone doesn't respond to a phone call or PDA signal, causing all items to be missing—but they are occasionally missing at the item level, such as when someone skips an item or hangs up early. Planned missing designs yield observations that are missing completely at random: the available data are a representative random sample of the total observations, and the Monte Carlo simulations reported here reflect this mechanism.

As McKnight et al. (2007) point out, however, patterns of missingness in real data typically reflect several mechanisms. In an experience sampling study, for example, some observations are missing completely at random (e.g., a technical failure in an IVR system or PDA that causes a missed signal), some are missing at random (e.g., people are less likely to respond earlier in the day, which can be modeled using time as a predictor; Courvoisier et al., 2012), and some are missing not at random (e.g., in a study of substance use, polydrug users are probably less likely to respond while and after using drugs; Messiah et al., 2011). These mechanisms might interact in complex ways. For example, a planned missing data design could reduce unplanned missingness by fostering higher compliance. Or, less favorably, when unplanned missingness is high, such as with volatile or low-functioning samples, the data could become sparse if planned missingness were added. In the absence of empirical guidance, researchers should take the expected effective response rates into account when estimating power and include likely predictors of missingness in the statistical model (Courvoisier et al., 2012).