Probabilistic measures of persistence and extinction in measles (meta)populations

Abstract

Persistence and extinction are fundamental processes in ecological systems that are difficult to accurately measure due to stochasticity and incomplete observation. Moreover, these processes operate on multiple scales, from individual populations to metapopulations.

Here we examine an extensive new dataset of measles case reports and associated demographics in pre-vaccine era U.S. cities, alongside a classic England & Wales dataset. We first infer the per-population quasi-continuous distribution of log incidence. We then use stochastic, spatially implicit metapopulation models to explore the frequency of rescue events and apparent extinctions. We show that, unlike critical community size, the inferred distributions account for observational processes, allowing direct comparisons between metapopulations.

The inferred distributions scale with population size. We use these scalings to estimate extinction boundary probabilities. We compare these predictions with measurements in individual populations and random aggregates of populations, highlighting the importance of medium-sized populations in metapopulation persistence.

Introduction

The persistence (and extinction) of species over space and time is an emergent property of multiple ecological processes. From conservation biology to disease ecology, local population dynamics and spatial connectivity are central to understanding species persistence. Host-pathogen interactions provide a natural framework in which to consider colonizer-invader trade-offs and the prerequisites for successful invasion and persistence (King et al., 2009). These problems have straightforward epidemiological and public health interpretations: the emergence and establishment of novel human pathogens, and their control and eradication in human populations. More generally, the study of disease dynamics can shed light on the ecologically significant interactions between demographic stochasticity, patch connectedness, and observational processes.

Measles has been a workhorse of theoretical ecology for more than 100 years (Hamer, 1906; Soper, 1929; Bartlett, 1956; Black, 1966; Anderson & May, 1991; Keeling & Rohani, 2008), particularly with respect to population-level persistence and extinction. A human pathogen that diverged from rinderpest in the pre-industrial era, measles has avoided eradication and still causes significant morbidity and mortality, particularly in regions with poor health care infrastructure (Ferrari et al., 2008). Originally noted for its dramatic yet regular epidemics, measles has become a model system in population ecology modeling. Epidemiological models of measles highlight the importance of non-linear feedbacks, transients, stochasticity, and non-stationarities in ecological processes (Bolker & Grenfell, 1993; Earn et al., 2000; Keeling et al., 2001; Rohani et al., 2002), as well as spatial structure and heterogeneity (Bolker & Grenfell, 1995; Grenfell & Bolker, 1998; Rohani et al., 2002).

Several factors make measles a useful model pathogen, including ease of diagnosis, abundant historical records, short latent and infectious periods, low mortality, lifetime immunity, and a lack of environmental or animal reservoirs. Seasonal aggregation of school-age children in developed countries also influences the basic reproductive ratio (R₀), controlling epidemic timing (London & Yorke, 1973; Fine & Clarkson, 1982; Keeling et al., 2001). These factors facilitate the interpretation of historical records by reducing uncertainty and constraining dynamics.

Population measures of persistence

Critical community size (CCS) is a threshold measure of within-population disease persistence. CCS has played a central organizing role in disease ecology since its introduction by Bartlett (1957). Though debate surrounds its precise definition (Bartlett, 1957; Nåsell, 2005; Conlan & Grenfell, 2007; Conlan et al., 2010), CCS is approximately the population size above which pathogen extinction is not observed, implying an unbroken within-population chain of infection. The CCS of measles has been extensively studied in the context of pre-vaccine era England & Wales (Grenfell et al., 2002), and with respect to vaccination and eradication thresholds (Griffiths, 1973; Bolker & Grenfell, 1996).

As defined, CCS depends fundamentally on both population and metapopulation-level processes, and serves as a measure of both. This ambiguity of the CCS concept is highlighted by vaccination, which is dynamically equivalent to lowering birth rates. As susceptible recruitment drops, the CCS of a given metapopulation increases. In the extreme case, endemic transmission of measles was eliminated in the U.S. circa 2000 (Orenstein et al., 2004). Using the traditional definition of CCS, the current CCS of the U.S. exceeds the size of every U.S. city, by definition, since continuous transmission is no longer observed in any U.S. city.

Minimum viable metapopulation (MVM) size is a complementary threshold measure of persistence that addresses this ambiguity, though does not consider individual population sizes (Hanski et al., 1996). The present work seeks, in part, to bridge a perceived gap between classic disease ecology and metapopulation literature, since these fields have historically approached similar questions from very different directions (e.g. the contemporaneous work of Hanski et al. (1996) and Bolker & Grenfell (1995)).

As measured, CCS is further confounded by observational processes such as sampling period and reporting rate, such that no straightforward between-metapopulation comparison exists. Here we present a new dataset consisting of over 20 years of weekly case reports of measles in 83 cities in the pre-vaccine era United States (from 1924 to 1945). Case reports are augmented by demographic records at the city, state and national level, and associated reporting rate estimates. We compare this dataset with the classic England & Wales dataset (biweekly, 1944 to 1965), also augmented with demographics and reporting rate estimates. We demonstrate the sensitivity of CCS to observational, within-population, and metapopulation processes, and provide an alternate measure of persistence.

We seek summary statistics that, similar to CCS, describe the long-term, marginal distribution of true measles incidence within and between populations. Here we use a distributional approach, augmented by stochastic metapopulation models that highlight the key dynamical and observational processes in these systems. Despite the presence of obvious autocorrelation and non-stationarity, we find conserved measures of measles incidence that scale with population size.

Three points deserve special notice. First, we find that U.S. reporting rates are lower and more variable than in England & Wales. This suggests a larger apparent CCS, for which we have corrected. Second, higher U.S. birth rates should favor increased persistence, which we do not observe. Finally, large U.S. intercity distances could result in smaller rescue effects and lead to decreased persistence, as observed here. These findings suggest that metapopulation processes play an important role in differentiating the U.S. from England & Wales. Nonetheless, a key remaining challenge in matching mechanistic models to data is the full differentiation of population-level processes such as seasonality of transmission from metapopulation-level processes such as migration.

Outline

An outline of the paper is as follows. We first infer weekly log incidence (ξ) from observed cases, reporting rate, and population size. Critically, we do not exclude observed zeros from our analysis. Instead we assume that each represents ≤ 1 observed case. We then fit a normal cumulative distribution function (CDF) to each city’s empirical cumulative distribution function (ECDF). Scaling of the inferred parameters (mean μ̂ and standard deviation σ̂, not sample mean and SD) with population size (N) is evident. For each inferred parameter and metapopulation, we fit a descriptive linear model using N as the independent variable. We construct a probabilistic measure of CCS, and compare patterns of persistence between random aggregates of populations and metapopulations.

For comparison, we construct a stochastic, spatially-implicit metapopulation model that includes fully-parametrized demographics. Model results highlight the effects of apparent extinctions on the proportion of observed zeros, particularly in intermediate-sized cities. We conclude with a discussion of the applicability and usefulness of the presented methodology to other systems.

Materials and Methods

Data collection and preparation

U.S weekly case reports were manually transcribed from United States Public Health Reports (U.S. Public Health Service, 1920–1950). Each report was double-entered; mis-matches were automatically identified and manually resolved. Populations with fewer than 20% missing values were used for subsequent analysis, for a total of 83 cities ranging in mean population from 16 thousand to 7.2 million. These cities account for 22.7% (1920) to 24.9% (1950) of the total U.S. population, and from 48% (1920) to 39% (1950) of the urban U.S. population. All cities with a 1930 population over 350 thousand are sampled; many smaller cities are missing. The period of record stretches from 1924-01-05 to 1945-12-29 (1148 weeks).

U.S. city decadal population was obtained from the U.S. decadal census (1920–1950) (U.S. Census Bureau, 1920–1950b). Yearly per capita state birth and death rates and US infant mortality rates were obtained from the U.S. Statistical Abstracts, 1920–1950 (U.S. Census Bureau 1920–1950a). Yearly U.S. city populations were estimated using an exponential growth model to interpolate between decadal population. Yearly U.S. city populations were then used to calculate births into each city from state birth and national infant mortality rates. Birth rates for the U.S. (states) and England & Wales (cities) are shown in Figure S1 in Supporting Information.

England & Wales case reports (every two weeks, no missing values, as presented by Grenfell et al. (2002)) were obtained from http://www.zoo.cam.ac.uk/zoostaff/grenfell/measles.htm, along with population size (Rohani, 2012) and births by year. Births were adjusted for infant mortality using yearly national rates (Southall, 2006). This dataset includes 60 cities ranging in (1955) population from 10.5 thousand to 3.25 million. The period of record covers 1944-01-09 to 1966-12-25; due to redistricting changes in 1965, only the period through 1964 was employed, resulting in 546 biweeks.

Migration was inferred for each population and year by subtracting live births from, and adding deaths to, the yearly change in population size. A proportion of migrants (1 − 1/R₀) was assumed to be recovered, with the remainder susceptible.

Reporting Rate

Reporting rate was assumed constant over the period of record; for the i^th population, a single reporting rate r_i was estimated. We assume that a proportion $1-\frac{1}{R_0}$ of available susceptibles contract and recover from measles (Anderson & May, 1991) over the period of record. The net yearly flow of susceptibles s_i into population i was estimated from births, infant mortality, and migration, as described above. Death of susceptibles was assumed to be minimal. Thus, the expected total number of actual cases in the i^th population, ${\mathrm{C̅}}_i={\sum }_t{s}_i(1-\frac{1}{R_0})$, and $r_i=\frac{{\sum }_t{C}_i}{{\mathrm{C̅}}_i}$, where C_i represents the observed case reports in population i at time t (Fine & Clarkson, 1982). See Figure S2 for a map of sampled U.S. cities showing estimated reporting rates.

Estimating lognormal distributions of incidence

For each city, we inferred the distribution of weekly per capita log incidence ξ_i (log₁₀ was used throughout). Missing values were excluded. Inferred cases Ĉ_i were estimated from reported cases C_i and reporting rate: ${Ĉ}_i=\frac{C_i}{r_i}$. Critically, we do not exclude observed zeros to avoid distorting the ECDF. Instead, we assume that each observed zero is equivalent to as many or fewer inferred cases as one observed case: $C_i=0\Rightarrow {Ĉ}_i\le \frac{Z}{r_i}$ for Z ≤ 1 (here Z = 1).

Weekly per capita log incidence ξ_i was estimated from inferred cases, the mean population size of each city N_i, and the number of weeks per observation n (2 for England & Wales): $\xi =\text{log}\frac{{Ĉ}_i}{n{N}_i}$. Nonlinear minimization (NLM) (Dennis & Schnabel, 1983) was used to fit a normal CDF to the ECDF of ξ_i using an L_∞ metric (equivalent to the Kolmogorov-Smirnoff (K-S) distance between the two distributions). Metapopulation mean μ̂ and σ̂ were used as initial conditions for another iteration of the NLM procedure to avoid local minima. Thus, the mean μ̂ and standard deviation σ̂ were chosen to minimize the maximum difference in probabilities (L_∞ metric) between each population’s empirical and estimated CDF of ξ.

In this way, we infer a quasi-continuous distribution of log incidence ξ from the discretized distribution of observed cases. The ECDFs and estimated normal CDFs are shown for select cities in Figure S4. This inference method explicitly accounts for the proportion of observed zeros as the integral of the normal probability density function (PDF) over the interval (−∞, $\text{log}\frac{1}{r{N}_i}$). Conceptually, this lower tail includes inferred cases below the observation threshold of ${Ĉ}_i=\frac{1}{r}$, as well as the effects of imported cases. To evaluate goodness-of-fit, parametric and nonparametric bootstrap replicates were conducted (see Figure S7).

To test for differences between metapopulations, we conducted an (unbalanced) ANCOVA using country identity as the independent variable and log population size N as the covariate. Separate linear models were tested for μ̂ and σ̂.

A metapopulation model of measles dynamics

We assessed the ability of simple epidemiological models to reproduce patterns observed in the data. We constructed a spatially implicit, stochastic, event-driven version of the standard exponential SEIR model as per Olsen et al. (1988). The resulting simulations also highlight unobservable yet important processes, including rescue events and apparent extinctions.

We employed the Gillespie τ-leap method (Gillespie, 2001) with a time-step of one day. Population sizes and demographics were fully specified from historical records. Births into the susceptible class account for infant mortality. We assume death occurs exclusively in the recovered class. A portion of migrants ($\frac{1}{R_0}$) was assumed to be susceptible; the remaining migrants enter or leave the population through the recovered class. Transitions into the exposed class due to imported infection were included at a rate proportional to metapopulation incidence. We tested both sinusoidal and term-time seasonal forcing of contact rates. Unlike England & Wales, U.S. term times are not national, and historical estimates are not available. The effect of varying term times remains under-explored in the literature. See Appendix S2 for model details.

Key transitions were summed on a weekly basis. These include total transitions into E (E_w), transitions into E caused by imports (E_wη), and total transitions into I (I_w). A binomial observation process was used to generate weekly observed cases I_wo from I_w, where the probability of successful observation was equal to the city’s reporting rate r_i. For Γ = E_w + I_w, we tabulated the total number of true extinctions (Γ = 0), rescue events (Γ = E_wη), and apparent extinctions (Γ > 0∩I_wo = 0). The proportion of weeks with zero case reports (P₀ = Pr(I_wo = 0)) was also tabulated.

An ensemble of 10 realizations was simulated for each of a range of parameter combinations (see Table S3). For each realization and population i, P_0i, μ̂_i, and σ̂_i were computed. For each of these 3 measures δ, the sum of squared residuals RSS_δ = ∑_i δ_i,model − δ_i,data was computed. See Figure S9 for final model selection details and Table S4 for final parameter values. For these parameter values, an ensemble of 50 realizations was run and within-city ensemble means of all estimates were computed.

Random aggregates of populations

Previous studies have examined case reports and incidence in both single populations and aggregate metapopulations. Here we construct random aggregates of various sizes. For each random aggregate, M = X² populations were sampled without replacement (X ∈ 2, …, 5). Timeseries, total cases, and total susceptibles were summed over sampled cities. Reporting rate and incidence distribution was computed as above. For each M, 100 aggregates were drawn.

Estimating extinction boundary probabilities

To predict the distribution of ξ for a given population size, a separate linear model was fit to each metapopulation and inferred parameter using N as the independent variable (Table S1). We use these descriptive linear models to compute the per-week probability $B=\mathit{\text{Pr}}(\xi \le \text{log}\frac{1}{N})$ for a range of N.

The ECDF of ξ is clearly discrete, while the normal CDF is continuous. Nonetheless, we propose that B yields a good estimate of the amount of time each population spends at or below 1 actual case, providing an approximate extinction boundary probability. This estimate is based on inferred (or actual) rather than observed cases, and thus accounts for rescue effects and is not biased by apparent extinctions.

Results

Distribution of inferred incidence

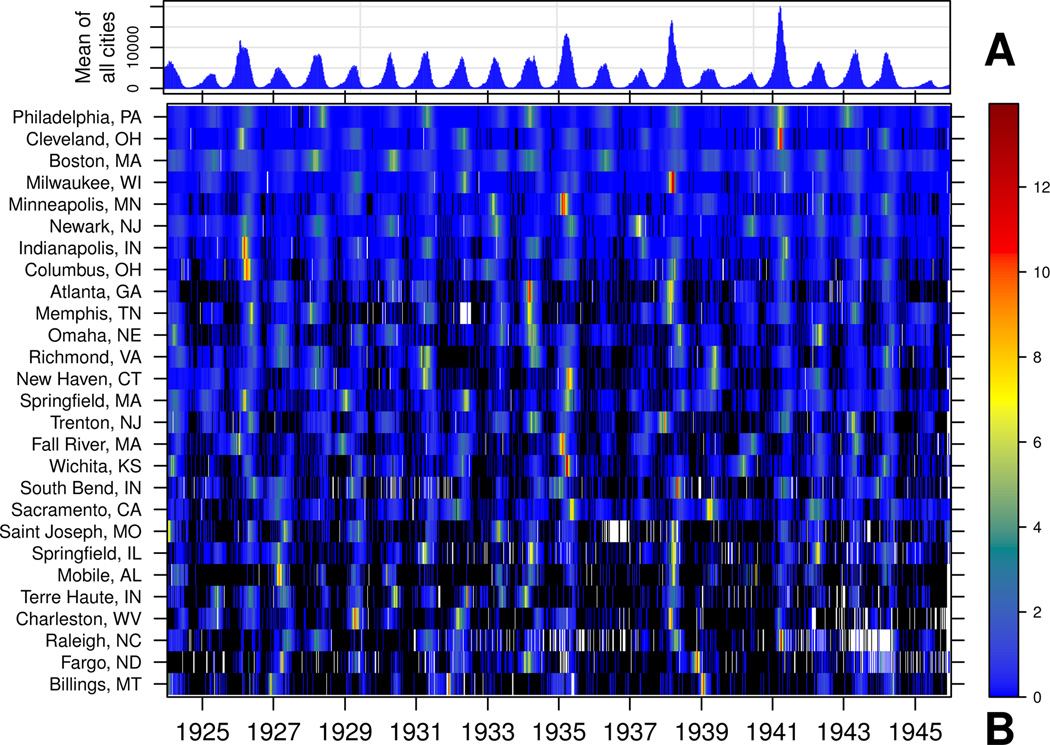
Figure 1 shows weekly scaled case reports for a subset of U.S. cities, and the weekly unscaled mean of city case reports (omitting missing values). We use this dataset, along with the previously-studied England & Wales dataset and a simple stochastic metapopulation model, to show that the distribution of weekly per capita log incidence (ξ) provides a unifying framework for comparing populations and metapopulations.

Figure 1. Weekly measles case reports for a subsample of United States cities, 1924-01-05 to 1945-12-29.

Zeros are black and missing values are white. (A) Weekly mean of unscaled case reports of all cities. (B) Heatmap for a subset of cities ordered by mean population size. Values are variance-scaled within each city.

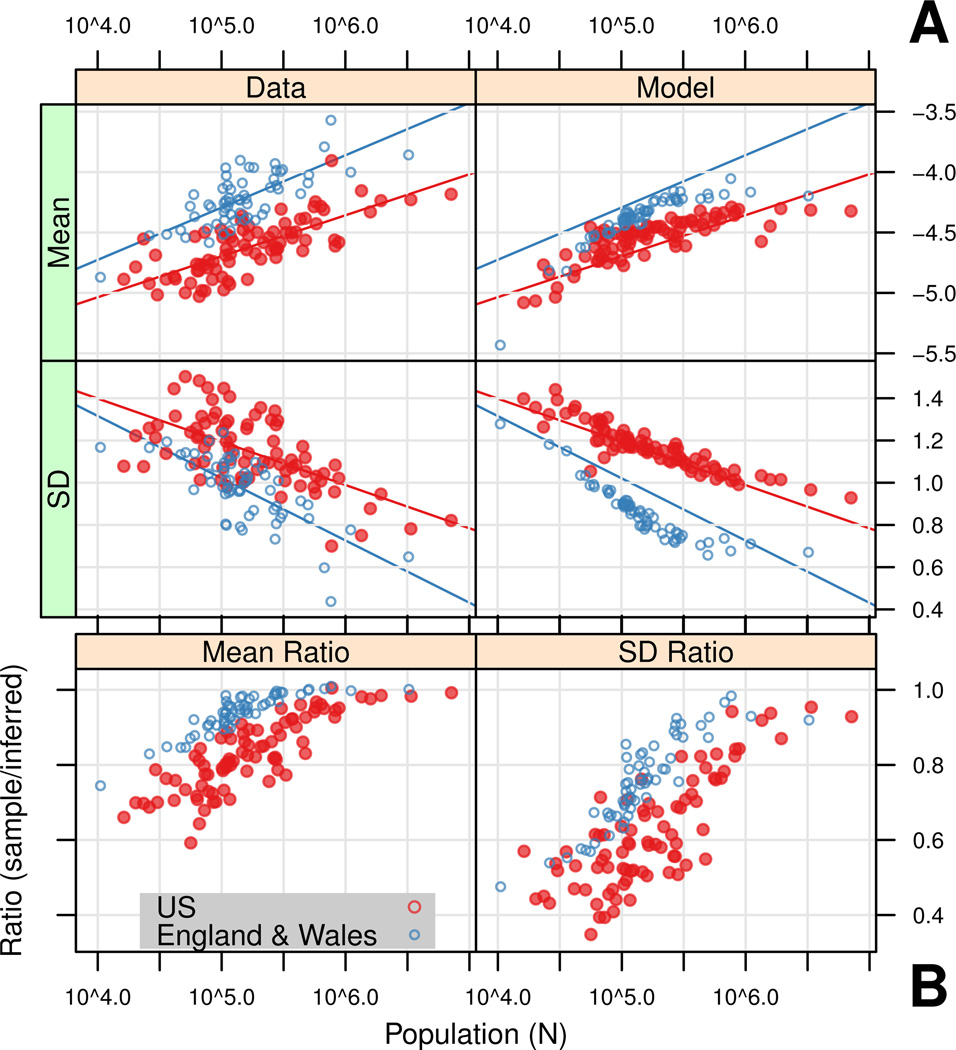
Figure 2A (Data column) shows the inferred mean (μ̂) and standard deviation (σ̂) for the per-city normal distribution of ξ. For comparison, the descriptive linear models of data are also plotted (see Table S1). Figure 2A (Model column) shows μ̂ and σ̂ inferred from the best-fit epidemiological model ensembles. See Figure S9 for epidemiological model fit details.

Figure 2. Inferred parameters for normal distributions of weekly log incidence (ξ).

(A) Left column: for each city, a normal CDF with mean (μ̂) and SD (σ̂) was fit to the ECDF of ξ by nonlinear minimization using an L_∞ metric (minimizing Kolmogorov-Smirnoff (K-S) distance). Right column: Simulation results, with (μ̂) and SD (σ̂) inferred as above, averaged over 50 realizations. See Table S4 for final epidemiological model parameters. For comparison, descriptive linear models of inferred parameters against log N of data (left column) are shown in both columns (see Table S1). (B) Ratio of sample statistics to inferred parameters (sample/inferred) for data. Sample statistics underestimate variation at small population sizes, and converge towards inferred parameters at large population sizes.

The inferred σ̂ of data (Figure 2A, left column) show more scatter in the U.S. than in England & Wales. One probable cause of this scatter is that reporting rate estimates appear less accurate in the U.S. (see Figure S8). Further, the geographical variation in the U.S. is extreme, where similarly-sized cities may range from close proximity to large cities to relative isolation. Lacking details of spatial connectivity, we explored simple measures of connectivity, including a rank gravity model, to explain the observed variance in inferred distributions. We did not identify a simple measure of connectivity that explains a significant proportion of this variance, though this area deserves more attention.

In simulation results (Figure 2A, right column), mean per capita incidence appears to saturate as population size increases. We might expect this because deterministic models of frequency-dependent transmission, where the force of infection depends only on the fraction infected, predict that per capita incidence does not depend on population size. The data do not clearly exhibit the same saturation behavior, which suggests future modeling efforts should investigate more flexible assumptions about transmission.

Figure 2B shows the ratio of sample statistics (sample mean and standard deviation of observed log per capita incidence, excluding zeros) to their associated inferred parameters (μ̂ and σ̂) for data. At small population sizes, sample statistics greatly underestimate the amount of variation observed in the data due to the exclusion of zero weeks (ξ = −∞). Sample statistics converge towards inferred values at large population size. This population size, near prior estimates of CCS, is the threshold above which ξ is normally distributed.

ANCOVA results are shown in Table 1. Country identity has a significant effect on intercept (though not both slope and intercept). Overall, U.S. populations exhibit less persistence than comparably sized populations in England & Wales. Goodness-of-fit results are shown in Figures S5–S7.

Table 1.

ANCOVA results. A separate linear model was constructed for each inferred parameter, using log N and country identity as predictors. Simulations were not modelled. England & Wales is the reference level. Mean (μ̂), R² = 0.74; SD (σ̂), R² = 0.55. For both inferred parameters, country identity has a significant impact on either intercept (shown here) or slope, but not both. Note the model is not balanced.

Inferred Parameter	Model Term	Estimate	Std. Error	t value	Pr(>|t|)
Mean	(Intercept)	−6.327	0.148	−42.842	<10−12
Mean	logN	0.367	0.028	12.967	<10−12
Mean	Country	−0.210	0.013	−16.021	<10−12
SD	(Intercept)	2.261	0.118	19.222	<10−12
SD	logN	−0.231	0.023	−10.263	<10−12
SD	Country	0.095	0.010	9.057	<10−12

Revisiting Critical Community Size

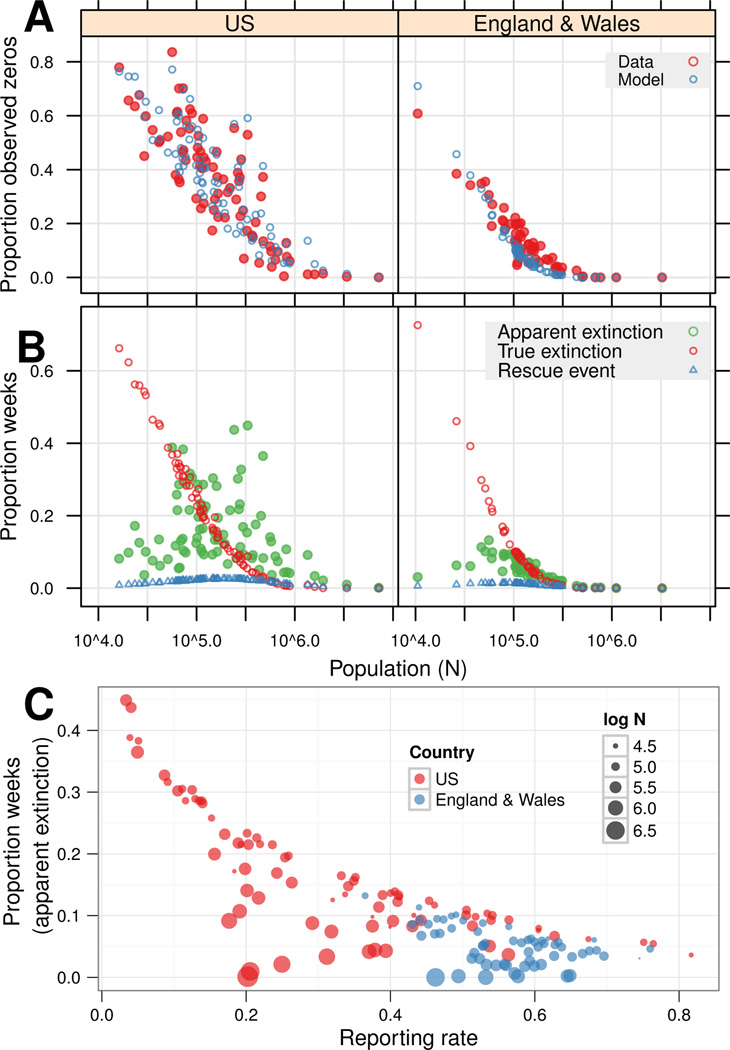
For comparison with previous results (Bartlett, 1957, 1960; Conlan et al., 2010), Figure 3A shows the relationship between population (logN) and the relative frequency of zero weeks (P₀) for both data and models. Cities in England & Wales show lower P₀, which might suggest a lower CCS in cities in England & Wales than in the U.S. in this era. Yet these curves are not directly comparable because reporting rates and sampling frequency differ, affecting the probability of observing zeros (see Figure S3).

Figure 3. Distribution of zeros, extinctions, and rescues.

For epidemiological models, values were calculated for each realization and an ensemble mean taken. (A) Proportion of observed zeros by population size. (B) Proportion of apparent extinctions (Γ > 0 ∩ I_wo = 0), true extinctions (Γ = 0), and rescue events (Γ = E_wη > 0) for Γ = E_w +I_w. True extinctions scale with population size; rescue events and apparent extinctions are highest at intermediate populations. Apparent extinctions cause scatter in observed zeros (A) in the U.S. (C) Apparent extinction versus reporting rate. As population size decreases, the apparent extinction rate becomes more sensitive to reporting rate.

Figures 3B and C use model results to examine key processes that are not readily observable in real systems. For Γ = E_w + I_w, Figure 3B shows true extinctions (Γ = 0), apparent extinctions (Γ > 0 ∩ I_wo = 0) and rescue events (Γ = E_wη) per week. Rescue events and apparent extinctions are most common in intermediate-sized cities. These cities spend more time on the edge of extinction, where the influence of stochastic observational processes and imports are maximal. True extinctions, on the other hand, show clear curvilinear scaling with population size, following the trend evident in P₀ (Figure 3A). The number of observed zeros is equivalent to the sum of true and apparent extinctions. Thus, Figure 3B suggests that the scatter in observed zeros (Figure 3A), particularly in the U.S., is caused in part by apparent extinctions, while rescue events play a much smaller role.

Figure 3C displays apparent extinctions as a function of reporting rate, highlighting the interaction between reporting rate and population size. A clear constraint curve is evident, where the maximum apparent extinction rate is a function of the reporting rate. Increasing population size lowers the apparent extinction rate from this maximum towards zero for the largest populations.

Surprisingly, the effect of per-city reporting rates and the variability thereof has not been previously examined in detail. In a few cases, individual population estimates have been reported (London & Yorke, 1973; Clarkson & Fine, 1985), as well as overall metapopulation estimates (Black, 1982; Finkenstädt & Grenfell, 2000). These generally agree with our findings of lower and more variable reporting rates in the U.S. than in England & Wales, though we found no previous estimates on within-metapopulation variance. Given the significant effect of variable reporting rates on observational bias shown in Figure 3C, this is a potentially fruitful avenue of study.

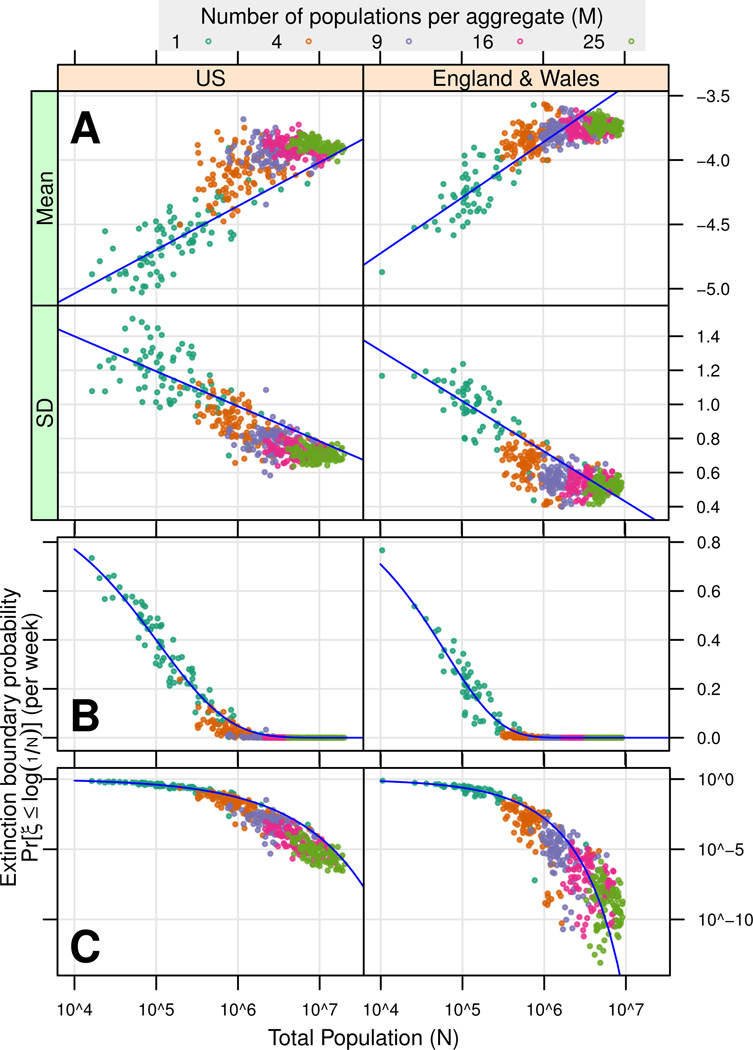
Figure 4 shows the effect of aggregation on the distribution of ξ. Random aggregates of smaller cities exhibit distributions of ξ similar to single, large cities, as shown by descriptive linear model predictions. In the US, aggregate μ̂ is consistently above the linear model prediction, while σ̂ is consistently below the prediction. Thus aggregation consistently reduces variation in the US, which would be expected amongst asynchronous populations. In England & Wales, the pattern is less clear-cut, with aggregates falling both above and below the linear model prediction for both inferred parameters. The above is consistent with the observation that the mean pairwise population correlation coefficient is much higher in England & Wales (0.29) than in the U.S. (0.15), indicating greater asynchrony in the U.S.

Figure 4. Inferred distributions (A) and extinction boundary probabilities (B,C) for single populations and random aggregates of populations.

100 random aggregates were drawn for each aggregate size (see legend).

(A) Inferred distributions and linear models (linear models exclude random aggregates, see Table S1). For random aggregate total population N ~≥ 10⁷, ξ converges to a limiting distribution.

(B, C) Points show the extinction boundary probability $B=\mathit{\text{Pr}}(\xi \le \text{log}\frac{1}{N})$, estimated from μ̂ and σ̂ for populations and random aggregates in (A). Curves show B for a range of population sizes, as predicted by linear models from (A). Any probability B = α has a corresponding population size, giving a probabilistic measure of critical community size CCS_α. The U.S. B curve is higher than in England & Wales, indicating higher probabilities of extinction across population sizes.

The observation that random aggregates generally follow the patterns of ξ predicted by linear models of single populations argues for a reconsideration of single large cities as key drivers in disease persistence in general and the emergence of measles in particular. Previous work used CCS to infer the possible historical era of measles zoonosis based on historical population sizes (Conlan & Grenfell, 2007). Our results argue strongly in favor of a metapopulation-level view of disease emergence, where interconnected aggregates of small populations can support disease persistence. This fact has important modern implications for zoonosis, which often occurs at the interface between human settlements and natural systems.

As the size of random aggregates grows, a central limiting distribution of ξ is reached, such that per capita log incidence is constant with increasing population size. This is the expected behavior for frequency-dependent transmission and is suggested by epidemiological model results, as mentioned above. This limiting distribution is very different for the U.S. and England & Wales, with the U.S. exhibiting relatively smaller μ̂ and larger σ̂.

The extinction boundary probability $B=\mathit{\text{Pr}}(\xi \le \text{log}\frac{1}{N})$, as computed from μ̂ and σ̂, is plotted for each population and random aggregate in Figure 4B and C. Intuitively, B forms an upper boundary for the per-week probability of a population being in the extinct state. The plotted curves show B for a range of population sizes N, as estimated from the descriptive linear models predicting μ̂ and σ̂ from individual city size (fit for each metapopulation, see Table S1). Thus, for N > 10⁷, we expect fewer than one extinction in a thousand years (B < 10⁻⁵) in both metapopulations. Figures 4B and C are identical except for log scaling of the Y axis in C.

Figures 4B and C highlight the difference between random aggregate and metapopulation estimates. In the U.S., random aggregates more closely match metapopulation estimates than in England &Wales. In addition, U.S. random aggregates are generally below (e.g. less likely to be extinct) what would be predicted from the metapopulation curve, as would be expected from the aggregation of asynchronous populations.

The extinction boundary probabilities give rise to a probabilistic interpretation of CCS. A given probability B_α has a corresponding critical community size CCS_α; for populations larger than CCS_α, the predicted per-week probability of being extinct is less than α. Indeed, the metapopulation curves reveal that B is higher in the U.S. than in England & Wales for all population sizes, yielding a larger CCS_α for all α.

Epidemiological model results

Even with a wealth of case report and demographic data, we still lack sampling of rural populations and patterns of spatial connectivity. We have thus chosen a relatively parsimonious epidemiological model formulation here that implicitly includes space. Despite the simple formulation, simulations do capture the overall scaling of μ̂ and σ̂, as well as the proportion of observed zeros P₀ (Figure 3A). Representative simulation timeseries are shown in Figure S10. Nonetheless, the observed scaling of μ̂ and σ̂ with population size N (Figure 2A) is not fully reproduced. Simulations yield nonlinear scaling, with per capita incidence approximately constant above a threshold N. Note, however, that Figure 2A shows ensemble means, which greatly reduces between-population scatter compared to individual simulations. We suggest that inferred μ̂ and σ̂ provide important probes that more complex mechanistic models can be tested against.

Epidemiological model results also clearly illustrate the influence of key dynamical processes that are difficult to observe in real systems (Figure 3B). Here we find that apparent extinctions greatly affect observational processes in midsized cities, an effect that is compounded by the low reporting rates of the US. A range of parameter values were found to produce similar results (see Figure S9). The final epidemiological models presented here are primarily for illustrative purposes, and different parameter choices do not affect overall results.

Discussion

Comparing metapopulations

The U.S. dataset presented here provides an important counterpoint to the highly successful England &Wales measles dataset (Fine & Clarkson, 1982; Bolker & Grenfell, 1995; Grenfell & Bolker, 1998; Rohani et al., 1999; Grenfell et al., 2001). First and foremost, it contains extensive spatial and temporal heterogeneity compared to England & Wales. Demographics and transportation vary over time, from boom years (1920s) to economic depression (1930s) to a major war and demographic boom (1940s), accompanied by racial and ethnic segregation within and between cities (U.S. Census Bureau, 1920–1950a; Tolnay, 2003; Middleton et al., 2007). Population density and transportation networks vary greatly in space, from dense and highly-connected Northeastern cities to isolated mountain West communities such as Billings, Montana and the island community of Galveston, Texas.

Both datasets sample a single, extensive metapopulation over a long, contiguous period of time. England & Wales offers dense coverage of a spatially compact metapopulation, while the U.S. dataset samples a much larger metapopulation, albeit less densely. The U.S. in this era is socially, economically, and even genetically more heterogeneous than England & Wales. In addition, key drivers of measles dynamics, such as school terms and family size, vary greatly throughout the U.S. during this era (Metzker, 2002), both temporally and spatially. Lacking data on these factors, we have used a simple “strategic” rather than detailed “tactical” model formulation that nonetheless largely reproduces observed patterns in the data.

Here we argue that the inferred distribution of weekly per capita log incidence ξ, and its consistent scaling with population size N, yields a robust comparison of patterns of incidence between metapopulations. Because our method accounts for reporting rate, population size and sampling frequency, we suggest that the remaining differences between metapopulation distributions result from differences in underlying ecological processes. The results presented here show significant differences in the distribution of ξ between countries (Table 1), as well as in the limiting distribution of ξ in random aggregates (Figure 4). Several key points deserve special notice. First, reporting rates are lower and more variable in the U.S. (Figure 3C), which suggests a larger apparent CCS, and which we have corrected for. Second, higher birth rates in the U.S. would generally favor increased persistence and a lower CCS, which we do not observe. Finally, large intercity distances in the U.S. could result in a smaller rescue effect, leading to a larger true CCS, as observed here.

Distributional measure of persistence and extinction

Diseases with relatively high R₀ and short infectious period, such as measles, are prone to local fade-outs. Large focal communities have been proposed as refugia that allow metapopulation persistence, thus highlighting the importance of CCS. Yet the usefulness of fixed population thresholds, such as CCS, has been criticized: Lloyd-Smith et al. (2005) points out that “thresholds are rarely abrupt and always difficult to measure”. By taking a distributional approach to understanding persistence and extinction in host-pathogen interactions, we aim to bypass some of the shortcomings of single threshold measures.

Our choice of log incidence (ξ) is motivated by the observation that incidence of acute infectious disease generally emerges from a multiplicative process, where the natural scale is logarithmic (Limpert et al., 2001). However, a log scale does not easily permit consideration of zero incidence and, in these situations, the true distribution of ξ is often thought of as a mixture of one process that describes presence/absence and another that conditions on presence and describes non-zero incidence (Fletcher et al., 2005). Yet observations of zero cases do not imply zero incidence in this system. Thus we subsume observed zeros into incidence at or below the minimum observable nonzero incidence, $\xi =\text{log}\frac{1}{rN}$. This approach preserves the within-city empirical CDF (ECDF) by including all the observed data points, yet is not overly biased by our inability to observe incidence between 0 and $\frac{1}{rN}(\xi \in (-\infty ,\text{log}\frac{1}{rN}))$.

Theory based on simple non-seasonal stochastic epidemiological models predicts that, for large enough population size, the distribution of infectives is approximately normal (Nåsell, 1999; Andersson & Britton, 2000), with mean and variance scaling linearly with population size. These results are obtained by conditioning on non-extinction to derive a quasi-stationary distribution of infectives. In fact, for average measles parameters, the threshold for this 12 approximation can be close to 10⁷, which is above the size of all cities in the two metapopulations considered here. For both datasets, we find that the normal CDF is a good description of the marginal distribution of log incidence for populations at or over the critical community size, so that sample mean and standard deviation can be used to infer this distribution (as shown in Figure 2). We argue that this is empirical evidence that the time series can be considered as weakly stationary, despite the intrinsic seasonality and autocorrelation present in the system. This supports theoretical work demonstrating that, if populations are above a critical size, the assumption that infectives follow a lognormal distribution is valid when closing moment equations (Keeling, 2000; Lloyd, 2004). In addition, for smaller populations, we can still characterize log incidence using a normal distribution by fitting a normal CDF to the truncated empirical CDF. Understanding how this inferred distribution relates to recent work by Black & McKane (2011), who derived an analytic approximation to the marginal distribution of infectives for a non-seasonal SIR model, could provide further insight into why the lognormal is a good fit for a wide range of population sizes.

Generality of approach and broader applications

The sensitivity of inferred distributions to the duration of study remains an important question. In particular, how long must populations be observed before log incidence is well-estimated by a normal distribution, and how do the inferred distributions change over time? The results presented here broadly hold if the data are divided into a small number of equal-length subdivisions (for details, see Figure S8). As subdivisions grow shorter, however, estimates diverge from those based on the full timeseries, and variance between subdivisions exceeds variance between populations within a subdivision. This is likely due to the fact that we are not able to observe enough of the distribution in a single short time series.

The above analysis assumes that processes in the studied metapopulations are weakly stationary over the period of examination. As such, the period of analysis should not include large perturbations, such as the onset of vaccination. This points to one potential application of this method: comparing metapopulation dynamics within a population pre- and post-vaccination. Thus metapopulation spatial structure remains static while effective birth rates decrease. In this case, both birth rates and vaccine uptake rates are required to estimate per-population reporting rate, and increased error is likely introduced. Nonetheless, this method could provide a direct measure of the efficacy of vaccination on incidence reduction.

Another outstanding question is whether this approach extends from measurements of incidence (e.g. per capita new cases in a unit of time) to more ecologically common measures of prevalence (e.g. per capita cases or occurrences at an instant in time). However, incidence and prevalence are very similar for diseases that are reported at intervals close to the average infectious period. For example, if we assume that incidence represents all newly recovered individuals over a reporting interval s then incidence $\xi =\gamma {\int }_t^{t+s}I(t)dt$, where 1/γ is the average infectious period. If s = 1/γ then incidence is the average prevalence over that interval.

Conversion between incidence and prevalence is important for several reasons. Prevalence is the ecologically relevant measure of disease burden, even though incidence is typically measured in human diseases (as case reports). On the other hand, in many ecological systems including non-human diseases, prevalence is the only obtainable measurement. We suggest the method presented is applicable to measurements of either prevalence or incidence, provided the sampling interval is short compared to the generation time and dynamics of the studied disease and host population.

Unraveling population and metapopulation dynamics from chance and observational processes is a difficult question in many systems. Stochasticity, spatial connectivity, and incomplete observation each play important and interconnected roles in this system. Here we present a framework that concisely infers the marginal distribution of measles incidence within populations. Comparison of inferred distributions between populations yields a high-level picture of metapopulation incidence patterns. The result is a probabilistic measure of persistence that can be used to compare and unify ecological models, data, and theory.

Whether the results shown here generalize to other systems remains an open question. The explosive population dynamics of measles are distinct but not unique. Influenza, pertussis, and polio, for example, exhibit epidemic peaks as well as immunity-mediated demographic extinction (though influenza’s rapid evolution precludes an estimation of reporting rate by the approach used here). More broadly, wildlife management is one field where metapopulation theory has long been applied, and where estimates of incidence distributions may prove useful. The establishment of an invasive species and the preservation of a threatened population are analogous to pathogen emergence and persistence. For infectious diseases, the host population is analogous to patch area, and prevalence becomes analogous to population density. Inferred distributions of incidence (or prevalence) permit the direct estimation of extinction or persistence risk from existing time series of population sizes or densities, and provide simple measures that link population and metapopulation ecology.