Abstract
Topological vortices with swirling ferroelectric, magnetic and structural anti-phase relationship in hexagonal RMnO3 (R = Ho to Lu, Y, and Sc) have attracted much attention because of their intriguing behaviors. Herein, we report the structure of multiferroic vortex domains in YMnO3 at atomic scale using state-of-the-art aberration-corrected scanning transmission electron microscopy (STEM). Two types of displacements were identified among six domain walls (DWs); six translation-ferroelectric domains denoted by α+, γ−, β+, α−, γ+ and β−, respectively, were recognized, demonstrating the interlocking nature of the anti-vortex domain. We found that the anti-vortex core is about four unit cells wide. In addition, we reconstructed the vortex model with three swirling pairs of DWs along the [001] direction. These results are very critical for the understanding of topological behaviors and unusual properties of the multiferroic vortex.
Topological defects are widespread in condensed matter physics, and interactions among topological defects and the resulting configurations of numerous topological defects can be associated with various intriguing phenomena1,2,3 because they are insensitive to continuous deformation or perturbation. Topological defects in hexagonal RMnO3 (R = Ho to Lu, Y, and Sc), domain walls/vortices, are responsible for their multiferroicity which is characterized by the coexistence of multi-ferroic orders. The ferroelectric domain walls (FEWs), structural translation domain walls (TWs) and antiferromagnetic domain walls (AFMW) in hexagonal RMnO3 are mutually coupled, thus the ferroelectric vortex can be also called multiferroic vortex. This vortex with multi-order parameters has been intensively studied experimentally and theoretically in recent years because of fascinating physics and promised potential applications such as information storage4,5,6,7,8,9,10,11,12,13,14,15,16. However, little is known concerning the structure of the multiferroic vortex at present, especially on the atomic scale.
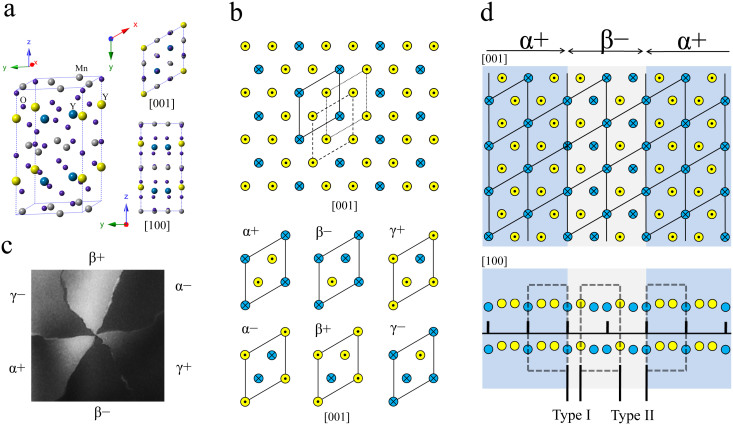
RMnO3 is a typical improper ferroelectrics, the size mismatch between the R ions with large radius and the Mn ions with small radius leads to the trimerization of MnO5 polyhedral and further induces the displacement of R ions17. The trimerization-polarization is produced by the uncompensated displacement of R ions along the c direction, where one third of R ions (Rup) shift upwards and two thirds of R ions (Rdown) shift downwards, producing the net polarization along the −z direction as shown in Fig. 1a. Thus, polarized domains in this system are 180° domains. Structurally, when RMnO3 transforms from paraelectric state (P63/mmc) to ferroelectric state (P63cm), tripling of the unit cell of the paraelectric phase leads to three translation domains–that are domains resulting from the breaking of translation rather than point symmetries, here we denote them as α, β and γ6,7. As labeled by three parallelograms in Fig. 1b, when the three types of translation domains coexist in a crystal lattice, corresponding to a same point, their relative positions are different and then their translation relationship can be recognized. Thus, six different translation-ferroelectric states denoted as α±, β±, γ± characterize the ferroelectric phase of hexagonal RMnO3 as shown in the lower half part of Fig. 1b. In practice, a striking six-state vortex shown by the dark-field image in Fig. 1c, where the sign of electric polarization changes six times around the vortex core, was visualized by the transmission electron microscopy (TEM) and piezoresponse force microscopy (PFM)6,7. It turns out to be the combination by the two electric polarization domains (denoted as + and −) and three anti-phase domains (denoted as α, β and γ). Two possible domain sequences: α+-β−-γ+-α−-β+-γ− (vortex) and α+-γ−-β+-α−-γ+-β− (anti-vortex) were identified, in which the periodic lattice has six different phases rotated by 60° with respect to each other18. The domain walls structures are also illustrated in Fig. 1d. In order to describe the two types of domain walls (Type I and Type II), we just simply put α+β− and β−α+ configurations togther along [001] and [100] directions to show their different translations.
Figure 1. The models of ferroeletric, translation-ferroelectric unit cell and the topology of experimental anti-vortex.
a. Ferroelectric unit cell and its projection along the [001] and [100] directions, yellow and blue spheres represent Yup and Ydown atoms, respectively. The grey spheres represent Mn atoms and the navy blue spheres represent O atoms. b. The translation relationship among three translation domains (α+, β+, γ+) are labeled by the three parallelograms along [001]. Six translation-ferroelectric unit cells with different origins and up-down configuration denoted by α+, β−, γ+, α−, β+and γ−, respectively. The yellow circles with a dot and blue circles with a cross represent Yup and Ydown atoms, respectively. c. Dark-field image of the anti-vortex domains along the [100] direction observed in our experiments. Bright and dark contrasts indicate opposite polarizations. α+, γ−, β+, α−, γ+ and β− are used to characterize the anti-vortex topology. d. The domain walls structures of α+β− and β−α+ configurations along [001] and [100] directions. The α+ and β− domains are indicated by different background colors. The same polarized unit cells are marked by broken rectangles. Two types of domain walls (Type I and Type II) with different translations can be idenfied. A black ruler with lattice periodicity projected along the [100] direction are added to illustrate their translation relationship.
As a promising route towards magnetoelectric switching, the multiferroic vortex in RMnO3 has attracted intensive attentions immediately after its discovery. Many scientists have engaged into this hottest subject with various methods and obtained numerous unusual phenomena and exciting physics. For example, the electric conduction of domain walls (DWs) is found quite different from the bulk, and different types of DWs display distinctly different electrical behaviors6,11,12; the topology and its evolution have been investigated from growth experiments and theoretical analyses by PFM and graph theory7,8,10,14, respectively; collective magnetism at multiferroic DWs was observed using cryogenic magnetic force microscopy9; the structural characteristics of the DWs at atomic level was explored by TEM and theoretical calculation13,15,16, etc. Despite of much exciting progress on the DWs and vortices, the true atomic configuration of the vortex has never been observed due to the difficulties in the TEM observation.
Herein, we successfully applied aberration-corrected high-angle annular-dark-field (HAADF) imaging technique to map the atomic shifts of the multiferroic vortex core, the domain configuration and atomic structure of the vortex were directly identified along the [100] direction. We found that six DWs can be classified into two types by the displacements across the DW, type-I: 1/6[210] and type-II: 1/3[210]. Six translation-ferroelectric domains denoted by α+, γ−, β+, α−, γ+ and β−, respectively, were recognized, demonstrating interlocking nature of the anti-vortex domain. The core region of nearly zero polarization was found to be about four unit cells wide. In addition, based on our experimental observation and previous proposed vortex model6, we reconstructed the atomic model of the vortex domains with three swirling pairs of DWs along the [001] direction, which is highly concerned by scientists who focus on the property measurements of the vortex. Our results provide a solid evidence for the understanding of topological behaviors and intriguing physics of the vortex in RMnO3 and pave the way for further theoretical calculation.
Results
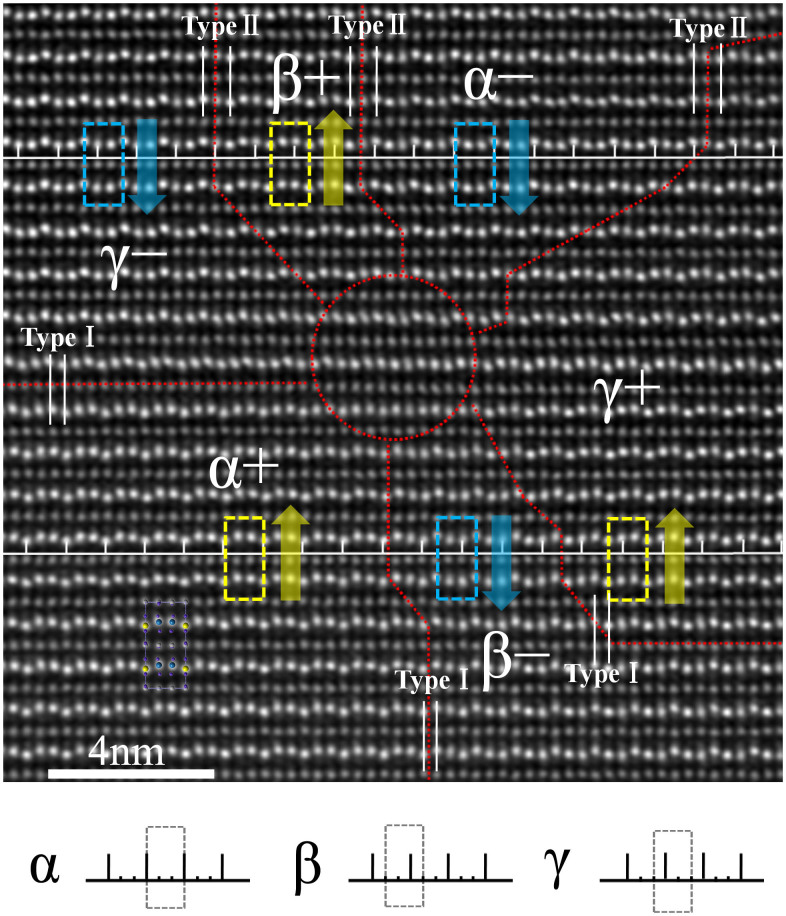
Figure 2 shows the HAADF image of the anti-vortex surrounded by six alternating ferroelectric domains (indicated by yellow and blue arrows) along the [100] direction. The structure of YMnO3 is labeled schematically in the image. Due to the Z-contrast characteristics of the HAADF imaging, the big bright spots correspond to Y atoms and the small bright spots correspond to Mn atoms. Note that [100] direction is the most suitable for imaging the DWs and identifying the location of the vortex core, where the shift of Y ions can be observed without overlapping. The different configurations of Yup and Ydown atoms comparing to the MnO5 polyhedra, which appears wavy-like, indicate that YMnO3 has two opposite polarized states. Since the HAADF contrast is generally less affected by small variation of specimen thickness, mapping the atomic position of heavier ions using HAADF approach is a reliable method to measure ion displacements and to further calculate the polarization. Herein we directly measured the displacement of Yup relative to that of Ydown within the domain and obtained an average value about 0.50 Å, which is in accord with the 0.465 Å determined by the x-ray measurement19. In each domain, the agreement between the structural model and Z-contrast image is good, which indicates that our experimental image is of high quality and can directly explain the ferroelectric polarization.
Figure 2. HAADF image of the anti-vortex domains.
Yellow and blue rectangles are used to mark the upward and downward polarized unit cells, respectively. The yellow upward and blue downward arrows indicate the different direction of polarization, respectively. Two white horizontal lines are superposed on the image to identify the relative translation relationship among α, β and γ domains. The DWs are marked by red dotted lines and the red circle is used to mark the region of the vortex core. The types of six DWs are also outlined by the white vertical lines, labeled by type-I and type-II. The schematics of the three translation domains are presented at the bottom. The broken rectangles are used to indicate the same polarized unit cells. The black ruler are scaled by the lattice periodicity projected along the [100] direction. The positions of the broken rectangles relative to the short vertical lines in the black ruler reflect their translation relationship.
Six ferroelectric domains can be distinguished clearly by the up-down-down and down-up-up arrangements of Y ions and their polarizations are marked by upward arrows and downward arrows, respectively, as shown in Fig. 2. In order to identify their translation relationship in this anti-vortex, we add two white horizontal lines with periodic short vertical lines which are scaled by an interval of the lattice periodicity projected along the [100] direction in the image, which are aligned with each other to represent the lattice of the whole image. This “lattice ruler” is used as a reference to identify the types of translation domains. Yellow (or blue) broken rectangular frames are superposed to label out the upward (downward) polarized unit cells. The ruler with lattice periodicity represents the crystal lattice. Please note that translating integral lattice periodicity will not change anything about translation domains. All the short vertical lines in the ruler are equivalent. Thus, we can distinguish α, β and γ domains clearly by their positions relative to the short vertical lines in the ruler, as shown in the bottom of Fig. 2. Consequently, the translation relationship among six domains can be recognized obviously: the β domain displaces 1/6[210] and γ domain displaces −1/6[210] relative to α domain. Thus, we directly observed the true domain configuration α+-γ−-β+-α−-γ+-β− of the anti-vortex at atomic level.
Discussion
In order to characterize the translation DWs along the [001] direction, we carefully examined the six DWs around the anti-vortex core, and found out that there are three type-I and three type-II DWs along [100] direction as marked in Fig. 2. In fact, this result can also be derived from the translation relationship among α, β, γ domains, if the three domains and orientation of DWs are identified. It should be noted that the displacements 1/6[210] and 1/3[210] are relative to the left-right relationship, for example, α|β and β|α sequences correspond to 1/6[210] and 1/3[210], respectively, which depends on the orientation of the DWs. The reason why translation domains always accompany ferroelectric domains can be attributed to the trimerization nature of improper ferroelectricity of YMnO3, which is almost an ‘‘accidental by-product'' of close packing due to the smallness of ion radius of Mn20. The Coulomb interaction would be very strong if the domains with opposite polarizations had no displacement, which is also energetically unstable. Therefore a displacement is needed for Y ions to release strong electrostatic repulsive force and the interlocking between TWs and FEWs is necessary.
In addition, the disorder of Y ions is more obvious at the charged DWs (head-to-head or tail-to-tail) than at the neutral DWs (head-to-tail). As we can see from Fig. 2, the vertical neutral DWs correspond to sharp atomic shifts while the horizontal and inclined charged DWs correspond to a blurred contrast and have a deviation from the typical ferroelectric arrangement. As well known, charged DWs are energetically unfavorable, so they need more adjustments of atomic shifts to release the effect of charge excess.
It is worthy to note that there are just slight decreasing and disordering of shifts of Y ions instead of obvious crystallographic defects in the core of the vortex as observed in our experiments. There are no evident changes in Mn ions; the inversion of polarization is realized mainly by the arrangement variation of Y ions. Unusually, we observed that the width of DWs is close to zero and the region of the vortex core is just several unit cells wide. Approaching the core the magnitude of shifts of Y ions, in other words, polarization becomes small till to be zero in the exact core demonstrated by the disordered shifts of Y ions. This could be corresponding to the adjustments of Y ions in order to satisfy the requirement of zero polarization in the core of vortex. Such a small transition region is related to the trimerization nature of ferroelectric origin17, thus the reverse of polarization can be sharply completed within one or two unit cells through the adjustment of shifts of Y ions.
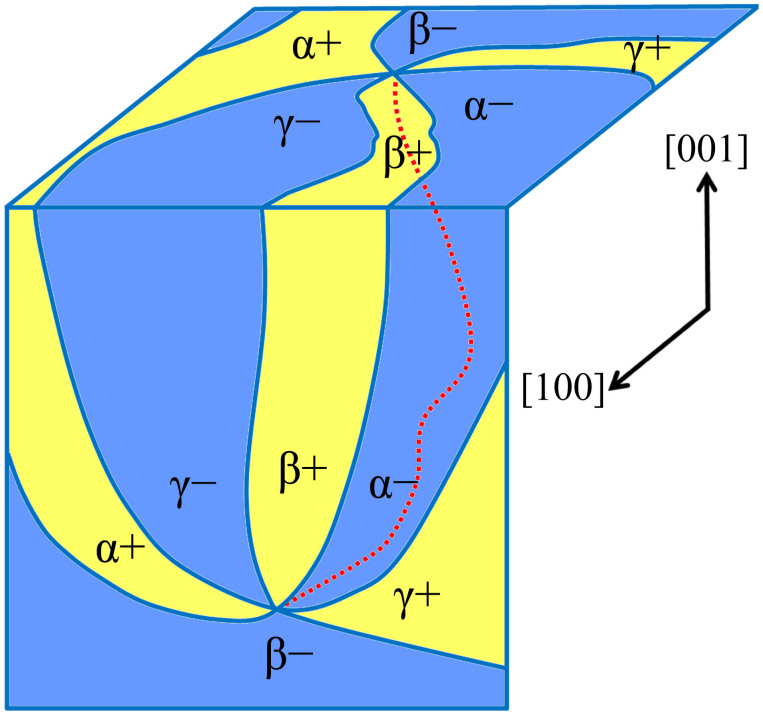
The vortex is a unique kind of topologically protected defect. Based on its topological invariance and our experimental observations, we can reconstruct the vortex model along the [001] direction. In the bulk, vortex cores are curved and the network of vortex can be resolved from all the three spatial dimensions by PFM7, as demonstrated by the cartoon in Fig. 3. This fact prompted us to reconstruct the vortex model along the [001] direction from that along the [100] direction, because the polarization is invisible at atomic level along the [001] direction in our TEM observations. It should be noted that two things can transform type-I to type-II or type-II to type-I: the viewing direction and the left-right sequence of neighboring domains. The observed configuration of the types of DWs varies with different viewing directions or orientation of domains. Thus, the anti-vortex α+-γ−-β+-α−-γ+-β− along the [100] direction can be recognized as the vortex α+-β−-γ+-α−-β+-γ− along the [001] direction because of the change of viewing direction in topology, as shown in Fig. 3.
Figure 3. The cartoon displaying the distribution of the vortex in three dimensions.
The anti-vortex α+-γ−-β+-α−-γ+-β− along the [100] direction turns to be the vortex α+-β−-γ+-α−-β+-γ− along the [001] direction. Yellow and blue regions represent upward and downward polarized domains. The red dotted line indicates the topology of the vortex in three dimensions.
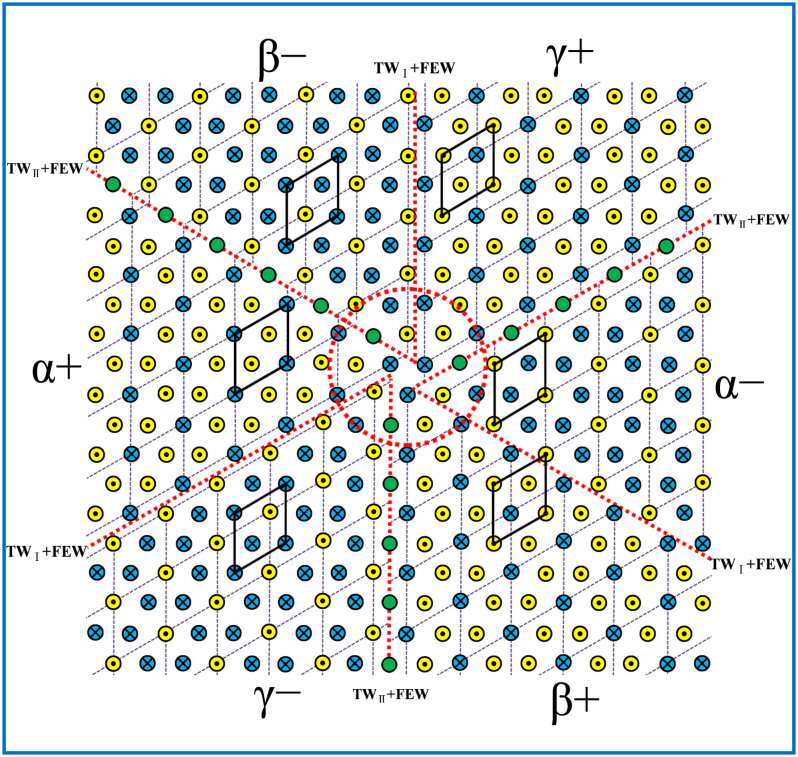
Based on our experimental results and the previous vortex model6, we reconstructed the vortex model along the [001] direction in Fig. 4. For simplicity, we just draw up Y ions with upward or downward shifts, which dominate polarization states of YMnO3. Black parallelograms are used to outline the unit cell of translation domain in each domain, demonstrating their relative translation relationship. Consequently, there are alternating sequence of type-I and type-II DWs indicated by red dotted lines among six DWs. It should be noted that such a sequence is the unique solution corresponding to the vortex topology, and the reverse is also true. A vortex surrounded by three swirling pairs of the DWs can be visualized obviously. A red dotted circle was superposed on the model to label out the region of the vortex core, in which three downward Y ions are triangularly neighbored instead of alternating up-down shifts in ferroelectric state. Considering the neutral nature of DWs in the vortex along the [001] direction, this assumption should be close to the real atomic arrangements. Although the atomic configuration in Fig. 4 near the vortex core in the model is just ideal, the first-principle calculations can be performed from it by optimizing the atomic positions in the core. We expect that the theorist would give a more precise atomic configuration including Mn and O ions in the future.
Figure 4. The reconstructed model of the vortex domains along the [001] direction.
The red dotted lines and the circle indicate the locations of DWs and the core of the vortex, respectively. The yellow circles with a dot and the blue circles with a cross represent Yup and Ydown atoms, respectively. The green circles represent Y atoms at the paraelectric position. Black parallelograms are used to outline the unit cell of translation domain in each domain, representing α+, β−, γ+, α−, β+ and γ−, respectively. TWI + FEW and TWII + FEW are used to label two types of translation-ferroelectric DWs.
Based on the vortex model we proposed, its topological stability can be discussed. In contrast to displacive ferroelectrics, it is difficult to convert YMnO3 into a single domain state. This incomplete poling behavior of ferroelectric domains can be understood by the interlock between ferroelectric DWs and structural translation DWs6,13, especially the coexistence of three kinds of translation domains. Supposing that the DWs between α+ and β− could be annihilated to form a single α+ domain, then α+ would neighbor γ+. That is to say, separated translation DWs would emerge, which is energetically unfavorable as calculated by Kumagai et al.16. Thus, due to strong interlock of ferroelectric vortex and structural translation vortex, the hexagonal RMnO3 cannot be polarized to a single domain by routine electric field. With regard to the stability of the vortex topology, the behavior of the vortex core is even stiffer. Han et al.15 applied electric field on the vortex and the immobility of the vortex core was observed in contrast to the migration of DWs, which can be attributed to the re-interlock of six translation-ferroelectric DWs by the three downward Y ions at the core of the vortex as shown in Fig. 4.
In summary, we successfully applied aberration-corrected STEM to map the polarizations of the multiferroic vortex and unveiled its atomic structure. Two types of displacements were identified among six DWs. Six translation-ferroelectric domains were recognized, demonstrating the interlocking nature of the anti-vortex domains. The core region with nearly zero polarization was found to be about four unit cells wide. These results demonstrated that polarization reverse can be realized efficiently by the adjustments of displacements of Y ions within several unit cells at both DWs and the anti-vortex core, demonstrating the trimerization nature of improper ferroelectricity of YMnO3. Based on our experimental observation and previous vortex model, we reconstructed the atomic model of the vortex with three swirling pairs of DWs along the [001] direction. Unusual stability of the vortex core is discussed. Our results provide a solid evidence for the understanding of topological behaviors and intriguing physics of the vortex in RMnO3 and pave the way for further theoretical calculations.
Methods
Single crystals of h-YMnO3 were grown by using the floating zone method. The [100] specimens for high-resolution scanning transmission electron microscopy (STEM) investigation were prepared by standard procedures including mechanical grinding, dimpling and polishing. The final thinning of the specimens by Ar-ion milling was carried out on a stage cooled with liquid nitrogen. High-resolution STEM investigation was carried out on an JEM-ARM200F microscope with double CS correctors for the condenser lens and objective lens. The available point resolution is better than 0.08 nm at an operating voltage of 200 kV. HAADF images were acquired at acceptance angles of 70–150 mrad. All of the images presented here are Fourier-filtered to minimize the effect of the contrast noise. The filtering does not have any effect on the results of our measurements.
Author Contributions
R.C.Y., Q.H.Z. planned and coordinated the experiments. G.T.T. grew the single crystal samples. Q.H.Z. carried out TEM experiments with the help of L.G., R.C.Y., Y.Y., C.Q.J., Y.G.W. and X.F.D. Q.H.Z. and R.C.Y. wrote the manuscript text. All authors reviewed the manuscript.
Acknowledgments
This work was supported by the State Key Development Program for Basic Research of China (Grant Nos. 2012CB932302 and 2010CB934202), the National Natural Science Foundation of China (Grant No. 11174336).
References
- Grigorenko A., Bending S., Tamegai T., Ooi S. & Henini M. A one-dimensional chain state of vortex matter. nature 414, 728–731 (2001). [DOI] [PubMed] [Google Scholar]
- Seidel J. et al. Conduction at domain walls in oxide multiferroics. Nat. Mater. 8, 229–234 (2009). [DOI] [PubMed] [Google Scholar]
- Mesaros A. et al. Topological defects coupling smectic modulations to intra-unit-cell nematicity in cuprates. Science 333, 426–430 (2011). [DOI] [PubMed] [Google Scholar]
- Gelard I. et al. Off-stoichiometry effects on the crystalline and defect structure of hexagonal manganite REMnO3 films (RE = V, Er, Dy). Chem. Mater. 23, 1232–1238 (2011). [Google Scholar]
- Chae S. C. et al. Self-organization, condensation, and annihilation of topological vortices and antivortices in a multiferroic. PNAS 107, 21366–21370 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi T. et al. Insulating interlocked ferroelectric and structural antiphase domain walls in multiferroic YMnO3. Nat. Mater. 9, 253–258 (2010). [DOI] [PubMed] [Google Scholar]
- Jungk T., Hoffmann A., Fiebig M. & Soergel E. Electrostatic topology of ferroelectric domains in YMnO3. Appl. Phys. Lett. 97, 012904 (2010). [Google Scholar]
- Chae S. C. et al. Direct observation of the proliferation of ferroelectric loop domains and vortex-antivortex pairs. Phys. Rev. Lett. 108, 167603 (2012). [DOI] [PubMed] [Google Scholar]
- Geng Y. N., Lee N., Choi Y. J., Cheong S. W. & Wu W. D. Collective magnetism at multiferroic vortex domain walls. Nano Lett. 12, 6055–6059 (2012). [DOI] [PubMed] [Google Scholar]
- Griffin S. M. et al. Scaling behavior and beyond equilibrium in the hexagonal manganites. Phys. Rev. X 2, 041022 (2012). [Google Scholar]
- Meier D. et al. Anisotropic conductance at improper ferroelectric domain walls. Nat. Mater. 11, 284–288 (2012). [DOI] [PubMed] [Google Scholar]
- Wu W., Horibe Y., Lee N., Cheong S. W. & Guest J. R. Conduction of topologically protected charged ferroelectric domain walls. Phys. Rev. Lett. 108, 077203 (2012). [DOI] [PubMed] [Google Scholar]
- Zhang Q. H. et al. Direct observation of interlocked domain walls in hexagonal RMnO3 (R = Tm, Lu). Phys. Rev. B. 85, 020102(R) (2012). [Google Scholar]
- Chae S. C. et al. Evolution of the domain topology in a ferroelectric. Phys. Rev. Lett. 110, 167601 (2013). [DOI] [PubMed] [Google Scholar]
- Han M.-G. et al. Ferroelectric switching dynamics of topological vortex domains in a hexagonal manganite. Adv. Mater. 25, 2415–21 (2013). [DOI] [PubMed] [Google Scholar]
- Kumagai Y. & Spaldin N. A. Structural domain walls in polar hexagonal manganites. Nature communications 4, 1540 (2013). [DOI] [PubMed] [Google Scholar]
- Van Aken B. B., Palstra T. T. M., Filippetti A. & Spaldin N. A. The origin of ferroelectricity in magnetoelectric YMnO3. Nat. Mater. 3, 164–170 (2004). [DOI] [PubMed] [Google Scholar]
- Mostovoy M. Multiferroics: A whirlwind of opportunities. Nat. Mater. 9, 188–190 (2010). [DOI] [PubMed] [Google Scholar]
- Abrahams S. C. Atomic displacements at and order of all phase transitions in multiferroic YMnO3 and BaTiO3. Acta cryst. B65, 450–457 (2009). [DOI] [PubMed] [Google Scholar]
- Khomskii D. I. Multiferroics: Different ways to combine magnetism and ferroelectricity. J. Magn. Magn. Mater. 306, 1–8 (2006). [Google Scholar]