Abstract
Brain activity often consists of interactions between internal—or on-going—and external—or sensory—activity streams, resulting in complex, distributed patterns of neural activity. Investigation of such interactions could benefit from closed-loop experimental protocols in which one stream can be controlled depending on the state of the other. We describe here methods to present rapid and precisely timed visual stimuli to awake animals, conditional on features of the animal’s on-going brain state; those features are the presence, power and phase of oscillations in local field potentials (LFP). The system can process up to 64 channels in real time. We quantified its performance using simulations, synthetic data and animal experiments (chronic recordings in the dorsal cortex of awake turtles). The delay from detection of an oscillation to the onset of a visual stimulus on an LCD screen was 47.5 ms and visual-stimulus onset could be locked to the phase of ongoing oscillations at any frequency ≤40 Hz. Our software’s architecture is flexible, allowing on-the-fly modifications by experimenters and the addition of new closed-loop control and analysis components through plugins. The source code of our system “StimOMatic” is available freely as open-source.
Keywords: Closed-loop, Local field potentials, Turtle cortex, Software, Detection of oscillations, Real-time system, Open source code freely available
1. Introduction
The brain’s response to an external stimulus is a complex combination of the activity triggered by the sensory stimulus itself and the brain’s internal state at the time the stimulus is presented (Arieli et al., 1996; Azouz and Gray, 1999; Leopold et al., 2003; Steriade, 2001). The internal state is a function of ongoing activity as well as past activity that resulted in structural changes through plasticity. This may explain why the neural response to a sensory stimulus can vary. It has been shown that some of this variability can be attributed to the immediately preceding ongoing activity (Arieli et al., 1996; Marguet and Harris, 2011). In the rat visual cortex response reliability can be modulated by stimulation of cholinergic afferents originating from the nucleus basalis (Goard and Dan, 2009). State-dependent effects depend also on precise timing, such as in the hippocampus where electrical stimulation can lead to synaptic potentiation or depotentiation depending on its phase, relative to ongoing theta oscillations (Pavlides et al., 1988).
Spontaneous and sensory driven events may occur only rarely or unpredictably, such as spontaneous bouts of theta oscillations in the temporal lobe, high-frequency ripples in the hippocampus, or attention-related gamma-band oscillations in the visual cortex. Some of these spontaneous events may or may not be observed in vitro or in anesthetized preparations. Thus, experiments are increasingly performed in awake behaving animals. Such experiments, however, reduce control of the experiment and restrict the time available for experimentation. The occurrence of “internal” events is also difficult to control. Hence, it would be useful to make the timing and nature of a stimulus presented to the animal conditional on the animal’s ongoing brain activity and behavior.
Such closed-loop experiments are challenging because they require that data analysis and stimulus generation occur fast enough with respect to the events of interest (Chen et al., 2011). There are three types of challenges: (i) data acquisition and processing needs to be fast enough, such that brain events of interest can be detected and used for conditional stimulation. This includes signal processing, detection and potential post-processing such as spike sorting, usually on many channels. (ii) Stimulus generation and presentation. Monitor refresh rates, for example, put constraints on how fast a visual stimulus can be updated. (iii) A closed-loop system should be easy to modify by experimenters, so as to allow rapid online adjustment.
We present and test a flexible software based closed-loop system that allows visual stimulation conditional on ongoing activity.2 The system accepts a large number of high-bandwidth channels in parallel, scales well and is based on standard computing and neurophysiology hardware. It runs in parallel on multiple cores and CPUs, making modifications comparatively easy without requiring extensive programming knowledge. This feature is useful for experimentation, enabling on-the-fly changes by experimenters rather than software specialists. Implementation relies greatly on Matlab rather than a compiled, low-level language, except for functions that do not require frequent modification, such as plotting and network communication.
We focus on the structure of local field potentials (LFPs) and use these signals in real-time to present visual stimuli conditional on features of the LFP. We quantified the system’s performance for different noise levels and oscillation frequencies using simulated data, re-played simulated data and experimental data recorded from awake turtles.
2. Methods
2.1. System architecture
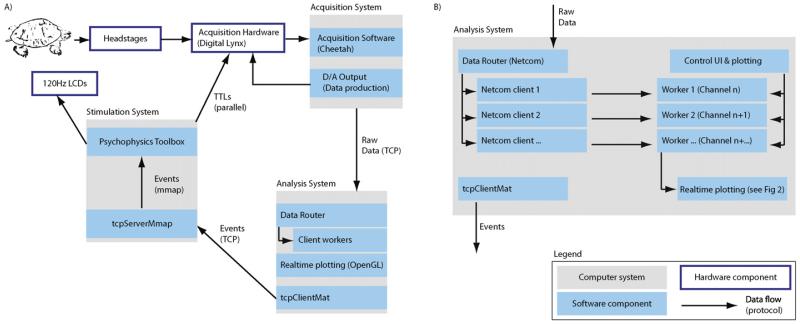
The StimOMatic system consists of three separate computers (Fig. 1): the acquisition, analysis and stimulation systems. All are connected to a common Gigabit Ethernet network. All systems run Windows and are equipped with hardware-accelerated OpenGL-capable graphics cards. The analysis system is most critical. We used a dual-CPU machine with 8 cores each (Dell T5500 workstation) and a Nvidia Quadro 600 graphics card, used to offload plotting functions. The CPU can thus be dedicated to computing. Online analysis was performed with 64-bit Matlab on Windows 7. Acquisition and visual stimulation machines ran 32-bit Matlab on 32-bit Windows XP.
Fig. 1.
System and software architecture (lower right corner shows the notation used). (A) There are three different PCs: (i) the stimulation computer, which produces visual stimuli on an LCD screen using psychophysics toolbox; (ii) the acquisition system, which receives the data, performs all pre-processing and stores data for later analysis and (iii) the real-time analysis system, which receives a continuous stream of data. Decisions made by the analysis system are sent to the stimulus system, which uses the commands received to produce accurately timed visual stimuli. (B) Software architecture of the analysis system. It runs several workers in parallel, each of which processes a number of channels. They send data to the real-time plotter and to the display system (tcpClientMat). The data router receives the data and delivers it to the individual workers.
2.2. Online data analysis – software architecture
Online analysis was performed by a dedicated system running Matlab and its parallel computing toolbox. Several workers (Matlab instances) were created, each of which processed one or several data acquisition channel. We used the single program multiple data (spmd) mode provided by the parallel computing toolbox. Workers ran simultaneously on the multi-core/multi-CPU, enabling parallel processing (We used a 16 core system on 2 CPUs). The parallel computing toolbox allows up to 12 workers, each running on a different core. More workers can be used with the Matlab Distributed computing toolbox. All experiments used a maximum of 10 workers. The selected channels were automatically distributed across all available workers as optimally as possible. For example, if 20 channels were selected for processing with 10 workers, each worker (thread) processed 2 channels. Each worker received data from its assigned channel(s) via the Netcom Router (Neuralynx Inc) that runs on the analysis system. Data were fed to the Router by the Cheetah acquisition software (Neuralynx Inc) that ran on the acquisition system (Fig. 1A). Netcom provides data in blocks of 15 ms. This is therefore the minimal system delay achievable with this architecture.
We developed a flexible plugin architecture so that users can modify and add functionality for specific experimental needs. Each plugin consists of a number of functions (see Appendix A), each of which typically consists of a few lines of code. Each plugin has its own GUI to enable parameter specification, and its own data processing function. There are two types of plugins: continuous and trial-based. The data processing function is called for every incoming block of data with continuous plugins and for every trial with trial-based plugins. Trial-based plugins can be used to update metrics such as the average evoked LFP, whereas continuous plugins can display the data continuously or perform real-time control. The following plugins were used (Table A.1): (i) closed-loop control, (ii) continuous data display and (iii) LFP trial-based response display, which shows the raw LFP as well as average spectrogram averaged over trials, aligned to stimulus onset.
2.3. Oscillation detection algorithm (real-time control plugin)
All online power and phase estimates were performed on LFPs using the Hilbert transform. Parameters specified by the user are the passband (in Hz, for example 22–28 Hz for a center frequency of 25 Hz and width of 3 Hz), window size (in ms), power detection threshold (in μV2) and the requested phase (in the range –π to π, only if phase-dependent stimulation is enabled). The power detection threshold can either be “larger than” or “smaller than”, meaning that stimuli are triggered when oscillatory power is larger or smaller than the requested value, respectively. The incoming LFP signal is reduced to 250 Hz sampling rate, then bandpass filtered with a zero-phase lag, 4th-order Butterworth filter with the provided center and width frequency. Appropriate measures are taken to avoid edge effects due to the blockwise incremental filtering (by choosing appropriate overlap). Every incoming block of 512 data points (approximately 15 ms, fixed block-size at which our acquisition system delivers data) is first appended to a 3 s long running buffer of raw unprocessed data. The plugin then uses the raw data in the entire buffer to filter, down-sample and estimate the instantaneous power and phase. Afterwards, the plugin evaluates whether the power threshold has been crossed for the newest data-point received. If so, a trigger signal is sent to the stimulus system.
For phase-conditional stimulation, after the power has been crossed, the current phase and oscillatory frequency are determined. The phase is determined using the Hilbert transform. The instantaneous frequency is estimated from the peak-to-peak interval duration of the bandpass filtered signal (Colgin et al., 2009). We found this method to be more reliable than one based on the Hilbert transform. The trial was aborted (no trigger sent) if the estimated instantaneous frequency was different by more than 3 Hz from the requested center frequency. Using instantaneous phase and frequency, one can predict the time when the requested phase will occur next. This value is sent to the stimulation computer, which triggers visual stimulation after this time minus the known system latency (transmission delays, display onset delays) has elapsed.
2.4. Timing synchronization
All timing is relative to the clock of the acquisition system (Cheetah Software, Neuralynx Inc). The stimulus display system sends synchronization data (stimulus on, stimulus off, delay on) via parallel port. This parallel port is sampled at the system sampling rate of 32,556 Hz, i.e. as fast as the data acquisition itself. Transmission delays over the parallel port are negligible.
2.5. Visual stimulus onset verification
LCD displays have been suggested to be unreliable for visual psychophysics (Elze, 2010). However, they have the advantage of relatively slow pixel decay times, making it less likely that neurons lock to the refresh frequency, as sometimes observed with CRTs. We verified that our display onset times were reliable. A photodiode (SFH300, Osram) was placed directly onto the LCD screen at the topmost corner, where the monitor starts its refresh. A resistor and the photodiode were connected in series and connected to a constant power source (1.2 V). One wide-band channel (0.1–9 kHz) of the acquisition system was used to measure the voltage difference across the resistor (the voltage difference was proportional to the luminance measured by the photodiode). The rise-and fall times of the photodiode (<10 μs) were rapid and negligible for our purposes.
2.6. Simulated LFP signals
Realistic 1/f background noise was simulated by summing sinusoidal pink noise (“red noise”, see page 235 in Rutishauser, 2008). The simulated signals were high-pass filtered at 0.5 Hz, followed by addition of normally distributed i.i.d. noise and superposition of the signal (simulated oscillation). Signal amplitude was varied while the noise amplitude was kept constant to achieve different SNR. The simulated signal was a sine wave, with initial phases chosen randomly from the uniform distribution –π to π. The same signals were used for simulations and replay for experimental verification.
2.7. Write-out of simulated data
Simulated data was converted to analog values for later recording via a digital-to-analog converter (National Instruments, PCIe-6259, sampling rate 25 kHz) and the Matlab DAQ toolbox. Resistors were used to reduce the produced voltage by 1:1000 to produce output signals in the <100 μV range. These signals were then recorded in the same way as signals from the electrodes themselves.
2.8. Offline data analysis
All data analysis was performed using custom-written Matlab routines (Mathworks, Inc). All filters were 4th order Butterworth non-causal filters. All LFP analysis was performed after downsampling to 1 kHz (low-pass filter followed by sampling rate reduction). Note that the methods used for offline data analysis differ from those used for online analysis, for performance reasons (e.g., 250 Hz online sampling rate vs. 1 kHz off-line). Raw data for each trial were loaded and filtered independently to avoid artifacts due to sampling-rate mismatches. Every trial was automatically screened for outliers and rejected if its amplitude lay outside the range of ±600 μV (a range that excluded eye-blink and muscle artifacts).
We calculated the oscillatory power of single trials using multitaper analysis (Chronux Toolbox (Mitra and Bokil, 2008)), a useful method to estimate single-trial frequency spectra (Jarvis and Mitra, 2001). We used 400 data points at 1000 Hz sampling rate, a time-bandwidth product of 2 and 3 tapers, resulting in a frequency resolution of 5 Hz. We moved a 400 ms window in steps of 50 ms to get oscillatory power as a function of time. Time–frequency spectra were computed for every trial and then averaged, followed by frequency-by-frequency baseline normalization to eliminate power differences due to 1/f power distribution. This resulted in normalized power spectra in units of a multiple of the baseline power at every frequency (no change = 1). The baseline for normalization was estimated before stimulus onset. When comparing conditions, normalization was made relative to the same baseline.
The phase of oscillations was estimated using the Hilbert transform. Single trials were first bandpass filtered in a band of ±3 Hz around the frequency of interest (22–28 Hz for 25 Hz), followed by the Hilbert transform. The strength of phase-locking across trials at a particular time, typically at stimulus onset, was evaluated using a Rayleigh-test (one phase value per trial) (Fisher, 1993) and visualized using a circular histogram. The phase was measured (in radians) in the range –π to π with zero at the peak (see Fig. 6). Phase angles rotate counter-clockwise in all circular histograms shown.
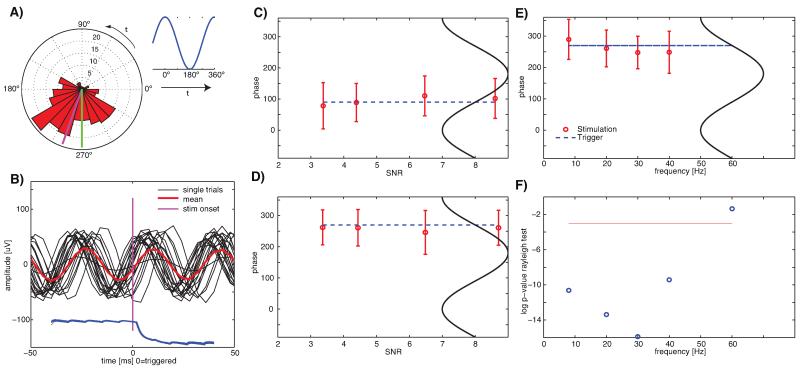
Fig. 6.
Experimental verification of phase-specific visual stimulation. Stimuli were shown at a particular phase (user specified) of the detected oscillations. (A) Rose diagram of the phase values achieved experimentally (n = 200 trials). The requested phase was 270° (green, upstroke) and the average achieved phase was 289.6° (magenta). The illustration (right) shows the notation used. The rose diagrams rotate counter-clockwise throughout as indicated. (B) Example traces (n = 20, random subset of trials shown in (A)), aligned at stimulus onset (t = 0). Display onset as measured by the photodiode (single trials, blue) was tightly locked to the measured phase. (C,D) Average achieved phase at stimulus onset for different requested phase values and SNR values. All are f = 20 Hz. The dashed line indicates the requested phase (downstroke, 90° for (C) and upstroke, 270° for (D)). All phase values where significant (p < 0.01, Rayleight test). Errorbars are ±s.d. (linear). Accuracy of phase was not dependent on SNR. (E,F) Accuracy and significancy of phase locking for different frequencies at SNR = 4.3. Shown is the achieved phase (E) and its significance (F). (F) shows the log of the p-value (Rayleigh test, red line is 0.05). The system could significantly lock to phases of oscillations up to 40 Hz, but not 60 Hz.
We further quantified the distribution of phases by fitting them with a von Mises distribution VM(μ, κ), a circular normal distribution. It is a function of the mean angle μ and the concentration parameter κ. The larger κ, the lower the variance of the phases around the mean value. κ = 0 is a uniform distribution (no phase preference). We used a maximum-likelihood procedure to estimate and (Fisher, 1993). Some circular statistical methods were used from the toolbox provided by Berens (2009).
We quantified the peak frequency of the evoked oscillations based on the multi-taper spectra shortly after stimulus onset (parameters as listed above). The frequency at which the observed power deviated most from what would be expected assuming a 1/f distribution was used as the center frequency of the observed oscillations. The background 1/f function was determined by estimating the parameters of the function Afα. We fitted a straight line to the power spectrum in log-log coordinates (the slope and offset of which are α and A, respectively). We subtracted (in log units) the fitted function from the observed data and took the maximum in the range of 15–40 Hz to determine the oscillation frequency for an experimental session or animal (see Table 1 for a summary and Fig. 7B for an example).
Table 1.
Animals used, dominant oscillation frequency, latency from stimulus onset till the peak of the mean VEP and latency from stimulus onset till the onset was noticeably above baseline (onset, defined as 75% of 1 s.d. above baseline). All errors are ±s.d. over recording days (as specified). In the text, F7 is “Animal 1” and D38 is “Animal 2”.
| Animal | Weight, Gender | VEP latency to max [ms] | VEP onset latency [ms] | Oscillation frequency [Hz] (days) | Impedance [MQ] |
|---|---|---|---|---|---|
| F7 | 889g, f | 164 ± 11 | 108 ± 6 | 26.9 ± 1.1 (5) | 1.97 ± 0.11 |
| D38 | 1160g, f | 114 ± 18 | 93 ± 7 | 33.4 ± 1.4 (5) | 1.81 ± 0.21 |
| D10 | 1053g, f | 146 ± 34 | 98 ± 19 | 24.5 ± 1.9 (6) | 1.74 ± 0.07 |
| D29 | 1032g, f | 234 ± 19 | 78 ± 48 | 26.2 ± 1.8(2) | n/a |
| D28 | 1200g, f | 238 ± 23 | 164 ± 34 | 22.4 ± 3.5(2) | 2.47 ± 0.28 |
| All | 179 | 108 | 26.7 ± 4.1 |
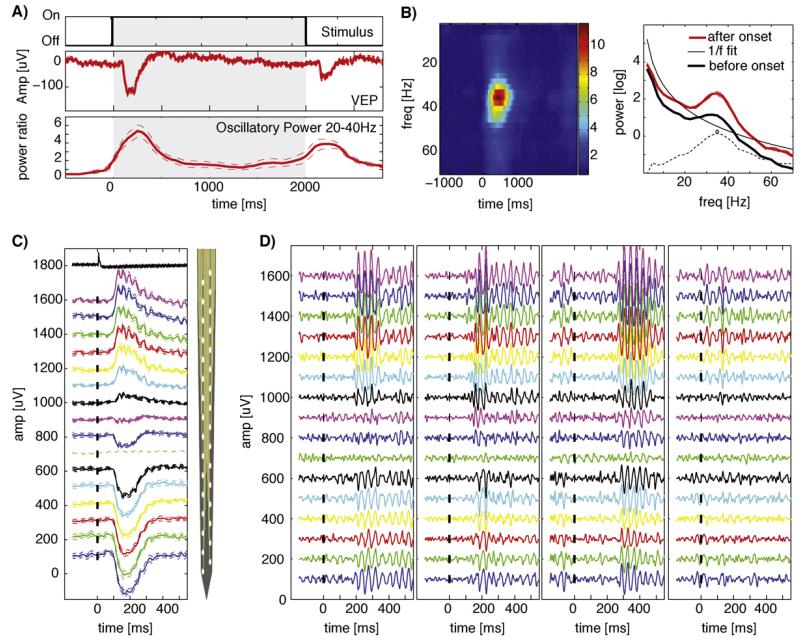
Fig. 7.
Properties of depth electrode LFP recordings in the visual cortex of awake turtles. (A) Response to static natural scenes for 2 s, preceded and followed by gray screen. Shown are the average broad-band response (middle, VEP) and the average 20–40 Hz power (bottom, normalized to baseline). (B) Time–frequency representation of the oscillatory response. Shown are the spectra before (at −700 ms) and after (300 ms) stimulus onset (right) and normalized spectra as a function of time (left). Dashed lines are ± SE. A frequency specific increase around ~35 Hz range can be observed, superimposed on a broadband increase. Time refers to the center of the bin, with a size of ±200 ms around the center. t = 0 is stimulus onset. Dashed lines show the difference between the after-stimulus power and the 1/f fit with the peak frequency 34.9 Hz marked. (C) Average broadband response in an example session, arranged topologically, from top (superficial) to bottom of the cortex (only left column shown). The vertical site spacing of the electrode (right) was 50 μm. Tickmarks show the stimulus onset. Vertical spacing of traces is 100 μV. The uppermost trace shows the photodiode current to verify stimulus timing. Dashed lines are ±SE over trials. (D) Single Trial examples (band-pass filter 20–100 Hz) from the same session shown in (C). Notice the variability of the response onset (early vs late) and strength. Notation is equivalent to (C).
All error bars stated in the text are ±s.d. over trials or sessions (as noted), unless specified otherwise.
2.9. Comparison of raw and normalized time-frequency spectra
The peak frequency in the power spectra (Fig. 7B, right) and normalized time-frequency representations (Fig. 7B, left) are not necessarily at the same value. This is due to the baseline normalization. The raw spectra show the absolute power, whereas the normalized spectra show relative power at each frequency, relative to baseline. The peak in raw spectra indicates the frequency at which the oscillations had peak amplitude. This value was not necessarily identical to that characterizing oscillations that increased most relative to baseline. The following calculations show that this shift in peak frequency can be attributed to different slopes of the 1/f spectra at baseline and stimulus conditions. Assume two spectra i = 1,2 with Pi(f) = Aifαi. The slopes of the spectra are dPi/df = Ai αi fαi−1. For two conditions with broad-band power differences A1(f) < A2(f) for all f and assuming α1 = α2, the derivative will (by definition) be larger for the condition in which broadband power increased. Thus, the derivative is not independent of the power.
What we wish to visualize with the normalized spectrum PN(f) = P1(f)/P2(f) is the narrow-band power changes superimposed on the broad-band power changes. If α1 = α2, this normalized spectrum will perfectly cancel the fαi term and recover the power constants Ai. This is the motivation for using a normalized spectrum (referred to as R-Spectrum by Burns et al., 2010a; Sridharan et al., 2011). Adding narrow-band power A′2(fj) = A2(fj) + d2(fj) only for some frequencies fj will further increase the slope at this particular frequency. Thus, situations can arise where d2(f1) > d2(f2) for f1 < f2 but where PN(f1) < PN(f2). This can be the case if f1,2 are nearby and if the slope at the lower frequency is sufficiently large to cancel the power difference d2(f1) − d2(f2) > 0 even if α1 = α2. Similar situations can arise even if there are no narrow-band increases but if α1 ≠ α2, i.e. if α depends on the stimulus (which has been observed, i.e. El Boustani et al., 2009). In conclusion, this peak shift does not represent an artifact but follows from the above definition. We used the raw spectra to calculate the peak oscillatory frequencies and the normalized spectra for visualization and for comparisons across animals.
2.10. Signal-to-noise ratio (SNR)
We used the SNR as a measure of task difficulty. Our aim was to detect oscillations embedded in a background of 1/f power. We thus defined SNR as a function of the oscillatory power at the frequency of interest relative to the background. The SNR of simulated signals was calculated as follows: (i) bandpass filter in the band of interest (e.g. 15–25 Hz). (ii) Hilbert-transform to estimate power: sqrt(real(X)2 + imag(X)2). (iii) The ratio of average Hilbert-estimated power when the signal is present over when the signal is absent is equal to the SNR. Since the background signal is 1/f distributed, the same signal amplitude will yield a different SNR value for different frequencies. Thus, to make SNR values comparable across different simulated frequencies, signal amplitudes were adjusted manually for each simulated oscillation frequency to achieve approximately comparable SNR values. All SNR values were determined empirically from the data; therefore, they vary across simulation runs.
2.11. Online data analysis – fast plotting
Matlab’s Parallel Computing Toolbox provides the tools to process data in parallel, both locally (on multiple CPUs) and remotely (on multiple computers). Using this technology, our system can operate in real-time, that is, it can process a block of data in less time than the data block-size in which the data arrives (15 ms). When it comes to data visualization, however, Matlab proves to be a bottle-neck. Unlike for data processing, rendering in Matlab is single threaded: all graphics-related calls are queued in a single Java thread, the Event Dispatch Thread (EDT). This thread runs at lower priority then the main processing thread (which manages the parallel processing) and is executed only if the processing thread is idle. It is possible to override this configuration manually and force the system to process all accumulated calls in the EDT using the drawnow() function. However, context switching between threads is expensive and therefore slows down processing. To achieve real-time parallel data visualization without interfering with data processing speed, we implemented an OpenGL-based plotting module written in Python (the Python OpenGL mmap plotter POMP). Each Matlab plugin exports to-be plotted data to shared memory files; they are then read by individual plotting processes that run concurrently. Rendering is further optimized by selectively transferring only the modified data points to the graphics cards (Fig. 2 shows a summary). We used Python 2.7 together with the libraries NumPy and pyglet 1.1 to implement the plotting-system, which is operating-system independent. Below, we summarize the Matlab component, the data transfer between the two components, and finally the Python-based plotting implementation.
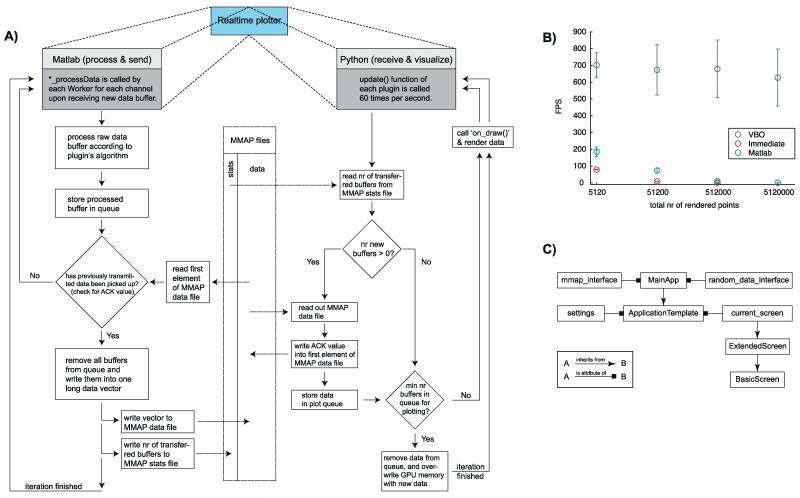
Fig. 2.
Software architecture and performance of the plotting component. (A) The real-time plotter (Fig. 1B) consists of two parts: a Matlab part that processes raw data and a Python part that visualizes the processed data (left and right column, respectively). Data is exchanged between these two parts via memory-mapped file (mmap, middle column). Both parts run concurrently. (B) Plotting performance for an implementation with Matlab (blue) and two different OpenGL implementations: Vertex Buffer Object (VBO, green) and immediate mode (red). The x-axis shows the number of data points that were plotted, the y-axis shows the frames per second (FPS, 1/time-to-plot). (C) Architecture of the Python OpenGL mmap plotter module (right column of panel A) in UML notation, following the Model-View-Controller design pattern.
2.11.1. Initial setup of shared memory and data queue
Inter-process communication (IPC) is a set of methods for the exchange of data between different applications. We used mmap, a POSIX-compliant system call, to map files into memory. mmap is supported by Matlab and Python on all platforms. Initializing a plugin (Fig. 2A) calls the setup_mmap_infrastructure function to create (i) a set of mmap files that are accessed by both the Matlab and Python side of each plugin; and (ii) a FIFO buffer that holds processed data buffers specific to each plugin and channel, in case the data cannot currently be transmitted via the mmap files (which may happen if the Python side blocks the file while reading from the shared memory). We use the org.apache.commons.collections.buffer.CircularFifoBuffer class for the FIFO buffer (included in Matlab). setup_mmap_infrastructure creates a set of mmap files: a stats file for information about the number of data channels, the plugin’s buffer size and the number of transmitted buffers, and one mmap data file for each data channel that will be plotted.
2.11.2. Data transfer from Matlab to Python
Upon receipt of new data, each plugin’s ‘*_processData’ function (Fig. 2A, left column) receives the new data buffer from the corresponding data channel. After processing, the to-be plotted data are first stored in the FIFO queue. send_databuffers_over_mmap reads out the first element of the data mmap file to check whether previously transmitted data has already been picked up by the Python side. If an acknowledgment value (ACK) is not found, no new data can be transmitted. This procedure implements a simple form of a file locking mechanism to assure that previously sent data is not accidentally overwritten. If the ACK value is found, all buffers are removed from the FIFO and are written into the mmap data file as one data vector (for efficiency reasons). Previously processed data are overwritten rather than deleted, making the transfer more efficient. The total number of individual buffers that constitute the transmitted data vector is written into the mmap stats file.
2.11.3. Data pickup by Python
The Python plotting is modularized (Fig. 2C), such that data management is independent of the current plotting style. The main process will schedule the update function of each plugin to be executed 60 times per second (Fig. 2A, right column). The update function consists of four major steps: (i) read out of new processed data from the mmap data file, (ii) confirmation of data pickup, (iii) storage of received data in queue, and (iv) data overwrite on the graphics card. To minimize performance bottlenecks and guarantee swift graphic updates, the number of transferred buffers from the mmap stats file are read first, and only those parts of the memory that changed are read. Once all data channels have been read, the ACK value is written for each channel so that the Matlab side can immediately write new data into the mmap data file. Finally, the incoming data are stored in a queue for later plotting. Lastly, the data are removed from the queue and transferred to the memory of the graphics card (Graphics Processing Unit – GPU). Importantly, only data points that have changed are transferred to the GPU. This removes what otherwise would be the main bottleneck, allowing high frame rates (see Fig. 2B for measurements). We went to great lengths to ensure that rendering is fast, using the Vertex Buffered Objects mode of OpenGL (see Appendix B).
2.11.4. POMP architecture
POMP was designed following the Model-View-Controller design pattern (Krasner and Pope, 1988), resulting in different classes for the application layers and objects (Fig. 2C). Each plugin instantiates an object of the MainApp subclass, which inherits its basic API from the Application Template superclass. The MainApp class is concerned with data management and provides access to both data received via mmap (mmap_interface), as well as data generated on the fly (random_data_interface). The latter enables easier debugging and testing of plugins. By contrast, the Application Template class is mainly responsible for managing the registration of events and rendering handlers that are defined in the current_screen class. This granular design allows switching between different plotting modes on the fly, without interference with data handling, or loss of application-specific state information (axes shown, threshold shown, etc.). There are three different plotting modes: Overwrite (keep old data on screen and overwrite with new data while moving to the right), clear at end (plot incoming data to the right and clear plot once end of x-axis is reached), and move left (for every incoming data point, move plot to the left and write new data to the rightmost position).
2.12. Online data analysis – communication between systems
The data analysis system makes decisions about when to trigger a particular visual stimulus. These trigger values need to be communicated reliably to the visual stimulation system with minimal system delay. For this purpose, we developed a TCP-based communication protocol and mechanism for data sharing between different processes on the same system. The sender is implemented in C and is called from Matlab using a mex file (by the real-time control plugin). A server process receiving the messages runs on the visual stimulation system. The server writes the values it receives into a shared memory file, which is continuously checked by the Matlab program providing the visual stimulation.
2.12.1. Communication protocol – sender
Client creates a TCP socket connection with the server and transmits the message (a single byte value). Client receives an ‘ok’ back from the server to confirm data transmission. Client returns 1 to Matlab if sending the message was successful and −1 other-wise. Finally, the TCP socket connection is closed. The loop time (message-response) is ~1 ms.
2.12.2. Communication protocol – receiver
The server is implemented in Python using the built-in SocketServer.TCPServer module for network communication. We set allow_reuse_address = True so that the same port can be reused immediately after a connection has been closed (this prevents ‘connection refused’ errors). We implemented our own request handler by subclassing SocketServer.BaseRequestHandler, which waits for incoming data and checks whether a valid value (integer number) was received. It appends the received value to the shared memory array and sends a confirmation back to the client. The shared memory array contains the last 100 values received – the oldest value is discarded before a new value is appended. To achieve the lowest latencies possible, we tuned the TCP server by disabling the Nagle algorithm so that single packages are sent immediately (see page 402 in Peterson and Davie, 2007), and limiting our transmission buffer to a size of 10 bytes.
2.12.3. Communication protocol – shared memory variables
For low-latency asynchronous communication between Matlab (which uses psychophysics toolbox to present the stimuli) and the Python TCP server we used memory-mapped shared files. These are accessed using the memmapfile class in Matlab and the mmap class in Python. Thus, we could communicate between two Matlab sessions on two different computers with a total latency of <1 ms (see Section 3 and Fig. 5A).
Fig. 5.
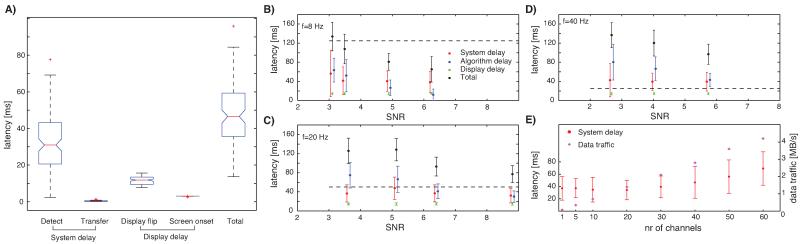
Experimental verification of oscillation detection performance and latency. All errors are ±s.d. (A) Experimentally determined system and display latencies, shown for the case of 20 Hz. Boxplots show the median (red line), the 25/75th quantile as the upper/lower limit of the blue box, outliers as red crosses, and wiskers the range of all values not considered outliers (±2.7× s.d., Matlab defaults for boxplot). (B)–(D) Latencies for different oscillation frequencies and SNR values. SNR values are slightly different between different simulations because the values are experimentally determined from the actually recorded data. The horizontal dashed lines indicate the cycle length of the simulated oscillation. Black lines is the total delay from the simulated oscillation onset till the screen changes. Red, blue and green lines show the components that the total delay is composed of (same notation panels B–D). System- and display delays are independent of SNR. (E) System delay (red, left axis) and data traffic generated (blue, right axis) as a function of the number of channels that are processed simultaneously for real-time oscillation detection (f = 20 Hz, SNR = 7.5).
2.13. Performance evaluation of oscillation-detection algorithm
LFP signals were simulated and oscillatory periods of known location and duration (1 s each) were randomly inserted as described above. For each simulation, 30 non-overlapping such oscillations were inserted into a trace of 130 s duration.
The oscillation frequency of each inserted episode was randomized (±3 Hz, centered on the target frequency). The amplitude of the inserted oscillation was varied to modify the difficulty, quantified by SNR as described above. The same signals were used to assess performance in simulations and experiments. Detection performance was quantified as the proportion of all correctly detected oscillations (TP, true positives) and the proportion of wrongly detected oscillation episodes (FP, false positives). Formally, TP = nTP/TPmax and FP = nFP/FPmax. There were TPmax = 30 oscillatory periods, thus if all these are detected TP = 1.0. Falsely detected oscillatory periods were each assumed to be of equal duration to the truly present episodes, to allow a fair comparison. There were thus FPmax = 100 possible false positives in each simulation. We swept through a range of possible thresholds to get pairs of (TP, FP) values at different thresholds. We used these to plot an ROC curve and to calculate the area under the curve (AUC; equal to 0.5 for chance performance and 1.0 for perfect performance). We use the AUC as a summary measure of the detector’s performance at a particular SNR value. The precision P of the detector is P = nTP/(nTP + nFP) where nTP and nFP are the number of true/false detections in a particular simulation, respectively. The precision is a useful metric to quantify the trade-off between latency and detection performance.
2.14. Experimental verification with simulated data (oscillation detection)
LFP signals were simulated as described above and re-played as described. The parameters of the real-time control plugin were adjusted accordingly for each oscillation frequency to achieve approximately equal hit rates. This was necessary because the parameters were specified in terms of power (μV2), which is a function of frequency due to the 1/f power nature of the LFP. Window-size was 200 ms throughout with thresholds 10, 35, and 200 respectively for 40, 20 and 8 Hz.
2.15. Experimental verification with simulated data (phase-specific stimulation)
Parameters of the real-time control plugin were adjusted for each frequency as described above. Window-size was 400 ms throughout with thresholds of 25, 30, 40 and 230, for 40, 30, 20, and 8 Hz, respectively. The assumed system delay was measured empirically and 29.8 ms for all simulations.
2.16. Turtle recordings
Recordings were made from the dorsal cortex of chronically implanted adult turtles (Trachemys scripta, m/f, weights 850–1200 g). Electrodes were 32-channel silicon probes (50 μm pitch, 177 μm2 surface area for each site; either in two rows of 16 contacts of the Poly2 type or all contacts in one row; H32 packaging; Neuronexus Inc; see Table 1 for impedances) mounted on a microdrive (nDrive32, Neuronexus Inc). The silicon probe (Vetter et al., 2004) was lowered in small steps (10–50 μm) into the brain till the polarity of the visually evoked potentials indicated that some recording sites had reached and passed the pyramidal cell layer. Implanted animals were used for experimental sessions of up to several hours per day with up to 20 sessions per animal. After removal from the water tank and drying, animals were placed into a shielded recording setup where their carapace and plastron were affixed to a stable post via a Velcro belt. Animals could move their head and limbs freely. Animals were presented visual stimuli (various natural scenes, full-screen) using Psychophysics toolbox (Brainard, 1997; Pelli, 1997) on an LCD Screen (120 Hz refresh rate, Alienware Inc.) approximately 30 cm from the animal’s head, contralateral to the implanted hemisphere (we always implanted the right hemisphere). Recordings were performed with a Digital Cheetah system and HS-36 headstages (Neuralynx Inc). This headstage had unity gain, high input impedance (~1TΩ) and produced no significant phase distortions at the frequencies of interest (Nelson et al., 2008). The headstage was placed on the carapace of the animal and connected to a plug on the head (Omnetics Inc.) using a flexible unshielded cable, permitting head movements during recording. Recordings were grounded and referenced against one of the skull screws. The polarity of all recordings was inverted as shown in all plots. Signals were sampled at 32,556 Hz wide band 0.1–9000 Hz. A photodiode was placed on the screen to verify stimulus update and its output recorded. After each final experiment, electrolytic lesions were made (40 μA DC, 5 s) through one of the upper contacts on the silicon probe (unipolar, vs ground screw, using a WPI A365 stimulator).
2.17. Turtle surgery
All surgical procedures and experiments were performed in accordance with permit F122/13 of the Regierungspraesidium Darmstadt (Hessen, Germany). Anesthesia was initiated with Ketamine (10–15 mg/kg) and Medetomidin (0.1 mg/kg) injected i.m., followed by intubation and maintained with 3–3.5% isoflurane (6 cycles/min, 5–12 ml volume, 8–15 mm Hg pressure). The animal was placed into a customized stereotactic apparatus (Knopf Inc) and fixated using custom-made ear bars. All surgical procedures were done under 20× magnification with a Zeiss neurosurgical microscope. The skin on top of the skull was carefully removed with a scalpel over both hemispheres and between the eyes to reveal the bone surface. A small cranial window was opened over the target area (see Fig. S2) (Powers and Reiner, 1980; Ulinski, 1990). Next, a part of the exposed dura was removed, followed by removal of the arachnoidea (using the sharp tip of a cannula, while carefully avoiding blood vessels). Electrode position was determined using anatomical landmarks (the rostro-caudal lateral ridge, which starts at the bulb-to-cortex border, indicates the transition between the dorsal and lateral cortex). The pia was penetrated with a customized pneumatic inserter (Blackrock Microsystems) (Rousche and Normann, 1992). The silicon probe was then inserted into the cortex through this opening. The probe was advanced using a small microdrive (nDrive, Neuronexus Inc), which also held the 36 pin connector. Three small holes were drilled into the skull around the microdrive, into which gold-plated screws were placed. These screws served both as external reference and ground (silver wire, which is connected to the plug) and as anchors for the cement holding the drive. After insertion, the microdrive was glued to the skull using UV-light curable orthodontic adhesive (Transbond XT, 3M Inc.). The craniotomy is filled with self-hardening liquid silicon (Flexitime medium flow, Heraeus Dental Inc.), allowing free movement of the electrode. The edges of the implant, the screws and the plug are then covered with dental cement for stability and protection. Because the drive exceeded 10 mm in height, preventing complete head retraction, we placed one screw between carapace and plastron on each side of the neck, to serve as head posts. Two holes (3 mm diameter) are drilled through the upper- and lower part of the shell to insert. These screws were stainless steel screws (surrounded by soft plastic), placed 3–5 mm from the anterior edge of the shell. The distance between the two screws was slightly smaller than the minimal width of the head, regardless of orientation. The chronic implants were functional for up to several weeks after implantation. This paper contains data from 5 chronically implanted animals (Table 1).
3. Results
We first evaluated our methods for real-time analysis of LFP signals using simulations and recording of simulated data. Next, we evaluated the feasibility of performing closed-loop visual stimulation experimentally in awake animals. For this, we presented visual stimuli to awake turtles conditional on the presence of oscillations in the LFP recorded from visual cortex.
3.1. Performance evaluation with simulated data
Our aim was to asses quantitatively the performance of our algorithm, given well defined signal characteristics. The algorithm had access to the simulated data in the same manner as the real-time implementation (block-by-block).
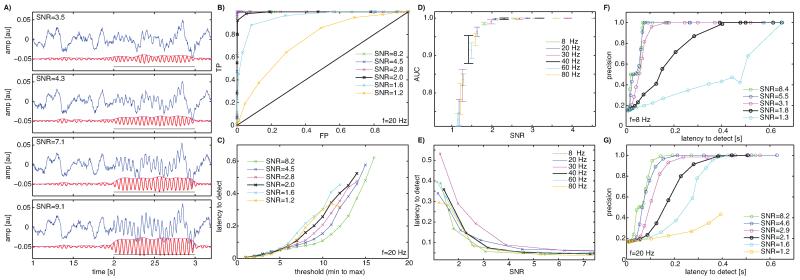
Simulated LFP signals with 1/f power similar to experimentally recorded LFPs were used as background “noise” and simulated oscillations of known amplitude, duration, start phase and location were inserted (see Section 2 for details and Fig. 3A for examples). We then evaluated the detection algorithm by comparing its performance (ROC analysis, latency to detect) for different SNR values and oscillation frequencies. We tested frequencies in the range of 8–80 Hz. We found that the algorithm could detect oscillatory periods reasonably reliably starting at an SNR value of 1.2 (AUC > 0.75, Fig. 3B, D). The latency to detect the oscillation was shorter with higher SNR (Fig. 3C, E) but did not depend strongly on oscillatory frequency except at very high thresholds (Fig. 3E). Similarly, detection performance was largely independent of oscillation frequency (Fig. 3D). This is because our definition of SNR normalizes signal amplitude as a function of frequency. If signal strength were calculated as absolute voltage amplitude, detection performance would depend strongly on signal amplitude, due to the 1/f nature of the underlying signal; indeed, background signal amplitude is higher for lower frequencies, and oscillations need to be of greater amplitude to be detected. We defined SNR on a per-frequency basis to normalize for this effect. Also note that for very low frequencies (<2 Hz) the detection latency would increase, due to the need to integrate over at least one period. The frequencies of interest here (>2 Hz) eliminated this problem (Fig. 3E).
Fig. 3.
Performance evaluation of the oscillation detection algorithm (Simulations). (A) Example traces of simulated LFP signals (blue) with superimposed oscillations (f = 20 Hz) to be detected. Red shows a bandpass filtered version (20–30 Hz) of the raw signal, magenta its envelope and the black line shows the ground truth. The 4 panels show 4 different SNR values (as indicated) of the very same signal. (B,C) Performance of the detection algorithm for the f = 20 Hz case, quantified with an ROC analyis (B) in terms of true positives (TP) and false negatives (FP) as well as latency to detect (C). Latency is measured from the theoretical oscillation onset till the onset of the oscillation is detected (20 Hz, 1 cycle = 40 ms). Each datapoint is a possible threshold value and a range of possible threshold values between the min/max range of the threshold signal is explored. Notice how detection accuracy and latency is a function of both SNR and the threshold. Each datapoint in (B,C) is the average of 30 trials. (D) Detection performance, quantified as the area under the curve (AUC) of the ROC, for different frequencies in the range of 8–80 Hz of the to-be-detected oscillation. Errors are ±s.d. over simulation runs for each datapoint (4 simulations with 30 trials each). (E) Latency to detect oscillations as a function of SNR at equal performance levels (FP = 0.12, resulting in average TP = 0.87). Notice that detection performance does not strongly depend on the frequency of the to-be-detected oscillation, but strongly depends on SNR regardless of frequency. (F,G) Tradeoff between detection accuracy and latency to detection, quantified as precision as a function of latency for the cases of 8 Hz (F) and 20 Hz (G).
We quantified the relationship between detection performance and latency (between oscillation onset and detection, see Section 2) as a function of oscillation frequencies (Fig. 3F, G). We found that there was a large tradeoff between the two, imposing that one prioritizes one or the other (low precision/short latency or high precision/long latency) in each experiment.
3.2. Performance evaluation with “recorded” data
Next, we used the same simulated data traces but in simulated recordings (Fig. 4). For this purpose, we converted the simulated data to analog voltage values using a digital-to-analog converter (see Section 2) and recorded these as if they were real signals from recording electrodes. Thus, performance can be evaluated precisely because the timing of the introduced event (oscillatory periods) is known.
Fig. 4.
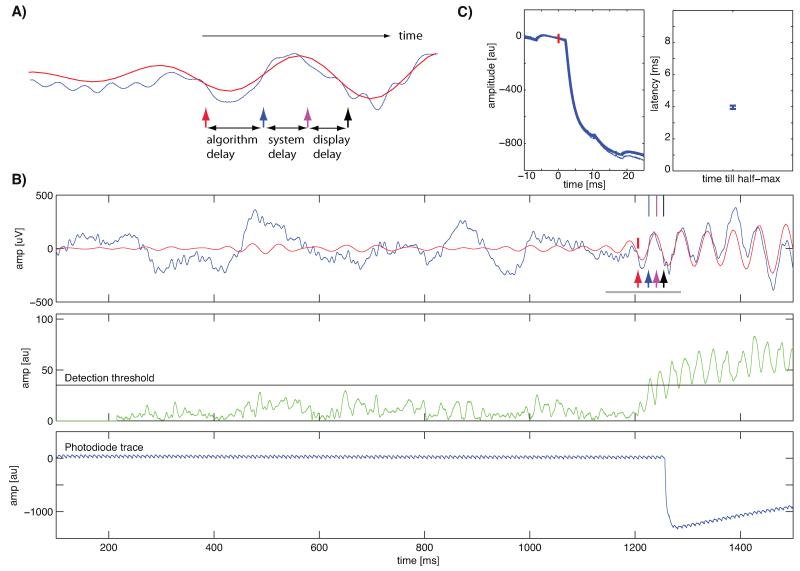
System setup for experimental verification of oscillation detection algorithm. (A) Illustration of an oscillation and points of time used in the text and in (B). Arrows indicate the location of different events: oscillation onset (ground truth, red arrow), theoretical first moment when the oscillation could have been detected (blue arrow), point of time when oscillation was detected by the analysis system (magenta arrow) and the point of time when the display change occurred (black arrow). (B) Single trial example with a 20 Hz oscillation. Shown are the raw (blue) and 15–25 Hz bandpass filtered (red) recorded traces (top), the signal computed by the detector and the threshold used (green and black, middle) and the trace from the photodiode on the screen (blue, bottom). Note the agreement of the black arrow with the photodiode trace (bottom). The small deviations in the photodiode trace are oscillations in the backlight of the LCD (at 240 Hz). The gray line indicates the time shown in (A). (C) Verification of display onset timing (n = 120 trials). Shown are the raw traces (top), aligned at t = 0 when the graphics card indicated that it had executed a refresh. The latency till the half-max luminance was reached was approximately 4 ms. Errorbars are ±s.d. Note that the y-axis values are different compared to (A) because of a different stimulus luminance used to conduct this experiment.
First, we evaluated the delays introduced by various components of the system. The delay from the onset of an event to a visual stimulus change is made up of three components (see Fig. 4A): (i) algorithm delay, (ii) system delay, and (iii) display delay. The first delay is the time between the onset of the event of interest and its detection. The type of algorithm used and its parameters determine this delay. For simple detection tasks (such as crossing of amplitude thresholds or detecting single spikes), the algorithmic delay could be reduced to almost zero. This delay is a lower bound in case of infinitely fast access to data and absence of computational delay. It can be calculated only for simulated data, because the true onset of an event is usually unknown. The system delay is the additional time that elapses until the analysis system detects the event. This delay is due to communication and computational overhead. For a perfect system, it would be 0. The third delay is due to the physical limits of the display. It is the time from when the analysis system detects the event to that when the visual stimulus changes on the screen, as verified by the photodiode.
We now focus on oscillatory events as the objective of our detection. We evaluated the different delays for our oscillation detection algorithm as follows. The raw signal (Fig. 4B, blue) was continuously band-pass filtered around the frequency of interest (Fig. 4B, red) and a detector signal was continuously updated (Fig. 4B, green). If the detector signal crossed a pre-defined threshold, an event was generated (magenta arrow) and sent to the display system to update the screen. When the actual screen update occurred the system generated another event (black arrow). The first time that the oscillation would have been detectable theoretically (blue arrow) was used to assess the latency. We verified that the timing returned by the display update is accurate by recording a photodiode trace (Fig. 4B, bottom). Timing of the screen was very accurate, with the half-max reached in approximately 4 ms after the psychophysics toolbox indicated execution of a screen refresh (Fig. 4C).
We next evaluated the system and display delays for different oscillation frequencies and SNR values. For 20 Hz oscillations with SNR 7.5, the detection delay was on average 32.6 ± 15.6 ms (Fig. 5A). It then took 0.4 ± 0.3 ms to transfer to the display system, 11.5 ± 2.3 ms to refresh the screen (flip time) and 3.0 ± 0.1 ms till the information appeared after a refresh (Fig. 5A). We varied the SNR as well as the average frequency of the oscillations and found that the system could detect oscillations with total onset to screen change latencies in the range of 50–150 ms (Fig. 5B-D). Shown is the total delay (black) till the screen changed as measured by the photodiode, as well as its components. Notice how the system delay (red) is independent of SNR, whereas the algorithmic delay (blue) decreases with higher SNR. This tradeoff is identical to that established above with simulations. With experimental data, the true onset time of the oscillations is of course not known or predictable. Hence, the algorithm delay is unknown and all that can be computed in this case is the time between when the real-time analysis system detected the oscillation and when a infinitely fast algorithm would have found it (Fig. 5B-D, red).
The latency results above were derived from real-time measurements with only one channel. We also assessed the delays as a function of system load (Fig. 5E), the number of channels processed in parallel. The same power-detection algorithm ran on each channel using the parallel architecture described above. We allowed a maximum of 10 workers (see Section 2). The to-be detected oscillations only appeared on one channel at random, so all channels had to be processed. Only the system delay is of interest here, because all other delays are independent of load. We used 20 Hz oscillations of high SNR (7.5) and enabled real-time plotting for one of the channels. System latencies increased from 37.0 ± 19.2 ms for a single channel to 69.1 ± 27.1 ms for 60 channels. The average latency was <40 ms for up to 30 channels. Because 10 parallel workers were used, we conclude that each worker could process 3 channels in parallel without introducing additional delays. If the load on each worker exceeds 3 channels, delays increased. These limits can be increased with a more powerful computer. Network traffic generated between acquisition and analysis machines was approximately 70 kB/s for every channel (resulting in 4.2 MB/s for 60 channels; Fig. 5E).
Next, we evaluated the system’s ability to change the visual stimulus at a particular phase of a detected oscillation. All simulated oscillations started at a random phase and, in the above evaluation, the screen change would thus occur at a random phase (as soon as the oscillation was detected). We extended our algorithm such that, when it detected an oscillation, it also estimated the instantaneous frequency of the oscillation as well as the current phase (see Section 2 for details). The algorithm calculated when the requested phase would occur next, assuming oscillation frequency remained unchanged and coherent. Taking into account the known delays (Fig. 5A) until screen update, the algorithm was thus able to send the trigger signal at the correct time.
The onset of visual stimuli could be timed such that they appeared at a phase chosen by the user (Fig. 6). For example, targeting the middle of the upstroke (270°, see Fig. 6A for illustration) at f = 20 Hz resulted in an average phase error of 19.6° (2.7 ms). Phase values were clustered significantly around the mean phase (Fig. 6A, Rayleight-test, p < 4e–26, R = 0.53, κ = 1.24). Single traces taken from this example (Fig. 6B, black) confirm that the stimulus appeared at the requested phase (Fig. 6B, blue). This was possible for arbitrary phases (Fig. 6C, D show two examples) at frequencies up to 40 Hz but not for 60 Hz (Fig. 6E, F). The frequency at which significant phase locking could be guaranteed is determined by the system’s variance (Fig. 5E, s.d. ~19.2 ms).
3.3. Performance evaluation – real-time plotting
Fast and direct data display is crucial for real-time analysis systems, because it facilitates on-line data exploration and rapid parameter fine-tuning (e.g., selection of channels, frequencies and thresholds). Data visualization, however, can be a critical problem. We thus implemented a plotting system based on OpenGL enabling data display independent of processing (see Section 2 and Appendix). We tested two possible modes of OpenGL: the immediate and vertex buffer object (VBO) modes. Immediate mode is straightforward, but scales poorly with rendered points, because all the data points must be transferred from CPU memory to GPU memory at each plot iteration (Fig. 2B, red). In VBO mode, by contrast, memory can be allocated on the GPU such that only new data points need to be uploaded. Plotting time thus becomes almost independent of the total amount of displayed data points (Fig. 2B, green). While Matlab plotting is fast with small numbers of data points (<51,200), the sampling rates required for spike and LFP data were between 1 and 32 kHz. We thus implemented the VBO mode (Fig. 2B).
3.4. Visual stimulation conditional on oscillatory power
We recorded with chronically implanted electrodes from the dorsal cortex of awake turtles (Fig. S2). Dorsal cortex receives visual input from the thalamic lateral geniculate nucleus (Zhu et al., 2005). Turtles were restrained at their carapace, and presented visual stimuli on an LCD screen positioned contra-laterally to the implanted electrode.
We presented images of natural scenes lasting up to 2 s each, with randomized inter-stimulus intervals of 10 ± 3 s. The LFP response consisted of two components: (i) a broad-band component, the visually evoked potential (VEP; Fig. 7A, middle), and ii) oscillations in a 25–35 Hz band (Fig. 7A, bottom). The oscillation frequency varied little (~1 Hz) across days in each animal but varied significantly across animals (22.4–33.2 Hz across five animals, Table 1, see Section 2 for definition of peak frequency). Both response components occurred after the onset and offset of the stimulus (Fig. 7A). Using 32-channel silicon probes inserted perpendicular to the cortical surface, we found that responses could be found at all depths of the cortex, but with variable amplitude and polarity (Fig. 7C, D). Response latency varied across trials, but very little across channels (Fig. 7D, Table 2). For this reason, we will restrict our description to the use of one channel.
Table 2.
Trial-by-trial variability, quantified from the same sessions used in Table 1. Shown are the average s.d. of the trial-by-trial variability. For peak VEP, the range to find the peak used was 50–400 ms; for the peak oscillatory power, it was 50–1000 ms.
| Animal | Mean s.d. of VEP peak latency [ms] |
Mean s.d. of peak oscillatory power [ms] |
|---|---|---|
| F7 | 75 | 301 |
| D38 | 107 | 339 |
| D10 | 67 | 242 |
| D29 | 92 | 191 |
| D28 | 70 | 268 |
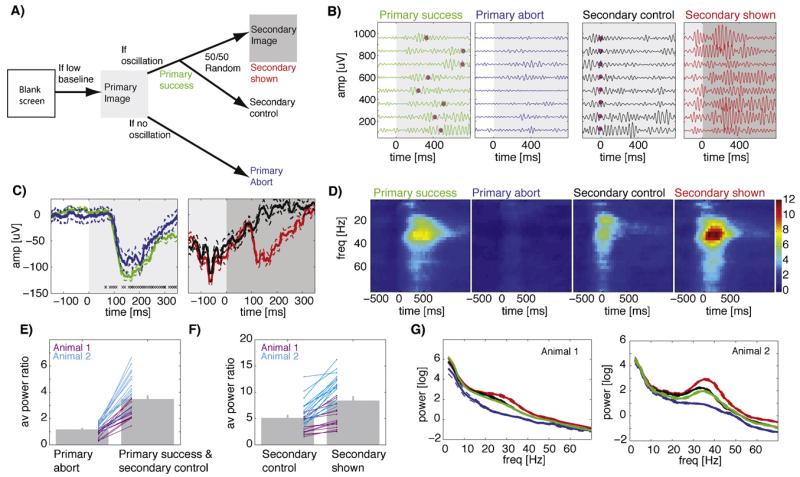
In an initial screening session (open-loop), we measured the frequency spectra of the evoked responses in (near) real-time enabling the choice of the optimal parameters (center oscillation frequency, detection threshold) in ~20 trials. The aim of our on-line stimulation system is to enable the choice of appropriate stimulus timing, conditional on the animal’s brain state, as assessed from LFPs and oscillatory signals. We presented a sequence of two images (Fig. 8A), called primary and secondary. The primary image was presented at low baseline activity, i.e., when the animal was quiet, immobile, and not actively engaged in processing sensory stimuli (which is usually associated with oscillatory activity). The secondary image was presented only if the primary image evoked an oscillatory response. The time delay to the onset of the secondary image depended on when oscillatory power (whose increase has been caused by the first stimulus) had crossed a threshold, and on the phase of the ongoing oscillation. For phase-conditional image onsets, the delay was such that the secondary image would appear at the specified phase. Thus, for each trial, the system first assessed whether the conditions for presentation of a primary stimulus were satisfied (low oscillatory power, see Section 2). Immediately after the primary stimulus, the system assessed whether oscillatory power exceeded a predetermined threshold (see below) within t ≤ 1 s. If so, the trial was noted as a “primary success” (Fig. 8A and B, green). If not, the trial was aborted (“primary abort”, Fig. 8A and B, blue). In a randomly determined subset of 50% of all “primary-success” trials, the secondary stimulus was presented, resulting in either a “secondary shown” or a “secondary control” trial (Fig. 8A and B black and red). The “secondary-control” trials were used to assess the choices made in response to the primary stimulus; the “secondary shown” trials were used to verify stimulus presentation timing and latency. High and low oscillation power thresholds were set manually at the beginning of each session based on responses recorded in the initial trials. Thresholds were kept constant throughout each experiment.
Fig. 8.
Closed-loop conditional presentation of a sequence of two images conditional on oscillatory power. (A) Schematic of the experiment. First, a “primary” image is shown, followed by a “secondary” image conditional on whether the primary resulted in sufficiently strong oscillations. Secondary images are shown probabilistically; omitted secondaries are used as controls. Regardless of whether a secondary was shown or not the screen reverts to blank 2 s after primary onset. (B) Single-trial examples (bandpass 20–40 Hz; 8 trials each), all on the same scale. Color indicates trial types and is matched to (A). t = 0 is the onset of the primary (left) and secondary (right). Magenta dots indicate onset of the secondary stimulus. The primary success trials are trials that are later followed by no further stimulus (secondary control). The same trials are shown in green and black, but aligned differently (note Magenta dots, which mark the control-onset time). Magenta dots indicate when the secondary stimulus would have been shown if these were not control trials. (C) Average broad-band responses (same session as B). A VEP was evoked by both the primary (left) and secondary (right) stimulus. Errorbars are ±SE over trials (left, n = 124 and 26; right, n = 80 and 43). Crosses mark points of time (one cross per trial) where the secondary stimulus would have been shown (not all shown, some are after 350 ms). (D) Oscillatory power (same session as in B,C). Shown are time-frequency spectra. Notice the absence of oscillatory power for primary abort trials, despite the presence of a VEP (see C). (E,F) Population statistics of oscillatory power for both animals. The average peak power was significantly different between primary only and secondary shown as well as secondary control and secondary control trials in both animals (p < 0.05, pairwise t-test). Lines show individual sessions. (G) Average powerspectra based on the period after stimulus onset. The difference between secondary control (black) and secondary shown (red) is due to the conditional presentation of a second stimulus. Errorbars are ±SE over sessions.
Primary and secondary stimuli always resulted in a VEP (Fig. 8C), even if the associated oscillatory power was low (Fig. 8C, blue). Presentation of the secondary stimulus during an ongoing oscillation, however, always resulted in a prominent increase of oscillatory power (Fig. 8B and D). A total of 32 sessions with 2 animals were used to quantify the reliability of our real-time stimulation system. All error bars that follow indicate ±s.d. across sessions. Primary stimuli evoked oscillations of sufficient strength in 75 ± 10% of trials (the range of failures across sessions was 10–47%). Note that trials were initiated only if pre-stimulus baseline oscillatory power was low. Despite this precaution, about 25% of primary trials failed to evoke oscillations. We quantified stimulus-evoked oscillatory power as the average power in a band ±5 Hz centered on the peak frequency after the stimulus onset, normalized to baseline power (Fig. 8E,F). We also quantified average raw power after stimulus onset for the same time periods (Fig. 8G). The stimulation system correctly distinguished between primary-abort and primary-success trials (Fig. 8E, normalized power 1.16 ± 0.08 vs. 3.47 ± 0.25, paired t-test p < 1e–11). As per our chosen threshold, power increased by 16% (relative to baseline) for aborted trials and by 247% for trials classified as successes (Fig. 8E). In contrast, peak VEP amplitude was only slightly less in aborted than successful trials (mean amplitude: −62 ± 45 μV vs. −77 ± 44 μV, p < 0.05, paired t-test). The secondary stimulus resulted in an additional power increase relative to the primary responses in which no secondary stimulus had been shown (Fig. 8F, normalized power of 5.09 ± 0.47 vs. 8.38 ± 0.72, p < 0.0001; Fig. 8B (red vs black) shows single trial examples). Thus, showing a second stimulus conditional on ongoing oscillations triggered by a previous stimulus further increases oscillatory power by approximately 65% (Fig. 8F). Note that the power for the secondary control trials is different in Fig. 8E and F because of different alignment (primary and secondary, respectively). The delay between onset of the first and second stimuli was 331 ± 166 ms (±s.d. across 3673 trials).
The average oscillatory response (normalized to baseline) to single primary stimuli (primary aborts and primary successes followed by control trials) was 2.51 ± 0.16 (Fig. 8E, average of both). In offline mode (no real-time control) this would be the best average power that could be expected, conditional on a quiet baseline. For this comparison, this selection would have been made post hoc rather than in real-time. By contrast, the secondary stimuli resulted in oscillatory power of 8.38 ± 0.75 (Fig. 8F, right), significantly different from 2.51 ± 0.16 (p < 1e–10). Selecting only the primary trials that were successful results in power of 3.47 ± 0.25, significantly less than 8.38 ± 0.75 (p < 1e–7). Is this power increase greater than would have been expected if power in response to the two successive stimuli summed linearly? Under this assumption, the power for two sequentially presented stimuli would be 5.02. Selecting only the subset of successful primary stimuli and adding the average power evoked by them to that evoked by unconditional stimulus presentations results in a value of 5.98 ± 0.4, significantly less than what observed after conditional sequence stimulation (p < 0.006). Note that this is the relevant comparison, because secondary-shown stimuli were not further subdivided into successes and failures (all trials were used regardless of the response). Thus, presenting two stimuli conditionally resulted in average power of 8.38 ± 0.75, significantly more than what would be expected if the oscillations were adding linearly 5.98 ± 0.4 (p < 0.006). We conclude (i) that our stimulation system successfully selected trials in real time based on instantaneous oscillatory power and (ii) that visual stimulation conditional on an ongoing and stimulus-evoked oscillation results in a supra-linear increase in oscillatory power.
3.5. Visual stimulation conditional on phase
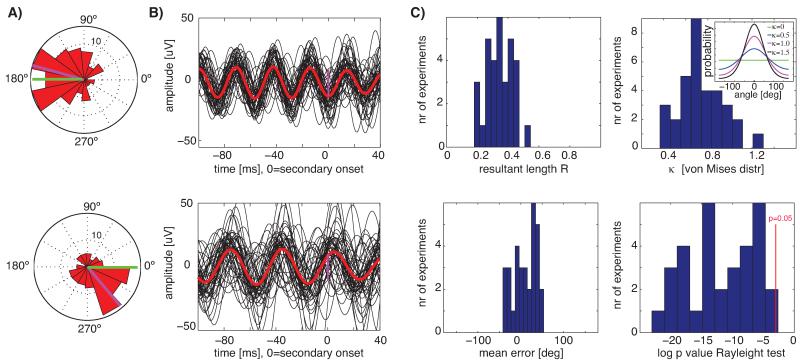
In each experimental session (same 32 sessions as above), we chose a target phase (peak, trough, upstroke, downstroke). In each trial, the secondary stimulus was presented such that it would appear on the screen at the requested phase (see Section 2). We calculated the phase of the ongoing oscillation (evoked by the first stimulus) at the onset of the secondary stimulus and evaluated whether this phase was consistent across trials using circular statistics. We could target arbitrary phases of the ongoing oscillations for oscillation frequencies up to 40 Hz (see Fig. 9A and B for 25 Hz and 35 Hz examples).
Fig. 9.
Presentation of visual stimuli conditional on the phase of ongoing oscillations. (A,B) Single-session examples from two different animals with different oscillation frequencies (26.9 Hz and 33.4 Hz respectively, top and bottom row). (A) Circular histograms of the phase of ongoing oscillations at the point of time the secondary image was displayed (t = 0 in (B)). The requested and achieved mean phase is indicated in green and magenta, respectively. Phases were significantly unimodal with p < 0.01 throughout: R = 0.4, k = 0.9 (top) and R = 0.3, k = 0.7 (bottom). (B) Bandpass filtered (30–40 Hz and 20–30 Hz, respectively) single-trials (black) and average (red); shown are 50 randomly chosen trials. (C) Population average of all sessions (n = 32 from 2 animals). The mean k of the von Mises distribution was 0.7 ± 0.2. The inset shows the shape of the von Mises distribution for different values of k. The mean error relative to the requested angle was 9 ± 28° and not significantly different from 0.
Averaging band-pass filtered trials (±5 Hz) aligned at the secondary stimulus onset resulted in phase-coherent oscillations with a phase at stimulus onset consistent with that specified by the user (Fig. 9B, magenta marker). The phase of the ongoing oscillations at stimulus time was significantly distributed around the requested phase in 31 of 32 sessions (Fig. 9C, p < 0.05, Rayleight test) with a mean resultant length of R = 0.35 ± 0.08 (Fig. 9C). The mean error relative to the requested phase was 9 ± 28° (Fig. 9C, not significantly different from zero). Oscillations were significantly phase locked for a total duration of 242 ± 20 ms (p < 0.05 Rayleigh test at each time point, uncorrected). Thus, oscillation bouts of about 250 ms (see also Fig. 7D) were sufficiently auto-coherent (see Burns et al., 2011) to enable accurate phase prediction and phase-locked stimulation.
Note that, while mean phase deviations can be corrected easily via a system delay, phase variance is harder to compensate for. We further quantified the variance of the measured phases, using von Mises distribution fits (circular equivalent of the normal distribution). The concentration parameter k (the inverse of the variance) was 0.7 ± 0.2 (Fig. 9C), a value at which the von Mises distribution contains 70% of its density within ±90°; Fig. 9C shows the von Mises probability density for different values of k for illustration.
In a first control, we assigned the system to choose a random target phase for every trial (3 sessions from 2 animals). This resulted in an absence of significant phase locking (p > 0.05, Rayleigh test), an average R = 0.08 ± 0.04 and k = 0.16± 0.07. In a second control, we quantified the phase of ongoing oscillations at the onset of the primary stimulus (only trials with no secondary stimulus were used). Because the primary stimulus had not been shown conditional on the phase, we expected no phase locking at stimulus onset. Over all 32 sessions, and consistent with this expectation, we found R = 0.1 ± 0.1 (0/32 were significant with p < 0.01 and 3/32 with p < 0.05) at response onset. The distribution of phases after onset of the phase-locked secondary stimulus was R = 0.35 ± 0.08 (significantly different from R = 0.1 ± 0.1, p < 1e–12 paired t-test).
4. Discussion
We designed a closed-loop system that can accurately detect the onset and phase of ongoing oscillations in the LFP and use this information in real time for conditional visual stimulation with low latencies and high accuracy. We demonstrated by simulations and experiments that our system detects oscillations with sufficiently low latency and high fidelity to allow phase-conditional presentation of visual stimuli for oscillations up to 40 Hz. The software was designed to exploit multi-core and multi-CPU processing, enabling parallel processing of large numbers of channels with inexpensive hardware. For example, a 2-CPU machine with 16 cores can process up to 30 channels in parallel without any increase in latency. Increasing the number of channels simply requires more CPUs, but necessitates no changes in our software.
4.1. Performance evaluation and system design considerations
Experiments with awake behaving animals are essential to understand brain function, but often generate limited data in conditions that vary, due to the animal’s own internal state and behavior. Sensory (or other) stimulation systems that can be conditioned on the animal’s instantaneous brain state could greatly improve and facilitate such experiments. For such systems to be useful, they should be modifiable easily and on the fly by experimenters. This makes closed-loop control with compiled code written in low-level languages such as C++ running on real-time operating systems such as QNX impractical, except to experienced programmers. Rather, we developed a system around a standard, commercially available data-acquisition system. We intentionally separated the data acquisition and real-time analysis components to ensure that data acquisition is not affected even when real-time analysis fails. We opted for a high-level programming language used by many neurophysiologists (Matlab), supplemented by a few time-critical components, written in other languages (C++, Python). These components provide infrastructure and do not require frequent modifications. We divided the software into components, consisting of the core and a number of data-processing plugins. The core takes care of data retrieval, parallel processing and distribution, plotting, and communication with the display system. The plugins implement specific real-time analysis and control algorithms, such as the detection of oscillations. Plugins are implemented by providing a small number of functions with an easy-to-use syntax. They are the primary means by which investigators can modify and extend the functionality of the real-time system.
Performing closed-loop experiments with awake animals poses several challenges. For example, electrodes, channels, power spectra, phases and thresholds must be assessed quickly and appropriate values chosen easily. Because such experiments are in closed-loop, the above operations must be carried out very fast. We implemented real-time analysis components that allow visualization of the responses as they emerge (updated at every trial). From these continuously updated metrics, we could quickly choose appropriate parameters for subsequent real-time control.
Delays due to display
We displayed natural scenes on standard 120 Hz computer screens. Techniques known from visual psychophysics (Brainard, 1997; Pelli, 1997) and gaze-contingent visual displays (Kotowicz et al., 2010; Perry and Geisler, 2002) enable frame-by-frame control of screen display while avoiding artifacts such as screen-updates during a refresh cycle. Nevertheless, a 120 Hz refresh rate implies that refresh cycles last between 8 and 17 ms (see Fig. 5) introducing an uncertainty and trial-to-trial variability of 8 ms. This delay and uncertainty could be reduced using different displays, and reduced to almost zero if feedback stimulation were provided electrically or optically.
Algorithmic delays
The nature of the signals used to assess brain state imposed a delay between onset and detection of the local field potential oscillations. This delay must be added to the system delay, which includes data transfer and computation. Depending on frequency and SNR of the oscillations, the algorithmic delay was 0.5–2 times the system delay for simulated data (Fig. 5). Thus the delays due to processing, transfer, and display accounted for only a minor fraction of the total delay (especially at high SNR). This supports the conclusion that our system architecture is fast enough to solve our task. Note that the true onset time of evoked oscillations is really unknown with experimental data. Consequently, the true SNR of the oscillation signal in an animal experiment is also unknown, and SNR could be calculated only for simulated data. We used a narrow band-pass filter followed by the Hilbert transform for oscillation detection, with a threshold that optimizes the precision-delay tradeoff (Fig. 3). Other power estimation methods, such as multi-taper estimates, might achieve better performance. Note also that using different features of the signal (such as a simple voltage threshold) would naturally reduce delays.
Phase-conditional visual stimulation
Locking a visual stimulus to a particular phase of an ongoing oscillation requires that future timing be predictable based on knowledge of that oscillation’s frequency and phase at a given time. This imposes that the oscillation be reasonably stationary (auto-coherent) over the delay (display + system delays, Fig. 5B-E) between oscillation detection and stimulus onset. This was true (by design) with our simulated data, but also with our experimental data (Fig. 9). In primate V1, the width of gamma-oscillation auto-coherence was not significantly longer than expected by chance (Burns et al., 2010b). Whether evoked or spontaneous oscillations in the turtle visual cortex are auto-coherent beyond what would be expected by chance is not known at present.
4.2. Experimental verification in awake turtles
We demonstrated that our system performed reliably during cortical recordings in awake turtles, exhibited by the accurate separation between ‘secondary abort’ and ‘secondary success’ trials in the sequential presentation experiment. The turtle visual cortex exhibits prominent oscillatory responses (Fig. 7) visible in singletrials (Bullock, 1993; Prechtl, 1994; Prechtl and Bullock, 1994; Prechtl et al., 1997, 2000). While prominent, these oscillations vary greatly in strength and duration across trials. These oscillations can be triggered by a change in visual input, but also occur spontaneously or following more complex processes such as the omission of expected stimuli (Prechtl and Bullock, 1993, 1994). As such, they have many similarities to gamma oscillations commonly observed in mammalian cortex. In turtle, these oscillations have been suggested to represent a signature of cortical processing (Prechtl and Bullock, 1994), partly because they are greatly diminished under anesthesia. In contrast, the VEP remains virtually unchanged in anesthetized animals (Prechtl and Bullock, 1992). While the role of such oscillations in the turtle cortex remains unknown, their ubiquitous nature represented an ideal model system to test our closed-loop system.
Our aim was to present visual stimuli at a particular phase of ongoing oscillations, when oscillatory power was high. The inherent variability of turtle visual cortex oscillations, together with the limited number of trials that can be run on any given day, makes it impractical to perform this experiment in an open-loop arrangement. This thus serves as a demonstration of the power of a closed-loop system, as it allows experiments that are otherwise impossible. In our sequential stimulation experiment, we designed two decision points conditional on ongoing brain activity: (i) oscillatory power should be low at baseline to initiate the first stimulus;(ii) oscillatory power should cross a power threshold to initiate the second stimulus. This stimulus sequence is only an example of what can be achieved. This sequence of conditions greatly facilitated the collection of useful trials: because up to ~50% of trials failed to pass condition ii, the trial could be aborted early and the next trial initiated quickly. Adding further conditionals, such as behavioral criteria, would further maximize return.
5. Potential applications
The receptive fields (RFs) of sensory neurons can be non-linear and high-dimensional, preventing exhaustive mapping of stimulus space. However, a small proportion out of all possible stimuli is often sufficient to define a RF, provided that the most informative stimuli are shown. For example, for non-linear RFs that are piecewise linear the most informative points are those that determine the non-linearities. A search mechanism that determines the most informative stimuli requires online access to the neuronal response. Such approaches have been used to define iso-response curves of V1 neurons in response to colored stimuli (Horwitz and Hass, 2012) and for responses to luminance-differences in the retina (Bolinger and Gollisch, 2012). The iso-response curves define the highly nonlinear response of these neurons well and could only be determined with the help of a closed-loop approach.
Closed-loop learning protocols are crucial in elucidating the role of different electrophysiological brain states in learning. Theories of learning suggest that the larger the impact of novel (to-be-learned) stimuli on ongoing brain activity, the faster can learning proceed. Certain brain states and activity patterns appear to be conducive to learning. Examples include hippocampal theta activity, and sharpwave ripple (SWR) complexes during rest shortly after learning. More recently, conditional learning protocols have provided crucial evidence for a causal role of such brain states in learning. For example, the conditional presentation of learning stimuli during hippocampal-dependent trace conditioning can be used to increase or decrease the learning rate by design (Asaka et al., 2005; Griffin et al., 2004). Transient disruption of SWRs shortly after learning or during sleep (Ego-Stengel and Wilson, 2010; Girardeau et al., 2009; Jadhav et al., 2012) results in learning deficits. Such disruption is achieved by electrical stimulation triggered in real time by the occurrence of ripples. These examples illustrate the types of experiments that are made possible by closed-loop systems and our system can be used to perform similar experiments.
Closed-loop systems can greatly facilitate the search for the appropriate stimuli to activate a given neuron, in particular in areas where neurons respond sparsely to abstract concepts or specifically to certain objects previously seen by the subject, such as animals, cars, specific people or faces (Kreiman et al., 2000; Mormann et al., 2011). Similar visual response specificity exists for the LFP-amplitude or oscillatory response (Kreiman et al., 2006). Since it is a priori impossible to predict what a particular neuron or LFP recording site will respond to, it is necessary to screen a wide variety of stimuli first, followed by presentation of stimuli related to the images that the neuron responded to in the screening. This requires quick data analysis followed by preparation of a new stimulus set, something which is routinely done in the course of hours in some experiments (Quiroga et al., 2005). A closed-loop system can greatly facilitate this process and allow repeated iteration and refinement of the stimulus set despite the limited availability of recording time.
Biofeedback and conditioning of neuronal responses requires closed-loop systems. Exposing an animal to the activity of its own neurons allows behavioral operant conditioning, such that activation of a particular neuron leads to reward (Fetz, 1969). In this classic study, a manually tuned single-channel hardware integrator was used; Similar experiments but on a larger scale and using more complex features such as oscillations are possible by using a closed-loop system such as ours. Such biofeedback has now also been used for recovery-of-function in neuroprosthesis and brain-machine interface (BCI) applications (Hwang and Andersen, 2009; Chapin et al., 1999; Hochberg et al., 2006; Moritz et al., 2008; Taylor et al., 2002). Some general-purpose software environments for BCI applications have emerged (Jerbi et al., 2009; Renard et al., 2010; Schalk et al., 2004). These could, in principle also be used for self-adapting experiments. However, to our knowledge, none of these environments has been systematically evaluated for this purpose.
Control theory and machine learning (see below) provide many rigorous quantitative concepts that can be used to systematically and optimally understand a complex non-linear system, such as populations of neurons. Adaptive control theory provides tools for online estimation of the parameters of an unknown system by systematically modifying its inputs such that appropriately rich dynamics are explored – a concept referred to as sufficient richness and persistent excitation in control theory (Slotine and Li, 1991).
Importantly, sufficient richness is a property of the signals in the feedback loop rather than the inputs and an online feedback loop is thus necessary to explore these concepts for systematic system exploration. Our system provides such a feedback loop, thus allowing application of the concepts that control theory provides. While control theory has been used surprisingly little so far to study neural circuits in vivo in awake animals, its powerful mathematical tools show much promise.
In machine learning, active learning methods (Settles, 2009) allow continuous estimation of what the next most informative stimulus would be by requesting labels (the output) selectively. This approach is motivated by the observation that the labeling cost for a given stimulus is high, whereas listing all possible stimuli is cheap. If we regard the spiking output of a particular neuron as the output of a classifier, this approach could be used to quantify the parameters of the classifier provably more efficient than by random exploration (active learning theory). Closed-loop experimental systems will allow utilizing such theoretical advances in machine learning and control theory for purposes of studying neural circuits.
6. Future improvements
We used a commercial electrophysiology acquisition system (Neuralynx Inc) to demonstrate our method. Other data acquisition systems can be incorporated without major changes since all data retrieval mechanisms are encapsulated in a separate set of functions. Except for these functions, the entire method is system-independent. We anticipate that providing the data retrieval functions for other acquisition systems that offer realtime access to the continuous data stream will be relatively easy and that our findings generalize to all such systems. Systems that provide data access in blocks of less than the 15 ms that our current system offers, will have a reduced system latency relative to what we showed.
Our display system relied on the Psychophysics toolbox (running on a dedicated computer), because this approach is a common one among vision scientists. It would be straightforward to use a different visual stimulation system: the commands received by the stimulation system are delivered via TCP; any system capable of processing a TCP stream would thus be compatible. Whereas this study focused on real-time control by features of LFPs, our approach could be adapted to spike signals and online spike sorting, using the infrastructure we provide. We plan to add a plugin that provides the functionality of the online spike sorting algorithm OSort (Rutishauser et al., 2006).
7. Conclusion
Advances in multi-electrode arrays have increased the number of recorded channels in an experiment into the hundreds. The amount and variability of data generated by such experiments makes it almost impossible for a human being to identify and explore responses while an experiment is ongoing. Later offline analysis typically takes up substantial amounts of time, preventing experimenters from rapidly identifying and further exploring potentially interesting phenomena that emerged in the data. Increasingly, such recordings are performed with awake behaving animals, which leads to further variability due to spontaneous ongoing behavior or changing brain states. In this paper, we demonstrated that the conditional presentation of stimuli facilitates data collection in such situations. Sophisticated algorithms and analysis systems will be necessary to efficiently work with large numbers of channels. The method we propose represents a first step into this direction and we hope that our work will facilitate efficient experimentation and advance the field of online data analysis.
Supplementary Material
Highlights.
Presentation of visual stimuli conditional on phase and power of oscillations.
Enables closed-loop experiments.
Processes up to 64 channels in real time.
Flexible software architecture facilitates use by experimenters.
Acknowledgements
We thank Christian Mueller for surgical instruction and training, Michaela Klinkmann for surgical assistance, Anja Arends for histology, Ingmar Schneider and Uri Maoz for discussion and Jean-Jacques Slotine for ideas regarding control-theoretic applications. This work was funded by the Max Planck Society and the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 322705.
Appendix A. Data processing plugins
Table A.1 lists the analysis and control components (plugins) of the system that we developed. Each is an independent plugin that can be loaded and enabled by the user in the GUI as desired.
Table A.1.
List of plugins provided.
| Name | Category | Type | Purpose |
|---|---|---|---|
| pCtrlLFP | Control | Continuous | Real-time oscillation detection, triggering of power-and phase conditonal events; send events to the visual stimulation system |
| pContinuous | Analysis | Continuous | Display of continuous data, broad-band, spike-band,LFP-band filtered |
| pLFPAv | Analysis | Trial-by-trial | Display of broad-band averages for the LFP and single-trial averaged time-frequency spectra |
| pRaster | Analysis | Trial-by-trial | Raster and PSTH that is updated with every trial |
| pSpikes | Analysis | Continuous | Display of waveforms ofdetected spikes |
Table A.2.
Plugin architecture (Matlab).
| Name | Executed on |
Inputs | Purpose |
|---|---|---|---|
| initCUI | Master | None | Prepare the plugin-specific GUI, such as plot elements to be updated later |
| initPlugin | Master | None | Load the plugin and its GUI |
| initWorker | Master | Channel(s) to be processed |
Initialize data structures that will later be transferred to the workers |
| prepareGUltransfer | Worker | Plugin-specific data, kept local on each worker |
Prepare data to be transferred to the master from the worker |
| processData | Worker | New data received, plugin-specific data |
Process new incoming information; This function is called either for every new block of data that arrived (continuous plugin) or for every new trial (trial-by-trial plugin) |
| updateGUI | Master | Subset of plugin-specific data indicated for transfer from worker to client |
Take the data provided by prepareGUItransfer and update the GUI elements with it |
Plugins have a standardized architecture, specified as a number of functions with appropriate parameters that have to be provided (see Table A.2). Developing a new plugin requires providing these functions, which are typically short. No other parts of the system have to be modified to implement new functionality, allowing the user to focus on the aspects of the experiment rather than system internals concerning data processing or parallel computing, which constitute the majority of the code we developed.
Appendix B. Optimizing OpenGL-based plotting
With OpenGL specification <= 1.2, we would have to implement all data rendering using the so-called immediate mode (see Fig. S1A). While this method provides the maximum amount of control and flexibility, the performance is poor. This is because each data point has to be rendered individually (Fig. S1A) and because all data has to been sent from the CPU to the GPU point by point, every time that a frame is rendered (even if to-be plotted data has not changed). Rendering performance will therefore scale with the number of data points n that have to be rendered (performance is ~ O(n)). Since OpenGL specification 1.5, Vertex Buffer Objects (VBO) provide a more elegant and efficient solution to high performance rendering: chunks of GPU memory can be ‘permanently’ allocated, specific regions of this allocated memory can be overwritten, and specific regions can be used for rendering of vertex data. The sample source code in Fig. S1B shows how efficient overwriting & rendering of a few data points becomes: glBindBuffer will bind a previously generated VBO. glBufferSubData will overwrite vertex data at the specified offset in the GPU memory. Finally, glVertexPointer (which parts of the VBO should be used for rendering) and glDrawArrays (how should the previously selected data be rendered) will render the data points. From this picture, one can immediately see, that the rendering performance does not depend on the number of data points n that have to be rendered. In contrast to the immediate mode, rendering performance is ~ O(1).
See Fig. 2B for a comparison of immediate mode, VBO and Matlab rendering (see Section 3 for details on these numbers).
Footnotes
We make the source code of StimOMatic and benchmark datasets of simulated LFP data publicly available on our website http://stimomatic.brain.mpg.de/ under an open-source license.
Appendix C. Supplementary data
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.jneumeth.2013.02.020 and at http://stimomatic.brain.mpg.de/.
References
- Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996;273:1868–71. doi: 10.1126/science.273.5283.1868. [DOI] [PubMed] [Google Scholar]
- Asaka Y, Mauldin KN, Griffin AL, Seager MA, Shurell E, Berry SD. Nonpharmacological amelioration of age-related learning deficits: the impact of hippocampal theta-triggered training. Proc Natl Acad Sci U S A. 2005;102:13284–8. doi: 10.1073/pnas.0506515102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999;19:2209–23. doi: 10.1523/JNEUROSCI.19-06-02209.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P. CircStat: A MATLAB Toolbox for Circular Statistics. J Stat Softw. 2009;31:1–21. [Google Scholar]
- Bolinger D, Gollisch T. Closed-loop measurements of iso-response stimuli reveal dynamic nonlinear stimulus integration in the retina. Neuron. 2012;73:333–46. doi: 10.1016/j.neuron.2011.10.039. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spat Vis. 1997;10:433–6. [PubMed] [Google Scholar]
- Bullock TH. How do brains work?: papers of a comparative neurophysiologist. Birkhäuser: Boston. 1993 [Google Scholar]
- Burns SP, Xing D, Shapley RM. Comparisons of the dynamics of local field potential and multiunit activity signals in macaque visual cortex. J Neurosci. 2010a;30:13739–49. doi: 10.1523/JNEUROSCI.0743-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns SP, Xing D, Shapley RM. Is gamma-band activity in the local field potential of V1 cortex a clock or filtered noise? J Neurosci. 2011;31:9658–64. doi: 10.1523/JNEUROSCI.0660-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns SP, Xing D, Shelley MJ, Shapley RM. Searching for autocoherence in the cortical network with a time-frequency analysis of the local field potential. J Neurosci. 2010b;30:4033–47. doi: 10.1523/JNEUROSCI.5319-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapin JK, Moxon KA, Markowitz RS, Nicolelis MAL. Real-time control of a robot arm using simultaneously recorded neurons in the motor cortex. Nat Neurosci. 1999;2:664–70. doi: 10.1038/10223. [DOI] [PubMed] [Google Scholar]
- Chen L, Madhavan R, Rapoport B, Anderson W. Real-time brain oscillation detection and phase-locked stimulation using autoregressive spectral estimation and time-series forward prediction. IEEE Trans Biomed Eng. 2011 doi: 10.1109/TBME.2011.2109715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colgin LL, Denninger T, Fyhn M, Hafting T, Bonnevie T, Jensen O, et al. Frequency of gamma oscillations routes flow of information in the hippocampus. Nature. 2009;462:353–7. doi: 10.1038/nature08573. [DOI] [PubMed] [Google Scholar]
- Ego-Stengel V, Wilson MA. Disruption of ripple-associated hippocampal activity during rest impairs spatial learning in the rat. Hippocampus. 2010;20:1–10. doi: 10.1002/hipo.20707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El Boustani S, Marre O, Behuret S, Baudot P, Yger P, Bal T, et al. Network-state modulation of power-law frequency-scaling in visual cortical neurons. PLoS Computational Biology. 2009:5. doi: 10.1371/journal.pcbi.1000519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elze T. Achieving precise display timing in visual neuroscience experiments. J Neurosci Methods. 2010;191:171–9. doi: 10.1016/j.jneumeth.2010.06.018. [DOI] [PubMed] [Google Scholar]
- Fetz EE. Operant conditioning of cortical unit activity. Science. 1969;163:955–8. doi: 10.1126/science.163.3870.955. [DOI] [PubMed] [Google Scholar]
- Fisher NI. Statistical analysis of circular data. Cambridge University Press; Cambridge [England]/New York, NY, USA: 1993. [Google Scholar]
- Girardeau G, Benchenane K, Wiener SI, Buzsaki G, Zugaro MB. Selective suppression of hippocampal ripples impairs spatial memory. Nat Neurosci. 2009;12:1222–3. doi: 10.1038/nn.2384. [DOI] [PubMed] [Google Scholar]
- Goard M, Dan Y. Basal forebrain activation enhances cortical coding of natural scenes. Nat Neurosci. 2009;12:1444–9. doi: 10.1038/nn.2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin AL, Asaka Y, Darling RD, Berry SD. Theta-contingent trial presentation accelerates learning rate and enhances hippocampal plasticity during trace eyeblink conditioning. Behav Neurosci. 2004;118:403–11. doi: 10.1037/0735-7044.118.2.403. [DOI] [PubMed] [Google Scholar]
- Hochberg LR, Serruya MD, Friehs GM, Mukand JA, Saleh M, Caplan AH, et al. Neuronal ensemble control of prosthetic devices by a human with tetraplegia. Nature. 2006;442:164–71. doi: 10.1038/nature04970. [DOI] [PubMed] [Google Scholar]
- Horwitz GD, Hass CA. Nonlinear analysis of macaque V1 color tuning reveals cardinal directions for cortical color processing. Nat Neurosci. 2012 doi: 10.1038/nn.3105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang EJ, Andersen RA. Brain control of movement execution onset using local field potentials in posterior parietal cortex. J Neurosci. 2009;29:14363–70. doi: 10.1523/JNEUROSCI.2081-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav SP, Kemere C, German PW, Frank LM. Awake hippocampal sharp-wave ripples support spatial memory. Science. 2012;336:1454–8. doi: 10.1126/science.1217230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvis MR, Mitra PP. Sampling properties of the spectrum and coherency of sequences of action potentials. Neural Comput. 2001;13:717–49. doi: 10.1162/089976601300014312. [DOI] [PubMed] [Google Scholar]
- Jerbi K, Freyermuth S, Minotti L, Kahane P, Berthoz A, Lachaux JP. Watching brain TV, playing brain ball: exploring novel bci strategies using real-time analysis of human intracranial data. Int Rev Neurobiol. 2009;86:159–68. doi: 10.1016/S0074-7742(09)86012-1. [DOI] [PubMed] [Google Scholar]
- Kotowicz A, Rutishauser U, Koch C. Time course of target recognition in visual search. Front Hum Neurosci. 2010:4. doi: 10.3389/fnhum.2010.00031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krasner GE, Pope ST. A cookbook for using the model-view-controller user interface paradigm in smalltalk-80. J Object-Orient Prog. 1988;1:41. [Google Scholar]
- Kreiman G, Hung CP, Kraskov A, Quiroga RQ, Poggio T, DiCarlo JJ. Object selectivity of local field potentials and spikes in the macaque inferior temporal cortex. Neuron. 2006;49:433–45. doi: 10.1016/j.neuron.2005.12.019. [DOI] [PubMed] [Google Scholar]
- Kreiman G, Koch C, Fried I. Category-specific visual responses of single neurons in the human medial temporal lobe. Nat Neurosci. 2000;3:946–53. doi: 10.1038/78868. [DOI] [PubMed] [Google Scholar]
- Leopold DA, Murayama Y, Logothetis NK. Very slow activity fluctuations in monkey visual cortex: implications for functional brain imaging. Cereb Cortex. 2003;13:422–33. doi: 10.1093/cercor/13.4.422. [DOI] [PubMed] [Google Scholar]
- Marguet SL, Harris KD. State-dependent representation of amplitude-modulated noise stimuli in rat auditory cortex. J Neurosci. 2011;31:6414–20. doi: 10.1523/JNEUROSCI.5773-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra PP, Bokil H. Observed brain dynamics. Oxford University Press; New York: 2008. [Google Scholar]
- Moritz CT, Perlmutter SI, Fetz EE. Direct control of paralysed muscles by cortical neurons. Nature. 2008;456:639–U63. doi: 10.1038/nature07418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mormann F, Dubois J, Kornblith S, Milosavljevic M, Cerf M, Ison M, et al. category-specific response to animals in the right human amygdala. Nat Neurosci. 2011;14:1247–9. doi: 10.1038/nn.2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson MJ, Pouget P, Nilsen EA, Patten CD, Schall JD. Review of signal distortion through metal microelectrode recording circuits and filters. J Neurosci Methods. 2008;169:141–57. doi: 10.1016/j.jneumeth.2007.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlides C, Greenstein YJ, Grudman M, Winson J. Long-term potentiation in the dentate gyrus is induced preferentially on the positive phase of theta-rhythm. Brain Res. 1988;439:383–7. doi: 10.1016/0006-8993(88)91499-0. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The videotoolbox software for visual psychophysics: transforming numbers into movies. Spat Vis. 1997;10:437–42. [PubMed] [Google Scholar]
- Perry JS, Geisler WS. Gaze-contingent real-time simulation of arbitrary visual fields. P Soc Photo-Opt Ins. 2002;4662:57–69. [Google Scholar]
- Peterson LL, Davie BS. Computer networks: a systems approach. Morgan Kaufmann. 2007 [Google Scholar]
- Powers AS, Reiner A. A stereotaxic atlas of the forebrain and midbrain of the eastern painted turtle (Chrysemys picta picta) J Hirnforsch. 1980;21:125–59. [PubMed] [Google Scholar]
- Prechtl JC. Visual motion induces synchronous oscillations in turtle visual cortex. Proc Natl Acad Sci U S A. 1994;91:12467–71. doi: 10.1073/pnas.91.26.12467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prechtl JC, Bullock TH. Barbiturate sensitive components of visual ERPs in a reptile. Neuroreport. 1992;3:801–4. doi: 10.1097/00001756-199209000-00020. [DOI] [PubMed] [Google Scholar]
- Prechtl JC, Bullock TH. Event-related potentials to omitted visual stimuli in a reptile. Electroencephalogr Clin Neurophysiol. 1994;91:54–66. doi: 10.1016/0013-4694(94)90018-3. [DOI] [PubMed] [Google Scholar]
- Prechtl JC, Bullock TH. Plurality of visual mismatch potentials in a reptile. J Cogn Neurosci. 1993;5:177–87. doi: 10.1162/jocn.1993.5.2.177. [DOI] [PubMed] [Google Scholar]
- Prechtl JC, Bullock TH, Kleinfeld D. Direct evidence for local oscillatory current sources and intracortical phase gradients in turtle visual cortex. Proc Natl Acad Sci U S A. 2000;97:877–82. doi: 10.1073/pnas.97.2.877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prechtl JC, Cohen LB, Pesaran B, Mitra PP, Kleinfeld D. Visual stimuli induce waves of electrical activity in turtle cortex. Proc Natl Acad Sci U S A. 1997;94:7621–6. doi: 10.1073/pnas.94.14.7621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quiroga RQ, Reddy L, Kreiman G, Koch C, Fried I. Invariant visual representation by single neurons in the human brain. Nature. 2005;435:1102–7. doi: 10.1038/nature03687. [DOI] [PubMed] [Google Scholar]
- Renard Y, Lotte F, Gibert G, Congedo M, Maby E, Delannoy V, et al. OpenViBE: an open-source software platform to design, test, and use brain-computer interfaces in real and virtual environments. Presence-Teleop Virt. 2010;19:35–53. [Google Scholar]
- Rousche PJ, Normann RA. A method for pneumatically inserting an array of penetrating electrodes into cortical tissue. Ann Biomed Eng. 1992;20:413–22. doi: 10.1007/BF02368133. [DOI] [PubMed] [Google Scholar]
- Rutishauser U. Computation&Neural Systems. California Institute of Technology; 2008. Learning and representation of declarative memories by single neurons in the human brain. PhD Thesis. Pasadena. [Google Scholar]
- Rutishauser U, Schuman EM, Mamelak AN. Online detection and sorting of extracellularly recorded action potentials in human medial temporal lobe recordings, in vivo. J Neurosci Methods. 2006;154:204–24. doi: 10.1016/j.jneumeth.2005.12.033. [DOI] [PubMed] [Google Scholar]
- Schalk G, McFarland DJ, Hinterberger T, Birbaumer N, Wolpaw JR. BCI2000: A general-purpose, brain-computer interface (BCI) system. IEEE Trans Bio-Med Eng. 2004;51:1034–43. doi: 10.1109/TBME.2004.827072. [DOI] [PubMed] [Google Scholar]
- Settles B. Computer Sciences Technical Report. University of Wisconsin; Madison: 2009. Active Learning Literature Survey. [Google Scholar]
- Slotine JJ, Li W. Applied nonlinear control. Prentice-Hall: 1991. [Google Scholar]
- Sridharan D, Boahen K, Knudsen EI. Space coding by gamma oscillations in the barn owl optic tectum. J Neurophysiol. 2011;105:2005–17. doi: 10.1152/jn.00965.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M. Impact of network activities on neuronal properties in corticothalamic systems. J Neurophysiol. 2001;86:1–39. doi: 10.1152/jn.2001.86.1.1. [DOI] [PubMed] [Google Scholar]
- Taylor DM, Tillery SIH, Schwartz AB. Direct cortical control of 3D neuroprosthetic devices. Science. 2002;296:1829–32. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- Ulinski PS. The cerebral cortex of reptiles. In: Jones EG, Peters A, editors. Comparative structure and evolution of cerebral cortex. Plenum; New York: 1990. pp. 139–215. [Google Scholar]
- Vetter RJ, Williams JC, Hetke JF, Nunamaker EA, Kipke DR. Chronic neural recording using silicon-substrate microelectrode arrays implanted in cerebral cortex. IEEE Trans Bio-Med Eng. 2004;51:896–904. doi: 10.1109/TBME.2004.826680. [DOI] [PubMed] [Google Scholar]
- Zhu D, Lustig KH, Bifulco K, Keifer J. Thalamocortical connections in the pond turtle Pseudemys scripta elegans. Brain Behav Evol. 2005;65:278–92. doi: 10.1159/000084317. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.