Genotype Imputation Reference Panel Selection Using Maximal Phylogenetic Diversity

Abstract

The recent dramatic cost reduction of next-generation sequencing technology enables investigators to assess most variants in the human genome to identify risk variants for complex diseases. However, sequencing large samples remains very expensive. For a study sample with existing genotype data, such as array data from genome-wide association studies, a cost-effective approach is to sequence a subset of the study sample and then to impute the rest of the study sample, using the sequenced subset as a reference panel. The use of such an internal reference panel identifies population-specific variants and avoids the problem of a substantial mismatch in ancestry background between the study population and the reference population. To efficiently select an internal panel, we introduce an idea of phylogenetic diversity from mathematical phylogenetics and comparative genomics. We propose the “most diverse reference panel”, defined as the subset with the maximal “phylogenetic diversity”, thereby incorporating individuals that span a diverse range of genotypes within the sample. Using data both from simulations and from the 1000 Genomes Project, we show that the most diverse reference panel can substantially improve the imputation accuracy compared to randomly selected reference panels, especially for the imputation of rare variants. The improvement in imputation accuracy holds across different marker densities, reference panel sizes, and lengths for the imputed segments. We thus propose a novel strategy for planning sequencing studies on samples with existing genotype data.

GENOTYPE imputation is an essential component of modern genetic association studies. This technique enables direct testing of untyped markers for associations with phenotypes of interest, thereby increasing the power to identify causal variants in association studies (Li et al. 2009). Imputation is especially useful in meta-analyses that combine data from genome-wide association studies (GWAS) conducted using different genotyping platforms (Zeggini et al. 2008; Scott et al. 2009). Moreover, genotype imputation performed using study-specific sequenced samples enables analysis of rare variants in large GWAS-genotyped data sets (Zawistowski et al. 2010).

Imputation methods typically use a reference panel of densely genotyped haplotypes to predict the missing genotypes in a less densely genotyped study sample. The choice of the reference panel then influences the imputation accuracy obtained in the study sample. It has been observed that in general, imputation accuracy is higher when the reference panel and the study sample derive from the same or similar populations than when they are from substantially different groups (Huang et al. 2009, 2011). However, high-diversity reference panels also contribute to increased imputation accuracy. Huang et al. (2009) found that increasing reference panel diversity by incorporating a mixture of different HapMap populations could improve imputation accuracy in comparison with the use of only a single HapMap population. Similarly, in imputing a study sample from a British birth cohort, Jostins et al. (2011) found that adding to the reference panel a proportion of HapMap samples from other populations (e.g., taking 17% of the reference panel from Toscani or 22% from Chinese and Japanese) yielded a higher imputation accuracy than using Northern European samples alone.

Most studies performed to date have selected reference panels from external databases such as the International HapMap Consortium (International Haplotype Map Consortium 2005; Frazer et al. 2007) and 1000 Genomes Project (1000 Genomes Project Consortium 2010). Dramatic reductions in sequencing cost now enable an alternative strategy: to select an internal reference panel for genotype imputation, that is, to sequence a subset of the study sample itself and then to use the sequenced subset as a reference panel for imputing the rest of the study sample. Using reference sequences derived from the study sample can prevent a mismatch in ancestral background between the study population and the reference population. It also enables novel variants distinctive to the study sample to be imputed. Employing sequences from a candidate gene and the 1000 Genomes Project, Fridley et al. (2010) demonstrated the feasibility of imputing genetic variants based on a sequenced proportion of a study sample, and they suggested sequencing “the largest and most diverse” subset. In a theoretical study, Jewett et al. (2012) found that including sequenced haplotypes from the study population in the reference panel improved imputation accuracy, even if the external panel was taken from a closely related population. Here, we develop criteria for the selection of an internal reference panel for genotype imputation. Our goal is to find a sensible approach for choosing an internal reference panel from the study sample, with the aim of (1) maximizing the number of polymorphic sites identified in the study sample and (2) achieving the maximal imputation accuracy.

The identification of maximally diverse subsets of a larger set of individuals has been a goal in other areas of genetics, such as in choosing diverse sets of plant accessions for inclusion in core collections targeted for agronomic development or experimental use (Brown 1989; McKhann et al. 2004; Reeves et al. 2012) and in choosing diverse species sets for biodiversity conservation (Faith 1992; Steel 2005) and genome sequencing (Pardi and Goldman 2005). In selecting a set of imputation templates, we borrow the concept of “phylogenetic diversity”, which, for a given subset of a larger set of taxa, measures the fraction of the total branch length of an evolutionary tree of the larger set that is included in the restriction of the tree to the taxon subset (Faith 1992; Nee and May 1997; Steel 2005). Conditional on a tree of n taxa, Pardi and Goldman (2005) and Steel (2005) proved that among all possible subsets of size m ≤ n taxa from the larger set, the globally maximal phylogenetic diversity can be obtained by a greedy algorithm. This greedy algorithm provides a computationally efficient solution to a form of combinatorial optimization problem that can usually be solved only via exhaustive analysis of all possible subsets. Further, if it becomes possible for investigators to increase the number of sequenced samples, for example, by an increase in budget, then the greedy algorithm guarantees that all of the previously selected individuals will be included in the larger optimal subset (Pardi and Goldman 2005).

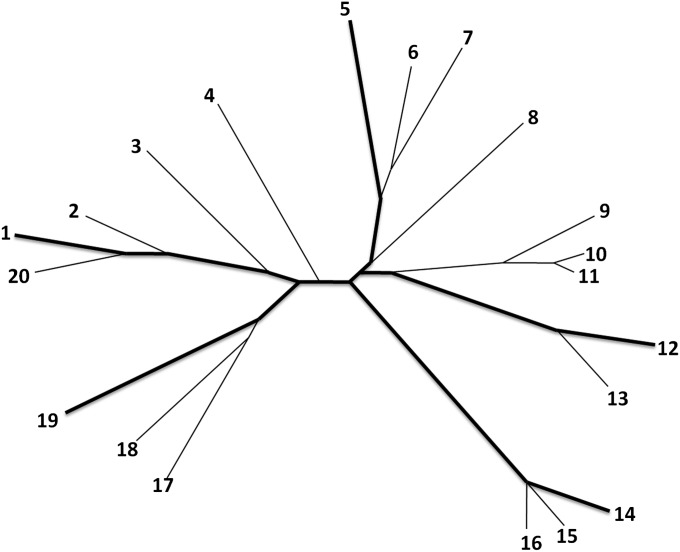
We propose the use of the most diverse reference panel for genotype imputation, adapting the greedy algorithm for maximizing phylogenetic diversity in our selection of an internal reference panel. We assume phased diploid individual genotypes are available, as phasing is not our focus. We approximate the ancestral relationships of haplotypes by constructing a neighbor-joining phylogenetic tree (Saitou and Nei 1987), using the pairwise Hamming distance matrix between the haplotypes in a study sample (Figure 1). We next apply the greedy algorithm of Pardi and Goldman (2005) and Steel (2005) to identify the subset at a given size with the maximal phylogenetic diversity conditional on the tree. The haplotypes chosen by our method are spread across the tree and tend to have long external branch lengths (Figure 1, thick lines), as our method prioritizes individual sequences that are more differentiated. We expect that in comparison with a random subset, the subset that is most phylogenetically diverse at the genotyped markers also carries a larger number of polymorphic sites that can be identified by sequencing and that are then available for imputation into the remaining sample when this subset is used as a reference panel. Thus, it can be predicted that this strategy enables more variants to be imputed in the study sample than does the use of a randomly selected reference panel.

Figure 1.

Illustration of the selection of the most phylogenetically diverse reference panel. Shown is the phylogenetic tree constructed from 20 simulated haplotypes as well as the most diverse subset of five taxa (thick lines). The selection algorithm first selects the most distant pair of taxa and then identifies haplotypes that are most distant conditional on the haplotypes already selected. To choose the five taxa, the greedy algorithm first selects pair 1 and 14 and then 12, 19, and 5 sequentially. Note how the haplotypes chosen are spread across the tree and possess long branch lengths.

To evaluate the performance of our “most diverse reference” panel in genotype imputation, we simulate sequences and create study samples similar to those observed in GWAS by masking the genotypes for a number of single-nucleotide polymorphisms (SNPs). We then impute the masked genotypes in the study sample by using either the most diverse reference panel or randomly selected reference panels. We also apply the “most diverse” method to sequences of European ancestry from the 1000 Genomes Project. The results from both the simulated sequences and the 1000 Genomes sequences show that the most diverse reference panel consistently provides higher imputation accuracy, independent of imputation lengths, reference panel sizes, and marker densities in the study sample. We thus provide a cost-effective strategy for designing sequencing studies for samples with existing genome-wide genotype data. As of 2013, thousands of GWAS have been performed, with >1 million genotyped individuals (http://www.genome.gov/gwastudies/). Effective use of these genotype data will make it possible to carry out large-scale sequencing studies on these individuals in silico with a limited budget.

Materials and Methods

Phylogenetic diversity

We use notation similar to that of Steel (2005). Assume a study sample T of n haploid individuals, each containing q polymorphic sites that are genotyped for k < q variable sites (referred to as markers) in a region of interest. We consider haploid data (phased diploid individuals for humans), as we do not focus on phasing. Based on the genotypes at those k markers, we aim to identify a subset $S \subset T$ of size m ≤ n to be sequenced. Sequencing reveals r ≤ q − k additional variable sites in the m individuals. S is then used as a reference panel to impute the genotypes of these r sites in the remaining n − m individuals in the study sample T.

To identify the optimal selection of S, let X_T be an unrooted tree constructed using all haplotypes in T on the basis of the k markers. Let λ_T be the sum of the branch lengths for all edges of X_T. We denote by X_S the induced tree obtained by restricting X_T to only the haplotypes in S and by λ_S the sum of the branch lengths of X_S. For m ≥ 2, we define the size-m subset of T with maximal phylogenetic diversity as pd_m:

$$p{d}_m=\text{arg max}\left\{{\lambda }_S:S\subseteq T\text{and}\left|S\right|=m\right\}.$$

Identifying the subset with maximal diversity

To find pd_m, we first generate an unrooted tree from the study sample T. Based on the genotypes of the k markers, we compute the Hamming distances between individual haplotypes and construct a pairwise distance matrix for T. Using this distance matrix, we construct a tree using the neighbor-joining (NJ) method, which recursively agglomerates pairs of nodes until all nodes have been incorporated into the tree (Saitou and Nei 1987). On this tree, we apply a greedy algorithm to identify the subset S with size m that has the maximal phylogenetic diversity. Briefly, we first select the pair of haplotypes with the greatest distance on the tree and add the pair to S. We then sequentially incorporate as the next haplotype in S the haplotype that adds the maximal length to the chosen tree at that step, repeating the process until S reaches size m. Pardi and Goldman (2005) and Steel (2005) proved that conditional on the tree, the subset chosen according to this greedy algorithm has the maximal phylogenetic diversity.

Simulations

We analyze simulated data sets to evaluate the performance of the “most diverse reference panel” in genotype imputation. We independently generate 50 data sets of 2000 haplotypes each with the program ms, a coalescent-based sequence sampling program, under the neutral Wright–Fisher model (Hudson 2002). We assume a basic population-genetic model with constant effective population size N_e = 10,000, a mutation rate µ = 1.0⁻⁸ per site per generation, and a recombination rate ρ = 1.0⁻⁸ per site per generation. We remove singletons from the simulated sequences to create the “true” imputable sequence data. All simulated sites are assumed to have at most two alleles. Emulating the density of current genotype arrays, we select the marker panel of the study sample (the “genotype data”) by randomly choosing 300 markers per megabase that have minor allele frequency (MAF) > 0.1 in the sequence data. We mask the genotypes for the remaining sites, which become the set of sites that will be imputed. We simulate haplotypes of length 1 Mb, imputing the middle 100 kb while keeping the genotypes for the marker panel in both 450-kb flanking regions to improve imputation accuracy and to avoid edge effects (Li et al. 2010). Based on these simulated marker genotype data sets, we apply our algorithm on the marker panel to obtain the most diverse reference panels of 200 haplotypes. To evaluate the performance of the most diverse reference panel, for each of the 50 simulated data sets, we generate 1000 random reference panels, by sampling without replacement 200 haplotypes each from the sequence data for comparison. Additionally, to model diploid samples, we assume that if one of the two chromosomes in a diploid individual is in the panel of most diverse haplotypes, both chromosomes are sequenced. We form the “diverse diploid panel” by ranking haplotypes with the greedy algorithm and incorporating diploid individuals into the panel who carry at least one of the top ranked haplotypes until we reach the number of diploid individuals we plan to sequence (100 in experiments that compare to the 200 most diverse haplotypes). In each selected reference panel, we unmask all imputable sites and use the resulting sequences as references for genotype imputations. For each data set, we perform one imputation with the most diverse reference panel, one imputation with the diverse diploid reference panel, and one imputation with each of the 1000 randomly selected reference panels.

To evaluate the impact of our parameter choices, we modify this basic design by changing the length of the imputation target, the reference panel size, and the number of genotyped SNPs in a study sample while maintaining the other parameters fixed as described above. We consider imputation target lengths of 100 kb, 500 kb, 1 Mb, and 2 Mb, each time adding 450-kb flanking regions. We select reference panel sizes of 100, 200, 300, 400, and 500 haplotypes among a total of 2000 haplotypes. We also vary the number of genotyped markers from 300 to 1000 in a 1-Mb region in a study sample. For each scenario, we simulate 50 data sets of 2000 haplotypes each. For each data set, we perform one imputation with the most diverse reference panel and 50 imputations with randomly selected reference panels.

Based on previous comparisons among imputation methods (Hao et al. 2009; Nothnagel et al. 2009; Pei et al. 2010), we employ minimac (Howie et al. 2012) as one of the best-performing methods. This method is an extension of MaCH (Li et al. 2010) for phased diploid data. To assess imputation accuracy on heterozygous genotypes, we then create n/2 diploid individuals by randomly combining pairs of haplotypes from the entire study sample. After imputation, we evaluate the predicted imputation accuracy by examining for each selected reference panel the mean of the estimated correlation coefficient ${\widehat{r}}^2$ across all markers. To evaluate the imputation accuracy of the r imputed sites for the n/2 diploid individuals in the imputed data sets, we compute two measures for the discordance rate between the imputed genotypes ${\widehat{g}}_{ij}$ and the simulated genotypes $g_{ij}$ at variant site j in target individual i. We allow ${\widehat{g}}_{ij}$ and $g_{ij}$ to equal 0, 1, and 2, based on their numbers of copies of one specific allele. First we calculate the discordance rate D across all sites:

$$D=\frac{{{\displaystyle \sum }}_{i=1}^{n/2}{{\displaystyle \sum }}_{j=1}^r|g_{ij}-{\widehat{g}}_{ij}|}{nr}.$$

As this error function is strongly affected by the minor allele frequencies of the variant sites examined (Huang et al. 2009), we also calculate imputation errors across all heterozygous genotypes ($g_{ij}=1$):

$$H=\frac{{{\displaystyle \sum }}_{i=1}^{n/2}{{\displaystyle \sum }}_{j=1}^r{1}_{g_{ij}=1}|g_{ij}-{\widehat{g}}_{ij}|}{2{{\displaystyle \sum }}_{i=1}^{n/2}{{\displaystyle \sum }}_{j=1}^r{1}_{g_{ij}=1}}.$$

Note that the evaluations use all n/2 simulated diploid individuals, both those with one or two haplotypes in the reference panel and those with two haplotypes that are imputed.

The 1000 Genomes Project data

We apply our method to sequence data from the 1000 Genomes Project. We consider the phased data of 381 diploid individuals (762 haplotypes) with European (EUR) ancestry, including 87 Utah residents with Northern and Western European ancestry (CEU), 93 Finnish from Finland (FIN), 89 British from England and Scotland (GBR), 14 Iberian populations in Spain (IBS), and 98 Toscani in Italy (TSI) (http://www.sph.umich.edu/csg/abecasis/MACH/download/1000G-PhaseI-Interim.html, the 1000G Interim Phase I Haplotypes 11/23/2010 release). We remove singletons from the sample, selecting eight 100-kb regions that are approximately evenly distributed across chromosome 20. We create study samples, using a similar procedure to that for the simulation above: for each region, we add a 450-kb flanking region on each side, randomly choose ∼300 genotyped SNPs per megabase among markers with MAF ≥ 0.1, and mask the genotypes of all other sites. In each region, we select the most diverse 160 haplotypes from the set of 762 total haplotypes as the diverse reference panel. For comparison, we sample without replacement 1000 random reference panels of 160 haplotypes each.

We next consider the entire chromosome 20 and create a study sample, using the same procedures as in the 100-kb regions. We select the most diverse reference panel using our method and 50 reference panels randomly without replacement. Using the selected reference panels, we impute all the masked genotypes and compute the discordance rate for each imputation.

Results

Number of imputed sites

Polymorphic sites in reference panels:

Only sites that are polymorphic in the reference panel can be imputed into the remaining study sample. Hence, we first evaluate the number of polymorphic sites in the reference panels selected. For each of the 50 simulated data sets, we choose one random reference panel and compare it to the most diverse reference panel. We find that for a total of 12,957 masked sites that are polymorphic in the study samples across the 50 data sets, 9642 sites (74.41%) are polymorphic in both types of reference panels. Among the remaining sites, 1492 sites (11.52%) are polymorphic only in the most diverse reference panels, whereas 760 sites (5.87%) are polymorphic only in the randomly selected reference panels. Thus, on average, 5.65% more sites are polymorphic in the most diverse reference panels than in the randomly selected reference panels.

Polymorphic sites in imputed data sets:

To ensure that the higher number of polymorphic sites in the most diverse reference panels also leads to a higher number of imputed polymorphic variants, we count the number of imputed sites that are polymorphic in data sets imputed with reference panels generated under three different selection strategies: (1) sampled at random, (2) selecting the 200 most diverse haplotypes, and (3) selecting the diploid individuals carrying the most diverse haplotypes (diverse diploid reference panel). As it is not currently practical to sequence only one chromosome in a diploid individual, strategy 3 represents a scenario in which the individuals that carry the most diverse haplotypes are identified and both of their chromosomes are sequenced.

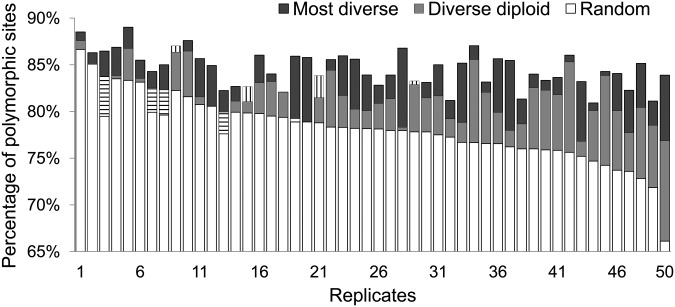
From the total of 12,957 imputed sites across the 50 data sets, 10,952 are polymorphic in data sets imputed with the most diverse reference panels (84.53%), 10,574 are polymorphic for the diverse diploid reference panels (81.61%), and 10,151 are polymorphic for randomly selected reference panels (78.34%). Figure 2 shows percentages of polymorphic sites in data sets imputed with the three reference types across the 50 data sets. In each of the 50 data sets, imputation with the most diverse reference panel captures more polymorphic sites than imputation with the random reference panel. The improvement by using the most diverse panel is greater when the randomly selected panel captures only a low percentage of polymorphic sites (e.g., replicates 46–50). Imputations with the diverse diploid panels result in higher percentages of polymorphic sites than with the random panels in 42 of the 50 data sets (84%) and in a higher percentage of polymorphic sites than with the most diverse panel in 4 of the 50 data sets (8%). Only in 4 data sets does the random reference panel perform substantially better than the diverse diploid reference panel (replicates 1, 2, 3, and 6) and in all these cases, the random panel captures a high (>83%) percentage of polymorphic sites.

Figure 2.

Percentages of polymorphic sites in data sets imputed with different types of reference panels for 50 data sets (replicates). The open bar represents the accuracy of a random panel, the shaded bar represents the accuracy of the diverse diploid panel, and the solid bar represents the accuracy of the most diverse reference panel. If the performance of the diverse diploid reference panel is lower than the performance of the random reference panel, this difference is indicated by the part of the open bar with horizontal stripes. If the accuracy of the diverse diploid panel is higher than the accuracy of the most diverse panel, this difference is indicated by the part of the shaded bar with vertical stripes. Data are sorted in decreasing order by percentage of polymorphic sites recovered by imputations with random reference panels.

Imputation accuracy

As a measurement of imputation accuracy, we evaluate the discordance rate between the simulated genotypes and the imputed genotypes for the 50 simulated data sets. For each data set, we compare the accuracy of the imputation using the most diverse reference panel to the empirical distribution of imputation accuracies from 1000 random reference panels.

Estimated imputation quality:

A predictor for the accuracy of an imputed site generated by minimac is the ${\widehat{r}}^2$, a quantity calculated by comparing the variance of observed genotype scores with the variance of expected genotype scores to estimate the squared correlation at a marker between the true allele counts and the estimated allele counts (Li et al. 2010). To compare this predicted imputation accuracy between the different choices of reference panels, we compute the average ${\widehat{r}}^2$ across the 12,957 total imputed sites across the 50 data sets. For imputations with the most diverse reference panels and the diverse diploid reference panels, we generate one value of ${\widehat{r}}^2$ for each site; to evaluate imputations with the 1000 randomly selected reference panels for each data set, we compute the mean ${\widehat{r}}^2$ for each site across 1000 imputations, and we then calculate the average across all imputed sites. Sites imputed with the most diverse reference panels have the highest mean ${\widehat{r}}^2$ (0.784), followed by sites imputed with the diverse diploid reference panels (0.758). Sites imputed with randomly selected reference panels have the lowest mean ${\widehat{r}}^2$ (0.723). As removing variant sites with ${\widehat{r}}^2<0.3$ filters most poorly imputed sites (Li et al. 2009), we also compare the number of sites that pass this imputation quality threshold. Across the 50 data sets, we observe that a higher percentage of sites imputed with the most diverse reference panels pass the threshold (83.17%) compared to sites imputed with the diverse diploid reference panels (80.53%) and sites imputed with the randomly selected panels (77.48%). For a higher ${\widehat{r}}^2$ threshold of 0.8 applied by typical association studies, 76.63% of sites pass the threshold for imputations with the most diverse reference panels, 74.76% for the diverse diploid reference panels, and 59.65% for the randomly selected reference panels.

Discordance rates:

For each simulated data set, we separately calculate discordance rates for all sites imputed with the most diverse reference panel, sites imputed with the diverse diploid reference panel, and the mean values for sites imputed with random reference panels, where the mean is taken across all 1000 random panels. Using the most diverse reference panel results in the lowest mean discordance rate across the 50 replicates (0.0019), followed by imputation with the diverse diploid reference panel (0.0022). Both quantities are lower than the mean discordance rates of imputation with the random reference panels (0.0031) (Figure 3). Ranking the discordance rate of selected reference panels together with the discordance rates of 1000 random panels from the lowest to the highest value, the most diverse reference panel is a clear outlier for 24 of the 50 data sets (48%), having a lower discordance rate than imputations with all 1000 randomly selected reference panels (rank 1). Across all 50 data sets, the mean rank of the most diverse reference panel is 13.5, ranging from 1 to 135 among 1001 panels. Across the same 50 data sets, the mean rank of the diverse diploid reference panel is 111.9, ranging from 1 to 906 among 1001 panels.

Figure 3.

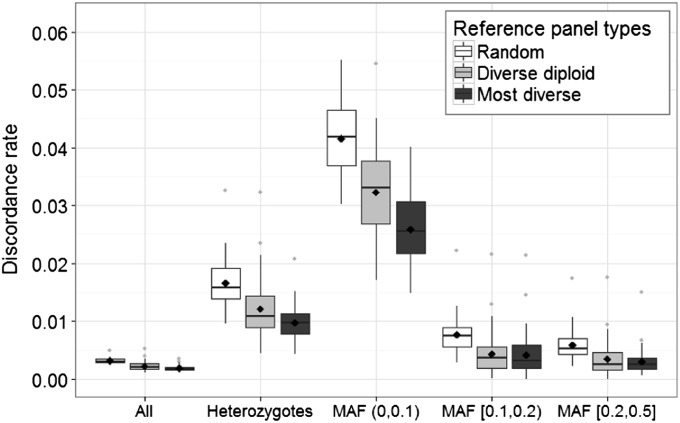
Box plots of discordance rates between imputed genotypes and simulated genotypes for imputations with randomly chosen reference panels, diverse diploid reference panels, and most diverse reference panels. The mean discordance rate across the 50 replicates for each comparison group is indicated by a diamond, and the median discordance rate across the 50 replicates for each comparison group is indicated by a middle line. The horizontal axis labels the comparison on the basis of all sites (All), all heterozygote sites (Heterozygotes), and heterozygotes in different MAF groups in the simulated sequence data.

To generate a more meaningful discordance measure for low-frequency variants, we compare the imputed genotypes and the simulated true genotypes across sites for which the true genotypes are heterozygotes. While the heterozygote discordance rate is higher than the overall discordance rate, the mean heterozygote discordance across the 50 replicates is again the lowest for sites imputed with the most diverse reference panels (0.0097), followed by the diverse diploid reference panels (0.0121) and the random reference panels (0.0165). Comparing across frequency bins, we observe that for all reference selection strategies, the heterozygote discordance rate decreases with increasing allele frequency. The mean heterozygote discordance rate across the 50 replicates for low-frequency variant sites (0 < MAF < 0.1) is considerably higher than the overall mean discordance rate for all heterozygote sites across the 50 replicates (0.0258 for the most diverse reference panels, 0.0329 for the diverse diploid reference panels, and 0.0415 for the random reference panels). In all frequency bins, considering heterozygote discordance rates, imputations with the most diverse reference panels generate the lowest discordance rates and imputations with the randomly selected reference panels generate the highest discordance rates, while imputations with the diverse diploid reference panels generate intermediate discordance rates (Figure 3). Combining the heterozygote discordance rate of the most diverse reference panel with the heterozygote discordance rates of 1000 random panels for each of the 50 simulated data sets and ranking from the lowest to the highest heterozygote discordance rate, the mean rank of the most diverse panel across all 50 data sets is 17.5 when comparing all heterozygote sites, 27.3 for sites with 0 < MAF < 0.1, 115.7 for sites with 0.1 ≤ MAF < 0.2, and 68.5 for sites with 0.2 ≤ MAF ≤ 0.5 among 1001 panels ranked. When comparing the diverse diploid reference panel to random panels, the mean rank across all 50 data sets is 147.9 for all heterozygote sites, 188.0 for sites with 0 < MAF < 0.1, 163.9 for sites with 0.1 ≤ MAF < 0.2, and 145.9 for sites with 0.2 ≤ MAF ≤ 0.5.

Imputation accuracy under different simulation settings

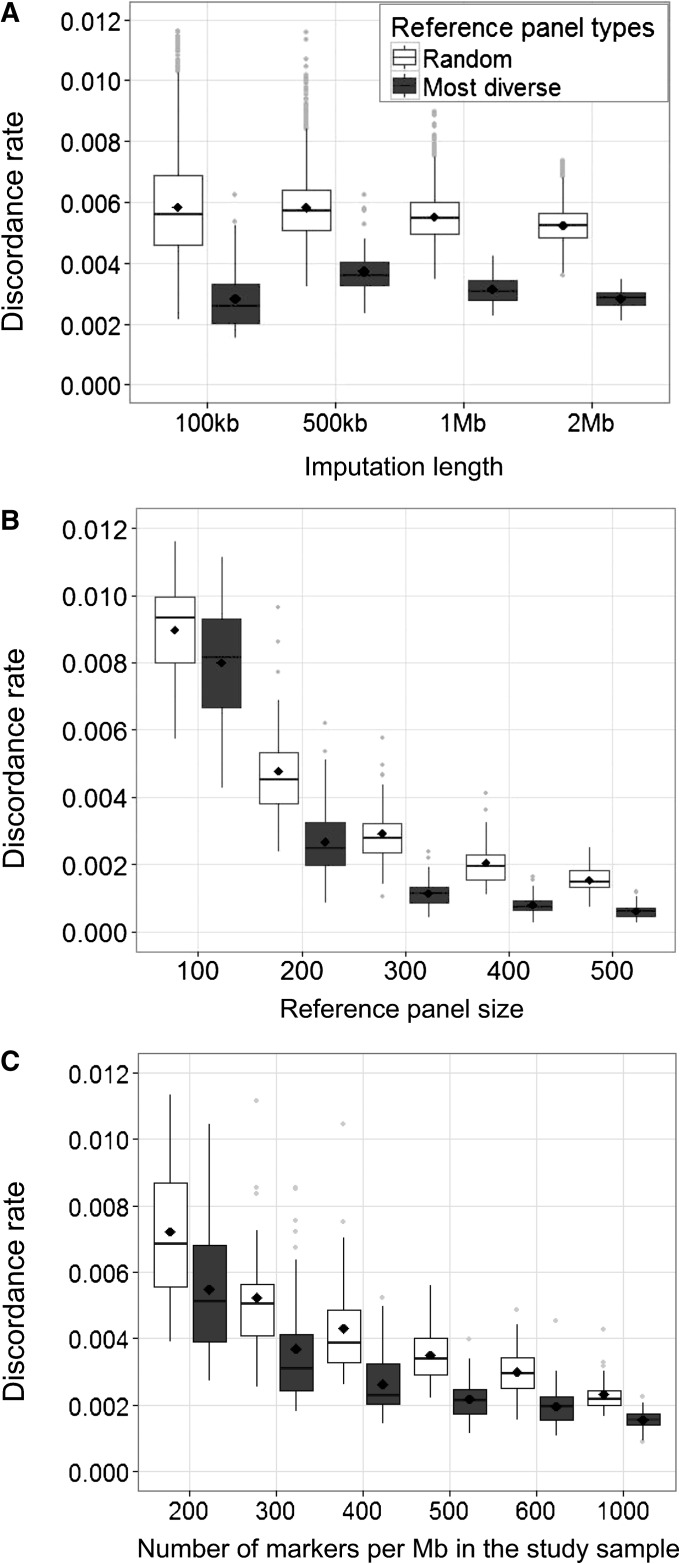
To assess the robustness of our results, we evaluate the performance of the most diverse reference panel under different simulation settings, considering different target sequence lengths, different reference panel sizes, and different marker densities in the study sample. We first investigate whether the lengths of the target regions affect the performance of the most diverse reference panels in imputations. We impute regions with lengths of 100 kb, 500 kb, 1 Mb, and 2 Mb, using both the most diverse reference panel and 50 random reference panels, each of which is compared to the true underlying genotypes; the mean of the 50 discordance rates is then compared with the discordance rate for the most diverse reference panel. As shown in Figure 4A, across the four different lengths, we observe little effect of the imputation length on the discordance rate. The mean discordance rate across the 50 replicates for each group ranges from 0.0028 (2 Mb) to 0.0037 (500 kb) for the most diverse reference panel and from 0.0052 (2 Mb) to 0.0058 (100 kb) for the random reference panels. For all sequence lengths considered, the most diverse reference panels provide lower discordance rates than the randomly selected reference panels.

Figure 4.

Box plots of discordance rates between imputed genotypes and simulated genotypes for imputations with randomly chosen reference panels and most diverse reference panels with varying simulation settings. (A) Imputation length. (B) Reference panel size. (C) Number of genotyped markers per megabase in the study sample. For each data set, we examine the mean of 50 random reference panels and the most diverse reference panel. The mean discordance rate across the 50 replicate simulated data sets for each comparison group is indicated by a diamond, and the median discordance rate is indicated by a middle line.

Second, we evaluate how the reference panel sizes affect the performance of the most diverse reference panel by comparing the genotype discordance rates for reference panels of size 100, 200, 300, 400, and 500 haplotypes. For both reference panels, the mean discordance rate across the 50 replicates decreases with larger reference panel sizes, from 0.008 to 0.0006 for the most diverse panel and from 0.009 to 0.0015 for the random reference panels. Especially for a reference panel of size 100 individuals, the discordance rate is considerably higher than for larger panel sizes. Across all reference panel sizes, imputations with the most diverse reference panels consistently provide lower discordance rates than do imputations with the randomly selected reference panels (Figure 4B).

Third, we examine how the number of markers genotyped initially in the study sample affects the performance of the most diverse reference panel by varying the density of markers in the study sample, considering 200, 300, 400, 500, 600, and 1000 markers per 1-Mb region. For both types of reference panels, the mean discordance rate across the 50 replicates decreases with a higher density of markers in the study samples, from 0.0055 to 0.0015 for the most diverse panel and from 0.0072 to 0.0023 for the random reference panels. Across all marker densities in the study sample, the most diverse reference panels consistently provide lower discordance rates than the randomly selected reference panels (Figure 4C). We also observe that the improvement in discordance rates for the most diverse reference panel over the randomly selected panels slightly decreases with more markers genotyped in the study sample.

Allele frequency bias and genotyping error

As the most diverse panel incorporates more variable sites than a randomly selected panel, it is plausible that the allele frequencies in the data sets imputed using the most diverse panel might systematically differ from allele frequencies in the simulated data sets or from those in data sets imputed using the randomly selected panels. To confirm that there is no such allele frequency bias, we compute allele frequency estimates in data sets imputed by the most diverse panels and data sets imputed by the random panels and compare them to the true allele frequencies in the simulated data sets.

We first estimate the bias for each type of reference panel by calculating the difference between the estimated and the true allele frequency for each locus and then averaging this difference across all loci in a MAF bin. As shown in Table 1, both imputation with a random panel and imputation with the diverse panel generate a subtle underestimate of allele frequency. The mean biases across loci from data sets imputed using the most diverse panel are smaller than the mean biases from data sets imputed with random panels for every MAF bin except the bin with 0.1 < MAF ≤ 0.5. Second, we calculate the mean squared error (MSE) of the estimated MAF for each locus and each reference panel and then calculate the average MSE in each MAF bin. The MSEs in data sets imputed with the most diverse panels are smaller than the MSEs in data sets imputed with the randomly selected panels across all loci and in every MAF bin except for the bin with 0.05 < MAF ≤ 0.1. Based on these results, we show that the most diverse panel provides less bias and more confident estimates of allele frequencies than a randomly selected panel, especially for less common variants.

Table 1. Mean bias and mean squared errors (MSEs) of the imputed genotypes for a total n = 12,957 markers from the 50 data sets.

	Variant groups
Reference types	MAF (0, 0.01]	MAF (0.01, 0.05]	MAF (0.05, 0.1]	MAF (0.1,0.5]	Overall
n	3,946	3,251	1,625	4,135	12,957
Most diverse
Mean bias	6.64 × 10−4	8.85 × 10−4	1.04 × 10−4	3.62 × 10−4	5.53 × 10−4
MSE	3.33 × 10−5	5.31 × 10−5	3.36 × 10−5	3.79 × 10−5	3.98 × 10−5
Random
Mean bias	1.41 × 10−3	1.22 × 10−3	9.42 × 10−4	8.15 × 10−5	8.81 × 10−4
MSE	3.56 × 10−5	9.50 × 10−5	1.12 × 10−5	9.84 × 10−5	8.02 × 10−5

The mean bias is calculated by ${{\displaystyle \sum }}_{i=1}^n({\text{MAF}}_{\text{sim}}-{\text{MAF}}_{\text{imp}})/n$ and MSE by ${{\displaystyle \sum }}_{i=1}^n{({\text{MAF}}_{\text{sim}}-{\text{MAF}}_{\text{imp}})}^2/n$. Shown here are the mean bias and the MSEs for different MAF bins as well as for all the imputed markers.

To evaluate the robustness of the most diverse reference algorithm to the presence of genotyping errors, we introduce genotype error uniformly at random to each of the 50 simulated genotype data sets and generate the most diverse subset based on the modified genotypes. We evaluate the selected subset by comparing a measure of its true diversity to that of the corresponding diversity of the subset generated without genotyping error.

For each of the 50 simulated data sets, we introduce genotyping error uniformly at random, using rates of 0.1%, 0.5%, and 1% for each site in the study samples, and we generate one new data set at each of the error rates. We then select a new most diverse subset of size 200 haplotypes for each of the data sets with genotyping error. After that, we compute the subtree length of the new diverse subset on the tree constructed with imperfect genotyping (imperfect subtree) and compare it to the subtree length of the original diverse set generated without genotyping error (optimal subtree). Our results show that with a genotyping error rate of 0.10%, the length of the imperfect subtree is nearly identical to the length of the optimal subtree (ranging between 99.65% and 100% of the optimal subtree length, with a mean of 99.99%). For a genotyping error rate of 0.50%, the length of the imperfect subtree ranges between 92.14% and 99.3% of the optimal subtree length, with a mean of 96.65%. For a genotyping error rate of 1%, the length of the imperfect subtree ranges from 90.11% to 98.29% of the optimal subtree length, with a mean of 94.67%. The reduction of subtree length caused by genotyping error is small when comparing to the subtree length reduction from a diverse subset to that from a random subset; for 50 simulated data sets, the length of a random subtree ranges from 56.80% to 75.37% of the optimal subtree, with a mean of 67.02%. Considering that study samples from genotyping arrays usually have a very low genotyping error (e.g., <0.1%) (Illumina 2010), our simulation results show that while the selection of the most diverse subset is affected by genotyping error, even with substantial genotyping error, the selected panel is still substantially more diverse than a random reference panel. This result is reminiscent of the result of Atteson (1999), who proved that the consistency of neighbor joining is robust to a certain degree of noise in the distance matrix, in that the method can still construct a correct tree when distances obtained on the basis of that tree are slightly perturbed.

Imputation accuracy on data from the 1000 Genomes Project

We apply our method to real sequence data of 381 phased individuals with EUR ancestry from the 1000 Genomes Project. Considering eight 100-kb regions across chromosome 20, we impute 3215 sites after removing singletons. Sites imputed with the most diverse reference panels have a mean ${\widehat{r}}^2$ of 0.749 across sites. Sites imputed with the 1000 randomly selected reference panels have a mean ${\widehat{r}}^2$ of 0.741. Slightly more sites pass the imputation quality threshold of ${\widehat{r}}^2$ ≥ 0.3 for the most diverse reference panels (85.75%) than for the randomly selected reference panels (84.23%). When applying a higher imputation threshold of ${\widehat{r}}^2$ ≥ 0.8, a similar percentage of sites pass the threshold for the most diverse reference panels (62.74%) and the randomly selected reference panels (62.89%).

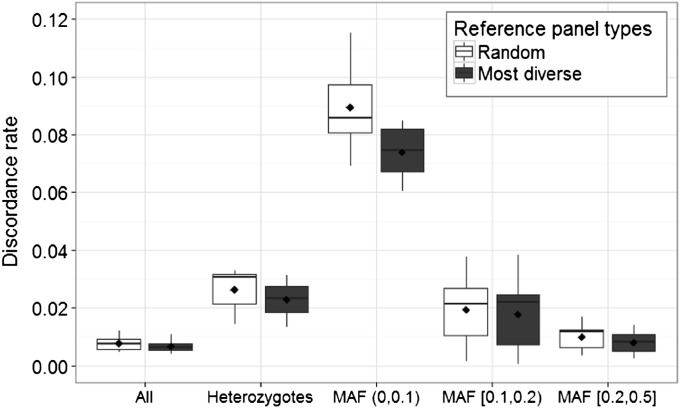
Considering all imputed sites for the eight 100-kb regions, the most diverse reference panels result in a lower mean discordance rate across the eight regions (0.0067) than that of the randomly selected reference panels (0.0077). When comparing imputed sites that are heterozygotes in real sequenced data sets, sites imputed with the most diverse reference panels have a lower mean discordance rate across the eight regions (0.0228) than sites imputed with the randomly selected reference panels (0.0262). The lower discordance rates from the most diverse reference panels are observed across all frequency bins for heterozygote sites. For sites with 0 < MAF < 0.1, the mean discordance rate across the eight regions is 0.074 using the most diverse reference panels vs. 0.0895 using random reference panels; for sites with 0.1 ≤ MAF < 0.2, the mean discordance rate across the eight regions is 0.0177 vs. 0.0193, and for sites with 0.2 ≤ MAF ≤ 0.5, the mean discordance rate across the eight regions is 0.0080 vs. 0.0099 (Figure 5). However, we also note that the performance of the most diverse reference panel varies widely across the eight regions. When ranking the discordance rate of the imputation by the most diverse reference panel with the discordance rates of the 1000 imputations by randomly selected reference panels from the lowest to the highest value for each of the eight regions, the most diverse reference panel has a mean rank of 116.1 across the eight regions, ranging from 3 to 496 of 1001 panels ranked. For heterozygote sites, the most diverse reference panel has a mean rank of 156.7, ranging from 1 to 508; for heterozygotes in different MAF bins, the most diverse reference panel has an average rank of 242.7 for sites with 0 < MAF < 0.1, an average rank of 311.0 for sites with 0.1 ≤ MAF < 0.2, and an average rank of 129.4 for sites with 0.2 ≤ MAF ≤ 0.5 among 1001 panels ranked.

Figure 5.

Box plots of discordance rates between imputed genotypes and simulated genotypes for imputations with randomly chosen reference panels and most diverse reference panels for eight 100-kb regions on chromosome 20. We analyzed 762 haplotypes of European ancestry from the 1000 Genomes Project. The horizontal axis represents the comparison of all sites (All), all heterozygote sites (Heterozygotes), and heterozygotes in different MAF groups in the simulated sequence data. The mean discordance rate across the eight regions for each comparison group is indicated by a diamond, and the median discordance rate across the eight regions for each comparison group is indicated by a middle line.

For the whole-chromosome 20 data, the sequence data set contains 259,618 sites after removing singletons. We select 18,000 sites with MAF ≥ 0.1 as “genotyped” markers and mask the genotypes for the remaining 241,618 sites to create a study sample. Based on the genotyped markers, we select the most diverse reference panel to impute the genotypes of the masked sites. For comparison, we sample 50 reference panels at random. We first compare the number of masked sites that are polymorphic in the selected reference panels. In the most diverse reference panel, 211,480 masked sites are polymorphic (87.53%), compared to an average of 210,137 across the 50 random reference panels (86.97%). After imputation, we observe that the imputation with the most diverse reference panel has 201,831 sites with ${\widehat{r}}^2$ ≥ 0.3 (83.53%), whereas 200,609 sites have mean ${\widehat{r}}^2$ ≥ 0.3 with a randomly selected reference panel (83.03%). For the higher imputation quality threshold of ${\widehat{r}}^2$ ≥ 0.8, 142,996 sites pass the threshold for the imputation with the most diverse reference panel (59.18%), whereas averaging 142,281 sites across imputations with the 50 randomly selected reference panels passes the threshold (58.89%). Moreover, sites are imputed with slightly higher accuracy with the most diverse reference panel than with random reference panels (Table 2). The discordance rate of the most diverse panel is lower than that of all except 2 of the 50 random panels (rank 3). To evaluate the imputation accuracy in different frequency bins, we again consider discordance rates of heterozygote genotypes. When ranking the discordance rate of the imputation by the most diverse reference panel with the discordance rates of the 50 imputations by randomly selected reference panels from the lowest to the highest value, we observe that the most diverse reference panel has a lower discordance rate than all 50 random panels (rank 1). Examining separate frequency bins, the most diverse reference panel has rank 4 for sites with 0 < MAF < 0.1, rank 3 for sites with 0.1 ≤ MAF < 0.2, and rank 14 for sites with 0.2 ≤ MAF ≤ 0.5. Averaging across sites, the numerical improvement in imputation accuracy by using the most diverse panel is modest, reducing imputation errors by 1% across all sites and by 2.3% at less common variants with 0 < MAF < 0.1.

Table 2. Discordance rates for genotype imputations with different reference panels, using chromosome 20 data with European ancestry in the 1000 Genomes Project.

	Variant groups
Reference types	All	Heterozygotes	MAF (0, 0.1)	MAF [0.1, 0.2)	MAF [0.2, 0.5]
Most diverse	1.02	3.53	10.31	2.77	1.92
Random
Mean	1.03	3.57	10.45	2.82	1.93
Standard deviation	0.004	0.019	0.076	0.019	0.014
Rank of the most diverse	3	1	4	3	14

Discordance rates are shown as percentages. We split 381 phased diploid individuals into a target sample of 301 target individuals and a reference panel of 160 haplotypes. Shown here are results from one imputation with the most diverse reference panel and the mean and standard deviation of the discordance rates from 50 imputations with randomly selected reference panels. We ranked discordance rates of the most diverse panel together with those of 50 random reference panels from the lowest to the highest value and display the rank of the most diverse panel.

Discussion

The cost reduction in modern sequencing technology enables investigators to generate a reference panel for genotype imputation by sequencing a subset of the study sample. We have proposed a selection strategy for such an internal reference panel by adapting an algorithm based on phylogenetic diversity. In simulated sequence data, our method consistently outperforms randomly selected reference panels, in that it provides higher imputation accuracy and recovers more polymorphic sites from the study sample. This improved performance holds across different imputation lengths, different reference panel sizes, and different marker densities in the study sample. Upon analyzing real sequence data with European ancestry from the 1000 Genomes Project, the most diverse reference panel provides higher imputation accuracy than do randomly selected reference panels. We observe this improved performance when imputing eight 100-kb regions on chromosome 20 and when imputing the entire chromosome 20, indicating that our method can be used to select reference individuals for imputing smaller target regions as well as for imputing the entire genomes. Our method may be particularly advantageous for imputing less common variants, as we found in our simulations that the most diverse reference panels incorporate more polymorphic sites than do randomly selected reference panels. Moreover, the accuracy gain from using the most diverse reference panel instead of randomly selected reference panels is greater for less common variants (e.g., 0 < MAF < 0.2) than for more common variants (e.g., MAF ≥ 0.2) (Table 2).

Comparable methods have been suggested by Pasaniuc et al. (2010) and Kang and Marjoram (2012). Pasaniuc et al. (2010) select an imputation template from an external data set based on similarity between haplotypes in the external data set and each individual haplotype in the study sample. Our method differs from that of Pasaniuc et al. (2010) in two major aspects. First, we select template individuals based on maximal differences among the template individuals, whereas Pasaniuc et al. (2010) select template individuals based on similarity to the imputation target. Second, as the method of Pasaniuc et al. (2010) is designed to be applied to haplotypes that have already been sequenced, it does not assume that the same reference panel is used for the study sample across the entire genome. Instead Pasaniuc et al. (2010) identify a different reference panel for each short window (e.g., 15 kb) of the target region for each study individual. Kang and Marjoram (2012) recently proposed a similar tree-based sample-selection strategy for next-generation sequencing motivated from the standpoint of coalescent theory instead of phylogenetic diversity. Similarly to our study, they aim to identify the subset with the maximal branch length. Although they use a different tree-building algorithm, they examined a similar greedy method, motivated by coalescent theory. In simulations that examined different marker densities, target imputation region lengths, and reference panel sizes, they found that their algorithm performed well, and we similarly find that our related method performs well under these scenarios. In addition, the work of Pardi and Goldman (2005) and Steel (2005) provides further theoretical justification for the phylogenetic-based method. Taken together, our study and that of Kang and Marjoram (2012) demonstrate the value of sensible use of genealogical relationships among samples to improve experimental design for sequencing studies.

We expect that the most diverse reference panel algorithm can work effectively either on a limited region of the genome or on whole chromosomes, provided the phylogenetic tree based on existing data reasonably captures the ancestral relatedness of the haplotypes in the study sample. This is possible only if the ancestral relatedness can be described well as a tree, a condition that depends on the population-genetic history of the sample and the size of the region of interest. When focusing on a single genomic region, relevant parts of its ancestral process can be approximated as a tree due to limited recombination events. This single tree can be estimated by a subset of genotyped markers, and thus our method can provide useful information for reference panel selection. On the other hand, many uncorrelated trees can be formed to represent the ancestral processes of a large region such as the entire genome. Hence, an approximation with a single tree might not capture many features of the data. In such a scenario, it is less likely that our method will produce a better reference panel than a random sample.

In a structured population, the underlying population structure generates a correlation of ancestries across the entire genome. The resulting clades can be approximated by the tree-building algorithm, and this tree can help in selecting a more diverse reference panel. It is encouraging that in a sample of five European subpopulations, the population structure was sufficient for the most diverse reference panel selected based on the entire chromosome 20 to outperform the randomly selected reference panels. Hence, relatively subtle population structure, such as that found in samples from geographically proximate European countries, is sufficient to create similarities in the underlying ancestral processes that can be captured by the tree-building algorithm and can result in improved reference panel selection. If subpopulations contribute different sample sizes, we expect that our algorithm will usually ensure that at least one haplotype from every subpopulation is included in the reference panel. As the algorithm collects the more diverse haplotypes, it may oversample subpopulations with a small contribution to the overall sample. This will ensure that for each subpopulation, enough haplotypes are in the template for reasonably precise imputation.

Our method is based on a locally estimated phylogenetic tree. The topology of the true underlying genealogy changes across the genome as a consequence of recombination events, and therefore, over long regions, the estimated tree obscures this underlying variability. Because the performance of our method is based on how well the local phylogenetic tree approximates the ancestral relatedness of the study individuals, we expect the gain in imputation accuracy using our method will eventually decrease with increasing length of the imputed region. As expected, the average improvement in imputation accuracy when imputing 100-kb regions is considerably higher than the average improvement across the entire chromosome, reflecting that the ancestry of a 100-kb region is more tree-like than the ancestry of an entire chromosome.

The method of reference panel selection described here can be adapted to address specific study design goals. Our method can be applied to incorporate other criteria in reference panel selection. For example, we have not specifically incorporated phenotype information when selecting reference haplotypes, so the selected reference panel is not guaranteed to include the individuals with traits of interest. To sequence certain individuals because of their phenotypes or other criteria unrelated to their phylogenetic placement, we can apply the selection algorithm conditional on including these individuals in the reference panel. The greedy algorithm still guarantees that the subsequent extension has optimal phylogenetic diversity, as proved by Pardi and Goldman (2005). Similarly, our method can be easily extended to form a reference panel by incorporating sequences partly from the study sample and partly from an external database such as the HapMap Project or the 1000 Genomes Project. For example, we can treat sequences from the HapMap Project as an initial set and apply the greedy algorithm to the study sample as an extension in a similar manner as in analyses treating other inclusion criteria.

We note that our method can be applied to select reference panels in species other than humans. There are many other species for which genomic mapping tools are under development (e.g., Atwell et al. 2010; Hickey et al. 2012; Badke et al. 2013), and indeed, the idea of locally estimating phylogenetic trees has been considered by Wang et al. (2012), who proposed to use a local phylogenetic tree to assess the confidence of imputed genotypes in inbred mice. The confidence in imputation quality is high when a study strain shares one or more genome intervals with the reference sequences, whereas the confidence in imputation accuracy is low when the strain does not share genome intervals with the reference sequences. Wang et al. (2012) suggested that strains with low confidence in imputation accuracy are the ones to sequence to achieve the maximal improvement in imputation accuracy if investigators plan to sequence a subset of the study sample. Our approach can supplement the strategy used by Wang et al. (2012) if only a subset of the low-confidence strains can be sequenced. In that scenario, our algorithm can condition on the strains that are already sequenced or strains imputed with high imputation accuracy, allowing researchers to identify the subset of low-confidence strains that can best be used to impute the full data set.

In summary, we have demonstrated that an innovative method of choosing an internal reference panel—the most diverse reference panel—can be a cost-effective approach for planning sequencing studies with existing genotype array data. The method can readily incorporate a variety of selection criteria, while still guaranteeing the maximal phylogenetic diversity for subsequent selections.

A program to select the most diverse reference panel using the greedy algorithm is available in C++ upon request.