Flooding Enzymes: Quantifying the Contributions of Interstitial Water and Cavity Shape to Ligand Binding Using Extended Linear Response Free Energy Calculations

Abstract

Glutamate racemase (GR) is a cofactor independent amino acid racemase that has recently garnered increasing attention as an antimicrobial drug target. There are numerous high resolution crystal structures of GR, yet these are invariably bound to either d-glutamate or very weakly bound oxygen-based salts. Recent in silico screens have identified a number of new competitive inhibitor scaffolds, which are not based on d-Glu, but exploit many of the same hydrogen bond donor positions. In silico studies on 1-H-benzimidazole-2-sulfonic acid (BISA) show that the sulfonic acid points to the back of the GR active site, in the most buried region, analogous to the C2-carboxylate binding position in the GR-d-glutamate complex. Furthermore, BISA has been shown to be the strongest nonamino acid competitive inhibitor. Previously published computational studies have suggested that a portion of this binding strength is derived from complexation with a more closed active site, relative to weaker ligands, and in which the internal water network is more isolated from the bulk solvent. In order to validate key contacts between the buried sulfonate moiety of BISA and moieties in the back of the enzyme active site, as well as to probe the energetic importance of the potentially large number of interstitial waters contacted by the BISA scaffold, we have designed several mutants of Asn75. GR-N75A removes a key hydrogen bond donor to the sulfonate of BISA, but also serves to introduce an additional interstitial water, due to the newly created space of the mutation. GR- N75L should also show the loss of a hydrogen bond donor to the sulfonate of BISA, but does not (a priori) seem to permit an additional interstitial water contact. In order to investigate the dynamics, structure, and energies of this water-mediated complexation, we have employed the extended linear response (ELR) approach for the calculation of binding free energies to GR, using the YASARA2 knowledge based force field on a set of ten GR complexes, and yielding an R-squared value of 0.85 and a RMSE of 2.0 kJ/mol. Surprisingly, the inhibitor set produces a uniformly large interstitial water contribution to the electrostatic interaction energy (⟨V^el⟩), ranging from 30 to >50%, except for the natural substrate (d-glutamate), which has only a 7% contribution of ⟨V^el⟩ from water. The broader implications for predicting and exploiting significant interstitial water contacts in ligand–enzyme complexation are discussed.

1. Introduction

Numerous studies have established the bacterial cell wall and the enzymes responsible for its construction as valid targets for broad-spectrum antibiotics.^1,2 An essential enzyme in this class, which has not been targeted by antibiotics, is glutamate racemase (GR), which produces d-glutamate, an essential molecule for a number of pathogenic bacterial species. GR is a member of a family of cofactor-independent racemases and epimerases, which employs 1:1-proton transfer using juxtaposed thiol/thiolate general acid-bases and hydrogen-bonding to the Cα-carboxylate. Previously, GR knockouts have resulted in d-glutamate auxotrophs, validating the essentiality of GR.^3,4 Structure-based,⁵ high-throughput screening (HTS),⁶ and quantative structure–activity relationship (QSAR)⁷ approaches to obtaining active site competitive inhibitors have been problematic for disparate reasons, including flexibility of the enzyme and the inconsistent presence of a hydrophobic pocket proximal to the active site from species to species. Thus, it is highly desirable to obtain effective inhibitory scaffolds against GR, which have favorable drug-like physicochemical properties. A greater understanding of the physical determinants of molecular recognition is the key to directing future efforts.

The essential and conserved active site residues of GR–ligand recognition have been well-established, especially for d-glutamate, by a number of methods, including: sequence conservation,⁸ mutagenesis studies,⁸⁻¹⁰ cocrystal structures,^5,6,11−16 and computational studies.^9,17 These residues include (using B. subtilis numbering): Asp10, Ser11, Cys74, Asn75, Thr76, Cys185, His187 and Thr186; where Cys74 and Cys185 act as the general acid/base for racemization. Asn75 is in a unique position, forming the back “wall” of the active site directly between the catalytic cysteines—a central location for forming strong hydrogen bonds with the Cα-carboxylate of d-glutamate, as well as contributing to active site volume. Previous computational studies have indicated that its amide functional group is a major source of electrostatic interaction energy with the glutamate carbanionic transition state.⁹ MD simulations in the current study also implicate the amide functional group of Asn75 as being a hydrogen bond donor to the Cα-carboxylate of d-glutamate. However, computational studies with a number of other active site ligands indicate that Asn75 is part of a network of interstitial waters, which are associated with charged and polar inhibitors in the active site of GR. This network also involves the conserved residues Thr76 and Thr118. Thus, based on its total sequence conservation, and its role in ligand recognition, Asn75 is the most important residue of GR that has, heretofore, not been subjected to a mutagenesis investigation. In the current study, we create the N75A and N75L mutants, both in vitro and in silico, in order to understand the importance of the amide functional group in both recognizing the native substrate, as well as several of the most efficient competitive inhibitors.

In addition to the Asn75, another major contributor to ligand-binding energy in GR is interstitial water, which was also identified as a major source of transition state stabilization.⁹ It is not surprising that the water-mediated contacts in GR are highly ligand dependent. A number of recent studies in other enzymes have indicated that water networks and interstitial water structure greatly depend on the particular nature of the enzyme-ligand contacts.¹⁸⁻²¹

An examination of GR crystal structures deposited in the RCSB Protein Data Bank reveals a heterogeneity in the location and number of the crystal-water oxygen atoms, which, in part, correlates to the type of ligand in the complex (Table 1). The scope of crystallographic data for GR–ligand complexes is limited to essentially d-Glu (and d-Glu analogs) and negatively charged oxygen-based buffers (acetate, citrate, phosphate, succinate, sulfate, and tartrate). A histogram comparing the numbers of interstitial waters between the former and the latter is illustrated in Figure 1. It is clear from the juxtaposition of these histograms that a variety of water-mediated GR–ligand contacts are possible. Unfortunately, although a number of recent competitive inhibitors for GR have been discovered, there remains a dearth of structural data, especially regarding tight binding complexes in the buried active site.

Table 1. Analysis of All Deposited GR Cocrystal Structures from the RCSB PDB^a.

PDB	species	ligand	monomer A	monomer B	monomer C	monomer D
1B74	A. pyrophilus	d-glutamine	1
1ZUW	B. subtilis	d-glutamate	1	1	1
2DWU	B. anthracis 1	d-glutamate	1	2	2
2GZM	B. anthracis 2	d-glutamate	0	1	0	1
2JFN	E. coli	d-glutamate	1
2JFO	E. faecalis	d-glutamate	0	1
2JFP	E. faecalis	d-glutamate	1	1
2JFQ	S. aureus	d-glutamate	1	2
2JFU	E. faecium	phosphate ions	2
2JFV	E. faecium	citrate	2
2JFW	E. faecium	tartaric acid	4
2JFX	H. pylori	d-glutamate	1	1
2JFY	H. pylori	d-glutamate	1	2
2JFZ	H. pylori	d-glutamate	2	1
2OHO	S. pyogenes	sulfate ion	0	3
2OHV	S. pyogenes	naphthylmethyl-d-glu	1
2VVT	E. faecalis	d-glutamate	1	1
2W4I	H. pylori	d-glutamate	2	1	2	1
3IST	L. monocyto.	succinic acid	2	2
3ISV	L. monocyto.	acetate ion	0
3OUT	F. tularensis	d-glutamate	2	2	2
3UHF	C. jejuni	d-glutamate	1	1
3UHO	C. jejuni	d-glutamate	1	1
4B1F	H. pylori	d-glutamate	2	2

^aThe number of interstitial waters is indicated per monomer for each structure. Structures were downloaded directly from the RCSB PDB, and hydrogen atoms were added using the “Clean All” function of YASARA v9.11.9. All non-hydrogen atoms were fixed, and an energy minimization was performed to relax hydrogen atoms. Interstitial waters are defined as a single water molecule forming at least two hydrogen bonds: one with the bound ligand and one with the enzyme. Monomer labeling is arbitrary and does not correspond to PDB labeling. Several deposited structures are unliganded and have been excluded from this analysis. Their PDB ID numbers correspond to 1B73, 3HFR, and 3UHP.

Figure 1.

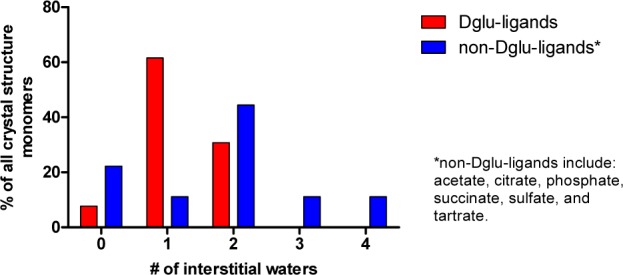
Frequency of interstitial waters in GR cocrystal structures. Results are separated by the indicated nature of the bound ligand. Each monomer in a particular crystal structure (where some contain dimers or trimers) is considered a single datum.

Previously, two attractive micromolar competitive inhibitors of GR from B. subtilis were identified. These compounds are 1H-benzimidazole-2-sulfonic acid (1, K_i = 9 μM)²² and croconic acid (2, K_i = 42 μM).²³ Both compounds possess high ligand efficiency, making them potentially attractive scaffolds for lead optimization. However, the source of the strength of their binding energy (as well as the lack of binding energy in many other negatively charged competitive inhibitors) remains elusive. The current work integrates experimental studies on wild-type GR and the Asn75 mutants with computational studies, in order to parse the contributions to binding free energies for a number of different classes of competitive GR inhibitors, using the extended linear response (ELR) method. The findings from these studies point to a stark difference in the use of water-mediated ligand contacts between the natural substrate (d-Glu) and the set of noncongeneric inhibitors. The extent of these differences and the implications for future drug design against GR are discussed below.

2. Materials and Methods

2.1. Materials

Croconic acid (LT00453399) was purchased from Labotest (Bremen, Germany). From Sigma Aldrich (St. Louis, MO), we obtained the following: 1H-benzimidazole-2-sulfonic acid (530646), d-glutamate (G1001), iodonitrotetrazolium (I8377), diaphorase (D5540), ATP (A7699), NAD+ (N7004), and l-glutamate dehydrogenase (G2501). All reagents related to buffer preparation for protein purification and circular dichroism were purchased from Sigma-Aldrich. Amicon centrifugal filtration devices were purchased from Millipore (Billerica, MA). Finally, HIS-Select Cobalt Affinity Gel (H8162) was purchased from Sigma-Aldrich.

2.2. Experimental Methods

2.2.1. Protein Expression and Purification

Recombinant protein was expressed in E. coli BL21 (DE3) cells containing a pET-15b plasmid with the N-terminal 6X-His-tagged gene of choice. Protein purification was achieved via cobalt-affinity chromatography followed by anion exchange chromatography. Details of both the expression and purification scheme were previously described by Whalen et al.²⁴

2.2.2. Mutant Construction

Mutant racE_N75A and racE_N75L were prepared using a QuickChange II XL Site-Directed Mutagenesis Kit (Stratagene, Santa Clara, CA) and primers obtained from Eurofins MWG Operon (Huntsville, AL). See Supporting Information Table S1 for primer sequences. Previously prepared and recently isolated pET15b containing the gene of interest was used as the template DNA. A BioRad MJ Mini Personal Thermal Cycler (BioRad, Hercules, CA) was used for all PCR reactions. Mutagenesis was confirmed via in-house DNA sequencing using an ABI 3730XL capillary sequencer.

2.2.3. Protein Secondary Structure Determination

Circular dichroism was employed in structure determination. A 10 μM solution of the enzyme of interest in an optically clear borate buffer (50 mM boric acid, 100 mM KCl, 0.7 mM DTT; pH 8.0) was measured from 190 to 260 nm, with five replicates. The averaged spectra was deconvoluted into respective secondary structure motifs (α-helix, β-sheet, and disordered) using the DichroWeb online server. The CDSSTR method was utilized with database 4 as a reference.

2.2.4. Enzyme Kinetics

Stereoisomerization of d-glutamate by glutamate racemase was assayed using a J-720 CD spectropolarimeter from JASCO (Easton, MD). A jacketed cylindrical cuvette with a volume of 750 μL and a path length of 10 mm was used for each assay. Readings were measured at 220 nm continuously. All measurements were conducted at 25 °C. Concentrations of d-glutamate were varied from 0.25–5 mM in an optically clear borate buffer (50 mM boric acid, 100 mM KCl, 0.7 mM DTT; pH 8.0). Reactions were initiated upon addition of enzyme (approximately 0.5 μM). Data acquisition was performed using JASCO Spectra Manager v1.54A software, and fitting was performed using GraphPad Prism v5.0 from GraphPad Software (San Diego, CA). Inhibitor IC₅₀ curves were obtained using a coupled-enzyme assay²⁵ with iodonitrotetrazolium absorbance at 500 nm as the readout, as both inhibitors studied were optically active at 220 nm. Assays were again conducted at 25 °C in the presence of 3–6 μM GR. For comparison with calculated binding energy values, experimental IC₅₀ values were converted to K_i values via the Cheng–Prussoff equation, and then, binding free energies were converted via the standard Gibbs free energy relation.

2.3. Computational Methods

2.3.1. Virtual Docking

The cocrystal structure of GR from B. subtilis bound to d-glutamate (1ZUW, chain C) was prepared for virtual docking by first deleting all water molecules, salt ions, peptide chains A and B, and the substrate, d-glutamate. A simulation cell was centered on the catalytic cysteine residues, Cys74 and Cys185, and dimensions of the cell were adjusted to encompass the entirety of the active site resulting in the following cell dimensions (x–y–z): 19.9–15.2–17.2 Å. Residue 75 was left unaltered in the case of docking to the wild-type model, but for docking to the N75A and N75L models, Asn75 was replaced with an alanine or leucine residue in silico, respectively. All ligands, including d-glutamate, were constructed and minimized in MOE v2011.10 (Chemical Computing Group)²⁶ and imported into YASARA for virtual docking. YASARA v12.4.1²⁷ employs AutoDock 4²⁸ in its docking functionality. Specific details regarding pose generation and scoring can be found in the wor of Whalen et al.²⁴ The top-ranking complexes were then used as starting structures for molecular dynamics simulations.

2.3.2. Molecular Dynamics Simulation

The molecular dynamics simulations of the docked complexes (based on the PDB 1ZUW, as described above) were performed with the YASARA Structure package version 12.4.1 (YASARA Biosciences).^27,29,30 A periodic simulation cell with boundaries extending 10 Å from the surface of the complex was employed with explicit solvent, and the cell was neutralized with NaCl (0.9% by mass). The YASARA2 force field was used with long-range electrostatic potentials calculated with the Particle Mesh Ewald (PME) method, with a cutoff of 7.86 Å.³¹⁻³³ The ligand force field parameters were generated with the AutoSMILES utility, which employs semiempirical AM1 geometry optimization and assignment of charges, followed by assignment of the AM1BCC atom and bond types with refinement using the RESP charges, and finally the assignments of general AMBER force field atom types. Optimization of the hydrogen bond network of the various GR–ligand complexes was obtained using the method established by Hooft et al., in order to address ambiguities arising from multiple side chain conformations and protonation states that are not well resolved in the electron density.³⁴ Following neutralization, a final density of 0.997 g/mL was employed. A previously described simulation annealing protocol²² was followed before initiation of simulations using the NVT ensemble at 298 K, and integration time steps of 1.25 and 2.5 fs for intra- and intermolecular forces, respectively. MD simulations of individual ligand in solvent and salt were performed as above, within a simulation cell having x–y–z dimensions of approximately 70–70–70 Å, and a total volume of ∼340 000 ų. Snapshots were saved for all cases at intervals of 25 ps, and the electrostatic interaction energy (⟨V^el⟩) and the van der Waals interaction energy (⟨V^vdW⟩) were calculated at each of the time points and averaged to yield the values in Table 5. Solvent accessible surface areas were constructed with a solvent probe radius of 1.4 Å, and the following radii for the solute elements: polar hydrogens 0.32 Å, other hydrogens 1.0717 Å, carbon 1.8 Å, oxygen 1.344 Å, nitrogen 1.14 Å, sulfur 2.0 Å. All surface area calculations were performed with the YASARA Structure package.

Table 5. Data Used in the Extended Linear Response Calculations^a.

complex	⟨Vel⟩ (kJ/mol)	⟨VvdW⟩ (kJ/mol)	Δ⟨Vel⟩ (kJ/mol)	Δ⟨VvdW⟩ (kJ/mol)	ΔGbind experiment (kJ/mol)	calculated ΔSASA (Å2)
1–WT	–617	–199	+9	–137	–28.8	277
1–N75A	–581	–224	+45	–162	–19.5	307
1–N75L	–590	–220	+36	–158	–23.9	294
1–wb	–626	–62
2–WT	–1643	–134	+60	–119	–25.0	232
2–N75A	–1671	–141	+32	–126	–26.4	231
2–N75L	–1684	–119	+19	–104	–26.4	230
2–wb	–1703	–15
3–WT	–1071	–150	+53	–149	–22.2	270
3–wb	–1124	–1.4
4–WT	–1717	–160	+167	–159	–19.4	247
4–wb	–1884	+0.6
5–WT	–532	–166	+73	–125	–18.4	311
5–wb	–605	–41
6–WT	–1753	–172	+140	–147	–15.4	274
6–wb	–1893	–25

^aBroken brackets, ⟨X⟩, indicate the average of an ensemble, where the ensemble of structures is obtained from molecular dynamics simulations. Abbreviations: el, electrostatic; vdW, van der Waals; SASA, solvent accessible surface area; wb, water box.

2.3.3. Ligand Interaction Maps and Reports

Ligand interaction maps were generated from the final snapshots of the 4-ns MD simulation using MOE v2011.10 (Chemical Computing Group).³⁵ Pocket analysis was conducted on the same structures using the Site Finder utility of MOE, using the default alpha sphere radius.

2.3.4. Multiple Regression Analysis Applied to Linear Response

Multiple regression analysis using the R statistical package, version 2.13.1,³⁶ was used to optimize the α, β, γ, and δ coefficients in eq 5. A linear model equating experimental binding free energies, listed in Table 5, and the computationally derived values from Table 5 (i.e., Δ⟨V^el⟩, Δ⟨V^vdW⟩, and ΔSASA) was employed to obtain optimized values for α–γ, and no restraints were used in the parameter optimization.

3. Results and Discussion

3.1. Steady-State Kinetics Shows Racemization Activity in Mutants, with Mild K_M Alterations

As discussed above, we predict Asn75 to be key to pocket volume and polarity, and thus, water accommodation. Two variations of Asn75 mutants were constructed, where asparagine was swapped for alanine or leucine. Wildtype and mutant variants of GR from B. subtilis were purified recombinantly from E. coli (see Supporting Information Figure S2 for SDS-PAGE). Circular dichroism shows that neither mutation causes significant changes to the secondary structure of GR (Figure 2, Table 2). Mutant and wild-type enzymes were assayed to determine steady-state kinetic constants, K_M and k_cat, in the d- to l- direction of racemization (Table 3). The apparent K_M values increased by a factor of 2- and 6-fold relative to wild-type for GR-N75L and GR-N75A, respectively. It is difficult to explain what causes the variation in Michaelis constants between GR variants from these studies due to the complicated nature of this constant, which includes association, dissociation, and catalytic steps. More striking is the 28-fold increase in k_cat caused by the N75A mutation. This phenomenon is currently the subject of a separate study.

Figure 2.

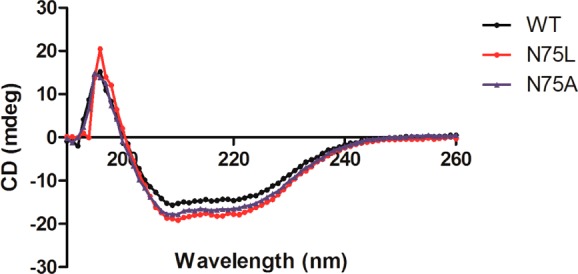
Comparison of the secondary structure of wild-type and mutant GRs confirms no unfolding or dramatic structural alteration induced by mutation to residue 75. Circular dichroism measurements are made in triplicate using a Jasco J-715 spectropolarimeter.

Table 2. Deconvolution of Circular Dichroism Spectra into Respective Secondary Structural Motifs^a.

protein	%-α-helix	%-β-sheet	%-disordered	NRMSD
GR-WT	60	14	24	0.001
GR-N75L	65	12	22	0.003
GR-N75A	59	16	25	0.001

^aDeconvolution performed using the online server, DichroWeb. The NRMSD given is for the comparison of experimental and calculated spectral data.

Table 3. Steady-State Kinetic Parameters (d- to l- Racemization) of Wild-Type and Mutant GR^a.

protein	KM (mM)	kcat (1/s)	kcat/KM (1/s·mM)
GR-WT	0.13 ± 0.01	1.64 ± 0.03	12.6 ± 0.08
GR-N75A	0.73 ± 0.09	45.6 ± 1.9	62.5 ± 0.13
GR-N75L	0.49 ± 0.10	0.15 ± 0.01	0.31 ± 0.10

^aSteady-state kinetics measured by monitoring ellipticity at 220 nm over time using a Jasco J-715 spectropolarimeter. d-Glutamate concentrations varied from 0.25 to 5.0 mM, and data fit to the Michaelis–Menten equation (with errors from nonlinear regression fitting).

3.2. Active Site Mutation Causes Ligand-Dependent and Residue-Dependent Binding Effects

1H-Benzimidazole-2-sulfonic acid (1) and croconic acid (2) are both competitive inhibitors with low-micromolar inhibitory constants that were previously discovered in virtual screening studies.^22,23 These compounds vary substantially in electrostatics and shape. The potency of each inhibitor was determined experimentally against either GR mutant. Compound 1 showed a 50% increase in IC₅₀ for the N75L mutation and a striking 600% increase in IC₅₀ for the N75A mutation, compared to the IC₅₀ for wild-type GR (Table 4). As suspected, the leucine and alanine substitutions cause binding energy changes of unequal magnitude, but surprisingly 1 suffers a greater binding energy loss in GR-N75A where we hypothesized additional water would be introduced to the active site. When comparing free energy binding values calculated from these IC₅₀ values, the same trend holds true. In the case of compound 2, only modest IC₅₀ decreases of 20% and 40% were observed for the N75L and N75A mutations, respectively, relative to the wild-type IC₅₀ value (Table 4). Although there is a statistically significant decrease in the value of the IC₅₀ for GR-N75A-2 compared to WT, the significance of this change does not hold with respect to their K_i values. Nevertheless, complexation of both of these compounds, to both wildtype and mutant GR, were subjected to more in-depth structural and computational analyses.

Table 4. GR Inhibitors and Substrate Examined in This Study^a.

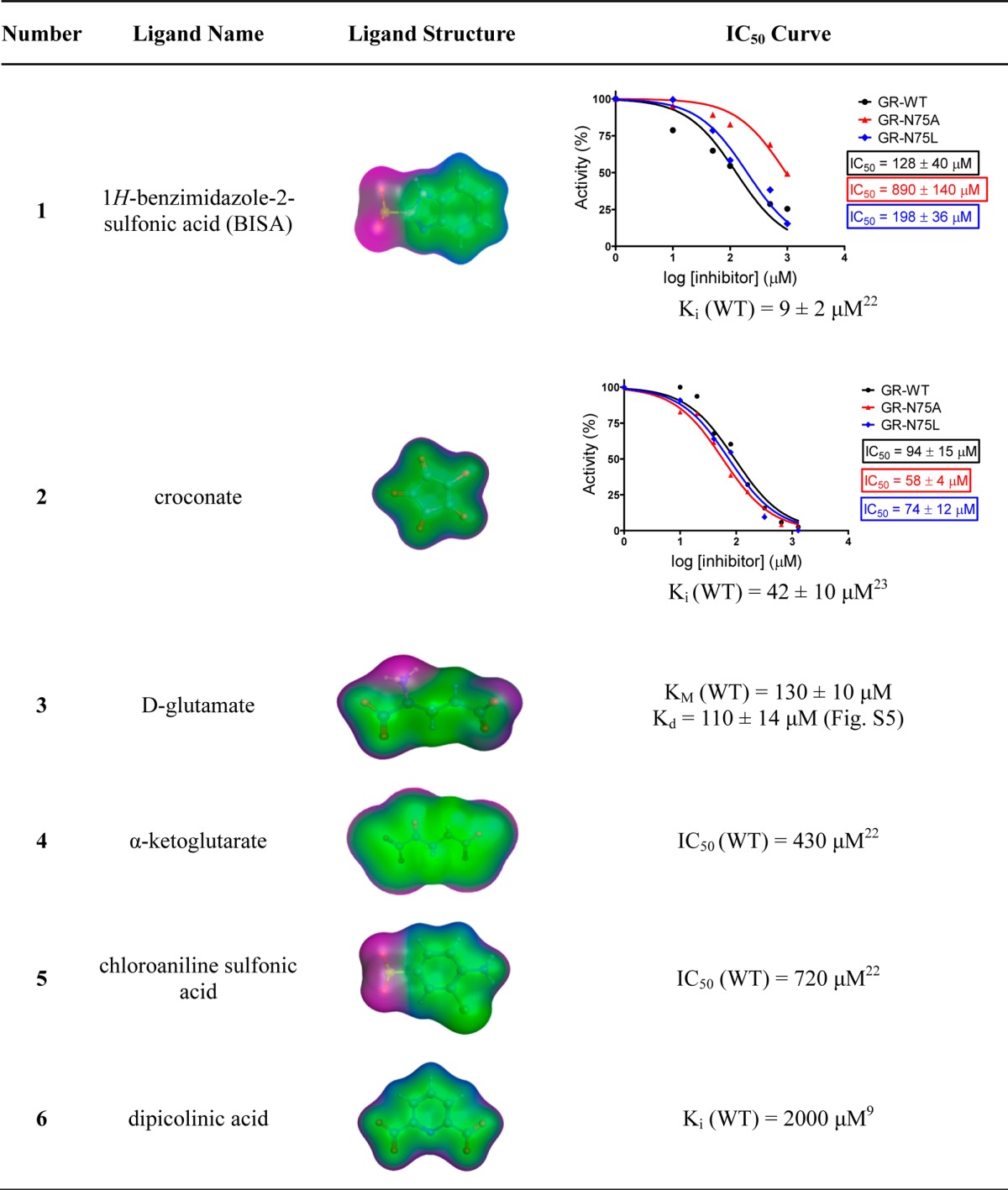
^aLigand structures shown with molecular surface (van der Waals) rendering. Hydrophobic regions are colored green, mildly polar regions are colored blue, and hydrogen bonding regions are colored purple. IC₅₀ curves were experimentally acquired via methods described in the Materials and Methods section.

3.3. Molecular Dynamics Simulations Indicate Morphological and Ligand-Binding Changes Resulting from N75A and N75L Mutations

In order to elucidate the nature and strength of the GR–ligand binding energies for a range of competitive inhibitors, we used a combination of docking, classical MD simulations, and extended linear response (ELR) free energy calculations. First, we describe the morphological characteristics of the GR–ligand complexes, followed by an analysis of the sources of binding free energy, including the role of interstitial water.

3.3.1. Placement of Ligands in GR Active Sites

A docking protocol, based on AutoDock 4.2, was used to place all of the ligands employed in the MD simulations (see Computational Methods section). Subsequently, these complexes were all subjected to the same protocols for simulated annealing energy minimization, followed by 4 ns of classical MD simulations, using the YASARA2 knowledge-based force field, using an explicit solvent model and periodic boundaries (see Computational Methods for details). These MD simulations were later used in ELR free energy calculations as described below. This type of hierarchical approach has proven successful in numerous LIE/ELR studies.³⁷⁻³⁹

3.3.2. Molecular Dynamics Simulations of GR–Ligand Complexes

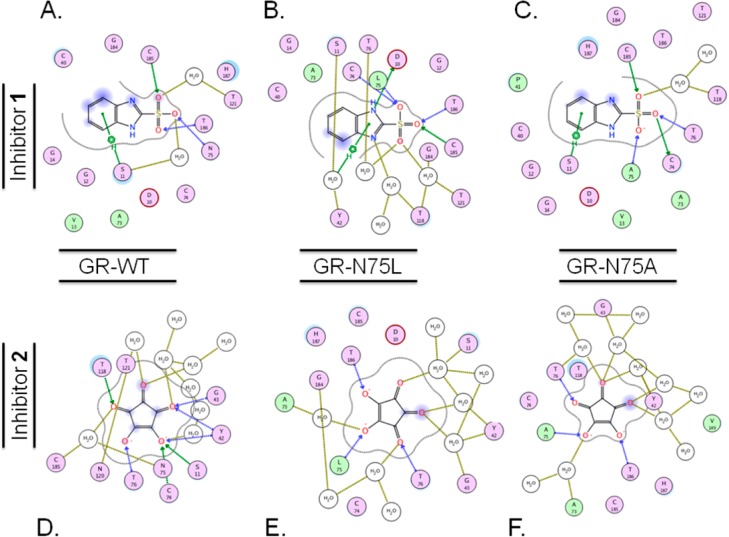
MD simulations were employed to obtain structural information for each inhibitor–GR complex. All ten complexes achieved RMSD equilibrium between 1 and 1.5 ns (Supporting Information Figure S1). Structures from the end of a 4 ns simulation were used to parse the GR–ligand interactions. GR–1 and −2 complexes were of particular interest, due to the reasons outlined above. A distinct characteristic of the GR-N75A–1 complex is that the ligand is less solvent exposed (than the GR-WT– and GR-N75L–1 complexes). The morphological characteristics of these various GR–ligand complexes may be described in a number of ways. A ligand pocket analysis of the three 1-bound complexes shows that the volume of the active site is markedly reduced for the GR-N75A–1 (Supporting Information Table S2), relative to GR-N75L– and GR-WT–1 complexes. Furthermore, in addition to the reduction in the size of the active site of GR-N75A, the openness of its cleft is significantly reduced, relative to wild-type and GR-N75L complexes, as described in Figure 3 and Supporting Information Figure S3. A cross-section of the three complexes of GR–1 from equilibrated MD snapshots at 4 ns are compared in Supporting Information Figure S4. The wild-type complex contains a water channel that leads out of the back of the active site (away from the entrance), while the GR-N75A and GR-N75L active sites are not contiguous with this water channel (Figure S4). The presence of this connected water channel in the wild-type GR (and its absence in the mutants) is a stable characteristic seen throughout the MD simulations. Additionally, while there are only two, or one, interstitial waters present in the wild-type and GR-N75A complexes, respectively, there are four interstitial waters in the GR-N75L complex (Figure 3). Lastly, the key hydrogen-bond contacts between 1 and GR are more optimal in the wild-type complex than in either Asn75 mutant, and this will be fully discussed below.

Figure 3.

Ligand interaction maps for the inhibitors, 1 (top) and 2 (bottom), bound to wild-type (A and D) GR-N75L (B and E), and GR-N75A (C and F) active sites support the energetic evaluations conducted via ELR. Maps generated from structures from the final snapshot of a 4-ns MD simulation. Residues are indicated with labeled circles. Direct hydrogen bonding interactions are indicated with blue (backbone) or green (side-chain) dashed lines. Interstitial water-hydrogen bonding interactions are indicated with gold dashed lines. Solvent exposure is indicated with light blue shading, and the active site surface proximal to the ligand is indicated with a gray line.

Given the gross morphological differences between the three GR species, it naturally follows that inhibitor 1 should be less solvent exposed in the N75A mutant, which is borne out in the ligand-interaction maps shown in Figure 3. Both the benzyl ring and sulfonate oxygens are somewhat less solvent exposed in GR-N75A, than in wild-type and GR-N75L complexes.

Although these MD simulations do provide some insight into the nature of GR–1 complexation, and more particularly the role of a key residue, Asn75, what is desired is a quantitative description of the free energy contributions of the GR pharmacophore. It is apparent from the relatively large plasticity exhibited by GR, from the MD analysis above, that diverse ligands may yield quite different GR–ligand complexes, particularly with regard to active site volume and interstitial water. In fact, a number of recent reports have also highlighted the idiosyncratic nature of interstitial water structure in enzyme active sites, where the presence of interstitial water can act as a favorable^21,40 or unfavorable component of the total binding energy.¹⁸⁻²⁰ In one particular study, Barandun and co-workers observed striking differences in binding energies between tRNA–guanine transglycosylase and sets of lin-benzoguanine and lin-benzohypoxanthine inhibitors.²⁰ Barandun et al. used X-ray crystallography to expose ligand-dependent conformational changes in key active site residues, which results in the import of interstitial water.²⁰ Without high-resolution structural information such as that obtained by Barandun and co-workers, enzyme plasticity and numerous water-mediated contacts make the determination of meaningful enzyme–ligand binding energies a nontrivial task. It would be extraordinarily useful to be able to predict the gross morphological changes as well as the specific active site alterations due to complexation with particular GR inhibitors, and more importantly, their binding free energies. To that end, we applied the extended linear response (ELR) method for calculating binding free energies, to a set of 10 different GR–ligand complexes (vide infra).

3.4. Binding Energy Calculations Using ELR

A permutation of the ELR methodology first described by Jorgensen has been applied to 10 different GR–ligand complexes.⁴¹ A number of ELR approaches⁴¹⁻⁴⁴ have been described and are based on the linear interaction energy (LIE) method, first described by Aqvist et al.⁴⁵ The seminal studies for utilizing the linear response approximation employ expressions for the hydration energy of ions, and it can be shown that the electrostatic portion of this free energy (ΔG_sol^el) is defined by eq 1.^46,47 This expression was then extrapolated by Aqvist and co-workers to the problem of considering ligand–protein binding, where they showed that the electrostatic contribution to the binding free energy was expressed by eq 2, where the ΔV term now refers to the difference between protein and water systems.⁴⁵

1

2

In the LIE approach, one obtains interaction energy components from molecular dynamics or Monte Carlo simulations, then parses the binding energy contributions into an electrostatic component (based on linear response) and a van der Waals component based on an empirically scalable parameter:

3

Δ⟨V^el⟩ indicates differences in the average electrostatic interaction energies between the two states (i.e., solvated and enzyme-bound systems). Statistical analysis of multiple systems by Aqvist and co-workers lead to an optimal set α value of 0.161.⁴⁵ Later studies employed a coefficient, called β, that is variable and ligand-dependent (ranging from 0.33 to 0.5) in place of the fixed Δ⟨V^el⟩ coefficient of 0.5, thus deviating from linear response.⁴⁸ These α and β parameter optimizations worked well for a number of systems,^45,48 but in the case of a thrombin target, it was necessary to add an additional offset term, γ, in order to reproduce the experimental binding free energies (eq 4).⁴⁹ In this case the γ term was a relatively large offset at −2.9 kcal/mol. These, and other studies, led Aqvist and co-workers to speculate that this constant offset value was highly dependent on the type of receptor site.⁵⁰

4

An augmented approach to the above model (eq 5), in which changes in ligand solvent accessible surface area (ΔSASA) are also empirically scaled was applied by Jorgensen and co-workers. Who, using the OPLS force field and investigating the binding of a set of sulfonamide inhibitors to human thrombin, arrived at solutions with significantly lower β values than the linear response approximation.⁴² Later studies, with various force fields, also found solutions with β values significantly different from linear response approximation.^44,51

5

While the meaning of the β parameter is based on the linear response approximation, which is derived from the potential of mean force from changing electric fields in polar solvents, the physical meaning of the α value is much more ambiguous. The α term has been empirically derived and lacks any clear a priori physical meaning. Kollman and co-workers determined that the α value is highly correlated to a weighted change in nonpolar SAS upon ligand binding,⁵² which they show to be dependent on the nature of the protein binding site (the more nonpolar the buried moiety, the more positive the weighting). Furthermore, optimization of the α parameter is expected to also implicitly include terms such as desolvation and entropy loss. Orthodox linear response-based methods are, however, not expected to explicitly account for long-range solvent–solute interactions, although more accurate methods for capturing such effects have been developed.⁵³ It is not surprising then that significant variation in the values of α and β (as well as γ and δ) exist across systems and methodological approaches.

In the current study, we are applying the above ELR approach, using ΔSASA and a constant offset value (δ) in order to reproduce the absolute binding free energies for the given set of ligands to GR. Furthermore, we are using the YASARA2 knowledge-based force field (KBFF) in 4-ns simulations for each GR–ligand complex (see Computational Methods for details). Ten different GR complexes, employing compounds indicated in Table 4 were used in ELR calculations; Table 5 lists the average ⟨V^el⟩ and ⟨V^vdW⟩ interaction energies for both solvated and enzyme-bound systems. In all cases, these highly polar ligands had negative values for ⟨V^el⟩ in both the enzyme-bound form and the solvated system. However, all of the ligands had more negative ⟨V^el⟩values in the solvated system than in the enzyme-bound form, leading to all positive values for Δ⟨V^el⟩. As expected, the converse of this was true for the Δ⟨V^vdW⟩, having all negative values. The change in solvent accessible surface area, as well as the experimentally determined binding values, are indicated in Table 5.

The adjustable parameters were then optimized using multiple regression analysis, and the results of this are indicated in Table 6. The residual standard error yielded a value of 2.0 kJ/mol, with an R value of 0.92 (Figure 4). It is remarkable that the β value here (0.07 ± 0.01) is within the error of the lowest RMS model of studies on sulfonamide inhibitors of thrombin (β = 0.071 ± 0.02⁴²), as well as a composite of ELR performed on three different protein kinases (β = 0.0848⁵⁴), laying in between β values determined for CYP1A2 (= 0.014–0.034⁵¹) and HIV-1 reverse transcriptase (0.144⁴³). Taken together, these ELR studies using three different force fields and six different enzymes converge on solutions of β values that are definitively lower than the original linear approximation but in toto are relatively precise.

Table 6. Multiple Regression Coefficients from Fitting to the Extended Linear Response Model^a.

	multiple regression estimate	regression standard error
α (van der Waals)	0.04	0.05
β (electrostatic)	0.07	0.01
γ (SAS) (kJ/Å2)	0.08	0.03
δ intercept (kJ/mol)	–43	6

^aThe residual standard error from the multiple regression fit was 2.0 kJ/mol. The multiple R-squared value was 0.85.

Figure 4.

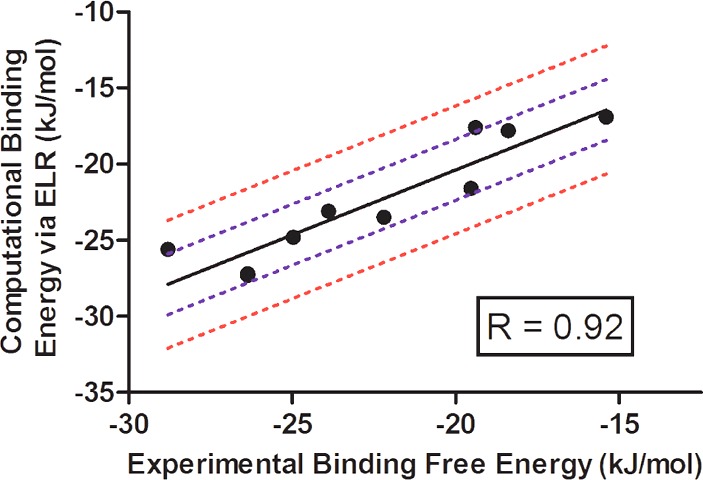
Plot of experimental versus computationally derived binding energies. Data is fit to a linear regression here (solid, black), and the ±4.2 kJ/mol (1 kcal/mol; red) and ±2.0 kJ/mol (mult regression error; blue) boundaries are shown. The calculated slope is 0.85 ± 0.13, Y-intercept is −3.3 ± 2.9 kJ/mol, and the R-squared value is 0.85.

The optimized α value in the current study is 0.04 ± 0.05. Previous LIE and ELR studies have shown that the α value has been arguably the most difficult parameter to estimate. Aqvist and co-workers obtained an optimized α value of 0.18 on a system composed of four different targets,⁵⁵ while other studies found diverse optimized values that ranged from being within error of zero⁴³ to being quite large (>0.5).⁵¹ A relatively large standard regression error on the α value was obtained for three different protein kinases by Tominaga and Jorgensen (α = 0.0771⁵⁴). The optimized γ value in this study indicates that larger buried solvent accessible surface area correlates with more unfavorable binding energy, which means that there is something other than simple cavitation being reported. One possibility is the ejection of stabilized, interstitial waters in the apo-GR structure. Ejection of such waters has been estimated to be ∼1.8 kcal/mol·water.⁵⁶ Previous steered MD studies on GR indicated that severe alterations in the global shape of the enzyme occur in a ligand-dependent manner.²² GR structures that exhibited greater degrees of active site cavity opening (induced by steered MD removal of ligands) also exhibited significantly greater free energies of protein solvation, suggesting that the ligand-induced changes in complex structure may have a number of nonobvious energetic implications.

3.5. Water Contributions to Total Binding Energy Are Strongly Ligand-Dependent

Another trend in the ELR data is that the relatively closed state of GR-N75A yields, not surprisingly, more favorable Δ⟨V^vdW⟩ (relative to wild-type and GR-N75L), for both inhibitors 1 and 2. This corresponds to the smaller active site volumes seen for the N75A mutant, its greater degree of cleft closure around the ligands as well as the solvent exposure, as presented in Figure 3. These enhanced van der Waals contacts do not necessarily track with greater binding affinities, as the quality of electrostatic interactions with the protein as well as the water network would need to be maintained in this reduced volume cavity. In order to parse the electrostatic contributions in terms of protein- and water-mediated contacts, for all of the GR–ligand complexes in this study, we determined the ⟨V^el⟩ in the absence of water (vide infra).

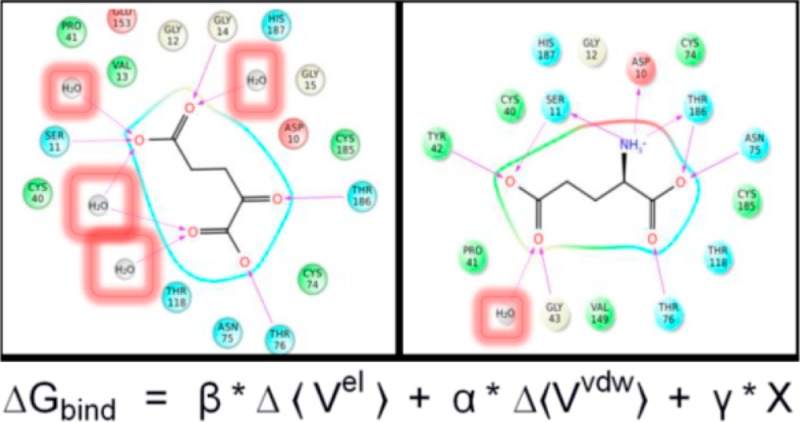
The striking conclusion from analyzing the ligand–protein and ligand–water-mediated contributions to ⟨V^el⟩ is that for most ligands there is a very large percentage of the interaction energy achieved through water contacts (Table 7). These values range from 7% for d-glutamate (3) to 54% for 4. However, the range for all ligands except for d-glutamate is 24–54%, indicating that all of the inhibitors here depend significantly more on water-mediated contacts for enzyme-binding than the natural substrate. In order to make the most stark comparison of these varying modes of water utilization, we juxtapose the ligand maps from the end of the MD simulation for d-glutamate- and 4-bound complexes (Figure 5). The ligand map of d-glutamate in Figure 5 illustrates the high efficiency of the natural substrate in making productive electrostatic protein contacts, which is highlighted by the presence of a singular water-mediated contact. Interestingly, this single water contact occurs at the γ-carboxylate, remote from the high-quality α-carboxylate-protein contacts in the rear of the cavity. This is not true of the inhibitors examined in this study. Compound 4 typifies this flooding of the active site of GR, in which there is extensive use of water-mediated contacts that contribute to the binding energy.

Table 7. Parsing the Contributions of Interstitial Waters to the Ligand Binding Set.

	electrostatic interaction energies in the absence of water (⟨Vel⟩protein [kJ/mol])	percent of ⟨Vel⟩ due to interstitial water–ligand interaction
1–WT	–419	32
1–N75A	–391	33
1–N75L	–314	47
2–WT	–777	53
3–WT	–993	7
4–WT	–798	54
5–WT	–377	29
6–WT	–1314	25

Figure 5.

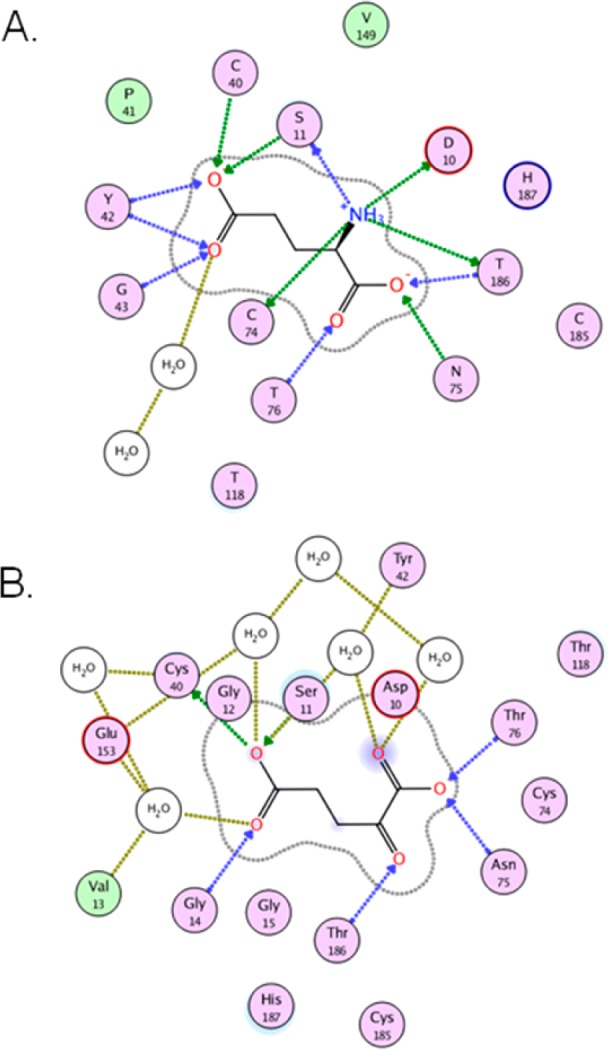
Ligand interaction maps for d-glutamate (A) and 4 (B) bound to wild-type GR. Residues are indicated with labeled circles. Direct hydrogen bonding interactions are indicated with blue (backbone) or green (side-chain) dashed lines. Interstitial water-hydrogen bonding interactions are indicated with gold dashed lines. Solvent exposure is indicated with light blue shading, and the active site surface proximal to the ligand is indicated with a gray line.

Another GR–ligand complex that exhibits this flooding phenomenon is GR-N75L–1, whose ligand map was presented earlier in Figure 3 and in which numerous water-mediated contacts could be seen. Table 7 shows that 1 bound to GR-WT has a 32% ⟨V^el⟩ due to water-mediated contacts, while 1 bound to GR-N75L exhibits a value of 47%, which is clearly reflected in the ligand interaction maps (Figure 3). Not surprisingly, 1 bound to GR-N75A has approximately the same dependence on water-mediated contacts as in the GR-WT complex. This reveals that the very poor quality of ligand–protein interaction energy, particularly in the hydrogen-bonding between the sulfonate of compound 1 and the back of the active site pocket (proximal to the mutated Asn75 position) which is present in GR-N75L. In other words, the damage due to the pharmacophore by swapping the amide of Asn75 for the isopropyl of leucine could be rescued by simply flooding this polar active site and increasing the number of water-mediated contacts. An astute observation made by Barandun and co-workers is that despite favorable interactions between imported water and the protein, these interactions are rarely sufficient to compensate for losses of direct ligand–protein interactions.²⁰ The difference in compound 1 binding energy between GR-WT and GR-N75A is most likely the result of an altered binding pose that produces suboptimal bond distances and angles for direct contacts between ligand and protein. This reduction in pose quality is quantified in Table 7 where electrostatic interaction energy is calculated in the absence of water (−419 vs −391 kJ/mol for WT vs N75A). Additionally, distances and angles were calculated and averaged for all protein–ligand hydrogen bonding interactions in the final three snapshots of either complex’s MD simulation (Supporting Information Figure S6). The results show an increase in overall bond distance and a reduction in bond angle in the case of N75A, consistent with its smaller electrostatic protein–ligand interaction energy (Table 7). In addition, there is one less bridging water molecule in the N75A complex compared to the wildtype complex.

4. Conclusions

The optimized ELR model resulted in an α = 0.04 and β = 0.07, both values within error of a number of published values on various enzymatic systems. This solution required an offset (δ value) or −43 ± 6 kJ/mol and yielded an R-squared value of 0.85 and an RMS error of 2.0 kJ/mol. The MD simulations indicated that GR-N75A had a reduced active site volume, less open active site cleft, and decreased solvent exposure with 1H-benzimidazole-2-sulfonic acid (1), a recently identified high-efficiency competitive inhibitor. Results of the ELR study indicated that Δ⟨V^vdW⟩ for GR-N75A with 1 and another attractive competitive inhibitor, croconate (2), are more favorable relative to their wild-type and GR-N75L counterparts.

Analysis of the contributions of water-mediated contacts to the GR–ligand electrostatic interaction energies reveals a surprisingly large role in all ligands (24–54%), except the natural substrate (7%). In the case of inhibitor 1, the N75A mutation results in nonoptimal sulfonate–protein hydrogen bonds in the rear of the active site and reduction in active site volume (relative to wild-type). While in the case of the N75L mutant, the sulfonate–protein hydrogen bonding is even poorer, yet the larger active site volume and degree of cleft openness led to water-mediated rescue of GR–ligand binding energy. These findings yield deep insight into potential antibacterial mutagenesis mechanisms. Despite the attractiveness of 1 as a scaffold, optimization should be pursued cautiously since it is possible to make a mutant that damages the pharmacophore and still produces a perfectly functional glutamate racemase.

Glossary

Abbreviations

GR

glutamate racemase

ELR

extended linear response

el

electrostatic

vdW

van der Waals

BISA

1H-benzimidazole-2-sulfonic acid

SASA

solvent accessible surface area

wb

water box

Supporting Information Available

Additional figures including: SDS-PAGE analysis of purified recombinant proteins, MOE computational pocket analysis, mutagenesis primers, d-Glu titration to GR, and MD simulation RMSD plots. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States