Unbiased comparison of sample size estimates from longitudinal structural measures in ADNI

Abstract

Structural changes in neuroanatomical subregions can be measured using serial magnetic resonance imaging scans, and provide powerful biomarkers for detecting and monitoring Alzheimer's disease. The Alzheimer's Disease Neuroimaging Initiative (ADNI) has made a large database of longitudinal scans available, with one of its primary goals being to explore the utility of structural change measures for assessing treatment effects in clinical trials of putative disease‐modifying therapies. Several ADNI‐funded research laboratories have calculated such measures from the ADNI database and made their results publicly available. Here, using sample size estimates, we present a comparative analysis of the overall results that come from the application of each laboratory's extensive processing stream to the ADNI database. Obtaining accurate measures of change requires correcting for potential bias due to the measurement methods themselves; and obtaining realistic sample size estimates for treatment response, based on longitudinal imaging measures from natural history studies such as ADNI, requires calibrating measured change in patient cohorts with respect to longitudinal anatomical changes inherent to normal aging. We present results showing that significant longitudinal change is present in healthy control subjects who test negative for amyloid‐β pathology. Therefore, sample size estimates as commonly reported from power calculations based on total structural change in patients, rather than change in patients relative to change in healthy controls, are likely to be unrealistically low for treatments targeting amyloid‐related pathology. Of all the measures publicly available in ADNI, thinning of the entorhinal cortex quantified with the Quarc methodology provides the most powerful change biomarker. Hum Brain Mapp, 2012. © 2011 Wiley Periodicals, Inc.

INTRODUCTION

Structural magnetic resonance imaging (MRI) is highly sensitive to the neurodegeneration that occurs in Alzheimer's disease (AD), even in prodromal stages [McEvoy et al., 2009; Vemuri et al., 2009]. Atrophy measures in neuroanatomical subregions correlate well with disease stage determined from histopathology [Vemuri et al., 2008], and with clinical measures of disease severity [Jack et al., 2004; McDonald et al., 2009]. They are predictive of clinical decline and conversion to AD in individuals with mild cognitive impairment (MCI) [Fan et al., 2008; Jack et al., 1999, 2004; Kovacevic et al., 2009; McEvoy et al., 2011; Vemuri et al., 2009]. Structural changes over time in neuroanatomical subregions can be quantified from serial MRI scans [Holland et al., 2009], and provide powerful biomarkers for tracking disease progression or slowing of progression with treatment. As a reflection of the progressive neurodegeneration that underlies the cognitive and functional decline in AD, anatomical change measures have high face validity as outcome measures for evaluating putative disease‐modifying effects of new therapeutic interventions, and are being evaluated in clinical trial settings as potential surrogates for standard clinical or cognitive outcomes.

To be useful as primary or secondary outcome measures in clinical trials, longitudinal MRI analysis methods must be able to detect with high fidelity subtle structural changes over time. Multiple methodologies have been developed to address this challenge. The Alzheimer's Disease Neuroimaging Initiative (ADNI), a large‐scale, multisite, longitudinal study of the natural history of AD [Mueller et al., 2005] was launched in 2003 with an overarching goal of determining the best set of in vivo biomarkers for early detection and tracking of AD (http://www.adni-info.org) [Mueller et al., 2005]. A related goal is to determine which methods provide maximum power for detecting treatment effects in clinical trials of potential disease‐modifying therapies [Cummings, 2010]. A unique aspect of ADNI is that all raw data are being made available publicly as they are collected (http://adni.loni.ucla.edu). Research groups funded by ADNI [Jack et al., 2010] have made their derived data publicly available as well, enabling a direct comparison of the relative sensitivity of different methods for detecting and tracking neuropathological changes related to AD. Here, we use ADNI's publicly available derived data to present a comparative analysis of measures of whole‐brain and subregional change, obtained from several widely used analysis methods. These methods amount to extensive processing streams and involve many factors, such as image exclusion decisions, quality control, the choice of using the pair of scans or choosing just the best single scan available for subject‐timepoints, and the quality of gradient‐field nonlinearity unwarping employed, and thus are composed of far more than change‐measurement algorithms. Given all these differences, it is only practical to evaluate each methodology based on the overall results individually available from applying them to the same large ADNI database. To compare methods, we use estimated sample size requirements, as these have become a standard metric for evaluating biomarkers, and are directly relevant to clinical trial design. We further provide statistical significance results (P values) for differences in sample size estimates obtained in strict head‐to‐head pairwise comparisons among all measures.

To obtain realistic sample size estimates from longitudinal neuroimaging measures, it is essential to control for potential bias that can arise in image analysis [Thompson and Holland, 2011]. The problem of bias in image registration has been known since the early days of nonrigid morphometric methods [Ashburner and Friston, 2000; Christensen, 1999; Christensen and Johnson, 2001] and has received a great deal of attention recently, including the development of some general and implementation‐specific solutions [Leow et al., 2007; Reuter et al., 2010; Yanovsky et al., 2009; Yushkevich et al., 2010]. Sources of bias include asymmetries in image smoothing and/or interpolation, and asymmetry in the image matching or regularization term in the cost function used in image registration. Such bias can be accentuated to varying degrees depending on the minimization scheme used [Yushkevich et al., 2010].

Another critical consideration when estimating sample sizes for treatment response is whether to include effects seen in normal aging as treatable effects. When performing power calculations based on a natural history (nonintervention) trial such as ADNI, sample size estimates are typically calculated for a hypothesized treatment effect expressed in terms of a percentage of the total disease‐related effect, for example, a 25% slowing in rate of decline on the outcome measure.

Compared to clinical or cognitive measures, neuroimaging measures are very sensitive to changes that occur over time in cognitively healthy older adults [Fjell et al., 2009; Fotenos et al., 2005; Fox et al., 2000; Jack et al., 2008]. When effect sizes are estimated based on absolute change measures, for example, 25% reduction in the total atrophy rate of a given anatomical structure, the usually implicit and probably false [Herrup, 2010] assumption is that all change over time is due to AD. Several ADNI presentations, the ADNI‐2 grant proposal (available at http://www.adni-info.org/Scientists/ADNIScientistsHome.aspx), and most ADNI studies evaluating or comparing sample size estimates for neuroimaging outcome measures make this assumption implicitly [Beckett et al., 2010; Cummings, 2010; Ho et al., 2010; Hua et al., 2009, 2010; Kohannim et al., 2010; Lorenzi et al., 2010; Nestor et al., 2008; Risacher et al., 2010; Schuff et al., 2009; Vemuri et al., 2010], with a few notable exceptions [Fox et al., 2000; Holland et al., 2009; Leung et al., 2010; McEvoy et al., 2010; Schott et al., 2010]. This is a critically important issue since sample size estimates will be substantially smaller if effect sizes are calculated based on absolute change measures rather than on the difference in change measures between patients and controls.

The use of absolute change measures is valid if all atrophy over time in cognitively healthy older individuals is due to AD, that is, if all cognitively healthy older individuals are in a preclinical state of AD. Current research suggests, however, that only 18% of cognitively healthy older individuals aged 60–69 show signs of amyloid‐β (Aβ) pathology, one of the key necessary features for AD, rising to 65% in those over 80 years [Rowe et al., 2010]. Pathological levels of cortical Aβ can be assessed directly through positron emission tomography (PET) imaging of amyloid‐sensitive ligands [Rabinovici and Jagust, 2009] or indirectly through cerebrospinal fluid levels of Aβ₄₂ [Blennow et al., 2010]. CSF and PET measures of Aβ pathology correlate highly with each other [Fagan et al., 2009] and with measures of Aβ at autopsy [Ikonomovic et al., 2008]. Proposed models of the trajectories of different AD biomarkers [Aisen et al., 2010; Frisoni et al., 2010; Jack et al., 2010] postulate that Aβ pathology is the earliest detectable sign of AD pathology, and may be apparent a decade or more before other signs of AD occur, such as neurodegeneration and cognitive impairment. These models further postulate that neurodegenerative changes, reflected in atrophy on structural MRIs, are downstream events that occur closer in time to, and underlie, the functional and cognitive impairment that characterize AD—and indeed for familial AD, gradual atrophy acceleration has been found in the prodromal stages [Ridha et al., 2006].

According to these models, atrophy observed in individuals who do not show signs of Aβ pathology would not be due to AD, as Aβ pathology appears prior to, and presumably triggers [Hardy and Selkoe, 2002], the AD‐related neurodegeneration. There would thus be no reason to expect that a treatment, such as an anti‐amyloid therapy, aimed at slowing progression of AD pathology, would affect atrophy that stems from causes other than AD pathology. Therefore, determination of disease‐specific effect sizes for neuroimaging outcome measures, based on a natural history trial of AD, would be best estimated as the difference in atrophy rates experienced by MCI or AD patients relative to atrophy rates observed in cognitively healthy individuals without Aβ pathology. It should be noted, however, that there is little evidence to date for differences in atrophy rates in AD‐vulnerable regions between Aβ‐positive and Aβ‐negative healthy older adults (or healthy older controls, HCs) [Chetelat et al., 2010; Fjell et al., 2010], though using variants of Boundary Shift Integral (BSI) for whole brain, ventricles, and hippocampus, a significant difference was found between 65 Aβ‐negative HCs (including two converters) and 40 Aβ‐positive HCs (including four converters) [Schott et al., 2010]. Here we compare atrophy rates in ADNI's full HC group, and in HCs separated into two subgroups, those who test negative for Aβ pathology and those who test positive, based on CSF Aβ₄₂ levels, and examine the implications of these findings for sample size estimation.

In this study, we analyze publicly available ADNI data from the application of five methodologies to serial brain scans to determine which method provides the most sensitive detection of anatomical change over time. These methodologies are: (1) Quarc (quantitative anatomical regional change, developed in our laboratory) [Holland and Dale, 2011; Holland et al., 2009], (2) FreeSurfer Longitudinal v.4.4, (3) FreeSurfer Cross‐sectional v.4.3 [Dale and Sereno, 1993; Dale et al., 1999; Fischl et al., 1999, 2002; Jack et al., 2010], (4) BSI [Freeborough and Fox, 1997; Leung et al., 2010], and (5) Tensor‐Based Morphometry (TBM) [Hua et al., 2008a, b, 2009, 2010]. (We note that “Tensor‐Based Morphometry” is sometimes used to refer to any nonlinear registration method, even if the only tensors involved are rank 1, that is, vectors. “Tensor‐Based Morphometry” is used in the title of several of the Hua et al. articles, referring to the full processing stream developed and implemented by those authors at LONI, UCLA; the tensors in question comprise the set of 3 × 3 Jacobian matrices, one at each voxel, which result from morphometric registration—the registration itself is not based on these tensors, but the analysis of structural change is based on statistical properties of the Jacobian field. In agreement with Hua et al., here we use “Tensor‐Based Morphometry” and “TBM” as identifiers referring exclusively to the complete UCLA‐LONI methodology.) Official ADNI data for Voxel‐Based Morphometry [Alexander et al., 2010; Ashburner and Friston, 2000; Chetelat et al., 2005; Tzourio‐Mazoyer et al., 2002] did not yield meaningful results and so was not included in our analysis. We assess the impact of measurement bias on sample size estimates derived from these neuroimage analysis methodologies and provide sample size estimates, with confidence intervals, for the bias‐corrected data, along with P values for pairwise head‐to‐head comparisons. We also evaluate the impact of failing to control for changes observed in healthy aging. Finally, to determine the sensitivity of neuroimaging variables as outcome measures, we compare sample size estimates derived using change in the neuroimaging measures to those derived using change on a standard clinical outcome measure, the Clinical Dementia Rating–Sum of Boxes (CDR‐SB) score.

The five methodologies under discussion have some aspects in common, and some unique features. FreeSurfer‐cross‐sectional performs independent tissue segmentations at each timepoint for each subject, and is the only method considered here that does not use any form of registration between longitudinal images; FreeSurfer‐longitudinal is conceptually an extension of the cross‐sectional variant, where input from all available time points for a subject is used to update the segmentations at each timepoint. Quarc and TBM are nonlinear registration methods, and estimate change by integrating a volume‐change field over anatomically predefined tissue ROIs or statistically defined ROIs; they differ significantly in their details, for example, image matching and regularization terms, minimization schemes, use or not of Jacobians, use or not of an atlas, intensity normalization, and so forth. BSI has evolved through several versions, but essentially estimates tissue (contrast) boundary displacements between pairs of affine registered images. Altogether, this is a rich set of methodologies that result in some remarkable similarities and differences, which we discuss below.

METHODS

ADNI

All data used in the preparation of this article were obtained from the ADNI database (http://www.loni.ucla.edu/ADNI). ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and nonprofit organizations, as a $60 million, 5‐year public–private partnership. ADNI's goal is to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations. ADNI has recruited 227 cognitively normal individuals to be followed for 3 years, 396 people with MCI to be followed for 3 years, and 193 with mild AD to be followed for 2 years (see http://www.adni-info.org). The research protocol was approved by each local institutional review board and written informed consent is obtained from each participant.

Participants

The ADNI general eligibility criteria have been described elsewhere [Petersen et al., 2010]. Briefly, subjects are not depressed, have a modified Hachinski score of 4 or less, and have a study partner able to provide an independent evaluation of functioning. HC subjects have a Clinical Dementia Rating (CDR) of 0. Subjects with MCI have a subjective memory complaint, objective memory loss measured by education‐adjusted scores on Wechsler Memory Scale Logical Memory II, a CDR of 0.5, preserved activities of daily living, and absence of dementia. Subjects with AD have a CDR of 0.5 or 1.0 and meet National Institute of Neurological Disorders and Stroke and Alzheimer's Disease and Related Disorders Association criteria for probable AD.

Data Processing

Analyses were performed on data sets available from http://www.loni.ucla.edu/ADNI/Data through April 16, 2011. These data sets comprise measures derived from longitudinal structural MRI processed with: Quarc; FreeSurfer‐longitudinal (FS); FreeSurfer‐cross‐sectional (FSx); BSI; and TBM. The measures in these data sets are for various ROIs, both predefined tissue regions and data‐driven regions, at baseline and follow‐up (generally 6‐months apart) through 36‐months. Images for Quarc were preprocessed locally, similarly to the preprocessing at Mayo Clinic performed by ADNI for the other methodologies, but using both images per time point where available, and using image correction procedures for site‐specific distortion effects updated for recent scanner changes. The other methodologies used only a single scan per timepoint—the best scan in the event of artifactual degradation in the other. Since one of the goals of ADNI is to identify biomarkers that are more powerful than current standard outcomes for tracking early disease progression, sample sizes were also determined using CDR‐SB as an outcome variable. Change with respect to baseline was the measure used in all cases (follow‐up images were directly registered with baseline). All data that passed quality control (as defined by the several methodologies) for all available time points were used. This provides for a global overview when comparing the full methodological processing streams, and implicitly takes into account differences in the methods' failure rates. We also carried out pairwise comparisons on identical subject‐timepoint data sets for a more narrowly focused assessment of relative performance.

For the FreeSurfer‐related methods, we focused primarily on the entorhinal, hippocampus, and whole brain, these being the ROIs traditionally of interest in AD studies, but we also provide results for other ROIs in Tables II and III; for BSI we used the whole‐brain measure “KN‐BSI,” described in [Leung et al., 2010]; and for TBM we used the “Stat‐ROI,” the statistically defined ROI in the temporal lobe that was designed to undergo a high degree of change from AD, as described in [Hua et al., 2009]. An earlier analysis of the TBM Stat‐ROI showed that the differences between 0 to 6 month and subsequent interval atrophy rates were highly significant for this measure for all diagnostic groups [Thompson and Holland, 2011], and an attempt to redress the issues raised [Hua et al., 2011] resulted in alternative sample size estimates, which we discuss below. Individual subject data from the modified method are not available on the ADNI website, but since a large number of publications have reported on the problematic TBM Stat ROI results [Beckett et al., 2010; Cummings, 2010; Ho et al., 2010; Hua et al., 2008a, b, 2009, 2010; Jack et al., 2010; Kohannim et al., 2010], and results from the modified method are similar, we provide a more detailed analysis here of this method, and compare results from the two approaches.

Table II.

Bias‐corrected sample size estimates for MCI

Measure	N MCI	N MCI‐HC(Aβ−)	N MCI‐HC
Quarc entorhinal	134 [110 171]	286 [201 446]	293 [214 432]
Quarc amygdala	165 [133 214]	297 [215 444]	366 [264 549]
Quarc hippocampus	164 [133 213]	388 [273 605]	444 [314 687]
Quarc fusiform	150 [121 194]	440 [302 707]	479 [338 742]
Quarc inf temporal	186 [149 246]	490 [334 800]	480 [340 742]
Quarc mid temporal	200 [159 266]	515 [347 856]	522 [364 825]
Quarc whole brain	149 [121 193]	555 [341 1057]	657 [433 1137]
Quarc ventricles	183 [146 241]	813 [465 1785]	1008 [623 1934]
FS hippocampus	175 [142 223]	327 [209 585]	576 [386 963]
FS entorhinal	413 [315 578]	694 [400 1505]	745 [490 1286]
FS inf temporal	449 [337 636]	988 [555 2240]	986 [617 1846]
FS mid temporal	488 [364 701]	825 [491 1679]	1013 [626 1936]
FS fusiform	518 [385 750]	799 [437 1932]	1121 [663 2326]
FS ventricles	164 [133 211]	1095 [542 3328]	1179 [695 2461]
FS amygdala	1113 [755 1842]	716 [423 1480]	1799 [974 4444]
FS whole brain	384 [294 531]	1769 [743 8642]	2179 [1053 7010]
FSx hippocampus	233 [190 298]	620 [377 1206]	771 [513 1310]
FSx ventricles	153 [126 194]	721 [434 1443]	991 [632 1803]
FSx mid temporal	549 [417 774]	1162 [701 2327]	1082 [703 1917]
FSx entorhinal	656 [494 935]	1592 [777 4928]	1121 [706 2080]
FSx inf temporal	661 [492 955]	2188 [992 8424]	1452 [863 2993]
FSx fusiform	763 [559 1129]	1870 [915 5740]	1661 [961 3608]
FSx whole brain	381 [299 512]	1445 [717 4353]	1961 [1052 4944]
FSx amygdala	1863 [1194 3371]	1856 [805 8164]	5169 [2114 27691]
KN‐BSI	142 [115 182]	500 [330 853]	715 [472 1221]
VBSI	181 [145 235]	778 [449 1675]	1173 [703 2368]
TBM Stat. ROI	287 [223 395]	1184 [523 4825]	1358 [712 3624]
CDR‐SB	542 [404 775]	608 [443 898]	638 [464 946]

See Methods section for methodology nomenclature; references are given in the Introduction. Values for selected measures are plotted in Figure 3. The 95% confidence intervals of the estimated sample sizes are shown in brackets. N MCI refers to sample size estimates required to detect 25% slowing in the total or absolute change seen in MCI, with 80% power and 5% significance. N MCI‐HC are sample size estimates for 25% slowing in the rate of change in MCI that is in excess of that seen in all HCs; ditto for N MCI‐HC(Aβ⁻), but with respect to the Aβ‐negative subgroup of HCs. P‐values for head‐to‐head pairwise comparisons of relative change sample sizes are in Table IV.

Table III.

Bias‐corrected sample size estimates for AD

Measure	N AD	N AD‐HC(Aβ−)	N AD‐HC
Quarc entorhinal	44 [33 63]	73 [53 113]	74 [54 113]
Quarc fusiform	57 [44 81]	98 [72 147]	102 [75 151]
Quarc inf temporal	73 [55 105]	118 [85 181]	117 [85 177]
Quarc mid temporal	76 [57 109]	123 [88 189]	124 [90 188]
Quarc hippocampus	71 [54 103]	118 [85 181]	126 [91 195]
Quarc amygdala	78 [59 113]	116 [83 179]	132 [94 205]
Quarc whole brain	84 [63 123]	179 [121 302]	196 [134 321]
Quarc ventricles	92 [69 135]	219 [144 382]	243 [164 409]
FS hippocampus	105 [79 152]	157 [105 265]	217 [150 355]
FS ventricles	90 [68 128]	247 [159 450]	255 [174 427]
FS entorhinal	240 [169 383]	326 [206 617]	340 [225 597]
FS inf temporal	226 [160 356]	352 [223 658]	352 [232 623]
FS fusiform	236 [167 375]	299 [188 564]	354 [231 637]
FS mid temporal	261 [182 423]	346 [223 631]	383 [248 692]
FS whole brain	252 [175 408]	629 [332 1658]	696 [393 1617]
FS amygdala	1410 [729 4074]	879 [441 2635]	2380 [971 13548]
FSx hippocampus	119 [91 169]	230 [153 396]	264 [183 428]
FSx ventricles	95 [73 131]	240 [163 396]	280 [195 451]
FSx mid temporal	347 [241 564]	516 [328 959]	498 [323 897]
FSx fusiform	360 [249 593]	547 [334 1092]	522 [333 969]
FSx whole brain	228 [162 359]	504 [295 1077]	586 [354 1193]
FSx entorhinal	429 [291 730]	713 [404 1645]	591 [370 1139]
FSx inf temporal	456 [305 790]	903 [489 2287]	729 [437 1515]
FSx amygdala	1399 [742 3747]	1395 [611 5996]	2604 [1095 13180]
KN‐BSI	75 [58 104]	152 [109 234]	180 [129 276]
VBSI	92 [70 128]	213 [144 353]	257 [177 417]
TBM Stat. ROI	110 [82 165]	243 [143 516]	260 [168 472]
CDR‐SB	279 [198 437]	292 [206 464]	298 [210 474]

See notes for Table II. Values for selected measures are plotted in Figure 4. P‐values for head‐to‐head pairwise comparisons of relative change sample sizes are in Table V.

Quality control information, using acronymic nomenclature, was explicitly provided by the individual research groups in the publicly available ADNI spreadsheets for FS, FSx, BSI, and Quarc data, and used here for filtering out subject visits that did not have values as follows: FS and FSx QVERALLQC = “Pass” or “Partial”; BSI VENTACCEPT = 1, REGRATING ≤ 3, KMNREGRATING ≤ 3; and Quarc QCPASS = 1. The total numbers of remaining subjects, categorized by diagnosis (and CSF‐Aβ status for HCs), for all methodologies and CDR‐SB are shown in Table I.

Table I.

Number of subjects

Methodology	AD	MCI	HCa	HC(Aβ+)	HC(Aβ−)
Quarc	131	311	182	35	58
FS	135	320	182	36	59
FSx	169	365	199	37	64
BSI	156	346	192	35	65
TBM	133	291	148	31	48
CDR‐SB	177	371	200	38	66

^aHC does not include 13 converters, based on clinical records up to and including the visit 36 months from baseline. Only 113 of 227 subjects diagnosed as HC at baseline had CSF Aβ‐status determined; six (2 Aβ⁻, 4 Aβ⁺) of these converted.

Bias Estimation

All measures were evaluated for potential bias by estimating the intercept based on a linear fit to the 6‐ and 12‐month timepoints [Yushkevich et al., 2010]. This linear fit was performed simultaneously across groups (AD, MCI, and HC), allowing different slopes for each group but requiring constant intercept, based on the assumption that additive bias, if arising from methodology, should equally affect measures from all groups.

More formally, we used the following linear model to fit for additive bias (intercept) b, and slopes (rates of change) s _H for HCs, s _M for MCI subjects, and s _A for AD subjects: Y = s _H × T _H + s _M × T _M + s _A × T _A + b. Here, Y, T _H, T _M, and T _A are vectors of length equal to the total number of all subject‐visits at 6‐ and 12‐months: Y is the vector of response measurements (percent volume change from baseline) for all subjects‐visits; T _H is the vector of times from baseline for all HC subject‐visits, with zeros at positions corresponding to non‐HCs; T _M, and T _A are similar vectors but for MCI and AD subjects, respectively. The general linear model was fit using Matlab, and the null hypothesis that the y‐intercept is zero, indicating no bias, was tested.

Measures were corrected for bias by subtracting the estimated b at all follow‐up timepoints. Bias‐corrected measures were then used for subsequent power calculations.

Power Calculations

Power calculations, modeling linear change over time, were performed for each methodology with standard methods briefly described in [Holland et al., 2009], using all available timepoints through 36‐months for each subject. Since we are measuring change from baseline, in plots of measured change versus time of measurement all intercepts are zero at baseline. Each subject, however, is assumed to change at an independent rate. Thus we have a linear mixed‐effects model (fixed intercepts, fixed group slopes, random individual subject slopes, random within‐subject additive or observational error) where, for a specific diagnostic group, the measurement Y _ij at time t _ij for subject i at follow‐up timepoint j is Y _ij = m _i t _ij+ε_ij. Here, ε_ij is the within‐subject error, assumed to be independent and identically normally distributed with zero mean and variance σ${}_{\text{e}}^{\text{2}}$; m _i = m + γ_i, where m is the fixed effect slope (mean rate of change for the group) and γ_i is the between‐subject random effect slope with variance σ${}_{\text{m}}^{\text{2}}$. We use the Matlab (version R2009b) nlmefit function in the Statistics Toolbox (http://www.mathworks.com) to obtain maximum likelihood point estimates of σ${}_{\text{e}}^{\text{2}}$, σ${}_{\text{m}}^{\text{2}}$, and m. These fixed and random effects parameter estimates can be used in power calculations to obtain point estimates of the sample sizes N, per arm, required for a hypothetical placebo‐controlled longitudinal study, as described in [Fitzmaurice et al., 2004]. This approach was used to calculate sample sizes required to detect a 25% slowing in mean rate of decline for a hypothetical disease‐modifying treatment versus placebo for a 24‐month, two‐arm, equal allocation trial, with 6‐month assessment intervals. Power calculations were performed with the requirement that the trial have 80% power to detect the treatment effect using a two‐sided significance level of 5%. When correcting for normal aging, the sample size estimates were calculated using the variance parameters (σ${}_{\text{e}}^{\text{2}}$, σ${}_{\text{m}}^{\text{2}}$) from the patient cohort, while the treatment effect size of interest was assumed to be 25% of the difference between the mean rates of change in the patient and healthy populations.

To determine 95% confidence intervals on the sample size estimates, the joint a posteriori probability density function for the mixed effects model parameters (σ${}_{\text{e}}^{\text{2}}$, σ${}_{\text{m}}^{\text{2}}$, and m) was computed based on the multivariate Gaussian likelihood function of the observed data, given the model parameters, evaluated at a regular mesh of points in the space spanned by the model parameters. The sample size values at the mesh points were then sorted, and the cumulative distribution calculated from the correspondingly sorted a posteriori probability values. The 95% confidence intervals were then computed from the cumulative distribution function (cdf) values of 0.025 and 0.975.

To calculate P values for pairwise comparisons of sample sizes required for different measures, we carried out a two‐tailed test for the null hypothesis of equal sample sizes (N ₁ − N ₂ = 0). We used the a posteriori probability distributions described above to compute the probability distribution for the difference between the sample sizes for the two measures; the latter is given by the convolution of the two sample size distributions, since N ₁ and N ₂ are independent random variables. Thus, p = 2 × min[P (N ₁ ≤ N ₂), P (N ₂ ≤ N ₁)], where P (N ₁ ≤ N ₂) = cdf_N1‐N2(0), and P (N ₂ ≤ N ₁) = 1‐cdf_N1‐N2(0) [Casella and Berger, 2002].

RESULTS

Bias

The TBM Stat‐ROI measure showed statistically significant bias, as illustrated in Figure 1. This figure shows the average cumulative atrophy detected by this method, as a percentage of baseline volume, for HC, MCI, and AD subjects up through 36‐months, along with the additive bias estimate. Without accounting for bias, the cumulative atrophy plots show that all three groups undergo an initial high rate of change (an average of 1.64% for HC, 1.93% for MCI, and 2.28% for AD over the first 6‐month interval of the study), with substantially lower rates of change after that (e.g., average change in the second 6‐month period of the study is 0.34% for HC, 0.55% for MCI, and 0.76% for AD subjects; for the final 12‐months of the study, the average change was 0.09% for MCI and −0.01% for HC—a pronounced deceleration that is indicative of higher‐order contributions to bias in TBM). Based on the simultaneous linear fit to the 6‐ and 12‐month timepoints of all three diagnostic groups, estimated additive bias was 1.31%, which is equal to 68% of the observed change in the MCI cohort and 57% of the observed change in the AD cohort at 6‐months. The P value for the null hypothesis of no bias was, to the precision of the Matlab numerical libraries, 0. Although subject data from the modified TBM Stat‐ROI method are not available, Hua et al. [ 2011] report a bias of 0.29% in the modified method, which is substantially reduced from 1.31% reported above. However, the new measures of change for the Stat‐ROI are also substantially reduced (average change measurement of 0.5% for HC, 0.6% for MCI, and 0.9% for AD over the first 6‐month interval of the study), so that the bias as a percentage of 6‐month change in MCI remains large: 48%. (We note that the bias reported in [Hua et al., 2011] would be slightly reduced if actual visit times were used, that is, not assuming that all visits happened exactly at 6‐month intervals.)

Figure 1.

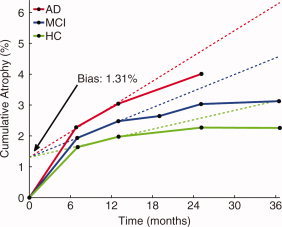
Average cumulative atrophy for TBM Stat‐ROI, as a percentage of baseline volume, for HC, MCI, and AD subjects, along with linear fits for the additive bias estimate. The additive bias of 1.31% is large, equal to 68% of the change in the MCI cohort, and 57% of the change in the AD cohort, at 6‐months, and highly statistically significant (P = 0 to precision of Matlab numerical libraries). The linear fits are conservatively restricted to the 6‐ and 12‐month visits. Note the slight shift to the right for follow‐up visits. On average, actual visit dates occurred later than the nominal interval dates.

The KN‐BSI measure also showed significant bias, accounting for 18% of the change observed in MCI subjects and 12% of the change observed in AD subjects at 6‐months (P = 0.042). None of the other methods showed significant bias.

Estimated sample sizes for absolute‐change were smallest for the bias‐uncorrected TBM Stat‐ROI measure. For example, using 291 MCI subjects, the sample size estimate to detect 25% slowing in the MCI population was N = 84, and the 95% confidence interval was CI = [71 103]. After bias correction, however, this estimate more than tripled, to N = 287, CI = [223 395], rendering this method significantly less powerful for detecting change than bias‐corrected KN‐BSI (head‐to‐head comparison of 266 MCI subjects: TBM N = 319, CI = [239 457]; KN‐BSI N = 147, CI = [117 197]; P value for difference in sample‐size estimates = 0.0002), Quarc entorhinal (236 MCI subjects: TBM N = 233, CI = [179 327]; ERC N = 150, CI = [118 202]; P = 0.029), and Quarc hippocampus (Hipp. N = 156, CI = [122 210]; P = 0.047). Sample size estimates for all methods, after bias‐correction, are shown in Table II for MCI and Table III for AD.

For the modified TBM Stat‐ROI method, the sample size estimate reported for absolute change in MCI is N = 129; correcting this for the 0.29% bias (and using the new estimated MCI annual rate of change of 1%, along with the standard sample size formula, ibid.), gives N = 129/(1 − 0.29)² = 256, close to the value N = 287, CI = [223 395], reported above and in Table II for the original TBM Stat‐ROI method.

Relative vs. Absolute Change: Defining the Potentially Treatable Effect

To determine whether atrophy rates in HCs are due to preclinical AD (the implicit assumption in numerous published studies that use absolute rather than relative change measures in sample size calculations), we examined atrophy rates in the two ROIs affected earliest in AD–entorhinal cortex and hippocampus—as well as in the whole brain in HCs who tested negative for Aβ pathology, based on the cut‐off value of CSF Aβ₄₂ levels >192 pg/mL as determined by Shaw et al. [ 2009], for all methodologies for which these ROIs are defined; we also similarly examined the TBM temporal lobe Stat‐ROI (note that CSF measures were obtained only on a subset of ADNI subjects—see Table I). Figure 2 shows bias‐corrected annual atrophy rates with 95% confidence intervals for the full HC group, the two HC subgroups who were, respectively, Aβ‐negative and Aβ‐positive, and the MCI group; these atrophy rates were calculated using a mixed‐effects regression model on all baseline data and follow‐up data available up to 3‐years, as described in the Methods section.

Figure 2.

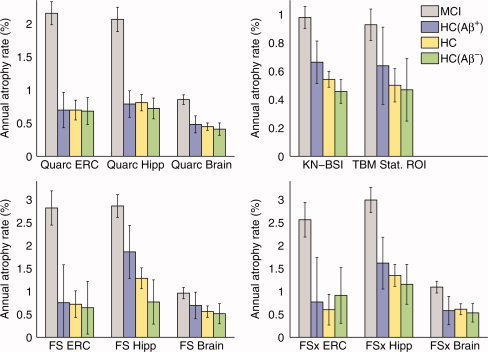
Annual rate of volume change in entorhinal cortex (ERC), hippocampus (Hipp), and whole brain (Brain and KN‐BSI), with 95% confidence intervals, calculated for all methodologies, along with the TBM Stat‐ROI. Aβ‐negative HCs are almost the same as all HCs, but have approximately a third to a half the change seen in MCI; Aβ‐positive HCs atrophy at a slightly higher rate than Aβ‐negative HCs. Thus, most HC change is not AD‐related; assuming it is leads to seriously underpowered clinical trials. All rates are corrected for bias, if any. Note that only a subset of all HCs had Aβ status determined.

As shown in Figure 2, longitudinal volumetric changes in entorhinal cortex, hippocampus, and whole brain are clearly present in Aβ‐negative HC subjects, and the annual percentage changes in these subjects do not substantially differ from those observed in the full HC group. Atrophy rates in Aβ‐negative HC subjects for all ROIs, regardless of methodology, are a substantial fraction (one‐third to one‐half) of the atrophy rates seen in MCI subjects. As the anatomical changes seen in Aβ‐negative HC subjects are not likely to be due to Aβ pathology, there is no reason to expect that they would be affected by therapeutic agents designed specifically to target amyloid pathology. The potentially treatable effect therefore would be most realistically defined as the amyloid‐negative aging‐corrected rate of change in the patient cohort, that is, the difference in rates of change between the patient group and the Aβ‐negative HC subjects. However, since there is little difference between the atrophic rates of change in the Aβ‐negative HC group and the full HC group (compared with the differences between either of these groups and the MCI or AD groups), the potentially treatable effect could conservatively be defined as the aging‐corrected rate of change in the patient cohort, that is, the difference in rates of change between the patient group and the full HC group–to take advantage of the larger N of the full control group.

The annual rates of change for the TBM Stat‐ROI shown in Figure 2 are very similar to those for the whole brain measure KN‐BSI, which in turn are fairly consistent with the whole brain measures for Quarc, FS, and FSx. (Note that the statistics for the HC(Aβ⁺) group are poorest, reflecting the relatively small number of subjects in that group—see Table I.) This is, on the face of it, an unexpected result because the TBM Stat‐ROI was specifically designed to identify the brain subregion undergoing the highest rate of change, yet the resulting rates are essentially the same as those for whole brain change obtained by the other methods. The estimates reported in [Hua et al., 2011] imply even smaller rates of change; for example, the TBM Stat‐ROI annual rate of change for MCI, when correcting for the remaining bias, is 1 − 0.29 = 0.71%, compared with 0.98%, CI = [0.90% 1.06%], for KN‐BSI.

Sample Size Estimates

Sample size estimates using disease‐specific (aging‐corrected) and absolute (aging‐uncorrected) rates of change for bias‐corrected data are shown in Figure 3 for MCI subjects and Figure 4 for AD subjects, for representative measures for each methodology (numerical values for these and other neuroimaging measures are shown in Tables II and III). For reference, the sample size estimate using CDR‐SB, the most sensitive standard clinical outcome measure, is also shown. P‐values for the significance of the difference in sample size estimates from all head‐to‐head pairwise comparisons of relative‐change (aging‐corrected) measures are in Tables IV and V, for MCI and AD, respectively. In the figures, data are arranged in ascending order for the conservative aging‐corrected sample size estimate, “MCI‐HC” or “AD‐HC.” CDR‐SB represents a demarcation for those neuroimaging measures that are competitive with current clinical outcome measure in tracking longitudinal change over time in MCI and mild AD. In the case of MCI, only the entorhinal cortex (ERC) as measured by Quarc has a conservative disease‐specific 95% confidence interval that is wholly below the CDR‐SB confidence intervals (head‐to‐head comparison involving 311 MCI subjects and 181 HC subjects gives: Quarc ERC N = 297, CI = [216 439]; CDR‐SB N = 582, CI = [417 884]; P value for difference in N's = 0.01). Head‐to‐head comparisons of the Quarc measures with measures from the other methodologies are shown in Figure 5 for MCI and Figure 6 for AD; P values presented in the first row in Table IV show that for MCI the Quarc entorhinal is significantly more powerful than all other measures of change, except the Quarc Hippocampus. From either the last column (MCI‐HC) or last row (MCI‐HC(Aβ⁻)) in Table IV, Quarc ERC is the only measure that is statistically significantly superior to CDR‐SB. From Figure 2, the measurement of rates of change for FS Hippocampus appears to be anomalous for the HC(Aβ⁻) and HC(Aβ⁺) groups, which show substantial and significant difference. This is in contrast with the much higher degree of similarity among these subject groups for all other measures. Furthermore, one would expect the point estimates for FS and FSx to be similar, as indeed they are for the hippocampus measured for all MCIs and all HCs, and for all subject groups for the whole brain. It should be noted that there are much fewer subjects in the HC(Aβ⁻) and, particularly, the HC(Aβ⁺) groups compared to all HCs (see Table I), so the estimates for these subgroups are not as robust.

Figure 3.

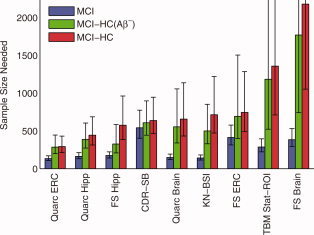
Estimated sample sizes, per arm, to detect a 25% reduction in rate of change in MCI subjects, at the P < 0.05 level with 80% power assuming a 24‐month trial with scans every 6 months. Sample sizes are estimated using a linear mixed effects model with fixed intercepts (no relative change at baseline) and random slopes applied to all data available up through 36 months. Results for the conservative aging‐corrected rates of change are shown in red; results for the more realistic amyloid‐negative aging‐corrected rates of change are shown in green; and results for absolute (aging uncorrected) rates of change are shown in blue. Error bars show the 95% confidence intervals. All numerical values are shown Table II. P‐values for all head‐to‐head pairwise comparisons of measures are in Table IV. FS is FreeSurfer‐longitudinal. FreeSurfer‐cross‐sectional (FSx) generally performs poorer than FS; it is not shown here, but values for it are in Tables II and IV.

Figure 4.

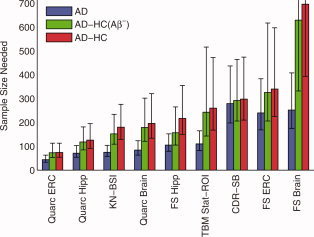
Estimated sample sizes, per arm, to detect a 25% reduction in rate of change in mild AD subjects, at the P < 0.05 level with 80% power assuming a 24‐month trial with scans every 6 months. See caption of Figure 3 for further details. Numerical values are shown in Table III. P‐values for all head‐to‐head pairwise comparisons of measures are in Table V.

Table IV.

P‐values for significance of difference in head‐to‐head comparisons of sample size estimates: MCI‐HC above diagonal, MCI‐HC(Aβ⁻) below diagonal

Measure	Quarc‐ Entorhinal	Quarc‐ Hippocampus	Quarc‐Whole‐ Brain	FS‐ Entorhinal	FS‐ Hippocampus	FS‐Whole‐ Brain	FSx‐ Entorhinal	FSx‐ Hippocampus	FSx‐Whole‐ Brain	KN‐ BSI	TBM‐ Stat‐ROI	CDR‐SB
Quarc‐ERC		0.12	0.005	0.005	0.014	4e‐6	1e‐5	0.013	7e‐6	0.008	2e‐4	0.01
Quarc‐Hipp	0.29		0.2	0.2	0.36	0.002	0.004	0.33	0.003	0.31	0.037	0.37
Quarc‐Brain	0.049	0.3		0.91	0.83	0.056	0.19	0.57	0.14	0.8	0.24	0.67
FS‐ERC	0.005	0.1	0.51		0.44	0.02	0.11	0.86	0.019	0.88	0.4	0.77
FS‐Hipp	0.24	0.95	0.41	0.065		0.003	0.02	0.39	0.003	0.77	0.074	0.88
FS‐Brain	3e‐4	0.015	0.16	0.12	3e‐4		0.43	0.031	0.95	0.026	0.49	0.004
FSx‐ERC	4e‐6	3e‐4	0.051	0.047	6e‐6	0.83		0.29	0.21	0.063	0.72	0.05
FSx‐Hipp	0.076	0.39	0.61	0.86	0.1	0.065	0.057		0.025	0.8	0.076	0.54
FSx‐Brain	0.004	0.04	0.48	0.13	4e‐4	0.84	0.88	0.085		0.04	0.51	0.003
KN‐BSI	0.026	0.53	0.56	0.3	0.26	0.16	0.006	0.93	0.23		0.23	0.96
TBM‐St.ROI	0.013	0.15	0.37	0.76	0.003	0.81	0.48	0.17	0.6	0.15		0.51
CDR‐SB	0.015	0.16	0.92	0.94	0.06	0.051	0.02	0.91	0.04	0.42	0.63

Values significant at the 5% level are bold and underlined. Sample size estimates calculated from all available (per measure) subject‐timepoints are in Table II. Sample size head‐to‐head comparisons with Quarc are in Figure 5.

Table V.

P‐values for significance of difference in head‐to‐head comparisons of sample size estimates: AD‐HC above diagonal, AD‐HC(Aβ⁻) below diagonal

Measure	Quarc‐ Entorhinal	Quarc‐ Hippocampus	Quarc‐Whole‐ Brain	FS‐ Entorhinal	FS‐ Hippocampus	FS‐Whole‐ Brain	FSx‐ Entorhinal	FSx‐ Hippocampus	FSx‐Whole‐ Brain	KN‐ BSI	TBM‐ Stat‐ROI	CDR‐ SB
Quarc‐ERC		0.048	7e‐4	<e‐6	7e‐5	4e‐6	<e‐6	6e‐5	3e‐6	0.009	1e‐4	4e‐6
Quarc‐Hipp	0.085		0.13	9e‐4	0.034	0.005	9e‐6	0.039	0.005	0.46	0.32	0.01
Quarc‐Brain	0.003	0.16		0.044	0.39	0.12	0.005	0.64	0.23	0.37	0.19	0.29
FS‐ERC	<e‐6	5e‐4	0.028		0.17	0.08	0.1	0.49	0.62	0.072	0.46	0.48
FS‐Hipp	0.001	0.13	0.74	0.039		0.002	0.003	0.51	0.072	0.39	0.45	0.43
FS‐Brain	5e‐5	0.013	0.18	0.16	8e‐4		0.92	0.03	0.33	0.047	0.032	0.012
FSx‐ERC	<e‐6	1e‐6	0.002	0.047	7e‐5	0.51		0.019	0.99	7e‐4	0.073	0.03
FSx‐Hipp	4e‐4	0.053	0.71	0.4	0.25	0.043	0.005		0.025	0.1	0.45	0.7
FSx‐Brain	1e‐4	0.022	0.44	0.79	0.027	0.34	0.46	0.044		0.006	0.042	0.04
KN‐BSI	0.012	0.57	0.53	0.026	0.89	0.13	1e‐4	0.21	0.027		0.094	0.062
TBM‐St.ROI	0.002	0.48	0.26	0.45	0.1	0.11	0.032	0.49	0.082	0.086		0.4
CDR‐SB	6e‐6	0.005	0.21	0.57	0.071	0.038	0.015	0.49	0.1	0.023	0.41

Values significant at the 5% level are bold and underlined. Sample size estimates calculated from all available (per measure) subject‐timepoints are in Table III. Sample size head‐to‐head comparisons with Quarc are in Figure 6.

Figure 5.

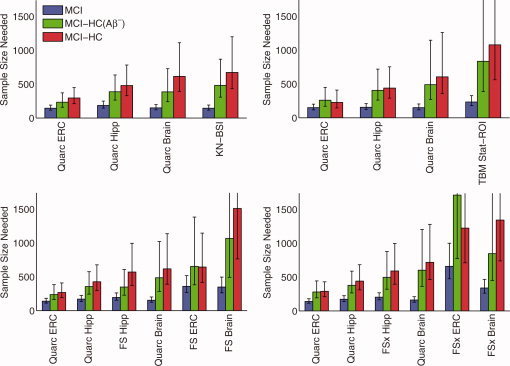
Estimated sample sizes for MCI, as in Figure 3, but from pairwise head‐to‐head comparison of Quarc with: BSI (subjects in common: 287 MCI, 170 HC, 55 HC(Aβ⁻)); TBM (236 MCI, 132 HC, 41 HC(Aβ⁻)); FreeSurfer‐longitudinal (267 MCI, 161 HC, 49 HC(Aβ⁻)); and FreeSurfer‐cross‐sectional (305 MCI, 178 HC, 56 HC(Aβ⁻)). P‐values for all head‐to‐head pairwise comparisons of measures are in Table IV.

Figure 6.

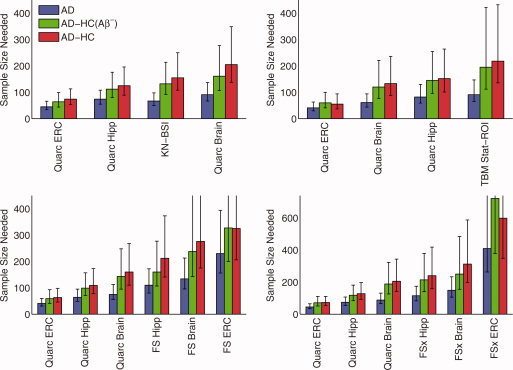
Estimated sample sizes for AD, as in Figure 4, but from pairwise head‐to‐head comparison of Quarc with BSI (123 AD subjects in common—see also Figure 5); TBM (97 AD); FreeSurfer‐longitudinal (FS; 107 AD); and FreeSurfer‐cross‐sectional (FSx; 129 AD; note different scale due to relatively poor performance for entorhinal cortex). P‐values for all head‐to‐head pairwise comparisons of measures are in Table V.

Sample size estimates for the more realistic amyloid‐negative aging‐corrected rates of change, that is, for “MCI‐HC(Aβ⁻)”, are generally lower compared with those for “MCI‐HC”, reflecting the slightly smaller atrophic rates for HC(Aβ⁻) compared with those for HC in Figure 2. Note that the point estimates for both the Quarc and FS entorhinal remain unchanged.

Using the estimated annual rates of change reported in [Hua et al., 2011] for MCI, and noting that additive bias is essentially eliminated when calculating relative change between groups, the sample size estimate from the modified TBM Stat‐ROI method for the change in MCI relative to that in all HCs is N = 129/(1 − 0.7)² = 1,433, close to the value N = 1,358, CI = [712 3624], reported in Table II for the original TBM Stat‐ROI method.

Sample size estimates for a trial involving mild AD patients, shown in Figure 4 and Table III, are substantially smaller, with most neuroimaging outcome measures yielding smaller estimated sample sizes than the CDR‐SB (significance of differences are in Table V). Sample size estimates based on absolute change are also shown for comparison. As expected, for any given neuroimaging measure, they are substantially smaller with much tighter confidence intervals than their disease‐specific counterparts.

Figures 5 and 6 show direct head‐to‐head comparisons of all methodologies with Quarc. In all cases, the entorhinal and hippocampal measures from Quarc were the strongest measures of change.

DISCUSSION

This study compared five widely used methodologies for quantifying longitudinal change measures from structural MRIs and examined two critical issues that significantly impact sample size estimation when neuroimaging measures are used as outcome variables: bias in image analysis and the definition of the potentially treatable effect. Failure to control for either of these factors can lead to dramatic underestimation of sample sizes needed to detect a potentially beneficial effect of a disease‐modifying therapy.

Potential bias in image registration is a well‐known problem in the analysis of serial MRIs that has received much attention in recent literature [Thompson and Holland, 2011]. Although most methodologies employ procedures to minimize bias, our results show that some commonly used methods, particularly TBM Stat‐ROI, are significantly affected. For TBM Stat‐ROI, correction for bias tripled (or doubled, using the alternative results from the modified method) the sample size estimates for detection of change in MCI subjects. Acquiring scans on the same day, where no deformation is expected, would provide ideal images for testing the presence of additive bias—though multiplicative bias would remain undetectable using such images. A simple way to eliminate bias due to registration methodology is to make the entire procedure symmetric by construction: register image A to image B, independently register image B to image A, and then combine the changes measured in both directions by algebraic or geometric averaging.

The definition of the potentially treatable effect is another critical factor that profoundly affects estimated sample sizes. The majority of publications in the ADNI literature, notably [Beckett et al., 2010; Cummings, 2010; Hua et al., 2010; Vemuri et al., 2010], implicitly define the potentially treatable effect as the absolute change from baseline, although as mentioned earlier there are exceptions [Fox et al., 2000; Holland et al., 2009; McEvoy et al., 2010; Schott et al., 2010]. The rationale for use of absolute change measures has not clearly been articulated in published reports, but presumably it arises from the assumption that atrophy in HCs is dominated by a subset of HCs who are in a preclinical stage of AD and experiencing disease‐related elevated rates of decline. We directly tested this assumption by examining atrophy rates in HCs who tested negative for Aβ pathology on the basis of CSF Aβ₄₂ levels and comparing these rates with those seen in all HCs. Since amyloid lesions neuropathologically partly characterize AD [Mirra et al., 1991], and CSF and PET measures of their prevalence are believed to be the earliest detectable signs of possible AD [Morris et al., 2010] (in which case clinical decline might not occur until a decade or so after the lesions become manifest [Price and Morris, 1999]), elderly individuals without Aβ pathology are highly unlikely to be in a preclinical stage of AD—and indeed since many elderly HCs have elevated plaque burden while remaining cognitively normal [Price et al., 2009], it might be that “Alzheimer's is not a part of normal aging any more than breaking your hip is a part of normal aging” [Herrup, 2010]. Our results show, however, that the Aβ‐negative HCs experienced an approximately similar rate of whole brain, entorhinal, and hippocampal atrophy as the full, undifferentiated HC group. Furthermore, as can be seen in Figure 2, apart from the anomalous “FS Hipp” result discussed above, hippocampal and entorhinal atrophy rates are similar for HC(Aβ⁺) and HC(Aβ⁻). This result is in agreement with neuropathological studies that show no significant difference in total entorhinal [Price et al., 2001] and hippocampal [West et al., 2004] neuron counts—even in CA1, the hippocampal sector most affected by neuron loss in the early stages of AD—between cognitively normal subjects essentially free of amyloid pathology and those exhibiting significant amounts of amyloid deposition, to a degree consistent with a neuropathological diagnosis of possible AD. Thus, the preponderance of atrophy in HCs must arise from causes other than Aβ pathology, and it would not be reasonable to expect an AD therapy, in particular one targeting Aβ pathology, to reduce atrophy rates for atrophy that occurs in the absence of such pathology. Neuropathological analysis of HCs who do not fulfill criteria for the neuropathological diagnosis of AD or other neurodegenerative disease [Freeman et al., 2008] supports this conclusion. Atrophy in such individuals can persist over an age range of five decades, likely reflects loss of dendritic complexity in neuropil and/or changes in neuronal size, but in contrast with AD‐related atrophy, preserves neuronal number. The neuropathological study shows further that in these subjects the presence of diffuse plaques did not correlate with cortical atrophy; that cortical atrophy correlates with age; and though neuritic plaque burden also correlates with age, the small number of plaques and tangles had no direct influence on cortical atrophy. Therefore, “cortical changes seen in aging are not simply the result of early AD changes but are related to aging itself” (ibid.).

It should be noted that in a clinical trial employing biomarkers for the natural history of the disease, care must be taken in assessing the disease modifying ability of the therapy [Citron, 2010; Salloway et al., 2008]. Correlation is not sufficient [Baker and Kramer, 2003]: the biomarker must also be in the causal pathway of the disease, and directly relate to clinically meaningful endpoints [Mani, 2004]. By the same token, therapy might affect atrophy in unexpected ways, as shown by the AN1792 Aβ immunotherapy trial [Gilman et al., 2005] where whole brain atrophy was greater in the approximately one‐fifth of subjects who were antibody responders than in the placebo group, a result possibly due to brain hydration state related to therapy, or to negative effects of the vaccination on fiber or white matter volume, and that was not reflected in worsening cognitive performance [Fox et al., 2005]. Though clinical improvement in this trial largely may have been precluded because the patient cohort was at a relatively advanced stage of the disease [Holmes et al., 2008; Hyman, 2011], this outcome nevertheless argues in favor of analyzing subregional, in particular cortical, change rather than global change when monitoring disease‐modifying effects of therapy.

Defining the potentially treatable effect based on absolute change from baseline is attractive in that it leads to small sample size requirements—often much smaller than those based on standard clinical outcome measures. This approach represents the most optimistic assessment of the potentially treatable effect. The more conservative approach of defining the potentially treatable effect relative to change experienced by all HCs, or the slightly more realistic approach of defining it relative to change experienced by Aβ‐negative HCs, may represent a more achievable goal, particularly since most current therapies target amyloid pathology. Requiring the treatment to slow all change, even that unrelated to the targeted mechanism of the drug, is likely to result in a trial that is substantially underpowered to detect slowing of disease‐specific atrophy. An additional advantage of using relative rather than absolute change measures is that any purely additive systematic bias in the results arising from errors in image acquisition or analysis methods will, by definition, be removed upon subtraction.

Consideration of these two factors together–bias correction and defining the potentially treatable effect as a measure of relative rather than absolute change–substantially alters the conclusions regarding the relative sensitivity of different neuroimaging biomarkers from what has been published in the literature [Beckett et al., 2010; Cummings, 2010; Jack et al., 2010]. From data available on the ADNI website through April 16, 2011, estimates of change in subregional cortical areas, as determined by Quarc, produce the smallest estimated sample sizes when change relative to HCs is taken into account. In particular, for the entorhinal cortex, the area known to be first affected by AD pathology, N = 293 CI = [214 432] for MCI‐HC, N = 74 CI = [54 113] for AD‐HC, and as can be seen in Table IV, sample size estimates based on the Quarc entorhinal are the only ones that are significantly smaller than those achieved using CDR‐SB as the outcome measure for either MCI‐HC or MCI‐HC(Aβ⁻). Several other temporal lobe structures quantified with Quarc (Tables II and III) also provided powerful relative‐change biomarkers, including the amygdala (N = 366 CI = [264 549] for MCI‐HC, N = 132 CI = [94 205] for AD‐HC) which suffers from a significant increase in the numbers of both neuritic plaques and NFTs when transitioning from HC to amnestic MCI, and again when transitioning from amnestic MCI to early AD [Markesbery et al., 2006]. Quarc was designed not only to capture large‐scale structural change, but also to measure change in small regions with high precision [Holland and Dale, 2011], and generally provides significantly improved measures of change compared with those of the standard (cross‐sectional) FreeSurfer and FreeSurfer‐longitudinal, the only other methods that attempt to quantify change in cortical regions. The results presented here for Quarc were derived using both the back‐to‐back scans per timepoint (which should improve signal to noise); the other methods used a single scan per timepoint (choosing the best scan from each pair should reduce the degrading impact of image artifacts). Though these effects have not been assessed here, when considering future trials the requirement for acquiring two scans to achieve these sample sizes should be borne in mind. Also, sample size estimates have not been modeled to account for attrition due to QC. (The methods used in Quarc are fully documented in [Holland and Dale, 2011], and are available to other researchers on a not‐for‐profit recharge basis through the UCSD Multimodal Imaging Laboratory, mmil.ucsd.edu.)

Although the current study is primarily concerned with issues that affect the use of neuroimaging biomarkers as outcome measures in clinical trials, it is important to point out that longitudinal MRI measures as provided by ADNI are also being used in the comparative investigation of disease‐related trajectories of various AD biomarkers [Caroli and Frisoni, 2010; Frisoni et al., 2010; Jack et al., 2010; Perrin et al., 2009; Trojanowski et al., 2010]. To ensure fidelity of the serial measurements, it has been proposed in a recent consensus article [Klein et al., 2009] that registration procedures be validated with respect to linearity (the inverse consistency of forward and reverse transformations between image pairs), and transitivity (e.g., the total change calculated when registering visit 3 to visit 1 should equal the sum calculated when registering visit 3 to visit 2, and visit 2 to visit 1). The methodologies used in ADNI, including Quarc, have not been validated in this respect. Therefore, caution is advised when considering the validity of the nonlinear trajectories that have been published based on ADNI data.

CONCLUSION

ADNI has been revolutionary in its pioneering of the open source model of data sharing, making raw data and derived measures freely accessible to the scientific community and industry as soon as they become available. It has been highly successful in advancing research on biomarkers in AD. ADNI results are being used by the pharmaceutical industry to aid in decision‐making on the choice of biomarkers for use as outcome measures, and for powering clinical trials. Ultimately, ADNI data and analyses may form the basis for regulatory qualification for imaging biomarkers.

It is thus essential that these biomarkers are validated and that the models used for power calculations be consistent with the biological mechanisms targeted by the therapy under investigation. It should be noted, however, that establishing imaging biomarkers as surrogates for clinical‐cognitive outcomes cannot be achieved with natural history studies, but will require successful clinical trials, that is, ones where cognitive outcomes are improved and where there is a clear and cogent biological connection with the imaging measures [Carrillo et al., 2009; Katz, 2004]. Establishing the surrogacy of biomarkers will be all the more difficult if those biomarkers are not correctly calibrated for non‐disease‐related effects. For therapies targeting Aβ pathology, it is not reasonable to expect that they will affect atrophy rates observed in healthy individuals without evidence of Aβ pathology. Since such individuals show atrophy rates in AD‐vulnerable structures equivalent to those of the larger HC group, the potentially treatable effect is best conservatively defined as change relative to that experience by HCs. It is also essential to provide confidence intervals for any sample size estimates to enable selection of biomarkers that estimate change with the highest certainty [Holland et al., 2009; McEvoy et al., 2010; Schott et al., 2010].

As part of the stated goals of the study, ADNI has been charged with statistically evaluating and comparing the different biomarkers and analysis methods to inform clinical trial design. To date, results presented and published by ADNI have not taken these critical issues into account. They report sample size estimates based only on absolute change measures; they have not considered issues of potential bias in image registration; and they have not provided a clear index of uncertainty of the results. If left uncorrected, these findings could lead to the adoption of suboptimal biomarkers for outcome measures, and to trials that are substantially underpowered for detecting potential disease‐modifying effects.