Automatic Classification of Left Ventricular Regional Wall Motion Abnormalities in Echocardiography Images Using Nonrigid Image Registration

Abstract

Identification and classification of left ventricular (LV) regional wall motion (RWM) abnormalities on echocardiograms has fundamental clinical importance for various cardiovascular disease assessments especially in ischemia. In clinical practice, this evaluation is still performed visually which is highly dependent on training and experience of the echocardiographers and therefore suffers from significant interobserver and intraobserver variability. This paper presents a new automatic technique, based on nonrigid image registration for classifying the RWM of LV in a three-point scale. In this algorithm, we register all images of one cycle of heart to a reference image (end-diastolic image) using a hierarchical parametric model. This model is based on an affine transformation for modeling the global LV motion and a B-spline free-form deformation transformation for modeling the local LV deformation. We consider image registration as a multiresolution optimization problem. Finally, a new regional quantitative index based on resultant parameters of the hierarchical transformation model is proposed for classifying RWM in a three-point scale. The results obtained by our method are quantitatively evaluated to those obtained by two experienced echocardiographers visually as gold standard on ten healthy volunteers and 14 patients (two apical views) and resulted in an absolute agreement of 83 % and a relative agreement of 99 %. Therefore, this diagnostic system can be used as a useful tool as well as reference visual assessment to classify RWM abnormalities in clinical evaluation.

Introduction

Cardiovascular disease (CVD) is one of the major causes of death throughout the world (34.3 % of mortality in 191 countries) [1]. Coronary artery disease causes more than half of CVD deaths per year [1]. This disease is the result of the occlusion of coronary arteries. When the blood flow to the heart muscle is reduced, contractility or motion of that piece of heart muscle fed by the obstructed artery will become impaired. This is known as ischemia. This disease can be diagnosed by measuring and scoring the regional wall motion (RWM) of the left ventricle (LV). Currently, echocardiography is the preferred method among other modalities (e.g., magnetic resonance (MR) and computed tomography) to assess RWM of LV because of its low cost, harmlessness to the human body, portability, and real-time imaging. In clinical practice, the evaluation of the RWM is mainly based on visual analysis of echocardiographic images. It relies on the ability of the echocardiographers to recognize patterns of endocardial and epicardial motion and thickening of each segment of the LV and then to assign a quantitative score to each segment according to a three-point scale—1: normal, 2: hypokinetic, 3: akinetic [2, 3]. This process which is usually denoted as visual RWM scoring facilitates and optimizes the treatment decision making. However, this visual assessment is highly dependent on experience and training of the echocardiographers and therefore suffers from significant interobserver and intraobserver variability [4]. Consequently, a robust and accurate automated method for detection and classification of RWM abnormality is highly desirable to obtain more objective and quantitative diagnosis, particularly for the novice echocardiographers.

Several methods have been proposed for quantifying the regional LV wall motion from two-dimensional (2-D) echocardiography images in the literature [5–35]. Two of these techniques are based on analyzing ultrasound radiofrequency (RF) signals [5–17]. The first method known as acoustic quantification is based on the detection of the interface between the tissue and the blood in each image. Synthesized color-coded images (color kinesis) are provided using this method to display the timing and magnitude of endocardial wall motion over time, either during the systolic phase or during the diastolic phase [5–11]. The various quantitative indices obtained from these synthesized images are proposed for assessment of RWM of LV [6–11]. However, this method is very dependent on the signal to noise ratio of RF signal. In addition, it only measures the movement of the endocardium and thickening of each segment is not considered. The second approach known as Tissue Doppler Imaging (TDI) estimates velocity, and strain/strain–rate values of the LV myocardial wall. The different quantitative indices obtained from these parameters are proposed to characterize the RWM [12–17]. However, this method is very dependent on the signal to noise ratio of the Doppler data. Moreover, it only measures the deformation of LV myocardial wall throughout the direction of the ultrasound beam. Other methods based on image post-processing techniques have been proposed for quantifying the RWM of LV in the literature [18–35]. In general, three types of methods have been proposed. The first studies the movement of the interior (endocardial) and exterior (epicardial) contours of the LV myocardium wall throughout the cardiac cycle after segmentation and tracking in echocardiography images. Then, several quantitative features are extracted to characterize the RWM of LV [18–26]. However, segmentation and tracking the interior and especially exterior contours of the LV myocardium wall in echocardiography images are difficult due to high level of uncorrelated speckle noise, shadowing and artifacts from valves and papillary muscles. The second type is based on methods of parametric imaging. In these methods, unlike approaches based on tracking a physical point, the variations in the grey levels measured in each pixel during a cardiac cycle are analyzed [27–31]. These methods provide synthesized color-coded images to summarize the information of LV myocardial contraction. The quantitative indices obtained from these synthesized images are proposed to classify RWM abnormality. However, these methods do not consider LV wall thickening and may be severely affected by cardiac translation. The third type is based on methods of tracking the speckle pattern or natural acoustic markers within the LV myocardium throughout the cardiac cycle [32–35]. These methods estimate displacement, velocity, and strain/strain–rate values of the LV myocardial wall. The different quantitative indices obtained from these parameters are proposed to quantify the RWM of LV. However, in the 2-D echocardiography images, the speckle pattern is decorrelated throughout the cardiac cycle because of the 3-D movement of the heart and the complex deformation of the myocardium.

In this paper, we attempt to overcome the underlying problems by proposing a new automatic method, based on nonrigid image registration, for detection and classification of RWM abnormalities of LV. In this algorithm, all pixels of an image (end-diastole) are tracked simultaneously over the cardiac cycle with a hierarchical parametric model, following an image registration algorithm as an optimization problem. The hierarchical model is based on an affine transformation for modeling the global LV motion and a free-form deformation (FFD) transformation based on B-spline for modeling the local LV deformation. The algorithm uses a multiresolution optimization strategy for higher speed and robustness. Consequently, the hierarchical transformation model together with a multiresolution optimization strategy provides a good framework for accurate estimation of the LV myocardial displacement field. Finally, a new regional quantitative index based on the resultant parameters of the hierarchical transformation model throughout the cardiac cycle is proposed for classification of RWM of LV.

Materials and Methods

Data Description

The study was approved by the Regional Committee for Medical Research Ethics and performed according to the Helsinki Declaration. Written informed consent was obtained from each participant. The 2-D image sequences of ten healthy volunteers and 14 patients (ischemic heart disease) from two apical views (apical four-chamber (A4C) and apical two-chamber (A2C)) were acquired. All recordings were made using a General Electric ultrasound machine with a frame rate of 46–74 per second, including the electrocardiogram (ECG) display. In the present study, for each view, one cardiac cycle was stored, with care being taken to ensure that there was no respiratory movement or probe displacement during the data acquisition. One cardiac cycle was identified by selecting the two consecutive R-wave of the ECG signal which is synchrone with the end of diastole phase. Echocardiography images were acquired during standard clinical examinations and no study was excluded because of image quality.

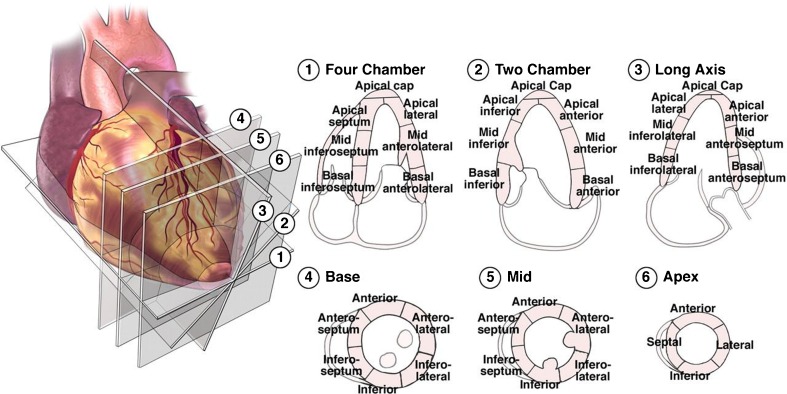
The American Heart Association (AHA) proposed a standard LV division of 17 segments that had a correspondence with the irrigation areas of the main coronary arteries (Figs. 1 and 2) [2]. In this study, RWM of LV myocardium was evaluated visually by examining the motion of the interior and exterior of the LV myocardium and also thickening of each segment. Then, each segment was scored according to a three-point standard scale—1: normal (normal wall thickening and motion), 2: hypokinetic (reduced wall thickening and motion), 3: akinetic (absence of wall thickening and motion) [2, 3]. The segments were analyzed and scored independently by two highly experienced echocardiographers, and then the consensual visual RWM scores between the two echocardiographers were used as reference scores (gold standard) for all comparisons. Currently, for each subject, we only used A2C and A4C views. Consequently, according to the reference scoring, among the 336 analyzed segments (48 sequences), 188 (56 %), 44 (13 %), and 104 (31 %) were normal, hypokinetic, and akinetic, respectively.

Fig. 1.

The recommended definition of LV division of 17 segments on echocardiographic views by the AHA [3]

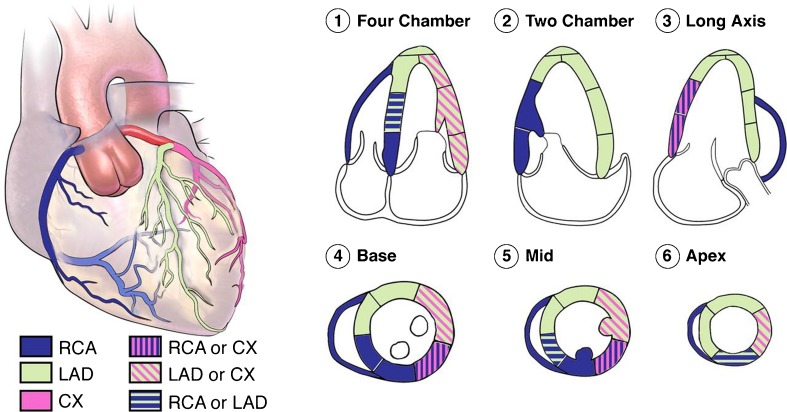
Fig. 2.

The distributions of coronary arteries perfusion in 17 segments of LV on echocardiographic views. The right coronary artery (RCA), the left anterior descending (LAD), and the circumflex (CX) are the coronary arteries [3]

LV Standardized Division

The approximate region of LV was extracted from echocardiography images (Fig. 3a) in each apical view. This was done by manually defining a rectangular region of interest (ROI) around LV on end-diastole image. This image was chosen because it has maximum LV volume at one cycle of heart and easily identified from the R-wave on the ECG signal. Then, the coordinates of the extracted rectangular ROI were automatically applied on all images of one cardiac cycle. These images are used for the following analysis in this study.

Fig. 3.

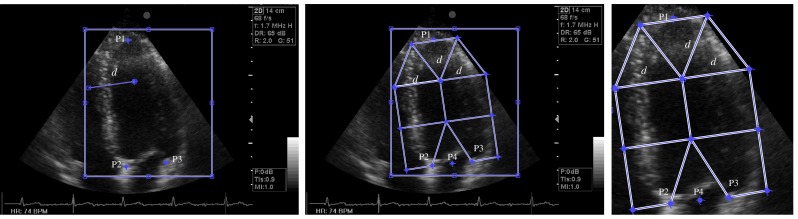
The LV standardized division in agreement with the guidelines of the AHA in A4C view. a A rectangular box around LV, three anatomic landmarks (P1, P2, P3) and a distance d manually positioned on the end-diastole image. b A mask with seven regions located on the LV excluding the mitral valves. c Extracted rectangular ROI

The LV in each apical view was divided up into seven regions in agreement with the LV standardized division by the AHA. To do this, for each view, three anatomical landmarks (the apex P1 and each side of the mitral valve P2, P3) and a distance d were manually located on end-diastole image by echocardiographer (Fig. 3a). Then, the LV division was automatically performed in three steps. First, the apex point P1 was connected to the mid-point P4 of the mitral valves points by a line, defined as the LV main axis. Second, the LV main axis was divided into three equal sections named apical, mid-, and basal using two orthogonal lines with length 2d. Third, apical section was divided into three equal regions by two radial lines with length d. Therefore, we defined a mask with seven regions located on the LV excluding the mitral valve (Fig. 3b). It should be noted that this LV division had been previously used for echocardiography images [27–31].

LV Displacement Field Estimation Using Image Registration

We consider an image sequence (images of one cardiac cycle) f(x, y, t) with t = t₀ (t = 0) ,… , t_I–₁ (t = I–1) and 0 ≤ x < X, 0 ≤ y < Y, where f(x, y, t) is the intensity of each pixel at position x, y and time t. Moreover, I is the total number of images of one cardiac cycle; X and Y denote the domain of the image.

Our goal is to estimate a displacement field, DF(x, y, t), for all pixels of end-diastole image (t = t₀) as a reference image over the cardiac cycle, that represents the position at time t of a pixel that was at position x, y at time t₀. In other words, we consider the end-diastole image as a spatial reference and we want to estimate the displacement field for all pixels of this image over the cardiac cycle. To do this, we register all images in a cardiac cycle to end-diastole image using a hierarchical transformation model [36]. The goal of image registration is to find the optimal parameters of the transformation model T(x, y). In conclusion, the displacement field for all pixels of the end-diastole image over the cardiac cycle is represented by the resultant transformation models as follow:

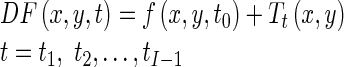1

T_t(x, y) is the estimated hierarchical transformation model using the image registration at time t to end-diastole image.

The motion of the LV is nonrigid. Moreover, it has a global motion and a local deformation. Therefore, in this paper, the transformation is represented by a nonrigid hierarchical model which consists of a global and a local model as follow [36]:

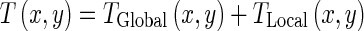2

The global motion model describes the overall motion of the LV over the whole sequence and is modeled by an affine transformation as follow:

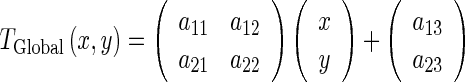3

The coefficients (a₁₁, a₁₂, a₂₁, a₂₂, a₁₃, a₂₃) parameterize the 6 degrees of freedom of the transformation, describing the rotation and translation of the LV.

The local deformation of the LV is modeled by a FFD transformation based on B-spline basis functions [37]. This nonrigid transformation is a powerful tool for modeling 2-D deformable objects and has been previously applied to the LV motion analysis in echocardiography images [38, 39]. FFD transformation deforms the shape of a 2-D object by manipulating an underlying mesh of control points [37]. The FFD is written as the 2-D tensor product of standard 1-D cubic B-spline:

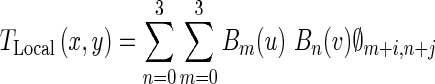4

Where i = ⌊x/n_x⌋ − 1, j = ⌊y/n_y⌋ − 1, u = x/n_x − ⌊x/n_x⌋, v = y/n_y − ⌊y/n_y⌋. Φ denotes a n_x × n_y mesh of control points (∅_i,j) with uniform spacing δ. Moreover, B_m(u) and B_n(v) are the basis functions of the B-spline evaluated at u and v, respectively as follow [37]:

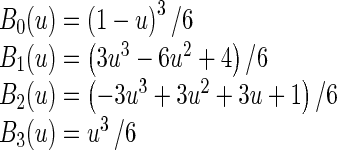The control points Φ act as parameters of the FFD transformation and the resolution of the control point mesh determines, simultaneously, the number of degrees of freedom of nonrigid deformation and consequently, the computational complexity. In the initial configuration, the control point mesh lies at their initial positions (Φ_initial) and by displacing or manipulating the control points, a desired deformation of the image is derived.

The result of image registration as an optimization problem is to estimate the optimal parameters of the hierarchical transformation (,Φ) so that a cost function defined in Eq. 5 associated with the image similarity and the smoothness of transformation is minimized.

5

We have used the sum of the squared intensities difference between homologous pixels in the two images as an image similarity criterion (Eq. 6). We chose to use this criterion because of its simplicity, fast computation time and good result even in the presence of decorrelated speckle noise. The similarity criterion is written as follow:

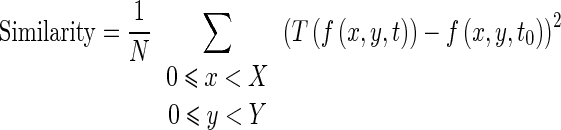6

Where N is the number of pixels in the image. Moreover, the transformation should be constrained to be smooth to prevent artifacts such as folding [40]. A common smoothing term which regularizes the transformation [40] is written as follow:

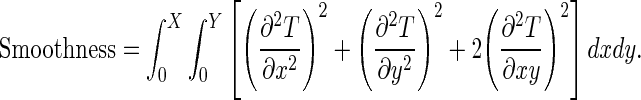7

In Eq. 5, λ is the weighting parameter which defines the tradeoff between the smoothness of the transformation and the image similarity criterion.

For computational efficiency, the optimization process proceeds in several stages. First, the affine transformation parameters are optimized by minimizing the cost function defined in Eq. 5. It is noted that the smoothness term of the cost function is zero for any affine transformation [40]. Then, the parameters of B-spline FFD transformation are optimized by minimizing the cost function defined in Eq. 5. In this step, we employ an iterative multiresolution optimization approach in which the resolution of the mesh of control points is increased, along with the image resolution, in a coarse to fine fashion to obtain a higher speed and robustness [41]. In addition, in each step, we apply an iterative gradient descent method [42] which steps in the direction of the gradient vector with a certain step size μ. The algorithm stops if the ║∇║ ≤ ε for some small positive threshold, where ∇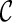 is the gradient vector of the cost function. Consequently, the final resultant positions of the control points of B-spline FFD (Φ_final) are the solution of our image registration problem.

A New Quantitative Regional Index

To quantify the RWM of LV, a new quantitative regional index which is related to final resultant position of control points of B-spline FFD model is proposed. To do this, after registering each image in one cycle of heart to the reference image, the sum of the squared Euclidean distance between homologous positions of initial (Φ_initial) and the final resultant (Φ_final) of the control points of B-spline FFD model for each region is computed. This value is divided by the number of control points in each region to normalize LV size and allow comparison between different cases.

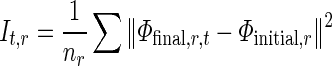8

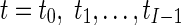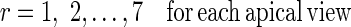Where n_r is the number of control points in region r and (Φ_final,r,t) is the final resultant positions of control points of B-spline FFD for image at time t and region r. Finally, for each myocardial region, the maximal value of the I_t,r through the images of one cardiac cycle is defined as the quantitative index for this region Ind_r.

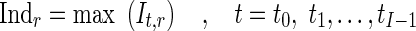9

Results

First, the LV in each apical view is divided up in a simple way into seven regions in agreement with the guidelines of the AHA, described in previous section (Fig. 3a). In this division, we reduce the influence of the mitral valve motion in the estimation of the LV myocardial motion. The coordinate of the seven regions are automatically saved for the next analysis. Then, we have computed the displacement field of every point of LV myocardium during a cardiac cycle by the proposed nonrigid image registration algorithm described in previous section in all data sets. For this purpose, we register all images in a cardiac cycle to end-diastole image using the hierarchical transformation model. We perform the image registration using the optimum parameter values (λ = 0.01, ε = 0.00001. A control point spacing of 5 mm). These values are chosen because these have provided a good compromise between the computing time and the accuracy of nonrigid image registration. Fig. 4 shows the image registration process between two images in A4C view for a healthy and a patient case. The left and middle parts show the end-diastole (reference) and end-systole images, respectively. The right part shows the corresponding image from registering end-systole image to the reference image. This figure also shows the positions of initial and final resultant mesh of control points of B-spline FFD model in two cases. As illustrated in these figures, the proposed image registration using the hierarchical transformation model (Fig. 4c) recovers the global motion and local deformation of the LV appropriately.

Fig. 4.

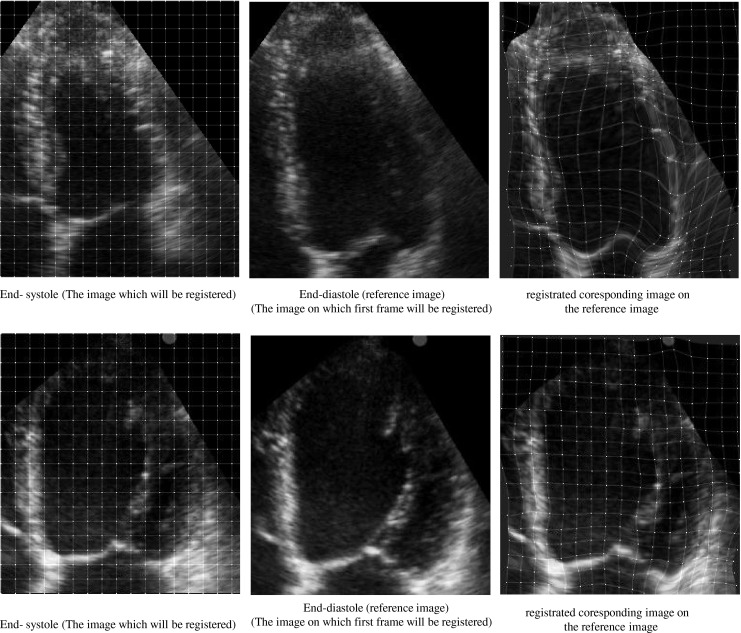
The image registration process between two images in A4C view for two cases. The left and middle parts show the end-diastole (reference) and end-systole images, respectively and the right part shows registrated coresponding image on the reference image. The positions of initial (left part) and final resultant (right part) mesh of control points of B-spline FFD model. Healthy case (top), patient case (bottom). According to the reference visual scoring, all segments for the healthy case are scored normal and all segments for the patient case are scored akinetic, except the basal lateral which is scored hypokinetic

Quantification of RWM of LV

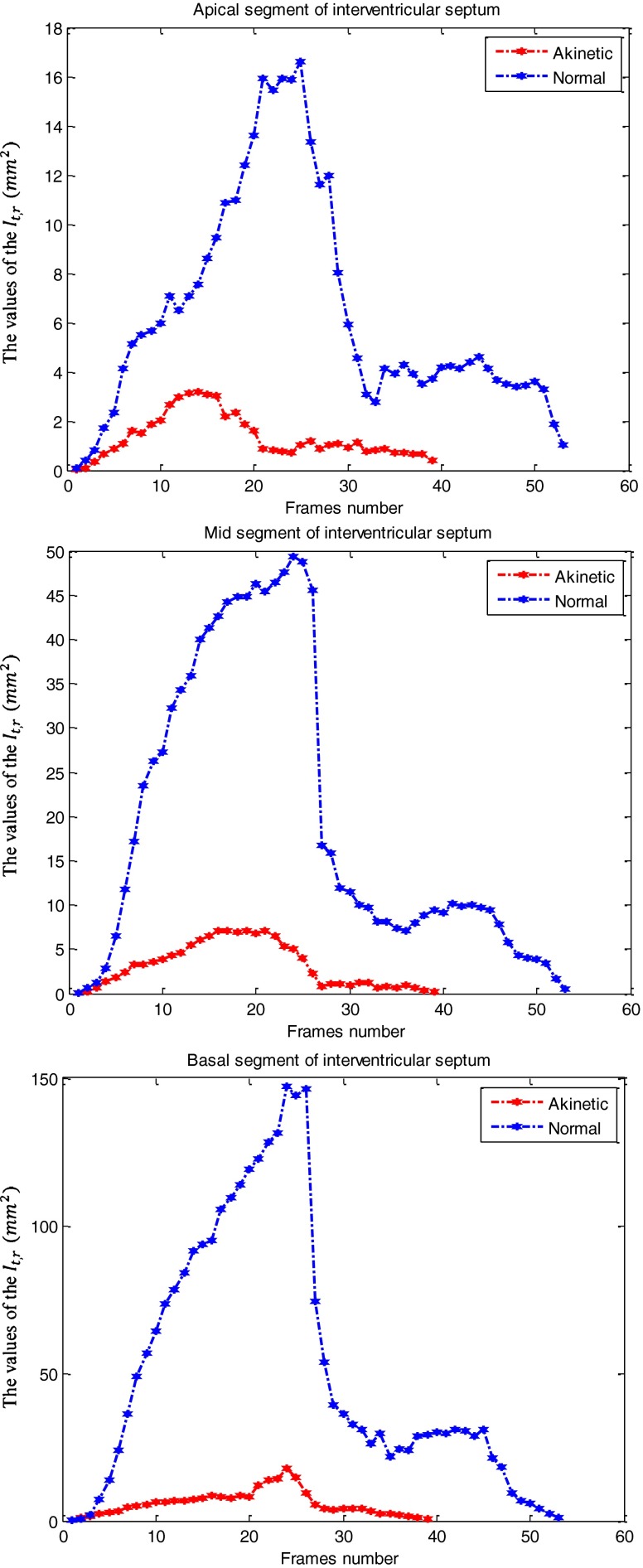
After registering each image in one cycle of heart to the reference image for each case, we have computed the quantitative index Ind_r for each of seven regions according to Eq. 9 to quantify the RWM of LV. This regional index Ind_r which is related to final resultant position of control points of B-spline FFD model over a cardiac cycle, reflects wall motion and thickening of each myocardial segment of the LV. Therefore, it decreases with the severity of the RWM abnormality, being the highest values in normal segments and the lowest values in akinetic segments. The curves obtained from the values of the I_t,r (Eq. 8) for the images of one cardiac cycle in the apical, mid-, and basal segments of interventricular septum (left wall of LV in A4C view), separately are demonstrated in Fig. 5 for the two above cases. According to the reference visual scoring, these segments for the healthy case and the patient case are scored normal and akinetic, respectively. The maximal value of each curve is defined the quantitative index for this region Ind_r. The mean values and standard deviations of the quantitative indices Ind_r for the apical, mid-, and basal segments (A4C and A2C views) independently, in the three reference visual scores (normal, hypokinetic, and akinetic) are calculated and summarized in Table 1. These values indicate that the proposed quantitative index decreases gradually according to the severity of RWM abnormality. Moreover, results show that the basal segments have slightly greater values than the mid- and apical segments. Besides, the mid-segments have slightly greater values than the apical segments. These results confirm the fact that the wall motion increases from apex to base.

Fig. 5.

The curve obtained from the values of the I_t,r (Eq. 8) for the images of one cardiac cycle in the apical (up), mid- (middle) and basal (bottom) segments of interventricular septum (left wall of LV in A4C view) for a healthy case and a patient case. It should be noted that the images of one cardiac cycle for the healthy and the patient cases are 40 and 54, respectively. The maximal value of each curve is defined the proposed quantitative index for this region Ind_r

Table 1.

Mean and standard deviation of the quantitative index Ind_r values (square millimeter) defined in Eq. 9 for the apical, mid- and basal segments (A4C and A2C views), independently corresponding to the three reference scores

Quantitative index	Reference scoring
Segment	Normal	Hypokinetic	Akinetic
Apical	39.27 ± 23.16	20.69 ± 11.11	9.45 ± 6.72
Mid	61.72 ± 25.20	28.83 ± 14.04	12.90 ± 6.04
Basal	195.66 ± 64.60	96.71 ± 38.82	38.99 ± 23.10

Classification of RWM of LV

Since the proposed regional quantitative index Ind_r decreases according to the severity of RWM abnormality, the estimation of two threshold values TH₁ and TH₂ separating akinetic from hypokinetic and respectively hypokinetic from normal is required to classify RWM of LV in a three-point scale. This process is done for apical, mid-, and basal segments of the LV, independently. Therefore, we must determine six threshold values (TH_1a, TH_2a, TH_1m, TH_2m, TH_1b, TH_2b).

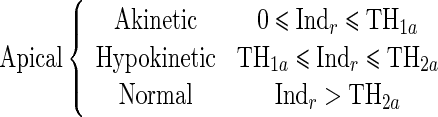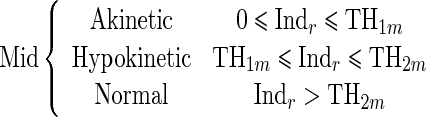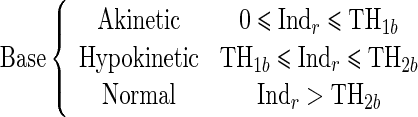To estimate the threshold values, a cross-validation procedure [43] is achieved and repeated ten times. For each trial, 2/3 of the cases (A2C and A4C views) are randomly selected for training and the remaining cases are used for validation. The distribution of the three reference RWM scores in randomly selected training subsets and the entire data sets is similar approximately to have an unbiased estimation of inter-scores thresholds during the training step. For each training subset, the thresholds are estimated by maximizing the weighted kappa coefficient [44] calculated from the 3 × 3 contingency table obtained from the comparison between the reference visual scoring and the proposed automated scoring. As mentioned above, this process is done for apical, mid-, and basal segments of the LV, independently. Consequently, for each trial, the six thresholds are estimated using this process. These thresholds are used for the quantitative scoring of wall motion of each segment of LV as normal, hypokinetic, or akinetic. The resultant scoring obtained from the proposed method is compared against those assigned by the reference visual analysis using two parameters, the absolute and the relative agreement. The absolute agreement is defined as the percentage of segments for which the scores obtained by the two methods are equal and the relative agreement is defined as the percentage of segments for which the scores obtained by the two methods differed is no more than 1. The values of agreement between two methods averaged over the ten subsets in the validation and training subsets for the apical, mid-, and basal segments, independently are demonstrated in Table 2. Results show that the apical segments which are known to be more complex to analyze have fewer absolute agreement values than the mid- and basal segments. Moreover, results show that the difference between the automatic and the reference visual scores in only apical segments is more than 1. In addition, there is absolute agreement of RWM scores between two methods averaged over the ten subsets in 88 ± 1.1 % of normal, 64 ± 2.2 % of hypokinetic, and 82 ± 1.3 % of akinetic segments as classified by the reference visual scoring. Finally, the same performances are obtained on both the validation and the training subsets indicating that the cross-validation procedure performs correctly without ‘over learning’.

Table 2.

The values of agreement (absolute and relative agreement) between the quantitative scoring of RWM obtained by the proposed method and those assigned by the reference visual analysis averaged over the ten subsets in the validation and training subsets for the apical, mid-, and basal segments, independently

	Apical		Mid		Basal
	Training	Validation	Training	Validation	Training	Validation
Absolute agreement (%)	74 ± 1.5	72 ± 3.5	89 ± 0.8	86 ± 2.6	94 ± 0.9	92 ± 1.8
Relative agreement (%)	98 ± 0.5	96 ± 1.6	100	100	100	100

Discussion

In this paper, a new suitable method, based on nonrigid image registration for classification of RWM of LV in a three-point scale with only minimal manual intervention (the placement of mitral annulus and the apex) is presented for 2-D echocardiography images. The clinical importance of having an automatic and objective method to classify RWM of LV as well as highly experienced echocardiographers is very high, because many clinical decisions and guidelines are based on this evaluation, but an experienced echocardiographer is not always present. This method can also be used as a second opinion when an experienced echocardiographer is available.

The proposed algorithm is able to accurately estimate the LV myocardial displacement field over the cardiac cycle using a hierarchical nonrigid transformation model, following an image registration algorithm as a multiresolution optimization problem. This model which is a combination of affine transformation and B-spline FFD transformation describes the global and local LV myocardial motion with a high degree of flexibility. Finally, a new quantitative index for each region of LV based on the resultant parameters of the hierarchical transformation model is proposed for the characterization of RWM scoring. It should be noted that the processing algorithm in Matlab (MathWorks Inc, USA) for each test sequence takes a few minutes on a standard laptop computer (2-GHz Dual Core, 4 GB ram), which makes the routine application in a clinical environment possible. We expect that the computation time is reduced significantly once the method is entirely recoded in C.

Our proposed method has some advantages rather than the other popular approaches of RWM scoring mentioned in the “Introduction” section. First, it is independent of analyzing of the RF signals which is very sensitive to the signal to noise ratio. Second, unlike TDI, it allows multidirectional (i.e. longitudinal, radial, and circumferential) assessment of the LV myocardial deformation. Third, any LV myocardial segmentation and tracking in the echocardiography images, which are very difficult, are not required. Fourth, a hierarchical parametric model is introduced to the displacement field of LV myocardium in order to overcome some of limitation of the 2-D echocardiography images (decorrelated speckle patterns throughout the cardiac cycle because of the 3-D movement of the heart and the complex deformation of the myocardium). Finally, our method can calculate the displacement of all points of the LV myocardium through the cardiac cycle not only the LV myocardial edges. Consequently, it considers the LV myocardial wall thickening in addition to endocardial and epicardial motion. In some approaches, color kinesis, parametric imaging, and segmentation only endocardial motion is considered and thickening of the myocardium which is an important clue for RWM scoring is disregarded. It should be noted that because of differences in databases, a direct comparison between our proposed method and other methods is not possible. However, in different databases, the results show that the proposed method yields an absolute agreement of 83 % and a relative agreement of 99 %, which is higher than the results achieved by other known algorithms.

Our method estimated the two threshold values for apical, mid- and basal segments, separately to classify the RWM of LV in a three-point scale. However, if we estimate the two threshold values for each segment of the LV (in A4C and A2C) separately, instead of only for apical, mid- and basal segments we could improve the performances of the proposed method largely. Although this would require a larger database which is our future work.

Results indicated a better classification of normal and akinetic segments (agreement in 88 and 82 %, respectively) than hypokinetic segments (64 %). Misclassification of hypokinetic segments is probably due to the definition of hypokinetic (reduced motion and wall thickening), which is much more subjective than the definition for both normal (normal motion and wall thickening) and akinetic segments (absence of motion and wall thickening). Moreover, akinetic segments may appear hypokinetic to the human eye in visual reference scoring because of the tethering of the neighbor segments but would be analyzed more accurately by the proposed algorithm.

Scoring the RWM of the LV has proven to be a reliable diagnosis parameter in the myocardial ischemia. It has a high prognosis value. Moreover, it has other clinical importance such as prognosis in patients undergoing heart surgery [45], subarachnoid hemorrhage and dialysis [46, 47]. It is also important for decision making in patients with chest pain in the emergency department [48] and in patients with congestive heart failure [49].

The absence of a true gold standard for RWM scoring is the limitation of this study. Visual scoring by experienced echocardiographer as reference scoring is not ideal; however, to reach clinical acceptance, any attempt for quantification should be compared against this clinically accepted and daily used technique. In the present study, the reference visual scoring was defined as the consensual visual scoring between the two highly experienced echocardiographers in order to reduce the possible observer variability. This reference scoring seems to be the best “gold standard”. In the future, we would like to use a more objective measure as gold standard such as MR imaging and coronary angiography. Further validation would facilitate the acceptance of this automatic method in routine clinical environment.

These results proved that the proposed algorithm is appropriate for the rest echocardiography images. Next, we are going to test the algorithm on stress echocardiography images, in order to define ischemia accurately. Moreover, the proposed algorithm could be adapted without theoretical difficulty to 3-D echocardiography images. Finally, the proposed algorithm is not modality specific and could be equally applied on cardiac MR images.

Conclusion

A new practical method, based on nonrigid image registration, is successfully used in the present study for automatic classification of RWM of LV in a three-point scale, with good agreement to visual assessment by highly experienced echocardiographers.