A Supervised Learning Approach for Crohn's Disease Detection Using Higher-Order Image Statistics and a Novel Shape Asymmetry Measure

Abstract

Increasing incidence of Crohn’s disease (CD) in the Western world has made its accurate diagnosis an important medical challenge. The current reference standard for diagnosis, colonoscopy, is time-consuming and invasive while magnetic resonance imaging (MRI) has emerged as the preferred noninvasive procedure over colonoscopy. Current MRI approaches assess rate of contrast enhancement and bowel wall thickness, and rely on extensive manual segmentation for accurate analysis. We propose a supervised learning method for the identification and localization of regions in abdominal magnetic resonance images that have been affected by CD. Low-level features like intensity and texture are used with shape asymmetry information to distinguish between diseased and normal regions. Particular emphasis is laid on a novel entropy-based shape asymmetry method and higher-order statistics like skewness and kurtosis. Multi-scale feature extraction renders the method robust. Experiments on real patient data show that our features achieve a high level of accuracy and perform better than two competing methods.

Introduction

Inflammatory bowel diseases (IBDs) constitute one of the largest healthcare problems in the Western world afflicting over 1 million European citizens. Out of these, nearly 700,000 suffer from Crohn’s disease (CD). Crohn’s disease is an autoimmune IBD that may affect any part of the gastrointestinal tract causing abdominal pain, diarrhea, vomiting, or weight loss. It is observed that, in most cases, the disease is localized in the most distant part of the small intestine, the terminal ileum. CD detection is essential to grade its severity, extent, and activity and also determines the subsequent therapeutic strategy. Currently, the reference standard for diagnosis relies on results of colonoscopy and biopsy samples [1]. Apart from therapeutic strategy, colonoscopy also has implications for patient prognosis. Through colonoscopy, a trained physician examines the ulcerations in the bowel and evaluates the severity and extent of inflammatory lesions using a standard scale called Crohn’s Disease Endoscopic Index of Severity. However, the procedure is invasive, requires extensive bowel preparation, and gives information only on superficial abnormalities. Therefore, it is beneficial to have a non-invasive approach to detect CD.

Several drawbacks of colonoscopy like invasiveness, procedure-related discomfort, and risk of bowel perforation have led to the exploration of imaging techniques to assess extension and severity of IBDs [2–4]. In Bodily et al. [5], sonography and computed tomography (CT) have been explored as alternatives to colonoscopy. For young patients, exposure to ionizing radiations is a serious limitation of CT. Assessment in sonography is limited due to gas interposition. MRI has the potential to overcome these limitations because of high tissue contrast, lack of ionizing radiations, and lower incidence of adverse events related to intravenous contrast employed in CT [6]. Horsthuis et al. [6] report the diagnostic accuracy of various signs for detection of active inflammation. However, this information is not sufficient to guide therapeutic decisions. Rimola et al. [2] determine that rate of contrast enhancement and bowel wall thickness identifies the presence of endoscopically active disease. But its reliance on explicit segmentation of the bowel wall and extensive manual scoring limits its effectiveness.

Related Work on Disease Classification

There do not exist abundant research on image analysis of abdominal MRI to identify Crohn’s Disease, although Bhushan et al. [7] look at dynamic contrast-enhanced (DCE) MRI for identifying colorectal cancer and [8] deal with ulcerative colitis. Atasoy et al. [9] addressed the tasks of localization, annotation, or classification of optical biopsies in colonoscopy. Our method will serve as a diagnostic tool for clinicians to localize the diseased area without the need for explicit segmentation of bowel wall.

Cheng et al. [10] propose the use of biologically inspired features for classification of different glaucoma types. The biological features are based on saliency maps predicting interesting regions for humans in pictures. Saliency-inspired features have been used in various applications like object tracking [11, 12], registration [13–15], and segmentation [16–19]. Automatic localization of multiple anatomical structures in medical images provides important semantic information for potential benefits in various clinical applications.

Pauly et al. [20] propose supervised regression techniques to detect and localize different parts in whole-body magnetic resonance (MR) sequences. They use 3D local binary patterns along with random ferns to achieve high segmentation accuracy. Kelm et al. [21] propose a random–regression-based method for detecting and grading coronary stenoses in CT angiography data. Their motivation is to provide an automated system that can rule out clinically relevant stenosis in the coronary arteries and serve as a second reader in the absence of an expert physician. Brain imaging data have seen a lot of applications of machine learning methods for classification, particularly Alzheimer’s disease [22–24]. Chest images have also generated a lot of interest with methods proposed for localization of chest pathologies in Avni et al. [25], pediatric tuberculosis in Irving et al. [26], and diffuse lung disease in Xu et al. [27].

Scope of Our Work

This paper proposes a semi-automated method to detect CD-afflicted regions from input abdominal MR images. Thus, we do not need an explicit segmentation of the bowel wall which turns out to be quite difficult based on MR imagery. Our method will serve as a tool to assist clinicians, reduce reliance on colonoscopy, and help in rapid diagnosis of CD. Many studies highlight the importance of low-level features in disease identification, e.g., intensity, texture, symmetricity in shape, and structure information [28, 29]. Kovalev et al. [30] showed the importance of anisotropy (a measure of feature asymmetry) from texture maps to detect abnormalities in diseased brain images. Anisotropy can be applied to other features for characterizing diseased regions. For example, in Liu et al. [28], reflectional asymmetry based on a pigmentation model was employed to detect skin lesions.

We propose a novel method to calculate shape asymmetry that uses the entropy of orientation angles. Our approach is simple to compute and gives accurate detection results. Intensity, texture, and shape asymmetry features from multiple scales are used to characterize normal and CD-affected regions in the bowel. This paper makes the following novelties: (1) a shape asymmetry measure based on entropy of the distribution of orientation angles is proposed; I2) it is combined with higher-order image statistics to identify diseased regions; and (3) the features are used for identification of CD areas in abdominal MRI, a novel application that has immense potential in assessing IBDs. We describe our method in “Materials and Methods,” present results in “Experiments and Results,” and conclude with the section on “Conclusions.”

Materials and Methods

Overview of Our Method

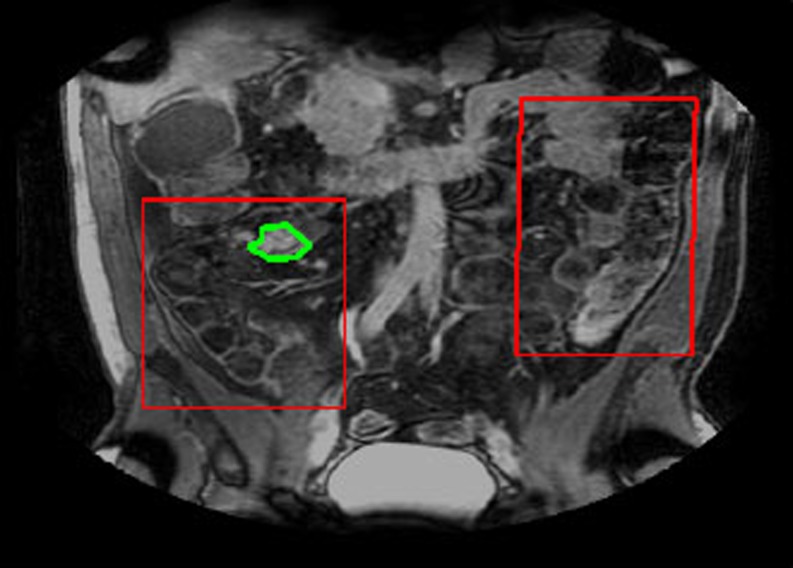
Our aim is to detect presence of Crohn’s Disease in a MRI volume. For that purpose, we have to classify a voxel in the volume. For a 400 × 400 × 100 volume, the processing time can be very high if we were to analyze each individual voxel. Since the bowel is visible in only a few slices, we focus on these slices to identify CD affected regions. Furthermore, in these slices, the bowel occupies part of the image. A rectangular region of interest (ROI) is manually defined which covers the regions most likely to contain diseased tissues but is smaller compared with the whole image. Physicians get an approximate idea of the ROI from the results of other tests like colonoscopy and DCE MRI. Since our proposed approach aims to assist expert doctors, this semi-automated approach seems reasonable. We employ a two-stage classification, details of which are described in the later sections. In the first stage (henceforth referred to as Stage 1), the pixels are first classified as either intestine or background. Those pixels that are labeled as intestine are further classified as either diseased or normal in the second classification stage (Stage 2). Figure 1 shows an example slice with the ROI outline shown in red and the diseased region shown in green.

Fig. 1.

Illustration showing the original slice image, the ROI in red and annotated region in green

Feature Extraction

Appropriate features are crucial in determining the accuracy rate of disease identification and its subsequent grading. We extract intensity, texture, and shape asymmetry features from three different scales for disease identification. For higher accuracy and robustness, features were extracted from neighborhoods centered around each pixel. Henceforth, we shall refer to these neighborhoods as a patch.

Intensity and Texture Features

To identify the exact area afflicted with CD, radiologists rely on the results of different tests like colonoscopy and biopsy, as well as different imaging protocols like MR-T1, MR-T2, and DCE-MRI. A simple visual examination of T1 MRI does not provide sufficient information to identify the diseased part. We propose to investigate features that are not discernible by the human eye but may provide discriminating features for our task. Psychophysical experiments have established that the human visual system is sensitive only to image features of the first- and second-order (mean and variance) [31]. It is common in MR images to have regions that do not form distinct spatial patterns but differ in their third order statistics, e.g., boundaries of some malignant tumors are diffuse and invisible to the naked eye [32]. However, with computational tools at our disposal, we can analyze higher-order statistics to determine their efficacy in disease classification. For every image patch (neighborhood of a pixel), we calculate the mean, variance, skewness, and kurtosis for intensity and texture features. Let us denote each patch as Si, the intensity of its jth pixel as Si(j), the mean intensity by Si, and the variance by 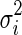. The skewness (third-order statistic) of the intensity distribution is given by

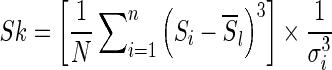1

where the term within the square brackets is the third-order moment. The skewness is a measure of symmetry of a distribution. Negative skew indicates that the bulk of the values lie to the right of the mean, and positive skew indicates the bulk of the values lie to the left of the mean. A zero value indicates that the values are relatively evenly distributed on both sides of the mean (e.g., a Gaussian distribution).

Kurtosis (the fourth-order statistic) is a measure of the “peakedness” of the probability distribution and along with skewness describes its shape. It is given by

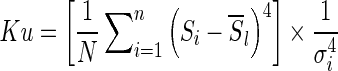2

where the term within the square brackets is the fourth-order moment. A high kurtosis distribution has a sharper peak and longer, fatter tails, while a low kurtosis distribution has a more rounded peak and shorter, thinner tails.

Texture Maps

Texture can be modeled as patterns which are distinguished by a high concentration of localized spatial frequencies. 2-D Gabor filter banks, which have optimal joint localization in the spatial and spatial-frequency domains, have been used for texture representation in Manjunath and Ma, and Liu and H. Wechsler [33, 34]. Due to its multiscale and multi-orientation structure, Gabor filter banks conform to the receptive fields profiles of simple cortical cells [35] and are able to capture rich visual properties such as spatial localization, orientation selection, and spatial frequency characteristics. Since Gabor filters incorporate Gaussian smoothing, they are robust to noise. Because of these desirable properties, we select the Gabor filter bank to characterize texture in our images. The Gabor filter bank can be represented as

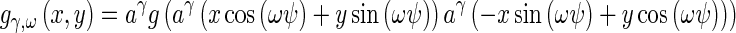3

where γ = 0,… Γ − 1, ω = 0,…Ω − 1. The mother function g is Gaussian defined as:

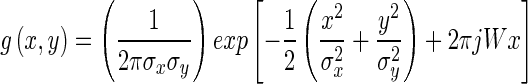4

Γ = 6 is the total number of orientations, Ω = 2 is the total number of scales. The rotation factor ψ = π/Ω and the scaling factor a = (Uh/Ul)^{1 Γ −1}. Uh and Ul are parameters that determine the frequency range of the filter bank, and W is a shifting parameter in the frequency domain. Texture maps are obtained using oriented Gabor filters along six directions (0°, 30°, 60°, 90°, 120°, and 150°).

Shape Asymmetry

In Liu et al. [28], the authors use reflectional asymmetry to identify skin lesions. Also, in Liu et al. [28], global point signatures (GPSs) were defined at each pixel to characterize color and orientation information, and the asymmetry descriptor is calculated based on bin differences about a principal axis of a histogram. The principal axis is chosen from one of 180 bins, and some of the bins are translated to ensure that there are 90 bins on each side of the principal axis. We propose a novel method for quantifying the shape asymmetry which is based on the entropy of the orientation distributions. Entropy-based measures have been used in computer vision studies to detect salient regions [12] and tracking [11]. This novel measure is simpler to calculate and also functions as a good descriptor.

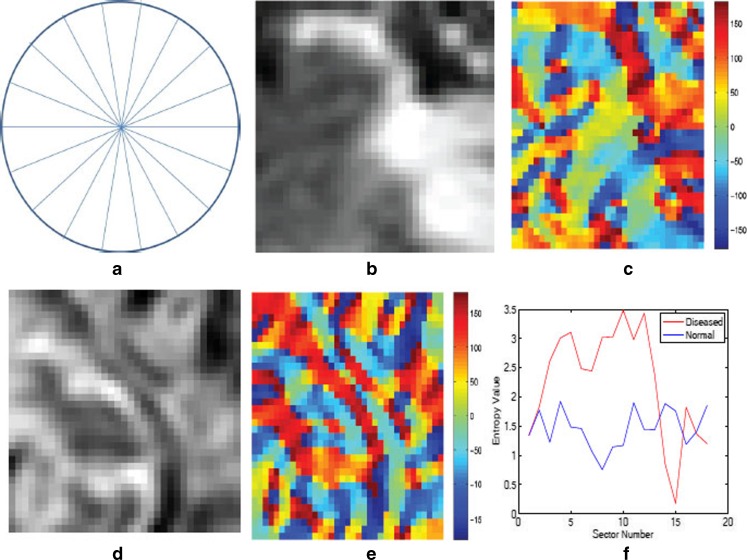
Each patch is divided into 18 sectors of a circle centered at the geometric center of the patch. For each sector, we calculate orientation angles of the pixels and determine the entropy of the angle distribution. Entropy measures the information in the respective distributions. A uniform distribution has high entropy while the entropy is low for a peaked distribution. If the orientation angles are distributed over many angle ranges, there is greater asymmetry in shape, leading to a higher entropy value. On the other hand, low entropy values indicate that most of the pixel orientation angles are distributed along a few directions leading to lower shape asymmetry. The shape asymmetry measure for a sector r is given by

5

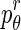denotes the angle distributions in sector r. Figure 2a shows an illustration of a circle divided into 18 sectors. Figure 2b shows a patch around a diseased pixel, and Fig. 2c shows a map giving the value of the corresponding orientation angles. Figure 2d shows a patch around a normal pixel with the corresponding angle map shown in Fig. 2e. The angle values are in the range [180°, 180°]. Figure 2f shows the plot of entropy values for each of the 18 sectors for the two patches shown in Fig. 2b and d. It is interesting to note that the orientation profile for the normal patch is quite regular as compared with the diseased patch. This is indicative of the fact that the orientation in diseased regions becomes distorted due to ulcerations or other abnormalities. Thus, they lose the regularity observed in healthy tissues. This is corroborated by the plot in Fig. 2f where the diseased patches show higher entropy, indicating greater randomness.

Fig. 2.

a Illustration of sectors for entropy, b, c diseased patch, and corresponding map of orientation angles; d, e normal patch and corresponding map of orientation angles; f plot of entropy values for the two patches. The color bars show the angle magnitude in degrees

The above set of features give a 46-dimension feature vector (intensity, 4; texture, 6 × 4 × 2 = 48; and shape, 18) for a single patch. In order to capture information over multiple scales, we extract similar features over neighborhood of different sizes. Thus, for each annotated pixel, features were extracted over three neighborhoods of sizes 25 × 25, 30 × 30, and 35 × 35. The final feature vector is of length 46 × 3 = 138. Although the Gabor texture maps are inherently multi-scale representations, intensity and shape measures are not derived from multiple scales. Thus, to include intensity and shape features from multiple scales, we consider three neighborhoods. Although the computation cost is slightly more, it leads to higher classification accuracy. A brief discussion is found in the section on “Importance of Multi-scale Feature Extraction” on the importance of such feature extraction.

Features for Comparison

We compare the effectiveness of our method with two other methods. The first is a wavelet–transform-based method (dual tree complex wavelet transform (DTCWT)) in Berks et al. [29]. The second is a shape–asymmetry-based method (Asy), where asymmetry is calculated similar to Liu et al.’s [28]. Instead of GPS, orientation angles are used.

DTCWT

Wavelet transforms have been used extensively in image processing and analysis to provide a rich description of local structure. The DTCWT has particular advantages because it provides a directionally selective representation with approximately shift-invariant coefficient magnitudes and local phase transformations [36]. DTCWT combines outputs of two discrete transforms (differing in phase by 90° to form the real and imaginary parts of complex coefficients. For 2-D images, it produces six directional sub-bands oriented at ±15°,±45°, and ±75° at a series of scales separated by a factor of 2. A feature vector is constructed by sampling DTCWT coefficients from six oriented sub-bands from a w × w neighborhood centered on the pixel. This gives an 18-dimension feature vector (i.e., six sub-bands from the three neighborhoods stated above). Details of the method can be found in Berks et al. [29].

Asy

Liu et al. [28] define a measure of reflectional asymmetry based on the pigmentation model of skin lesions. We use a similar approach for an alternative shape asymmetry metric where, instead of the GPS, we calculate shape asymmetry based on orientation angle information. For every patch, the distribution of orientation angles is calculated such that the magnitude of angles lies between 180° and 180° and the number of bins equals 40 with an equal number of bins for positive and negative magnitudes. The shape asymmetry is determined as

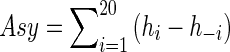6

Here h − i denotes the histogram count of ith bin of negative magnitudes, and hi denotes the histogram count of the corresponding bin of positive magnitudes. Note that we do not take the absolute value of differences. A net positive value of Asy indicates that the orientation angles have a net positive leaning, while a negative Asy indicates a net negative leaning. Thus, the sign and magnitude of Asy indicates an “asymmetry vector.”

Experiments and Results

The datasets comprised of samples from 26 patients diagnosed with CD (mean age, 36 years; range, 19–72 years; 17 females and 9 males) at the Academic Medical Center (AMC), Amsterdam, The Netherlands. Two radiologists with more than 7 years of experience with dealing with abdominal MR images annotated regions (with consensus) corresponding to diseased, normal, and background (normal nonintestine) on the 26 patients. Patients fasted 4 h before a scan and drank 1,600 ml of mannitol (2.5 %) (Baxter, Utrecht, The Netherlands) 1 h before the scan. Images were acquired with patients in supine position using a 3-T MR imaging unit (Intera, Philips Healthcare, Best, The Netherlands) with a 16-channel torso phased array body coil. The protocol consists of axial and coronal single-shot fast-spin echo (SSFSE) sequences followed by a coronal fat saturated SSFSE sequence and coronal 3D T1-weighted spoiled gradient echo sequence. The spatial resolution of the images was 1.02 × 1.02 × 2 mm, and the acquired volume dimension was 400 × 400 × 100 pixels.

The number of samples was 6,827 from diseased regions, 5,156 from normal, and 3,725 from background regions. Here, each sample refers to the feature vector from a pixel’s multiple neighborhoods. We employ a tenfold cross-validation (leave-one-out) approach for testing our classifier’s performance. Each sample class is divided into roughly ten equal parts, of which nine parts are used for training and the other one for testing. The study was approved by the AMC’s ethics committee and waived informed consent. The study was in accordance with the rules of the European Community’s Seventh Framework Programme. Our method was compared with DCTWT and Asy. Each of the three methods was evaluated using three different classifiers, random forests (RF), support vector machines (SVM), and a Bayesian classifier (BC).

Classifiers

Random forests [37] have been successful in a variety of domains and compare favorably with other state-of-the-art algorithms [38]. A random forest is an ensemble of decision trees where each tree is trained with a different subset of the training data to improve the classifier’s generalization ability. Training finds the set of tests that best separate the training data into different classes. Random forests and their variants have been used to detect abnormalities in mammograms [29] and identify coronary artery stenoses [21] and semantic segmentation in CT images [39]. In our experiments, 100 trees were used for the RF classifier.

SVMs construct a hyperplane or set of hyperplanes in a high-dimensional space, which can be used for classification, regression, or other tasks. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training data of any class (so-called functional margin). In general, the larger the margin, the lower the generalization error of the classifier. SVMs have also seen wide application in classification tasks like brain tumor segmentation [40, 41], chest pathologies [25], and glaucoma classification [10], among others. For SVMs, we use the LIBSVM package [42] and define a radial basis function (RBF) as the kernel.

The default naive Bayesian classifier in MATLAB was the third classifier. A Bayesian classifier was chosen to highlight the linearly non-separable nature of the data and the advantages of having a RBF kernel in SVMs. We have two classification stages for all classifiers. For all classifiers, we employ tenfold cross-validation (leave-one-out with ten subsets of the original data) approach.

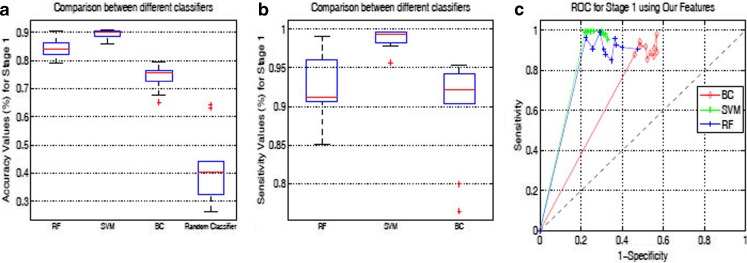
Classification Results for Stage 1

Table 1 shows the average accuracy and sensitivity of the first classification stage using tenfold cross-validation. Here, each sample is classified as either intestine or background. The highest classification accuracy is obtained using our features, the results of which are shown in the box plots of Fig. 3. In this stage, we desire a high sensitivity or true-positive rate (TPR) even at the expense of low overall accuracy. True positive refers to an intestine sample correctly classified as intestine. We do not want an intestine sample to be incorrectly labeled as background, thus increasing the false-negative rate (FNR). In such a situation, the diseased samples (which are part of intestine in the first stage) get classified as background and, hence, escape the scrutiny of the next stage. This is particularly undesirable in a clinical decision making system.

Table 1.

Quantitative measures for the Stage 1 classification for various features and using different classifiers

	Asy			DTCWT			OurFeatures
	SVM	BC	RF	SVM	BC	RF	SVM	BC	RF
Accuracy (%)	80.4 (2.6)	72.0 (2.3)	79.9 (2.2)	82.2 (2.4)	71.3 (2.9)	80.1 (2.5)	86.4 (1.5)	73.2 (4.4)	83.3 (4.1)
Specificity (%)	67.9 (1.8)	41.5 (1.8)	68.0 (1.7)	68.1 (1.6)	42.7 (1.7)	67.6 (1.8)	71.1 (1.8)	49.1 (2.1)	70.6 (2.2)
Sensitivity (%)	86.2 (1.9)	81.5 (1.4)	84.6 (1.8)	93.9 (2.7)	88.3 (2.1)	85.7 (1.9)	96.7 (1.2)	90.1 (6.5)	92.1 (4.1)
Precision (%)	90.1 (1.1)	77.9 (1.8)	89.6 (1.3)	92.1 (2.1)	78.8 (1.7)	89.5 (1.1)	96.3 (1.8)	80.4 (4.2)	90.9 (2.9)

Values indicate mean (standard deviation)

Fig. 3.

Box plots for Stage 1 classification: a Accuracy; b Sensitivity. c ROC curves for three classifiers using OurFeatures

In trying to reduce the FNR, we observe an increase in false-positives, i.e., increasing number of background regions are identified as intestine. This situation does not adversely affect the outcome of the decision system. The background regions classified as intestine are invariably identified as normal in the second classification stage. Those background regions identified as diseased in the second stage can be discarded by examination of a clinician.

Classifiers’ Performance in Stage 1

A comparison of ROC curves of all three methods using RF classifier in Stage 1 is shown in Fig. 3c. During tenfold cross-validation, sensitivity and specificity values are obtained for each run which are then used to draw the ROC curves. All the three methods give high sensitivity (more than 90 %), but their specificity values are comparatively lower, indicating a large number of false-positives. The overall accuracy (i.e., correct classification percentage of both intestine and background samples) is lower than 86 % in all cases. This indicates a high number of false positives, i.e., many background samples are classified as intestine. This is not a disadvantage since these incorrectly labeled background samples are invariably identified as normal in Stage 2. It is interesting to note that BC has an overall accuracy less than 75 %, because of a high number of false-positives. This is reflected in the specificity values in Table 1 and the ROC curves in Fig. 3c. This gives some interesting insight into the nature of data and performance of classifiers. BC can find a good decision boundary for data which are linearly separable, or which have low overlap amongst the feature values. For different classes which have similar feature values, BC produces lots of errors. The performance of different classifiers suggests that our data have such characteristics. In spite of the low specificity, BC shows an accuracy of 74 % because the number of background samples is about a third of the number of intestine samples. Had the number of samples been equal, then BC’s accuracy would have been still lower. All classifiers perform better than a random classifier.

In order to achieve good discrimination, it is important that the samples in the training set represent all possible variations in the real world. However, this is not always possible in practice. Feature selection plays an important role in order to make the best use of the available samples. Intensity, texture, and shape asymmetry provide lot of important discriminating information between the different classes. An additional factor is multi-scale feature extraction which overcomes issues like choosing an appropriate neighborhood and sufficient neighbors to get a stable statistical measure.

Importance of Different Features

We also investigate the importance of different features in our classification framework. Here, we report the results of a combination of different features using the RF classifier. Table 2 shows different quantitative measures for Stage 1 classification using only intensity, texture, and shape asymmetry and their different combinations. As expected, the sensitivity and accuracy for the individual features are lower than the values in Table 1. The combination of texture and shape features produces results that are closest to the values in Table 1. However, this does not indicate that intensity information is unimportant. Conducting a t test on the values for Tex + Shape (Table 2) and All Features (Table 1) gives p < 0.032 which clearly indicates statistically different results. Furthermore, we also conduct t tests for features Tex versus Tex-Int, and Shape versus Shape-Int. In both cases, we find that p < 0.04, thus clearly showing that inclusion of intensity statistics improves classification accuracy.

Table 2.

Quantitative measures for individual and different combination of features using RF classifier

	Int	Tex	Shape	Tex + Int	Shape + Int	Shape + Tex
Accuracy (%)	77.1 (2.3)	81.6 (2.1)	79.1 (2.7)	79.2 (1.3)	79.5 (2.4)	82.3 (1.3)
Sensitivity (%)	79.3 (3.2)	86.9 (2.1)	82.3 (1.9)	83.1 (3.1)	83.8 (2.3)	86.6 (2.8)

Values indicate mean (standard deviation)

DTCWT Versus Tex

DTCWT also calculates texture maps of an image. While DTCWT only calculates the mean across different orientations and scales, Tex calculates mean, variance, skewness, and kurtosis across orientation and scales. Thus, it is expected that Tex would be a more accurate measure than DTCWT, and it is reflected in the quantitative measures for Tex (Table 2) and DTCWT (Table 1).

Asy Versus Shape

The difference between the two features is that, while Asy operates on the whole patch, Shape operates on different sectors of the patch. They also differ in their approach to determining asymmetry. Asy calculates asymmetry as the difference in “positive” and “negative” histograms of orientation distributions. On the other hand, Shape characterizes asymmetry as the entropy of orientation angles in each sector. A comparison of the results for Shape (Table 2) and Asy (Table 1) show that their performance is very similar, with p = 0.13.

Classification Results for Stage 2

Those samples that are identified as intestine in the first stage are considered in Stage 2 for further classification into diseased or normal. Suppose there are N number of intestine samples at the beginning of Stage 1, out of which Nd are diseased and Nn are normal, i.e., Nd + Nn = N. In Stage 1, let N2 intestine samples be correctly classified, out which Nd2 are diseased and Nn2 are normal. The sensitivity of Stage 1 is calculated using N2 and N. The N2 number of samples is now considered for classification in Stage 2. At the end of Stage 2, suppose the number of correctly classified diseased samples to be Nd3 and the number of correctly classified normal samples, Nn3. The different quantitative measures for Stage 2 are based on the original number of samples at the beginning of Stage 1, i.e., Nd and Nn. Below, we shall define the different measures:

1. Accuracy: the number of diseased and normal samples that were correctly classified, i.e., (Nd3 + Nn3)/N.

2. True-positives (TP): number of correctly classified diseased samples(Nd3).

3. True-negatives (TN): number of correctly classified normal samples (Nn3).

4. False-positives (FP): number of normal samples classified as diseased (Nn-Nn3).

5. False-negatives (FN): number of diseased samples identified as normal. (Nd-Nd3).

6. True-positive rate (TPR) : 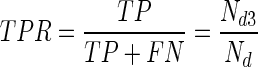. It is the same as sensitivity and recall.

7. True-negative rate (TNR) : 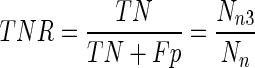. It is the same as specificity.

8. 8. 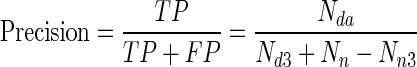. It is the fraction of retrieved instances that are relevant. In this case, retrieving diseased samples is relevant.

Table 3 shows the accuracy and sensitivity after the final classification stage, i.e., an indicator of performance over the original N samples. Although BC’s accuracy and TPR in Stage 1 was comparable to RF and SVM, it showed significantly worse results for Stage 2. From the results of BC, we infer that the feature values of diseased and normal samples are not linearly separable. This supports our use of features from multiple scales. The high difference of measures between BC and the other classifiers in Stage 2 as compared with the corresponding values in Stage 1 can be explained as follows. The extracted features of diseased and normal samples have lower differences than the feature values of background and intestine (normal and diseased) samples. Thus, in Stage 1, BC did a good job because intestine and background samples formed “clusters” which were reasonably distant. However, diseased and normal samples seem to form clusters that are not very far apart. This would explain the low accuracy, sensitivity, and specificity values for BC in Stage 2. These observations make a stronger case for RF and SVMs using RBF kernels.

Table 3.

Quantitative measures for the Stage 2 classification for various features and using different classifiers

	Asy			DTCWT			OurFeatures
	SVM	BC	RF	SVM	BC	RF	SVM	BC	RF
Accuracy (%)	81.5 (1.3)	59.1 (0.9)	81.7 (1.2)	82.2 (1.4)	58.4 (6.1)	81.9 (1.2)	89.5 (2.6)	62.8 (5.4)	88.9 (1.5)
Specificity (%)	80.8 (3.1)	35.1 (4.8)	83.4 (2.4)	82.8 (1.4)	37.7 (2.7)	84.2 (1.9)	90.2 (1.7)	39.3 (4.1)	90.1 (1.6)
Sensitivity (%)	84.5 (1.9)	60.5 (1.2)	84.9 (1.8)	86.9 (1.7)	61.3 (8.2)	86.1 (1.9)	91.9 (2.6)	64.8 (9.7)	90.4 (1.2)
Precision (%)	82.9 (1.4)	59.7 (1.9)	82.7 (1.5)	85.3 (1.4)	59.7 (5.4)	84.9 (1.4)	90.2 (2.0)	63.3 (4.3)	88.9 (1.3)

Values indicate mean (standard deviation)

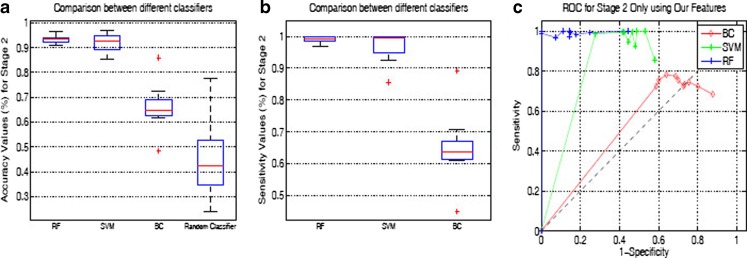
Figure 4 shows the box plots of accuracy and sensitivity, and ROC curves when we consider Stage 2 as different classification process without any link to Stage 1. The accuracy and sensitivity are calculated only over the samples that pass Stage 1, i.e., TRP (Sensitivity) = 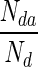; Accuracy = (N_d3 + N_n3)/(N_d2 + N_n2). Obviously, the values will be higher than those reported in Table 3 (which are based on all the original number of samples). The box plots and ROC curves indicate that a high percentage of each sample type is correctly classified by both SVM and RF. This is highly desirable because, ultimately, we would like to detect the diseased regions from abdominal MRI. During tenfold cross-validation, sensitivity and specificity values are obtained for each run which are then used to draw the ROC curves.

Fig. 4.

Box plots for Stage 2 classification: a Accuracy; b Sensitivity. c ROC curves for three classifiers using Ourfeatures

Results on Real Patient MRI

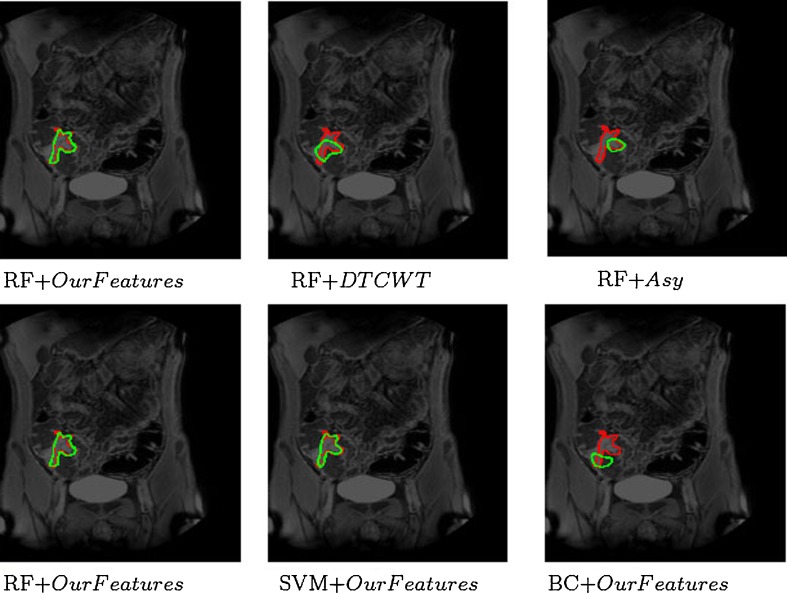
Figure 5 shows visual results for CD detection in Patient 23. After classification, we generally get one large cluster and smaller isolated clusters. Isolated clusters with less than 10 pixels were removed, and the large cluster was transformed into a single continuous region using contour fitting. The first row shows the detection results obtained using the RF classifier with the three methods namely our features, DTCWT and Asy. The manually annotated diseased regions are shown in red while the result of automatic detection is shown in green. The figures show that our features give the best performance. DTCWT and Asy both detect less number of diseased pixels, which can prove to be critical in decision making systems. They also identify many background or normal pixels as diseased (false-positives), while using our features the number of false-positives is very low.

Fig. 5.

Visual results for CD detection in Patient 23. First row shows results of RF using different features (our features, DTCWT, and Asy). Second row shows performance of different classifiers (RF, SVM, and BC) using our features. The two images in the first column are identical and are shown for continuity

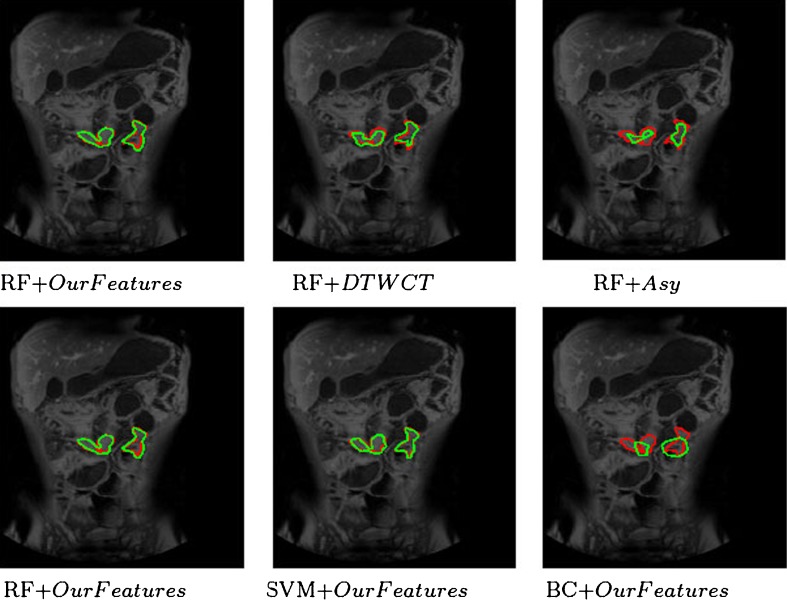
The second row of the same figure shows the detection results using our features with different classifiers, namely RF, SVM, and BC. The two figures in the first column are the same but have been shown for consistency. Although our features give the best performance using RF, the results vary depending upon the choice of classifier. SVM’s performance is close to that of RFs in terms of high true-positives and low false-positives. However, BC shows significantly poor performance than the other two classifiers with low true-positives and high false-positives because of its limited ability to handle non-linearly separable data. We would like to point out that, if we use a linear kernel in SVMs, it performs poorly than RFs, and is closer to BC’s performance. Figure 6 shows the detection results on Patient 16, where there are two diseased regions to be detected. Again, our features perform better than DTCWT and Asy; RF and SVM show similar performance, and BC performs poorly.

Fig. 6.

Visual results for CD detection in Patient 16. First row shows performance of RF using different features (our features, DTCWT, and Asy). Second row shows performance of different classifiers (RF, SVM, and BC) using our features. The two images in the first column are identical and are shown for continuity

The manual annotations can be treated as ground truth segmentations. The pixels identified as diseased or normal can be grouped together to form automatic segmentations. Thus, we can calculate measures like Dice metric (DM) and Hausdorff distance (HD) between the two regions. The average DM and HD values are summarized in Table 4.

Table 4.

Average DM and HD values after Stage 2 using different features and classifiers

	Asy			DTCWT			OurFeatures
	SVM	BC	RF	SVM	BC	RF	SVM	BC	RF
DM (%)	84.1 (1.1)	79.3 (2.4)	84.7 (1.5)	85.3 (2.1)	80.1 (2.3)	85.6 (1.4)	90.3 (2.1)	81.8 (2.1)	90.9 (1.2)
HD (pixels)	3.4 (2.1)	6.3 (2.8)	3.5 (1.8)	3.1 (1.2)	6.7 (2.2)	3.2 (2.1)	2.1 (1.1)	4.8 (1.6)	2.0 (1.1)

Values indicate mean (standard deviation)

Importance of Multi-scale Feature Extraction

Although multi-scale feature extraction leads to a slight increase in computation time, it contributes toward to higher classification accuracy. Table 5 summarizes the performance of our features for different neighborhoods using RF classifiers over all samples. Results are shown only after Stage 2, although the analysis was carried out for both Stage 1 and Stage 2. 1 Scale refers to features extracted from a 25 × 25 neighborhood; 2 Scales refers to features extracted from a 25 × 25 and 30 × 30 neighborhoods. The computation time is shown for the whole pipeline consisting of Stage 1 and Stage 2 for a 100 × 30 manually drawn ROI. The results clearly indicate that Our Features (multi-scale feature extraction) improves accuracy measures significantly over 1 Scale (p < 0.01 from t tests) and 2 Scales (p < 0.018). However, the corresponding extra computation time is not significantly high. Therefore, we can include multi-scale features without a large increase in computation time.

Table 5.

Accuracy percentage and computation time for multi-scale feature extraction and comparison with other methods

	Asy	DTCWT	Our Features	1 Scale	2 Scales
Accuracy (%)	81.7 (1.2)	81.9 (1.2)	88.9 (1.5)	84.3 (1.9)	80.1 (1.5)
Computation time (s)	349 (14)	404 (21)	463 (24)	415 (22)	381 (17)

Values indicate mean (standard deviation)

Conclusion

In this paper, we have proposed a method to identify regions in the human gastrointestinal tract that are afflicted with Crohn’s disease. Higher order intensity and texture statistics, and shape asymmetry information are extracted at multiple scales and used to discriminate between diseased, normal, and background regions. Higher-order statistics capture image properties that are not discernible to the human eye. Our shape asymmetry measure is simple to compute and is informative in detecting diseased regions. We compare our features with a wavelet–transform-based feature (DTCWT) and asymmetry descriptor (Asy) using three standard classifiers. Experimental results show that our designed feature vector performs better than Asy and DTCWT. Our results indicate that Crohn’s disease can be detected from MR images and, thus, reduce reliance on invasive procedures like colonoscopy and biopsy. With further improvements of our method in the future, we can hope to build a reliable detection and CD classification system.

Our system also has its limitations: (1) manual definition of ROI is not always possible. Therefore, we are working on a reliable method to detect regions of disease activity (i.e., the ROIs). Once an approximate ROI is identified, each pixel within it can be further analyzed for disease activity; (2) a two-stage classification takes lot of time which can be reduced by efficient coding and faster feature extraction; (3) post-processing to remove isolated pixel clusters increases the manual involvement. We are working on a solution using segmentation frameworks (like graph cuts) that inherently impose spatial smoothness constraints and produce a coherent segmentation of diseased regions.