The effect of cross-link distributions in axially-ordered, cross-linked networks

Abstract

Cross-linking between the constituent chains of biopolymers has a marked effect on their materials properties. In certain of these materials, such as fibrillar collagen, increases in cross-linking lead to an increase in the melting temperature. Fibrillar collagen is an axially-ordered network of cross-linked polymer chains exhibiting a broadened denaturation transition, which has been explained in terms of the successive denaturation with temperature of multiple species. We model axially-ordered cross-linked materials as stiff chains with distinct arrangements of cross-link-forming sites. Simulations suggest that systems composed of chains with identical arrangements of cross-link-forming sites exhibit critical behavior. In contrast, systems composed of non-identical chains undergo a crossover. This model suggests that the arrangement of cross-link-forming sites may contribute to the broadening of the denaturation transition in fibrillar collagen.

1. Introduction

Many important biopolymers contain cross-links between constituent chains, and changes to the cross-links can result in vastly different materials characteristics [1, 2]. Fibrillar collagen, e.g. tendon, is a stiff, axially ordered, cross-linked protein [3] with a high tensile strength. In fibrillar collagen, increasing cross-linking between polymer chains leads to an increase in the melting temperature [4]. Wallace et al. find a broad specific-heat peak around the nominal melting temperature of fibrillar bovine collagen, compared to a sharp peak in the melting of non-fibrillar collagen, attributing the broadened peak to the presence of three distinct molecular or fibrillar species, each denaturing at a characteristic temperature [5, 6]. The polymer-in-a-box mechanism [7], in which the configurations of the chains are limited due their proximity to one another, has been proposed to explain the multiple denaturation temperatures specifically of decalcified bone and rat-tail tendon [8]. However, when constituent polymers are rod-like, the polymer-in-a-box mechanism adds no additional constraint and should not have a significant broadening effect on the denaturation temperature. The range in denaturation temperatures has also been attributed to uneven fibril cross-linking (see Ref. [9, 10, 11]) and to inconsistencies in cross-linking [12].

Alternatively, variations in the density or strength of cross links will also change the melting temperature. The importance of the number density is demonstrated in the tanning of leather, while the effect of cross-link binding strength is substantiated in dermal stiffening in echinoderms [13, 14]. We propose that even with fixed density and strength, the distribution of cross links within an axially ordered network of stiff polymer chains may account for broadening of the melting transition.

We consider two classes of cross-link-forming site arrangements along individual chains. Homogeneous systems are those in which these sites appear identically for all chains. Our work suggests that homogeneous systems will yield sharp phase transitions. The critical temperature is independent of the cross-link number density but does depend on the spatial distribution of cross-links. To the authors’ knowledge, experiments involving materials composed of chains with identical arrangements of cross-link-forming sites have not been conducted. In contrast to homogeneous systems, the cross-link- forming sites in heterogeneous systems are determined stochastically, so that the chains are not identical. We find that heterogeneous systems denature over a broad range of temperatures without the need to invoke multiple, discrete denaturation transitions.

This paper presents a three-dimensional lattice model of axially-aligned, cross-linked polymer chains. We systematically vary the number density of cross-link-forming sites per unit length of chain and the arrangements of cross-link-forming sites along each chain. In the following sections we describe the model and the results of Monte Carlo simulations, drawing particular attention to the difference between homogeneous and heterogeneous systems.

2. Model and Simulations

We treat a network of axially-ordered, stiff, cross-linked polymer chains as parallel bundles of rods that interact with one another only through the cross-links between adjacent rods. Treatment of the physical chains as rods is a reasonable approximation, because, depending on the biological source of the fibril, chains represented by this model are on the sub-micron scale, while estimates of the persistence length of collagen fibrils range to the meter scale [15]. The radial organization of the chains with respect to one another is approximated as a two-dimensional square lattice such that all model chains are parallel to one another and each chain has four nearest neighbors (see Fig. 1(a)).

Figure 1. Representations of a model system, four chains with binding sites, and the shifting of one chain.

(Color online) (a) The cross-section of systems consists of M × M chains stacked in the xy-plane. Chain lengths extend in the z-direction. (b) A representation of a set of four adjacent chains. In the figure, “active binding sites” (ABSs) are represented by dark cells. When ABSs on adjacent chains (say chains i and j) align at some particular z, a cross-link is formed, thereby contributing an energy −J. (c) A representation of the shifting of one chain during Monte Carlo simulations. Microstates are generated by the shifting of all binding sites along the length of a randomly selected chain in either the +z or −z direction by one binding site. In this example, the middle chain is chosen and is shifted in the +z direction, as indicated by the shifting of the dark cells along the middle chain by one cell.

We suppose that a total of N binding sites appear with a fixed periodicity along the length of each chain and that cross-links form between nearest-neighbor chains only at particular binding sites. We call these binding sites “active binding sites” (or ABSs). The periodicity of binding sites and the existence of ABSs are two aspects of the model that are inspired specifically by the collagen fibrils found in tendon. These fibrils are well-aligned and have periodic (D-band) locations at which proteoglycans capable of forming cross-links may attach (see Ref. [16]). An ABS then represents a D-band location at which such a proteoglycan is attached and is capable of cross-linking to a proteoglycan on an adjacent chain (see Ref. [17]). We suppose that cross-links necessarily form when ABSs on neighboring chains align. On each chain, the locations of n ≤ N/2 ABSs (the same n for each chain) are fixed, defining a density per unit length ρ = n/N (see Figure 1(b)). We investigate the effect of variability in cross-linking on denaturation temperatures by exploring the effects of density and arrangements of ABSs.

A model system is constructed by arranging M × M parallel chains on a square lattice. We choose the coordinate system such that the length of each chain (of N sites) extends along the z-direction. We propose an Ising-like Hamiltonian

$$E=-\frac{1}{2}J\sum _{\langle i,j\rangle }\sum _z{S}_{iz}{S}_{jz}$$ (1)

for nearest-neighbor chains labeled i, j and index 1 ≤ z ≤ N along each chain. The s_iz are either 0 or 1, indicating that the corresponding binding site is either inactive or active. Later, we shall find it expedient to replace the value 1 with values taken from a Gaussian distribution clustered around 1. The isotropic coupling constant, J > 0, represents the strength with which ABSs bond to one another to form cross-links. The first sum is over the four nearest-neighbor chains, while the second sum is over the possible locations of binding sites along length of chains i and j. Systems are characterized by unique values of the ABS density (ρ), size (M), length (N), and a particular arrangement of ABSs.

We use Monte Carlo (MC) numerical simulations to equilibrate the model. The Metropolis MC method [18] is utilized to generate the microstates as follows. A chain is selected at random with uniform probability. An MC move is proposed for the selected chain by first choosing a direction (+z or −z) with equal probability, and displacing the chain by one unit in the chosen direction (see Fig. 1(c)). The change in energy, ΔE, due to the proposed move is calculated. The configuration is accepted if ΔE ≤ 0; otherwise the move is accepted with a probability equal to the Boltzmann weight(e^{−Δ E/k_BT}). We define one MC step as a set of M² proposed MC moves.

2.1. Thermalization Procedure

For homogeneous systems, periodic boundary conditions are imposed in the two directions transverse to the chains. Since all the chains are identical, there are no unsatisfied ABSs, so the ground state energy is E₀ = −2JM²Nρ. In order to determine when a system is thermalized, an exponential function E(m) = (E_i−E_∞)e^−m/µ + E_∞ is fitted to the energy dependence on MC step, where m is the number of MC steps. We identify µ as a scale to estimate the number of MC steps required for thermalization. After a minimum of 10⁵ MC steps, systems are considered thermalized when one of the following conditions is satisfied:

1. the number of MC steps exceeds 5µ and the uncertainty in µ during the fit is on the order of 1% or less; or

2. the number of MC steps exceeds 20µ indicating that the data are noisy but consistent; or

3. |E_∞ − E_i| ≤ k_BT, in which case the energy is not changing significantly.

During and after this thermalization stage, all chain displacements are recorded along with MC step. Hence the precise displacement of each chain for each MC step is known.

The process by which heterogeneous systems are constructed yields systems in random energy states; therefore, these systems are first thermalized via the same procedure as above but under periodic boundary conditions in the z-direction, in addition to the x- and y-directions. Upon completion of this initial thermalization process, periodic boundaries in the z-direction are removed, and the thermalization process is again performed for the non-z-periodic systems. Figure 2 shows a representative example of the dependence of E on MC step for a heterogeneous system for ρ = 0.30 and T = 3.03 J/k_Band an exponential fit E(m), during the initial (z-periodic) thermalization stage. For each set of ρ, T, M, and N, multiple systems were simulated and the results averaged.

Figure 2. Energy vs thermalization MC step, and an exponential fit, for a heterogeneous system during the initial thermalization stage.

(Color online)

2.2. The Observables

2.2.1. Specific Heat

To compare our results to scanning-calorimetry experiments [5], we examine the temperature dependence of the heat capacity as determined through the fluctuation-dissipation theorem: C = 〈(δE)² 〉 /(k_BT²), where E is the internal energy. A power-law divergence in heat capacity at a well-defined critical temperature is a hallmark of a continuous phase transition, as from an ordered to a disordered phase, while a broadened peak may indicate a subtler crossover without a qualitative change in symmetry or order (see also Appendix).

2.2.2. Order Parameter

We observe that for each ABS density there is a temperature below which a cross-sectional “surface,” defined by the ends of the chains, appears distinct (again see Fig. 1(a), above). Above this temperature the distinguishability of the cross-sectional “surface” is lost, because many chains have obtained large displacements. We define an order parameter f as the fraction of chains that are essentially frozen. To define f we first define two quantities: (1) the average displacement of the chains in a system for each MC step, d̄, and (2) the number of chains, n_f, whose displacements (d_i, i = 1, …, M²) are less than one lattice spacing from the average, |d_i− d̄| < 1. Then f = n_f/M². The average displacement of the entire system, d̄, is subtracted in order to remove any (irrelevant) net displacement incidentally acquired by the entire system. Essentially, f is a measure of the fraction of chains that have zero displacement in a microstate consistent with equilibrium.

2.2.3. Experimental Analogue to the Order Parameter

As an experimentally measurable analogue to f, we introduce 1/〈đ〉, where đ is the root-mean-squared displacement of the system of chains, at each MC step,

$$đ=\sqrt{\frac{1}{M^2}\sum _{i=1}^{M^2}{(d_i-\mathrm{d̄})}^2}$$ (2)

and 〈đ 〉is the ensemble-averaged 〈đ 〉. This 〈đ 〉 is analogous to the “surface width” in studies of surface roughening during surface growth [19]. Surface roughening, however, is an interfacial phenomenon, and the roughening transition describes the change in the properties of the interface, not the materials properties of the sample. In our case, 〈đ 〉 reflects bulk interactions well removed from the surface.

3. Results and Discussion

3.1. Heterogeneous Systems

The random arrangements of ABSs in heterogeneous systems result in highly degenerate ground states, preventing convergence. To break the degeneracy, it is expedient to choose the binding strength s_iz of each ABS from a Gaussian distribution centered around 1.0. We choose a standard deviation of 0.2 with the constraint that 0 < s_iz < 2; a different choice of Gaussian width (0.10) has no discernible effect on the results. The assumption of a distribution in ABS binding strengths is not inconsistent with experimental evidence (see Ref. [20]), which indicates that there is a broad range of interaction strengths in the cross-linking of decorin between collagen fibrils.

Figure 3 shows the temperature dependence of the heat capacity per chain (specific heat) at constant volume for several ABS densities. The specific heat is small at low and high temperatures for each ABS density. A gradual onset of a peak is also apparent for each density at mid-temperatures. We denote the temperature at which the peak appears as T_m, which increases with increasing ABS density, ρ, consistent with the increasing bond-energy density.

Figure 3. Temperature dependence of heat capacity per chain (specific heat), C_V /M², for systems of heterogeneous chains.

(Color online) Low-and high-temperature specific heats are near zero for each ρ. The specific heat for each density also exhibits a gradually-onset peak for mid-temperatures. The temperature at which this onset occurs increases with increasing ρ, as do the widths. We denote the temperature at which the peak occurs as T_m, to correspond with conventional notation (Ref. [5]). T_m also increases monotonically with increasing ρ ≤ 0.50.

Additionally, the peak widths increase as ρ approaches 0.50, the point at which quenched disorder reaches its maximum. The extent of broadening does not seem to depend on system size, suggesting a crossover instead of a transition except in the limit ρ → 0 (see Appendix).

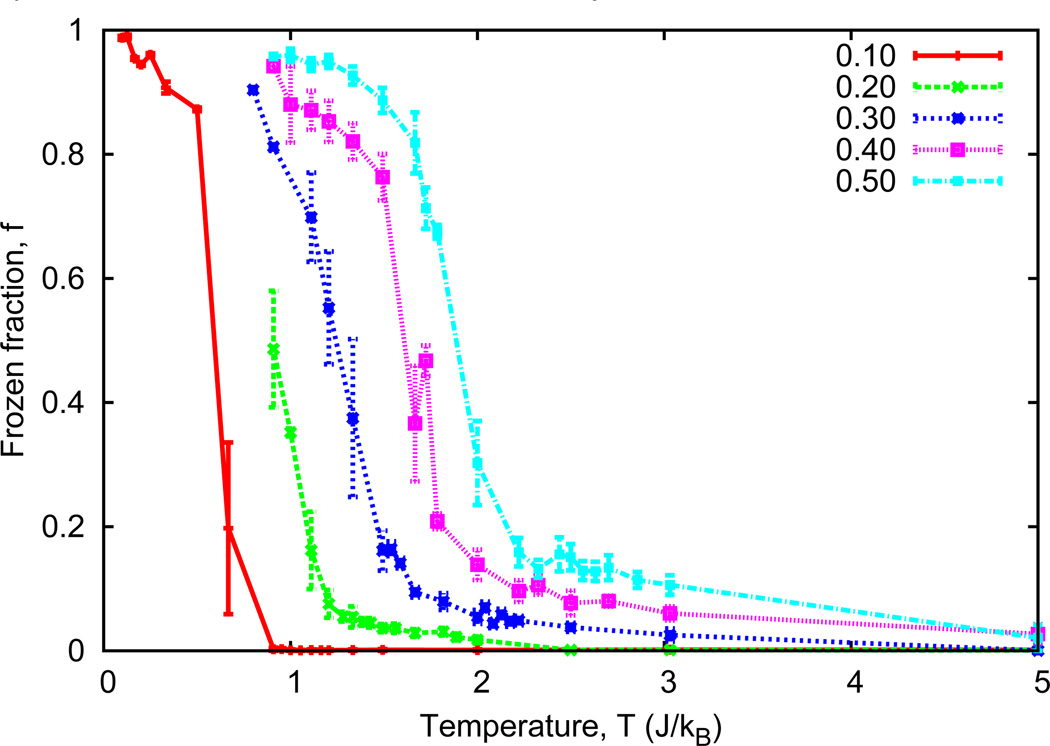
The fraction of frozen chains (Fig. 4) indicates that for all densities there is a locally ordered, low-temperature region in which a significant portion of the system remains essentially frozen. Likewise there is a disordered, high-temperature region in which nearly all chains are displaced. The temperature range over which the change from ordered to disordered states occurs depends on ρ.

Figure 4. Order parameter, f vs T.

(Color online) The fraction f of chains that are within one lattice spacing of the average indicates that there is a range of temperatures for each ρ for which a significant portion of the systems change from ordered (or frozen) to disordered states. The breadth of this range is also ρ dependent.

Figure 4 shows the temperature dependence of the frozen fraction for various ABS densities. Each density exhibits high order for low temperatures with a change to disorder with increasing temperature. Low-density systems exhibit a change in order at low temperatures that becomes more step-like in the limit as ρ → 0. Higher density systems, on the other hand, pass through this crossover at higher temperatures and do so more gradually compared to low-density systems. The point at which f tends to level off in the disordered region is consistent with the melting temperature identified by the peaks in heat capacity (Fig. 3). For each ABS density, the peak in heat capacity occurs at a higher temperature than the change from ordered to disordered states, and this difference in temperature increases with increasing ρ. This behavior is similar to a glass transition in that it is not a true phase transition [21].

Figure 5 shows the dependence of 1/〈đ 〉 on temperature. The behavior of 1/〈đ 〉 corresponds well to the crossover displayed by f. In the high-temperature (disordered) region, f and 1/〈đ 〉 suggest that the chains have many accessible configurations. Low-density systems in this region interact so weakly as to be essentially independent.

Figure 5. 1/〈 đ 〉 vs T.

(Color online) The temperature at which the change from ordered to disordered states occurs, as observed in 1/〈 đ 〉, increases with increasing cross-link density. These correspond accurately to the change in order predicted by f.

Because ABS locations on neighboring chains do not match, the systems are frustrated, broadening the heat-capacity peak and the crossover observed in f and 1/〈đ 〉 Systems with lower ABS densities display a narrower peak and sharper change in order parameter, corresponding to the smaller quenched disorder.

3.2. Homogeneous Systems

Quenched disorder is absent in the unfrustrated, homogeneous systems, so we expect a sharp transition.^‡ We first investigate systems in which all ABSs along each chain are sequentially arranged immediately adjacent to one another. Such a sequence of adjacent ABSs along a chain is said to make up a domain. Figure 6 shows the specific heat versus temperature for three ABS densities (0.10, 0.30, and 0.50). The peak in specific heat of homogeneous systems with one domain exhibits a sharp transition (see Appendix), unlike the heterogeneous systems, and is independent of ABS density.

Figure 6. Temperature dependence of heat capacity per chain (specific heat), CV/M², for systems of homogeneous chains.

(Color online) Specific heat for three values of ABS density, ρ (0.10, 0.30, and 0.50), each show the same narrow peak at the same melting temperature, independent of ρ. Low-temperature heat capacities are near zero for each ρ. High-temperature heat capacities show a dependence on ABS density. See Fig. 7(a) for a visual representation of such a system.

The effect of separating the ABSs into two domains for ρ = 0.30 is shown in Figure 7. Figure 7 (a) depicts homogeneous systems of (A) one domain per chain, (B) two domains of equal size separated by a single inactive binding site, (C) two domains of equal size separated by (1 − ρ)N inactive binding sites, and (D) two domains of unequal sizes also separated by (1 − ρ)N inactive sites, along with the temperature dependencies of (b) the order parameter f and (c) the specific heat. Both the order parameter and the specific heat indicate that the melting temperature almost doubles from $T_m^{(A)}\simeq 1.1J/k_B$ to $T_m^{(B)}\simeq 2.1J/k_B$ when the single domain is split into two equal domains that are separated by one inactive binding site. When the two domains are arranged far apart, the melting temperature increases only slightly from $T_m^{(B)}\simeq 2.1J/k_B$ to $T_m^{(C)}\simeq 2.3J/k_B$ The effect on the melting temperature due to the proximity of the domains is much less apparent than the effect due to changing the number of ABS domains. Unlike in the heterogeneous systems, T_m as determined from f and the peak in the specific heat coincide.

Figure 7. Comparison of melting temperatures based on domain boundaries for ρ = 0.30.

(Color online) (a) Depictions of four homogeneous sample systems with (A) one domain (all ρN ABSs are clustered), (B) two equal domains separated by one inactive binding site, (C) two equal domains separated by (1 − ρ)N inactive binding sites, and (D) one small (two ABSs) and one large domain (ρN − 2) separated by (1 − ρ)N inactive sites; (b) The order parameter and (c) the heat capacity indicate that the increase in melting temperature is primarily associated with the number of domain boundaries, not the manner in which they are organized.

We infer that in homogeneous systems, the melting temperature is determined by the number of domains and not their proximity to one another. The melting temperatures are dictated by the number of cross-links that must be broken simultaneously in order to transition from the ground state. ABSs near the edge of a domain are more likely to become unsatisfied. ABSs away from a domain edge simply change which ABSs with which they are cross-linked. The most important aspect in determining the behavior of a given chain within a system, then, is the domain boundaries on neighboring chains. When a chain samples a configuration in which an ABS crosses a domain boundary on an adjacent chain, cross-links are broken. Systems melt only when thermal fluctuations are similar to the energy associated with breaking cross-links on ABSs near the boundaries. We expect a linear increase in melting temperature with an increasing number of domain boundaries (two per domain). Figure 8 shows the dependence of melting temperature on the number of domains, n_d, for ρ = 0.30 and for n_d =1, 2, 3, and 5. From Figure 6, we infer that the melting temperature is again independent of ABS density, by extension of the independence of T_m on ρ for the one-domain systems.

Figure 8. Melting temperature T_m versus number of domains, for ρ = 0.30.

The melting temperature shows an approximately linearly-increasing dependence on the number of domains of ABSs for homogeneous systems.

3.3. The Role of Active Binding Site Domains

Any homogeneous system will exhibit a sharp phase transition, as shown above, but the melting temperature will be determined primarily by the number of domain boundaries present. The frustration in the heterogeneous systems of Section 3.1 also can be discussed in terms of ABS domains (or domain boundaries). Clustering of ABSs seldom occurs in heterogeneous systems with low ABS densities. Therefore the variation in the number of domains in low-ρ, heterogeneous systems is expected to be small. The increased blurring of a would-be phase transition observed in this model with increasing ρ can be explained as a result of the widened distribution of values of n_d over chains in such systems. Figure 9(a) shows the ρ-dependence of the probability of a given number of domains for heterogeneous systems with randomly distributed ABSs, for N = 100. With increasing ABS density, the probability distribution of the number of domains broadens until ρ = 0.50. (The probability distributions for ρ and 1 − ρ are the same.) Figure 9(b) shows the ρ-dependence of the standard deviation σ of the number of domains, n_d. For ρ = 1/N = 0.01, there can exist only one domain per chain; hence the standard deviation is zero. σ increases monotonically up to ρ = 0.50; i.e., the higher the density, the greater the variation in the number of domains. Increasing density also increases the bond frustration, since the number of distinct placements of ABSs increases. The broadening of the crossover is thus the direct result of the distinct arrangements of fixed ABSs along each chain.

Figure 9. Standard deviation of the number of domains per chain vs ABS density.

The number of domains in low-ρ systems is expected to be similar to the number of ABSs, with little variance. The number of domains increases withρ; however, the probability of ABS clustering also increases; therefore the variance in the number of domains increases.

The model proposed here provides insight into a new fundamental mechanism for the multiple denaturation transitions observed in fibrillar collagen: inherent disorder in the arrangements of cross-links between neighboring chains.

Results from the heterogeneous systems are consistent with phenomena observed in some echinoderms, for example, which are known to increase their dermal rigidity while under duress. This is due to their ability effectively to increase the cross-link strength at physiological temperature [13, 14]; in terms of our model, this is equivalent to lowering T at fixed J. The model is also consistent with results that indicate that age-related changes in the properties of axially-ordered, cross-linked tissues may be the result of changes in cross-linking strength [12]. The model suggests that additional cross-links may form or perhaps cross-links become more organized, resulting in the shifting of the broad melting temperature toward higher temperatures. Additionally, the model suggests that in the case of well ordered cross-link distributions, sharp denaturation transitions may be observed and perhaps engineered as desired.

Heterogeneous systems may constitute a glassy material due to their quenched disorder. Simulations of these systems of heterogeneous chains have long thermalization times at temperatures near the crossover, similar to those of glasses. The observation that the change in the order parameter occurs at a lower temperature than the peak in heat capacity is also of interest. The heat capacity increases when fluctuations in the energy become large, which occurs when chain displacements have a large enough range to explore configuration space. The decrease in the order parameter, however, occurs because the energy landscape [21] in heterogeneous systems may often provide nearby configurations with the same energies. These nearby configurations of similar energies provide no significant fluctuation in the energy yet provide for the displacement that reduces the order parameter.

4. Conclusions

The model presented in this work predicts that axially-ordered networks with identical chains will exhibit a sharp phase transition. The melting temperature for these homogeneous systems depends linearly on the number of domains of ABSs but not on their proximity nor on the overall density ρ of ABSs. In contrast, systems composed of quenched, stochastic chains exhibit crossover behavior. The temperature at which the crossover occurs depends on ρ. The presence of this crossover behavior is the direct result of the frustration introduced by the non-identical arrangements of fixed ABSs along each chain. The application of this model to axially-ordered cross-linked materials sheds light on possible mechanisms by which the properties of materials may be tuned for specific behavior, artificially and naturally.

Appendix

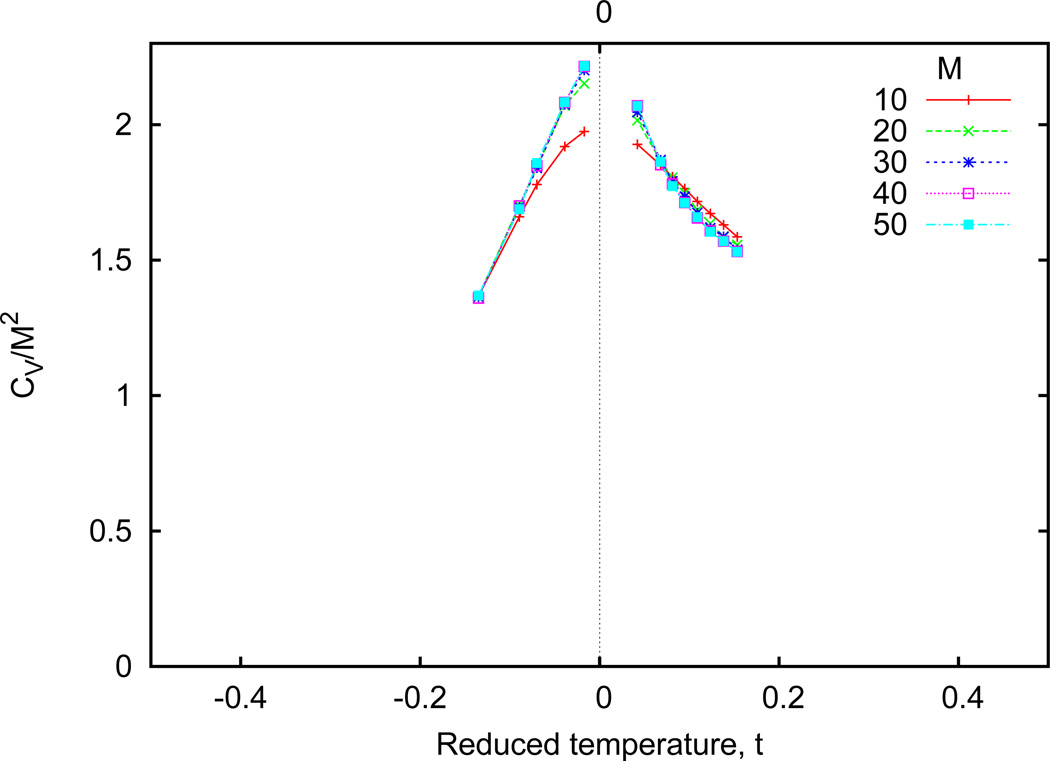
Scaling with system size supports the existence of a continuous phase transition in the homogeneous case but of a crossover for heterogeneous systems. A continuous phase transition may be characterized by, among other properties, a power-law divergence in the heat capacity at T_C, C ~ |t|^−α, where t = (T − T_C)/T_C is the reduced temperature. Since true critical behavior is manifest only in the infinite system, we examine the effect of lattice size on the heat-capacity peak, fixing ρ = 0.30 and estimating σ for M = 10, 20, 30, 40, and 50.

Figure A1 shows that the specific-heat peak narrows and increases in height as the lattice size increases, consistent with a phase transition.

Figure A1. Specific heat dependence on reduced temperature for homogeneous systems.

The peak specific heat appears to narrow with increasing lattice size. Values within about 3% of the critical temperature are neglected due to increased instability.

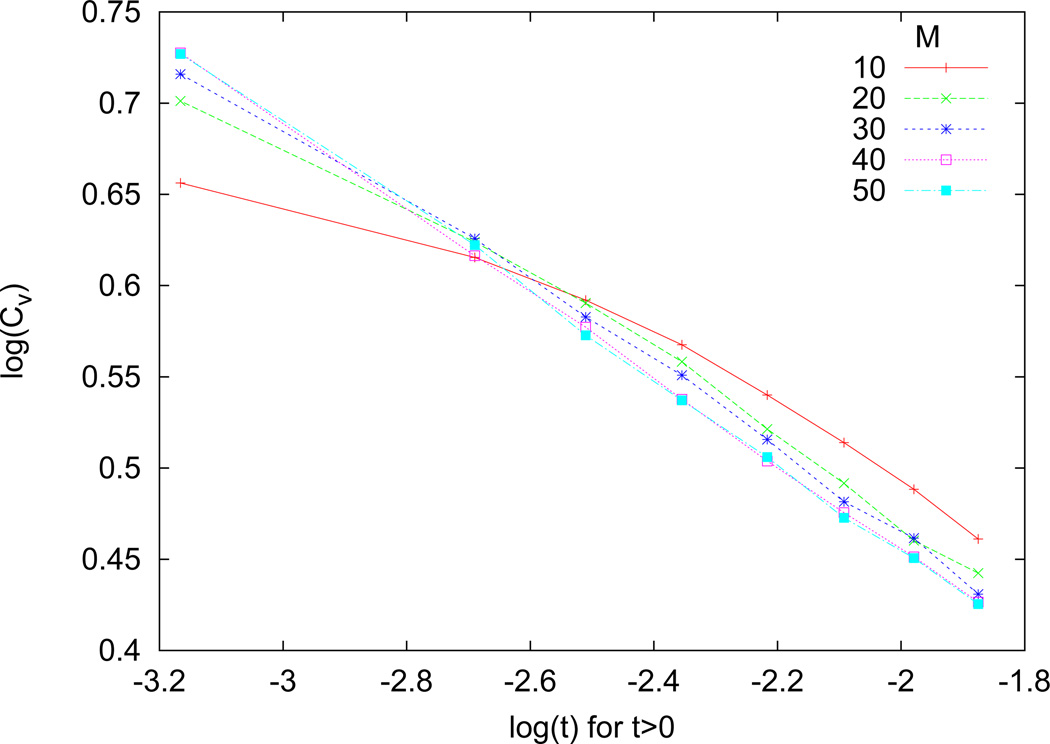
Figure A2 shows log(C_V) vs log(t) for t > 0. With increasing system size, the behavior of log(C_V) becomes linear. The critical exponent σ is determined from the linear fit of log(C_V) vs log(t), for t > 0.

Figure A2. Homogeneous system: log(C_V) vs log(t) for t > 0.

With increasing system size, the behavior of log(C_V) becomes increasingly linear and appears to be saturating. The critical exponent α is determined from a linear fit.

Figure A3 shows the linear-fit estimates for α for each M. α appears to approach asymptotically the approximate value 0.25. We conclude that, in the thermodynamic limit, homogeneous systems would exhibit a phase transition.

Figure A3. Homogeneous system: the critical exponent, α, vs system size, M.

α approaches ≈ 0.25 with increasing system size

The effect of lattice size on the heterogeneous systems is less clear. Figure A4 shows the specific heat versus reduced temperature t for three lattice sizes, M = 15, 30, and 100, of heterogeneous systems with ρ = 0.30. With increasing lattice size the peak shows little or no increase in height nor significant narrowing. We conclude there is no phase transition in the heterogeneous systems.

Figure A4. Specific heat dependence on reduced temperature for heterogeneous systems.

With increasing lattice size the peak shows little to no increase in height nor significant narrowing, as would be expected for finite-size effects.