Efficient Design for Mendelian Randomization Studies: Subsample and 2-Sample Instrumental Variable Estimators

Abstract

Mendelian randomization (MR) is a method for estimating the causal relationship between an exposure and an outcome using a genetic factor as an instrumental variable (IV) for the exposure. In the traditional MR setting, data on the IV, exposure, and outcome are available for all participants. However, obtaining complete exposure data may be difficult in some settings, due to high measurement costs or lack of appropriate biospecimens. We used simulated data sets to assess statistical power and bias for MR when exposure data are available for a subset (or an independent set) of participants. We show that obtaining exposure data for a subset of participants is a cost-efficient strategy, often having negligible effects on power in comparison with a traditional complete-data analysis. The size of the subset needed to achieve maximum power depends on IV strength, and maximum power is approximately equal to the power of traditional IV estimators. Weak IVs are shown to lead to bias towards the null when the subsample is small and towards the confounded association when the subset is relatively large. Various approaches for confidence interval calculation are considered. These results have important implications for reducing the costs and increasing the feasibility of MR studies.

Mendelian randomization (MR) is a study design used to test or estimate the causal relationship between an exposure and an associated outcome using data on inherited genetic variants that influence exposure status (1, 2). Because associations between exposures and outcomes are potentially attributable to unmeasured confounding and reverse causation, using a genetic determinant of the exposure as an instrumental variable (IV) allows the causal component of the observed association to be estimated. An IV is required to be 1) associated with the exposure, 2) independent of the outcome conditional on the exposure and confounders of the exposure-outcome association (measured or unmeasured), and 3) independent of all unmeasured confounders of the exposure-outcome association (1–3). Genetic variants are attractive as candidate IVs because they are randomly assigned at conception and are not affected by potentially confounding environmental factors.

If the exposure and outcome of interest are continuous traits, and a single IV is used, the MR estimator can be conceived of as a ratio of 2 estimates: the “reduced-form” estimate (the coefficient for the association between the IV and the outcome) and the “first-stage” estimate (the coefficient for the association between the IV and the exposure). In the traditional MR setting, these 2 estimates are obtained using a single sample, where data on the IV, exposure, and outcome are available for all participants. However, in practice, complete data may not always be obtainable. For researchers conducting MR investigations in the context of large genetic association studies, it may not be possible to obtain exposure data for all participants. For example, if the exposure is a biomarker, measurements may be prohibitively expensive to conduct for a large study or impossible to conduct because of the lack of appropriate biospecimens available for analysis (for example, lack of prospectively collected or adequately preserved samples for biomarker measurement). Thus, the exposure of interest may only be measurable for a subset of individuals.

In this paper, we use simulated data to explore the implications of incomplete exposure data for statistical power and bias in MR studies using “subsample IV estimators.” We show that generating exposure data for a subset of study participants, rather than all participants, does not substantially decrease power when the IV is relatively strong. In fact, generating exposure data for all participants can be an extremely cost-inefficient strategy. We show that this concept also applies to “2-sample IV estimators” (4–6), where the first-stage and reduced-form estimates are obtained from independent (nonoverlapping) samples drawn from the same population. In addition, we demonstrate the effects of weak IVs (genetic variants that explain a small proportion of the variation in the exposure) in the context of subsample and 2-sample IV methods and compare various methods for estimating standard errors and confidence intervals.

Large sample sizes are needed for MR studies (7, 8), and the costs associated with exposure measurement can be substantial. The subsample and 2-sample IV approaches described here have broad relevance for MR investigations of exposures that are expensive or impossible to measure for large samples, including biomarkers. Our findings should increase the feasibility and cost-efficiency of MR, enabling the use of existing genetic data sources, such as large-scale genetic association studies, for MR analyses.

MATERIALS AND METHODS

We define subsample and 2-sample IV estimation as follows. Assuming that data on the IV (G) are available for all participants, subsample IV estimation can occur when data on the exposure (X) are available for only a subset of participants but outcome data (Y) are available for all participants. The samples with data on X and Y have sample sizes defined as n_X and n_Y, respectively. Subsample IV estimation could also occur when data on Y are available for a subset of participants but data on X are available for all participants, although this strategy is not considered further here. Two-sample IV estimation occurs when data on G and X are available for one sample and data on G and Y are available on an independent sample, such that no participants have data on both X and Y.

We used simulated cohort data sets to investigate the effect of varying the sample size for subsample and 2-sample IV estimators on power, precision, and bias. For each simulated scenario, we generated 10,000 data sets with 10,000 observations on 4 variables: a genetic susceptibility score used as the IV (G), an exposure (X) influenced by G, an outcome (Y) influenced by X, and a confounding variable (U), assumed to be unmeasured, with effects on both X and Y. G and U were generated randomly from a standard normal distribution. X was also a randomly generated standard normal variable with linear effects exerted by G and U:

(1)

X was standardized to have a variance of 1. Values of β_GX were chosen to produce specific R² values for the first-stage regression of X on G using the following equation:

(2)

Y was a randomly generated standard normal variable with linear effects of X and U:

(3)

In order to vary n_X, X values were randomly set to missing. IV strength in a given data set is measured by the F statistic from the first-stage regression of X on G. IVs with an average first-stage F value less than 10 are conventionally considered weak, although this threshold is arbitrary, and some bias persists even for nonweak IVs (9). F is defined as the ratio of the variance explained by the model to the residual variance in the model. F can be expressed as a function of the first-stage R², the sample size (n), and the number of IVs (k):

(4)

Thus, F increases as R² and n increase and as k decreases. The IV used here is continuous; however, our results apply to any IV or IV set with the same first-stage R², including categorical or ordinal IVs and multi-IV scenarios (7) (see Discussion).

We conducted 4 sets of simulations in order to assess power and bias for subsample IV estimators. In order to assess how power varies according to the size of the subsample (simulation 1), we varied n_X from 25 to 10,000 and β_XY from 0 to 0.3, with n_Y set to 10,000 and the first-stage R² set to 0.025. In order to assess how IV strength affects power (simulation 2), we varied n_X from 25 to 10,000 and the first-stage R² from 0.002 to 0.05, with n_Y set to 10,000 and β_XY set to 0.2. In order to assess bias when IVs are weak (simulation 3), we varied the n_X:n_Y ratio from 0.1 (a small subsample) to 1.0 (the complete-data scenario) and varied the average first-stage F statistic from approximately 1 to approximately 20, with β_XY set to 0.1. Varying of F was accomplished as follows: For each n_X:n_Y ratio, the first-stage R² was held constant (to a value that produced an average first-stage F of 20 when n_Y = 10,000) and n_Y was varied from 100 to 10,000, with the value n_X determined by the n_X:n_Y ratio. This approach allowed us to assess weak IV biases for a wide spectrum of values for F and n_X:n_Y. We also evaluated bias for weak IVs by varying n_X:n_Y (from 0.1 to 1.0) and R² (from 0.001 to 0.03), with β_XY set to 0.1 and n_Y set to 10,000, 3,000, or 1,000 (simulation 4). Similar simulations were also conducted for 2-sample IV estimators, where the first-stage sample (n_X) and the reduced-form sample (n_Y) consisted of independent sets of participants. Confounder effects β_UX and β_UY were set to 0.2 in simulations 1 and 2, leading to positive confounding. β_UX and β_UY were set to 0.3 in simulations 3 and 4 to better demonstrate weak IV bias. Simulations were repeated in the absence of confounding, although it is known that X-Y confounding does not produce substantial bias for traditional IV analyses when IVs are strong (7).

MR estimates were obtained using the Wald ratio method (1). For each simulation, 2 linear regressions were performed: a regression of X on G (the first-stage regression) and a regression of Y on G (the reduced-form regression). The ratio of these estimates (the Wald estimate) and corresponding confidence intervals were obtained using the suest and nlcom commands in Stata (10). The suest (seemingly unrelated regression (SUR)) command combines the regression estimates into 1 parameter vector and a simultaneous sandwich (robust) variance-covariance matrix. The nlcom command computes standard errors and confidence intervals for nonlinear combinations of parameter estimates using the delta method. We did not use the traditional 2-stage least-squares procedure (11), because this method discards persons with missing data on X, whereas the Wald method can include such persons in the reduced-form regression. Power was defined as the proportion of the 10,000 data sets in which a statistically significant effect of X on Y was observed (2-sided P < 0.05).

For 3 randomly chosen data sets from simulation 2, comprising strong, moderate, and weak IV scenarios, we compared 5 strategies for calculating standard errors and 95% confidence intervals for the MR estimate. First, we used a sequential regression approach, where linear regression was used to generate a coefficient for the G-X association; this coefficient was then used to generate predicted values of X for all persons with data on Y (n_Y). The association between the predicted X and Y was assessed using linear regression with robust standard errors to mitigate the failure of the method to account for the uncertainty in the predicted X. We also used the SUR/delta method described above; Fieller's theorem, which is a method for calculating confidence intervals for a ratio of 2 normally distributed variables (12); and a Bayesian method using weakly informative prior distributions (13). Finally, we used a bootstrap method for confidence interval estimation in which 1,000 random samples equal in size to the original sample were drawn, with replacement, from each of the samples used to generate the first-stage and reduced-form estimates.

RESULTS

Simulation 1

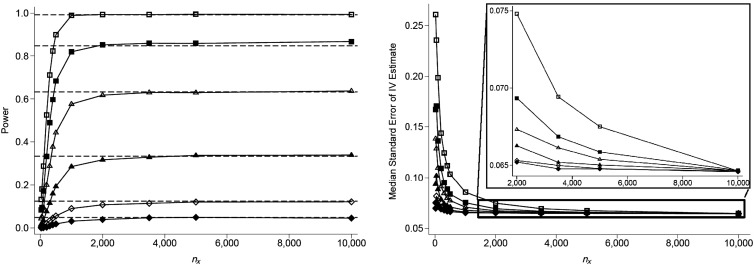
For a study of 10,000 persons with data on Y, Figure 1 (left panel) shows how varying the size of the subsample (n_X) affects power to detect a significant effect of X on Y. For all effect sizes considered, the power of the subsample IV estimator has an upper bound approximately equal to the power of the reduced-form estimator (shown as horizontal dashed lines), which is approximately equal to the power for a traditional IV approach for these scenarios, where complete data are available for all n_Y individuals. As n_X increases, power approaches this upper bound, and gains in power diminish. For these scenarios, our results indicate that more than 90% of the maximum power can be achieved by obtaining exposure data on only 20% of the sample. Figure 1 (right panel) shows the standard errors for these scenarios. In general, the standard errors for subsample IV estimates are larger when the effect size is larger, and standard errors decrease as n_X increases. Standard errors converge to the full analysis standard error of 0.063 for all effect sizes as n_X approaches n_Y. Using a 2-sample IV approach, results are very similar (see Web Figure 1, available at http://aje.oxfordjournals.org/). Power for the 2-sample approach appears to be very slightly lower than that for the subsample approach, and standard errors do not converge to a common value as n_X approaches n_Y.

Figure 1.

Power (left) and median standard error (right) of the subsample instrumental-variable (IV) estimate for different values of the causal effect size (β_XY) and the sample size of the first-stage regression (n_X), with a strong IV (R² = 0.025), a sample size for the reduced-form regression (n_Y) of 10,000, and a confounding variable with equal effects on X and Y (β_UX = β_UY = 0.2). β_XY values are 0.0 (filled diamond), 0.05 (open diamond), 0.1 (filled triangle), 0.15 (open triangle), 0.2 (filled square), and 0.3 (open square).

Simulation 2

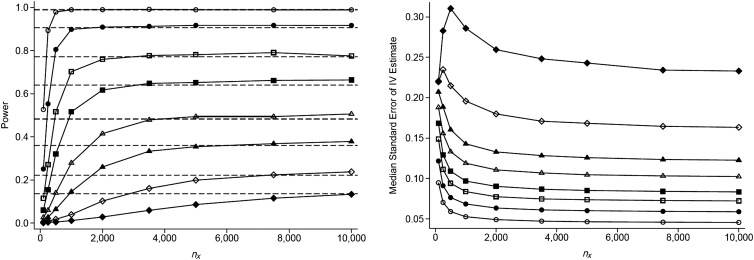
When we vary the strength of the IV (as measured by R²), holding the effect size constant at 0.2, we observe that as R² decreases, power approaches its maximum more slowly as n_X increases (Figure 2). Thus, the value of n_X needed to obtain more than 90% of the maximum power is higher when the first-stage R² is low. In the scenarios simulated here, to achieve greater than 90% power, n_X needed to be approximately 2,000 (20% of n_Y), 3,500 (35%), 5,000 (50%), and 7,500 (75%) for first-stage R² values of 0.015, 0.01, 0.007, and 0.004, respectively. Using a 2-sample IV approach, results were very similar (Web Figure 2), with slightly lower power for most scenarios compared with the subsample IV approach.

Figure 2.

Power (left) and median standard error (right) of the subsample instrumental-variable (IV) estimate for different values of the first-stage R² and the sample size of the first-stage regression (n_X), with a constant effect size (β_XY = 0.2), a sample size for the reduced-form regression (n_Y) of 10,000, and a confounding variable with equal effects on X and Y (β_UX = β_UY = 0.2). First-stage R² values are 0.002 (filled diamond), 0.004 (open diamond), 0.007 (filled triangle), 0.01 (open triangle), 0.0015 (filled square), 0.2 (open square), 0.03 (filled circle), and 0.05 (open circle).

Simulation 3

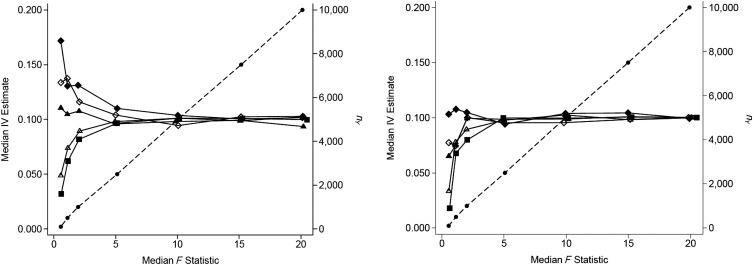
It is well known that traditional “complete-data” IV estimators are biased towards the confounded association and that bias is most severe when the IV is weak (7, 14). In contrast, 2-sample IV estimates are known to be biased towards the null, even when the confounded estimate is biased away from the null (4, 5). In Figure 3 (left panel), we show that the direction of the weak IV bias for subsample MR analyses depends on the n_X:n_Y ratio. If n_X represents a small percentage of n_Y, bias moves towards the null as F decreases, similar to the 2-sample case. In contrast, if the n_X:n_Y ratio is close to 1, bias moves towards the observational estimate as F decreases, similar to the complete-data scenario. The total number of participants (n_Y) is shown as a diagonal line, and the first-stage R² is fixed for each ratio. Figure 3 (right panel) shows the same simulations conducted in the absence of confounding; hence, no bias towards the confounded association is observed. For weak IVs, bias towards the null is present for all subsample scenarios, and the estimate moves closer to the null as n_X:n_Y decreases. For the 2-sample approach (Web Figure 3), bias towards the null increases as F decreases, regardless of the value of n_X:n_Y. This is true for both the confounded and unconfounded scenarios.

Figure 3.

Bias in the subsample instrumental-variable (IV) estimate in confounded (left) and unconfounded (right) scenarios for different values of the average first-stage F statistic and the relative size of the subsample used in the first-stage regression (n_X:n_Y), with a constant causal effect size (β_XY = 0.1) and a confounding variable with equal effects on X and Y (β_UX = β_UY = 0.3). Values for n_X:n_Y are 1 (filled diamond), 0.75 (open diamond), 0.5 (filled triangle), 0.25 (open triangle), and 0.1 (filled square). The sample size for the reduced-form regression equation (n_Y, on the right vertical axis) is shown as dots connected with a dashed line.

In the traditional complete-data setting, weak IV bias can be explained as resulting from a correlation between the 2 terms in the Wald estimator: the first-stage and reduced-form estimates (14). In the 2-sample setting, these estimates are uncorrelated, since they are derived from different data sources. In this case, imprecision in the estimation of the G-X and G-Y associations is analogous to nondifferential measurement error in an observational estimate and results in bias towards the null similar to regression dilution bias (15). In the subsample setting, the bias towards the null and the bias in the direction of the observational association (which is usually in the same direction as the causal effect when this is present) can balance each other out, as demonstrated in the left-hand panel of Figure 3 when the ratio n_X:n_Y is 0.5. The precise ratio required to give unbiased estimates is likely to depend on the characteristics of a given example rather than to be a generalizable result.

Simulation 4

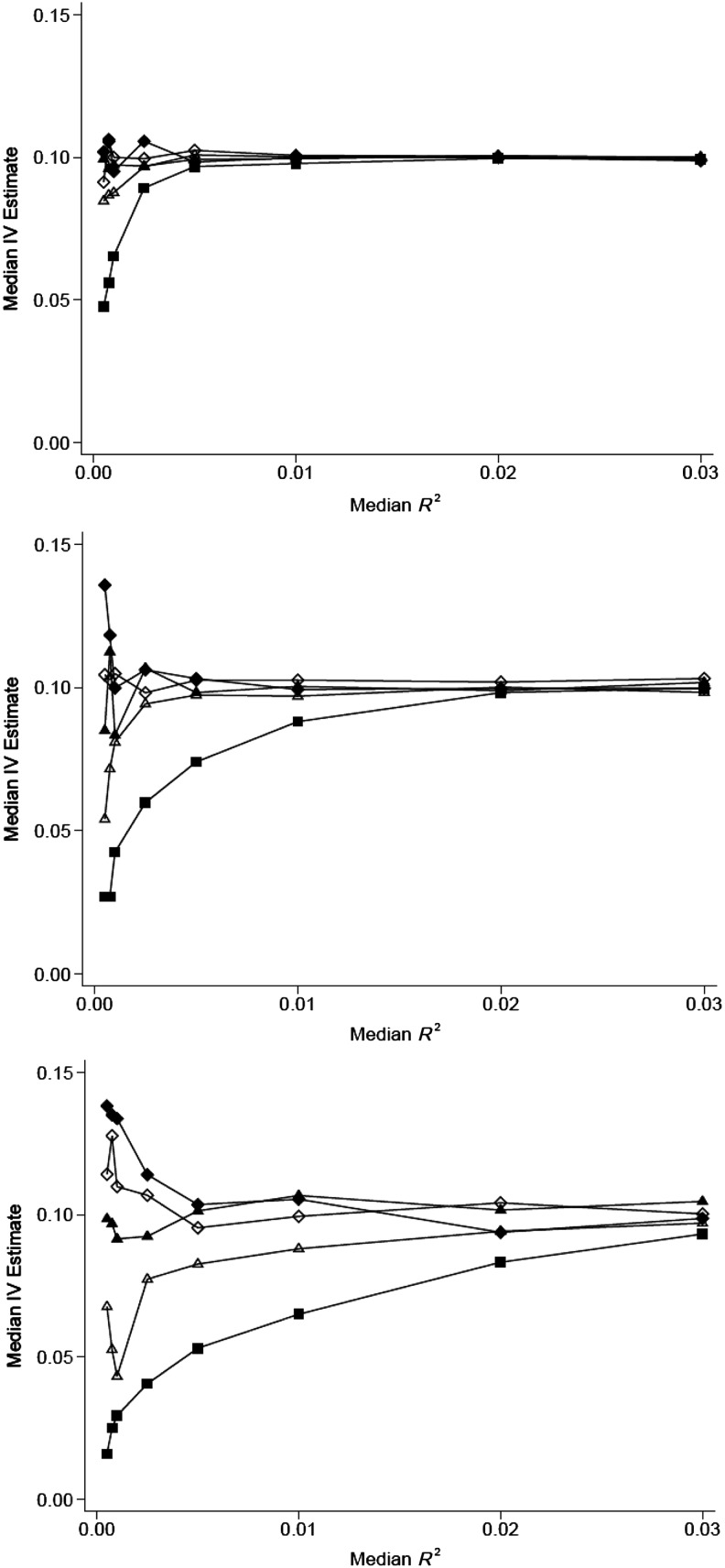
We assessed weak IV bias for subsample IV scenarios varying the R² for the regression of X on G (rather than F), as R² may be a more meaningful parameter to MR practitioners (Figure 4). However, because weak IV bias is related to F rather than to R², bias does not vary with the n_X:n_Y ratio in a uniform way, since increasing n_X both increases the proportion of participants in the subsample (leading to a greater bias towards the confounded association) and increases the F statistic, leading to a reduction in weak IV bias. Thus, weak IV bias towards the confounded association is much more pronounced when n_Y is small, because n_Y limits the size of n_X, reducing the F statistic.

Figure 4.

Bias in the subsample instrumental-variable (IV) estimate for different values of the first-stage R² and the relative size of the sample used in the first-stage regression (n_X:n_Y). The sample size for the reduced-form regression equation (n_Y) is 10,000 (top), 3,000 (middle), and 1,000 (bottom), with a constant causal effect size (β_XY = 0.1) and a confounding variable with equal effects on X and Y (β_UX = β_UY = 0.3). Values for n_X:n_Y are 1 (filled diamond), 0.75 (open diamond), 0.5 (filled triangle), 0.25 (open triangle), and 0.1 (filled square).

Calculating standard errors and confidence intervals

All simulations were conducted using SUR and the delta method (with sandwich variance estimates) for calculating confidence intervals. Stata code for using this method is provided in the Web Appendix. Table 1 shows results obtained using several other methods for standard error and confidence interval estimation, for three randomly selected subsample data sets and three 2-sample data sets. For both the subsample and the 2-sample strong IV scenarios, the SUR/delta method, sequential regression, Fieller's theorem, and the Bayesian method produced very similar confidence intervals, with the bootstrap method producing slightly wider confidence intervals. For the moderate IV and weak IV scenarios, the delta and sequential regression methods produce similar results; however, the Fieller, bootstrap, and Bayesian confidence intervals become substantially wider than the confidence intervals produced by these methods and often asymmetrical in the presence of a weak IV. This reflects the true sampling distribution of the IV estimate with a weak IV, which has long tails and is asymmetrical and is modeled poorly by a normal distribution. In the complete-data MR setting, the reliance on normality assumptions for constructing confidence intervals has been shown to lead to poor coverage properties with weak IVs (13). In our work, coverage under the null was not underestimated when IVs were strong, but it was overestimated, with increasingly conservative confidence intervals, as IV strength decreased (Web Table 1).

Table 1.

A Comparison of Different Methods of Estimating 95% Confidence Intervals for Selected Simulated Data Sets^a

	Strong IV (R2 = 0.025) (Theoretical F = 50)b			Moderate IV (R2 = 0.005) (Theoretical F = 10)			Weak IV (R2 = 0.002) (Theoretical F = 5)
	β	SE	CI	β	SE	CI	β	SE	CI
Subsample IV approach
Delta method	0.148	0.057	0.037, 0.259	0.152	0.132	−0.108, 0.411	0.081	0.161	−0.234, 0.397
Sequential regressionc		0.055	0.039, 0.256		0.128	−0.099, 0.403		0.159	−0.231, 0.394
Fieller's theorem		N/A	0.040, 0.272		N/A	−0.108, 0.562		N/A	−0.291, 0.602
Bootstrapd		0.068	0.014, 0.280		0.137	−0.117, 0.421		0.551	−0.999, 1.162
Bayesian	0.143	0.056	0.040, 0.258	0.174	0.289	−0.161, 0.778	0.089	0.443	−0.563, 0.975
2-sample IV approach
Delta method	0.117	0.068	−0.015, 0.250	0.051	0.119	−0.182, 0.284	−0.086	0.163	−0.405, 0.232
Sequential regressionc		0.065	−0.011, 0.245		0.118	−0.181, 0.282		0.160	−0.440, 0.227
Fieller's theorem		N/A	−0.012, 0.267		N/A	−0.201, 0.336		N/A	−0.610, 0.280
Bootstrapd		0.071	−0.023, 0.257		0.138	−0.221, 0.322		0.997	−2.041, 1.868
Bayesian	0.119	0.072	−0.013, 0.273	0.055	0.169	−0.232, 0.390	−0.100	0.456	−1.012, 0.554

Abbreviations: CI, confidence interval; IV, instrumental variable; N/A, not applicable; SE, standard error.

^a The simulated data sets consisted of 10,000 persons with data on G and Y and 2,000 persons with data on G and X. The true effect of X on Y was set to 0.1, and a confounding variable U had the effect of 0.2 on both X and Y.

^b Theoretical F values were obtained using the following equation: F = R² (n_X − 1)/(1 − R²).

^c For the second-stage regression (of sequential regression), robust SEs are reported.

^d Bootstrapping was conducted using 1,000 replications, with samples of size n_X and n_Y randomly selected (with replacement) from the original samples of size n_X and n_Y.

DISCUSSION

In this paper, we have described how subsample and 2-sample IV methods can be used to increase the feasibility and cost-efficiency of MR studies. Our primary conclusion is that for epidemiologic studies with available genetic data and outcome data, MR investigations can be conducted by generating exposure data for a limited representative sample of the study population with very little loss of power as compared with a study with exposure data for all participants. For example, in our simulated data set of 10,000 participants, a realistic sample size for large-scale genetic association studies, obtaining exposure data for approximately 20% of the full sample achieves maximum power when the first-stage R² is greater than 0.015. This finding is of critical relevance for causal evaluations of exposures that are expensive to measure or impossible to obtain for the full set of participants due to lack of prospectively collected or adequately preserved samples. For IVs with weaker effects on the exposure of interest (R² < 0.015), a larger subsample with exposure data may be required. Additional analytical information clarifying the relationships among n_Y, n_X, R², and power is provided in the Web Appendix.

We have also demonstrated that the upper limit for power in an MR study is approximately the power for the reduced-form estimator, although this upper limit appears to be slightly higher for subsample IV estimators than for 2-sample IV estimators. This may be due to the slight residual bias in the direction of the observational estimate in the subsample case and in the direction of the null in the 2-sample case. Thus, in theory, exposure data are not needed for a fully powered test of the hypothesis that an exposure is causally related to an outcome if the reduced-form estimator is used (2). However, the reduced-form method does not produce a causal estimate for the effect of the exposure on the outcome and so does not allow the researcher to know whether a null finding is due to lack of a causal association or lack of power (for example, if the confidence interval for the IV estimate still includes the observational estimate).

Because the reduced-form power is the approximate upper limit for power, power for MR is most efficiently increased by increasing the size of the sample used for estimation of the reduced-form equation, rather than the first-stage equation (assuming exposure data are available for a sufficient subset of participants). This conclusion is somewhat intuitive because the reduced-form association (the numerator of the Wald estimator) is typically quite weak and difficult to estimate with statistical confidence, since the association between the IV and the outcome is mediated entirely through the exposure. In contrast, the first-stage association (the denominator) should be well-established and easily detectable in a large epidemiologic study.

Thus, the potential gains in cost-efficiency we describe in this paper relate only to reducing the amount of exposure data that are needed. For most MR studies, genetic data and outcome data will be needed for very large numbers of participants to achieve adequate power (7), regardless of how much exposure data are generated. This is a major challenge for MR study design, especially considering that most genetic IVs are not especially strong. A possible solution to this is the use of multiple IVs, when available (7, 16).

Our simulations also show that similar efficiency gains can be achieved using 2-sample IV estimators, where the first-stage and the reduced-form estimation are conducted using data from nonoverlapping sets of study participants. The validity of this method depends strongly on the assumption that the first-stage sample and the reduced-form sample are randomly drawn from the same population (similar to the assumption for subsample IVs, where the first-stage sample is a random sample of the reduced-form sample).

As compared with standard IV estimators, subsample IV estimators exhibit different behavior in the presence of weak IVs. For traditional IV estimators, estimates are biased towards the confounded observational association. In contrast, subsample IV estimators are biased towards the null when the subsample is relatively small, similar to 2-sample IV estimators (5). However, they are biased towards the confounded association when the subsample is increased, similar to traditional IV estimators.

As a guide to practitioners, we describe a variety of methods for obtaining standard errors and confidence intervals for subsample and 2-sample IV estimators. When the IV is strong, the SUR/delta method used in this work is appropriate and produces quite similar confidence intervals compared with the other methods examined. However, for moderate and weaker IVs, the Fieller, bootstrap, and Bayesian confidence intervals are considerably larger than those derived from the SUR/delta methods and sequential regression. The SUR/delta and sequential regression methods are problematic for weak IV scenarios, since they do not adequately account for the error that accompanies estimation of the effect of the IV on the exposure, and they assume that the sampling distribution of the IV estimate is normal. Thus, in the presence of a weaker IV, more robust methods for confidence interval calculation may be needed, such as bootstrapping. Unfortunately, bootstrapping was not computationally feasible for the simulation-based work presented here. Fieller's theorem is a straightforward alternative strategy for confidence interval calculation without the assumption of a normal distribution for the IV estimate; details on how this is implemented are provided in the Web Appendix. An additional limitation of the SUR/delta method is that it is only applicable when one IV is used (5, 6).

In this paper, we simulate data sets that represent random samples drawn from a single population. However, in practice, MR investigations may be conducted with data from several studies, using either pooled data or a meta-analysis approach (17–19). Meta-analyses that derive their first-stage and reduced-form estimates from different studies are actually employing a form of 2-sample IV analysis, similar to that described here. Our results suggest that such approaches should focus on maximizing the number of participants in the meta-analysis with data on the IV and the outcome, even if data on the exposure are absent. A cautionary remark is that the magnitude of association of the IV with the exposure may be different in studies which derive their participants from different underlying populations, and heterogeneity in this association should be acknowledged where possible (17). Similarly, subsample IV approaches should utilize subsamples that are representative of the full sample. This issue may be especially problematic for MR studies of biomarkers if biospecimens are available for a subsample that is not representative of the full sample.

In this work, we have used a continuous variable as an IV, representing a genetic score comprised of multiple variants. Such a score may be problematic to obtain for exposures with few genetic determinants which are valid IVs. However, we have previously shown that the first-stage R² is the key parameter influencing power, regardless of what type of IV is used (i.e., single or multiple IVs; dichotomous, ordinal, or continuous IVs). Thus, our findings for a given first-stage R² will apply to any type of instrument, be it continuous or discrete, or a set of multiple instruments.

In summary, this work has demonstrated how subsample and 2-sample IV methods can be used to substantially enhance cost-efficiency for MR studies. For large studies with available genetic and outcome data, it will not be essential to obtain exposure data for all participants. Generating exposure data for a subset of participants will typically have a very limited impact on power, with the optimal size of this subset being determined by the strength of the IV. Furthermore, these methods potentially allow for the inclusion of participants for whom it is not feasible to collect biomarker data. These findings should increase the feasibility of MR for epidemiologists, especially those interested in utilizing existing genetic data or DNA samples from large-scale genetic association studies.