Rationally designed coiled-coil DNA looping peptides control DNA topology

Abstract

Artificial DNA looping peptides were engineered to study the roles of protein and DNA flexibility in controlling the geometry and stability of protein-mediated DNA loops. These LZD (leucine zipper dual-binding) peptides were derived by fusing a second, C-terminal, DNA-binding region onto the GCN4 bZip peptide. Two variants with different coiled-coil lengths were designed to control the relative orientations of DNA bound at each end. Electrophoretic mobility shift assays verified formation of a sandwich complex containing two DNAs and one peptide. Ring closure experiments demonstrated that looping requires a DNA-binding site separation of 310 bp, much longer than the length needed for natural loops. Systematic variation of binding site separation over a series of 10 constructs that cyclize to form 862-bp minicircles yielded positive and negative topoisomers because of two possible writhed geometries. Periodic variation in topoisomer abundance could be modeled using canonical DNA persistence length and torsional modulus values. The results confirm that the LZD peptides are stiffer than natural DNA looping proteins, and they suggest that formation of short DNA loops requires protein flexibility, not unusual DNA bendability. Small, stable, tunable looping peptides may be useful as synthetic transcriptional regulators or components of protein–DNA nanostructures.

INTRODUCTION

DNA looping is essential to the control of gene expression in both prokaryotes and eukaryotes. The short-range looping (typically <500 bp) characteristic of transcriptional activation and repression in prokaryotes requires DNA curvature, with an attendant free energy cost. The structure and flexibility of the protein components of the loop also determine the range of accessible loop conformations. The Lac repressor (LacI) has been the classic model for looping-mediated repression. The X-ray co-crystal structure of LacI bound to two DNA operators is a V-shaped dimer of dimers, with nearly parallel DNA segments (1). LacI can anchor loops as small as 52 bp in vitro (2), which would require a nearly circular DNA loop smaller than one gyre of the nucleosome to fit to V-shaped LacI. The related Gal repressor (GalR) forms a 113-bp loop stabilized by HU protein (3). Biochemical, topological and spectroscopic experiments suggest that very small LacI loops can be enabled by headpiece flexibility and/or open protein conformations (4–8). Non-specific bending proteins also act to decrease the free energy cost of the substantial DNA deformation required to form small loops. Widom and others have proposed that spontaneous sharp bending and twisting of sub-persistence length DNA also decrease the free energy of small loops, relative to the free energy predicted from classical persistence length and torsional modulus values (9,10). However, there is ongoing controversy about the existence of extreme DNA bendability (11,12). The results are of wide interest in part because they bear on the stability of in vivo loops, which are also stabilized by DNA supercoiling (13), specific DNA bending proteins like integration host factor (IHF) (14) and non-specific DNA bending proteins like HU (15). In vivo loops (as identified by periodicity of repression efficiency as a function of operator separation) can be as small as 55–59 bp (16), and loops this short must require sharp DNA bending that cannot all be provided by supercoiling (17). Resolution of the primary intrinsic sources of flexibility that stabilize DNA loops, and by extension a deeper understanding of the quantitative thermodynamics of looping in general, requires experimental separation of protein and DNA flexibility. To this end we sought to design a rigid looping protein, basing the design on the continuous coiled-coil of α-helices as a small and well-understood motif (18,19).

Electron microscopy, atomic force microscopy, tethered particle microscopy, X-ray crystallography and theoretical analysis suggest that the coiled-coil is at least as stiff as DNA, both in terms of bending persistence length and torsional modulus (20–24). The simplicity of the coiled-coil makes it an attractive template for protein engineering, and it is well understood how α-helices self-assemble in parallel versus anti-parallel orientations and in different oligomeric states (25,26). This palette has been used to engineer peptides with new ligand-binding properties (27,28). The GCN4 basic region leucine zipper (bZip) DNA-binding domain has been a common template, and Oakley and coworkers (29) have shown that transposing its N-terminal basic DNA-binding helix to the C-terminus provides a new sequence-specific DNA-binding protein. Here, we have extended the diversity of coiled-coil applications to include DNA looping, by appending both N- and C-terminal DNA-binding domains to a central coiled-coil dimerization domain, creating leucine zipper dual-binding (LZD) peptides. We demonstrate here using the electrophoretic mobility shift assay (EMSA) and DNA ligation, cyclization and topology assays that two designed LZD peptides loop DNA, and that loop formation requires >254 bp of DNA. The results can be quantitatively simulated without invoking extreme DNA bendability.

MATERIALS AND METHODS

Chemicals, DNA and proteins

Oligonucleotide polymerase chain reaction (PCR) primers and EMSA sequences were from IDT. T4 polynucleotide kinase, T4 DNA ligase and restriction enzymes were purchased from New England Biolabs (NEB). Radioactive triphosphates were from Perkin-Elmer or MP Biomedical. Proteins were expressed in Escherichia coli from pRSET A plasmids (Life Technologies) bearing commercially synthesized genes (BioMatik) and variants derived by QuikChange site-directed mutagenesis (Stratagene/Agilent). Peptides were purified from lysates on a metal affinity column with elution by imidazole gradient. The Supplementary Information includes details of the protein purification and all DNA sequences.

Ligation substrates

Templates used to generate cyclization substrates were made by using standard cloning methods to insert both a single CREB site (5′-ATGACGTCAT-3′) and a single Inv-2 site (5′-GTCATATGAC-3′) into modified pRSET A plasmids (complete plasmid sequences available on request). Changing the separation between the binding sites required a separate plasmid for each fragment. The sequence outside of the two cloned binding sites was held constant for the Vx(152-448) 414 templates and nearly constant for the Vx(435-458) templates, except for the small changes needed to maintain a constant total length of 862 bp for the latter set. This allowed the use of a single forward and reverse primer set when generating PCR products for cyclization experiments, except for Vx(448)212. Terminal XhoI restriction sites were introduced into cyclization substrates by PCR with the Vx templates, using forward and reverse primers that both include a non-complementary XhoI sequence at their 5′-ends.

The cyclization substrates were internally radiolabeled during PCR using [α-³²P]dATP (0.133 μM), in 50 μl of reaction mixtures, including 100 μM each of the four deoxynucleoside triphosphates 200 nM primers, 1 U Phusion polymerase (Finnzymes/NEB) and 1× Phusion HF buffer. The cycling protocol was as follows: initial denaturation at 99°C for 3 min, followed by 33 cycles of 95°C for 30 s, 65°C for 20 s and 73°C for 25 s. The PCR products were subjected to a Qiaquick (Qiagen) PCR clean-up column to remove polymerase and unincorporated nucleotides and eluted in 50 μl of H₂O. The Qiaquick step at this point was found to be essential to give efficient ligation and cyclization. The samples were then digested with 20 U of XhoI for 1 h in a total volume of 57 μl of NEB buffer 2 (10 mM Tris–HCl, 50 mM NaCl, 10 mM MgCl₂ and 1 mM dithiothreitol (DTT), pH 7.9) at 37°C. The digested products were purified by native polyacrylamide gel electrophoresis (PAGE) (7%, 75:1 acrylamide:bis) run in Tris borate EDTA (TBE) buffer for 1 h at 20 V/cm, excised from the gel and then eluted overnight in 500 μl of 50 mM potassium acetate, 1 mM ethylenediaminetetraacetic acid (EDTA), pH 7.1. The eluted samples were concentrated to 100 μl by SpeedVac and then subjected to a second Qiaquick PCR clean-up column step. The samples were eluted in water and quantitated using Cerenkov counting, and the radioactivity in the product was used to estimate final concentration and yield.

Electrophoretic mobility shift assay

Complementary synthetic oligonucleotides were used to assemble the 30 bp and 58 bp dsDNA fragments, with Inv-2 and CREB-binding sites, respectively, as in Figure 2. One strand (5 μM) of each fragment was end labeled with 2 μM [γ-³²P]rATP, using 10 U of T4 polynucleotide kinase in the manufacturer's supplied buffer (70 mM Tris–HCl, 10 mM MgCl₂ and 5 mM DTT, pH 7.6). The kinase was heat inactivated, and the complementary strands were annealed by mixing equal amounts of each oligonucleotide in an Eppendorf tube (2.5 μM each, 50 μl of total volume) and placing the sample in a beaker containing 300 ml of boiling water. The beaker was allowed to cool to nearly room temperature for >1 h. The dsDNA products were purified by native PAGE and then buffer exchanged into TE buffer using a BioSpin 6 column (Bio-Rad). Final concentration was determined using ultraviolet absorption.

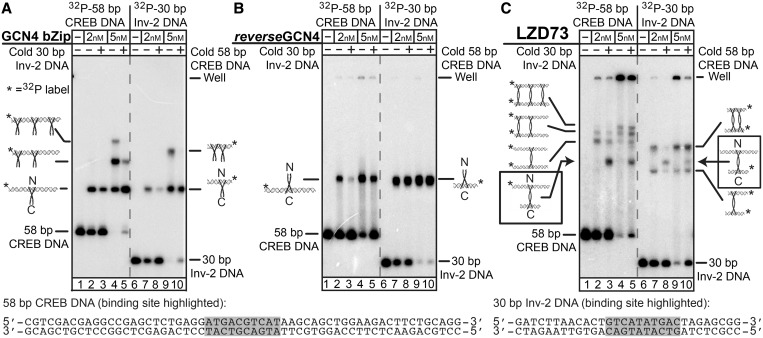
Figure 2.

Demonstration of LZD73:DNA sandwich complexes by EMSA. In each panel, lanes 1–5 contain 1 nM ³²P-labeled 58-bp CREB DNA, with 1 nM unlabeled 30-bp Inv-2 DNA in lanes 3 and 5. Lanes 6–10 have 1 nM ³²P-labeled 30 bp Inv-2 DNA, with 1 nM unlabeled 58-bp CREB DNA in lanes 8 and 10. Cartoons show binding ratios do not imply details of non-specific protein:DNA structures. (A) EMSA with the GCN4 bZip single-binding control peptide shows a weak preference for CREB DNA, and non-specific protein binding is seen when protein is in excess. (B) EMSA with the single-binding reverseGCN4 peptide, with a C-terminal DNA-binding domain shows a strong preference for binding to Inv-2 over CREB and a much lower extent of non-specific binding than GCN4. (C) EMSA with LZD73 shows complexes with lower mobility, suggesting they are sandwich complexes, and the presence of both DNAs in the same complex in the bands indicated with the arrows confirms binding of two DNAs to one peptide. Identification of 58/58 and 30/30 sandwiches is by comparative mobility. Bands that appear only with increased protein concentration are assigned to non-specific binding.

Protein and DNA stocks were diluted to working concentrations in a binding/ligation (B/L) buffer consisting of 50 mM Tris–HCl, pH 7.7, 4 mM NaCl, 4 mM KCl, 4 mM MgCl₂, 2 mM ATP, 0.2% glycerol, 100 μg/ml bovine serum albumin, 10 mM DTT and 0.01% Nonidet-P40 (IGEPAL). This low ionic strength formulation was required to perform the EMSA and the ligase-mediated cyclization experiments under identical conditions. All DNAs were mixed with each other before peptides being added. Peptides were added to the final concentrations indicated in Figure 2, in a final volume of 10 μl and binding reactions were incubated for 10 min at room temperature. Immediately before gel loading, 2 μl of 6× DNA loading dye (30% glycerol, 0.25% each bromophenol blue and xylene cyanol in water) was added to each sample.

Previous results on leucine zipper proteins showed large electrophoretic mobility shifts even for small GCN4 fragments (30), and our experiments with standard acrylamide gels (≥6%) frequently led to retention of all the bound DNA in the well. To obtain the results here, we used a hybrid agarose/acrylamide gel matrix consisting of 0.5% agarose and 5% acrylamide (75:1 acrylamide:bis) in TBE buffer with 7.5 mM NaCl added (50 mM Tris–HCl, pH 8.1, 50 mM boric acid, 7.5 mM NaCl and 1 mM EDTA), which improved band resolution compared with gels that were cast and run in TBE alone. This formulation also served as the running buffer. Gels were run for 1 h at 20 V/cm in a gel box maintained at 15°C (Hoefer). The gels were dried on filter paper and exposed to storage phosphor screens overnight. Images were captured using a Storm 860 Phosphorimager (GE Healthcare Sciences/Molecular Dynamics) and visualized using ImageJ, with correction for the GE/Molecular Dynamics intensity scaling algorithm.

DNA ligation and topoisomer distribution experiments

DNA samples were diluted to 1 nM, and LZD peptide samples were diluted to 30 nM in B/L buffer. T4 DNA ligase was diluted in the same buffer to 10 U/μl immediately before use. The protein and DNA samples were mixed (5 μl each) and allowed to equilibrate for 10 min at room temperature. DNA-only samples (5 μl) were mixed with 5 μl of B/L buffer to maintain consistent concentration. A 5 μl aliquot of the T4 DNA ligase dilution was then added and mixed by gentle pipetting. The final concentrations during ligation were 0.33 nM DNA, 10 nM LZD or control peptide and T4 DNA ligase at 3.3 U/μl. The reaction was allowed to proceed at room temperature for 60 min. After ligation, some samples (as indicated in Figure 3 and all samples in Figure 4) were treated with BAL 31 DNA nuclease (NEB) to remove any linear multimer background bands, which can interfere with the analysis of topoisomer products. For these samples, 15 μl of 2× Bal-31 reaction buffer (40 mM Tris–HCl, 1.2 M NaCl, 24 mM CaCl₂, 24 mM MgCl₂ and 2 mM EDTA, pH 8.0) followed by 0.25 U of BAL 31 were added to each sample and mixed by pipetting. The reaction was allowed to proceed at 30°C for 30 min. After the digestion, 4 μl of 2 mg/ml proteinase K in B/L buffer with 50 mM EDTA was added, and samples were incubated at 37°C for 15 min. For ligation reaction mixtures that were not BAL-31 digested, 4 μl of the proteinase K mix was added immediately after the 60 min ligation, and the samples were incubated at 37°C for 15 min to digest the T4 DNA ligase and LZD peptides. All samples were ethanol precipitated and resuspended in 15 μl of 1× DNA loading solution (0.05% bromophenol blue, 0.05% xylene cyanol, 3% Ficoll 400 and 10% glycerol; without the added glycerol these samples tended to ‘float’ on gel loading). The intercalator chloroquine was also added to 7.5 μg/ml, to resolve the topoisomers. The samples were moved to a 50°C bath for 5 min before electrophoresis to improve re-suspension after the precipitation. Topoisomer products were resolved by electrophoresis on 6% polyacrylamide gels (75:1 acrylamide:bis), containing 50 mM Tris, 50 mM boric acid, 1 mM EDTA, 7.5 mM NaCl and 7.5 μg/ml chloroquine, pH 8.3. The same buffer was used as the running buffer. Gels were run at 4 V/cm for 18 h [Figure 3, Vx(153–448) samples] or 42 h [Figure 4, Vx(435–458) samples]. The gels were dried and imaged as described earlier in the text. Topoisomer products were quantitated using the volume integration function on ImageQuant (GE/Molecular Dynamics).

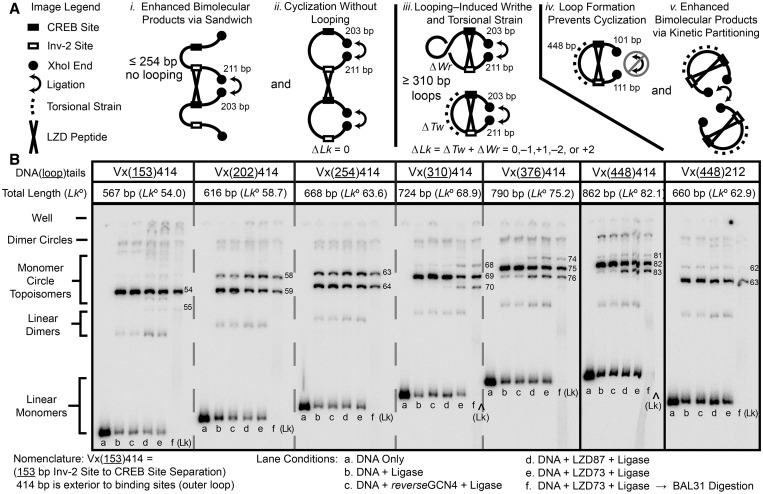
Figure 3.

Ligation reactions of DNA fragments with CREB and Inv-2 sites separated by variable DNA lengths demonstrate looping through the appearance of new topoisomers on ring closure. DNA fragments were synthesized by PCR from plasmids with CREB and Inv-2-binding sites separated by 153–448 bp. The CREB-XhoI spacing was 203 bp and Inv-2-XhoI was 211 bp except for the Vx(448)212 construct at the far right. (A) The LZD peptide could affect the distribution of ligation products in several ways. LZD can enhance bimolecular reactions (i and v), or it can form a loop that alters the cyclization probability and/or the topology of the ligation products through ΔTw and ΔWr (iii and iv), or it may have no effect on cyclization (ii). (B) Variable length DNA fragments with XhoI overhangs were treated with T4 DNA ligase. Deproteinized samples were analyzed by native PAGE on a 6% 75:1 gel containing 7.5 μg/ml chloroquine to resolve topoisomers. Each set of six lanes shows starting DNA, ligated DNA, ligation in the presence of the control GCN4 peptide, ligation with LZD73, ligation with LZD87 and ligation with LZD87 followed by BAL31 digestion to identify DNA minicircles. The calculated Lk for cyclized products assumes a DNA helical repeat of 10.55 bp/turn. New positive and negative topoisomers diagnostic for looping are seen only for molecules with ≥310-bp site spacing (inner loops) and >212-bp outer loops. Slight enhancement of bimolecular ligation is also seen, especially for molecules that do not loop.

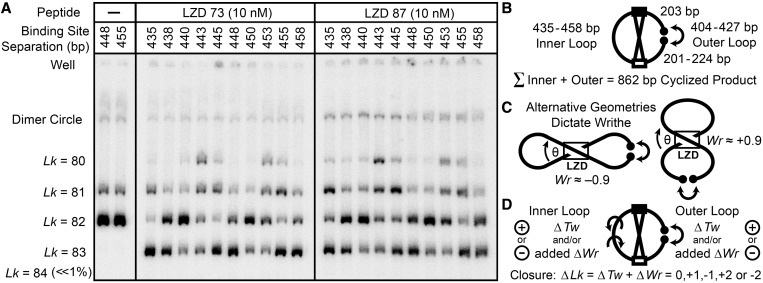
Figure 4.

Topological effects of protein-induced looping, for ten 862 bp cyclized DNA fragments with CREB and Inv-2 sites separated by 435–458 bp. DNA (0.3 nM) was cyclized by T4 DNA ligase in the presence of LZD73 or LZD87, treated with BAL31 nuclease and analyzed as in Figure 3. Cyclization of DNA alone is shown for the 448 and 455 constructs on the left; all the other constructs give the same results. The distribution of topoisomers in the presence of LZD peptides, including new positive and negative supercoils, is a periodic function of binding site separation. (B) Schematic of the variation of inner and outer loop lengths at a constant 862 bp total length. (C) Looping introduces a writhe crossover, which can be of either sign because the binding sites are palindromic. The peptide can also introduce a local ΔTw. (D) A ΔTw in the inner lobe is required to bring binding sites into alignment to form a protein-mediated loop, and a ΔTw in the outer loop is required for ring closure. Both twist changes and any writhe in the lobes contribute to the total observed ΔLk.

Topoisomer population model calculations

The topoisomers formed by cyclization of different constructs were simulated according to simple models for loop structure and the bending and twisting energetics of DNA. There are always two topologies in which a loop can connect, parallel and antiparallel with respect to the central binding sites. Defining θ as the angle between DNA sites viewed along the coiled-coil axis as in Figure 5, there are two values of the oriented crossover angle, θ′ = θ and θ′ = θ − 180°. For non-zero θ, one connection orientation has positive writhe and the other has negative writhe. All the calculations below are carried out in parallel for both θ′ angles. Each lobe of the assumed figure 8 shape is assumed to be a teardrop shape, which allows straightforward computation of the xyz coordinates along the DNA, from which the writhe integral (31) is calculated. The writhe results are insensitive to θ, as long as θ is not too small and the center-to center distance between sites z is not too large. The two writhe values are within the limits Wr = ± (0.90 ± 0.06) for θ >15° and 9 bp < z <27 bp.

Figure 5.

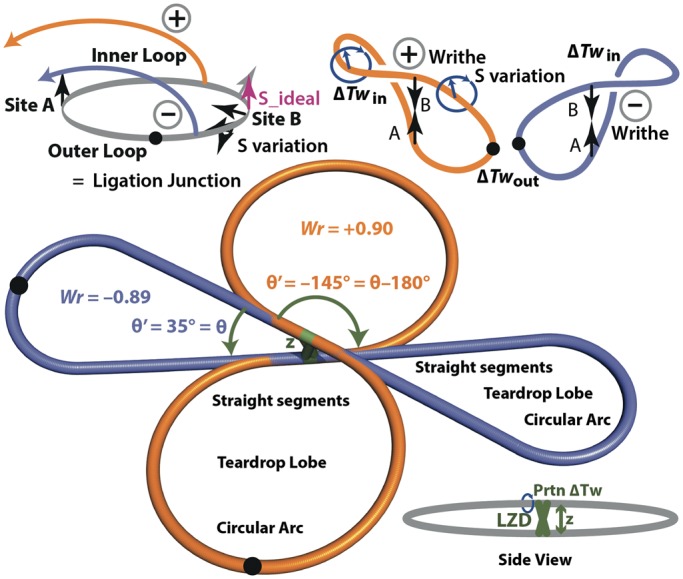
Dual-teardrop model for cyclized minicircles containing a DNA loop. The models shown are the basis for calculations of the DNA bending and twisting energies for the possible topoisomers. The xyz coordinates for pseudoatoms representing each base pair are computed in MATLAB, and the results are output as PDB files for visualization in Pymol. PDB files for the two minicircles shown here are provided in Supplementary Information. The sketch at the top illustrates formation of the two different writhed loops, with opposite signs for writhe Wr, starting from a planar molecule with aligned sites. Helical rotation of the sites relative to each other leads to different ΔTw values in the two lobes as in Figure 4.

To simulate topoisomer distributions for comparison with the experiment of Figure 4, we calculate the energy of all of the combinations of Wr and Tw for each topoisomer and then apply the Boltzmann distribution. The energy is given by the sum of the DNA bending and twisting energies, for which we assume independence and additivity. The bending energy of a teardrop (with θ in radians) is given by

per Sankararaman and Marko, section IIIA of (32), calculated for each lobe of each of the two writhed forms. A is the persistence length, taken to be 150 (bp). This analysis ignores the influence of z on the teardrop bending energy, which is reasonable for z << L. For θ near 0°, the energy of the teardrop with the acute included angle is large; therefore, the teardrop is probably not a good model for the real loop. In this case, the ‘double circle’ crossover geometry, with its large included angle, should be strongly preferred; hence, the inaccuracy in the energy of the high-energy state should not affect population estimates.

The twist in each lobe must be calculated independently because the protein isolates the two sides topologically when the loop exists (33). ΔTw, the difference between the actual twist and the relaxed twist, is determined by initially considering a planar circle with two binding sites perfectly aligned (parallel) on one face of the helix. The total local twist change introduced by the protein (the sum of the changes introduced by the two binding domains) is denoted Prtn_Tw. Net unwinding introduced by GCN4 has been estimated as −53° (34); we assume all unwinding appears as twist. The unwinding introduced by the reverseGCN4 is unknown. The relaxed linking number of the circle is, therefore, Lk° = L/hr + Prtn_Tw, where hr is the helical repeat. The helical repeat is constrained by the observed topoisomer distribution in the absence of looping; we find that hr = 10.55 bp/turn gives the 80:20 distribution observed for Lk = 82:Lk = 81. The most stable achievable linking number is Lk_m, the integer closest to Lk°. The residual twist strain is ΔTw = Lk_m − Lk°. The twist in each half of the circle must be integral because the sites are assumed to be helically in phase and are, therefore, separated by an integral number of helical turns. Given all this, we can calculate the ideal DNA-binding site spacing, corresponding to minimum twist energy with twist strain partitioned equally to both sides, as S_ideal = ½ Lk_m × hr, in base pairs.

We then consider forming the figure 8 writhed loop. As the linking number on looping does not change, the looping ΔTw = ΔLk − ΔWr = −ΔWr, and as the initial writhe of the planar circle is zero, the change in writhe ΔWr on looping is equal to the writhe Wr calculated as aforementioned. At S = S_ideal, the ΔTw is partitioned equally to each lobe; therefore, the twist strain in each lobe is given by ΔTw_ideal = ½ (Lk_m − L/hr − Prtn_Tw − Wr). We then consider the true binding site separations. For the inner loop, the twist strain becomes ΔTw_in = ΔTw_ideal + (S − S_ideal)/hr, and for the outer loop it is ΔTw_out = ΔTw_ideal − (S − S_ideal)/hr. In calculating ΔTw_in and ΔTw_out and considering their energetic consequences, we ignore writhe in the individual lobes; the writhe in a ∼450 bp circle is small (31,35), and the energy of the lobe should be close to the twist energy plus the bend energy calculated ignoring writhe. With the ΔTw values for the inner and outer lobes in hand, we calculate the twist energy on each side given by E_twist = 4π²CΔTw²/2ℓN, where C is the torsional modulus (taken to be 2 × 10⁻¹⁹ erg•cm), ℓ is the base pair separation 3.4 × 10⁻⁸ cm and N is the number of base pairs in the lobe. Thus, given a value for θ we have two values of θ′, writhe and bending energy, and then for each value of S we calculate a total twisting energy for each θ′, giving two total energies for the two ways to make a ΔLk = 0 topoisomer.

We then consider formation of all additional topoisomers by assuming that the writhed shapes stay the same and calculating the twist energies corresponding to ΔTw = ΔTw_in + m and ΔTw_out + n, with m and n = 0, ±1, or ±2. The resulting observable ΔLk is m + n. The energies of all 25 possible combinations of m and n for each value of Wr are calculated, and their populations are calculated from the Boltzmann distribution:

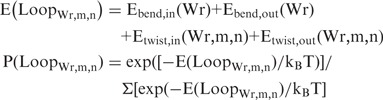where Loop_Wr,m,n indicates the DNA loop with the designated Wr, m and n values, and the summation to give the partition function is over all 50 possible loops. The total probability P(ΔLk) of observing a particular ΔLk = m + n = 0, ±1, ±2, ±3 or ±4 is the sum of the corresponding P(Loop_Wr,m,n) values. In practice, we find that for most choices of θ, Prtn_Tw, hr and z there is one dominant topoisomer and one minor topoisomer for each Wr, giving four values of ΔLk with nonzero populations, as observed in the experiment.

The populations for each ΔLk were calculated for each spacing S. The fit to experiment was measured as the sum of squared errors in P(ΔLk, S) versus experiment. The best fit was optimized by varying hr, Prtn_Tw, z and θ individually for each peptide, arriving at locally optimum sets of parameters given in Table 1. A single variable offset was applied to all of the calculated sets of curves to account for possible variation in the helical repeat between the two lobes. This offset was optimized to be ∼1.3 bp, corresponding to an average helical repeat difference of 1.3/431 = 0.3%. The value of hr = 10.55 bp/turn was optimized independently, but it matched the observed topoisomer distribution in the absence of protein.

Table 1.

Optimized LZD–DNA geometric parameters

Peptide	θ (°)	z (bp)	Prtn_Tw (°)	Hr (bp/turn)	Offset (bp)	Error
LZD73	35	16	−50	10.55	−1.2	0.86
LZD87	33	21	−50	10.55	−1.4	1.00

The θ angle and center to center distance z are defined in Figure 5. Prtn_Tw is the total ΔTw introduced by protein binding at the two sites. Hr is the DNA helical repeat, and the offset is a shift applied uniformly to the all of the curves in Figure 6. The error is the sum over all lengths of the squared error in the probability of observing each topoisomer.

All calculations were carried out in MATLAB. The experimental data from Figure 4 and replicate experiments is provided as a Microsoft Excel spreadsheet in the Supplementary Information. The xyz coordinates for the loops were output as PDB files for visualization in Pymol. Sample PDB files for the loops in Figure 5 are available in the Supplementary Information, and code is available on request to jdkahn@umd.edu.

RESULTS

LZD peptide design and synthesis

The basic region-leucine zipper (bZip) domain of the yeast transcription factor GCN4 binds DNA as a homodimer (36), with the leucine zipper forming a coiled-coil of α-helices that separate near the N-terminus into positively charged helices that grip the DNA (37,38). The GCN4 bZip is a common template for protein design (19,39,40). Our DNA looping peptides were inspired by the work from the Oakley laboratory in which the basic DNA-binding region was fused to the C-terminus of the leucine zipper instead, to make the reverseGCN4 peptide (29). They demonstrated that reverseGCN4 has high affinity and specificity for a DNA target in which the palindromic CREB binding site recognized by GCN4 (5′-ATGAC|GTCAT-3′) is inverted to give the Inv-2 site (5′-GTCAT|ATGAC-3′); the underlining indicates the specific half-site recognized by each basic region.

We combined reverseGCN4 with GCN4 itself to give the LZD peptide denoted LZD73, containing both N- and C-terminal DNA-binding domains (Figure 1). The coiled-coil axis of GCN4 in the GCN4–DNA complex is perpendicular to the DNA helix axis. This geometry suggests that a change in coiled-coil length should translate to a change in the crossover angle of the DNA fragments in the putative LZD–DNA sandwich complex, as viewed along the coiled-coil axis. Different crossover angles should translate to different, and predictable, loop geometries. To test this hypothesis, we also constructed the LZD87 peptide by inserting 14 amino acids, lengthening the coiled-coil by two heptad repeats. The inserted sequence is duplicated from the GCN4 leucine zipper, and an extended GCN4 that included this sequence was soluble and able to bind DNA (data not shown).

Figure 1.

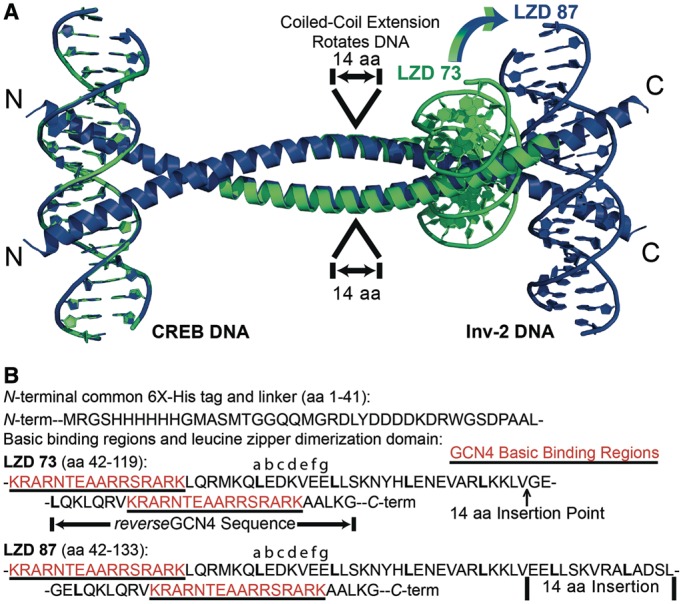
Designed DNA looping peptides. (A) Models for the LZD73 (green) and LZD87 (blue) LZD peptides bound to DNA at each end, overlapped at their identical N-terminal GCN4:DNA side. The coordinates are based on GCN4:DNA and coiled-coil geometry. A 14 amino acid insertion in LZD87 introduces relative rotation of the C-terminal binding sites. The N-terminal 41 amino acids of the peptides are omitted for clarity. PDB files for the models of the LZD73:DNA and LZD87:DNA complexes are provided in Supplementary Information. (B) Amino acid sequences for LZD73 and LZD87. (top) Shared His-tag and enteropeptidase cleavage site sequences from the pRSET A vector. (bottom) The sequences of the DNA-binding regions (red) and the leucine zipper domains of LZD73 and LZD87. The 73/87 nomenclature corresponds to the number of amino acids between the first residue in the N-terminal basic region and the last residue in the C-terminal basic region, giving relative lengths of the two coiled-coils.

Figure 1 shows a model for two DNA sandwich complexes, including the engineered LZD peptides. The models were assembled from the GCN4 bZip:CREB DNA co-crystal [PDB ID 2DGC (38)], a segment with coordinates taken from the structure of cortexillin to provide the peptide backbone between DNA-binding helices [1D7M (41)] and inverted portions of 2DGC to give the C-terminal structure. Cortexillin is a well-characterized coiled-coil (41,42), and a fusion peptide of cortexillin and the GCN4 leucine zipper forms a homodimeric coiled-coil of uninterrupted α-helices (43); therefore, the coordinates should be suitable for modeling even though the LZD protein sequences are not derived from cortexillin. The starting model side chains were replaced by those of the actual sequence in Pymol, and the C-terminal DNA-binding domains were docked by hand to remove steric conflicts. The structure was subjected to molecular dynamics (50 ns), and no substantial changes were observed. Even if this model is not correct in detail, it illustrates how varying the coiled-coil should allow programmed changes in the geometry of peptide–DNA complexes and the resulting DNA loops.

Synthetic genes coding for these peptides were cloned in E. coli, and the peptides were expressed and purified as in the ‘Materials and Methods’ section and the Supplementary Information. The peptides are toxic to cells, perhaps because they non-covalently cross-link chromosomal DNA. Circular dichroism showed that they are mostly α-helical at 1.2 µM, and the α-helical content increases slightly on DNA addition (Supplementary Figure S1).

Assessing dual DNA-binding capacity of LZD peptides with the electrophoretic mobility shift assay

Any DNA looping protein must have two binding sites for DNA; therefore, it must be able to bind two separate molecules of dsDNA in a stable ‘sandwich complex’ (2) if the DNA concentration exceeds the effective local concentration provided by looping. In the electrophoretic mobility shift assays (EMSAs) of Figure 2, sandwich complexes with LZD peptides were identified using mixtures in which either a 58-bp DNA containing a CREB site (the N-terminal target) or a 30 bp DNA containing the Inv-2 site (the C-terminal target) was ³²P-labeled. Competition with unlabeled DNA reported on specificity. A 5% polyacrylamide/0.5% agarose hybrid gel was used to increase the electrophoretic mobility of the complexes relative to that in gels with higher acrylamide density (44), as leucine zipper complexes migrate anomalously slowly (30).

Figure 2A shows that a GCN4 bZip control peptide, with its N-terminal binding domain, binds with high affinity to both the 58 bp and the 30 bp fragments. Non-specific binding to both fragments can be competed away with either unlabeled 58 or 30 bp DNA. The GCN4 peptide shows a weak preference for the CREB site over the Inv-2 site. Panel B shows that the reverseGCN4, bearing the C-terminal-binding region, shows a strong preference for the Inv-2 site over the CREB site and a significantly decreased extent of non-specific binding.

Panel C of Figure 2 shows a band of unique mobility that requires both the 58 bp and the 30 bp DNA fragments and contains radiolabel from either DNA, which we assign as a sandwich complex (45) containing both fragments bound to LZD73. The gel also shows bands assigned as 58/58 and 30/30 sandwich complexes based on their mobilities relative to the 58/30 complex, as well as more slowly migrating species that grow in at higher protein concentration and, therefore, presumably contain non-specifically bound LZD peptide. Non-specific dual-binding events could be stabilized by high local DNA concentrations established by the specific sandwich complex. At high peptide concentrations there are also aggregates in the well, but they are released by added DNA. We do not observe bands that can be assigned to 1:1 peptide:DNA complexes, suggesting that a DNA-binding helix that is not occupied by specific DNA potentiates aggregation. These aggregates could be protein–DNA networks linked by non-specific protein–DNA binding or protein–protein interaction.

The existence of a stable specific sandwich complex confirms that the LZD peptides have two active DNA-binding domains. When the two DNA-binding sites are placed on the same DNA molecule, enhanced local concentration favors specific binding of one LZD peptide to CREB and Inv-2 sites embedded in a DNA loop, assuming that the DNA concentration is less than the effective concentration of the second DNA site in the neighborhood of a peptide anchored by binding at the first DNA site. If the loop is too short or torsionally misaligned, then the effective concentration of the second site will be very low, and sandwiches or singly bound DNA will be preferred.

Assaying looping by ligation of variable length DNA fragments

DNA looping can be detected by EMSA, footprinting, electron microscopy or atomic force microscopy, Förster resonance energy transfer (FRET) and tethered particle microscopy (TPM) (6,46–48). Initially we attempted to apply EMSA to DNA looping by the LZD peptides, but the large DNA size required and also competition with sandwich complexes made the results difficult to interpret. We turned to DNA ligation because the assay depends on the reactivity of molecules that are entirely in free solution, not immobilized or in gels. Ligation can also detect transient or unstable loops because formation of a sandwich complex can potentiate irreversible intermolecular ligation when the DNA ends hybridize to form a DNA loop (49). Ring closure of a single DNA that is looped to bridge two internal sites (as opposed to ‘looping’ of DNA to bring the ligatable ends together) can be especially diagnostic for protein-mediated looping. Ring closure of the complex to form a covalently closed minicircle DNA captures twist and writhe changes induced by the internal loop as a permanent change (relative to free DNA) in the linking number (Lk) distribution of the minicircle products (5). Modeling described later in the text suggests that an almost any LZD-mediated loop should introduce diagnostic changes in writhe. Finally, cyclization can be interpreted quantitatively to give estimates of the geometric parameters of the loop as well as the DNA or peptide-DNA deformability (5,50–52).

Figure 3 shows ligation experiments that measure the DNA length required for the LZD peptides to induce a loop, as indicated by changes in ligation efficiency or in the topology of the circular ligation products. After preliminary negative bimolecular ligation results on shorter DNAs, we constructed the Vx(153–448)414 series of looping/ligation substrates, in which the separation between CREB and Inv-2-binding sites (forming the inner loop on peptide binding) was varied from 153 to 448 bp. The total distance between the two binding sites and terminal XhoI overhangs, forming the outer loop on cyclization, was held at 414 bp. The Vx(448)212 construct, with a 448-bp inner loop and outer segments totaling 212 bp, was used to verify that the results should be independent of which side of the final looped minicircle product was initially continuous.

The amount of bimolecular products at all lengths increases on LZD binding because of enhanced ligation of DNA in sandwich complexes [or in the case of Vx(448)212 because of inhibition of cyclization]. The effect is enhanced at separations of ≤254 bp, for which no looping takes place. For 202 and 254 bp separations, the Vx(202 or 254)414 constructs, a subtle shift to the circular product with a lower Lk is consistent with local protein-induced DNA untwisting (34) but not with writhe at a node, which would lead to a larger |ΔLk|. DNA bending by bZip proteins is controversial (53); significant bending should enhance cyclization of these short DNAs, but this is not observed. At site separations of ≥310 bp, new topoisomers are observed with ΔLk = ±1 in addition to the original product, suggesting the formation of loops with both positive and negative writhe. A ΔLk = + 1 cannot result from protein-induced untwisting. The Vx(448)212 results show that when the DNA tails exiting a loop are too short, cyclization is inhibited, and no ΔLk = ± 1 topoisomers are observed, in accord with the results showing that when the internal segment is too short, the loops also fail to form.

These results strongly suggest that loops of ≥310 bp can be formed by the LZD peptides, and shorter loops cannot be formed, but the results do not establish a precise lower limit for loop length because the particular lengths we tested could be torsionally strained. The lower limit set by bending strain could be resolved by exploring closely spaced loop lengths. In summary, cyclization as a function of loop length shows that the DNA length needed to form a loop anchored by a small, rigid protein is much longer than the length needed for looping by flexible proteins like LacI.

Cyclization of a series of 862-bp DNAs with helically phased binding sites

To sample the diversity of accessible loop topologies and shapes systematically, we varied the loop length at a constant total DNA length and characterized the minicircle topoisomers produced by ring closure (Figure 4). This approach is modeled after classic demonstrations of looping as the cause of periodic variation of in vivo repression efficiency with DNA spacing (16,17,54,55). Ten DNA fragments in which the CREB to Inv-2 inner loop spacing ranged from 435 to 458 bp were constructed. A total length of 862 bp was maintained by concurrently reducing the outer loop length from 427 to 404 bp. Cyclization of each of the ten 862 bp fragments in the absence of LZD resulted in the same yields of a major product (Lk = 82, assuming a helical repeat of 10.55 bp/turn) and a minor product (Lk = 81). The distribution of topoisomers is strikingly different in the presence of LZD peptides: it is a periodic function of binding site separation, definitively confirming DNA looping, and it includes new Lk = 80 and Lk = 83 topoisomers. The near-disappearance of the original Lk = 82 topoisomer for some lengths suggests that the DNA, at least at those lengths, is almost exclusively found in looped complexes.

Modeling and analysis of topoisomer distributions

To model the results of Figure 4A quantitatively, we took advantage of the simplicity and assumed rigidity of the LZD peptides to construct a straightforward numerical model that combines reasonable assumptions for the peptide–DNA geometry with the established worm-like coil treatment of DNA bending and flexibility (31,32,34,35). Much more sophisticated treatments are possible (51,56,57), but here we are only trying to assess whether the observed oscillations in topology are reasonable based on the assumed protein–DNA geometry and the flexibility of DNA. As shown in Figure 5, we assume that the protein makes a sandwich complex with a fixed crossover angle θ between two DNA-binding site segments (0 < θ <180° for symmetric sites) that lie in parallel planes separated by a distance z. The shape of the loop is assumed to be a figure 8, with the two lobes each adopting teardrop shapes, of length S for the continuous inner loop and length L–S for the outer loop, which is formed on ligation. The z-coordinate of each point is chosen to give an elliptical cross-section for the final figure 8. The protein–DNA model parameters are the angle θ, the distance z, and the total local twist change Prtn_Tw. DNA is described by its persistence length P = 150 bp, torsional modulus C = 2 × 10⁻¹⁹ erg·cm, and average helical repeat hr near 10.5 bp/turn. Based on the design of Figure 1, z should be ∼27 bp, which is small relative to the DNA contour length; therefore, the modeling enforces the correct contour length, but it does not explicitly consider changes in z in calculating the energy. For each pair of DNA lengths S and L, the writhe Wr and the bending energy (32) are calculated for the two loop topologies of Figures 4C and 5. The twist Tw is treated for each lobe of each loop independently because the protein isolates the lobes topologically (33). An initial Tw required to make Lk = Tw + Wr an integer is set for each lobe, chosen to minimize ΔTw relative to relaxed DNA for lengths S and L–S. The variation in S provides a set of different required Tw values for the inner and outer loops. The twist energies for ΔTw of 0, ± 1 or ± 2 relative to the initial ΔTw as well as the total energies for each combination of Tw and Wr are then calculated. The Boltzmann distribution provides the population of each combination and the combined populations comprising each Lk simulate the experimentally observed topoisomer distribution. Details of the calculation are given in the ‘Materials and Methods’ section.

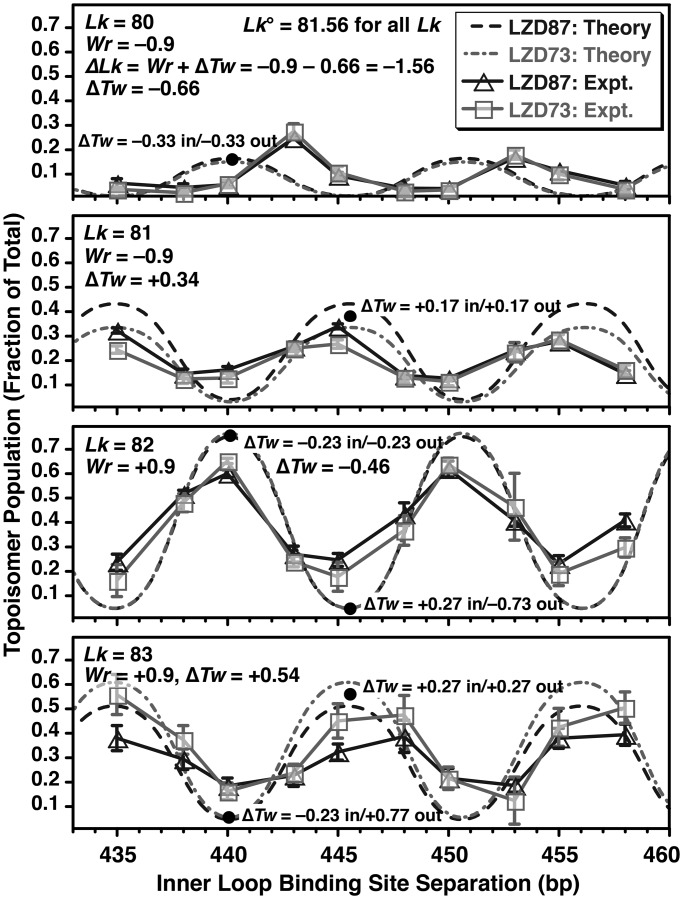
Figure 6 compares the experimental topoisomer distributions as a function of site separation from Figure 4 with the predicted distributions, using the best fit θ, z, Prtn_Tw and hr values found in Table 1. It was also necessary to fit a ∼1 bp offset to allow for an apparent difference in the intrinsic twist between the inner and outer loops. The essential features of the experiment are that there are four populated topoisomers, the peak population for each topoisomer is offset by about half a helical turn from the next topoisomer and Lk = 82 and 83 topoisomers are more abundant than Lk = 80 and 81. The simulation explains these observations in qualitatively understandable ways as follows: first, Lk°, the ideal linking number for the 862 bp circle, changes from 81.71 for free DNA to 81.57 with the inclusion of LZD-induced untwisting parameterized by Prtn_Tw = −50°, or 25° of untwisting per site, midway between the untwisting previously inferred for GCN4 at the CREB site (34) and the twist observed in the X-ray co-crystal structure (38). For all S, the Lk = 82 and 83 topoisomers have Wr ≈ +0.9 because of the crossover node created by the LZD loop. The Lk = 82 topoisomer is untwisted, with ΔTw = ΔLk − ΔWr = (Lk − Lk°) − Wr = (82 − 81.57) − 0.9 = −0.47 turns distributed over the two lobes, and the Lk = 83 is overtwisted in each lobe, with total ΔTw = +0.53. The peak abundance of the Lk = 83 topoisomer is lower because of the larger absolute value of total ΔTw and, hence, higher twist energy. The loop length S that gives the peak abundance for each Lk occurs when ΔTw is equal in each lobe (for lobes of similar size); distributing twist strain evenly minimizes total energy because of the quadratic dependence of twist energy on ΔTw. This idea provides a straightforward explanation for the half helical turn offset between the Lk = 82 and 83 curves. For example, the peak at ∼440 bp for Lk = 82 represents a loop with ΔTw = −0.23 in each lobe. A change in S of +½ hr to ∼445 bp, at constant Lk and total Tw, gives ΔTw = +0.27 for the inner and −0.73 for the outer loop. The addition of one helical turn to the outer loop gives evenly distributed ΔTw = +0.27 in each lobe at Lk = 83; therefore, there is a peak at 445 bp for Lk = 83. Lk = 80 and 81 results are all analogous starting from Wr ≈ −0.9, with lower overall abundance because the LZD geometry (θ ≈ 33°) favors a loop with positive Wr, the orange DNA in Figure 5, with θ′ = θ − 180° = −147°.

Figure 6.

Comparison of experimental and theoretical probabilities for observing each topoisomer of Figure 4 as a function of DNA-binding site separation. The solid lines and symbols show the experimental results. The error bars represent the average ± standard deviation for three experiments. Free DNA gives 78% Lk = 82 and 22% Lk = 81, for Lk = 81.71 and the best-fit local protein-induced untwisting gives Lk = 81.56 for the protein-bound DNA. The dashed lines show theoretical predictions using a rigid protein geometry (Figures 1 and 5) with the optimized parameters of Table 1 and the worm-like coil model for DNA energetics. The model captures the general features of the experiment, including the amplitudes and ∼5 bp phase shifts of the four observed topoisomers. At each peak in a distribution, twist strain is equally distributed in the inner loop and the outer loop. For each writhe (Wr = +0.9 for Lk = 82 and 83, or Wr = −0.9 for Lk = 80 and 81), a peak in the distribution for the smaller value of Lk corresponds to undertwisting in each lobe, and the peak for the larger Lk, offset by half a helical turn, is overtwisting in each lobe. The model does not explain the ∼3-bp phase shift in the Lk = 80 curve, and proteins as in Figure 1 that are rigid were expected to show larger differences between LZD73 and LZD87 because of different θ angles.

This crude model is not perfect. It predicts peak values of S for Lk = 80 that are offset by ∼3 bp between theory and experiment, and there are smaller errors in the peak positions for the other topoisomers. Improved modeling of the DNA energetics would probably lead to changes in the amplitudes rather than the positions of peaks. Also, by design θ should be ∼120° for LZD73 and 0 for LZD87, but the two peptides actually gave similar results in the experiment of Figure 4, with the best fit θ estimated at +33–35° for both peptides. Finally, the best-fit values of z are ∼8 bp less than the values estimated from Figure 1. These discrepancies between theory and experiment could be due to incorrect modeling of the orientation of the C-terminal DNA-binding domain, protein torsional flexibility or coupling between DNA deformation and protein conformation. These issues notwithstanding, we suggest that the agreement between the worm-like coil model for DNA and the experimental results of Figure 3 argues that DNA does not exhibit extreme bendability, and the agreement between the worm-like coil predictions and the results of Figure 4 argues against unusual twisting flexibility for DNA.

DISCUSSION

Demonstration of DNA looping by rationally designed coiled-coil peptides

The DNA binding, cyclization and topology results aforementioned show that addition of a C-terminal basic region to a GCN4 bZip coiled-coil provides peptides that bind two DNA sites simultaneously and thereby loop DNA efficiently, for loops of ≥310 bp. Four-helix bundle proteins with pendant DNA-binding domains have been observed to form loops or sandwich complexes (45,49,58), but the LZD peptides described here are the first to form a more stable loop in which each polypeptide strand contacts both DNA partners. The topological results of Figures 4 and 6 showing modulation of DNA topoisomer distributions by changes in the separation between protein-binding sites and their helical phasing demonstrate that the looping is amenable to quantitative analysis. The model of Figure 5 combined with calculations assuming a rigid peptide and canonical worm-like chain values of the DNA persistence length and torsional modulus captures the essential features of the topoisomer distributions. Both positive and negative supercoils formed by ring closure of looped complexes are quantitatively explained by the existence of two loop topologies, which give either positive or negative writhe and have slightly different total bending energies.

Although the essential properties of the LZD peptides matched the design of Figure 1, two peptides that were intended to give markedly different crossover (θ) angles yielded surprisingly similar topoisomer distributions. The coiled-coil structure could be deformable, so that the two peptides explore the same range of θ; experiments on the myosin coiled-coil suggest that the motif can unfold under mechanical strain (59). Alternatively, the peptides could be stiff but θ could be nearer to 90° for both: topoisomer distributions depend on θ mainly through differences in DNA-bending energy for the two writhes, and for larger θ, the bending energy depends only weakly on θ. The peak inter-site spacing for the Lk = 80 topoisomer was also not predicted accurately. This could be due to coupling between protein and DNA deformation (60), and we have shown previously that cyclization can preferentially capture distorted protein–DNA geometry (61,62). These structural and dynamic questions can be addressed with FRET, TPM or high-resolution structures, coupled with rod mechanics models for DNA shape (51,56,57).

Length dependence of DNA looping by natural and artificial proteins

The separation of DNA and protein flexibility contributions to looping free energy was one motivation for the LZD peptide design. Figures 3 and 4 show that loop shape and stability are indeed strongly dependent on DNA length, suggesting that systematic exploration of the shortest loop lengths will provide a sensitive test for theories of enhanced DNA flexibility (63,64). The LZD peptides are ideal for such tests because as long as the DNA-binding sites lie roughly perpendicular to the coiled-coil axis, the protein should be under tension in a loop; therefore, protein bending away from the extended form should be suppressed and should not affect the minimum-energy loop conformation. The shortest loops seen in Figure 3 are ∼310 bp, much longer than the ∼50-bp loops formed in vitro by the natural repressors LacI (2) and λ phage cI (65), or the ∼100–150-bp loops seen for the type II restriction enzymes FokI (60) and SfiI (66). The repressors can probably bridge DNA sites that lie on a continuous curved segment (17,67), and the FokI restriction enzyme includes a flexible linker between the recognition domain and the catalytic domain (68). The SfiI:DNA co-crystal structure (69) does not show obvious flexibility, but the loop length estimates for SfiI are based on cleavage activity that could reflect transient binding (66). In vivo loops such as those characterized for GalR (15), LacI (17), AraC (55) and the NtrC-RNA polymerase complex (14,70) can be <100 bp, but these are stabilized by supercoiling or bending proteins.

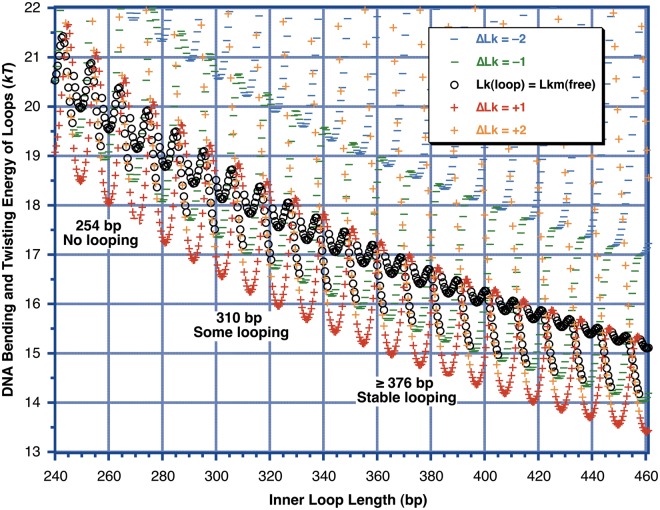
Figure 7 shows that the estimated DNA deformation energy at 254 bp is roughly comparable with the free energy available from protein–DNA binding for 1 nM binding affinity at one site, ΔG° = −kTln(10⁻⁹) = −20.7 kT; therefore, it is reasonable that loops of this length are unstable. We conclude that stabilization of shorter loops depends substantially on protein flexibility for proteins with ∼1 nM binding affinity for each DNA binding domain. Our results do not provide evidence in support of enhanced DNA flexibility. In these measurements based on the stability of small DNA loops in free solution, all of the DNA that is strongly bent or twisted over short length scales is contained within a longer DNA that is completely double-stranded, with no ends, single-stranded regions or chemical modifications. This avoids potential artifacts in ligation-mediated cyclization experiments; the cyclization to form minicircles in our experiments occurs within a 400-bp segment of a figure 8 shape, a length range at which all the models for DNA converge on the results of the worm-like coil. Systematic evaluation of loop stability and topology for 200–300-bp loops coupled with thermodynamic measurements of protein–DNA binding should allow more stringent tests of extreme bendability models.

Figure 7.

Calculated DNA strain energy for different loop-containing minicircle topoisomers as a function of loop length (inner loop binding site separation), using the model of Figure 5 and the worm-like coil as in Figure 6. The ΔLk is defined relative to the Lk_m of free DNA at each DNA length. The outer loop length is held fixed at 414 bp as in the experiment of Figure 3, and the qualitative results of Figure 3 are noted within the figure. All model parameters were those for LZD87 from Table 1 except that no offset was included. The energies of all of the topoisomers seem to be discontinuous because the reference Lk_m of the free DNA changes by 1 abruptly as the DNA length crosses (n + ½) helical turns. Because of the large writhe induced on looping, the topoisomer with Lk equal to the Lk_m of free DNA never corresponds to the lowest-energy topoisomer. In this model, the overall minimum possible energy, where there is no twist strain and the total strain energy is equal to the bending energy, occurs for helically out-of-phase sites. This initially surprising result arises because for the protein geometry assumed here the out-of-phase sites can be brought together with no change in twist for the inner loop. This introduces a change of ΔTw = (−ΔWr) in the outer lobe, which will then relax by the introduction of a twist change of ΔTw = +ΔWr ≈ ±1 to return the outer lobe to its relaxed twist. The end result is a loop with almost no twist strain, with ΔLk = ±1 ≈ +ΔWr relative to relaxed DNA. ΔLk = +1 is lower in energy than ΔLk = −1 because the best-fit value θ = 33° leads to a lower bend energy for the Wr = +0.9 geometry.

Uses of rigid and readily modifiable looping proteins

Sequence-specific rigid looping proteins could find practical uses. They could act as repressors that are controlled through cooperative binding at a remote binding site, which in turn could be modulated by a second protein. Artificial looping could also potentiate the interaction of natural transcription factors. Retroviral integration is aided through localization of integrase via protein–protein interactions (71). Bridging of two DNA sites could similarly be used to enhance genome editing, for example, by localizing DNA ends generated by zinc-finger nuclease (72) activity near a homologous chromosomal location. Finally, small, rigid, readily modified looping proteins with tunable crossover angles might enable synthesis of self-assembled protein–DNA nanostructures that could link the well-developed DNA nanotechnology and protein-nanotechnology fields. Natural looping proteins are less suitable for this purpose because of their size and flexibility.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online: Supplementary Figure 1, Supplementary Methods, Supplementary DNA Sequences, Supplementary PDB Files and Supplementary Data set.

FUNDING

Wiley Dissertation Fellowship (to D.B.G.); Howard Hughes Medical Institute (HHMI) to E.J.K.; National Science Foundation CAREER award (to J.D.K.); National Institutes of Health [5R01CA136938-03 to J.D.K. and A.J. Mixson]. Funding for open access charge: HHMI.

Conflict of interest statement. None declared.