Learning Incoherent Sparse and Low-Rank Patterns from Multiple Tasks

Abstract

We consider the problem of learning incoherent sparse and low-rank patterns from multiple tasks. Our approach is based on a linear multi-task learning formulation, in which the sparse and low-rank patterns are induced by a cardinality regularization term and a low-rank constraint, respectively. This formulation is non-convex; we convert it into its convex surrogate, which can be routinely solved via semidefinite programming for small-size problems. We propose to employ the general projected gradient scheme to efficiently solve such a convex surrogate; however, in the optimization formulation, the objective function is non-differentiable and the feasible domain is non-trivial. We present the procedures for computing the projected gradient and ensuring the global convergence of the projected gradient scheme. The computation of projected gradient involves a constrained optimization problem; we show that the optimal solution to such a problem can be obtained via solving an unconstrained optimization subproblem and an Euclidean projection subproblem. We also present two projected gradient algorithms and analyze their rates of convergence in details. In addition, we illustrate the use of the presented projected gradient algorithms for the proposed multi-task learning formulation using the least squares loss. Experimental results on a collection of real-world data sets demonstrate the effectiveness of the proposed multi-task learning formulation and the efficiency of the proposed projected gradient algorithms.

1. INTRODUCTION

In the past decade there has been a growing interest in the problem of multi-task learning (MTL) [Caruana 1997]. MTL aims to enhance the overall generalization performance of the resulting classifiers by learning multiple tasks simultaneously in contrast to the single-task learning (STL) setting. It has been applied successfully in many areas of data mining and machine learning [Ando 2007; Ando and Zhang 2005; Bi et al. 2008; Bickel et al. 2008; Si et al. 2010; Xue et al. 2007]. A common assumption in MTL is that all tasks are intrinsically related to each other. Under such an assumption, certain information is allowed to be shared across the tasks, implying what is learned from one task is beneficial to another. This is particularly desirable when there are a number of related tasks but only a limited amount of training data is available for learning each task.

MTL has been investigated by many researchers from different perspectives. Hidden units of neural networks are shared among similar tasks [Caruana 1997]; task relatedness are modeled using the common prior distribution in hierarchical Bayesian models [Bakker and Heskes 2003; Schwaighofer et al. 2004; Yu et al. 2005; Zhang et al. 2005]; the parameters of Gaussian Process covariance are learned from multiple tasks [Lawrence and Platt 2004]; kernel methods and regularization networks are extended to the multi-task learning setting [Evgeniou et al. 2005]; a convex formulation is developed for learning clustered tasks [Jacob et al. 2008; Zhou et al. 2011]; a shared low-rank structure is learned from multiple tasks [Ando and Zhang 2005; Chen et al. 2009]; the relatedness of multiple tasks is modeled using various structured sparsity penalties such as the tree-guided group lasso and the graph-guided fused lasso [Kim and Xing 2010; Chen et al. 2010; Chen et al. 2010]. Recently, trace norm regularization has been introduced into the multi-task learning domain [Abernethy et al. 2009; Argyriou et al. 2008; Ji and Ye 2009; Obozinski et al. 2010; Pong et al. 2010] to capture the task relationship via a shared low-rank structure of the model parameters, resulting in a tractable convex optimization problem [Liu et al. 2009b].

In many real-world applications involving multiple (related) tasks, the underlying predictive hypothesis structure [Ando and Zhang 2005; Shapiro 1982] may be complex, e.g., the predictive classifiers may admit a low-rank structure as well as a (entry-wise) sparse structure. For example, for the problems of reconstructing natural scene images via the multi-scale approximation approaches [Gonzalez and Woods 2002], the images usually have sparse representations (corresponding to a low-rank structure) in the form of a linear combination of certain bases; meanwhile, the images obtained under different illumination conditions or using different equipments may have only a small (sparse) sets of discriminative features (corresponding to a sparse structure). Analogously, for the problem of predicting disease progression in different geographic locations, the underlying progression patterns for all locations may share a set of basis factors, while the progression pattern for a specific location is also distinguished from other locations by a sparse set of features. Moreover in collaborative filtering or recommender system, a few factors contribute to the common taste of the individuals, while each individual's taste also relies on the personal inclination. Therefore it is desirable to utilize both the low-rank structure (representing the tasks relatedness) and the sparse structure (representing the task-wise discriminative patterns) for improved generalization performance and easily interpretable models for certain applications, e.g., the aforementioned real-world applications.

In this paper, we consider the problem of learning incoherent sparse and low-rank patterns from multiple related tasks. We propose a linear multi-task learning formulation, in which the model parameter can be decomposed as a sparse component and a low-rank component. Specifically, we employ a cardinality regularization term to enforce the sparsity in the model parameter, identifying the essential discriminative feature for effective classification; meanwhile, we use a rank constraint to encourage the low-rank structure, capturing the underlying relationship among the tasks for improved generalization performance. The proposed multi-task learning formulation is non-convex and leads to an NP-hard optimization problem. We convert this formulation into its tightest convex surrogate, which can be routinely solved via semi-definite programming. It is, however, not scalable to large scale data sets in practice. We propose to employ the general projected gradient scheme to solve the convex surrogate; however, in the optimization formulation, the objective function is non-differentiable and the feasible domain is non-trivial. We present the procedures for computing the projected gradient and ensuring the global convergence of the projected gradient scheme. The computation of the projected gradient involves a constrained optimization problem; we show that the optimal solution to such a problem can be obtained via solving an unconstrained optimization subproblem and an Euclidean projection subproblem separately. We also present two algorithms based on the projected gradient scheme and analyze their rates of convergence in details. In addition, we present an example of the proposed multi-task learning formulation using the least squares loss and illustrate the use of the presented projected gradient based algorithms in this case. We conduct extensive experiments on a collection of real-world data sets. Our results demonstrate the effectiveness of the proposed multi-task learning formulation and also demonstrate the efficiency of the projected gradient algorithms.

The remainder of this paper is organized as follows: in Section 2 we propose the linear multi-task learning formulation; in Section 3 we present the general projected gradient scheme for solving the proposed multi-task learning formulation; in Section 4 we present efficient computational algorithms for solving the optimization problems involved in the iterative procedure of the projected gradient scheme; in Section 5 we present two algorithms based on the projected gradient scheme and analyze their rates of convergence in details; in Section 6 we present a concrete example on the use of the projected gradient based algorithms for the proposed multi-task learning formulation using the least squares loss; we report the experimental results in Section 7 and the paper concludes in Section 8.

Notations

For any matrix $A\in {\mathbb{R}}^{m\times n}$, let a_ij be the (i, j)th entry of A; denote by ∥A∥₀ the number of nonzero entries in A; let ${\Vert A\Vert }_1={\sum }_{i=1}^m{\sum }_{j=1}^n\mid a_{ij}\mid$; let ${\left\{{\sigma }_i\left(A\right)\right\}}_{i=1}^r$ be the set of singular values of A in non-increasing order, where r = rank(A); denote by ∥A∥₂ = σ₁ (A) and ${\Vert A\Vert }_{\ast }={\sum }_{i=1}^r{\sigma }_i\left(A\right)$ the operator norm and the trace norm of A, respectively; let ∥A∥_∞ = max_i,j |a_ij|.

2. MULTI-TASK LEARNING FRAMEWORK

Assume that we are given m supervised (binary) learning tasks, where each of the learning tasks is associated with a predictor $f_{\ell }$ and a set of training data as ${\left\{(x_i^{\ell },y_i^{\ell })\right\}}_{i=1}^{n_{\ell }}\subset {\mathbb{R}}^d\times \{-1,+1\}(\ell =1,\cdots ,m)$. We focus on linear predictors as $f_{\ell }\left(x^{\ell }\right)=z_{\ell }^T{x}^{\ell }$, where $z_{\ell }\in {\mathbb{R}}^d$ is the weight vector for the $\ell \text{th}$ learning task.

2.1 Proposed Formulation

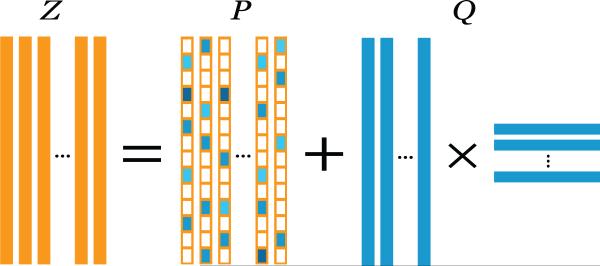
We assume that the m tasks are related using an incoherent rank-sparsity structure, that is, the transformation matrix can be decomposed as a sparse component and a low-rank component. Denote the transformation matrix by $Z=[z_1,\cdots ,z_m]\in {\mathbb{R}}^{d\times m}$; Z is the summation of a sparse matrix $P=[p_1,\cdots ,p_m]\in {\mathbb{R}}^{d\times m}$ and a low-rank matrix $Q=[q_1,\cdots ,q_m]\in {\mathbb{R}}^{d\times m}$ given by

$$Z=P+Q,$$ (1)

as illustrated in Figure 1. The ${\ell }_0\text{-norm}$ (cardinality) [Boyd and Vandenberghe 2004], i.e., the number of non-zero entries, is commonly used to control the sparsity structure in the matrix; similarity, matrix rank [Golub and Van Loan 1996] is used to encourage the low-rank structure. We propose a multi-task learning formulation with a cardinality regularization and a rank constraint given by

$$\begin{array}{cc}\hfill \underset{\{Z,P,Q\}\in {\mathbb{R}}^{d\times m}}{\text{min}}& \sum _{\ell =1}^m\sum _{i=1}^{n_{\ell }}\mathcal{L}(z_{\ell }^T{x}_i^{\ell },y_i^{\ell })+\gamma {\Vert P\Vert }_0\hfill \\ \hfill \text{subject to}& Z=P+Q,\text{rank}\left(Q\right)\le \tau ,\hfill \end{array}$$ (2)

where $\mathcal{L}(\cdot )$ denotes a smooth convex loss function, γ provides a trade-off between the sparse regularization term and the general loss component, and τ explicitly specifies the upper bound of the matrix rank. Both γ and τ are non-negative and determined via cross-validation in our empirical studies.

Fig. 1.

Illustration of the transformation matrix Z in Eq. (1), where P denotes the sparse component with the zero-value entries represented by white blocks, and Q denotes the low-rank component.

The optimization problem in Eq. (2) is non-convex due to the non-convexity of the components ∥P∥₀ and rank(Q); in general solving such an optimization problem is NP-hard and no efficient solution is known. We consider a computationally tractable alternative by employing recently well-studied convex relaxation techniques [Boyd and Vandenberghe 2004].

Define the function $f:\mathbb{C}\to \mathbb{R}$, where $\mathbb{C}\subseteq {\mathbb{R}}^{d\times m}$. The convex envelope [Boyd and Vandenberghe 2004] of f on $\mathbb{C}$ is defined as the largest convex function g such that g(Ẑ) ≤ f(Ẑ) for all $\widehat{Z}\in \mathbb{C}$. The ${\ell }_1\text{-norm}$ has been known to be the convex envelope of the ${\ell }_0\text{-norm}$ as [Boyd and Vandenberghe 2004]:

$${\Vert P\Vert }_1\le {\Vert P\Vert }_0,\forall P\in \mathbb{C}=\{P\mid {\Vert P\Vert }_{\infty }\le 1\}.$$ (3)

Similarly, the trace norm (nuclear norm) has been shown to be the convex envelop of the rank function as [Fazel et al. 2001]:

$${\Vert Q\Vert }_{\ast }\le \text{rank}\left(Q\right),\forall Q\in \mathbb{C}=\{Q\mid {\Vert Q\Vert }_2\le 1\}.$$ (4)

Note that both the ${\ell }_1\text{-norm}$ and the trace-norm functions are convex but non-smooth, and they have been shown to be effective surrogates of the ${\ell }_0\text{-norm}$ and the matrix rank functions, respectively.

Based on the heuristic approximations in Eq. (3) and Eq. (4), we can replace the ${\ell }_0\text{-norm}$ with the ${\ell }_1\text{-norm}$, and replace the rank function with the trace norm function in Eq. (2), respectively. Therefore, we can reformulate the multi-task learning formulation as:

$$\begin{array}{cc}\hfill \underset{\{Z,P,Q\}\in {\mathbb{R}}^{d\times m}}{\text{min}}& \sum _{\ell =1}^m\sum _{i=1}^{n_{\ell }}\mathcal{L}(z_{\ell }^T{x}_i^{\ell },y_i^{\ell })+\gamma {\Vert P\Vert }_1\hfill \\ \hfill \text{subject to}& Z=P+Q,{\Vert Q\Vert }_{\ast }\le \tau .\hfill \end{array}$$ (5)

Note that in Eqs. (2) and (5), the transformation matrix is denoted by Z and it is the superposition of an entry-wise sparse matrix P and a low-rank matrix Q. The optimization problem in Eq. (5) is the tightest convex relaxation of Eq. (2). Such a problem can be reformulated as a semi-definite program (SDP) [Vandenberghe and Boyd 1996], and solved using many off-the-shelf optimization solvers such as SeDuMi [Sturm 2001]; however, SDP is computationally expensive and can only handle several hundreds of optimization variables. Since the proposed MTL formulation in Eq. (5) is convex, it admits a globally optimal solution; however, its (globally) optimal solution may not be unique, as the uniqueness of the solution is dependent on the involved training data, e.g., whether the resulting optimization formulation is strictly convex.

2.2 Related Work

Our multi-task learning formulation in Eq. (5) resembles the Alternating Structure Optimization algorithm (ASO) proposed in [Ando and Zhang 2005]. However, they differ in several key aspects: (1) In ASO, the tasks are coupled using a shared low-dimensional structure induced by an orthonormal constraint, and the formulation in ASO is non-convex. Our formulation encourages the low-rank structure via a trace norm constraint and the resulting formulation is convex. (2) In ASO, in addition to a low-dimensional feature map shared by all tasks, the classifier for each task computes an independent high-dimensional feature map specific to each individual task, which is in general dense and does not lead to interpretable features. In our formulation, the classifier for each task constructs a sparse high-dimensional feature map for discriminative feature identification. (3) The alternating optimization algorithm in ASO can only find a local solution with no known convergence rate. The proposed algorithm for solving the formulation in Eq. (5) finds a globally optimal solution and achieves the optimal convergence rate among all first-order methods.

Our formulation is also closely related to the concept of dirty models for multi-task learning [Jalali et al. 2010]. Specifically in [Jalali et al. 2010] a dirty model is proposed for the joint learning of multiple linear regression functions via a composite structured sparsity regularization; this model expresses the transformation matrix (of multiple regression functions) as a superposition of two matrix parameters and regularizes them respectively via the ${\ell }_{1,1}\text{-norm}$ and the ${\ell }_{1,\infty }\text{-norm}$, in order to perform biased statistical estimation tailored to certain types of data.

Recent works in [Candès et al. 2009; Chandrasekaran et al. 2009; Wright et al. 2009] consider the problem of decomposing a given matrix into its underlying sparse component and low-rank component in a different setting: they study the theoretical condition under which such two components can be exactly recovered via convex optimization, i.e., the condition of guaranteeing to recover the sparse and low-rank components by minimizing a weighted combination of the trace norm and the ${\ell }_1\text{-norm}$.

3. PROJECTED GRADIENT SCHEME

In this section, we propose to apply the general projected gradient scheme [Boyd and Vandenberghe 2004] to solve the constrained optimization problem in Eq. (5). The projected gradient scheme is a first-order method; it require only the computation of the first-order information and hence it is suitable for large scale data analysis. This type of methods has recently attracted intense interest in machine learning and data mining areas [Bach et al. 2011; Nemirovski 1995; Liu et al. 2009b]. Specifically it has been employed for solving mathematical formulations arising from different multi-task learning scenarios [Chen et al. 2009; Zhang et al. 2010; Liu et al. 2009a].

In Eq. (5), the objective function is non-smooth and the feasible domain is associated with a trace norm constraint. For simplicity, we denote the optimization in Eq. (5) as

$$\begin{array}{cc}\hfill \underset{T}{\text{min}}& f\left(T\right)+g\left(T\right)\hfill \\ \hfill \text{subject to}& T\in \mathcal{M},\hfill \end{array}$$ (6)

where the functions f(T) and g(T) are defined respectively as

$$f\left(T\right)=\sum _{\ell =1}^m\sum _{i=1}^{n_{\ell }}\mathcal{L}({(p_{\ell }+q_{\ell })}^T{x}_i^{\ell },y_i^{\ell }),g\left(T\right)=\gamma {\Vert P\Vert }_1,$$

and the set $\mathcal{M}$ is defined as

$$\mathcal{M}=\left\{T\mid T=\left(\begin{array}{c}\hfill P\hfill \\ \hfill Q\hfill \end{array}\right),\phantom{\mid }P\in {\mathbb{R}}^{d\times m},{\Vert Q\Vert }_{\ast }\le \tau ,Q\in {\mathbb{R}}^{d\times m}\right\}.$$

Note that f(T) is a smooth convex function with a Lipschitz constant L_f [Bertsekas et al. 2003] as:

$${\Vert \nabla f\left(T_x\right)-\nabla f\left(T_y\right)\Vert }_F\le L_f{\Vert T_x-T_y\Vert }_F,\forall T_x,T_y\in \mathcal{M},$$ (7)

g(T) is a non-smooth convex function, and $\mathcal{M}$ is a compact and convex set [Bertsekas et al. 2003]. It is known that the smallest Lipschitz constant L̂_f in Eq. (7), i.e, L̂_f = min L_f, is called the best Lipschitz constant for the function f(T); moreover, for any L ≥ L̂_f, the following inequality holds [Nesterov 1998]:

$$f\left(T_x\right)\le f\left(T_y\right)+\langle T_x-T_y,\nabla f\left(T_y\right)\rangle +\frac{L}{2}{\Vert T_x-T_y\Vert }^2,$$ (8)

where $T_x,T_y\in \mathcal{M}$.

The projected gradient scheme computes the global minimizer of Eq. (6) via an iteratively updating procedure. That is, given T_k as the intermediate solution of the kth iteration, we update T_k as

$$T_{k+1}=T_k-t_k{\mathcal{P}}_k,\forall k,$$ (9)

where ${\mathcal{P}}_k$ and t_k denote the appropriate projected gradient direction and the step size, respectively. The appropriate choice of ${\mathcal{P}}_k$ and t_k is key to the global convergence of the projected gradient scheme. The computation in Eq. (9) depends on ${\mathcal{P}}_k$ and t_k; in the following subsections, we will present a procedure for estimating appropriate ${\mathcal{P}}_k$ and t_k, and defer the discussion of detailed projected gradient based algorithms to Section 5. Note that since the determination of ${\mathcal{P}}_k$ is associated with T_k and t_k, we denote ${\mathcal{P}}_k$ by ${\mathcal{P}}_{1∕t_k}\left(T_k\right)$, and the reason will become clear from the following discussion. It is worth pointing out that throughout this paper we focus on using a smooth convex loss function in the proposed multi-task learning formulation as described in Eq. (2) and hence the objective function (of the proposed multi-task learning formulation) can be expressed as the combination of a smooth component and a non-smooth component as in Eq. (6); for this case the projected gradient scheme is applicable; when the loss function is non-smooth convex, we can resort to the subgradient algorithms [Bertsekas 1999].

3.1 Projected Gradient Computation

For any L > 0, we consider the following construction associated with the smooth component f(T) of the objective function in Eq. (6):

$$f_L(S,T)=f\left(S\right)+\langle T-S,\nabla f\left(S\right)\rangle +\frac{L}{2}{\Vert T-S\Vert }_F^2,$$

where S, $T\in {\mathbb{R}}^{d\times m}$. It can be verified that f_L(S, T) is strongly convex with respect to the variable T. Moreover, we denote

$$G_L(S,T)=f_L(S,T)+g\left(T\right),$$ (10)

where g(T) is the non-smooth component of the objective function in Eq. (6). From the convexity of g(T), G_L(S, T) is strongly convex with respect to T. Since

$$G_L(S,T)=f\left(S\right)-\frac{1}{2L}{\Vert \nabla f\left(S\right)\Vert }_F^2+\frac{L}{2}{\Vert T-\left(S-\frac{1}{L}\nabla f\left(S\right)\right)\Vert }_F^2+g\left(T\right),$$

the global minimizer of G_L(S, T) with respect to T can be computed as

$$\begin{array}{cc}\hfill T_{L,S}& =\underset{T\in \mathcal{M}}{\text{arg min}}{G}_L(S,T)\hfill \\ \hfill & =\underset{T\in \mathcal{M}}{\text{arg min}}\left(\frac{L}{2}{\Vert T-\left(S-\frac{1}{L}\nabla f\left(S\right)\right)\Vert }_F^2+g\left(T\right)\right).\hfill \end{array}$$ (11)

We can then obtain the projected gradient of f at S via

$${\mathcal{P}}_L\left(S\right)=L(S-T_{L,S}).$$ (12)

It is obvious that 1/L can be seen as the step size associated with the projected gradient ${\mathcal{P}}_L\left(S\right)$ by rewritting Eq. (12) as

$$T_{L,S}=S-\frac{1}{L}{\mathcal{P}}_L\left(S\right).$$ (13)

Note that if the inequality f(T_L,S) ≤ f_L(S, T_L,S) is satisfied, ${\mathcal{P}}_L\left(S\right)$ is called the L-gradient of f at S [Nemirovski 1995].

3.2 Step Size Estimation

From Eq. (12), the step size associated with ${\mathcal{P}}_L\left(S\right)$ is given by 1/L. Denote the objective function in Eq. (6) as

$$F\left(T\right)=f\left(T\right)+g\left(T\right).$$ (14)

Theoretically, any step size 1/L of the value L larger than the best Lipschitz constant L̂_f guarantees the global convergence in the projected gradient based algorithms [Nemirovski 1995]. It follows from Eq. (8) that

$$F\left(T_{L,S}\right)\le G_L(S,T_{L,S}),\forall L\ge L_f.$$ (15)

In practice we can estimate an appropriate L (hence the appropriate step size 1/L) by ensuring the inequality in Eq. (15). By applying an appropriate step size and the associated projected gradient in Eq. (9), we can verify an important inequality [Beck and Teboulle 2009; Nemirovski 1995], as summarized in the following lemma.

Lemma 3.1. Let L_f be the Lipschitz continuous gradient associated with the function f(T) as defined in Eq. (7). Let $S\in {\mathbb{R}}^{d\times m}$, and let T_L,S be the minimizer of G_L(S, T) as defined in Eq. (11). Then if L ≥ L_f, the following inequality holds

$$F\left(T\right)-F\left(T_{L,S}\right)\ge \langle T-S,{\mathcal{P}}_L\left(S\right)\rangle +\frac{1}{2L}{\Vert {\mathcal{P}}_L\left(S\right)\Vert }_F^2$$ (16)

for any $T\in \mathcal{M}$.

Proof. Following from the convexity of f(·) and g(·), we have

$$f\left(T\right)\ge f\left(S\right)+\langle T-S,\nabla f\left(S\right)\rangle$$ (17)

$$g\left(T\right)\ge g\left(T_{L,S}\right)+\langle T-T_{L,S},\partial g\left(T_{L,S}\right)\rangle ,$$ (18)

where ∂g(T_L,S) denotes the subgradient [Nesterov 1998] of g(·) at T_L,S. It is well known that T̂ minimizes G_L(S, T) (with respect to the variable T) if and only if 0 is a subgradient of G_L(S, T) at T̂, that is,

$$0\in L(T_{L,S}-S)+\nabla f\left(S\right)+\partial g\left(T_{L,S}\right).$$ (19)

From Eqs. (10), (14), (17) and (18), we have

$$\begin{array}{cc}\hfill F\left(T\right)-G_L(S,T_{L,S})& =(f\left(T\right)+g\left(T\right))-(f_L(S,T_{L,S})+g\left(T_{L,S}\right))\hfill \\ \hfill & \ge \langle T-T_{L,S},\nabla f\left(S\right)+\partial g\left(T_{L,S}\right)\rangle -\frac{L}{2}{\Vert S-T_{L,S}\Vert }_F^2\hfill \\ \hfill & =-L\langle T-T_{L,S},T_{L,S}-S\rangle -\frac{L}{2}{\Vert S-T_{L,S}\Vert }_F^2\hfill \\ \hfill & =\langle T-S,{\mathcal{P}}_L\left(S\right)\rangle +\frac{1}{2L}{\Vert {\mathcal{P}}_L\left(S\right)\Vert }_F^2,\hfill \end{array}$$

where the second and third equalities follow from Eqs. (19) and (12), respectively. This completes the proof of this lemma.

By replacing S with T in Eq. (16), we have

$$F\left(T\right)-F\left(T_{L,T}\right)\ge \frac{1}{2L}{\Vert {\mathcal{P}}_L\left(T\right)\Vert }_F^2.$$ (20)

Note that the inequality in Eq. (16) characterizes the relationship of the objective values in Eq. (6) using T and its updated version via the procedure in Eq. (9).

4. EFFICIENT COMPUTATION

The projected gradient scheme requires to solve Eq. (11) at each iterative step. In Eq. (11), the objective function is non-smooth and the feasible domain set is associated with a trace norm constraint; we show that its optimal solution can be obtained by solving an unconstrained optimization problem and an Euclidean projection problem separately.

Denote T and S in Eq. (11) respectively as

$$T=\left(\begin{array}{c}\hfill T_P\hfill \\ \hfill T_Q\hfill \end{array}\right),S=\left(\begin{array}{c}\hfill S_P\hfill \\ \hfill S_Q\hfill \end{array}\right).$$

Therefore the optimization problem in Eq. (11) can be expressed as

$$\begin{array}{cc}\hfill \underset{T_P,T_Q}{\text{min}}& \frac{L}{2}{\Vert \left(\begin{array}{c}\hfill T_P\hfill \\ \hfill T_Q\hfill \end{array}\right)-\left(\begin{array}{c}\hfill {\widehat{S}}_P\hfill \\ \hfill {\widehat{S}}_Q\hfill \end{array}\right)\Vert }_F^2+\gamma {\Vert T_P\Vert }_1\hfill \\ \hfill \text{subject to}& {\Vert T_Q\Vert }_{\ast }\le \tau ,\hfill \end{array}$$ (21)

where Ŝ_P and Ŝ_Q can be computed respectively as

$${\widehat{S}}_P=S_P-\frac{1}{L}{\nabla }_{P}f\left(S\right),{\widehat{S}}_Q=S_Q-\frac{1}{L}{\nabla }_{Q}f\left(S\right).$$

Note that ∇_P f(S) and ∇_Q f(S) denote the derivative of the smooth component f(S) with respect to the variables P and Q, respectively. We can further rewrite Eq. (21) as

$$\begin{array}{cc}\hfill \underset{T_P,T_Q}{\text{min}}& \beta {\Vert T_P-{\widehat{S}}_P\Vert }_F^2+\beta {\Vert T_Q-{\widehat{S}}_Q\Vert }_F^2+\gamma {\Vert T_P\Vert }_1\hfill \\ \hfill \text{subject to}& {\Vert T_Q\Vert }_{\ast }\le \tau ,\hfill \end{array}$$ (22)

where β = L/2. Since T_P and T_Q are decoupled in Eq. (22), they can be optimized separately as presented in the following subsections.

4.1 Computation of T_P

The optimal T_P can be obtained by solving the following optimization problem:

$$\underset{T_P}{\text{min}}\beta {\Vert T_P-{\widehat{S}}_P\Vert }_F^2+\gamma {\Vert T_P\Vert }_1.$$

It is obvious that each entry of the optimal matrix T_P can be obtained by solving an optimization problem as

$$\underset{\widehat{t}\in \mathbb{R}}{\text{min}}\beta {\Vert \widehat{t}-\widehat{s}\Vert }^2+\gamma \mid \widehat{t}\mid .$$ (23)

Note that ŝ denotes an entry in Ŝ_P, corresponding to t̂ in T_P from the same location. It is known [Tibshirani 1996] that the optimal t̂ to Eq. (23) admits an analytical solution; for completeness, we present its proof in Lemma 4.1.

Lemma 4.1. The minimizer of Eq. (23) can be expressed as

$${\widehat{t}}^{\ast }=\{\begin{array}{cc}\hfill \widehat{s}-\frac{\gamma }{2\beta }\hfill & \hfill \widehat{s}>\frac{\gamma }{2\beta }\hfill \\ \hfill 0\hfill & \hfill -\frac{\gamma }{2\beta }\le \widehat{s}\le \frac{\gamma }{2\beta }\hfill \\ \hfill \widehat{s}+\frac{\gamma }{2\beta }\hfill & \hfill \widehat{s}<-\frac{\gamma }{2\beta }\hfill \end{array}\phantom{\}}.$$ (24)

Proof. Denote by h(t̂) the objective function in Eq. (23), and by t̂* the minimizer of h(t̂). The subdifferential of h(t̂) can be expressed as

$$\partial h\left(\widehat{t}\right)=2\beta (\widehat{t}-\widehat{s})+\gamma \text{sgn}\left(\widehat{t}\right),$$

where the function sgn(·) is given by

$$\text{sgn}\left(\widehat{t}\right)=\{\begin{array}{cc}\hfill \left\{1\right\}\hfill & \hfill \widehat{t}>0\hfill \\ \hfill [-1,1]\hfill & \hfill \widehat{t}=0\hfill \\ \hfill \{-1\}\hfill & \hfill \widehat{t}<0\hfill \end{array}\phantom{\}}.$$

It is known that t̂* minimizes h(t̂) if and only if 0 is a subgradient of h(t̂) at the point t̂*, that is,

$$0\in 2\beta ({\widehat{t}}^{\ast }-\widehat{s})+\gamma \text{sgn}\left({\widehat{t}}^{\ast }\right).$$

Since the equation above is satisfied with t̂* defined in Eq. (24), we complete the proof of this lemma.

4.2 Computation of T_Q

The optimal T_Q can be obtained by solving the optimization problem:

$$\begin{array}{cc}\hfill \underset{T_Q}{\text{min}}& \frac{1}{2}{\Vert T_Q-{\widehat{S}}_Q\Vert }_F^2\hfill \\ \hfill \text{subject to}& {\Vert T_Q\Vert }_{\ast }\le \tau ,\hfill \end{array}$$ (25)

where the constant 1/2 is added into the objective function for convenient presentation. In the following theorem, we show that the optimal T_Q can be obtained via solving a simple convex optimization problem.

Theorem 4.1. Let ${\widehat{S}}_Q=U{\Sigma }_S{V}^T\in {\mathbb{R}}^{d\times m}$ be the SVD of Ŝ_Q, where q = rank(Ŝ_Q), $U\in {\mathbb{R}}^{d\times q}$, $V\in {\mathbb{R}}^{m\times q}$, and ${\Sigma }_S=diag({\varsigma }_1,\cdots ,{\varsigma }_q)\in {\mathbb{R}}^{q\times q}$. Let ${\left\{{\sigma }_i\right\}}_{i=1}^q$ be the minimizers of the following problem:

$$\begin{array}{cc}\hfill \underset{{\left\{{\sigma }_i\right\}}_{i=1}^q}{\text{min}}& \sum _{i=1}^q{({\sigma }_i-{\varsigma }_i)}^2\hfill \\ \hfill subjectto& \sum _{i=1}^q{\sigma }_i\le \tau ,{\sigma }_i\ge 0.\hfill \end{array}$$ (26)

Denote $\Sigma =diag({\sigma }_1,\cdots ,{\sigma }_q)\in {\mathbb{R}}^{q\times q}$. Then the optimal solution to Eq. (25) is given by

$$T_Q^{\ast }=U\Sigma V^T.$$

Proof. Assume that the optimal $T_Q^{\ast }$ to Eq. (25) shares the same left and right singular vectors as Ŝ_Q. Then the problem in Eq. (25) is reduced to the problem in Eq. (26). Thus, all that remains is to show that $T_Q^{\ast }$ shares the same left and right singular vectors as Ŝ_Q. Denote the Lagrangian function [Boyd and Vandenberghe 2004] associated with Eq. (25) as

$$H(T_Q,\lambda )=\frac{1}{2}{\Vert T_Q-{\widehat{S}}_Q\Vert }_F^2+\lambda ({\Vert T_Q\Vert }_{\ast }-\tau ).$$

Since 0 is strictly feasible in Eq. (25), i.e., ∥0∥_* < τ, the Slater's condition [Boyd and Vandenberghe 2004] is satisfied and strong duality holds in Eq. (25). Let λ* ≥ 0 be the optimal dual variable [Boyd and Vandenberghe 2004] in Eq. (25). Therefore,

$$\begin{array}{cc}\hfill T_Q^{\ast }& =\underset{T_Q}{\text{arg min}}H(T_Q,{\lambda }^{\ast })\hfill \\ \hfill & =\underset{T_Q}{\text{arg min}}\frac{1}{2}{\Vert T_Q-{\widehat{S}}_Q\Vert }_F^2+{\lambda }^{\ast }{\Vert T_Q\Vert }_{\ast }.\hfill \end{array}$$

Let $T_Q^{\ast }=U_T{\Sigma }_T{V}_T^T\in {\mathbb{R}}^{d\times m}$ be the SVD of $T_Q^{\ast }$ and $r=\text{rank}\left(T_Q^{\ast }\right)$, where $U_T\in {\mathbb{R}}^{d\times r}$ and $U_T\in {\mathbb{R}}^{m\times r}$ are columnwise orthonormal, and ${\Sigma }_T\in {\mathbb{R}}^{r\times r}$ is diagonal consisting of non-zero singular values on the main diagonal. It is known [Watson 1992] that the subdifferentials of ${\Vert T_Q\Vert }_{\ast }$ at $T_Q^{\ast }$ can be expressed as

$$\partial {\Vert T_Q^{\ast }\Vert }_{\ast }=\{U_T{V}_T^T+D:D\in {\mathbb{R}}^{d\times m},U_T^{T}D=0,D{V}_T=0,{\Vert D\Vert }_2\le 1\}.$$ (27)

On the other hand, we can verify that $T_Q^{\ast }$ is optimal to Eq.(25) if and only if 0 is a subgradient of H(T_Q, λ*) at $T_Q^{\ast }$, that is,

$$0\in \partial H(T_Q^{\ast },{\lambda }^{\ast })=T_Q^{\ast }-{\widehat{S}}_Q+{\lambda }^{\ast }\partial {\Vert T_Q^{\ast }\Vert }_{\ast }.$$ (28)

Let $U_T^{\perp }\in {\mathbb{R}}^{d\times (d-m)}$ and $V_T^{\perp }\in {\mathbb{R}}^{m\times (m-r)}$ be the null space [Golub and Van Loan 1996] of U_T and V_T, respectively. It follows from Eq. (27) that there exists a point $D_T=U_T^{\perp }{\Sigma }_d{\left(V_T^{\perp }\right)}^T$ such that

$$U_T{V}_T^T+D_T\in \partial {\Vert T_Q^{\ast }\Vert }_{\ast }$$

satisfies Eq. (28), and ${\Sigma }_d\in {\mathbb{R}}^{(d-m)\times (m-r)}$ is diagonal consisting of the singular values of D_T on the main diagonal. It follows that

$$\begin{array}{cc}\hfill {\widehat{S}}_Q& =T_Q^{\ast }+{\lambda }^{\ast }(U_T{V}_T^T+D_T)\hfill \\ \hfill & =U_T{\Sigma }_T{V}_T^T+{\lambda }^{\ast }{U}_T{V}_T^T+{\lambda }^{\ast }{U}_T^{\perp }{\Sigma }_d{\left(V_T^{\perp }\right)}^T\hfill \\ \hfill & =U_T({\Sigma }_T+{\lambda }^{\ast }I)V_T+U_T^{\perp }\left({\lambda }^{\ast }{\Sigma }_d\right){\left(V_T^{\perp }\right)}^T\hfill \end{array}$$

corresponds to the SVD of Ŝ_Q. This completes the proof of this theorem.

Note that the optimization problem in Eq. (26) is convex, and can be solved via an algorithm similar to the one in [Liu and Ye 2009] proposed for solving the Euclidean projection onto the ${\ell }_1$ ball.

5. ALGORITHMS AND CONVERGENCE

We present two algorithms based on the projected gradient scheme in Section 3 for solving the constrained convex optimization problem in Eq. (6), and analyze their rates of convergence using techniques in [Nemirovski 1995; Nesterov 1998].

5.1 Projected Gradient Algorithm

We first present a simple projected gradient algorithm. Let T_k be the feasible solution point at the k-th iteration; the projected gradient algorithm updates T_k by recycling the following two steps: find a candidate T̂ for the subsequent feasible solution point T_k+1 via

$$\widehat{T}=T_{L,T_k}=\underset{T\in \mathcal{M}}{\text{arg min}}{G}_L(T_k,T),$$

and meanwhile ensure the step size $\frac{1}{L}$ satisfying the condition

$$F\left(\widehat{T}\right)\le G_L(T_k,\widehat{T}).$$

Note that both T_k and T̂ are feasible in Eq. (6). It follows from Eq. (20) that the solution sequence generated in the projected gradient algorithm leads to a non-increasing objective value in Eq. (6), that is,

$$F\left(T_{k-1}\right)\ge F\left(T_k\right),\forall k.$$ (29)

The pseudo-code of the projected gradient algorithm is presented in Algorithm 1, and its convergence rate analysis is summarized in Theorem 5.1. Note that the stopping criterion in line 11 of Algorithm 1 can be set as follows: the change of objective values in two successive steps are smaller than some pre-specified value (e.g., 10^–5).

Algorithm 1.

Projected Gradient (PG) Method

1:	Input: T0, $L_0\in \mathbb{R}$, and max-iter.
2:	Output: T.
3:	for i = 0,1, · · · , max-iter do
4:	while (true)
5:	Compute T̂ = TLi,Ti via Eq. (11).
6:	if F(T̂) ≤ GLi (Ti,T̂) then exit the loop.
7:	else update Li = Li × 2.
8:	end-if
9:	end-while
10:	Update Ti+1 = T̂ and Li+1 = Li.
11:	if the stopping criterion is satisfied then exit the loop.
12:	end-for
13:	Set T = Ti+1.

Theorem 5.1. Let T* be the global minimizer of Eq. (6); let L̂_f be the best Lipschitz continuous gradient defined in Eq.(7). Denote by k the index of the iteration, and by T_k the solution point at the kth iteration of Algorithm 1. Then we have

$$F\left(T_k\right)-F\left(T^{\ast }\right)\le \frac{\widehat{L}}{2k}{\Vert T_0-T^{\ast }\Vert }_F^2,$$

where L̂* = max{L₀, 2L̂_f}, and L₀ and T₀ are the initial values of L_k and T_k in Algorith m 1, respectively.

Proof. It follows from Eq. (12) we have

$$T_{i+1}=T_{L_i,T_i}=T_i-\frac{1}{L_i}{\mathcal{P}}_{L_i}\left(T_i\right).$$

Moreover, from Eq. (16), we have

$$\begin{array}{cc}\hfill -{\epsilon }_{i+1}& \ge \langle T^{\ast }-T_i,{\mathcal{P}}_{L_i}\left(T_i\right)\rangle +\frac{1}{2L_i}{\Vert {\mathcal{P}}_{L_i}\left(T_i\right)\Vert }_F^2\hfill \\ \hfill & =\frac{L_i}{2}(-{\Vert T_i\Vert }_F^2+{\Vert T_{i+1}\Vert }_F^2+2\langle T^{\ast },T_i-T_{i+1}\rangle ),\hfill \end{array}$$ (30)

where ε_i+1 = F(T_i+1) – F(T*). Moving L_i/2 to the left side in Eq. (30) and summing such a reformulation from i = 0 to i = k, we have

$$\begin{array}{cc}\hfill \sum _{i=0}^k\frac{2}{L_i}{\epsilon }_{i+1}& \le {\Vert T_0\Vert }_F^2-{\Vert T_{k+1}\Vert }_F^2+2\langle T^{\ast },T_{k+1}-T_0\rangle \hfill \\ \hfill & ={\Vert T_0-T^{\ast }\Vert }_F^2-{\Vert T_{k+1}-T^{\ast }\Vert }_F^2\hfill \\ \hfill & \le {\Vert T_0-T^{\ast }\Vert }_F^2.\hfill \end{array}$$

Since L_i ≥ L_i–1 from line 7 in algorithm 1, and ε_i ≤ ε_i–1 from Eq. (29) for all i, we have

$${\epsilon }_{k+1}\le \frac{L_k}{2(k+1)}{\Vert T_0-T^{\ast }\Vert }_F^2.$$

Moreover, it can be verified that L₀ ≤ L_k ≤ 2L̂_f for all k. This completes the proof of this theorem.

5.2 Accelerated Projected Algorithm

The proposed projected gradient method in Section 5.1 is simple to implement but converges slowly. We improve the projected gradient method using a scheme developed by Nesterov [Nesterov 1998], which has been applied for solving various sparse learning formulations [Liu et al. 2009b].

We utilize two sequences of variables in the accelerated projected gradient algorithm: (feasible) solution sequence {T_k} and searching point sequence {S_k}. At the i-th iteration, we construct the searching point as

$$S_k=(1+{\alpha }_k)T_k-{\alpha }_k{T}_{k-1},$$ (31)

where the parameter α_k > 0 is appropriately specified as shown in Algorithm 2. Similar to the projected gradient method, we refine the feasible solution point T_k+1 via the general step as:

$$\widehat{T}=T_{L,S_k}=\underset{T\in \mathcal{M}}{\text{arg min}}{G}_L(S_k,T),$$

and meanwhile determine the step size by ensuring

$$F\left(\widehat{T}\right)\le G_L(S_k,\widehat{T}).$$

The searching point S_k may not be feasible in Eq. (6), which can be seen as a forecast of the next feasible solution point and hence leads to the faster convergence rate in Algorithm 2. The pseudo-code of the accelerated projected gradient algorithm is presented in Algorithm 2, and its convergence rate analysis is summarized in the following theorem.

Algorithm 2.

Accelerated Projected Gradient (AG) Method

1:	Input: T0, $L_0\in \mathbb{R}$, and max-iter.
2:	Output: T.
3:	Set T1 = T0, t–1 = 0, and t0 = 1.
4:	for i = 1, 2, · · · , max-iter do
5:	Compute α = (ti–2– 1)/ti–1.
6:	Compute S = (1 + αi)Ti – αiTi–1
7:	while (true)
8:	Compute T̂ = TLi,S via Eq. (11).
9:	if F(T̂) ≤ GLi (S, T̂) then exit the loop
10:	else update Li = Li × 2.
11:	end-if
12:	end-while
13:	Update Ti+1 = T̂ and Li+1 = Li.
14:	if the stopping criterion is satisfied then exit the loop.
15:	Update $t_i=\frac{1}{2}(1+\sqrt{1+4t_{i-1}^2})$.
16:	end-for
17:	Set T = Ti+1.

Theorem 5.2. Let T* be the global minimizer of Eq. (6); let L̂_f be the best Lipschitz continuous gradient defined in Eq.(7). Denote by k the index of the iteration, and by T_k the solution point at the kth iteration of Algorithm 2. Then we have

$$F\left(T_{k+1}\right)-F\left(T^{\ast }\right)\le \frac{2\widehat{L}}{k^2}{\Vert T_0-T^{\ast }\Vert }_F^2,$$

where L̂ = max{L₀, 2L̂_f}, where L₀ and T₀ are the initial values of L_k and T_k in Algorithm 2, respectively.

Proof. Denote ε_i = F(T_i)–F(T*). Setting T = T_i, S = S_i, and L = L_i in Eq. (16), we have

$${∊}_i-{∊}_{i+1}\ge \langle T_i-S_i,{\mathcal{P}}_{L_i}\left(S_i\right)\rangle +\frac{1}{2L_i}{\Vert {\mathcal{P}}_{L_i}\left(S_i\right)\Vert }_F^2,$$ (32)

where the left side of the inequality above follows from

$$T_{i+1}=T_{L_i,S_i}=\underset{T\in \mathcal{M}}{\text{arg min}}{G}_{L_i}(S_i,T_i).$$

Similarly, setting T = T*, S = S_i, and L = L_i in Eq. (16), we have

$$-{∊}_{i+1}\ge \langle T^{\ast }-S_i,{\mathcal{P}}_{L_i}\left(S_i\right)\rangle +\frac{1}{2L_i}{\Vert {\mathcal{P}}_{L_i}\left(S_i\right)\Vert }_F^2.$$ (33)

Multiplying Eq. (32) by t_i–1 – 1 and summing it with Eq. (33), we have

$$(t_{i-1}-1){\epsilon }_i-t_{i-1}{\epsilon }_{i+1}\ge \langle (t_{i-1}-1)(T_i-S_i)+T^{\ast }-S_i,{\mathcal{P}}_{L_i}\left(S_i\right)\rangle +\frac{t_{i-1}}{2L_i}{\Vert {\mathcal{P}}_{L_i}\left(S_i\right)\Vert }_F^2.$$ (34)

Moreover, multiplying Eq. (34) by t_i–1, we have

$$t_{i-2}^2{\epsilon }_i-t_{i-1}^2{\epsilon }_{i+1}\ge \frac{1}{2L_i}{\Vert t_{i-1}{\mathcal{P}}_{L_i}\left(S_i\right)\Vert }_F^2+\langle t_{i-1}{\mathcal{P}}_{L_i}\left(S_i\right),(t_{i-1}-1)(T_i-S_i)+T^{\ast }-S_i\rangle .$$ (35)

where the left side is obtained via the equation

$$t_{i-1}^2-t_{i-1}=t_{i-2}^2$$

from the line 15 in Algorithm 2. On the other hand, it follows from Eq. (12) we have

$${\mathcal{P}}_{L_i}\left(S_i\right)=L_i(S_i-T_{L_i,S_i})=L_i(S_i-T_{i+1}).$$ (36)

From Eq. (31) and the line 5 in Algorithm 2, we have

$$t_{i-1}{S}_i=t_{i-1}{T}_i+(t_{i-2}-1)(T_i-T_{i-1}).$$ (37)

Denote

$$C_{i-2}=t_{i-2}{T}_i-(t_{i-2}-1)T_{i-1}-T^{\ast }.$$ (38)

From Eqs. (36), (37) and (38), we can verify that

$$t_{i-1}{\mathcal{P}}_{L_i}\left(S_i\right)=t_{i-1}{L}_i(S_i-T_{i+1})=L_i(C_{i-2}-C_{i-1}).$$ (39)

Moreover, we have

$$\begin{array}{cc}\hfill (t_{i-1}-1)(T_i-S_i)+T^{\ast }-S_i& =(t_{i-1}-1)T_i+T^{\ast }-t_{i-1}{S}_i\hfill \\ \hfill & =-t_{i-2}{T}_i+(t_{i-2}-1)T_{i-1}+T^{\ast }=-C_{i-2}.\hfill \end{array}$$ (40)

Substituting Eqs. (39) and (40) into Eq. (35), we obtain

$$\begin{array}{cc}\hfill {\Vert C_{i-1}\Vert }_F^2-{\Vert C_{i-2}\Vert }_F^2& \le \frac{2}{L_i}(t_{i-2}^2{\epsilon }_i-t_{i-1}^2{\epsilon }_{i+1})\hfill \\ \hfill & \le \frac{2}{L_{i-1}}{t}_{i-2}^2{\epsilon }_i-\frac{2}{L_i}{t}_{i-1}^2{\epsilon }_{i+1}.\hfill \end{array}$$ (41)

Summing Eq. (41) from i = 1 to i = k, we have

$${\Vert C_{k-1}\Vert }_F^2-{\Vert C_{-1}\Vert }_F^2\le \frac{2}{L_0}{t}_{-1}^2{\epsilon }_1-\frac{2}{L_k}{t}_{k-1}^2{\epsilon }_{k+1}.$$

Therefore, we have

$$\begin{array}{cc}\hfill \frac{2}{L_k}{t}_{k-1}^2{\epsilon }_{k+1}& \le {\Vert C_{-1}\Vert }_F^2-{\Vert C_{k-1}\Vert }_F^2+\frac{2}{L_0}{t}_{-1}^2{\epsilon }_1\hfill \\ \hfill & \le {\Vert C_{-1}\Vert }_F^2+\frac{2}{L_0}{t}_{-1}^2{\epsilon }_1={\Vert T_0-T^{\ast }\Vert }^2,\hfill \end{array}$$ (42)

where the equality follows from t_–1 = 0 in Algorithm 2. From line 15 in Algorithm 2, we have

$$2t_i=1+\sqrt{1+4t_{i-1}^2}\ge 2t_{i-1}+1.$$ (43)

Summing Eq. (43) from i = 1 to i = k, we have

$$t_k\ge \frac{1}{2}(k+1),\forall k.$$ (44)

Substituting Eq. (44) into Eq. (42), we complete the proof.

The proof of Theorem 5.2 uses standard techniques in [Nemirovski 1995; Nesterov 1998] yet with simplification in several aspects for easy understanding. Note that the convergence rate achieved by Algorithm 2 is optimal among all first-order methods [Nesterov 1998; Nemirovski 1995].

6. EXAMPLE: LEARNING SPARSE AND LOW-RANK PATTERNS WITH LEAST SQUARES LOSS

In this section, we present a concrete example of learning the sparse and low-rank patterns from multiple tasks, i.e., the MTL formulation in Eq. (5) using the least squares loss function; we also illustrate the use of the PG and AG algorithms in this case. Mathematically, the specific MTL formulation can be expressed as

$$\begin{array}{cc}\hfill \underset{P,Q}{\text{min}}& {\Vert {(P+Q)}^{T}X-Y\Vert }_F^2+\gamma {\Vert P\Vert }_1\hfill \\ \hfill \text{subject to}& {\Vert Q\Vert }_{\ast }\le \tau ,\hfill \end{array}$$ (45)

where $X=[x_1,x_2,\cdots ,x_n]\in {\mathbb{R}}^{d\times n}$, and $Y=[y_1,y_2,\cdots ,y_n]\in {\mathbb{R}}^{m\times n}$. For simplicity in Eq. (45) we assume that all of the m tasks share the same set of training data, and the derivation below can be easily extended to the case where each learning task has a different set of training data.

6.1 Efficient Computation for the Key Component

The computation of Eq. (11) is involved at each iteration of the projected gradient scheme. For the specifical MTL formulation in Eq. (45), given the intermediate solution pair {P_i, Q_i} at the i-th iteration, the subsequent solution pair {P_i+1, Q_i+1} can be obtained via

$$\begin{array}{cc}\hfill \underset{\widehat{P},\widehat{Q}}{\text{min}}& \frac{L_i}{2}{\Vert \widehat{P}-{\tilde{P}}_i\Vert }_F^2+\frac{L_i}{2}{\Vert \widehat{Q}-{\tilde{Q}}_i\Vert }_F^2+\gamma {\Vert \widehat{P}\Vert }_1\hfill \\ \hfill \text{subject to}& {\Vert \widehat{Q}\Vert }_{\ast }\le \tau ,\hfill \end{array}$$ (46)

where L_i specifies the step size of the i-th iteration. The optimal P̂ and Q̂ to Eq. (46) can be obtained via solving two separate problems as below.

Computation of P̂ The optimal P̂ can be obtained via solving

$$\underset{\widehat{P}}{\text{min}}\frac{L_i}{2}{\Vert \widehat{P}-{\tilde{P}}_i\Vert }_F^2+\gamma {\Vert \widehat{P}\Vert }_1.$$ (47)

Based on the results in Section 4.1, the optimization problem in Eq. (47) can be further decomposed into entry-wise subproblems in the form of Eq. (23), which admits an analytical solution (Lemma 4.1).

Computation of Q̂ The optimal Q̂ can be obtained via solving

$$\begin{array}{cc}\hfill \underset{\widehat{Q}}{\text{min}}& {\Vert \widehat{Q}-{\tilde{Q}}_i\Vert }_F^2\hfill \\ \hfill \text{subject to}& {\Vert \widehat{Q}\Vert }_{\ast }\le \tau .\hfill \end{array}$$ (48)

Based on the results in Section 4.2, the optimal solution to Eq. (48) can be obtained via the following two steps:

• —Compute the SVD of ${\tilde{Q}}_i=U_{Q_i}{\Sigma }_{Q_i}{V}_{Q_i}^T$, where $\text{rank}\left({\tilde{Q}}_i\right)=q,U_{Q_i}\in {\mathbb{R}}^{d\times q}$, $V_{Q_i}\in {\mathbb{R}}^{m\times q}$, and ${\Sigma }_{Q_i}=\text{diag}({\widehat{\varsigma }}_1,\cdots {\widehat{\varsigma }}_q)\in {\mathbb{R}}^{q\times q}$.

• —Compute the optimal solution ${\left\{{\sigma }_i^{\ast }\right\}}_{i=1}^q$ to the following problem

  $$\begin{array}{cc}\hfill \underset{{\left\{{\sigma }_i\right\}}_{i=1}^q}{\text{min}}& \sum _{i=1}^q{({\sigma }_i-{\widehat{\varsigma }}_i)}^2\hfill \\ \hfill \text{subject to}& \sum _{i=1}^q{\sigma }_i\le \tau ,{\sigma }_i\ge 0.\hfill \end{array}$$

The optimal Q̂ can be constructed as $\widehat{Q}=U_{Q_i}{\Sigma }_Q{V}_{Q_i}^T$, where ${\Sigma }_Q=\text{diag}({\sigma }_1^{\ast },\cdots {\sigma }_q^{\ast })$.

6.2 Estimation of the Lipschitz Constant

An appropriate step size 1/L in Eq. (13) is important for the global convergence of the projected gradient based algorithms and its value can be estimated via many sophisticated line search schemes [Boyd and Vandenberghe 2004] in general. In Algorithm 1 (lines 6 ~ 7) and Algorithm 2 (lines 9 ~ 10), the value of L is updated until the inequality in Eq. (15) is satisfied; however, this updating procedure may incur overhead cost in the computation.

Denote the smooth component of the objective function in Eq. (45) by

$$f(P,Q)={\Vert {(P+Q)}^{T}X-Y\Vert }_F^2.$$ (49)

It can be verified that any Lipschitz constant L_f of the function f(P, Q) can satisfy Eq. (15). Note that the gradient of f(P, Q) with respect to P and Q can be expressed as

$${\nabla }_{P}f(P,Q)={\nabla }_{Q}f(P,Q)=2(X{X}^T(P+Q)-X{Y}^T).$$

To avoid the computational cost of estimating the lipschitz constant for f(P, Q), we directly estimate its best value (the smallest lipschitz constant), as summarized in the following lemma.

Lemma 6.1. Given $X\in {\mathbb{R}}^{d\times n}$ and $Y\in {\mathbb{R}}^{m\times n}$, the best Lipschitz constant L̂_f of the function f(P, Q) in Eq. (49) is no larger than $2{\sigma }_X^2$, where σ_X denotes the largest singular value of X.

Proof. For arbitrary $P_x,P_y,Q\in {\mathbb{R}}^{d\times m}$, we have

$$\begin{array}{cc}\hfill {\widehat{L}}_P=\frac{{\Vert {\nabla }_{P_x}f(P_x,Q)-{\nabla }_{P_y}f(P_y,Q)\Vert }_F}{{\Vert P_x-P_y\Vert }_F}& =\frac{{\Vert 2X{X}^T(P_x-P_y)\Vert }_F}{{\Vert P_x-P_y\Vert }_F}\hfill \\ \hfill & \le \frac{2{\sigma }_X^2{\Vert (P_x-P_y)\Vert }_F}{{\Vert P_x-P_y\Vert }_F}=2{\sigma }_X^2.\hfill \end{array}$$ (50)

Similarly, for arbitrary $P,Q_x,Q_y\in {\mathbb{R}}^{d\times m}$, we have

$${\widehat{L}}_Q=\frac{{\Vert {\nabla }_{Q_x}f(P,Q_x)-{\nabla }_{Q_y}f(P,Q_y)\Vert }_F}{{\Vert Q_x-Q_y\Vert }_F}\le 2{\sigma }_X^2.$$ (51)

Therefore it follows from Eq. (7) that

$${\widehat{L}}_f\le \text{max}\left({\widehat{L}}_P,{\widehat{L}}_Q\right)=2{\sigma }_X^2.$$ (52)

This completes the proof.

6.3 Main Algorithms

The pseudo-codes of the PG and AG algorithms for solving Eq. (45), i.e., Eq. (5) with the least squares loss, are presented in Algorithm 3 and Algorithm 4 respectively. The main difference between PG and AG lies in the construction of S_Pi and S_Qi: in line 4 of Algorithm 3, S_Pi and S_Qi are set as the pair of feasible points from the previous iteration; in line 6 of Algorithm 4, S_Pi and S_Qi are set as the a linear combination of the feasible points from the previous and the current iterations, which are not necessarily feasible in Eq. (45). The different construction leads to different rates of convergence, i.e., $\mathcal{O}(1∕k)$ in Algorithm 3 and $\mathcal{O}(1∕k^2)$ in Algorithm 4.

Algorithm 3.

Projected Gradient Algorithm (PG) for Solving Eq. (45)

1:	Input: P0, Q0, $L=2{\sigma }_X^2$, and max-iter.
2:	Output: P, Q.
3:	for i = 0, 1, · · · , max-iter do
4:	Set Li = L, SPi = Pi, SQi = Qi.
5:	Compute P̃i = SPi – ∇P f (P, Q)|P=SPi,Q=SQi,
6:	Q̃i = SQi – ∇Q f (P, Q)|P=SPi,Q=SQi.
7:	Compute P̂ via Eq. (47) and Q̂ via Eq. (48).
8:	Set Pi+1 = P̂, Qi+1 = Q̂.
9:	if the stopping criterion is satisfied then exit the loop.
10:	end-for
11:	Set P = Pi+1, Q = Qi+1.

Algorithm 4.

Accelerated Projected Gradient Algorithm (AG) for Solving Eq. (45)

1:	Input: P0, Q0, $L=2{\sigma }_X^2$, and max-iter.
2:	Output: P, Q.
3:	Set P1 = P0, Q1 = Q0, t–1 = 0 and t0 = 1.
4:	for i = 1, 2, · · · , max-iter do
5:	Compute αi = (ti–2 – 1)/ti–1.
6:	Set Li = L, SPi = (1 + αi)Pi – αiPi–1, SQi = (1 + αi)Qi – αiQi–1.
7:	Compute P̃i = SPi – ∇P f (P, Q)|P=SPi,Q=SQi,
8:	Q̃i = SQi – ∇Q f (P, Q)|P=SPi,Q=SQi.
9:	Compute P̂ via Eq. (47), and Q̂ via Eq. (48).
10:	Set Pi+1 = P̂, Qi+1 = Q̂.
11:	if the stopping criterion is satisfied then exit the loop.
12:	Update $t_i=\frac{1}{2}(1+\sqrt{1+4t_{i-1}^2})$.
13:	end-for
14:	Set P = Pi+1,Q = Qi+1.

7. EMPIRICAL EVALUATIONS

In this section, we evaluate the proposed multi-task learning formulation (MixedNorm) in comparison with other seven representative methods; we also conduct numerical studies on the proposed projected gradient based algorithms. The employed optimization algorithms are implemented in MATLAB.

We employ six benchmark data sets in our experiments. One of them is AR Face Data [Martinez and Benavente 1998]: we use a subset consisting of 1400 face images corresponding to 100 persons. The other three are LIBSVM multi-label data sets¹: for Scene and Yeast, we use the entire data sets; for MediaMill, we generate several subsets by randomly sampling 8000 data points with different numbers of labels. References and Science are Yahoo webpages data sets [Ueda and Saito 2002]: we preprocess the data sets following the same procedures in [Chen et al. 2009]. All of the benchmark data sets are normalized and their statistics are summarized in Table I. Note that in our multi-task learning setting, each task corresponds to a label and we employ the least squares loss function for the following empirical studies.

Table I.

Statistics of the benchmark data sets.

Data Set	Sample Size	Dimension	Task Number	Type
Face	1400	19800	100	image
Scene	2407	294	6	image
Yeast	2417	103	14	gene
MediaMill1	8000	120	80	multimedia
MediaMill2	8000	120	100	multimedia
References	7929	26397	15	text
Science	6345	24002	22	text

7.1 Demonstration of Extracted Structures

We apply the proposed multi-task learning algorithm on synthetic data and face data to demonstrate the extracted sparse and low-rank structures.

Demonstration on Synthetic Data

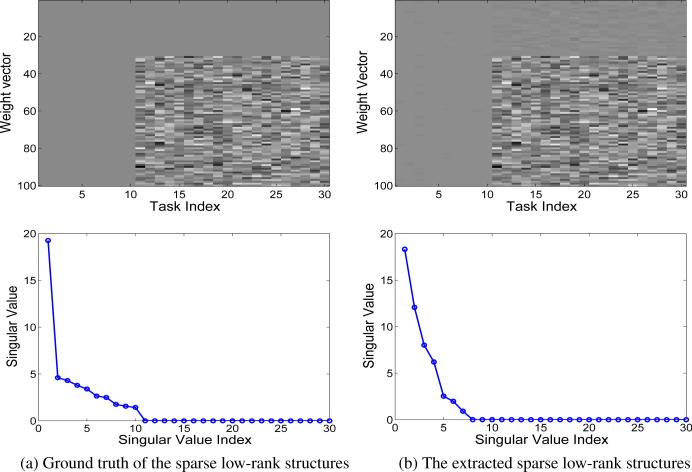
We apply the proposed multi-task learning algorithm on a synthetic data and also demonstrate the extracted sparse and low-rank structures. The synthetic data is constructed as follows: set the task number m = 30, the training sample size of each task $n_{\ell }=60$, and the training sample dimensionality d = 100; generate the entries of the training data (of the $\ell \text{-th}$ task) $X^{\ell }=[x_1^{\ell },\cdots ,x_{n_{\ell }}^{\ell }]\in {\mathbb{R}}^{d\times n_{\ell }}$ from $\mathcal{N}(0,25)$; generate the entries of the sparse component P = [p₁, · · · , p_k] (of size k × d) from $\mathcal{N}(0,100)$ and then set the entries of its first 10 rows and its first 30 columns as zero; generate the entries of the low-rank component Q = [q₁, · · · , q_k] (of size k × d) from $\mathcal{N}(0,9)$ and then set its smallest 20 singular values as zero; construct the response vector of each task as $y^{\ell }=X^{{\ell }^T}(p_{\ell }+q_{\ell })+{\delta }^{\ell }\in {\mathbb{R}}^{n_{\ell }}$, where the entries in ${\delta }^{\ell }$ are generated from $\mathcal{N}(0,1)$. By this construction, we have 30 related tasks, where each task has 60 training samples of feature dimensionality 100; moreover, the transformation matrix for all 30 tasks consists of a sparse component as well as a low-rank component.

In the left column of Figure 2, we present the ground truth of the sparse and low-rank structures; in the right column we present the extracted sparse and low-rank structures via solving Eq. (45) with γ = 150 and τ = 50. From the first row of the plots in Figure 2, we can observe that the extracted sparse structure (right plot) is similar to the ground truth of the sparse structure (left plot), i.e., most of the entries in the first 10 columns and the first 30 rows of the sparse component are zero; moreover from the second row of the plots, we can observe that the patterns of the extracted low-rank structure (right plot) is similar to the patterns of the ground truth of the low-rank structure (left plot), i.e., they have a similar number of non-zeros singular values. Our observation empirically demonstrates the potential of the proposed multi-task learning formulation for extracting sparse and low-rank structures (of multiple tasks).

Fig. 2.

Demonstration of the sparse and low-rank structures: the left column corresponds to the ground truth (of the sparse structure and the low-rank structure), and the right column corresponds to the extracted (sparse and low-rank) structures from Eq. (45); the first row shows the sparse components, and the second row shows the singular values of the low-rank components.

Demonstration on AR Face Data

We use a subset of AR Face Data for this experiment. The original size of these images is 165 × 120; we reduce the size to 82 × 60. We convert the face recognition problem into a multi-task learning problem, where one task corresponds to learning a linear classifier, i.e., $f_{\ell }\left(x\right)={(p_{\ell }+q_{\ell })}^{T}x$, for recognizing the faces of one person. By solving Eq. (45), we obtained $p_{\ell }$ (sparse structure) and $q_{\ell }$ (low-rank structure); we reshape $p_{\ell }$ and $q_{\ell }$ and plot them in Figure 3. We only plot p₁ and q₁ for demonstration. The first two plots in Figure 3 are obtained by setting γ = 11, τ = 0.08 in Eq. (45): we obtain a sparse structure of 15.07% nonzero entries and a low-rank structure of rank 3; similarly, the last two plots are obtained by setting γ = 14, τ = 0.15, we obtain a sparse structure of 5.35% nonzero entries and a low-rank structure of rank 7. We observe that the sparse structure identifies the important detailed facial marks, and the low-rank structure preserves the rough shape of the human face; we also observe that a larger sparse regularization parameter leads to higher sparsity (lower percentage of the non-zero entries) and a larger rank constraint leads to structures of higher rank.

Fig. 3.

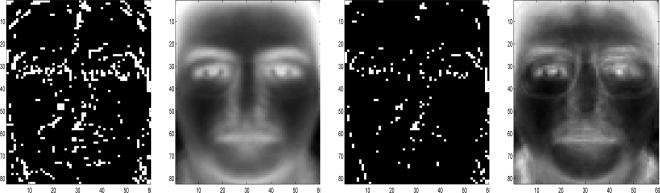
Extracted sparse (first and third plots) and low-rank (second and fourth plots) structures on AR face images with different sparse regularization and rank constraint parameters in Eq. (45): for the first two plots, we set γ = 11, τ = 0.08; for the last two plots, we set γ = 14, τ = 0.15.

7.2 Performance Evaluation

We compare the proposed multi-task learning formulation with other seven representative algorithms including the multi-task relationship learning (MTRL) algorithm [Zhang and Yeung 2010], the multi-task learning with a sparse matrix-normal penalty (MTL[Ω&Σ]) algorithm [Zhang and Schneider 2010], the alternating structure optimization (ASO) algorithm [Ando and Zhang 2005], the least squares with trace norm regularization (TraceNorm) [Ji and Ye 2009; Pong et al. 2010], the least squares with one norm regularization (O-neNorm) [Tibshirani 1996], the independent support vector machines (IndSVM) [Schölkopf and Smola 2002], and the ridge regression (RidgeReg). Note that in [Zhang and Schneider 2010], the authors propose various configurations of their MTL learning formulation; in our experiments, we focus on the most general one, i.e., MTL(Ω&Σ), in which the two covariance matrices are automatically learned.

In this experiment, we employ Average AUC (the averaged area under the curve), Macro F1 (the global calculation of F1 regardless of the tasks), and Micro F1 (the averaged F1 scores of all tasks) as the performance measures [Yang and Pedersen 1997]. The reported experimental results are averaged over five random repetitions of the data sets into training and test sets of a ratio 1 : 9. In this experiment, we stop the iterative procedure of the algorithms if the change of the objective values in two consecutive iterations is smaller than 10^–5 or the iteration numbers larger than 10⁵. The experimental setup is summarized as below. Note that in our experiments, OneNorm, RidgeReg, and IndSVM represent the single task learning (STL) algorithms; they are employed as baseline algorithms; the comparison among MixedNorm, OneNorm, and TraceNorm is used to verify the effectiveness of the combination of OneNorm and TraceNorm.

1. MixedNorm (the proposed multi-task learning formulation with the least squares loss) The trace-norm constraint parameter is tuned in ${\{{10}^{-2}\times i\}}_{i=1}^{10}\cup {\{{10}^{-1}\times i\}}_{i=2}^{10}\cup {\{2\times i\}}_{i=1}^p$, where $p=\lfloor k∕2\rfloor$ and k is the label number; the one-norm regularization parameter is tuned in ${\{{10}^{-3}\times i\}}_{i=1}^{10}\cup {\{{10}^{-2}\times i\}}_{i=2}^{10}\cup {\{{10}^{-1}\times i\}}_{i=2}^{10}\cup {\{2\times i\}}_{i=1}^{10}\cup {\{40\times i\}}_{i=1}^{20}$.

2. MTRL (the multi-task relationship learning formulation) The two regularization parameters (λ₁ and λ₂) in MTRL are tuned in the range ${\{{10}^{-3}\times i\}}_{i=1}^{10}\cup {\{{10}^{-2}\times i\}}_{i=2}^{10}\cup {\{{10}^{-1}\times i\}}_{i=2}^{10}\cup {\{2\times i\}}_{i=1}^{10}\cup {\{40\times i\}}_{i=1}^{20}$.

3. MTL(Ω&Σ) (the multi-task learning formulation with a sparse matrix-normal penalty) Following [Zhang and Schneider 2010], we set ${\lambda }_{\Omega }={\lambda }_{\Sigma }=\widehat{\lambda }$. The two regularization parameters λ and $\widehat{\lambda }$ are tuned in the range ${\{{10}^{-3}\times i\}}_{i=1}^{10}\cup {\{{10}^{-2}\times i\}}_{i=2}^{10}\cup {\{{10}^{-1}\times i\}}_{i=2}^{10}\cup {\{2\times i\}}_{i=1}^{10}\cup {\{40\times i\}}_{i=1}^{20}$.

4. TraceNorm (the formulation of the least squares loss with the trace-norm constraint) The trace-norm constraint parameter is tuned in ${\{{10}^{-2}\times i\}}_{i=1}^{10}\cup {\{{10}^{-1}\times i\}}_{i=2}^{10}\cup {\{2\times i\}}_{i=1}^p$ where $p=\lfloor k∕2\rfloor$ and k denotes the label number.

5. ASO (the alternating structure optimization algorithm) The regularization parameter is tuned in ${\{{10}^{-3}\times i\}}_{i=1}^{10}\cup {\{{10}^{-2}\times i\}}_{i=2}^{10}\cup {\{{10}^{-1}\times 2\}}_{i=1}^{10}\cup {\{2\times i\}}_{i=1}^{10}\cup {\{40\times i\}}_{i=1}^{20}$; the dimensionality of the shared subspace is tuned in ${\{2\times i\}}_{i=1}^p$, where $p=\lfloor k∕2\rfloor$ and k denotes the label number.

6. OneNorm (the formulation of the least squares loss with the one-norm regularization) The one-norm regularization parameter is tuned in ${\{{10}^{-3}\times i\}}_{i=1}^{10}\cup {\{{10}^{-2}\times i\}}_{i=2}^{10}\cup {\{{10}^{-1}\times i\}}_{i=2}^{10}\cup {\{2\times i\}}_{i=1}^{10}\cup {\{40\times i\}}_{i=1}^{20}$

7. IndSVM (independent support vector machines) The regularization parameter is tuned in ${\left\{{10}^{-i}\right\}}_{i=1}^3\cup {\{2\times i\}}_{i=1}^{50}\cup {\{200\times i\}}_{i=1}^{20}$.

8. RidgeReg (ridge regression) The regularization parameter is tuned in ${\{{10}^{-3}\times i\}}_{i=1}^{10}\cup {\{{10}^{-2}\times i\}}_{i=2}^{10}\cup {\{{10}^{-1}\times 2\}}_{i=1}^{10}\cup {\{2\times i\}}_{i=1}^{10}\cup {\{40\times i\}}_{i=1}^{20}$.

The averaged performance (with standard deviation) of the competing algorithms are presented in Table II and Table III. We have the following observations: (1) MixedNorm achieves the best performance among the competing algorithms on all benchmark data sets in this experiment, which gives strong support for our rationale of improving the generalization performance by learning the sparse and low-rank patterns simultaneously from multiple tasks; (2) TraceNorm outperforms OneNorm on Scene and Yeast data sets, which implies that the shared low-rank structure may be important for image and gene classification tasks; meanwhile, OneNorm outperforms TraceNorm on MediaMill and yahoo web-page data sets, which implies that sparse discriminative features may be important for multimedia learning problems; (3) the multi-task learning algorithms in our experiments outperform or perform competitively compared to OneNorm, IndSVM and RidgeReg, which verifies the effect of improved generalization performance via multi-task learning.

Table II.

Average performance (with standard derivation) comparison of eight competing algorithms on three data sets in terms of average AUC (top section), Macro F1 (middle section), and Micro F1 (bottom section). All parameters of the eight methods are tuned via cross-validation, and the reported performance is averaged over five random repetitions.

Data (n, d, m)		Scene (2407, 294, 6)	Yeast (2417, 103, 14)	References (7929, 26397, 15)
Average AUC	MixedNorm	91.602 ± 0.374	79.871 ± 0.438	77.526 ± 0.285
	MTRL	90.821 ± 0.512	78.437 ± 0.610	75.133 ± 0.410
	MTL(Ω&Σ)	90.217 ± 1.139	78.515 ± 0.393	76.249 ± 0.277
	TraceNorm	90.205 ± 0.374	76.877 ± 0.127	71.259 ± 0.129
	ASO	86.258 ± 0.981	64.519 ± 0.633	75.960 ± 0.104
	OneNorm	87.846 ± 0.193	65.602 ± 0.842	75.444 ± 0.074
	IndSVM	84.056 ± 0.010	64.601 ± 0.056	73.882 ± 0.244
	RidgeReg	85.209 ± 0.246	65.491 ± 1.160	74.781 ± 0.556
Macro F1	MixedNorm	60.602 ± 1.383	55.624 ± 0.621	37.135 ± 0.229
	MTRL	58.873 ± 0.814	53.913 ± 0.785	36.492 ± 0.575
	MTL(Ω&Σ)	59.212 ± 0.671	54.854 ± 0.803	36.218 ± 0.157
	TraceNorm	57.692 ± 0.480	52.400 ± 0.623	35.562 ± 0.278
	ASO	56.819 ± 0.214	45.599 ± 0.081	34.462 ± 0.315
	OneNorm	55.061 ± 0.801	42.023 ± 0.120	36.579 ± 0.157
	IndSVM	54.253 ± 0.078	38.507 ± 0.576	31.207 ± 0.416
	RidgeReg	53.281 ± 0.949	42.315 ± 0.625	32.724 ± 0.190
Micro F1	MixedNorm	64.392 ± 0.876	56.495 ± 0.190	59.408 ± 0.344
	MTRL	63.958 ± 0.324	55.127 ± 0.922	58.112 ± 0.322
	MTL(Ω&Σ)	63.219 ± 0.769	54.235 ± 0.318	58.118 ± 1.246
	TraceNorm	61.172 ± 0.838	54.172 ± 0.879	57.497 ± 0.130
	ASO	59.015 ± 0.124	45.952 ± 0.011	55.406 ± 0.198
	OneNorm	59.951 ± 0.072	47.558 ± 1.695	58.798 ± 0.166
	IndSVM	57.450 ± 0.322	52.094 ± 0.297	54.875 ± 0.185
	RidgeReg	56.012 ± 0.144	46.743 ± 0.625	53.713 ± 0.213

Table III.

Average performance comparison of eight competing algorithms on three data sets in terms of average AUC, Macro F1, and Micro F1. See the caption of Table II for detailed explanations.

Data (n, d, m)		Science (6345, 24002,22)	MediaMill1 (8000, 120, 80)	MediaMill2 (8000, 120, 100)
Average AUC	MixedNorm	75.746 ± 1.423	72.571 ± 0.363	65.932 ± 0.321
	MTRL	73.389 ± 0.417	71.447 ± 0.185	64.980 ± 0.522
	MTL(Ω&Σ)	75.165 ± 0.439	70.625 ± 0.570	64.303 ± 0.241
	TraceNorm	71.478 ± 0.293	69.469 ± 0.425	60.882 ± 1.239
	ASO	75.535 ± 1.591	71.067 ± 0.315	65.444 ± 0.424
	OneNorm	74.456 ± 1.076	70.453 ± 0.762	64.219 ± 0.566
	IndSVM	70.220 ± 0.065	67.088 ± 0.231	57.437 ± 0.594
	RidgeReg	69.177 ± 0.863	66.284 ± 0.482	56.605 ± 0.709
Macro F1	MixedNorm	38.281 ± 0.011	9.706 ± 0.229	7.981 ± 0.011
	MTRL	36.320 ± 0.421	8.625 ± 0.507	7.112 ± 0.303
	MTL(Ω&Σ)	38.198 ± 0.348	8.225 ± 0.108	6.785 ± 0.624
	TraceNorm	36.447 ± 0.055	8.562 ± 0.027	6.765 ± 0.039
	ASO	36.278 ± 0.183	8.023 ± 0.196	6.150 ± 0.023
	OneNorm	37.981 ± 0.200	8.579 ± 0.157	6.447 ± 0.133
	IndSVM	35.175 ± 0.177	6.207 ± 0.410	5.175 ± 0.177
	RidgeReg	35.066 ± 0.196	7.724 ± 0.190	5.066 ± 0.096
Micro F1	MixedNorm	52.619 ± 0.042	61.426 ± 0.062	60.117 ± 0.019
	MTRL	51.212 ± 0.165	60.217 ± 0.311	59.443 ± 0.508
	MTL(Ω&Σ)	52.612 ± 1.192	59.578 ± 0.631	59.848 ± 1.140
	TraceNorm	49.124 ± 0.409	59.090 ± 0.117	58.317 ± 1.010
	ASO	49.616 ± 0.406	59.415 ± 0.005	59.079 ± 1.720
	OneNorm	52.733 ± 0.394	60.594 ± 0.026	59.221 ± 0.390
	IndSVM	48.574 ± 0.265	57.825 ± 0.272	56.525 ± 0.317
	RidgeReg	47.454 ± 0.255	57.752 ± 0.210	56.982 ± 0.455

7.3 Sensitivity Study

We conduct sensitivity studies on the proposed multi-task learning formulation, and study how the training ratio and the task number affect its generalization performance.

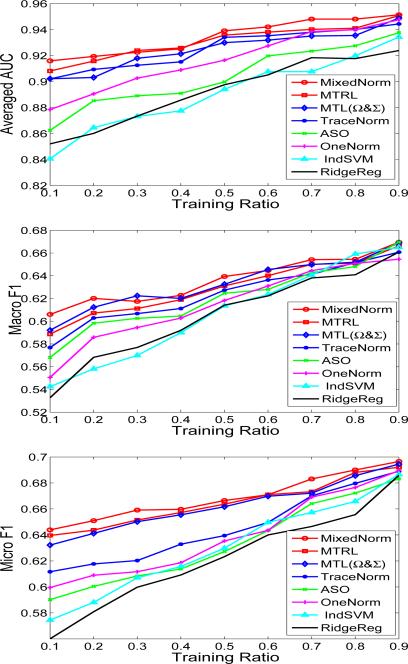
Effect of the training ratio

We use Scene data for this experiment. We vary the training ratio in the set ${\{0.1\times i\}}_{i=1}^9$ and record the obtained generalization performance for each training ratio. The experimental results are depicted in Figure 4. We can observe that (1) for all compared algorithms, the resulting generalization performance improves with the increase of the training ratio; (2) MixedNorm outperforms other competing algorithms in all cases in this experiment; (3) when the training ratio is small (e.g., smaller than 0.5), multi-task learning algorithms can significantly improve the generalization performance compared to IndSVM and RidgeReg; on the other hand, when the training ratio is large, all competing algorithms achieve comparable performance. This is consistent with previous observations that multi-task learning is most effective when the training size is small.

Fig. 4.

Performance comparison of eight multi-task learning algorithms with different training ratios in terms of average AUC (top plot), Macro F1 (middle plot), and Micro F1 (bottom plot). The index on the x-axis corresponds to the training ratio varying from 0.1 to 0.9.

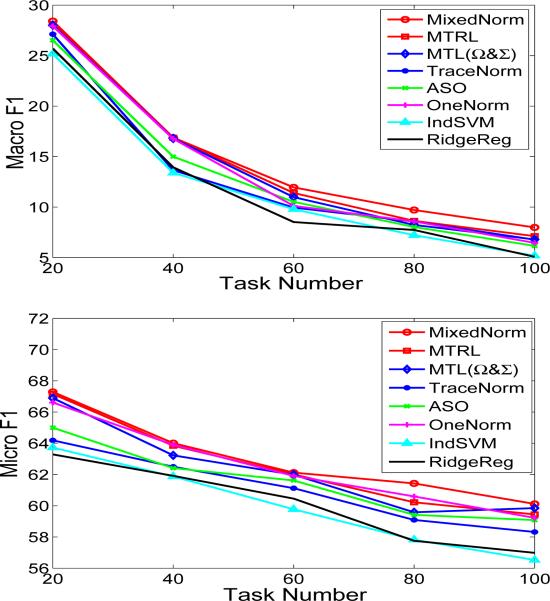
Effect of the task number

We use MediaMill data for this experiment. We generate 5 data sets by randomly sampling 8000 data points with the task number set at 20, 40, 60, 80, 100, respectively; for each data set, we set the training and test ratio at 1 : 9 and record the average generalization performance of the multi-task learning algorithms over 5 random repetitions. The experimental results are depicted in Figure 5. We can observe that (1) for all compared algorithms, the achieved performance decreases with the increase of the task numbers; (2) MixedNorm outperforms or performs competitively compared to other algorithms with different task numbers; (3) all multi-task learning algorithms outperform IndSVM and RidgeReg. Note that the learning problem becomes more difficult as the number of the tasks increases, leading to decreased performance for both multi-task and single-task learning algorithms. We only present the performance comparison in terms of Macro/Micro F1; we observe a similar trend in terms of the average AUC in the experiments.

Fig. 5.

Performance comparison of the eight competing multi-task learning algorithms with different numbers of tasks in terms of Macro F1 (top plot) and Micro F1 (bottom plot).

7.4 Comparison of PG and AG

We empirically compare the projected gradient algorithm (PG) in Algorithm 1 and the accelerated projected gradient algorithm (AG) in Algorithm 2 using Scene data. We present the comparison results with γ = 1, τ = 2 and γ = 6, τ = 4 in Eq. (45); for other parameter settings, we observe similar trends in our experiments.

Comparison on convergence rate

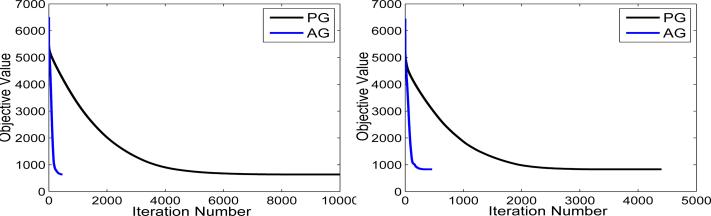
We apply PG and AG for solving Eq. (45) respectively, and compare the relationship between the obtained objective values and the required iteration numbers. The experimental setup is as follows: we terminate the PG algorithm when the change of objective values in two successive steps is smaller than 10^–5 and record the obtained objective value; we then use such a value as the stopping criterion in AG, that is, we stop AG when AG attains an objective value equal to or smaller than the one attained by PG. The experimental results are presented in Figure 6. We can observe that AG converges much faster than PG, and their respective convergence speeds are consistent with the theoretical convergence analysis in Section 5, that is, PG converges at the rate of $\mathcal{O}(1∕k)$ and AG at the rate of $\mathcal{O}(1∕k^2)$, respectively.

Fig. 6.

Convergence rate comparison between PG and AG: the relationship between the objective value of Eq. (45) and the iteration number (achieved via PG and AG, respectively). For the left plot, we set γ = 1, τ = 2; for the right plot, we set γ = 6, τ = 4.

Comparison on computation cost

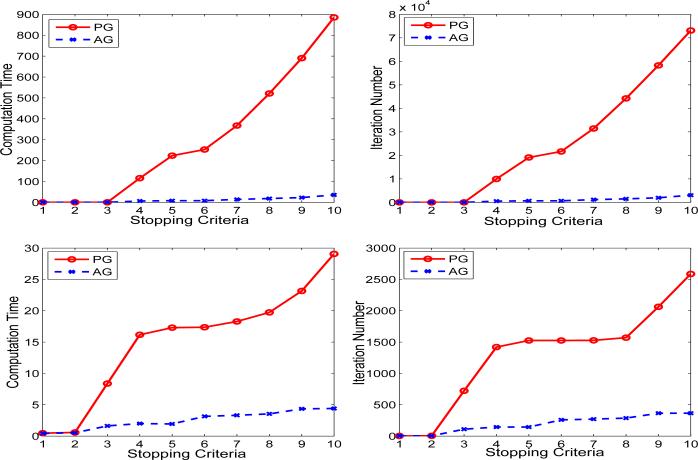
We compare PG and AG in terms of computation time (in seconds) and iteration numbers (for attaining convergence) by using different stopping criteria ${\left\{{10}^{-i}\right\}}_{i=1}^{10}$. We stop PG and AG if the stopping criterion is satisfied, that is, the change of the objective values in two successive steps is smaller than 10^–i. The experimental results are presented in Table IV and Figure 7. We can observe from these results that (1) PG and AG require higher computation costs (more computation time and larger numbers of iterations) for a smaller value of the stopping criterion (higher accuracy in the optimal solution); (2) in general, AG requires lower computation costs than PG in this experiment; such an efficiency improvement is more significant when a smaller value is used in the stopping criterion.

Table IV.

Comparison of PG and AG in terms of computation time (in seconds) and iteration number using different stopping criteria.

	γ = 1, τ = 2				γ = 6, τ = 4
stopping criteria	iteration		time		iteration		time
	PG	AG	PG	AG	PG	AG	PG	AG
10–1	2	2	0.6	0.4	3	3	0.5	0.4
10–2	4	4	0.6	0.4	5	4	0.6	0.5
10–3	17	15	0.6	0.5	722	110	8.4	1.6
10–4	9957	537	116.1	6.5	1420	144	16.2	1.9
10–5	19103	683	223.7	8.3	1525	144	17.3	1.9
10–6	21664	683	253.0	8.3	1525	259	17.4	3.1
10–7	31448	1199	367.9	14.3	1527	271	18.3	3.3
10–8	44245	1491	521.3	18.4	1570	287	19.7	3.5
10–9	58280	1965	690.5	23.0	2062	365	23.1	4.2
10–10	73134	3072	885.4	35.9	2587	365	29.1	4.4

Fig. 7.

Comparison of PG and AG in terms of the computation time in seconds (left column) and the iteration number (right column) with different stopping criteria. The x-axis indexes the stopping criterion from 10^–1 to 10^–10. Note that we stop PG or AG when the change of the objective value in Eq. (45) is smaller than the value of the stopping criterion. For the first row, we set γ = 1, τ = 2; for the second row, we set γ = 6, τ = 4.

7.5 Discussion on Computation Cost of MixedNorm

The proposed multi-task learning formulation (MixedNorm) is formulated as a mathematical programm which minimizes a non-smooth objective function subject to a trace norm constraint. We employ the projected gradient based algorithms to solve MixedNorm (described in Algorithms 3 and 4). From the pseudo-codes, we can observe that the key component for solving MixedNorm lies in the computation of Eq. (46), i.e., Eq. (11) with the least squares loss. Moreover, it follows from Section 6.1 that the dominant computation cost for solving Eq. (46) includes an SVD operation as well as an singular value projection.

To illustrate the trade-off between the computation cost and the generalization performance, we conduct a comparison among MixedNorm, OneNorm, RidgeReg, and IndSVM in terms of the obtained average AUC and the required computation time (in seconds). From Table V, we can observe that MixedNorm requires more computation time; however it leads to significantly better performance in terms of average AUC. It is worth pointing out that our algorithms are implemented in Matlab, while the LIBMSVM package [Chang and Lin 2011] (for solving IndSVM) is implemented in C and highly optimized as well.

Table V.

Comparison of the proposed multi-task learning algorithm and the representative single task learning algorithm in terms of average AUC and computation time (in seconds). Note that data size corresponds to sample size, feature dimensionality, and task number.

	Scene		Reference
Data Size	2406 × 294 × 6		7929 × 26397 × 15
Measures	Average AUC	Computation Time	Average AUC	Computation Time
MixedNorm	91.602	0.5460	77.526	159.868
OneNorm	87.846	0.4836	75.444	141.257
RidgeReg	85.209	0.2496	65.491	80.200
IndSVM	84.056	0.2946	73.882	5.479

7.6 Automated Annotation of the Gene Expression Pattern Images

We apply the proposed multi-task learning formulation for the automated annotation of the Drosophila gene expression pattern images from the FlyExpress² database. Note that for this biological application, we focus on comparing the performance of MixedNorm and its special cases, i.e., OneNorm and TraceNorm; we also use the single task learning algorithms, i.e., OneNorm, IndSVM, and RidgeReg, as baselines. The Drosophila gene expression pattern images capture the spatial and temporal dynamics of gene expression and hence facilitate the explication of the gene functions, interactions, and networks during Drosophila embryogenesis [Fowlkes et al. 2008; Lécuyer et al. 2007]. To provide text-based pattern searching, the gene expression pattern images are annotated manually using a structured controlled vocabulary (CV) in small groups based on the genes and the developmental stages as shown in Table VI. However, with a rapidly increasing number of gene expression pattern images, it is desirable to design computational approaches to automate the CV annotation process.

Table VI.

Sample images and the associated controlled vocabulary (CV) terms in FlyExpress database.

Stage Range	7 ~ 8	11 ~ 12
Gene	Pfrx	Ran
Images Groups
CV Terms	anterior endoderm anlage dorsal ectoderm primordium head mesoderm primordium P4 mesectoderm primordium posterior endoderm primordium P2 procephalic ectoderm anlage trunk mesoderm primordium P2 ventral ectoderm primordium P2 ventral nerve cord anlage visual anlage	anterior midgut primordium brain primordium posterior midgut primordium ventral nerve cord primordium

We preprocess the Drosophila gene expression pattern images (of the standard size 128 × 320) from the FlyExpress database following the procedures in [Ji et al. 2009]. The Drosophila images are from 16 specific stages, which are then grouped into 6 stage ranges (1 ~ 3, 4 ~ 6, 7 ~ 8, 9 ~ 10, 11 ~ 12, 13 ~ 16). We manually annotate the image groups (based on the genes and the developmental stages) using the structured CV terms. Each image group is then represented as a feature vector based on the bag-of-words and the soft-assignment sparse coding. Note that the SIFT features [Lowe 2004] are extracted from the images with the patch size set at 16 × 16 and the number of visual words in sparse coding set at 2000. The first stage range only contains 2 CV terms and we do not report the performance for this stage range. For other stage ranges, we consider the top 10 and 20 CV terms that appear most frequently in the image groups and treat the annotation of each CV term as one task. We generate 10 subsets for this experiment, and randomly partition each subset into training and test sets using the ratio 1 : 9. Note that the parameters in the competing algorithms are tuned following the experimental setting in Section 7.2.

We report the averaged AUC (Avg. AUC), Macro F1 (Mac. F1), and Micro F1 (Mic. F1) over 10 random repetitions in Table VII (for 10 CV terms) and Table VIII (for 20 CV terms), respectively. We can observe that MixedNorm achieves the best performance among the five algorithms on all subsets. In particular, MixedNorm outperforms its special cases, i.e., OneNorm and TraceNorm; MixedNorm also outperforms other single-task learning algorithms: IndSVM and RidgeReg. The experimental results demonstrate the effectiveness of learning the sparse and low-rank patterns from multiple tasks for improved generalization performance.

Table VII.

Performance comparison of five competing algorithms for the gene expression pattern images annotation (10 CV terms) in terms of average AUC (top section), Macro F1 (middle section), and Micro F1 (bottom section). All parameters of the six methods are tuned via cross-validation, and the reported performance is averaged over five random repetitions. Note that n, d, and m denote the sample size, dimensionality, and term (task) number, respectively.

Stage Range (n, d, m)		4 ~ 6 (925, 2000, 10)	7 ~ 8 (797, 2000, 10)	9 ~ 10 (919 , 2000 , 10 )	11 ~ 12 (1622, 2000, 10)	13 ~ 16 (2228, 2000, 10)
Avg. AUC	MixedNorm	75.44 ± 0.87	75.55 ± 0.42	77.18 ± 0.50	83.82 ± 0.93	85.54 ± 0.25
	OneNorm	74.98 ± 0.12	73.80 ± 0.55	75.80 ± 0.24	82.78 ± 0.27	84.77 ± 0.20
	TraceNorm	73.04 ± 0.79	74.06 ± 0.46	76.71 ± 0.72	81.77 ± 1.10	83.64 ± 0.27
	IndSVM	71.00 ± 0.53	72.13 ± 0.70	73.58 ± 0.48	79.01 ± 0.58	82.06 ± 1.04
	RidgeReg	72.46 ± 0.15	72.51 ± 0.82	73.10 ± 0.38	80.83 ± 0.67	82.02 ± 0.15
Mac. F1	MixedNorm	43.71 ± 0.32	48.31 ± 0.56	53.11 ± 0.56	61.11 ± 0.58	61.81 ± 0.40
	OneNorm	42.24 ± 0.14	47.40 ± 0.23	51.04 ± 0.10	59.36 ± 0.60	61.02 ± 0.10
	TraceNorm	41.38 ± 0.36	46.51 ± 0.67	51.13 ± 0.95	61.05 ± 0.78	60.15 ± 0.45
	IndSVM	40.88 ± 0.49	46.73 ± 0.51	50.28 ± 0.65	59.82 ± 0.83	59.62 ± 0.94
	RidgeReg	41.65 ± 0.45	46.91 ± 0.94	50.69 ± 0.77	59.46 ± 0.95	60.59 ± 0.79
Mic. F1	MixedNorm	46.98 ± 0.90	62.73 ± 0.93	63.46 ± 0.07	69.31 ± 0.37	67.13 ± 0.41
	OneNorm	44.55 ± 0.38	60.02 ± 0.56	61.78 ± 0.10	68.54 ± 0.17	66.30 ± 0.55
	TraceNorm	43.88 ± 0.73	61.29 ± 0.78	61.33 ± 1.04	68.68 ± 0.27	66.37 ± 0.26
	IndSVM	42.05 ± 0.61	60.09 ± 0.78	60.57 ± 0.75	67.08 ± 0.99	65.95 ± 0.80
	RidgeReg	43.63 ± 0.41	59.95 ± 0.75	60.59 ± 0.66	66.87 ± 0.11	65.67 ± 1.10

Table VIII.

Performance comparison of five competing algorithms for the gene expression pattern images annotation (20 CV terms).

Stage Range (n, d, m)		4 ~ 6 (1023, 2000, 20)	7 ~ 8 (827, 2000, 20)	9 ~ 10 (1015, 2000, 20)	11 ~ 12 (1940, 2000, 20)	13 ~ 16 (2476, 2000, 20)
Avg. AUC	MixedNorm	76.27 ± 0.53	72.03 ± 0.63	73.97 ± 1.10	82.27 ± 0.42	82.16 ± 0.16
	OneNorm	75.13 ± 0.03	70.95 ± 0.14	72.49 ± 1.00	81.73 ± 0.36	81.03 ± 0.08
	TraceNorm	74.69 ± 0.39	69.43 ± 0.46	71.59 ± 0.79	81.53 ± 0.16	80.88 ± 1.10
	IndSVM	73.82 ± 0.78	69.74 ± 0.19	70.84 ± 0.85	80.86 ± 0.56	79.94 ± 0.19
	RidgeReg	74.66 ± 1.44	70.77 ± 0.62	69.36 ± 1.44	80.40 ± 0.43	78.29 ± 0.42
Mac. F1	MixedNorm	31.90 ± 0.11	31.13 ± 0.68	32.28 ± 1.13	43.48 ± 0.39	43.44 ± 0.60
	OneNorm	30.48 ± 0.12	30.07 ± 0.56	30.50 ± 1.13	41.89 ± 0.24	42.64 ± 0.47
	TraceNorm	29.22 ± 0.31	30.24 ± 0.78	31.28 ± 0.54	42.07 ± 0.67	41.11 ± 0.52
	IndSVM	29.47 ± 0.46	28.85 ± 0.62	30.03 ± 1.68	41.63 ± 0.58	40.80 ± 0.66
	RidgeReg	28.92 ± 1.24	28.76 ± 0.95	29.94 ± 1.84	41.51 ± 0.39	40.84 ± 0.40
Mic. F1	MixedNorm	42.50 ± 0.63	57.04 ± 0.13	57.37 ± 0.71	61.97 ± 0.51	56.75 ± 0.40
	OneNorm	40.80 ± 0.48	56.55 ± 0.22	56.82 ± 0.04	60.59 ± 0.32	55.87 ± 0.11
	TraceNorm	41.26 ± 1.16	56.47 ± 0.27	55.37 ± 0.38	59.27 ± 0.93	54.08 ± 0.51
	IndSVM	39.24 ± 0.82	55.40 ± 0.15	55.75 ± 1.70	58.33 ± 0.53	53.61 ± 0.36
	RidgeReg	38.46 ± 0.41	56.08 ± 0.46	54.23 ± 0.85	59.13 ± 0.67	53.75 ± 0.31

8. CONCLUSION

We consider the problem of learning sparse and low-rank patterns from multiple related tasks. We propose a multi-task learning formulation in which the sparse and low-rank patterns are induced respectively by a cardinality regularization term and a low-rank constraint. The proposed formulation is non-convex; we convert it into its tightest convex surrogate and then propose to apply the general projected gradient scheme to solve such a convex surrogate. We present the procedures for computing the projected gradient and ensuring the global convergence of the projected gradient scheme. Moreover, we show that the projected gradient can be obtained via solving two simple convex subproblems. We also present two detailed projected gradient based algorithms and analyze their rates of convergence. Additionally, we illustrate the use of the presented projected gradient algorithms for the proposed multi-task learning formulation using the least squares loss. Our experiments demonstrate the effectiveness of the proposed multi-task learning formulation and the efficiency of the proposed projected gradient algorithms. In the future, we plan to conduct a theoretical analysis on the proposed multi-task learning formulation and apply the proposed algorithm to other real-world applications.