Abstract
Probing biomolecules at the single-molecule level can provide useful information about molecular interactions, kinetics and motions that is usually hidden in ensemble measurements. Techniques with improved sensitivity and time resolution are required to explore fast biomolecular dynamics. Here, we report the first observation of DNA hybridization at the single-molecule level using a carbon nanotube field-effect transistor. By covalently attaching a single-stranded probe DNA sequence to a point defect in a carbon nanotube, we are able to measure two-level fluctuations in the nanotube conductance due to reversible hybridizing and melting of a complementary DNA target. The kinetics are studied as a function of temperature, allowing the measurement of rate constants, melting curves and activation energies for different sequences and target concentrations. The kinetics show non-Arrhenius behavior, in agreement with DNA hybridization experiments using fluorescence correlation spectroscopy. This technique is label-free and has the potential for studying single-molecule dynamics at sub-microsecond time-scales.
Studies at the single molecule level have revealed intramolecular dynamics and conformational changes in many biomolecular systems. The intramolecular chain diffusion of nucleic acids, particularly the hairpin configuration, has been extensively studied by optical techniques such as fluorescence correlation spectroscopy (FCS)1-3. In these studies, labels are attached to the DNA hairpin and the opening and closing rates of a small number of molecules can be monitored at sub-microsecond time-scales. One of the disadvantages of FCS, however, is that observation time is limited to the diffusion time of molecules through the observation volume4. Single-molecule fluorescence resonance energy transfer (smFRET) has also been used to study conformational changes in biomolecules5 but provides only tens of millisecond time-scales for kinetic studies. Label-free technologies for biomolecular detection include nanowires6, microcavities7, mechanical cantilevers8, optical waveguides9 and optical tweezers10, but none have combined high enough sensitivity for label-free detection with the high temporal resolution necessary to monitor the kinetics of biomolecular processes to sub-microsecond time-scales.
One-dimensional (1D) conductors such as single-walled carbon nanotubes (SWCNTs) act as high-gain field-effect sensors whose conductance varies strongly with local charge density. However, initial experiments with both specific adsorption with coated nanotubes11 and non-specific adsorption with pristine nanotubes12 have not demonstrated sufficient sensitivity to detect single biomolecules with the highest reported sensitivity for DNA detection of 14 pM12. Other studies have employed carbon nanotubes as electrodes. Small gaps are etched into the tubes, bridged by molecular junctions, the conductance of which is monitored for sensing. These devices are able to distinguish between fully complementary bridging DNA duplexes and ones with a single mismatch but DNA hybridization kinetics could not be measured13.
Recently it has been shown that single point defects can be electrochemically created in nanotubes in a controllable manner and can be used to covalently bind biomolecules at the scattering site14. The resulting device has been demonstrated to exhibit sensitivity to the binding of a single molecule (with a conductance change of more than 100 nS for binding of a reactive carbodiimide), due to Coulomb interaction between the molecule and the defect which modulates scattering in the 1D channel15. Compared with molecular-bridge devices, these devices can be prepared with much higher yield due to the real-time monitoring of conductance during defect generation. In this report, we exploit such defect-dominated conductance in nanotubes to produce the first measurements of DNA hybridization kinetics in which sufficiently high signal-to-noise ratio (SNR) and bandwidth have been achieved to measure single-molecule kinetics and thermodynamics through a label-free field-effect-based approach.
Carbon-nanotube transistors are fabricated using standard fabrication techniques. Nanotubes with a diameter less than 2 nm are grown by chemical vapor deposition16 on degenerately doped silicon wafers with 300 nm of thermally grown silicon oxide and contacted by multiple titanium electrodes using optical lithography. Oxygen plasma ion etching is used on a selectively exposed area in a second lithography step to electrically isolate neighboring devices, leaving only one nanotube between a pair of electrodes. After fabrication, the devices are placed in an electrochemical cell, contacted by fixed wire-bonds that are encapsulated with epoxy and sealed with a small glass tube. A platinum counter electrode is used in a pseudo-reference configuration to control the liquid potential both during oxidation and in subsequent aqueous experiments15,17.
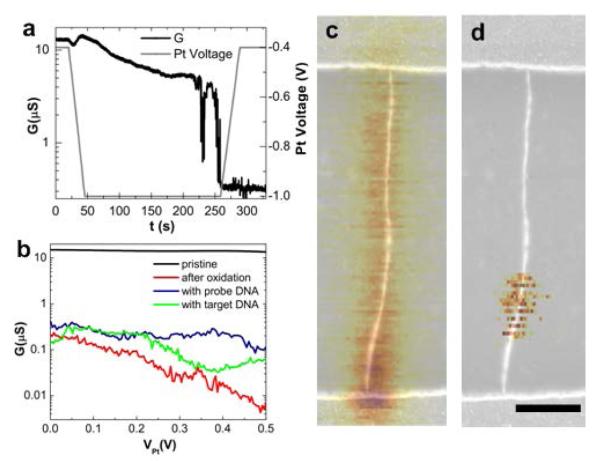
The point functionalization of the nanotubes is achieved similarly to the electrochemical method described previously14. An oxidation potential, slightly greater than the oxidation threshold (between −0.9 and −1V), is applied through the platinum electrode in sulfuric acid (1M H2SO4 in deionized water) until a sharp drop in the nanotube conductance down to about 10% of the original conductance is observed. When we terminate oxidation at a 90% reduction in the conduction level, we find that 88% (23 out of 26) of the devices remain conductive out of which 19% yield functional single molecule devices for measuring DNA hybridization kinetics. At a greater than 99% reduction in the conductance level14, the percentage of conductive devices decreased to 18% (7 out of 38) out of which 28% yield functional single molecule devices. We attribute the low yield in this final step to a number of factors including the possibility of generating unreactive C-O and C=O defects18, multiple reactive defects and over-oxidation that yields insulating devices. Fig. 1a shows a typical conductance-controlled oxidation. After the drop in device conductance, the oxidation potential is reduced and the device is immersed in 6.5 mM KMnO4 in order to create a carboxyl functional group on the freshly created defect. Overall, we fabricated seven functional devices (out of 64), which are characterized by the two-level conductance fluctuations described below when functionalized with probe DNA in the presence of complementary target.
Figure 1. Electrochemical oxidation of carbon nanotube.
a, Conductance-controlled oxidation of nanotube in 1 M H2SO4 with 30 mV bias. b, Conductance as a function of potential on Pt electrode relative to the source-drain potential of the nanotube (VPt) at different stages in the process: before oxidation, after oxidation, after overnight coupling with probe DNA and after exposure to target DNA at 100 mV source-drain bias. Initially the nanotube is metallic but shows large gate response after oxidation. c,d, A combined topography/SGM image of a semiconducting nanotube. Scale bar is 500 nm. In the overlayed SGM image, the darker yellow color corresponds to lower current at a fixed bias voltage of 100 mV. Before oxidation (c) current is enhanced near the source where the Schottky barrier forms. After oxidation (d) the well localized region of highest sensitivity shows up in the middle of the tube, indicating the defect site.
We investigate the local defects generated by this process using scanning gate microscopy (SGM) of the nanotube before and after oxidation14,19. By applying a local gate through the cantilever of an AFM to a small region of the nanotube while monitoring the conductance, we can spatially map out the sensitivity of the conductance to local gating. The spatial resolution of this technique is expected to be around 50 nm. Fig. 1c and 1d show an SGM image overlaid with the device topography before and after oxidation, respectively. This device is a semiconducting nanotube, and Fig. 1c shows that the Schottky barriers20 at the contacts dominate the device’s gate sensitivity. After oxidation, however, the sensitivity is localized to the location of the defect on the nanotube and no longer depends on the initial band structure. Both metallic and semiconducting nanotube devices have been used and they generally show large gate dependence after oxidation. A representative current-voltage (I-V) characteristic is shown in Fig. 1b of a device in its pristine state and after oxidation.
Devices are used to study the kinetics and thermodynamics of DNA hybridization for two different 10mer duplex DNAs. Probe DNA, terminated with an amine group and a three-carbon linker at the 5′ end is covalently attached to the carboxyl defect on the nanotube through a standard coupling reaction using sulfo-N-hydroxysuccinimide (sulfo-NHS) and 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDCI). After thoroughly rinsing the device with de-ionized water, all subsequent measurements are carried out in phosphate buffered saline solution (1X PBS pH=7.4). After attaching the probe DNA to the point defect in the nanotube, we surround the setup with a thermal water bath (±0.1 °C). When thermal equilibrium is reached (~10 minutes), we monitor the device conductance for periods of 10 minutes at different temperatures. Without the presence of target DNA, the devices show no particular features in a conductance dominated by flicker (1/f) noise (Supplementary Fig. S2 and S10). The intrinsic bandwidth of the device is approximately 10 kHz but we apply external measurement filters to reduce the bandwith to 5 kHz for the measurements presented here. This results in an overall input-referred noise level of 450 pArms at 100 mV source to drain bias (Supplementary Table S1).
When the device is immersed in buffer containing 1 μM target DNA, however, large-amplitude two-level fluctuations appear as shown in Fig. 2a with a conductance difference of approximately 70-100 nS, well above the noise floor to give a signal-to-noise ratio (SNR) of approximately 15-22. Control devices without probe DNA modifications do not show this conductance behavior either before or after the addition of target DNA (Supplementary Fig S7). Neither AFM nor SGM techniques have enough spatial resolution to determine if the change in the device happens at a single bond or if only a single DNA molecule covalently attaches to the nanotube. However, because of the strong two-level fluctuations, we conclude that only a single DNA interaction dominates the conductance modulation and the fluctuations are fit to a two-level model.
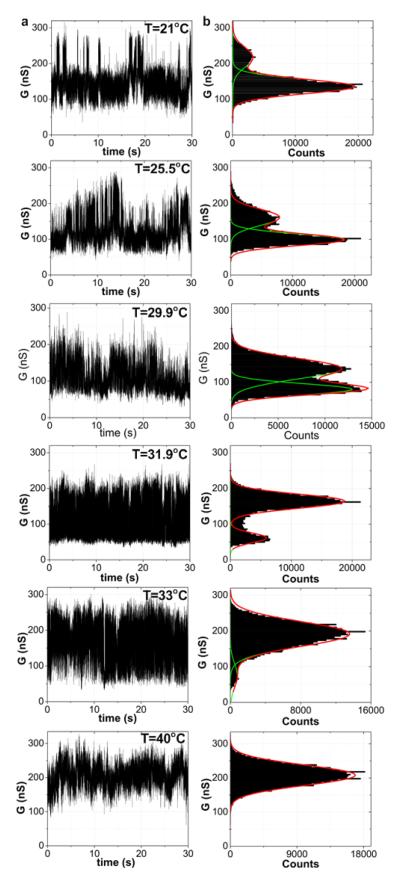
Figure 2. Real time measurements of DNA kinetics.
a, Conductance recordings of Device 1 over one-minute interval with DNA oligonucleotide probe NH2-5′-GGAAAAAAGG-3′ (A6) after exposure to complementary DNA target in 1X PBS. The temperature is varied from 21 to 40°C at 100 mV source-drain bias and zero VPt. b, Conductance-based histograms of time intervals shown in Fig. 2a. The two levels are fit to Gaussian distributions.
In Fig. 2a, the real time conductance data of a representative device (Device 1) is shown with the probe ssDNA NH2-5′-GGAAAAAAGG-3′ (probe A6) and 1 μM complementary target ssDNA. The low-conductance state, which dominates at low temperature, represents a device with duplex DNA, while the high-conductance state, which dominates at high temperatures and prior to the addition of target DNA, represents a device containing unbound probe DNA. Around the melting temperature (~28 °C), the two states are similarly occupied. This result is consistent with other observations that target DNA reduces conductance through a nanotube12 due to increased scattering and charge transfer. We can relate the conductance modulation to a change in the transmission probability at the defect using the Landauer-Büttiker formalism19 as where Rc is the resistance of the device before oxidation and T is the transmission probability through the defect. For this particular device, Rc = 53 kΩand the transmission probability changes from 0.0055 before adding DNA target to roughly 0.0018 with target; that is, when the target DNA binds, the transmission probability is modulated by a factor of three.
By taking the ratio of the areas under the low and high conductance state curves from the Gaussian fits in Fig. 2b, we obtain the melting curve shown in Fig. 3a. We also obtain melting curves of the same DNA duplex in solution through ultraviolet-visible absorption spectroscopy (UV-Vis) (Supplementary Fig. S9). Assuming a two-state model where the DNA strands are either in single or in duplex form, the equilibrium constant, K, in solution is given by K = 2α/(1–α)2 where α is the fraction of total strand concentration C that is in duplex form21. For surface based hybridization, the equilibrium constant can be written as the Langmuir isotherm K =α/(1–α)C22. For both surface- and solution-based hybridization, we can then relate the temperature to the fraction of DNA in duplex form through the thermodynamic relation, −RTln(K) = ΔH0 – TΔS0. The melting temperature of the DNA duplex (where α=0.5) as measured by the nanotube (Tm = 27.7°C) is slightly lower and the transition is sharper compared to the free DNA (Tm = 32.3°C). A similar observation has been made for DNA linked to gold nanoparticles23 and RNA adsorbed to carbon nanotubes24 due to interactions between the molecules and the surface25. This is considered further below in the context of analyzing the results of the kinetic studies.
Figure 3. DNA melting curves.
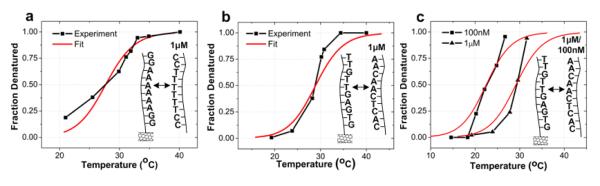
a, Melting curve extracted from nanotube two-level fluctuations (Device 1) for probe DNA NH2-5′-GGAAAAAAGG-3′ (A6) and complementary target with van’t Hoff fit. b, Melting curve extracted from nanotube two-level fluctuations (Device 2) for probe DNA NH2-5′-GTGAGTTGTT-3′ (A1) and complementary target with van’t Hoff fit. c, Melting curve showing two different target concentrations (1 μM and 100 nM) with DNA probe NH2-5′-GTGAGTTGTT-3′ (A1) and complementary target with van’t Hoff fit using Device 3.
Figs. 3b and 3c show the melting curves extracted for the different probe oligonucleotide NH2-5′-GTGAGTTGTT-3′ (probe A1). We show results for a nanotube device (Device 2) with 1 μM complementary target concentration (Fig. 3b) and another device (Device 3) with both 1 μM and 100 nM complementary target concentrations (Fig. 3c). We observe that the lower target concentration reduces the melting temperature, similar to what has been observed in bulk solution. We summarize the thermodynamic properties for both DNA strands and compare them to results with standard UV-Vis analysis in Table 1.
Table 1.
Thermodynamic properties of DNA hybridization comparing solution based UV-Vis measurements and conductance-based single-molecule nanotube experiments.
| DNA | Method | ΔH° (kJ/mol) |
ΔS° (J/Kmol) |
Tm(°C) (1μM) |
Ea (kj/mol) (binding) |
Ea (kJ/mol) (melting) |
|---|---|---|---|---|---|---|
| Probe(A6): NH2-5′-GGAAAAAGG-3′ | Solution | 383.7 | 1134 | 32.3 | — | — |
| Target : 3′-CCTTTTTTCC-5′ | Nanotube | 311.8 | 922 | 27.7 | −164 | 59/411 |
| Probe(A1): NH2-5′-GTGAGTTGTT-3′ | Solution | 356.6 | 1025.8 | 36.2 | — | — |
| Target : 3′-CACTCAACAA-5′ | Nanotube | 256.7 | 733.6 | 28.9 | −147 | 204 |
In order to study the kinetics of DNA hybridization and obtain further insight into the thermodynamics observed through time averaging of a single molecule system, we extract (as shown in Fig. 4a) the dwell times in the high (τhigh) and low states (τlow) in the presence of flicker noise by idealizing the transitions using a hidden Markov model (incorporated in the vbFRET software package)26, which has been used in smFRET experiments to study conformational changes in biomolecules27. The lifetime in each state is extracted by exponentially fitting the dwell time histograms (Supplementary Fig. S3 and S6).
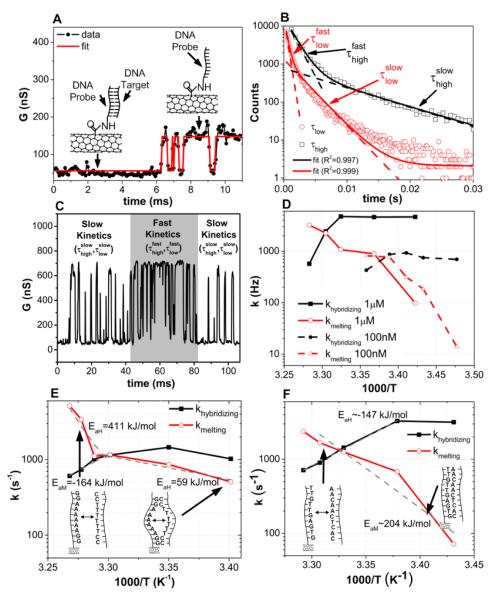
Figure 4. DNA kinetics analysis.
a, Conductance of Device 1 (Fig. 2a) showing experiment data and idealized fits resulting from hidden-Markov-model analysis using vbFRET. Inset: Associated bound and unbound states of the probe DNA. b, Example of double exponential fitting at 1 μM target concentration and 32°C showing both fast and slow lifetimes (Device 3). c, Conductance data, showing intervals with both fast and slow kinetics (Device 3). d, Arrhenius plot showing hybridizing and melting rates for 100 nM and 1 μM complementary target concentrations (Device 3). e, Arrhenius plot of Device 1 showing hybridizing and melting rates. There is no sharp transition in the activation energy. f, Arrhenius plot of Device 2. Sharp transition in activation energy is shown around melting temperature and is attributed to bubble kinetics at lower temperatures.
From this lifetime analysis, we determine that the dwell time histograms can be best fit by a double exponential function with time constants, and , as shown in Fig. 4b. This is the consequence of two distinct kinetic modes28,29, which can also be seen in the real-time conductance data as shown in Fig. 4c. In the solution mode, we assume the probe DNA interacts directly with the target from the solution through 3D diffusion as it would in solution. In the surface mode, we assume that the target reaches the probe through a combination of non-specific adsorption and 1D diffusion along the nanotube. Similar models have been used to describe the kinetics of surface based detection systems on silicon or glass30 and how proteins find specific target sites on DNA strands31,32.
How these time constants are associated with solution-based or surface-based kinetics is determined by examining the concentration dependence of the associated dwell times. From chemical kinetics, we expect the solution hybridization rate (khybridization) to be proportional to DNA target concentration (bimolecular process) and the solution melting rate (kmelting) to be independent of concentration (unimolecular process). Fig. 4d shows the Arrhenius plot for Device 3 with 100 nM and 1 μM complementary target concentration using and for the 1 μM concentration and and for the 100 nM concentration so that the hybridizing and melting rates behave as expected based on solution ensemble experiments and as described above. The target concentration at which khybridization (kmelting) goes from being determined by to being determined by depends on the ratio of one-dimensional and three-dimensional diffusion rates and the concentration dependence of the surface-based hybridization and melting rates (Supplementary Fig. S13 and S14).
Arrhenius plots for khybridization and kmelting at 1 μM for Devices 1 (probe A6) and 2 (probe A1) are presented in Figs. 4e and 4f, respectively. The Arrhenius plot of Device 2 (Fig. 4f) looks very similar to ones reported2,3 for DNA duplex kinetics studied with DNA hairpins. The melting rates (kmelting) follow Arrhenius-like behavior and are very dependent on temperature while the hybridization rates (khybridizing) have anti-Arrhenius behavior and are only slightly temperature-dependent. This anti-Arrhenius behavior yields a negative activation energy, which implies that the reaction rate decreases with increasing temperature and the the free energy barrier arises from a significant loss of entropy33. The slight curvature in the Arrhenius plot has also been observed with DNA hairpin hybridization3 and protein folding34 and is attributed to a change in the rate limiting step of the reaction as a function of temperature, because of a significant temperature dependence in either the activation entropy or enthalpy35,36.
The Arrhenius plot of Device 1 (Fig 4e) shows a remarkably different behavior for kmelting, with a sharp change in activation energy around the melting temperature. At temperatures less than the melting temperature, kmelting has a small activation energy (59 kJ/mol) that can be seen from the shallow slope in the Arrhenius plot. We attribute this to breathing of the DNA duplex (probe A6 for Device 1) which consists of six adeninethymine (AT) base pairs that are enclosed by guanine-cytosine (GC) bases. This differs from the A1 duplex (for Devices 2 and 3), which has at most two neighboring AT bases. We assign the fluctuations well below the melting point for Device 1 to bubble dynamics of the AT region which have been previously reported37,38.
In addition to the solution and surface modes, we also observe occasional several-second-long non-ergodic time intervals when the fluctuations stop (Supplementary Fig. S12), which translates into long tails in the dwell time histograms. This behavior could be due to reversible states in which the DNA complex may adhere to the nanotube surface in a conformation that impedes the binding dynamics. From the dwell time histogram, we estimate the percentage of non-ergotic time intervals to be approximately 10% of the total monitored time.
In conclusion, we have presented a novel single-molecule label-free bioanalytical system capable of probing molecular dynamics at sub-microsecond time scales. We expect this method to be powerful for the immediate exploration of applications in single molecule studies with fast time resolution, such as label free single-nucleotide polymorphism (SNP) detection and sequencing-by-synthesis (SBS). In addition, this methodology may prove powerful for single molecule studies of protein folding and enzymatic activity. Future work will also involve incorporating these devices on active substrates with integrated measurement electronics to reduce both parasitic impedances and measurement noise in order to probe kinetics at even higher rates and SNR.
Methods
Device fabrication
The catalyst solution for nanotube growth is composed of p-methyl methylacetoxy calix[6]arene (MC6, Tokuyama Corp.) and Fe(III) acetylacetonate (Fe(Acac)3, Aldrich) in monochlorobenzene16. A solution of 1.0 Wt% MC6 and 0.1 Wt% Fe(Acac)3 is brushed onto one edge of a piranha-cleaned silicon dioxide substrate (300 nm SiO2) and then subjected to a pre-heated (500 °C) furnace for 10 minutes in air to remove the resist. After flushing the system with argon at the same temperature for 10 minutes, the temperature is ramped to 750 °C and connected to the reducing gases of argon and hydrogen (642 sccm and 115 sccm, respectively) to activate the iron nanoparticles for one hour. Carbon nanotubes are then grown at 880 °C for one hour by a chemical vapor deposition (CVD) process from the iron nanoparticles using ethanol as the carbon source39. The flow rates for growth are 138 sccm for argon and 18 sccm for hydrogen. In general, the nanotubes grown are several millimeters long and have a spacing of approximately 50 μm.
For device fabrication, nanotubes are grown on degenerately doped silicon substrates (ρ=0.01 Ωcm) with a 300 nm thermally grown SiO2 layer. Electrodes to the nanotubes are defined using optical lithography in a bilayer (120 nm LOR1A/1.3 μm Shipley S1813) resist, followed by electron beam evaporation of a 75 nm titanium film and lift off in PG Remover. Scanning electron microscopy (SEM) and atomic force microscopy (AFM) are used to locate the nanotubes relative to alignment marks and electrodes on the substrate and to measure their diameter (only tubes with a diameter less than 2 nm are chosen). Afterwards, another lithography step is used to cover a selected nanotube followed by an oxygen plasma etch (Technics Series 800 RIE machine, 50 W RF power, oxygen 250 mTorr for 10 s) to remove all other nanotubes. This etching step is crucial since it guarantees that only a single tube bridges the electrodes and that neighboring electrodes are electrically isolated (see Figs. S1A and S1B in Supplementary Information). After fabrication, the substrates are annealed in forming gas (a mixture of hydrogen/argon) for at least two hours at 400°C to remove the resist residue completely (see Figs. S1C and S1D in Supplementary Information)40.
Measurement Instrumentation and device oxidation
After wire-bonding the chips to 44-pin J-leaded chip carriers (Chelsea Technology), the wirebonds are electrically and mechanically insulated by standard epoxy (EPO-TEK GE120 and EPO-TEK 302-3M for damming and filling). A small glass tube is fixed on top of the epoxy to create a 3-ml cavity for the aqueous experiments. A platinum wire in a pseudo-reference configuration is used to modulate the liquid gate potential while the back gate is held at zero potential. We have also run the experiment with an Ag/AgCl electrode both in a pseudo-reference configuration and a potentiostat configuration (using both the platinum and Ag/AgCl elecrode in a feedback system) and have determined that the choice of electrode does not affect the results. The advantage of a Pt electrode is that it can withstand the harsh electrochemical environment and that it can be easily cleaned between experiments by grinding away the outer layer with fine sandpaper and then rinsing it with de-ionized water.
For the conductance plots as a function of gate voltage, we use an Agilent 4155C Semiconductor Parameter Analyzer to sweep the electrolyte gate while monitoring the conductance in a two-probe configuration with 100 mV source-to-drain bias. The gate leakage is always negligible (<1 nA) with respect to the source drain current. This is a good indication that the native oxide of the titanium electrodes sufficiently reduces any electrochemical leakage currents. The real time experiments are monitored with a Labview program. A voltage source (Keithley 2400 Source Meter) is used to set the electrolyte voltage while the conductance through a selected device is monitored with a transimpedance current amplifier (Stanford Research SR570) that is sampled at either 10 kHz or 15 kHz using a NIDAQ card. The transimpedance amplifier also sets the source drain voltage to 100 mV and the bandwidth is 5 kHz (at 200 nA/V sensitivity, 10 kHz/12 dB lowpass filter). Devices that have been oxidized in sulfuric acid (1 M H2SO4(aq)) are connected to a second voltage source that is always kept 0.4 V above the Pt potential to avoid further oxidation or accidental reduction. This allows several devices to be oxidized at once. Afterwards, we flush the glass chamber with de-ionized water (while keeping the potential fixed) and then immersing the devices in 6.5 mM potassium permanganate (KMnO4(aq)) for 45 s.
DNA functionalization
The carboxylate defects created in the nanotube during the oxidation process are covalently linked to the DNA in a two-step process 41. First, the carboxylic acid group in the nanotube is activated for 30 minutes in MES buffered saline solution (pH=4.7, Pierce Biotechnology) with 1 mM EDC (1-Ethyl-3-[3-dimethylaminopropyl]carbodiimide Hydrochloride) and 2 mM Sulfo-NHS (N-hydroxysulfosuccinimide) (Pierce Biotechnology). Then, the devices are rinsed with fresh buffer solution, followed by rinsing in 1X PBS buffer (pH=7.4). We then incubate the devices in 2 μM single stranded probe DNA with an amine group at the 5′ end in 1X PBS buffer (pH=7.4) with 1 mM EDC and 2 mM Sulfo-NHS overnight (14 h). The devices are then rinsed with de-ionized water and immersed in 1X PBS for further characterization.
Scanning gate microscopy
Scanning gate microscopy (SGM) is done with a Park Systems Corp. XE-100 AFM using a Cr/Au tip (NSC 14-Cr/Au) at room temperature. Both SGM and electron force microscopy (EFM) are done concurrently and the tip is lifted to 30 nm above the nanotube. For SGM, a small 50 mV bias is applied across the nanotube using a lock-in amplifier (Stanford Research SR830) and the tip is biased at −2 V. The device is slightly p-type (see Figs. S8 in Supplementary Information) and this negative bias increases the conductance through the local tip gating. Both the topography image and the SGM image are leveled but no further processing is done. The conductance of the pristine device increases by about 8% when the tip is over the Schottky barrier while the conductance of the point-functionalized device increases by more than 22% when the tip is over the defect.
Supplementary Material
Contributor Information
Sebastian Sorgenfrei, Department of Electrical Engineering, Columbia University, New York, New York 10027, USA.
Chien-yang Chiu, Department of Chemistry, Columbia University, New York, New York 10027, USA.
Ruben L. Gonzalez, Jr., Department of Chemistry, Columbia University, New York, New York 10027, USA
Young-Jun Yu, Department of Physics, Columbia University, New York, New York 10027, USA.
Philip Kim, Department of Physics, Columbia University, New York, New York 10027, USA.
Colin Nuckolls, Department of Chemistry, Columbia University, New York, New York 10027, USA.
Kenneth L. Shepard, Department of Electrical Engineering, Columbia University, New York, New York 10027, USA
References
- 1.Bonnet G, Krichevsky O, Libchaber A. Kinetics of conformational fluctuations in DNA hairpin-loops. Proc. Natl. Acad. Sci. U. S. A. 1998;95:8602–8606. doi: 10.1073/pnas.95.15.8602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Li HT, Ren XJ, Ying LM, Balasubramanian S, Klenerman D. Measuring single-molecule nucleic acid dynamics in solution by two-color filtered ratiometric fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2004;101:14425–14430. doi: 10.1073/pnas.0404295101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wallace MI, Ying L, Balasubramanian S, Klenerman D. Non-Arrhenius kinetics for the loop closure of a DNA hairpin. Proc Natl Acad Sci U S A. 2001;98:5584–5589. doi: 10.1073/pnas.101523498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Deniz AA, Mukhopadhyay S, Lemke EA. Single-molecule biophysics: at the interface of biology, physics and chemistry. J. R. Soc. Interface. 2008;5:15–45. doi: 10.1098/rsif.2007.1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fei J, Kosuri P, MacDougall DD, Gonzalez RL., Jr. Coupling of ribosomal L1 stalk and tRNA dynamics during translation elongation. Mol Cell. 2008;30:348–359. doi: 10.1016/j.molcel.2008.03.012. [DOI] [PubMed] [Google Scholar]
- 6.Patolsky F, et al. Electrical detection of single viruses. Proc Natl Acad Sci U S A. 2004;101:14017–14022. doi: 10.1073/pnas.0406159101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Armani AM, Kulkarni RP, Fraser SE, Flagan RC, Vahala KJ. Label-free, single-molecule detection with optical microcavities. Science. 2007;317:783–787. doi: 10.1126/science.1145002. [DOI] [PubMed] [Google Scholar]
- 8.Burg TP, et al. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature. 2007;446:1066–1069. doi: 10.1038/nature05741. [DOI] [PubMed] [Google Scholar]
- 9.Hughes RC, Ricco AJ, Butler MA, Martin SJ. Chemical Microsensors. Science. 1991;254:74–80. doi: 10.1126/science.254.5028.74. [DOI] [PubMed] [Google Scholar]
- 10.Cecconi C, Shank EA, Bustamante C, Marqusee S. Direct observation of the three-state folding of a single protein molecule. Science. 2005;309:2057–2060. doi: 10.1126/science.1116702. [DOI] [PubMed] [Google Scholar]
- 11.Besteman K, Lee JO, Wiertz FGM, Heering HA, Dekker C. Enzyme-coated carbon nanotubes as single-molecule biosensors. Nano Lett. 2003;3:727–730. [Google Scholar]
- 12.Star A, et al. Label-free detection of DNA hybridization using carbon nanotube network field-effect transistors. Proc Natl Acad Sci U S A. 2006;103:921–926. doi: 10.1073/pnas.0504146103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Guo X, Gorodetsky AA, Hone J, Barton JK, Nuckolls C. Conductivity of a single DNA duplex bridging a carbon nanotube gap. Nat Nanotechnol. 2008;3:163–167. doi: 10.1038/nnano.2008.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Goldsmith BR, et al. Conductance-controlled point functionalization of single-walled carbon nanotubes. Science. 2007;315:77–81. doi: 10.1126/science.1135303. [DOI] [PubMed] [Google Scholar]
- 15.Goldsmith BR, Coroneus JG, Kane AA, Weiss GA, Collins PG. Monitoring single-molecule reactivity on a carbon nanotube. Nano Lett. 2008;8:189–194. doi: 10.1021/nl0724079. [DOI] [PubMed] [Google Scholar]
- 16.Ishida M, Hongo H, Nihey F, Ochiai Y. Diameter-controlled carbon nanotubes grown from lithographically defined nanoparticles. Jpn. J. Appl. Phys. Part 2 - Lett. Express Lett. 2004;43:L1356–L1358. [Google Scholar]
- 17.Chen RJ, et al. Noncovalent functionalization of carbon nanotubes for highly specific electronic biosensors. Proc Natl Acad Sci U S A. 2003;100:4984–4989. doi: 10.1073/pnas.0837064100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kosynkin DV, et al. Longitudinal unzipping of carbon nanotubes to form graphene nanoribbons. Nature. 2009;458:872–876. doi: 10.1038/nature07872. [DOI] [PubMed] [Google Scholar]
- 19.Bachtold A, et al. Scanned probe microscopy of electronic transport in carbon nanotubes. Phys Rev Lett. 2000;84:6082–6085. doi: 10.1103/PhysRevLett.84.6082. [DOI] [PubMed] [Google Scholar]
- 20.Freitag M, et al. Imaging of the Schottky barriers and charge depletion in carbon nanotube transistors. Nano Lett. 2007;7:2037–2042. doi: 10.1021/nl070900e. [DOI] [PubMed] [Google Scholar]
- 21.Borer PN, Dengler B, Tinoco I, Jr., Uhlenbeck OC. Stability of ribonucleic acid double-stranded helices. J Mol Biol. 1974;86:843–853. doi: 10.1016/0022-2836(74)90357-x. [DOI] [PubMed] [Google Scholar]
- 22.Gong P, Levicky R. DNA surface hybridization regimes. Proc Natl Acad Sci U S A. 2008;105:5301–5306. doi: 10.1073/pnas.0709416105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sun Y, Harris NC, Kiang CH. Melting transition of directly linked gold nanoparticle DNA assembly. Physica A. 2005;350:89–94. [Google Scholar]
- 24.Karachevtsev VA, et al. Adsorption of poly(rA) on the carbon nanotube surface and its hybridization with poly(rU) Chemphyschem. 2008;9:2010–2018. doi: 10.1002/cphc.200800182. [DOI] [PubMed] [Google Scholar]
- 25.Brewood GP, et al. Electrical detection of the temperature induced melting transition of a DNA hairpin covalently attached to gold interdigitated microelectrodes. Nucleic Acids Res. 2008;36:e98. doi: 10.1093/nar/gkn436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bronson JE, Fei J, Hofman JM, Gonzalez RL, Jr., Wiggins CH. Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys J. 2009;97:3196–3205. doi: 10.1016/j.bpj.2009.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fei J, et al. Allosteric collaboration between elongation factor G and the ribosomal L1 stalk directs tRNA movements during translation. Proc Natl Acad Sci U S A. 2009;106:15702–15707. doi: 10.1073/pnas.0908077106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lu HP, Xun L, Xie XS. Single-molecule enzymatic dynamics. Science. 1998;282:1877–1882. doi: 10.1126/science.282.5395.1877. [DOI] [PubMed] [Google Scholar]
- 29.English BP, et al. Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited. Nat Chem Biol. 2006;2:87–94. doi: 10.1038/nchembio759. [DOI] [PubMed] [Google Scholar]
- 30.Chan V, Graves DJ, McKenzie SE. The biophysics of DNA hybridization with immobilized oligonucleotide probes. Biophys J. 1995;69:2243–2255. doi: 10.1016/S0006-3495(95)80095-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.von Hippel PH, Berg OG. Facilitated target location in biological systems. J Biol Chem. 1989;264:675–678. [PubMed] [Google Scholar]
- 32.Halford SE, Marko JF. How do site-specific DNA-binding proteins find their targets? Nucleic Acids Res. 2004;32:3040–3052. doi: 10.1093/nar/gkh624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ansari A, Kuznetsov SV, Shen Y. Configurational diffusion down a folding funnel describes the dynamics of DNA hairpins. Proc Natl Acad Sci U S A. 2001;98:7771–7776. doi: 10.1073/pnas.131477798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Oliveberg M, Tan YJ, Fersht AR. Negative activation enthalpies in the kinetics of protein folding. Proc Natl Acad Sci U S A. 1995;92:8926–8929. doi: 10.1073/pnas.92.19.8926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dobson CM, Sali A, Karplus M. Protein folding: A perspective from theory and experiment. Angew. Chem.-Int. Edit. 1998;37:868–893. doi: 10.1002/(SICI)1521-3773(19980420)37:7<868::AID-ANIE868>3.0.CO;2-H. [DOI] [PubMed] [Google Scholar]
- 36.Chalikian TV, Volker J, Plum GE, Breslauer KJ. A more unified picture for the thermodynamics of nucleic acid duplex melting: a characterization by calorimetric and volumetric techniques. Proc Natl Acad Sci U S A. 1999;96:7853–7858. doi: 10.1073/pnas.96.14.7853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Altan-Bonnet G, Libchaber A, Krichevsky O. Bubble dynamics in double-stranded DNA. Phys Rev Lett. 2003;90:138101. doi: 10.1103/PhysRevLett.90.138101. [DOI] [PubMed] [Google Scholar]
- 38.Metzler R, Ambjornsson T, Hanke A, Fogedby HC. Single DNA denaturation and bubble dynamics. J Phys-Condens Mat. 2009;21 doi: 10.1088/0953-8984/21/3/034111. [DOI] [PubMed] [Google Scholar]
- 39.Huang LM, Cui XD, White B, O’Brien SP. Long and oriented single-walled carbon nanotubes grown by ethanol chemical vapor deposition. J. Phys. Chem. B. 2004;108:16451–16456. doi: 10.1021/jp060693r. [DOI] [PubMed] [Google Scholar]
- 40.Ishigami M, Chen JH, Cullen WG, Fuhrer MS, Williams ED. Atomic structure of graphene on SiO2. Nano Lett. 2007;7:1643–1648. doi: 10.1021/nl070613a. [DOI] [PubMed] [Google Scholar]
- 41.Hermanson GT. Bioconjugate techniques. Elsevier ; Academic Press; Amsterdam ; Boston ; London ; Burlington, MA: 2008. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.