Trace Ratio Linear Discriminant Analysis for Medical Diagnosis: A Case Study of Dementia

Abstract

Dementia is one of the most common neurological disorders among the elderly. Identifying those who are of high risk suffering dementia is important to the administration of early treatment in order to slow down the progression of dementia symptoms. However, to achieve accurate classification, significant amount of subject feature information are involved. Hence identification of demented subjects can be transformed into a pattern recognition problem with high-dimensional nonlinear datasets. In this paper, we introduce trace ratio linear discriminant analysis (TR-LDA) for dementia diagnosis. An improved ITR algorithm (iITR) is developed to solve the TR-LDA problem. This novel method can be integrated with advanced missing value imputation method and utilized for the analysis of the nonlinear datasets in many real-world medical diagnosis problems. Finally, extensive simulations are conducted to show the effectiveness of the proposed method. The results demonstrate that our method can achieve higher accuracies for identifying the demented patients than other state-of-art algorithms.

I. Introduction

Dementia, which causes a progressive decline in cognitive functions, is one of the most common neurolog-population, its prevalence is expected to increase [1]. However, there exists considerable regional variation in diagnosis practice because of the differences in available resources even within a country, e.g. lack of trained general practitioners and/or time to administer and analyze full cognitive function assessments. For example, it was approximated that only a third of people who were actually suffering dementia in the US ever received a formal medical diagnosis. Thus, limited patients suffering dementia are offered appropriate medical treatment or care, which can potentially slow down the progression of symptoms. To separate probably or possibly demented patients from normal subjects, a large amount of data with features for describing symptoms are currently required [1]. In that way, the identification of demented subjects can be transformed into a pattern recognition problem with a high-dimensional dataset.

But dealing with high-dimensional data has always been a major problem in pattern recognition. Hence finding a low-dimensional representation of high-dimensional data, namely dimensionality reduction is thus of great practical importance. Among the dimensionality reduction methods, linear discriminant analysis (LDA) [10] is the most popular method, which is to find the optimal low-dimensional presentation by maximizing the between-class scatter matrix while minimizing the within-class scatter matrix. Several variants of LDA have been proposed during the past decades, and trace ratio LDA (TR-LDA) is one of the most widely used variants [2], [11], [12]. TR-LDA is based on the trace ratio criterion, which can directly reflect Euclidean distances between data points of inter- and intra-classes. In addition, the optimal projection obtained by TR-LDA is orthogonal. As described in [2], when evaluating the similarities between data points based on Euclidean distance, the orthogonal projection can preserve such similarities without any change. Thus, TR-LDA tends to perform empirically better than the classical LDA and other variants of LDA in many problems.

In this paper, improved ITR algorithm (iITR), an efficient algorithm is proposed for solving TR-LDA problem, which can handle nominal attributes and missing values in many real-world medical diagnosis problems. To validate the effectiveness of the proposed method to assist medical screening, the performance of TR-LDA with iITR and other state-of-art dimensionality reduction methods will be compared here by a case study in the screening of demented subjects using only demographic data, medical history, and behavioral attributes, without the use of cognitive function assessment data. In our current study, results show that TR-LDA method can assist the identification of demented patients with higher accuracies even with less training data comparing to other state-of-art dimensionality reduction methods. The proposed dimensionality reduction method can be incorporated into computational screening program to identify probable or possible patients such that general practitioners can refer these subjects to specialists for full diagnosis.

II. Trace Ratio Linear Discriminant Analysis

A. Review of Linear Discriminant Analysis

LDA uses the within-class scatter matrix S_w to evaluate the compactness within each class and between-class scatter matrix S_b to evaluate the separability of different classes. The goal of LDA is to find a linear transformation matrix W ∈ R^D×d, for which the between-class scatter matrix is maximized, while the within-class scatter matrix is minimized. Let X = {x₁, x₂, … X_l} ∈ R^D×l be the training set, each x_i belongs to a class c_i = {1, 2, … c}. Let l_i be the number of data points in the ith class and l be the number of data points in all classes. Then, the between-class scatter matrix S_b, within-class scatter matrix S_w, and total-class scatter matrix S_t are defined as follows:

$$\begin{array}{l}{S}_t=\sum _{i=1}^c\sum _{x\in c_i}(x-\mu ){(x-\mu )}^T\\ S_w=\sum _{i=1}^c\sum _{x\in c_i}(x-{\mu }_i){(x-{\mu }_i)}^T\\ S_b=\sum _{i=1}^c{l}_i({\mu }_i-\mu ){({\mu }_i-\mu )}^T\end{array}$$ (1)

where μ_i = 1/l_i Σ_xi∈ci x_i is the mean of the data points in the ith class, and $\mu =1/l{\sum }_{i=1}^l{x}_i$ is the mean of the data points in all classes. The original formulation of LDA, called Fisher LDA [10], can only deal with binary classification. Two optimization criteria can be used to extend Fisher LDA to solve the multi-class classification problem. The first one is in the ratio trace form (we refer it as LDA):

$$W^{\ast }=arg{max}_{W}Tr\left\{{(W^T{S}_{w}W)}^{-1}{W}^T{S}_{b}W\right\}$$ (2)

and the second one is in the trace ratio form (we refer it as TR-LDA):

$$W^{\ast }=arg{max}_{W^{T}W=I}\frac{Tr(W^T{S}_{b}W)}{Tr(W^T{S}_{w}W)}$$ (3)

The optimal solution of LDA can be formed by the top eigenvectors of $S_w^{-1}{S}_b$. On the other hand, the optimization problem of TR-LDA in (3) has no close-form solution and has to calculate it by an Iterative Trace Ratio method (ITR) [7]. Specifically, if W_t denotes the solution at the tth iteration, then at the (t + 1)th solution, W_t+1 can be formed by the top eigenvectors of S_b − λ_tS_w, where ${\lambda }_t=Tr(W_t^T{S}_b{W}_t)/Tr(W_t^T{S}_w{W}_t)$. This procedure can be proved to converge to the globally optimal solution given any initialization W₀ [2].

B. A More Efficient Algorithm for Solving the TR Problem

Though the ITR algorithm works well for solving the TR problem, it has its own drawback. The ITR algorithm method has chosen d eigenvectors corresponding to the d largest eigenvalues of S_b − λ^*S_w to form W^*. These eigenvectors can only maximize the trace difference value Tr(W^T(S_b − λ^*S_w)W), but these eigenvectors cannot maximize trace ratio value $TR(W_t^T{S}_b{W}_t)/Tr(W_t^T{S}_w{W}_t)$. Thus, how to find eigenvectors to maximize the trace ratio value is an important question. Motivated by this issue, we then, in this subsection, propose a more efficient algorithm, called improved ITR algorithm (iITR), which can solve this problem.

Given any initial λ_t, by performing the eigen-decomposition of S_b − λ_tS_w, we can obtain the D eigenvectors of S_bλ_tS_w. The problem is then to choose the d eigenvectors W_t = {w_i1, w_i2, …, w_iD} maximizing ${\sum }_{k=1}^d{w}_{i_k}^T{S}_b{w}_{i_k}/{\sum }_{k=1}^d{w}_{i_k}^T{S}_w{w}_{i_k}$, where i = {i₁, i₂, …, i_d} is a certain permutation chosen from {1, 2, …, D}. Here, if we define f = {f₁, f₂, …, f_D} ∈ R^1×D, g = {g₁, g₂, …, g_D} ∈ R^1×D with each element satisfying $f_i=w_i^T{S}_b{w}_i$ and $g_i=w_i^T{s}_w{w}_i$, the above problem can be converted to find the optimal selection vector b = {b₁, b₂, … b_D} ∈ R^1×D as:

$$\begin{array}{c}{b}^{\ast }=arg{max}_b\frac{f_1{b}_1+f_2{b}_2+\cdots +f_D{b}_D}{g_1{b}_1+g_2{b}_2+\cdots +g_D{b}_D}.\\ \mathit{subject}to{b}_i\in \{0,1\},b{1}^T=d\end{array}$$ (4)

Note that the above problem is a linear fractional programming (LFP) problem [4], [9], [14]. It can be solved by Dinkelbach’s algorithm which is a general algorithm for optimizing γ = Φ(b)/Ψ(b) with Ψ(b) > 0. In Dinkelbach’s algorithm, it converts the problem to a sequence of sub-problems for optimizing Φ(b) − γΨ(b). Hence in our case, by initializing γ₀ = λ_t and let f, g be defined as above, the optimal selection vector b^* can then be obtained by iteratively solving the following sub-problem:

$$\begin{array}{l}\left\{\begin{array}{c}{\gamma }_0={\lambda }_t\\ f,g\end{array}\right\}\to \left\{\begin{array}{c}{b}^k=arg{max}_{b}b{(f-{\gamma }_{k}g)}^T\\ \mathit{subject}to{b}_i^k\in \{0,1\},b^k{1}^T=d\\ {\gamma }_{k+1}=\frac{b^k{f}^T}{b^k{g}^T}\end{array}\right\}\\ \to \left\{\begin{array}{c}{b}^{\ast }:b^k=b^{k-1}\\ {\gamma }^{\ast }=\frac{b^{\ast }{f}^T}{b^{\ast }{g}^T}\end{array}\right\}\end{array}$$ (5)

After b^* is obtained, we can output W_t by choosing the d eigenvectors with $b_i^{\ast }=1$. The basic steps of the algorithm are listed in Table I.

TABLE I.

iITR Algorithm for Solving the Trace Ratio Problem

Initialize λ0 = 0. Compute the eigen-decomposition of Sb − λtSw as (Sb − λtSw) wi = τiwi, where wi (i = 1,2,…D) is the eigenvector of Sb − λtSw. Calculate $f_i=w_i^T{S}_b{w}_i$ and $g_i=w_i^T{S}_w{w}_i$ for i ∈ {1,2,…,D} and initialize γ0 = λt and $b^0=\left[b_1^0,b_2^0,\dots b_D^0\right]$ be a zero vector, iteratively solving the sub-problem of Eq. (5) until convergence: Sort fi − γkgi and set $b_i^k=1$ corresponding to the d largest value of fi − γkgi, $b_i^k=0$ otherwise. Update γi+1 = bkfT/bkgT. If bk = bk−1, output b* = bk and γ* = b*fT/b*gT. Form Wt by choosing the d eigenvectors of wi, with $b_i^{\ast }=1$ and Update λt+1 = γ*. Iterate the steps (2–4) until |λt+1 − λt| < ε. Output W*.

C. Convergence Analysis of iITR Algorithm

Here the convergence of the proposed iITR algorithm is also analyzed. In fact, as pointed in [3], [13], the algorithm of TR-LDA is Newton method, hence the convergence rate is quadratic and the very fast convergence of the algorithm of TR-LDA is theoretically guaranteed. It has been rigorously proved that for ITR algorithm, given any initial λ_t, the updated λ_t+1 satisfying 1) ${\lambda }_{t+1}^{\mathit{ITR}}\ge {\lambda }_t$ and 2) ${\lambda }_{t+1}^{\mathit{ITR}}\le {\lambda }^{\ast }$. Hence we only need to prove that for the proposed iITR algorithm, the updated ${\lambda }_{t+1}^{\mathit{iITR}}$ is no smaller than ${\lambda }_{t+1}^{\mathit{ITR}}$. Following (5), this can be equivalent to prove that given the initial γ₀ = λ_t, the updated γ_k+1 satisfying i) γ_k+1 ≥ γ_k and ii) γ_k+1 ≤ γ^*. We next prove the two inequalities.

Proof

Let h(γ_k) = max_b b(f − γ_kg)^T, since γ_k+1 = b^kf^T/b^kg^T, we have b^kf^T − γ_k+1b^kg^T = 0 → b^k (f − γ_k+1g)^T = 0. In addition, since b^k+1 = arg max_b b(f − γ_k+1g)^T, it follows h(γ_k+1) = b^k+1 (f − γ_k+1g)^T ≥ b^k (f − γ_k+1g)^T = 0. This indicates that h(γ_k+1) ≥ 0. We then have h(γ_k+1) ≥ 0 → b^k+1 f^T/b^k+1g^T ≥ γ_k+1 → γ_k+2 ≥ γ_k+1. By simply performing the notation substitution, i.e. k + 1 → k, we thus prove the first inequality γ_k+1 ≥ γ_k. We next prove the second inequality. Recall that γ^* = max_b bf^T/bg^T = b^*f^T/b^*g^T, it follows b^*f^T − γ^*b^*g^T = 0 → b^*(f_T − γ^*g)^T = 0. Since h(γ^*) = max b(f − γ^* g)^T = b^*(f − γ^* g) = 0, it can be rewritten as h(γ^*) = h(γ^k+1) + (γ^k+1 − γ^*)g^T = 0. Note that h(γ_k+1) ≥ 0 and g is a semi-positive vector, the equality can only holds as γ^k+1 ≤ γ^*, hence we prove the second inequality, i.e. γ_k+1 ≤ γ^*.

III. Identifying Demented Patients via TR-LDA

A. Data Descriptions

The proposed method will be used to screen the demented subjects which meet the criteria for dementia in accordance with standard criteria for dementia of the Alzheimer’s type or other non-Alzheimer’s demented disorders in their first visits to Alzheimer disease Centers (ADCs) throughout the United States. Data from 289 demented subjects and 9611 controls collected by approximately 29 ADCs from 2005 to 2011 are studied. These data are organized and made available by the US National Alzheimer’s Coordinating Center (NACC). Among the demented patients studied, 97% of them were classified as probable or possible Alzheimer’s disease (AD) patients. Those with dementia and with neither probable AD nor possible AD have other types of dementia such as Dementia with Lewy Bodies, and Frontotemporal Lobar Degeneration. 5 nominal, 142 ordinal, and 9 numerical attributes of the subjects are included in the study. These attributes include demographic data, medical history, and behavioral attributes, with 5% being missing values. To make the classification problem more difficult, no cognitive assessment variable, such as Mini-Mental State Examination score, is included as attribute.

B. Prediction Stage

The next step is to apply TR-LDA in identifying demented patients from normal persons. Note that NACC dataset includes nominal attributes and missing values. It should be transferred to a numerical data before performing dimensionality reduction. To handle this problem, we use kernel method to map NACC dataset to a high-dimensional Hilbert space. We then use the data in such space to perform dimensionality reduction. The kernel function used is the radial basis function (RBF) defined by K_ij = exp(−||x_i − x_j||²/σ²). Here, to construct the kernel function, we use VDM (Value difference Metric) [8] to calculated the distance between x_i and x_j instead of only relying Euclidean distance. In detail, given two samples x_i and x_j, suppose the first j attributes of them are nominal, the following k ones are numeric and normalized to [0,1], and the remaining D − j − k ones are missing if either x_i or x_j lacks the values in these attributes, the distance between x_i and x_j can be calculated by:

$$D(x_i,x_j)={\left(\sum _{h=1}^j\mathit{VDM}(x_{h,i},x_{h,j})+\sum _{h=j+1}^{j+k}{\mid x_{h,i}-x_{h,j}\mid }^2\right)}^{\frac{1}{2}}$$ (6)

Here, the VDM distance between two values z₁ and z₂ on nominal attribute Z can be calculated by:

$$\mathit{VDM}(z_1,z_2)\sum _{k=1}^c{\left|\frac{N_{Z,z_1,k}}{N_{Z,z_1}}-\frac{N_{Z,z_2,k}}{N_{Z,z_2}}\right|}^2$$ (7)

where N_Z,z denotes the number of training examples holding value z on Z, N_Z,z,k denotes the number of training examples belonging to the kth class and holding value z on Z, c denotes the number of classes. Hence after we define the distance as in (6), we can either use it to construct the kernel function or to train a nearest neighbor classifier for evaluating the accuracies of test set.

IV. Simulations

This simulation aims at differentiating normal persons from demented persons by using TR-LDA and compares it with other state-of-the-art methods such as PCA, LPP, MMC and LDA. In this simulation, we randomly choose 500, 1000 and 2000 samples in AD data as training set and the remaining as test set. The data is preliminarily processed with KPCA operator to eliminate the null space of training set [7]. Then, each method uses the training set in the reduced output space to train a nearest neighborhood classifier to classify the demented and non-demented persons in test set.

The average accuracies over 20 random splits under different dimensionalities are in Table II and Fig. 2. As shown in Table II, the classification accuracies of all methods change greatly with the increase in the number of labeled samples. Another important observation is that the supervised methods such as LPP [6], MMC [5], LDA [10], TR-LDA outperform the unsupervised methods such as PCA and LPP. Among all the supervised methods, the proposed TR-LDA performs the best due to the trace ratio criterion. We also compare the convergence between ITR and iITR algorithms as in Fig. 1. From Fig. 1, we can see both algorithms can converge to the optimal trace ratio value. The iITR algorithm converges faster than ITR algorithm due to reason as in Section II-C.

TABLE II.

The Average Accuracies Over 20 Random Splits

Method	500 samples		1000 samples		1500 samples		2000 samples
	mean ± var	dim	mean ± var	dim	mean ± var	dim	mean ± var	dim
1NN	71.76 ± 3.89	-	73.09 ± 1.68	-	75.45 ± 1.26	-	77.32 ± 1.14	-
KPCA+1NN	72.08 ± 4.09	23	73.35 ± 2.14	25	75.26 ± 2.37	24	80.02 ± 2.05	23
KPCA+LPP+1NN	71.94 ± 3.65	24	75.09 ± 2.35	33	77.12 ± 2.23	30	80.55 ± 1.50	32
KPCA+MMC+1NN	79.56 ± 3.50	1	82.46 ± 2.00	1	84.63 ± 2.56	1	87.90 ± 1.22	1
KPCA+LDA+1NN	79.94 ± 3.86	1	82.09 ± 2.41	1	84.82 ± 2.29	1	87.46 ± 1.02	10
KPCA+TR-LDA+1NN	81.12 ± 3.29	10	84.35 ± 2.10	7	86.83 ± 2.52	15	90.01 ± 1.25	15

Fig. 2.

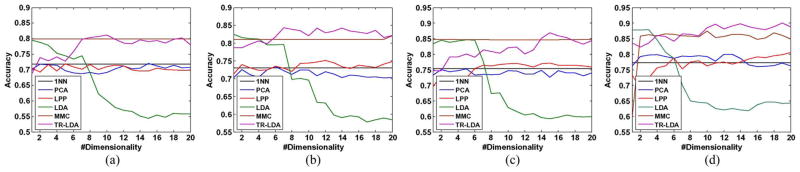
Average accuracies under different dimensionalities: (a) 500 samples; (b) 1000 samples; (c) 1500 samples; (d) 2000 samples.

Fig. 1.

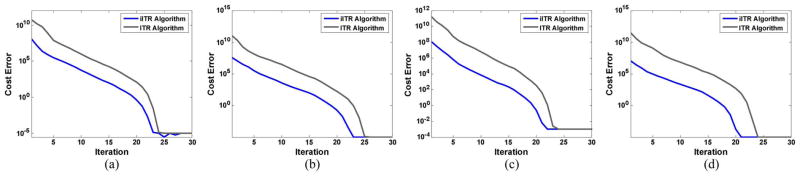
Convegence between ITR and iITR algorithms: (a) 500 samples; (b) 1000 samples; (c) 1500 samples; (d) 2000 samples.

V. Conclusion

Dementia is one of the most common neurological disorders among the elderly. Identification of demented patients from normal subjects can be transformed into a pattern recognition problem with high-dimensional nonlinear datasets. In this paper, we introduce trace ratio linear discriminant analysis (TR-LDA) for dementia diagnosis and propose an improved ITR algorithm (iITR) to solve the TR-LDA problem. The new proposed algorithm can handle nominal attributes and missing values in many real-world medical diagnosis problems. Finally, extensive simulations are presented to show the effectiveness of the proposed algorithms. The results demonstrate that our proposed algorithm can achieve higher accuracies for identifying the demented patients than other state-of-art algorithms.