In vivo quantification of serotonin transporters using [¹¹C]DASB and positron emission tomography in humans: modeling considerations

Abstract

Positron emission tomography (PET) studies of the serotonin transporter (5-HTT) in the human brain are increasingly using the radioligand [¹¹C]N, N-dimethyl-2-(2-amino-4-cyanophenylthio) benzylamine. A variety of models have been applied to such data in several published articles; however to date, these models have not been validated with test–retest data. We recruited 11 healthy subjects and conducted two identical scans on each subject on the same day. We considered four different models (one- and two-tissue compartment kinetic models, likelihood estimation in graphical analysis (LEGA; a bias-free alternative to the graphical method), and basis pursuit) along with fast noniterative approximations to the kinetic models. We considered four different outcome measures (total volume of distribution (V_T), binding potential with (BP) and without (BP₁), free-fraction adjustment, and specific-to-nonspecific equilibrium partition coefficient (BP₂)). To assess the performance of each model, we compared results using six different metrics (percent difference (PD) and within-subject mean sum of squares for reproducibility, interclass coefficient for reliability, variance across subjects, identifiability based on bootstrap resampling of residuals for each method, and time stability analysis to determine minimal required scanning time). We considered analysis of both at the voxel level and at the region of interest (ROI) level and compared results from these two approaches to assess agreement. We determined that 100 mins of scanning time is adequate and that for ROI-level analysis, LEGA gives best results. Average PD is 5.51 for V_T, 20.7 for BP, 17.2 for BP₁, and 16.5 for BP₂ across all regions. For voxel-level analysis we determined that the one-tissue compartment noniterative model is best.

Introduction

The serotonin transporter (5-HTT) is the primary target for selective serotonin reuptake inhibitors (SSRIs), which are used to treat mood and anxiety disorders. Selective serotonin reuptake inhibitors bind to the transporter, blocking the reuptake of serotonin, and stimulate a chain of intracellular events including desensitization of 5-HT_1A autoreceptors, increases in neuronal firing rate, and downstream trophic effects that are temporally associated with clinical response (Blier and de Montigny 1999; Duman et al, 1997). In vivo imaging studies report less 5-HTT binding in major depression (Malison et al, 1998; Parsey et al, 2006). Finally, positron emission tomography (PET) studies report on the relationship of 5-HTT occupancy in vivo, to oral doses and plasma levels of SSRIs (Meyer et al, 2001, 2004; Parsey et al, in press) to determine the level of 5-HTT occupancy by SSRI that is required to achieve a therapeutic effect. Such studies rely on valid quantification of 5-HTT bindig using PET or SPECT.

[¹¹C]N, N-Dimethyl-2-(2-amino-4-cyanophenylthio) benzylamine ([¹¹C]DASB), binds with high affinity (1.1 nmol/L) and selectivity to 5-HTT and offers advantages over other PET 5-HTT radioligands (Frankle et al, 2004; Ginovart et al, 2001; Houle et al, 2000; Wilson et al, 2002, 2000). While these initial publications have addressed different methods of quantification of the transporter with [¹¹C]DASB, none have presented the test–retest reproducibility for any method to permit a data-based choice of the optimal method of quantification for a given study. Interpretation of the significance of repeated measurements in the same subjects after an intervention such as administration of an SSRI (Parsey et al, in press) or acute tryptophan depletion (Talbot et al, 2005), depends in part on knowledge of the variability of repeated measures on the same subject.

The objective of our present study is to comprehensively evaluate aspects of modeling of data with this ligand, with the ultimate goals being to determine (1) the optimal scanning duration; (2) the best model to fit; and (3) the reliability of the results. We address these questions with data from repeated scans on the same subjects rather than through simulation studies so as not to rely on assumptions about the noise structure and so that we are not required to set ‘true’ parameter values to generate data. In particular, we consider estimation of four common outcome measures: total volume of distribution (V_T), binding potential (BP₁ and BP), and specific-to-nonspecific equilibrium partition coefficient (BP₂), which are defined here. The solution to the linear first-order differential equations that constitute the system of compartmental models typically applied in neuroreceptor PET studies is

$$C(t)=\sum _{j=1}^m{\phi }_j{e}^{-{\theta }_{j}t}\otimes C_{\mathrm{p}}(t)$$ (1)

where C_p(t) is the concentration of the radioligand in the plasma (corrected for metabolism) over time and m is the number of tissue compartments in the model. For these models, V_T is defined as

$$V_{\mathrm{T}}=\sum _{j=1}^m\frac{{\phi }_j}{{\theta }_j}.$$ (2)

The other outcome measures can be derived from V_T. Binding potential is defined as

$$BP=\frac{V_{\mathrm{T}}-V_{\mathrm{T}\text{REF}}}{f_1}$$ (3)

for a suitably chosen reference region, where f₁ is the plasma-free fraction. The other outcome measures considered (also called ‘binding potential’ in some references) are:

$$\begin{array}{cc}B{P}_1=f_1\times BP;& B{P}_2=f_2\end{array}\times BP=B{P}_1/V_{\mathrm{T}\text{REF}}$$ (4)

Thus, both BP₁ and BP₂ can be computed without measuring free fraction.

In addition to region of interest (ROI)-based fitting, we also considered modeling on a voxel-by-voxel basis, since vastly different signal-to-noise ratios at the voxel level may require different modeling techniques. We considered six metrics for judging among the various methods, including a novel measure of identifiability (ID) based on bootstrapping the data. To determine the optimal time needed for scanning, all metrics were considered for all outcome measures for a range of scanning times. In addition, we assessed the agreement between analysis methods at the voxel level with those at the ROI level since these approaches should be complementary.

Materials and methods

Subjects

Healthy volunteers were recruited for the study. Inclusion criteria were assessed by the after: history, Structured Clinical Interview for DSM IV (First et al, 1997), review of systems, physical examination, routine blood tests, pregnancy test, urine toxicology, and EKG. Inclusion criteria included: (1) age 18 to 65 years; (2) no Axis I DSM-IV psychiatric diagnoses; (3) absence of any psychotropic medications for at least 2 weeks; (4) absence of lifetime history of alcohol or substance abuse or dependence; (5) absence of lifetime exposure to 3,4-methylenedioxymethamphetamine (ecstasy); (6) absence of significant medical conditions; (7) absence of pregnancy; and (8) capacity to provide informed consent. The Institutional Review Boards of Columbia University Medical Center and the New York State Psychiatric Institute approved the protocol. Subjects gave written informed consent after an explanation of the study. Eleven subjects were enrolled in the study (four men, seven women; mean age 27 ± 6 years, range 18 to 36). All subjects underwent two identical scans, test–retest, on the same day.

Radiochemistry

Preparation of [¹¹C]DASB was as previously described (Belanger et al, 2004). The chemical purity of [¹¹C]DASB was >99%, and the radiochemical purity was >90%. Mean specific activity at injection was 1.5 mCi/nmole, and mean injected dose was 15.4 ± 2.8 mCi.

Positron Emission Tomography Protocol

A venous catheter was used for injection of the radioisotope and an arterial catheter to obtain arterial samples for the input function. A polyurethane head holder system (Soule Medical, Tampa, FL, USA) was molded around the subject’s head for immobilization purposes. Positron emission tomography imaging was performed with the ECAT HR+ (Siemens/CTI, Knoxville, TN, USA). A 10 mins transmission scan was obtained before radiotracer injection. At the end of the transmission scan, between 5 and 20 mCi of [¹¹C]DASB was administered intravenously as a bolus over 30 secs. Emission data were collected in three-dimensional (3D) mode for 120 mins with 21 frames of increasing duration: 3 at 20 s, 3 at 1 min, 3 at 2 mins, 2 at 5 mins, and 10 at 10 mins. Images were reconstructed to a 128 × 128 matrix (pixel size of 2.5 × 2.5 mm²). Reconstruction was performed with attenuation correction using the transmission data, and scatter correction was carried out using model-based scatter correction (Watson et al, 1995). The reconstruction filter and Estimated Image Filter were Shepp 0.5 (2.5 FWHM), Z filter was All Pass 0.4 (2.0 FWHM), and Zoom Factor was 4.0, leading to a final image resolution of 5.1mm FWHM at the center of the field of view (Mawlawi et al, 2001).

Input Function Measurement

Arterial samples were collected with an automated sampling system every 5 secs for the first 2 mins, and manually thereafter for a total of 31 samples. Centrifuged plasma samples were collected in 200 µL aliquots, and the radioactivity was measured in a well counter. A high-pressure liquid chromatography assay of six samples (collected at 2, 12, 20, 50, 80, and 100 mins) provided unmetabolized parent compound levels (Parsey et al, 2000). The six parent fraction levels were fit with a biexponential function, which was damped by a power function to take into account the low initial value (Parsey et al, submitted). The input function was calculated as the product of the interpolated parent fraction and the total plasma counts. The measured input function values were fitted to a sum of three exponentials, and the fitted values were used as input to the analyses.

Free Fraction Measurement

To determine the plasma-free fraction (f₁), blood samples were taken before radioligand injection and spiked with [¹¹C]DASB. Aliquots (200 µl) were pipetted into ultracentrifuge units (Centrifree, Millipore Corp., Bedford, MA, USA). After centrifugation for 20 mins at 4000 r.p.m., all parts of the ultrafiltration unit were counted individually. Counts for each fraction were summed and divided into ultrafiltrate counts to determine free fraction. Average f₁across all studies was 12.7%±1.15%.

This procedure resulted in three replications for each scan and was also replicated three times each scan for a pooled sample. The pooled plasma sample was obtained by combining plasma samples from over 30 subjects and freezing aliquots for use on scan days. To control for any daily variation of the process, the measurements for all subjects and all scans, including the pooled sample, were fitted with a linear mixed model with random effects for subject and day and based on the fitted model a subject-specific value of f₁ was obtained.

Magnetic Resonance Imaging

Magnetic resonance images (MRIs) were acquired on a GE 1.5-T Signa Advantage system. A sagittal scout (localizer) was performed to identify the anterior commissure– posterior commissure (AC–PC) plane (1 min), followed by a transaxial T1-weighted sequence with 1.5mm slice thickness in a coronal plane orthogonal to the AC–PC plane over the entire brain under the after parameters: 3D spoiled gradient recalled acquisition in the steady state, 34 ms TR, 5 ms TE, 45° flip angle, 1.5 mm slice thickness and zero gap, 124 slices, 22 × 16 cm² field of view, with a 256 × 192 matrix, reformatted to 256 × 256, yielding a voxel size of 1.5 × 0.9 × 0.9 mm³, and acquisition time of 11 mins.

Image Analysis

Image analysis was performed using MEDX software (Sensor Systems Inc., Sterling, VA, USA). The last 13 frames of an individual study were coregistered to the eighth frame using the Functional Magnetic Resonance Imaging of the Brain’s Linear Image Registration Tool (FLIRT) v5.0 (Jenkinson and Smith 2001) to correct for subject motion during the scan. A mean motion-corrected PET image was created and coregistered to its corresponding MRI using FLIRT. The resulting transformation was applied to all motion-corrected frames. Region of interests were traced based on brain atlases (Duvernoy 1991; Talairach and Tournoux 1988) and published reports (Kates et al, 1997; Killiany et al, 1997). Region of interests included the anterior cingulate, cingulate cortex, amygdala, hippocampus, insular cortex, temporal cortex, dorsal caudate, midbrain (MID), ventral striatum (VST), thalamus, dorsal putamen, dorsolateral prefrontal cortex (DOR), occipital cortex (OCC), orbital prefrontal cortex, entorhinal cortex, cerebellar gray matter, medial prefrontal cortex, parietal lobe, parahippocampal gyrus, and posterior parahippocampal gyrus. Magnetic resonance images were cropped utilizing the exbrain v.2 utility (Lemieux et al, 2003) and then segmented utilizing FMRIB’s automated segmentation tool. Within the cortex, only gray matter voxels were used to measure PET activity distribution. Region of interests were drawn by three different data analysts who were blinded to condition. Test–retest variability of V_T between the three raters over all ROIs is < 3%.

Modeling

Six modeling approaches were considered for fitting the time activity curves (TACs) extracted from the imaging data: two kinetic models fit by nonlinear least-squares methods, the same two models each fit by a fast approximation algorithm, and two model-free approaches. All models considered in this manuscript involve an arterial input function. The same weighting scheme (weights equal to frame duration) was applied to all methods. Each model is described here and all model abbreviations and descriptions are given in Table 1 for reference.

Table 1.

Abbreviations and descriptions for all models considered

	Abbreviations
	Description
1TC	One-tissue compartment kinetic model (iterative fit)
2TC	Two-tissue compartment kinetic model (iterative fit)
1TCNI	One-tissue compartment kinetic model (noniterative fit)
2TCNI	Two-tissue compartment kinetic model (noniterative fit)
LEGA	Likelihood estimation in graphical analysis from Ogden (2003)
Basis	Basis pursuit from Gunn et al (2002)

Kinetic models

The solution to the linear first-order differential equations that constitute the system of compartmental models typically applied in neuroreceptor PET studies is given by equation (1). For these models, V_T, the integral of the impulse response function, is defined in equation (2). We consider both one- and two-tissue compartment models.

These models are customarily fit by an iterative nonlinear least-squares algorithm, but this can be rather computationally expensive when fitting all voxel TACs (or when applying a bootstrap algorithm to calculate s.e.). An alternative to this iterative approach is to first create a library of functions e^−θ_kt ⊗ C_p (t) for a range of θ_k values (Simpson et al, 2003). For a one-tissue model, the noisy TAC is regressed (using fast non-negative least-squares methods) on each function in the library in turn. The fitted model is chosen to be that, which gives the smallest sum of weighted squared errors. Similarly, for a two-tissue compartment model, the noisy TAC curve is regressed on each possible pair of library functions, the smallest sum of weighted squared errors determining the final fit.

Besides the obvious computational advantages of such an approach, this also can avoid some of the numerical problems of nonconvergence or convergence to a local minimum that can arise with standard iterative methods. In addition, extreme outliers in V_T estimation can be avoided by setting the minimum value of θ_k appropriately. The limitations of such an approach are that estimation can be negatively affected by poor choices for such settings, and that estimation of time constants is not as precise as when parameters are estimated iteratively (since this approach is intended merely as a fast approximation to iterative model fitting).

For application to [¹¹C]DASB data, we selected 35 functions with the θ_k values equally spaced in the log domain. The minimum and maximum values for θ_k were set as in Gunn et al (2002).

Graphical method

One useful model-free approach to fitting of TAC data is the graphical analysis originally put forth by Logan et al (1990). For the purposes of this paper, we considered the bias-free approach (likelihood estimation in graphical analysis (LEGA)) (Ogden 2003; Parsey et al, 2003). For this approach, the estimate of V_T is taken to be the estimated slope of the Logan expression. In application to [¹¹C]DASB data, the linearity point was chosen such that the last eight points are used in fitting.

Basis pursuit

The last approach considered in this study is the model-free basis pursuit strategy proposed by Gunn et al (2002). As in the noniterative kinetic modeling, a library of basis functions is created e^−θ_kt ⊗ C_p (t). Estimation is made by minimizing the weighted sum of squared errors plus an L₁ penalty term thereby ensuring sparseness of the selected model. The parameter contained in the penalty term, controlling the trade-off between model complexity and model fit, is determined based on a cross-validation algorithm. For this study, we applied the DEPICT software created by Gunn et al. We used 30 basis functions and set the range for θ_k as in Gunn et al (2002).

Outcome Measures

In addition to V_T, three other common outcome measures were considered, each being derived from V_T. The most relevant outcome measure is BP (equivalent to B_max/K_D, where B_max is the receptor concentration and K_D is the reciprocal of the tracer affinity) and it can be derived from V_T as given in equation (3). We also considered BP1 and BP₂ as defined in equation (4) which can be useful if f₁cannot be reliably estimated. For this study, the reference region is taken to be a circular sample of the cerebellar cortex as this region has the lowest V_T and least displacement of all regions examined (Parsey et al, in press).

Metrics for Comparison of Modeling Strategies

Results of fitted models were assessed according to six metrics: percent difference (PD) and within-subject mean sum of squares (WSMSS) to measure reproducibility; interclass correlation coefficient (ICC) to measure reliability; variance (Var); ID; and time stability (TS). Each of these is described below.

Percent difference

The test–retest reliability was calculated as the absolute difference between the test and retest values divided by their average.

Within-subject mean sum of squares

Within-subject variability was estimated according to

$$\text{WSMSS}=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^2{(X_{ij}-{\overline{X}}_i)}^2$$

Here, X_i1 represents the ‘test’ value of an outcome measure for subject i, X_i2 represents the ‘retest’ value for the same subject, n is the number of subjects, and X̄_i = (X_i1 + X_i2)/2. This represents the variance in the estimation of a subject-specific outcome measure and cannot be estimated except when repeated measurements are available.

Variance

The variance of an outcome measure is simply the sample variance (across subjects) of all observations for each ROI.

Interclass correlation coefficient

The measure of within-subject variability relative to between-subject variability was computed using the ICC:

$$\text{ICC}=\frac{\text{BSMSS}-\text{WSMSS}}{\text{BSMSS}+(k-1)\text{WSMSS}}$$ (5)

where BSMSS is the mean sum of squares between subjects, WSMSS is the mean sum of squares within subjects and k is the number of repeated observations (k = 2 in the current study). The coefficient value ranges from –1 (no reliability) to 1 (maximum reliability).

Identifiability

To assess the stability of each estimation strategy, we computed 100 bootstrap samples (Ogden and Tarpey, 2006) for each subject’s ROI and estimated the outcome measure for each of these samples. Since interest in this paper centers on variability in the modeling of the brain TACs rather than that for plasma and metabolite modeling, bootstrap samples were taken only of the TAC data. We measured the variability of these estimates using the robust median absolute deviation criterion:

$$\mathit{\text{median}}\left[\right|Z_j-\mathit{\text{median}}(Z_1,Z_2,\dots ,Z_{100})|,j=1,2,\dots ,100]$$

This approach to assessing ID may be preferred to the more customary technique of using the asymptotic formulas for s.e. in nonlinear regression since it does not rely on distributional assumptions of the noise.

Time stability

It may appear logical that the longer the acquisition time, the more accurate the estimation. However, because of the physical decay of the radionuclide (¹¹C: T_1/2 = 20 mins) as well as subject head motion, the acquired data becomes increasingly noisy towards the end of the scan and does not necessarily contribute useful information. Considerations of subject comfort would also dictate that the data acquisition time be as short as possible.

All studies analyzed here included a full 120 mins of scanning. To assess performance of each method with shorter scan-duration data, each model was fit to data with later frames deleted. This was carried out for total scan times of 120, 110, 100, 90, 80, and 70 mins. For each ROI for each study, we computed the ratio of the outcome measure for the shorter scan time to that for the full scan. An estimation procedure for a ROI was considered stable at a given scanning duration if the mean of these ratios across all studies was between 95% and 105% and if their standard deviation was <10%. In addition, all the other metrics described in this section were recalculated for each of the candidate scan durations.

Results

Results of the analysis for the various metrics considered are presented in tabular and graphical form. The two-tissue kinetic model (both the iterative and noniterative fitting methods) performed quite poorly for all the metrics and is thus not presented in this section. Since BP is the outcome measure closest to B_max, we first analyzed the results for BP. These results were generally representative of the results for the other outcome measures considered, so unless otherwise specified, all results are for BP.

The modeling procedures considered here depend on numerical algorithms that occasionally result in unreasonable large estimates for V_T. To limit the effect that these outliers can have on summary measures (across subjects and/or ROIs) of the various metrics considered, we summarized results (unless otherwise specified) using the median rather than the mean.

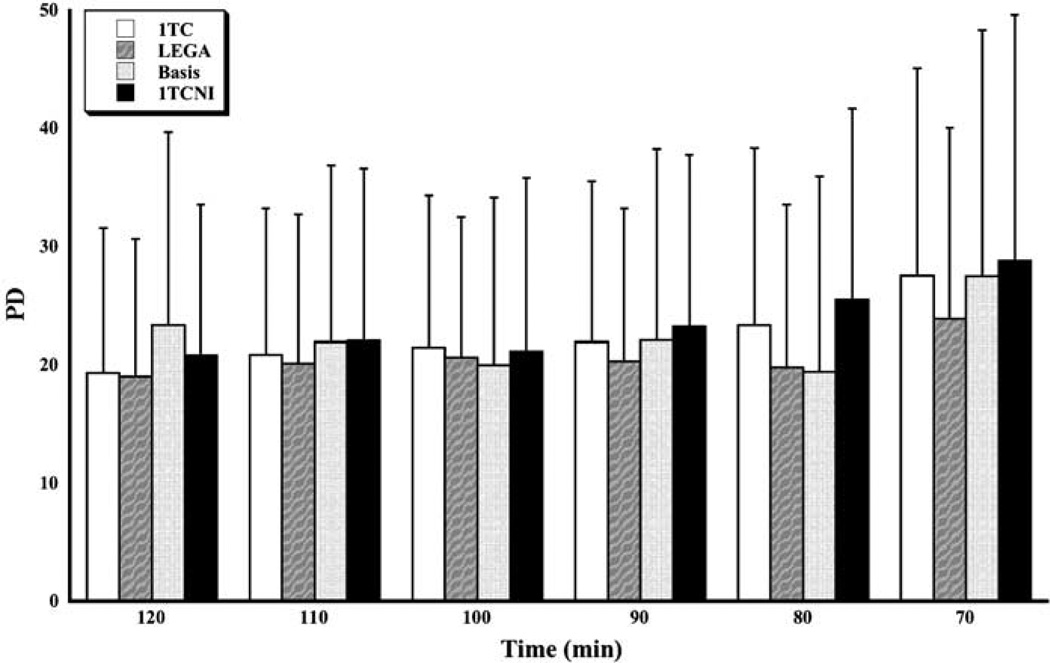
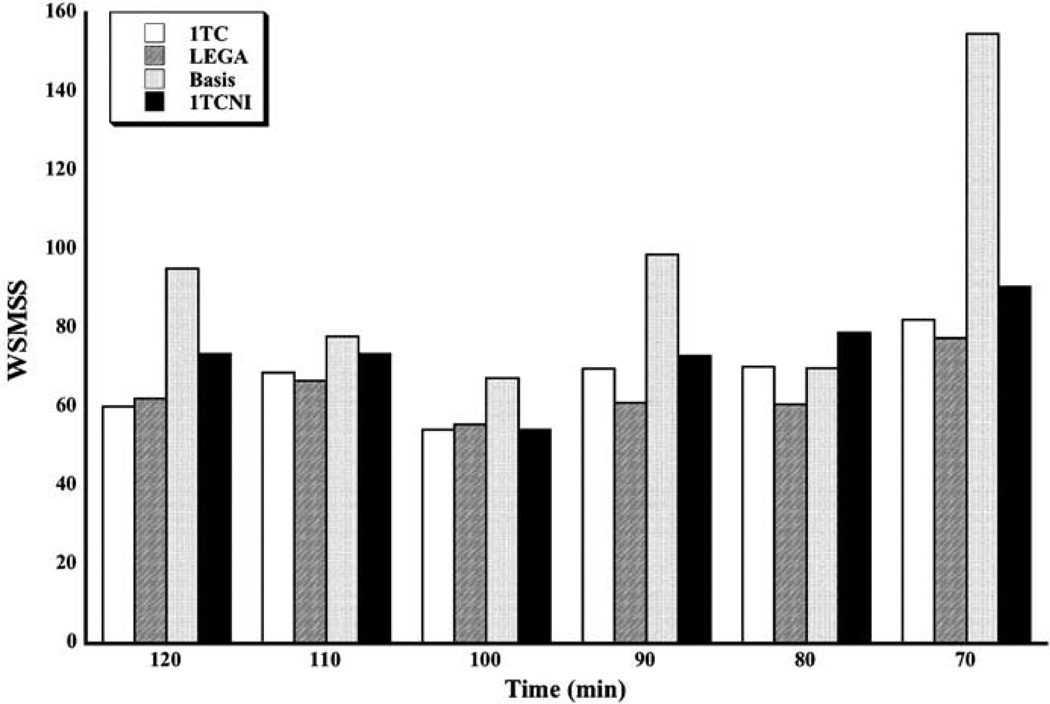
Reproducibility results are presented in Figures 1 and 2. The PD criterion (Figure 1) varies from about 20% to 25% (median across all subjects and across all ROIs) for all methods, with a small increase for shorter scanning times. The LEGA method seems to be somewhat better than the others for most time durations, although the difference is slight. The WSMSS criterion (Figure 2) seems to be minimized for all methods at 100 mins of scanning time. The 1TC and LEGA methods are generally better than the other methods and basis pursuit is quite high for some scanning durations.

Figure 1.

Median percent difference (PD) in test–retest for all scanning times and methods. The medians are taken across all subjects and all ROIs.

Figure 2.

Median WSMSS for all scanning times and methods. The medians are taken across all subjects and all ROIs.

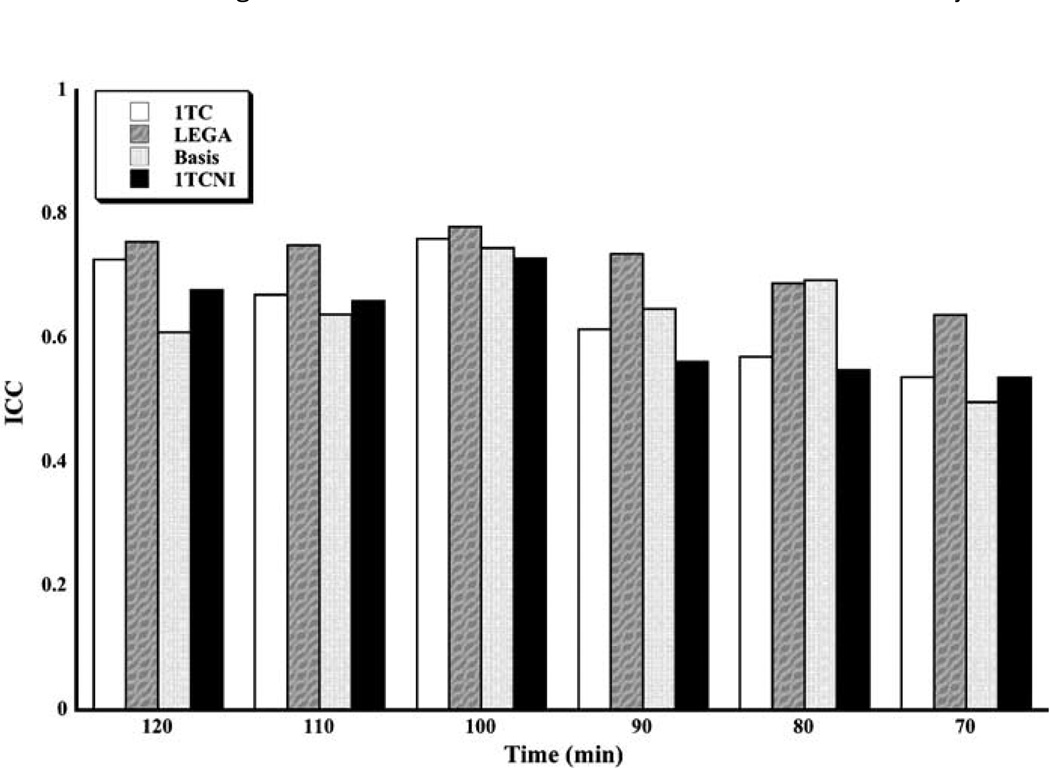
Reliability results are shown in Figure 3. Overall, highest ICC is achieved at 100 mins of scanning. The LEGA method has somewhat higher (better) ICC than the other methods for most scan times.

Figure 3.

Median ICC for all scanning times and methods. The medians are taken across all subjects and all ROIs.

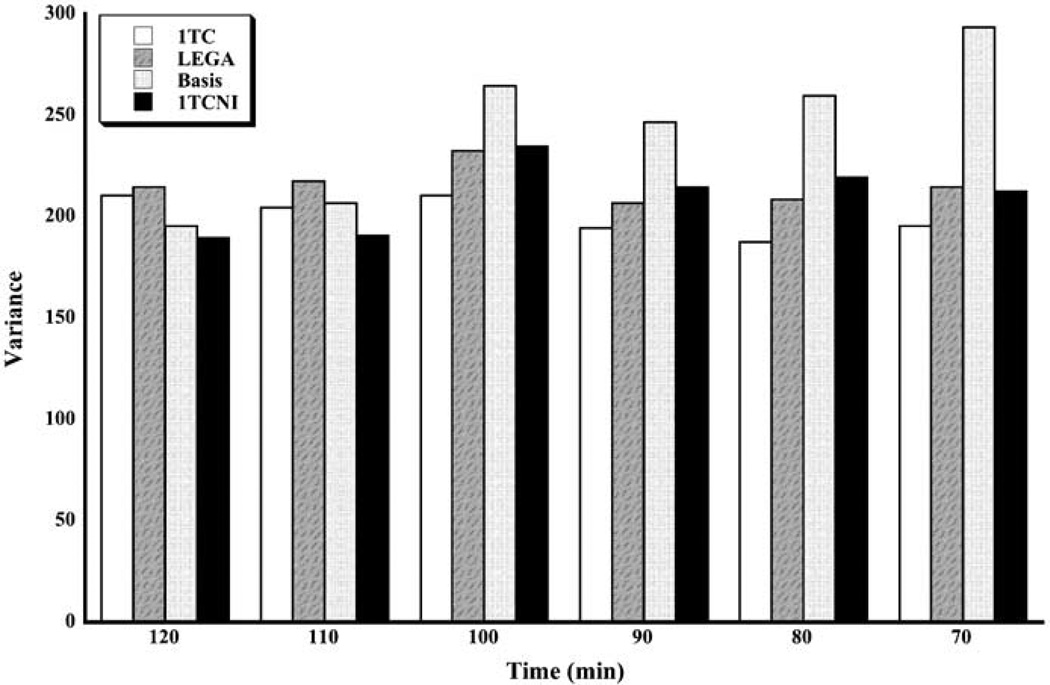
Results for the variance metric are displayed in Figure 4. Variances are generally smallest for the two longest scanning durations, for which the 1TCNI method is slightly better than the others. For shorter scanning times, the 1TC model seems to do better than the others.

Figure 4.

Median variance (Var) for all scanning times and methods. The medians are taken across all subjects and all ROIs.

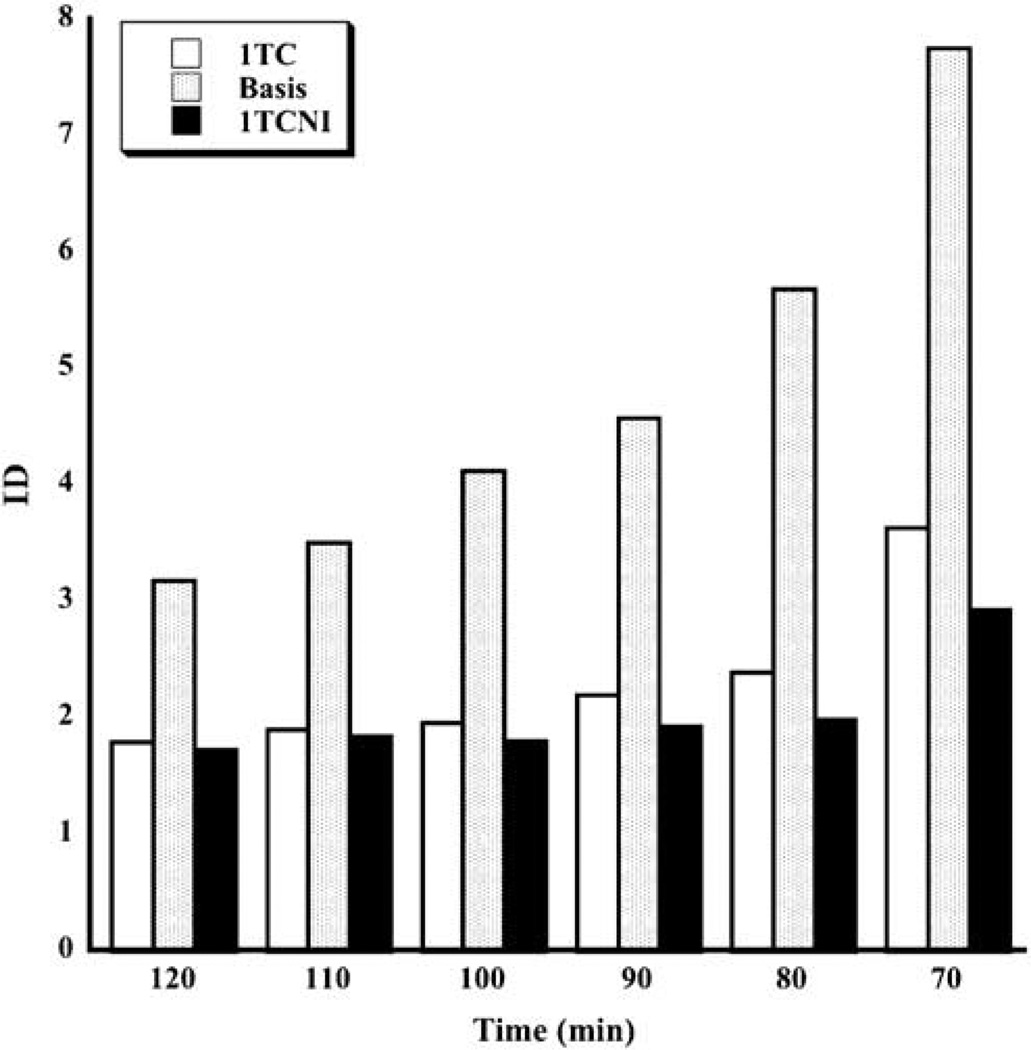
Identifiability results are given in Figure 5 for all methods except LEGA. The bootstrap-based ID measure cannot be applied to LEGA since there are only eight data points that are modeled with the graphical analysis even at the longest acquisition times, and thus the bootstrap samples cannot be expected to have the proper distribution. Identifiability is best for longest scanning times and gradually worsens for shorter scanning times. According to this metric, 1TCNI is generally preferred to the others, although its advantage over 1TC is slight at longer scanning times.

Figure 5.

Median identifiabilty (ID) for all scanning times and three methods. The medians are taken across all subjects and all ROIs. Identifiability is not available for LEGA since there are too few residuals for valid resampling.

Time stability results are displayed in Table 2. Each tabled element represents the minimum scanning time for which the TS criterion is satisfied. BP₁ results are identical to those for BP and thus omitted from the table. For all methods considered, V_T is remarkably stable, even for scanning times as short as 70 mins. For the other outcome measures, more scanning is required for each method. Based on this criterion, we concluded that the 1TC and LEGA methods require less scanning time than the others.

Table 2.

The minimal time scan required for stable outcome measures of V_T, BP₁ (BP is the same as BP₁) and BP₂ for models 1TC, LEGA, Basis and 1TCNI

Models	1TC			LEGA			Basis			1TCNI
ROIs	VT	BP	BP2	VT	BP	BP2	VT	BP	BP2	VT	BP	BP2
ACN	70	90	80	70	90	70	70	100	100	70	80	80
AMY	70	70	70	70	70	70	70	70	80	80	100	100
MED	70	100	100	70	100	100	70	110	110	70	100	100
MID	70	80	80	70	80	80	70	80	70	100	100	100
VST	70	70	70	70	70	70	70	70	70	80	80	90
Mean±s.d.	71±2	84±15	82±13	70±0	84±14	80±12	71±2	95±15	96±14	73±7	93±15	93±16

ACN: anterior cingulate; AMY: amygdala; MED: medial prefrontal cortex; MID: midbrain; 1TC: one-tissue compartment kinetic model (iterative fit); 1TCNI: One-tissue compartment kinetic model (noniterative fit); VST: ventral striatum.

Results are displayed for representative ROIs, but the mean and standard deviation given in the last table row is taken over all ROIs.

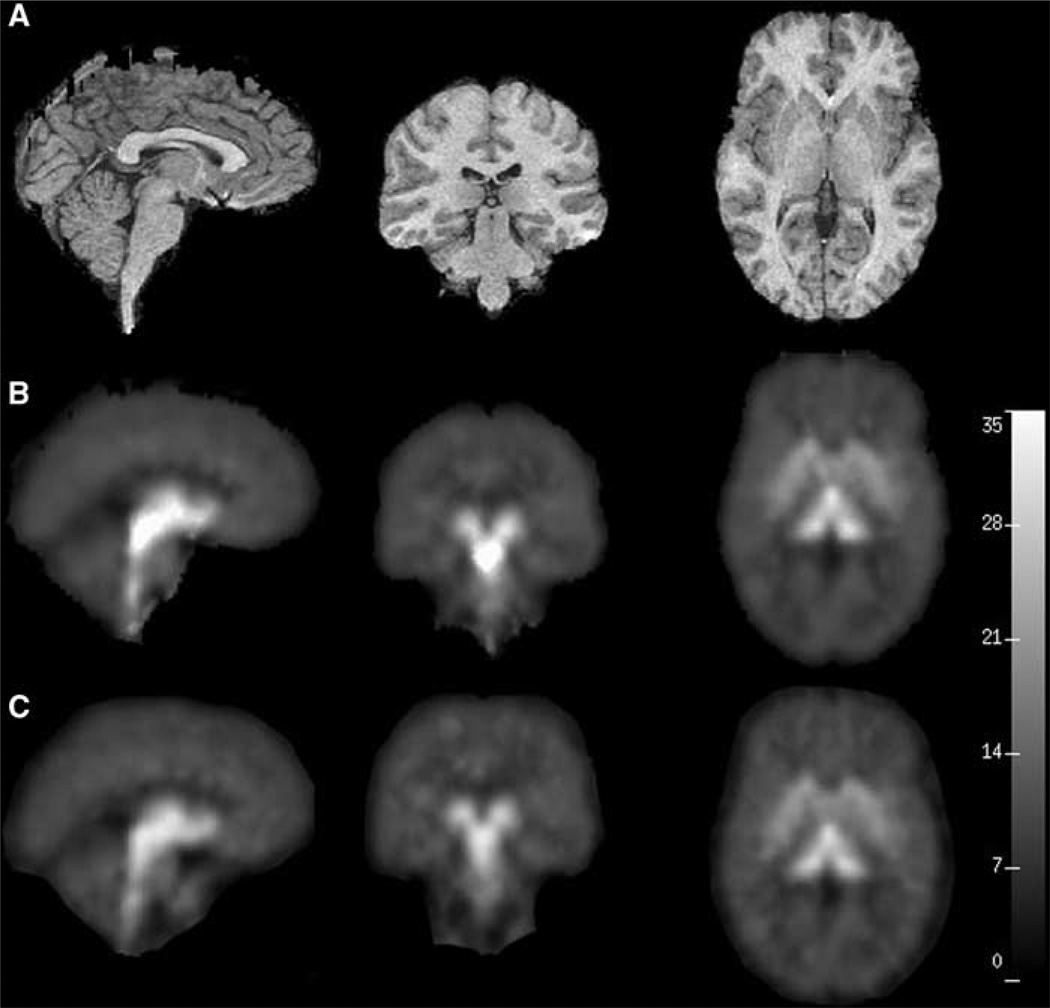
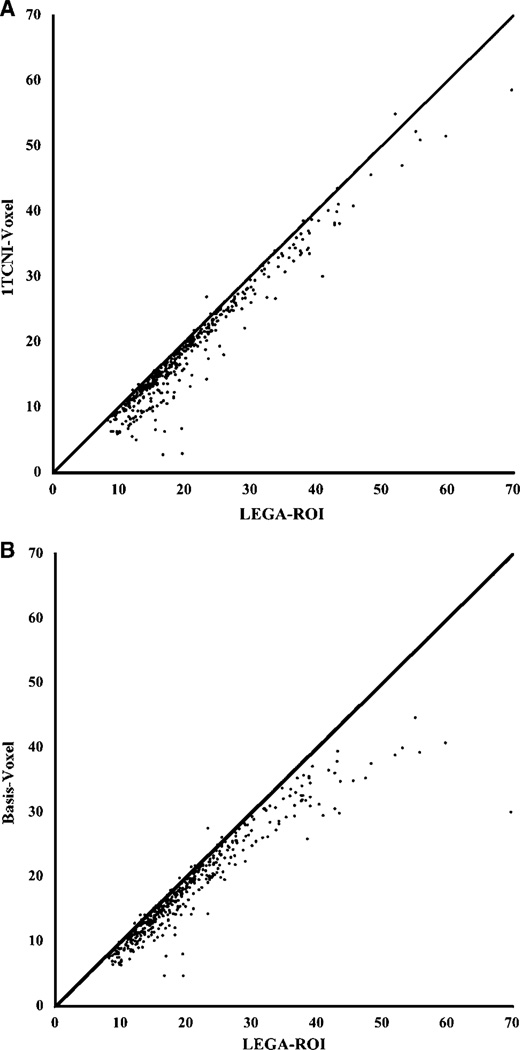
Results from the voxel-based analysis are displayed in Figure 6, Figure 7 and in Table 3. Figure 6 displays the V_T calculated for each voxel using two methods. At the voxel level a key consideration is computational time requirements so we limited our analysis to the ‘fast’ methods: 1TCNI and basis pursuit. To assess agreement between estimation at the voxel level and that at the ROI level, we plotted the estimated V_T for each region for each study (mean across all voxels in the corresponding region) against the V_T estimate from an ROI-based analysis with LEGA in Figure 7. Both of these voxel-based methods tend to slightly underestimate V_T relative to LEGA at the ROI level. This disagreement is greater for regions of higher binding for the basis pursuit method. Table 3 gives values of the various metrics considered for V_T estimates obtained by averaging 1TCNI voxel-level estimates. The ICC and WSMSS criteria are optimized for 1TCNI at 120 mins of scanning, the variance at 100 mins, and PD at 110 mins. Considering all metrics, 100 mins gives a value for 1TCNI that is fairly close to the optimal; for shorter scanning times the values worsen.

Figure 6.

(A) shows the subject’s cropped MRI. (B) and (C) show the PET images generated using 1TCNI and basis pursuit models, respectively. The three views displayed in all the panels from left to right are sagittal (slice 124), coronal (slice 71), and transverse (slice 134).

Figure 7.

Scatterplots of V_T values estimated using LEGA in ROI analysis (X-axis) versus average (all voxels in the ROI) of V_T values estimated through voxel-based analysis (Y-axis) for ITCNI (left panel) and basis pursuit (right panel). The line of identity is added to each panel for reference.

Table 3.

The values of all the metrics for the 1TCNI model obtained from the parametric images of the parameter V_T

Time (mins)	ICC	WSMSS	Var	PD
120	0.951	0.590	12.3	4.99±4.25
110	0.951	0.639	12.0	4.85±4.17
100	0.946	0.776	10.5	5.75±4.51
90	0.927	0.964	11.3	6.22±4.93
80	0.908	1.125	11.0	6.77±5.39
70	0.887	1.413	10.9	6.83±5.83

Results for the models considered at 100 mins are summarized in terms of their rankings in Table 4.

Table 4.

Ranks (1 being the best of each criterion) of four methods considered for all metrics

	1TC	LEGA	Basis	1TCNI
PD	2	1	3	4
ID	2	–	3	1
WSMSS	3	1	2	4
ICC	2	1	3	4
Var	2	4	1	3

Discussion

Our primary objective is to compare in a test/retest setting some of the various modeling approaches that have previously been used for [¹¹C]DASB imaging data. The conclusion in Ginovart et al (2001), based on fitting five subjects, was that the 1TC model provides better fit and more stable estimation than the 2TC model, and that 80 mins of scanning is sufficient. Frankle et al (2004) determined that 95 mins of scanning is sufficient for estimating V_T for the MID using a one-tissue model. We considered outcome measures that are in common use in neuroreceptor mapping studies and we compared them using six metrics that were chosen to assess properties that an optimal method will have. We considered the results both for ROI-based analyses and for voxel-based analyses. In addition, we considered all the metrics over a range of scanning durations in order to determine the optimal scanning time and modeling method.

Kinetic modeling is typically performed on TACs for ROIs, which are generated by averaging the TACs from all voxels contained within anatomically defined regions. Modeling is also often performed for each voxel separately. The advantage of the former approach is that it is more robust from a mathematical point of view, since there will be less noise as a consequence of the averaging procedure. However, this approach may miss important information in areas that do not correspond closely enough to predefined ROIs. It is therefore generally advantageous to use both approaches. Since TAC data used in the two approaches can differ widely in terms of their noise characteristics, there is no reason to believe that the same method would necessarily be superior for both ROI and voxel approaches and so these are considered separately.

Region of interest-based analysis

To simplify the comparisons, we divided the candidate methods into two groups—model-based methods (1TC, 1TCNI) and data-driven methods (basis pursuit, LEGA). We compared methods within each group according to our six metrics and determined the best overall model for each group. These methods are then compared with each other to give an overall best model for ROI-based analysis.

Model-based methods

Comparing 1TC with 1TCNI, the following can be concluded from Figures 1–5: ID is better for 1TCNI for most scanning durations; reproducibility (PD, WSMSS) is slightly better for 1TC; variability (Var) is less for 1TCNI at the two longest acquisition times, while at shorter times, it is less for 1TC; and reliability (ICC) and TS are generally better for 1TC. In summary, it appears that 1TC is generally better than its noniterative counterpart. The better ID of 1TCNI is almost certainly because of the limited number of solutions available to that method. We therefore concluded that, for ROI-based analysis, 1TC is the best of the model-based methods.

Data-driven methods

Comparing basis pursuit with LEGA, it can be seen that reproducibility (PD, WSMSS) is better for LEGA for most scanning durations; variability (Var) is lower for basis pursuit for the two longest acquisition times, while at shorter times, it is lower for LEGA; and reliability (ICC) and TS are in general better for LEGA. Based on these other metrics, we therefore concluded that, for ROI-based analysis, LEGA was the better data-driven method.

Model-based versus data-driven methods

Comparing the selected methods from each of the two groups (1TC and LEGA), we conclude that: reproducibility (PD, WSMSS) was in general better for LEGA, while variability (Var) is less for 1TC; reliability (ICC) was better for LEGA; and TS was very similar for the two methods. In summary, while conclusions about reproducibility and variability opposed each other, the reliability measure differentiated the two methods, and therefore we concluded that LEGA is the best overall method for ROI analysis.

Acquisition time

For LEGA, the reproducibility (PD, WSMSS) was quite stable with acquisition times as short as 80 mins. The normalized variance reached a minimum for a 90 mins scanning time, and the reliability measure (ICC) indicated that optimal results would be obtained by scanning for 100 mins. The TS results show that only two of the ROIs (DOR, OCC) required longer scanning time (110 mins) for BP only, according to the predefined criteria. Thus, we conclude that the optimal scanning time for these data, considering all these criteria as well as subject comfort, is 100 mins.

Considering that the data presented here were obtained from healthy volunteers, it could be argued that the results may not be valid for a patient population, especially the optimum scanning time. However, both patients with major depression (Parsey et al, 2006) and patients taking SSRIs (Parsey et al, 2006) should have lower specific binding than healthy volunteers, which would lead to faster equilibration. Therefore, the selected scanning time should be adequate in these cases as well.

In addition to the above comparisons, we also compared the methods by examining their relative ranks (Table 4). Although LEGA had higher variance than the other models considered, it had the highest rank for all other criteria and is thus the preferred model for ROI-based analysis.

Although complete results for all outcome measures are not provided here, it is noteworthy that the metrics applied to V_T data are quite good relative to those for BP. Average PD for V_T as estimated by LEGA across all subjects and ROIs is 5.51% as compared with 20.7% for BP. Also, average ICC is 0.96 for V_T as compared with 0.78 for BP. We attribute this to two factors: error in estimating f₁, but more importantly, a relatively high level of nonspecific binding throughout the brain. Thus, the reference region will have relatively high V_T values (and thus, greater noise), resulting in worse performance in these metrics, most notably in cortical regions (BP PD = 11.9 in VST, Table 7) that have less transporter than subcortical regions (BP PD = 35.8 in DOR). It may be that any ligand for 5-HTT will have high nonspecific binding and suffer from the same problem. To our knowledge no test/retest binding potential data has been published for [¹¹C]McN5652, another common ligand used in 5-HTT studies, so we are not able to compare performance of these two ligands according to these metrics. One advantage [¹¹C]DASB does have over [¹¹C]McN5652 is that it is possible to measure f₁ for [¹¹C]DASB.

Table 7.

All metrics for all regions considered for LEGA with 100 min acquisition time

ROI	PD	ICC	WSMSS	ID	Var
ACN	17.6	0.820	34.8	21.5	185
AMY	11.1	0.808	170	78.1	801
CIN	22.5	0.772	50.6	22.8	211
DCA	13.1	0.924	64.3	45.5	697
DOR	35.8	0.800	11.0	10.3	54.8
DPU	13.3	0.792	183	58.1	815
ENT	23.2	0.570	109	31.8	246
HIP	15.0	0.892	35.5	31.6	307
INS	11.0	0.763	65.6	33.4	276
MED	37.5	0.700	19.7	11.4	64.2
MID	12.6	0.926	389	169	5150
OCC	39.6	0.452	37.6	10.5	70.5
ORB	25.6	0.638	16.4	11.7	45.5
PAR	35.2	0.782	16.5	10.1	76.2
PIP	20.7	0.696	69.2	29.7	221
PPH	22.4	0.750	61.2	24.8	245
TEM	26.2	0.455	36.1	14.7	67.9
THA	17.0	0.906	214	62.5	2160
VST	11.9	0.852	282	88.7	1690

ACN: anterior cingulate; AMY: amygdala; CIN: cingulate cortex; DCA: dorsal caudate; DOR: dorsolateral prefrontal cortex; DPU: dorsal putamen; ENT: entorhinal cortex; HIP: hippocampus; INS: insular cortex; MED: medial prefrontal cortex; MID: midbrain; OCC: occipital cortex; ORB: orbital prefrontal cortex; PAR: parietal lobe; PIP: parahippocampal gyrus; PPH: posterior parahippocampal gyrus; TEM: temporal cortex; THA: thalamus; VST: ventral striatum.

Voxel-based analysis

We suggest that an appropriate voxel-based method should necessarily have close agreement with the best ROI-based method. Two analysis methods were implemented on a voxel-by-voxel basis: the model-driven 1TCNI method and the data-driven basis pursuit method. These were chosen for practical reasons, considering computational expense. When comparing the two voxel-based methods with ROI-based LEGA, we found that 1TCNI resulted in the closest agreement, and therefore this method was chosen for voxel-based analysis.

Some comments on modeling

In addition to the LEGA approach considered here, there are several other methods that have been developed in the graphical analysis framework to reduce or eliminate the noise-dependent bias demonstrated by Slifstein and Laruelle (2000). We considered LEGA because it represents an exact solution to the estimation problem by modeling the TAC noise directly and thus it inherits optimality properties associated with likelihood theory. Also, among several approaches considered in a simulation study, LEGA was found to have smallest bias, although its variance was not as small as some of the others (Joshi et al, 2005).

We did not consider any of the numerous reference-tissue-based approaches to modeling because there is detectable, displaceable SERT binding in the cerebellum (Parsey et al, 2006). In the absence of a true reference region, we use methods requiring an input function so as to minimize the error associated with estimating the outcome measures. Reference tissue approaches are limited in that the only outcome measure that is an index of B_max is BP₂; the outcome measure most sensitive to changes in cerebellar binding ((V_{T ROI}–V_{T Cer})/V_{T Cer}).

Conclusions

Based on the six metrics used to judge among competing models, we determined: 100 mins of scanning time is sufficient for quantification, the LEGA method is preferred for ROI-based analysis, and 1TCNI is the best for voxel-based analysis. Median results for the LEGA method applied to data using 100 mins scanning time are given in Table 5. The preferred outcome measure is BP, but these basic conclusions are the same for the other outcome measures as well. Estimates of all outcome measures for all subjects using the LEGA method and 100 mins scanning time, along with PD, are given in Table 6. Summary statistics for all metrics and all regions using LEGA with 100 mins of scanning time are displayed in Table 7.

Table 5.

Median metrics across all ROIs considered for LEGA with 100 mins acquisition. Note that units differ across columns

Metric	VT	BP	BP1	BP2
PD	5.51	20.73	17.2	16.46
ID	10.7	27.3	3.49	0.180
WSMSS	0.649	55.9	0.455	4.00E-03
ICC	0.963	0.782	0.890	0.775
Var	13.8	233	3.76	1.85E–02

Table 6.

All outcome measures and percent differences for midbrain (mid) and amygdala (amy) for all subjects for LEGA with 100 min acquisition time

			Subject
	ROI		1	2	3	4	5	6	7	8	9	10	11	Median
VT	AMY	Test	38.1	24.7	20.4	29.9	18.3	23.3	32.4	28.0	34.3	21.1	35.8	28.0
		Retest	35.7	21.9	19.5	29.8	19.4	25.0	28.2	27.8	33.2	23.8	35.0	27.8
		PD	6.50	11.9	4.54	0.336	5.89	6.85	13.7	0.441	3.06	12.1	2.39	5.89
	MID	Test	50.6	30.8	27.6	38.9	23.3	38.1	57.7	39.7	49.0	31.9	64.7	38.9
		Retest	50.0	30.6	25.8	41.0	27.0	36.1	55.3	38.4	47.1	34.3	58.1	38.4
		PD	1.23	0.607	6.77	5.09	14.6	5.53	4.33	3.39	4.04	7.26	10.8	5.09
BP	AMY	Test	146	95	100	123	80.8	105	131	129	169	97.7	166	123
		Retest	166	96.0	91.7	121	85.0	147	104	130	142	117	162	121
		PD	12.7	0.845	9.12	1.14	5.07	33.4	23.2	0.167	17.6	18.1	2.74	9.12
	MID	Test	232	136	160	186	124	216	324	222	285	189	382	216
		Retest	280	172	143	199	147	253	293	213	239	208	345	213
		PD	18.5	23.2	11.1	6.8	17.1	15.9	10.0	4.3	17.5	9.6	10.3	11.1
BP1	AMY	Test	21.1	14.1	12.2	17.6	9.3	14.0	17.2	16.4	21.6	11.6	22.3	16.4
		Retest	20.8	11.0	11.2	17.4	10.3	15.3	14.8	16.4	20.2	13.5	20.5	15.3
		PD	1.47	25.1	7.97	0.712	10.0	9.17	14.9	0.158	6.61	15.6	8.35	8.35
	MID	Test	33.6	20.2	19.3	26.6	14.3	28.8	42.5	28.2	36.3	22.4	51.2	28.2
		Retest	35.0	19.7	17.5	28.6	17.8	26.4	41.9	27.0	34.0	24.0	43.6	27.0
		PD	4.30	2.80	9.94	7.27	22.0	8.58	1.57	4.27	6.51	7.05	15.94	7.0
BP2	AMY	Test	1.24	1.34	1.48	1.42	1.04	1.49	1.13	1.42	1.70	1.21	1.65	1.4
		Retest	1.39	1.00	1.36	1.41	1.13	1.58	1.11	1.44	1.55	1.31	1.42	1.4
		PD	11.7	28.5	8.31	0.91	8.62	5.88	2.43	1.45	9.29	7.83	15.05	8.3
	MID	Test	1.97	1.91	2.35	2.16	1.59	3.07	2.80	2.43	2.86	2.35	3.78	2.4
		Retest	2.35	1.80	2.12	2.31	1.96	2.72	3.13	2.36	2.61	2.33	3.01	2.3
		PD	17.39	6.24	10.28	7.08	20.6	11.9	10.9	2.98	9.19	0.70	22.6	10.3
Free fraction		Test	0.144	0.148	0.121	0.143	0.116	0.133	0.131	0.127	0.127	0.118	0.134	0.131
		Retest	0.125	0.114	0.123	0.144	0.121	0.104	0.143	0.127	0.142	0.115	0.126	0.125
		PD	14.2	25.9	1.15	0.431	4.96	24.4	8.43	0.0097	11.0	2.57	5.62	5.6

AMY: amygdala; MID: midbrain.