Prospective High-Resolution Respiratory-Resolved Whole-Heart MRI for Image-Guided Cardiovascular Interventions

Abstract

Cardiovascular diseases, including arrhythmias and heart failure, are commonly treated with percutaneous procedures guided by X-ray fluoroscopy. The visualization of the targeted structures can be enhanced using preacquired respiratory-resolved anatomic data (dynamic roadmap), which is displayed as an overlay onto X-ray fluoroscopy images. This article demonstrates how dynamic roadmaps using an affine motion model can be obtained from one respiratory-resolved three-dimensional whole-heart acquisition using the previously introduced Radial Phase Encoding-Phase Ordering with Automatic Window Selection method. Respiratory motion in different regions of the heart was analyzed in 10 volunteers, and it was shown that the use of dynamic roadmaps can reduce misalignment errors from more than 10 down to less than 1.5 mm. Furthermore, the results suggest that reliable motion information can be obtained from highly undersampled images due to the advantageous undersampling properties of the radial phase encoding trajectory. Finally, results of a three-dimensional dynamic roadmap obtained from a patient before catheter ablation for atrial fibrillation treatment are presented.

INTRODUCTION

Image-guided percutaneous procedures are commonly used to assess and treat cardiovascular diseases. Their applications include diagnosis and treatment of ischemic and congenital heart disease (1) as well as cardiac arrhythmia (2–4) and heart failure (5). All these procedures benefit from high quality three-dimensional (3D) anatomical images for an accurate diagnosis, accurate treatment planning, and reliable guidance during the interventional procedure. In particular, the treatment of cardiac arrhythmias requires detailed anatomical information about the atria, ventricles, pulmonary veins, and coronary sinus. In order to ensure optimal depiction of the complex geometries this image data should be acquired with a high isotropic resolution to avoid image degradation such as partial volume effects.

The common imaging modality for catheter guidance is X-ray fluoroscopy. It offers high spatial and temporal resolution and a good catheter visualization. However, X-ray fluoroscopy suffers from low soft tissue contrast and only yields two-dimensional projection images making it difficult to visualize structures in 3D. Therefore, preacquired cardiac computer tomography (CT) data are more frequently used as a “roadmap” to provide 3D anatomical information during the procedure. Nevertheless, cardiac computer tomography data are obtained during breathhold, whereas the patient is breathing during the intervention. This can result in misalignments between the roadmap and the actual position of the anatomy (6). These alignment errors can be minimized using dynamic 3D computer tomography data, but it involves a significant radiation dose for the patient.

Magnetic resonance imaging (MRI) has recently been reported to be able to provide roadmaps for catheterization with excellent soft tissue contrast (1, 7, 8). Furthermore, it can provide additional information about cardiac function, blood flow, and myocardial scar tissue. Respiratory motion has been reported as a major challenge leading to misalignments between the roadmap and the X-ray fluoroscopy images (8). Therefore, “dynamic roadmaps” have been proposed to minimize these errors (9–11). The shape and position of the roadmap are updated according to a preacquired motion model and a motion surrogate recorded during the interventional procedure.

The complexity of respiratory motion models has been studied by several groups using X-ray angiography (12), multiple MR pencil beams (13), and cardiac 3D MR images (14, 15). It has been shown that patient-specific 3D affine motion models can describe the respiratory motion of the heart with a satisfactory degree of accuracy (10, 12, 15). In order to create such 3D affine motion models, dynamic MR data have to be acquired in addition to the 3D anatomical data, which prolong the overall scan time (10).

Here, we present an approach that yields all necessary information for a dynamic roadmap within one 3D whole-heart MR scan. It is based on the recently published Radial Phase Encoding-Phase Ordering with Automatic Window Selection (RPE-PAWS) acquisition scheme (16). It was shown that RPE-PAWS leads to an efficient acquisition of a high-resolution 3D whole-heart image while providing undersampled 3D data sets at different stages in the breathing cycle.

In this article, we investigate the use of these respiratory-resolved 3D image datasets to create a 3D affine motion model without the need for any additional data acquisition. Affine motion is determined between the different image data sets, and a motion model is created by polynomial fitting of the affine parameters over time. In contrast to previous methods (10), high-resolution data sets are used both to obtain the anatomical information for the roadmap and to determine the respiratory motion information. The images available for the motion estimation can be impaired by undersampling artefacts. Therefore, the effect of image quality on the results of the motion estimation is assessed. The 3D affine motion models are evaluated using data from 10 healthy volunteers, which have been acquired with RPE-PAWS. The motion of important anatomical landmarks (LMs) of the heart is determined, and differences between volunteers are reported. The accuracy of the affine model is quantitatively assessed. An analysis of the respiratory motion and results of the 3D dynamic roadmap from a patient before catheter ablation for atrial fibrillation treatment are presented.

METHODS

Data Acquisition and Reconstruction

Previously we have introduced RPE-PAWS to overcome the problem of long scan times due to low efficiencies using respiratory gating. In contrast to respiratory gating, where data are only recorded if a corresponding navigator signal lies within a predefined navigator window, PAWS acquires data for different respiratory motion bins, and the final image is reconstructed using data from adjacent bins (17). This approach is especially helpful for irregular breathing patterns where respiratory gating can lead to excessively long scan times (5, 18).

RPE-PAWS combines RPE (19) with a PAWS approach that uses two adjacent respiratory motion bins. RPE uses Cartesian frequency encoding with phase encoding along radial lines (Fig. 1a,b). The interleaved bit-reversed RPE scheme ensures a homogeneous distribution of acquired k-space data over the two-dimensional phase-encoding plane for undersampled data sets. Furthermore, data from two adjacent bins are complementary and can be combined for image reconstruction using a sliding window approach to improve the sampling density (Fig. 1b).

FIG 1.

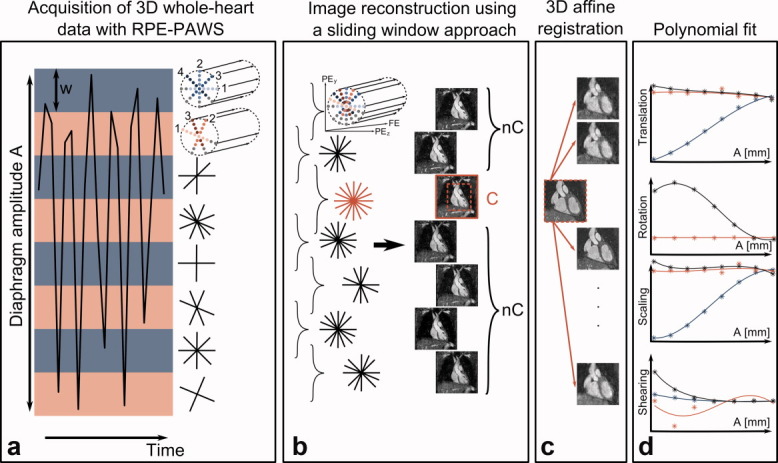
a: RPE-PAWS acquires data simultaneously in multiple bins (red/blue bars) covering the entire amplitude A of the respiratory motion of the diaphragm. The width w is defined prior to the acquisition and the number of the acquired respiratory phases N is given by A/w. Data are acquired with an interleaved bit-reversed radial phase encoding (RPE) trajectory which leads to a homogeneous covering of k-space during the entire scan and allows for the optimal combination of k-space data from adjacent bins (numbers indicate the sampling order in each bin). A further decrease of scan time can be achieved using a partial Fourier acquisition along the radial direction (color/gray = sampled/unsampeld k-space positions). bs: The scan is successfully finished if one combination of two bins yields the desired k-space information and a complete image (C) can be reconstructed. Additional images can be reconstructed from the noncomplete (nC) bin combinations. c: After selecting a region of interest around the heart the complete image (C) is registered to the noncomplete images (nC) using a 3D affine registration. d: This yields 12 affine parameters (stars) which are fitted with a third-order polynomial (line) for the final motion model. The graphs show the affine parameters for translation, rotation, scaling and shearing as a function of A for foot-head (blue), left-right (black) and anterior-posterior (red).

The scan is successfully finished if the desired k-space information is acquired in one combination of two bins. The latter shall be referred to as “complete” bin combination and the images obtained from this data as “complete” images. It is important to note that the complete data does not necessarily have to be fully sampled to provide a high-resolution image with an iterative reconstruction method. All other combinations of bins contain less data and will be referred to as “noncomplete,” i.e., higher undersampling factors depending on respiratory motion.

The respiratory bins are positioned to cover the entire amplitude A of the navigator signal. The width w of the bins has to be set prior to the data acquisition and determines the residual motion and therefore the image quality of each respiratory motion state. In addition, w defines the number of bins, i.e., number of acquired respiratory phases N = A/w (Fig. 1a). For all data presented here, the width of the bins was set to 3 mm.

For high undersampling factors, and therefore short scan times, a non-Cartesian SENSE reconstruction (20) is used. This ensures reconstruction of complete images with excellent quality and isotropic resolution as well as good image quality for noncomplete data sets. In order to speed up the data acquisition further the RPE scheme is combined with a half-Fourier approach along the radial direction (Fig. 1a,b). The image data is reconstructed off-line by performing a homodyne reconstruction along the radial direction and a subsequent non-Cartesian SENSE reconstruction.

The 3D data sets are reconstructed using a sliding window approach. Therefore, from N acquired respiratory phases, N − 1 respiratory-resolved images are obtained.

Three-Dimensional Affine Motion Model

The respiratory motion of the heart was modeled using a subject-specific 3D affine motion model M, which describes the temporal behavior of translation, rotation, shearing, and scaling. The main steps of this registration process are summarized in Fig. 1c,d. The 12 affine parameters were obtained using a custom 3D affine registration algorithm, which was applied to a 3D rectangular region of interest around the heart. The normalized cross-correlation function was used as a similarity measure. The complete image was registered to the different noncomplete images, which represent the different respiratory phases. This yielded a set of 12 affine parameters (θ₁… θ₁₂) for each registration, i.e., N − 1 different respiratory phases rph_n:

[1]

In order to create a motion model M, each of the 12 parameters θ_i [rph₁, rph₂,…rph_N-1] were fitted by a third-order polynomial as a function of the diaphragm position in millimetres. Therefore, the affine parameters are not just defined at discrete positions of the diaphragm given by the respiratory bins but can be interpolated for a continuous range of breathing stages. The fitted θ_i were then used to create a matrix defining the 3D affine transformation between the complete and the noncomplete images.

Evaluation of Heart Motion

The effect of respiratory motion was evaluated for different areas in the heart, i.e., ventricles, atria, and coronary arteries. For that, eight anatomical LMs were selected manually as lateral/medial apex, lateral/medial tricuspid valve, lateral/medial annulus, and origin of the left/right coronary artery (Fig. 3a).

FIG 3.

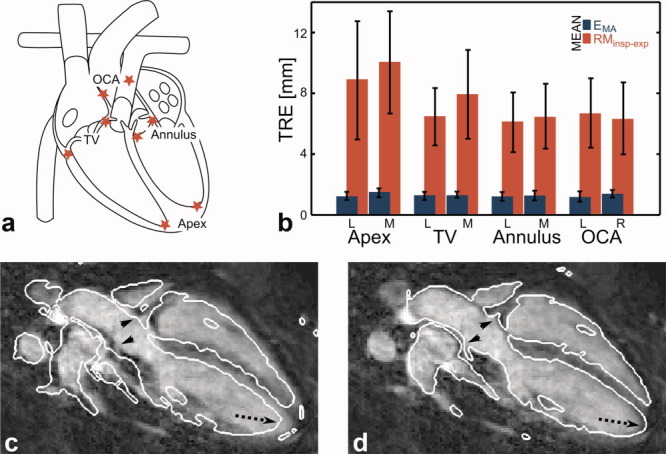
a: Eight landmarks were selected at anatomically well defined positions in the heart: lateral/medial apex, lateral/medial tricuspid valve (TV), lateral/medial annulus and origin of left/right coronary arteries (OCA). b: Mean values and standard deviation (error bars) of the displacement of landmarks between end-inspiration and end-expiration (RM_insp-exp) and the model accuracy (E_MA). c,d: The grayscale image shows an oblique plane through the heart at end-inspiration. c: The white contours were obtained from the same plane but in end-expiration exhibiting significant displacements not just in the apex (dashed arrow) but also in the area of the origin of the coronary arteries (arrow heads). d: Applying the obtained 3D affine transformation to the end-expiration image corrects for these displacements. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Effect of Undersampling on Motion Estimation

All 3D image sets, which were reconstructed from the RPE-PAWS data, had the same high isotropic resolution. However, the noncomplete images, which were used to form the motion model, could be impaired by undersampling artefacts. Therefore, their quality depended mainly on the amount of acquired k-space data in each bin, which was determined by the individual breathing pattern and thus cannot generally be predicted. The influence of image quality on the accuracy of the motion model was assessed on data that were retrospectively undersampled. For this, noncomplete sets of images containing 40, 30, 20, 15, 10, and 5% of k-space data were generated (100% correspond to the complete image) in one specific volunteer exhibiting an irregular breathing pattern allowing for this analysis, which will be discussed in more detail in the “Results” section. The k-space data were undersampled such that the data were distributed the same as if the scan had originally been stopped at 40, 30, … 5%.

In a previous study introducing RPE-PAWS, image quality parameters were analyzed as functions of k-space undersampling (16). Here, the effect of undersampling was analyzed with respect to the accuracy of motion models. For this, six motion models (M_40%, M_30%,..) were derived from the undersampled data sets and were applied to the LMs determined in the complete image. This led to six sets of predicted LMs, LM_40%, LM_30%,.., which were then compared with the LM positions predicted by the motion model M_ref created from the original data. As a means of comparison the maximum and root mean square (RMS) error of the distance between the positions of the LM points LM_ref and LM_40%, LM_30%,… were calculated:

[2]

with i = 40, 30, 20, 15, 10, and 5%, with rph = C referring to the complete image and with lm and rph describing the different LMs and respiratory phases, respectively.

The RMS error (E_US) averaged over all LMs and all respiratory phases and an increase in E_US for individual targets might not have been immediately obvious from that value. The maximum error on the other hand is sensitive to the behavior of single LMs. Therefore, a different behavior of the RMS and the maximum error as a function of undersampling would have indicated that E_US did not change evenly but showed a dependency on the LM position.

It is important to note that for this analysis the LM positions predicted by M_ref were compared to the ones predicted by M_40%, M_30%….M_5%. Therefore, any errors introduced by inaccurate selection of the position of LM were avoided and could not distort the result.

Model Accuracy

The accuracy of motion models is usually assessed using the target registration error, which describes the distance between different pairs of LMs (21). For this study, the 3D target registration error was determined for eight LM points by measuring their position in each of the noncomplete images and the position of the LMs predicted by applying the motion model M to the LM positions determined in the complete image (rph = C). In addition to the mean value and standard deviation the RMS error of the model accuracy E_MA is given as the RMS error over all N_v volunteers and all N respiratory phases:

[3]

where lm = 1…8 described the different LMs.

The LM points were visually selected, and therefore, the intraobserver and interobserver variabilities of the model accuracy were determined in order to assess the reproducibility of the evaluation.

Motion Model Application

For the final roadmap, five regions of interest for cardiac catheterization (left/right ventricle, left/right atrium, and coronary arteries) were segmented in the complete images using a semiautomatic approach (ITK-SNAP; www.itksnap.org) (22). The motion model M was applied to this roadmap and the position and shape of it were analyzed qualitatively for different respiratory phases.

EXPERIMENTS

Volunteer and Patient Studies

Three-dimensional whole-heart data were acquired in 10 healthy volunteers and one patient (43 years, due to undergo catheter ablation for paroxysmal atrial fibrillation treatment) on a 1.5-T MRI scanner (Philips Medical Systems, Best, The Netherlands) with a balanced steady-state free precession sequence using the following specifications: T₂-prep pulse (TE = 50 ms), isotropic FOV: 288 mm³, isotropic resolution: 1.5 mm³, fat suppression, 90° flip angle, TR/TE = 4.3/2.2 ms, segmented approach (TFE factor = 24) with low-high profile order. The images of the volunteers were obtained with a 32-channel cardiac phased array coil, and patient data were acquired with a 5-channel cardiac phased array coil. The data were undersampled in the angular direction, and a partial Fourier factor of 0.75 was used along the radial direction which resulted in an overall undersampling factor of 4 for the complete image. The acquisition matrix consisted of 144 phase encoding points in the radial direction and 64 radial lines. Mid-diastolic triggering was applied and each respiratory bin covered a diaphragm displacement of 3 mm. Therefore, an image for each 3 mm of the respiratory cycle is available. Written informed consent was obtained from all participants.

The effect of undersampling on the motion estimation was analyzed using data from a volunteer exhibiting a highly irregular breathing pattern. This led to a homogeneous distribution of k-space data in a wide range of bin combinations rather than a clear most probable breathing state (e.g., end-expiration) as with regular breathing patterns. Furthermore, for this volunteer, the behavior of the individual affine parameters describing the motion models was studied as a function of undersampling.

The motion of the LMs was studied between the different volunteers, and the mean motion between end-inspiration and end-expiration was calculated and standard deviation was given. Furthermore, the intraobserver and interobserver variabilities were assessed in one volunteer by determining the model accuracy E_MA for the eight LMs in all respiratory phases by the same observer twice and by two different observers, respectively. The mean and standard deviation of E_MA over the LM positions were used as a quantitative parameter.

In the data set acquired from the patient before catheter ablation treatment, the respiratory motion and the model accuracy were assessed for LMs close to the atrium (origin of coronary arteries, tricuspid valve, and annulus). Furthermore, a 3D roadmap was segmented from the complete image data, and the motion model was applied.

RESULTS

The scan was successfully finished in all 10 volunteers. The total acquisition time ranged from 8.4–14.8 min with a mean navigator efficiency of 52%. The number of obtained bins/respiratory phases was between 4 and 9 (mean 6.3) depending on the individual breathing patterns, i.e., the amplitude of the respiratory movement of the diaphragm in foot-head direction. A summary of the individual breathing parameters is given in Table 1.

Table 1.

Summary of Volunteer Study

Volunteer	NE	# Bins	# Bins ≥40%	# Bins ≥10%	# Bins rejected	Resp. amp (mm)
1	0.63	5	3	5	0	7.65
2	0.49	10	4	8	2	18.00
3	0.64	4	3	4	0	6.71
4	0.49	6	4	6	0	9.49
5	0.34	9	7	9	0	13.58
6	0.41	8	7	8	0	11.05
7	0.33	7	6	7	0	9.12
8	0.62	3	3	3	0	6.18
9	0.50	9	5	7	2	14.15
10	0.63	5	4	5	0	9.00

Navigator efficiency (NE), total number of respiratory bin combinations (# Bins), number of bin combinations containing more than 40 and 10% of k-space data compared to the complete bin combination (# Bins ≥40%, # Bins ≥10%), number of rejected bins (# Bins rejected) and the maximum of respiratory motion amplitude over all landmarks in each volunteer. Data from volunteer 5 (bold) were used to study the effect of undersampling on the accuracy of the motion estimation.

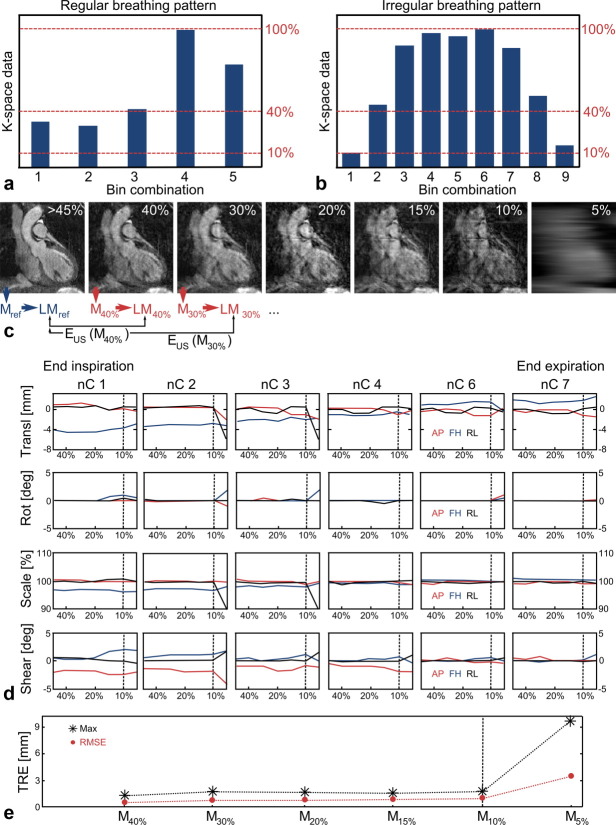
The majority of volunteers showed regular breathing patterns, which led to a well-defined most probable breathing state in end-expiration and therefore one highly populated bin combination and several other bins with considerably less data (Fig. 2a). Data from these subjects were not suitable for the analysis of the effect of undersampling on the motion model, because only a few respiratory phases were available due to the small amount of data in the noncomplete bins and only a small range of undersampling factors could have been analyzed. Therefore, for the assessment of the effect of undersampling on the motion model a volunteer exhibiting a highly irregular breathing pattern was selected (Fig. 2b). For this subject, a large number of respiratory bins with a high amount of acquired data in each of them were available. This data set consisted of one complete bin combination (100% k-space data) and eight noncomplete bin combinations containing 9.6, 45, 88, 97, 95, 87, 52, and 16% of k-space data. The percentage values describe the amount of k-space data in each combination of bins relative to the complete image. The first and the last bin combinations were not included in this analysis in order to achieve more homogeneously distributed data with at least 45% of k-space data. Figure 2c shows one slice of the reference image and one of each of the data sets, which were retrospectively undersampled to 40, 30, 20, 15, 10, and 5%. The outline of the heart is still visible for a wide range of undersampling ratios but image quality decreases strongly for the 5% case as it contains as few as three-sampled RPE lines.

FIG 2.

Assessment of the effect of undersampling on the motion model accuracy. a,b: Histogram showing the amount of k-space data acquired in different respiratory bin combinations for a regular (a) and irregular (b) breathing pattern. Only an irregular breathing pattern leads to a high number of bins with a large amount of acquired k-space data sufficient for this analysis. c: The noncomplete bin combinations (>45%) of one volunteer with an irregular breathing pattern were retrospectively undersampled to 40%, 30%, …5% of k-space data (100% correspond to the complete image). The prediction of the six motion models M_40%, M_30%,…M_5% of the position of the landmarks LM were compared to the original model M_ref. d: Behavior of 4 × 3 affine parameters for different undersampling factors. Each column represents the results of the registration of one of the non complete images (nC1, nC2,…) to the complete image. The complete image represents a respiratory phase between nC4 and nC6. Each individual image shows either translation (transl), rotation (rot), scaling (scale) or shearing (shear) in anterior-posterior (AP, red), foot-head (FH, blue) and right-left (RL, black) as a function of the undersampled motion models (>45%, 40%, 30%,…5%). The scaling of the figures was set to visualize significant changes of the parameters. e: The RMS and maximum error for different motion models. The latter were obtained from retrospectively undersampled images and compared to the motion model determined from the original data. The amount of k-space data used for the noncomplete images is given in percent relative to the complete image. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 2d shows the 4 (translation, rotation, scaling, and shearing) × 3 [anterior-posterior (AP), foot-head (FH) and right-left (RL)] affine parameters as functions of undersampling for different respiratory phases. Each column describes the results of the registration of one of the non-complete images (nC1, nC2,…) to the complete image. The complete image describes a respiratory phase between nC4 and nC6. The different columns visualize the behavior of the affine parameters for different respiratory phases. Relative to the complete data set, nC6 and nC7 show increasing translation in FH but no scaling or shearing. Moving from the complete image toward end inspiration, translation in the opposite direction, and additional scaling and shearing occurs. All parameters reach a maximum change relative to the complete data set at end inspiration.

The affine parameters show little variation for images using at least 10% of k-space data. For higher undersampling factors some parameters change strongly, which suggests that the image quality is not sufficient for a reliable image registration.

The RMS and maximum error of the motion model due to undersampling (E_US) over all seven respiratory phases and over all eight LMs for the different motion models are depicted in Fig. 2e. Both errors show a similar behavior, which suggests that the motion models describe the respiratory motion of the heart for all eight LMs equally well and the errors do not depend on the position of the LMs.

The assessment of the effect of undersampling is also summarized in Fig. 2c.

The behavior of both the individual affine parameters and of E_US suggests that a threshold of 10% of k-space data is sufficient to ensure accurate motion estimation. Therefore, this threshold was applied to all volunteer data, which meant that for two volunteers two bins each were discarded.

The quantitative analysis of the motion between end-expiration and end-inspiration of the eight LM points and the model accuracy for the different LMs was carried out on the data after excluding four bins as mentioned above. Eight LMs were selected in each respiratory phase from all 10 volunteers with a mean number of 6.3 respiratory bins leading to a total of 504 LMs. Eight points had to be removed because their visibility was strongly impaired by undersampling artefacts. The results of the analysis of the remaining 496 LMs are shown in Fig. 3b. The motion decreases with increasing distance from the diaphragm, but it is still in the range of 6 mm even for the origin of the coronary arteries. In addition, there is a considerable standard deviation between different volunteers. The mean error of E_MA lies below the voxel size (1.5 mm) for all LMs with a standard deviation between ±0.22 and ±0.41 mm (Table 2). Table 2 also includes the RMS and maximum error of E_MA. All values do not exhibit an explicit dependency on the position of the LMs.

Table 2.

Respiratory motion (RM_insp-exp) between end-inspiration and end-expiration and model accuracy (E_MA) for eight landmarks

		Apex		Tricuspid valve		Annulus		Origin of CA
		L	M	L	M	L	M	L	R
RMinsp-exp	Mean (Std) (mm)	8.85 (±3.89)	10.01 (±3.34)	6.43 (±1.90)	7.93 (±2.95)	6.10 (±1.98)	6.46 (±2.14)	6.69 (±2.29)	6.33 (±2.39)
	Min – Max (mm)	4.97 – 18.00	6.18 – 15.00	3.67 – 9.12	3.35 – 13.83	3.00 – 9.60	3.67 – 11.02	3.00 – 10.61	3.00 – 11.32
EMA	Mean (Std) (mm)	1.24 (±0.27)	1.48 (±0.36)	1.28 (±0.30)	1.30 (±0.22)	1.20 (±0.32)	1.28 (±0.36)	1.22 (±0.41)	1.38 (±0.30)
	RMSE (Max) (mm)	1.47 (2.78)	1.70 (2.73)	1.52 (2.77)	1.52 (2.71)	1.44 (2.76)	1.52 (2.75)	1.43 (2.50)	1.61 (2.70)

Mean value (Mean), standard deviation (Std), minimum/maximum (Min/Max) value and root mean square error (RMSE). CA, coronary arteries.

The intraobserver and interobserver variabilities of E_MA were found to be −0.13 mm (±0.34 mm) and −0.13 mm (±0.33 mm), respectively.

Figure 3c and d depicts an oblique plane of the 3D whole-heart data in end-inspiration. The white contour in Fig. 3c is obtained from the corresponding end-expiration image showing misalignments at the apex and also at the origin of the coronary arteries. Figure 3d shows the contour of the end-expiration image, which was transformed to end-inspiration with the obtained 3D affine motion model.

The acquisition of the patient data took 9.3 min with a respiratory gating efficiency of 59%. All of the six bin combinations contained more than 10% of k-space data and no data had to be discarded. Figure 4 summarizes the results of the patient scan. The obtained affine parameters for translation and scaling are displayed in Fig. 4a,b and snapshots of the final dynamic roadmap are shown in Fig. 4c,d for end-inspiration and end-expiration. The dominant breathing motion is scaling and translation in foot-head direction, which can be seen in Fig. 4a,b. Figure 4e shows the left and right atrium and the measured and predicted positions of 33 LMs. The amplitude of respiratory motion was more than 9 mm and the model accuracy E_MA was 1.17 mm ± 0.36 mm.

FIG 4.

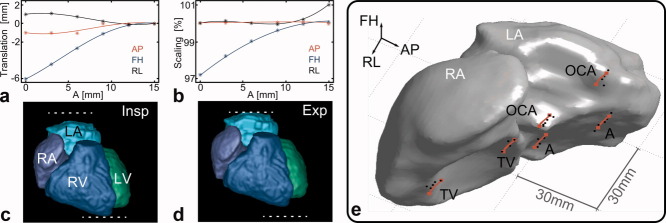
Results of the patient scan. a,b: Affine parameters describing translation and scaling in anterior-posterior (AP), foot-head (FH) and right-left (RL) direction (star: measured, line: third polynomial fit). c,d: Snapshots showing the segmented dynamic roadmap at end-inspiration (Insp) and end-expiration (Exp) (LA/RA left/right atrium, LV/RV left/right ventricle). The dominant motion components are a translation and scaling in FH. e: The measured positions (black dots) and the positions predicted by the obtained motion model (red line) of the selected landmarks displayed on the segmented RA and LA. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

DISCUSSION

The dynamic information provided by RPE-PAWS can be used to create an accurate 3D affine motion model from a single scan describing the respiratory motion of the heart in order to minimize alignment errors due to breathing. A qualitative and quantitative analysis of respiratory heart motion shows significant displacements not only at the apex but also at the base of the heart. Furthermore, a strong variability between different subjects is reported. Both the results are in good agreement with earlier studies (12, 14, 15) and emphasize the importance of patient specific dynamic roadmaps.

The mean error of the accuracy of the motion model E_MA lies below the acquired resolution of 1.5 mm. This suggests that E_MA is limited by how accurate the LM points can be defined by the observer rather than how well the affine motion model describes the respiratory motion of the heart.

The effect of undersampling on the motion model accuracy was studied on only one volunteer. Nevertheless, the obtained threshold value of 10% of k-space data has been verified in the analysis of the model accuracy on 11 subjects as it led to an accurate motion model for all volunteers and one patient.

The number of respiratory bins (e.g., the number of acquired respiratory phases) depends on the individual breathing pattern, the amplitude of the diaphragm movement A and the predefined bin width w. Some volunteers exhibit small A, which can lead to as few as four acquired respiratory phases. This could be overcome using a 3D Golden RPE trajectory (23), which would allow for a retrospective definition of different widths w.

For several volunteers bin combinations had to be excluded from the registration and motion modeling, because they did not contain enough data for reliable motion estimation. This was due to the current stopping criteria of RPE-PAWS, which has been defined for the shortest possible scan time of the complete data set rather than obtaining all noncomplete images with a certain amount of k-space data. In order to optimize the data acquisition for motion modelling a new stopping criteria based on the results from the analysis of the motion model stability could be defined. The results of Fig. 2d and e suggest that a threshold of 10% of k-space data would be enough to ensure a sufficient image quality in each bin combination for accurate affine motion estimation. Therefore, the RPE-PAWS acquisition could also be carried out until each bin combination contains at least 10% of k-space data. In this case, the k-space trajectory for complete bin combinations could be rotated by half of the angular gap between adjacent lines in order to increase the sampling density and therefore the image quality of the complete images and avoid the acquisition of redundant data. This would lead to a more predictable population of the respiratory bins and to an accurate motion model for the entire extent of the respiratory cycle with only a slight increase in scan time. Our simulations have shown that an additional scan time of about 2 min would have halved the number of excluded bins in our volunteer study.

The reported total scan time of our whole-heart acquisition is higher than commonly used respiratory gated Cartesian 3D acquisitions. This is due to the fact that RPE-PAWS provides an acquired isotropic resolution in contrast to the majority of 3D Cartesian trajectories, which use retrospective interpolation methods usually in the slice encoding direction to achieve a reconstructed isotropic resolution.

Previous studies have shown that the difference between inspiration and expiration translation can reach up to 6 mm (14). Our presented approach does not model the inspiration and expiration cycle separately. In principle, this is possible but would require the acquisition of more k-space data and thus a longer scan time. In addition, the positive effect of modeling the inspiration and expiration cycle separately has so far not been shown for cardiac roadmaps (10).

The motion model is obtained as a function of the diaphragm movement but this information is not always available during interventional procedures. Nevertheless, the 3D affine motion model also allows the use of different surrogates such as the position of a catheter at a certain anatomical location in the heart.

The non-Cartesian reconstruction of the image data is carried out iteratively, which is computationally demanding. Nevertheless, an implementation of the iterative SENSE algorithm on a graphical processor unit is possible and can strongly reduce reconstruction times (24).

CONCLUSION

We have shown that RPE-PAWS yields all the necessary information to obtain accurate dynamic cardiac roadmaps with one 3D whole-heart scan without the need of additional data acquisition. The motion of the heart during the respiratory cycle can lead to misalignment errors of more than 10 mm. The 3D affine motion models obtained from the RPE-PAWS data reduce this error to less than the acquired resolution (1.5 mm). The accuracy of the motion models is influenced by image quality and the results suggest that at least 10% of k-space data compared to the complete image is required for reliable motion estimation. Nevertheless, the beneficial undersampling properties in combination with flexible stopping criteria of RPE-PAWS can ensure an accurate motion model for all breathing phases. Finally, results from a patient scan emphasize the importance of respiratory-resolved roadmaps for cardiovascular interventions targeting thin structures such as the atrial wall and demonstrate the accuracy of our 3D dynamic roadmaps.