Predicting Gene Function from Uncontrolled Expression Variation among Individual Wild-Type Arabidopsis Plants

This study shows that expression variations among individual wild-type Arabidopsis plants grown under the same macroscopic growth conditions contain as much information on the underlying gene network structure as expression profiles of pooled plant samples under controlled major-effect perturbations, opening up new avenues to generate sufficient amounts of data for reverse engineering algorithms.

Abstract

Gene expression profiling studies are usually performed on pooled samples grown under tightly controlled experimental conditions to suppress variability among individuals and increase experimental reproducibility. In addition, to mask unwanted residual effects, the samples are often subjected to relatively harsh treatments that are unrealistic in a natural context. Here, we show that expression variations among individual wild-type Arabidopsis thaliana plants grown under the same macroscopic growth conditions contain as much information on the underlying gene network structure as expression profiles of pooled plant samples under controlled experimental perturbations. We advocate the use of subtle uncontrolled variations in gene expression between individuals to uncover functional links between genes and unravel regulatory influences. As a case study, we use this approach to identify ILL6 as a new regulatory component of the jasmonate response pathway.

INTRODUCTION

A classical dogma in systems biology states that in order to study a biological system, one needs to systematically perturb the system, measure the response, and construct a model that predicts the outcome of future perturbations (Ideker et al., 2001). For instance, molecular biologists often profile the mRNA expression response to controlled perturbations, such as environmental or chemical treatments or genetic knockouts. Because reproducibility is a cornerstone of the scientific method, such experiments are invariably performed in a tightly controlled setup (Richter et al., 2011). Great care is taken to control the boundary conditions and to keep unwanted external influences in check. Variability among individuals is smoothed out by pooling biological materials and averaging over biological replicates. Moreover, in order to overpower any residual uncontrolled effects, the perturbations applied to the system under study are often rather harsh, causing the system to operate outside its normal range.

Even when taking such precautions, the reproducibility of expression profiling experiments is often poor, in part because reproducing particular experimental conditions is hard even when detailed information on the original setup is available (Schilling et al., 2008). To assess the within- and between-lab reproducibility of leaf growth-related (molecular) phenotypes, Massonnet et al. (2010) recorded the gene expression profiles of 41 individual leaves at the same developmental stage (leaf 5, stage 6.0), taken from Arabidopsis thaliana plants of three accessions (Columbia-4, Landsberg erecta, and Wassilewskija) grown in six different laboratories. Despite the fact that the participating labs adhered to a standardized and very detailed protocol, significant intra- and interlaboratory variability in gene expression was found. The authors concluded that small variations in growth conditions within and across labs may lead to substantially different gene expression profiles.

The key question addressed in this study is whether we can use such uncontrolled expression variations to our advantage in a reverse engineering context (i.e., to unravel the wiring of an organism). We reanalyze the gene expression data set of Massonnet et al. (2010) and compare its functional prediction performance to that of same-sized compendia of Arabidopsis gene expression experiments profiling the response to controlled perturbations on pooled plant samples. We show that, from a guilt-by-association perspective, subtle uncontrolled variations among individual leaves are as informative as experiments monitoring more severe controlled perturbations in pooled samples. Since it is often practically infeasible to define and perform the tens to hundreds of controlled perturbations needed to unravel (part of) a transcriptional regulatory network, our findings may open up novel avenues to generate sufficient amounts of data for reverse engineering algorithms.

RESULTS

Residual Gene Expression Differences Yield Biologically Relevant Expression Modules

The gene expression data set of Massonnet et al. (2010) contains expression profiles of leaves of three accessions grown in six different labs (see Supplemental Table 1 online), which causes a substantial proportion of the expression variance among leaves to result from lab and accession effects (see Supplemental Figure 1 online). Accession, lab, and lab × accession effects explain on average 14.9, 19.7, and 12.8% of the expression variance of a single gene, respectively, whereas the residual error contains 52.5% of the variance on average (median values 9.9, 17.0, 11.4, and 53.8%, respectively). Although the variance induced by lab or accession effects may well contain biologically relevant information, we were primarily interested in analyzing the gene expression variation among comparable individual plant leaves grown under comparable macroscopic growth conditions. Substantial lab and accession effects, by virtue of not being independent and highly redundant across the leaves profiled, are expected to largely overpower the residual variation of interest when calculating coexpression links (see below). Therefore, we used a two-way unbalanced design analysis of variance (ANOVA) model to remove lab, accession, and lab × accession effects from the data set (see Methods). The residuals of this ANOVA analysis (i.e., the unexplained expression differences among the 41 individual leaves, further referred to as the residuals data set) are the basis of all following analyses.

We used the ENIGMA algorithm (Maere et al., 2008) to calculate expression modules from the residuals data set and 1000 randomly assembled compendia of 41 gene expression profiles of controlled perturbational treatments on pooled Arabidopsis leaf or shoot material (referred to as the sample data sets; see Methods). The log-scaled residuals data set is best fit by a Student's t location-scale distribution with a df parameter of 3.70, whereas the sample data sets exhibit a t distribution with df in the range 1.41 to 2.31, indicating that the log ratio distributions of the sample data sets contain somewhat heavier tails (i.e., more expression values that are substantially up- or downregulated with respect to the normal expectation) (see Supplemental Figure 2 online). This may not come as a surprise given that the sample data sets include experiments profiling gene expression responses to major-effect perturbations, as opposed to the residuals data set. The ENIGMA algorithm requires discretization of expression values into the categories “upregulated,” “downregulated,” and “unchanged” (or “undecided”) (Maere et al., 2008). The algorithm was originally intended for detecting significant “co-differential expression,” a hybrid measure between coexpression and differential expression that essentially indicates whether two genes are significantly up- or downregulated together over at least a subset of the conditions profiled. The underlying rationale is that simple coexpression measures, such as Pearson's correlation, may be misleading in cases where coregulated genes respond qualitatively the same, but quantitatively different to a series of different regulatory inputs. Discretization of the gene expression response into up/down/unchanged removes some of the quantitative disturbances that may obfuscate coexpression patterns and allows for the use of combinatorial statistics to assess significant codifferential expression relationships over part of the condition set instead of the entire set (Maere et al., 2008). Since statistically motivated differential expression P values can only be computed for perturbational data sets with biological replicates, such as the sample data sets, but by design not for the residuals data set, we used a uniform log ratio threshold instead to define up- and downregulated gene expression values in all data sets. Therefore, “differential” expression in this context is not motivated in terms of statistically rigorous differential expression P values, but merely serves as a means to discretize the expression values for ENIGMA analysis and to separate noise (technical noise and some forms of intrinsic stochastic noise) from potentially valuable signal. All mentioning of “differential” expression in the remainder of the article should be interpreted accordingly. For thresholds in the appropriate range (i.e., before the distribution tails start flattening out), the residuals and sample data sets contain numbers of differential log ratio expression values in the same range. We fixed the log₂ ratio threshold at 0.3498 (i.e., the standard deviation of the residuals data set), corresponding to a fold change threshold of 1.274 (see Supplemental Figure 3 online).

Interestingly, we observed that the residuals data set still provides enough signal to discriminate biologically relevant expression modules (Figure 1; see Supplemental Data Sets 1 and 2 online). Sister plants (same lab, same ecotype) often exhibit different residual expression responses in a given module (i.e., the module genes are upregulated in one sibling plant and downregulated in another; Figure 1), indicating that the modules are not formed by lingering lab or accession effects that were not removed by ANOVA analysis (i.e., effects that are nonlinear on log scale; see Methods), in contrast with many of the modules learned from the original data set (see Supplemental Data Sets 3 and 4 online). The set of modules learned from the residuals data set contains modules that are significantly enriched in, among other processes, photosynthesis, ribosome and chromatin assembly, proteolysis, secondary metabolism, response to wounding, bacteria, chitin and jasmonic acid (JA) stimulus, response to temperature, water, and nutrient levels, and starch catabolism (see Methods and Supplemental Data Set 2 online). The fact that the recovered modules are enriched for a variety of biological processes indicates that the residuals are not merely noise, but are to a large extent defined by genuine differences in the expression response of particular regulons, presumably caused by subtle uncontrolled variations in the growth conditions of individual plants (see below).

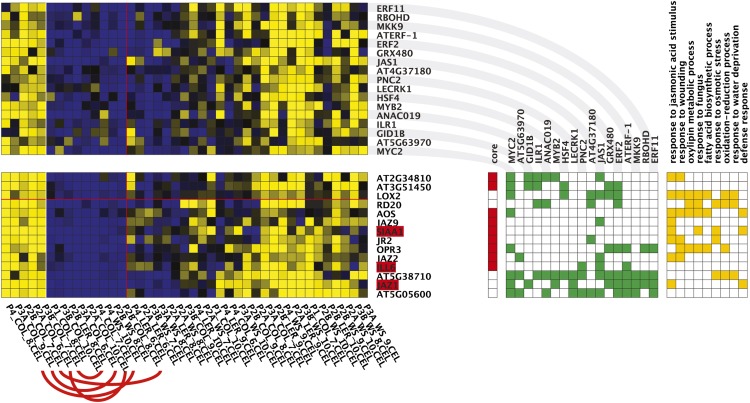
Figure 1.

Co-differential Expression Module Enriched for Response to JA Stimulus Genes, Obtained with ENIGMA (Maere et al., 2008) on the Residuals Data Set.

Yellow/blue squares indicate up-/downregulated gene expression with respect to the baseline leaf expression of the gene concerned. The bottom matrix contains the expression profiles of the module genes, while the top matrix contains the expression profiles of predicted regulators of the module. Significant co-differential expression links between the regulators and the module genes are indicated in the green matrix to the right. Genes highlighted in red are regulators that are part of the module. Genes indicated as core genes belong to the original module seed, and other genes were accreted by the seed in the course of module formation (Maere et al., 2008). Gene annotations for enriched GO categories are indicated in the orange matrix to the right. Sister plants (same lab, same ecotype, indicated by red arcs for the first two condition leaves) often end up in different condition leaves in the module, indicating that expression variations between individual plants, and not residual lab or accession effects, are responsible for the formation of the module.

Gene Function Prediction Performance

The co-differential expression networks obtained in the first step of the ENIGMA algorithm were used to assess the gene function prediction performance of the residuals and sample data sets. Topologically, the residuals network and the sample networks contain comparable numbers of genes and co-differential expression links (edges) and a similar network density and clustering coefficient (Table 1). Forty-eight genes in the residuals network are not observed in any sample network, but there is no obvious functional theme among them. For most Gene Ontology (GO) (Ashburner et al., 2000) categories, the residuals network contains similar numbers of annotated nodes as the average sample network (see Supplemental Data Set 5 online), but the residuals network contains a significantly higher fraction of genes which are not annotated in the GO database (Table 1). Well-represented categories in the residuals network (relative to the sample networks) include categories related to secondary and lipid metabolism, cell wall biogenesis, and pollination. Several photosynthesis- and amino acid metabolism-related categories are relatively poorly represented (see Supplemental Data Set 5 online).

Table 1. Topological Parameters for the Residuals and Sample Co-differential Expression Networks.

Topological Parameters	Residuals Network	Sample Networks	P Value
No. of nodes	11,474	10,695 ± 2,606	0.409
No. of edges	165,455	152,017 ± 156,476	0.314
Network density	0.0025	0.0021 ± 0.0012	0.240
Clustering coefficient	0.2388	0.2111 ± 0.0371	0.211
Unannotated gene fraction	0.2210	0.1841 ± 0.0139	0.005

For the sample networks, mean values ± 1 sd are indicated. Approximate P values are based on the rank of the residuals network relative to the 1000 sample networks.

The presence of a particular gene or biological process in a network does not automatically indicate that the network provides biologically relevant connections for that gene/process. To evaluate the function prediction performance of the residuals and sample networks, we predicted the function of all genes based on the function of their network neighbors and used the available GO annotations as a gold standard to score precision (proportion of predictions that are true positives) and recall (proportion of known annotations recovered by the predictions) for each network over the prediction false discovery rate (FDR) threshold range 10e-2 to 10e-11 (see Methods). The F-measure (harmonic mean of precision and recall) was used as a single integrated measure of prediction performance. An unavoidable pitfall in this approach is the occurrence of false positive and false negative functional annotations in the GO reference set, undermining its use as a gold standard. Although the calculated precision and recall values may therefore deviate from the real values, our approach is still useful for comparative purposes, since similar biases presumably exist for all networks. If any differential bias would exist, one may be inclined to think it might be a bias favoring the sample networks, since comparatively more of the existing GO annotations and supporting experimental evidence can be assumed to derive from major effect perturbations on pooled plant samples, as in the sample data sets, than from minor effect perturbations on individual plants, as in the residuals data set. The fact that significantly more functionally nonannotated genes are recovered in the residuals network than in the average sample network (Table 1) may point in this direction, but this can hardly be taken as solid evidence for a differential bias.

Overall, the residuals network produces slightly more predictions for slightly more genes than the average sample network at each FDR threshold (see Supplemental Figure 4 online). For more stringent FDR thresholds, the resulting number of predictions per predicted gene is substantially larger for the residuals network than for the average sample network, reaching the 90th sample networks percentile at FDR = 10e-11. The prediction performance of all networks was assessed for a wide range of GO categories (see Supplemental Figure 5 online), which were classified in five performance categories depending on their F-measure scores for the residuals network relative to the sample networks over the entire prediction FDR range (see Methods). Performance plots for some representative GO categories are depicted in Figure 2 (see Supplemental Data Set 6 and Supplemental Figure 5 online for other categories). The residuals network outperforms the majority of the sample networks for functional categories, such as response to wounding, defense response, response to fungus, drought and salt stress responses, response to JA, abscisic acid (ABA), and ethylene stimulus, cell communication, lipid and carbohydrate metabolism, and leaf development. On the other hand, the residuals network scores comparatively worse for categories such as response to light intensity, desiccation, insect, virus, UV and DNA damage, photosynthesis, responses to auxin and brassinosteroids, cell cycle, cell differentiation, tropic responses, and root and flower development. Other categories such as oxidative stress, temperature and starvation responses, response to bacteria, salicylic acid–mediated signaling, translation, and secondary metabolism score average. A noticeable trend for many GO categories is that for more stringent FDR thresholds, the function prediction performance of the residuals network increasingly improves relative to that of the sample networks (see, for example, “response to mechanical stimulus” in Figure 2).

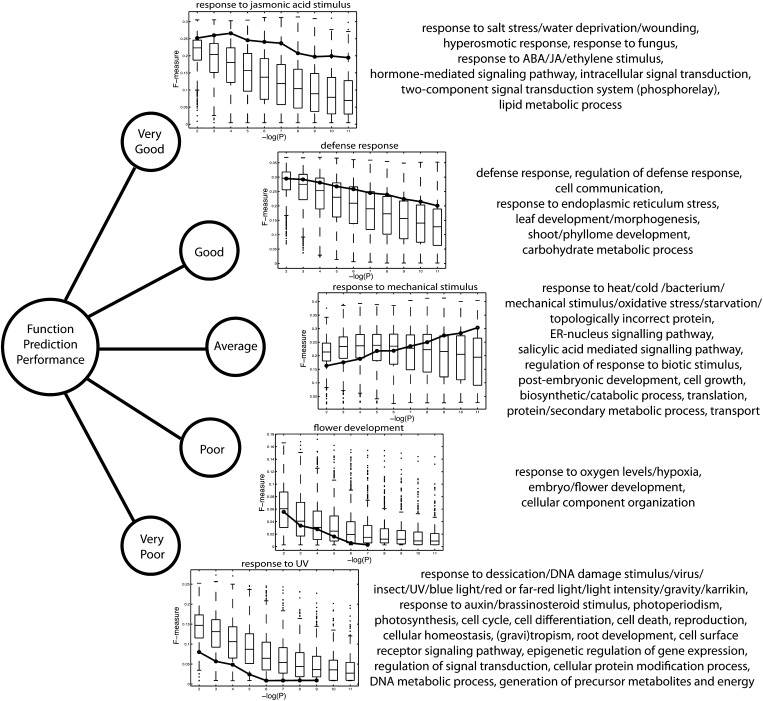
Figure 2.

Process-Specific Function Prediction Performance.

Biological processes were subdivided into five performance categories based on the average deviation of the residuals network F-measure from the 25th, 50th, and 75th percentiles of the sample network F-measures over the entire FDR range (very good = above the 75th percentile on average; good = on average between the 50th and 75th percentile but closer to the 75th percentile; average = closest to the 50th percentile on average; poor = on average between the 25th and 50th percentile but closer to the 25th percentile; very poor = below the 25th percentile on average; see Methods). An F-measure versus -log(P) (FDR threshold) plot is shown for one representative process per category. Box-and-whisker plots indicate the F-measure distribution over all 1000 sample networks at any given FDR threshold, and the solid line depicts the F-measure trend for the residuals network. Boxes extend from the 25th to the 75th percentile, with the median indicated by the central black line. Whiskers extend from each end of the box to the most extreme values within 1.5 times the interquartile range from the respective end. Data points beyond this range are displayed as little black circles. The categorization of other processes is shown on the right (see Supplemental Data Set 6 online for performance plots and Supplemental Figure 5 online for a depiction of the tested categories in their GO context). Categories related to environmental stress factors that cannot easily be homogenized across plants generally score above average, as well as the corresponding hormonal responses, while categories related to stresses that are largely absent under lab growth conditions score below average.

Next to the process-centric performance assessment described above, we used a gene-centric method to score the overall gene function prediction performance of all networks (see Methods; Figure 3). Recall values for the residuals network are situated around the 50th percentile of the sample networks over the entire FDR range, but precision scores generally stay below the 25th percentile. The lower precision values of the residuals network with respect to the sample networks may be taken to indicate a genuinely larger amount of false positive gene function predictions. Alternatively, given the incompleteness of the Arabidopsis GO annotation (Lamesch et al., 2012), it could conceivably be caused by the positive identification of a larger amount of false negative functional annotations in the GO reference set, in particular if, as hypothesized above, there were a bias of known GO annotations toward predictions made by the sample data sets, which remains to be proven. As a result of the lower precision values, the global gene function prediction performance of the residuals network at FDR = 10e-2 scores below the 27th percentile of the sample networks (Figure 3), but as was the case for many individual GO categories, the residuals network performance increases relative to that of the sample networks for more stringent FDR thresholds, culminating in an F-measure equal to the 55th sample network percentile for FDR = 10e-11. A relative increase of the residuals performance with respect to the sample networks for more stringent FDR thresholds may be expected if there were a bias of the existing GO annotations toward the sample data set predictions. In that case, one would expect a more fair performance balance between the residuals and sample networks for the most confident predictions (which are arguably the most likely to be recovered from any data set) and an increasing bias for predictions at the higher end of the FDR range, as observed in Figure 3. But again, despite being suggestive, this can hardly be taken as solid evidence for the existence of any bias.

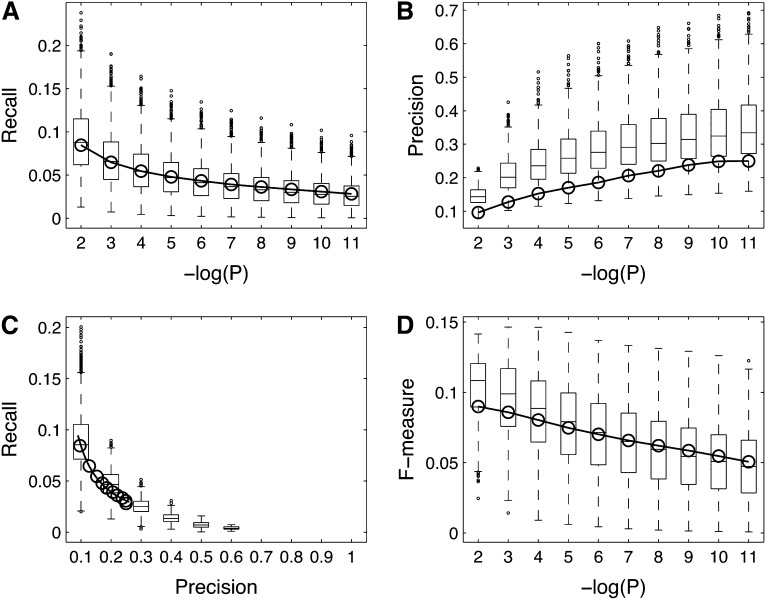
Figure 3.

Global Function Prediction Performance.

Plots in (A) to (D) depict the performance of the residuals network (open circles and solid line) and the sample networks (box-and-whisker plots) based on the use of a gene-centric method (Deng et al., 2004) to score the recall and precision of function predictions across all genes in a given network. Boxes extend from the 25th to the 75th percentile, with the median indicated by the central black line. Whiskers extend from each end of the box to the most extreme values within 1.5 times the interquartile range from the respective end. Data points beyond this range are displayed as little black circles.

(A) Recall as a function of the prediction FDR threshold.

(B) Precision versus prediction FDR threshold.

(C) Precision-recall curve.

(D) F-measure as a function of the FDR threshold. Whereas the recall values for the residuals network are situated around the 50th percentile of the sample networks, precision values are generally below the 25th percentile. The combined F-measure score of the residuals network ranges from the 27th sample network percentile for FDR = 10e-2 to the 55th percentile for FDR = 10e-11.

JA Signaling Case Study

Response to JA stimulus (GO:0009753) is one of the best scoring functional categories in the functional prediction performance assessment described above. To assess whether the residuals data set can be used to successfully predict the involvement of novel genes in this process, we screened all networks for novel candidate genes that are a priori annotated as biological regulators (GO:0065007) but are not known to be involved in the JA signaling response (see Methods). ILL6 came out as the top predicted novel candidate regulator in the residuals network (P = 3.33e-09), with a substantial lead over other candidate genes (see Supplemental Table 2 online). The ILL6 prediction was supported by 598 out of 1000 sample networks and ranked as the top prediction in 285 of those networks. At least one other computational study also predicted ILL6 to be involved in the response to JA stimulus (Heyndrickx and Vandepoele, 2012), but hard experimental evidence has been lacking until now.

We took a reverse-genetics approach to investigate the possible role of ILL6 in jasmonate signaling. Two homozygous T-DNA insertional mutant lines, ill6-1 and ill6-2, were identified in which no full-length transcript of ILL6 was detectable by RT-PCR (see Supplemental Figure 6 online). To examine the mutants’ sensitivity to the hormone, these plant lines and the wild-type, Columbia-0 (Col-0), were grown on various concentrations of methyl jasmonate (MeJA), and the root lengths and shoot weights were determined (Figures 4A and 4B). Analysis of these data indicate that the roots of ill6-1 and ill6-2 are significantly shorter and the rosettes weigh significantly less than those of the wild type across all levels of MeJA treatment (P = 0.0011 and P < 0.0001, respectively; see Methods for details on statistical analyses). There is also a slight but significant (P = 0.0298) genotype × MeJA treatment effect in terms of shoot weight response to MeJA. Thus, the mutants are slightly but significantly more sensitive to exogenous jasmonate than the wild type. Furthermore, liquid chromatography–tandem mass spectrometry analysis revealed that the two mutants both accumulate substantially more wound-induced jasmonoyl-Ile (JA-Ile) than the wild type (Figure 4C; P = 0.0001 for the genotype effect and P = 0.0003 for the genotype × time interaction effect). Together, these data are consistent with ILL6 acting as a negative regulator of the jasmonate response. It is an attractive hypothesis that ILL6 could be a JA-Ile hydrolase, cleaving the JA-Ile amide bond in vivo and releasing Ile and molecularly inactive JA. ILL6 is a member of a family of proteins whose founding member, ILR1, has been characterized as an auxin-Leu hydrolase (Bartel and Fink, 1995), while a second member, IAR3, is known to be an auxin-Ala hydrolase in Arabidopsis (Davies et al., 1999). Furthermore, the IAR3 homolog from Nicotiana attenuata, Na IAR3, was recently shown to be a JA-Ile hydrolyzing enzyme (Woldemariam et al., 2012). We expressed a recombinant ILL6 protein in Escherichia coli, but to date we have not detected any JA-Ile hydrolase activity from this protein, nor have we seen in vitro activity on several other tested JA–amino acid conjugates.

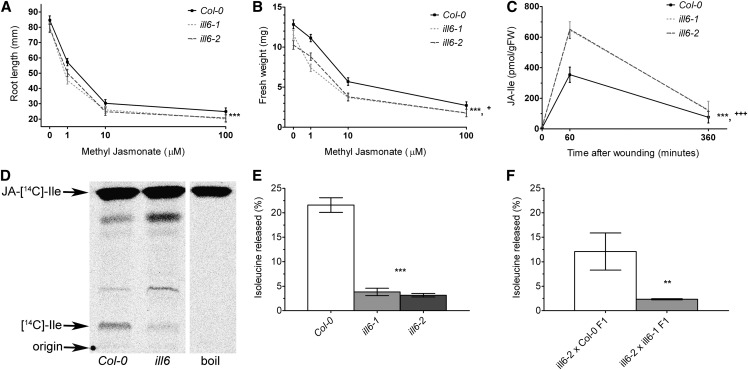
Figure 4.

ILL6 Negatively Regulates JA Response and Wound-Induced JA-Ile Accumulation, Likely through Hydrolysis of JA-Ile.

(A) Response of mutant and wild-type Arabidopsis seedlings' root length to exogenous MeJA. Seedlings were exposed to media containing 0, 1, 10, or 100 µM MeJA for 8 d (n ≥ 16 seedlings).

(B) The rosettes of the plants in (A) were excised from the roots and weighed (n ≥ 16 seedlings).

(C) Time course of wound-induced JA-Ile accumulation. Plants were wounded and damaged leaves were harvested at the indicated time points after wounding and JA-Ile accumulation was analyzed by liquid chromatography–tandem mass spectrometry (n = 6 plants across two independent experiments).

(D) Representative in vivo JA-[¹⁴C]Ile hydrolysis assay. JA-[¹⁴C]Ile was applied to individual plant leaves of the indicated genotype, and extracts were separated by thin layer chromatography and visualized by autoradiography.

(E) In vivo hydrolysis of JA-[¹⁴C]Ile in ill6 mutants and the wild type. Autoradiograms were quantified by densitometry (n ≥ 9 plants across five independent experiments).

(F) ill6-1 and ill6-2 are allelic mutations. The two F1 hybrids indicated were subjected to an in vivo hydrolysis assay as in (D) and (E) (n = 3 plants).

For all plots, data represent mean ± se, and asterisks indicate significance of genotype effects: *P ≤ 0.05, **P ≤ 0.01, and ***P ≤ 0.001. The plus sign indicates P ≤ 0.05 for the genotype × MeJA interaction effect in (B), and three plus signs indicates P ≤ 0.001 for the genotype × time interaction effect in (C) (see Methods for details on statistical analyses).

To address the in vivo activity of this protein, we examined the metabolic fate of exogenously applied radiolabeled JA-Ile (see Methods). JA-[¹⁴C]Ile was applied to individual leaves of wild-type and ill6 mutant plants, and after 24 h, ethanolic extracts of these treated leaves were separated by thin layer chromatography (Figure 4D). Autoradiographic detection revealed that whereas boiled leaf controls produced no detectable radiolabeled metabolic products of JA-[¹⁴C]Ile, ∼20% of the radioactivity applied to the wild-type Col-0 was released as free [¹⁴C]Ile. This result was in marked contrast to either ill6 mutant, in which only 4% of applied radioactivity was released as [¹⁴C]Ile (Figure 4E; log₁₀-transformed one-way ANOVA F-test P < 0.0001). Next, for a complementation test, we crossed ill6-2 as the pollen donor to both Col-0 and ill6-1. In the F1 hybrids between the mutant and wild type, we observed a release of 12% of applied radioactivity as [¹⁴C]Ile, whereas in the F1 hybrids between the two mutants, we observed little release of [¹⁴C]Ile, similar to both mutant parents (Figure 4F; t test on log₁₀-transformed data, P = 0.0067). This complementation test thus indicates that the biochemical defect in JA-[¹⁴C]Ile hydrolysis is due to the ill6 mutant lesions. Collectively from these data, we conclude that ILL6 is a negative regulator of jasmonate accumulation and response, likely through its role as an amidohydrolase of JA-Ile, though formally we cannot exclude the possibility that ILL6 acts on an in planta–produced derivative of JA-Ile.

Literature Screen for Direct and Indirect Evidence Supporting the Top 10 Residuals Predictions for Various GO Categories in the “Very Good” Performance Class

Above, we provide evidence validating the functional prediction of a gene (ILL6) that is also predicted to be involved in the JA signaling response by the majority of sample networks and that as such cannot be regarded as a prediction that is unique to the residuals network. In fact, for most of the categories we screened, there are barely any residuals predictions that are not supported by at least one sample data set (e.g., there are only two such predictions out of 31, for “response to JA stimulus;” see Supplemental Table 2 online), showing that the residuals data set does generally not make predictions that are beyond the reach of any other data set. Although high-confidence residuals predictions that are made by a higher number of randomly sampled compendia, such as the ILL6 prediction, may to some extent be viewed as being more supported and may be prioritized as such for wet-lab testing, residuals predictions that are rarely recovered by the sample data sets may, if validated, point to specific advantages of profiling uncontrolled expression variation across individuals.

To investigate the added value of profiling expression responses to micro-environmental variability among individuals in more detail, we screened literature for direct or indirect evidence supporting the top 10 novel predictions for six GO categories that were classified in the “very good” prediction performance category, namely, the response to JA, ABA, and ethylene stimulus, response to fungus, response to salt stress, and response to water deprivation. Although literature screens can arguably never be all-encompassing, we did find reports describing direct (indirect) experimental evidence for one (two) JA predictions, three (one) ABA predictions, one (two) ethylene predictions, two (two) response to fungus predictions, one (0) response to salt stress predictions, and 0 (one) response to water deprivation predictions out of the top 10 for each category (see Supplemental Tables 2 to 7 online). As for the direct evidence, these are essentially earlier findings that have not yet been incorporated in the GO database, and our associated predictions can as such not really be regarded as novel, although supported. The indirect evidence references given in Supplemental Tables 2 to 7 online link the predicted gene to a process or pathway related to the target process or describe direct evidence for a homolog of the predicted gene in another species. Although more than half (10/16) of the top 10 residuals predictions for which we recovered supporting experimental evidence in literature are also predicted by a sizeable proportion of sample networks (14.6 to 41.7%), we did find a substantial number (6/16) of supported residuals predictions that are only predicted by <10% of the sample networks, in particular among the indirectly supported predictions (4/8, as opposed to 2/8 for directly supported predictions). Directly supported residuals predictions that are uncovered by <10% of the sample networks include the involvement of AZF1 (3.8%) in the response to ABA stimulus (Kodaira et al., 2011) and TGA5 (0.3%) in ethylene signaling (Zander et al., 2010) (numbers in parentheses indicate sample network prediction percentages). Indirectly supported residuals predictions include the involvement of APK1 (8.8%) in JA signaling, MPK1 (0.7%) and JAZ1 (7.0%) in ethylene signaling, and CRT3 (1.6%) in the response to water deprivation. APK1 was previously reported to be involved in the synthesis of glucosinolates and sulfated 12-hydroxyjasmonate (Mugford et al., 2009). MPK1 activity was shown earlier to be repressed by the ethylene response regulator CTR1, but the physiological relevance of MPK1 downregulation for ethylene signaling responses is still unclear (Yoo et al., 2008). JAZ1 was reported to interact with and repress the ethylene-stabilized transcription factors EIN3 and EIL1 (Zhu et al., 2011). And a putative ortholog of CRT3 in wheat (Triticum aestivum) was previously shown to be involved in drought stress response (Jia et al., 2008). Although we do not claim that the residuals data set is superior for all functional prediction purposes, these results suggest that the residuals data set can produce valid novel predictions that are seldom recovered from randomly sampled perturbational data sets.

DISCUSSION

We reanalyzed a set of gene expression profiles of single wild-type Arabidopsis leaves of three accessions grown in tightly controlled growth room conditions across six labs. We focused on the residual expression differences that remain among the profiled leaves after controlling for lab and/or accession-dependent gene expression effects. Intriguingly, these residuals, generally considered experimental noise, still harbor a remarkable amount of biologically relevant expression variation, comparable to the information content of same-sized expression compendia incorporating traditional large-effect perturbations on pooled plant samples. Our analyses show that the expression variations among the individual plants are not random, but most likely reflect subtle differences in their growth environment, in spite of the detailed protocol used to control the experimental growth conditions (Massonnet et al., 2010). In support of this notion, many of the stress responses to environmental factors that are difficult to rigorously homogenize in even the best of experimental setups, such as salt, water, and infestations by fungi, score above average in our gene function prediction performance assessment, while responses to factors that are more easily controlled or homogenized across plants in lab conditions, such as oxygen levels, light intensity, UV, and insects, score below average. In between these extremes are responses to factors that may have been controlled to an intermediate extent in the original setup, such as temperature, oxidative stress, mechanical stimulus (e.g., through plant handling), and starvation (Massonnet et al., 2010). Responses to relatively harsh stresses, such as desiccation, which arguably did not impact the lab-grown plants in the original experiment (Massonnet et al., 2010), score comparatively worse than responses to milder or more generally defined stresses, such as water deprivation. In addition, processes that are thought to have a low impact on gene expression in fully expanded leaves as profiled in the original study (Massonnet et al., 2010) (e.g., cell cycle, cell differentiation, and auxin and brassinosteroid signaling) are generally not well represented in the gene network learned from the residuals data set, whereas several hormone signaling pathways associated with responses to various biotic and abiotic stresses (JA, ABA, and ethylene) score well above average.

In addition to assessing its capacity to recapitulate known gene functions, we used the residuals data set to predict the involvement of novel genes in regulating six of the best performing processes in our prediction performance screen, and we sought to experimentally validate the top predicted novel regulator of the JA signaling response, ILL6. We found increased phenotypic sensitivity to exogenous jasmonate, increased wound-induced JA-Ile accumulation in ill6 mutants versus wild-type plants, and a decreased capacity to release Ile from exogenously applied JA-Ile, consistent with a negative regulatory role of ILL6 in the jasmonate response. These results highlight the role of jasmonate as a sentinel of environmental stress and, more generally, show that expression responses to uncontrolled subtle variations in plant growth conditions can be used effectively to point to novel regulatory relationships.

Noisy gene expression caused by variability in environmental parameters or intracellular stochastic effects is often considered a nuisance, although some authors have recently used intrinsic expression noise propagation to decipher regulatory influences in single-celled organisms (Dunlop et al., 2008; Munsky et al., 2012; Stewart-Ornstein et al., 2012). It is currently impossible to assess which proportion of the residuals is due to true stochastic variation emanating from the stochastic nature of cellular processes, instead of micro-environmental variation, as the two are impossible to separate in the setup used by Massonnet et al. (2010). Even if it were possible to separate inherent stochastic effects from micro-environmental effects, it is unclear to what extent inherent stochastic variations on the cellular level, if they would propagate through the cellular regulation network, would contribute to coordinated expression variation across genes in the context of a multicellular organism, as they would likely be averaged out to some degree across all cells in an individual plant or leaf. As outlined above, our results suggest that the observed residual expression variation derives mostly from subtle variations in the micro-environmental growth conditions of individual plants and that this expression “noise” contains valuable information on the wiring of biological networks, on par with the amount of information that can be extracted from controlled perturbations. In the prevailing perception of the scientific method, the stochastic features of uncontrolled experimental setups could be considered diametrically opposed to the experimental design features needed to ensure reproducibility. In the classical view, reproducibility is understood as the capacity to obtain the same results under the same controlled conditions. But from a systems biology perspective, reproducibility may be assessed on a different level. Reproducibility of a reverse-engineered gene network entails that the same interconnections among genes can be recovered from comparable data sets, which in this context are not necessarily copies that are systematically generated under exactly the same conditions. In fact, for large-scale gene network inference, the exact nature of the experimental conditions is secondary in importance to the requirement that similar conditions occur across the condition set when performing repeat experiments. In this respect, profiling the expression response of individuals to uncontrolled conditions can be regarded as sampling from a multivariate probability distribution, with each dimension being a random environmental factor. Given a large enough sample size, the effect size distributions in uncontrolled expression profiling experiments should therefore essentially be reproducible and so should the gene networks recovered from them.

The data set reanalyzed here contained only a limited sample of 41 individuals, resulting in poor function prediction F-measures in the range 0 to 0.4. In addition, the data set was suboptimal because of the multiple ecotypes and labs involved in the original study (Massonnet et al., 2010), leading to systematic biases that may not have been pruned out entirely by ANOVA analysis. Nevertheless, it is clear that the uncontrolled residuals contain a significant amount of information on the underlying gene network structure. The results presented here suggest that expression profiling of wild-type individuals under uncontrolled conditions should be considered as an alternative data generation strategy for unraveling the wiring of biological networks. Algorithms used for this purpose are notoriously data-demanding, to the extent that unraveling a substantial part of an organism's transcriptional wiring easily requires hundreds of independent, controlled perturbations (Hughes et al., 2000; Chua et al., 2004; Ma et al., 2007; He et al., 2009; Lee et al., 2010). Given the substantial resource and time expenditure associated with controlling growth conditions and treatments, generating mutant lines, and profiling biological replicates, profiling uncontrolled individuals may prove more cost-effective for generating sufficient amounts of data for large-scale reverse engineering efforts.

In addition, uncontrolled data sets are fundamentally different from traditional data sets with respect to the perturbation structure across experimental conditions. In traditional data sets, only a single major perturbation is usually applied in any given experiment, while in an uncontrolled data set, multiple unidentified (mild) perturbations may impact the expression profile of an individual simultaneously. For instance, an individual plant may have been subjected to both watering and temperature conditions that are subtly different from its neighbors. This multifactorial setup is exactly the setup encountered by plants in the field, where they are irregularly and often simultaneously impacted by several abiotic and biotic stresses, the responses to which often operate in synergistic or antagonistic interaction to modulate plant fitness. In this respect, uncontrolled field data sets screening multifactorial phenotypic responses under natural variation in the growth environment may prove useful to identify and quantify crosstalk between pathways, an issue that is not easily tackled in a lab environment but is of paramount importance for predicting the phenotypic effects of candidate yield or stress tolerance-enhancing mutations in the field. Although the use of natural variation on the genotype level has become mainstream in recent years, e.g. in genome-wide association studies and expression quantitative-trait-locus (eQTL) analyses (Kliebenstein, 2009; Nayak et al., 2009; Chan et al., 2011; Cubillos et al., 2012; Weigel, 2012), the potential use of natural variation in gene expression triggered by variations in environmental conditions has only recently begun to gather attention (Nagano et al., 2012; Richards et al., 2012). In most species, natural variation other than on the genotype level is still considered a nuisance rather than a potential asset. However, our results suggest that sampling natural environmental variation may be of general use for reverse engineering genetic networks, not only in plants, but also in species such as human, for which uncontrolled environmental variation is largely unavoidable and controlling experimental conditions and treatments is often impossible due to ethical constraints.

METHODS

Data Sets and Extraction of Codifferential Expression Networks

Raw microarray data for 41 individual Arabidopsis thaliana leaves (Massonnet et al., 2010), profiled using the AGRONOMICS1 microarray platform (Rehrauer et al., 2010), were obtained from the AGRON-OMICS repository (http://www.agron-omics.eu/). The raw data were RMA normalized using the Bioconductor R package, version 2.5 (Gentleman et al., 2004). We retained only the Affymetrix ATH1 probe sets present on the AGRONOMICS1 array for calculating gene expression levels (using the agronomics1_ath1probes.cdf file), to facilitate comparisons between this data set and the sampled data sets for pooled plants (see below). The log-transformed expression profiles were subjected to gene-specific ANOVA models of the form:

with i (= 1..41) indexing the number of expression values obtained per gene, μ the baseline expression level of a given gene, L_j the lab effect (j = 1..6), A_k the accession effect (k = 1..3), LA_jk the lab × accession interaction, and ε_ijk the residual error on the log expression level. The residuals ε_ijk were used for all further analyses. Supplemental Table 1 online indicates the numbers of samples on which unbalanced design ANOVA estimation of lab, accession, and lab × accession effects was based. Although the overall number of data points is limited, the numbers of leaves are fairly balanced across labs and accessions, and with one exception, there are always three data points to estimate a particular interaction effect.

To construct same-sized sample data sets on perturbed and pooled plants, 688 Affymetrix ATH1 microarray experiments profiling the response to various perturbations on leaf and shoot tissues were extracted from the CORNET database (De Bodt et al., 2010), and the resulting compendium was randomly sampled without replacement to obtain 1000 data sets containing 41 experiments each. These were preprocessed as described above, and expression ratios (perturbations versus their respective control conditions) for 19,937 Arabidopsis genes were obtained using a custom cdf file designed to minimize cross-hybridization effects (Casneuf et al., 2007). In all data sets, only the 19,760 nuclear genes in common between the AGRONOMICS1 and ATH1 cdf files were retained for further analysis.

Co-differential expression networks and expression modules for the residuals data set and sample data sets were obtained using ENIGMA 1.1 (Maere et al., 2008). ENIGMA requires the definition of up- and downregulation thresholds, either based on differential expression P values or expression log ratio thresholds. Since differential expression P values can by design only be computed for the sample data sets, but not for the residuals data set, we standardized the treatment of all data sets using a log ratio threshold of 0.3498 to define up- and downregulation of gene expression (see Results). Note that the residuals can also be considered log ratios with respect to the baseline expression level of a gene over all leaves after correcting for lab and accession effects (Equation 1). The FDR level for detecting significant codifferential expression links was set to 0.01. For functional annotation on the level of expression modules, GO ontology information and annotations for Arabidopsis were obtained from the GO database (www.geneontology.org, annotation version 10/23/2012), and annotations with nonexperimental evidence codes IEA, ISS, and RCA were discarded. GO enrichment of gene modules was assessed using hypergeometric tests, and the resulting P values were corrected for multiple testing using the Benjamini and Hochberg FDR correction at FDR = 0.05. Potential regulators of a module were predicted from the set of genes annotated to “biological regulation” in GO (GO:0065007) at FDR = 0.01. The remaining ENIGMA parameters were set to default values. For use in gene function predictions, negative correlation edges were removed from the codifferential expression networks. Basic network topology parameters (network density and clustering coefficient for the major connected component of each network) were obtained using NetworkX 2.6.4 (http://networkx.github.com/).

Gene Function Prediction

We predicted the function of a given gene from a given network by performing GO enrichment analysis on its network neighborhood using a custom-tailored derivative of PiNGO, a software tool to screen biological networks for genes that may be involved in a process of interest (Smoot et al., 2011). Gene functions were predicted with hypergeometric tests, and the resulting P values were corrected (per network) with the Benjamini and Hochberg multiple testing correction. The resulting GO predictions were then compared with the known GO annotations, and precision, recall, and F-measure (harmonic mean of precision and recall) were scored for every network for a wide array of GO categories (see Supplemental Figure 5 online) at prediction FDR thresholds ranging from 10e-2 to 10e-11. For every functional category, the relative prediction performance of the residuals network with respect to the sample networks was classified as very good, good, average, poor, or very poor (see Figure 1 legend) based on the root mean square deviation of the residuals network F-measures from the 25th, 50th, and 75th percentiles of the sample network F-measures over the FDR subrange in which the residuals network exhibited defined F-measures, with deviations normalized to the square root of the residuals F-measure.

The global function prediction performance of a given network was calculated using a gene-centric method described by Deng et al. (2004), based on assessing the overlap between predicted and annotated GO functional paths for a given gene (i.e., the path from an annotated or predicted GO term to the root of the GO hierarchy), while taking into account the depth of predictions and annotations in the hierarchical GO structure. Recall and precision were calculated for every gene as described (Deng et al., 2004). The overall prediction recall and precision score of an entire gene network are then defined as the arithmetic mean of the recall and precision values across all genes. Recall, precision, and F-measure were calculated for every network at prediction FDR thresholds ranging from 10e-2 to 10e-11.

JA Signaling Response Gene Prediction

PiNGO (Smoot et al., 2011) was used to screen all networks for known regulators that are potentially involved in the JA signaling response. To obtain high-confidence functional predictions, computationally derived GO annotations with evidence codes IEA, ISS, and RCA were discarded. The set of 19,760 genes present in all data sets was used as the reference set. “Biological regulation” (GO:0065007) was set as the “start” GO category, while “response to JA stimulus” (GO:0009753) was used as the “target” and “filter” GO category. P values were calculated with hypergeometric tests and corrected with the Benjamini and Hochberg multiple testing correction at FDR = 0.01. The same protocol was used for predicting novel regulators for the other processes listed in Supplemental Tables 3 to 7 online, with the “target” and “filter” GO categories defined accordingly.

Plant Material, Growth Conditions, and Genetic Analysis

Plants were grown at 22°C in Sunshine Mix LC1 potting soil (wounding experiments) or Jiffy 7 peat pellets (in vivo hydrolysis assays; Jiffy Products) and 10 h (wounding, in vivo hydrolysis assays) or 16 h (growth inhibition assay) of light at 100 to 120 µmol/photons/m²/s. Arabidopsis accession Col-0 was obtained from the ABRC (ABRC stock CS70000). The ill6 mutant lines were derived from ABRC stocks Salk_024894C (ill6-1) and CS852193 (ill6-2), both in the Col-0 background. To identify homozygous T-DNA insertion mutants, genomic DNA of individual plants of these lines was used as template in a three-primer PCR reaction. ILL6 transcript accumulation in these lines was examined by RT-PCR. The sequences of primers used in these analyses are included in Supplemental Table 8 online.

Growth Inhibition Assay

Surface-sterilized and cold-stratified seeds were plated on half-strength Murashige and Skoog media, pH 5.8, containing 0.8% Suc, 0.8% agar, and 0.5 g/L MES. After 3 to 4 d, seedlings of equal root length (∼1 cm) were transferred to plates of the same media containing various concentrations of MeJA or an equal volume of carrier (DMSO); to reduce interassay variability, these plates were always allowed to air-dry in a laminar flow hood for exactly 1 h. Each plate contained an equal number of seedlings of all three genotypes. In the data presented in Figures 4A and 4B, the seedlings were transferred to three replicate plates per concentration of MeJA and each replicate was placed on a separate shelf of a plant growth chamber. After 8 d on JA-containing media, the length of the primary root of each seedling was measured, and the shoot tissue was removed and weighed. A minimum of 16 seedlings was analyzed for each genotype at each concentration.

A linear mixed model was fitted to the data and analyzed using the residual maximum likelihood method. The model included fixed effects due to genotype, MeJA concentration, their interaction, and random effects due to the replicate plate and shelf. The significance of fixed effects was judged by F-test. Differential sensitivity of the mutants’ root elongation and shoot weight were seen in other independent experiments.

Wounding Treatments and JA-Ile Analysis

Thirty-day-old plants of Col-0, ill6-1, and ill6-2 were wounded evenly with a hemostat twice across the width of each of three fully expanded leaves, crushing 40 to 50% of the leaf surface area. At various time points after wounding, 200 to 300 mg of damaged leaves from two individual plants was harvested together and immediately frozen in liquid nitrogen and stored at −80°C until jasmonate extraction.

Extraction and quantification of endogenous JA-Ile from plant tissue were according to previously described methods (Koo et al., 2009, 2011). A known amount of [¹³C₆]JA-Ile was added to the frozen samples at the beginning of extraction as an internal standard. Compounds were separated on an Ascentis C18 column (1.7 µM, 2.1 × 3 × 50 mm) using an Acquity ultraperformance liquid chromatography system (Waters). A Quattro Premier XE tandem quadrupole mass spectrometer (Waters) was used in an electrospray negative mode to detect JA-Ile (322 → 130) and [¹³C₆]JA-Ile (328→ 136).

The data from two independent experiments were analyzed together. A linear mixed model was fitted to the data and analyzed using residual maximum likelihood, including fixed effects due to genotype, time, their interaction, and random effects due to the replicated experiments. The significance of fixed effects was judged by F-test.

JA-[¹⁴C]Ile Synthesis and in Vivo Hydrolysis Assay

JA was obtained by base-catalyzed hydrolysis (Farmer et al., 1992) of MeJA (Bedoukian Research) and purified by reverse-phase HPLC (Fonseca et al., 2009). For synthesis of JA-[¹⁴C]Ile, JA (14 mg), l-Ile (8 mg), and l-[¹⁴C]Ile (5.5 µCi, specific activity 55 mCi/mmol; American Radiolabeled Chemicals) were coupled and purified by open-column silica chromatography as detailed (Suza et al., 2010). For plant treatments, 50,000 dpm of JA-[¹⁴C]Ile in an aqueous 20% DMSO solution was applied in a single 10-μL drop to individual leaves of individual plants. After 24 h, leaves were excised and extracted individually in 4 mL of 95% ethanol at 70°C for 45 min. These extracts were dried under a stream of nitrogen, resuspended in 50 μL of 95% ethanol, and separated by thin layer chromatography (silica gel 60; EMD Millipore) in chloroform:methanol:acetic acid (70:30:2, v:v:v). Radioactivity was detected with a Typhoon FLA 7000 phosphor imager (GE Healthcare Life Sciences). Images were background subtracted and bands quantified using ImageJ (Schneider et al., 2012). [¹⁴C]Ile was identified by cochromatography with an authentic standard. The log₁₀-transformed data of Figure 4E were analyzed by one-way ANOVA, and the significance of the genotype effect was judged by F-test. The log₁₀-transformed data of Figure 4F were analyzed by Student’s t test.

Accession Number

Sequence data from this article can be found in the Arabidopsis Genome Initiative or GenBank/EMBL data libraries under accession number At1g44350/NM_103546.3 (ILL6) and in Supplemental Tables 2 to 7 online.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure 1. Effect Size of Accession, Lab, Lab × Accession, and Residual Effects in the Massonnet et al. (2010) Data Set.

• Supplemental Figure 2. Distributional Characteristics of Log-Ratio Expression Values in the Residuals and Sample Data Sets.

• Supplemental Figure 3. Numbers of “Differential” Expression Values in the Residuals and Sample Data Sets, for the Purpose of ENIGMA Analysis.

• Supplemental Figure 4. Functional Prediction Statistics for the Residuals and Sample Data Sets.

• Supplemental Figure 5. Category-Specific Function Prediction Performance in the Context of the GO Hierarchy.

• Supplemental Figure 6. Identification of ill6 Mutants.

• Supplemental Table 1. Number of Individual Leaves Profiled per Lab and Accession in the Massonnet et al. (2010) Study.

• Supplemental Table 2. Regulatory Genes Predicted to Be Involved in the Response to JA Stimulus Based on the Residuals Co-differential Expression Network.

• Supplemental Table 3. Regulatory Genes Predicted to Be Involved in the Response to ABA Stimulus Based on the Residuals Co-differential Expression Network.

• Supplemental Table 4. Regulatory Genes Predicted to Be Involved in the Response to Ethylene Stimulus Based on the Residuals Co-differential Expression Network.

• Supplemental Table 5. Regulatory Genes Predicted to Be Involved in the Response to Fungus Based on the Residuals Co-differential Expression Network.

• Supplemental Table 6. Regulatory Genes Predicted to Be Involved in the Response to Salt Stress Based on the Residuals Co-differential Expression Network.

• Supplemental Table 7. Regulatory Genes Predicted to Be Involved in the Response to Water Deprivation Based on the Residuals Co-differential Expression Network.

• Supplemental Table 8. Sequences of Oligonucleotide Primers Used for ILL6 PCR Analyses.

• Supplemental Data Set 1. Module Figures for All Modules Learned from the Residuals Data Set.

• Supplemental Data Set 2. Excel File Containing Predicted GO Annotations for All Modules in Supplemental Data Set 1.

• Supplemental Data Set 3. Module Figures for All Modules Learned from the Original Data Set, without Removing Lab and Accession Effects.

• Supplemental Data Set 4. Excel File Containing Predicted GO Annotations for All Modules in Supplemental Data Set 3.

• Supplemental Data Set 5. Excel File with Gene Counts in the Residuals and Sample Networks for all GO Processes with at Least 10 Nodes in the Residuals Network.

• Supplemental Data Set 6. Category-Specific Function Prediction Performance Figures for All GO Categories Scored in Supplemental Figure 5.

Glossary

ANOVA

analysis of variance

GO

Gene Ontology

FDR

false discovery rate

JA

jasmonic acid

ABA

abscisic acid

JA-Ile

jasmonoyl-Ile

Col-0

Columbia-0

MeJA

methyl jasmonate