The Effect of Spatial Resolution on Wall Shear Stress Measurements Acquired Using Radial Phase contrast Magnetic Resonance Angiography in the Middle Cerebral Arteries of Healthy Volunteers

Abstract

Introduction

Low wall shear stress (WSS) values are frequently observed in arterial regions that are prone to atherosclerotic plaque formation and have also been implicated in the pathogenesis of saccular cerebral aneurysms. Acquisition of WSS values in-vivo has been challenging, especially using non-invasive techniques and within clinically-useful imaging times. We have recently implemented radial phase-contrast techniques that allow high resolution angiograms with velocity information to be acquired within clinically-useful imaging times.

Methods

10 healthy volunteers were scanned using PC-VIPR and PC-SOS, two high resolution phase-contrast techniques at spatial resolutions of 0.67×0.67×0.67mm3 and 0.4×0.4×1mm3 respectively. Velocity data from the two acquisitions was imported into a custom Matlab runtime environment that automatically calculated WSS values using Green’s Theorem and B-spline interpolation.

Results

Time average axial WSS was 1.069 N/m2 (95% confidence interval: 0.8628 < x < 1.276) in the left and right middle cerebral arteries of the 10 healthy volunteers (n=20) when scanned by PC-VIPR, and 1.670 N/m2 when scanned by PC-SOS (95% confidence interval: 1.395 < x < 1.946). This difference in means was statistically significant (p < 0.002).

Discussion

Previous investigators have found that higher spatial resolution results in higher WSS measurements because smaller voxel size results in fewer partial volume effects. This was true in our study as well. In this study, we found that PC-SOS has significantly higher spatial resolution than PC-VIPR and this followed in the WSS measurements.

Conclusion

Higher in-plane spatial resolution allows WSS calculations to be performed more accurately because of increased precision near the vessel boundary.

INTRODUCTION

Low wall shear stress (WSS) values are frequently observed in arterial regions that are prone to atherosclerotic plaque formation. Non-laminar flow, which leads to abnormal shear stress, has been shown to change endothelial gene expression and homeostasis as well as increased boundary zone proliferation, leading to increased atherosclerotic plaque deposition.^1.2 Both increases and decreases in wall shear stress have been associated with the formation and progression of intracranial aneurysms.³ Thus, WSS analysis may be of value in identifying areas vulnerable to atherosclerotic plaque and aneurysm formation,^4.5 as well as areas vulnerable to disease progression. This information has many potential clinical applications including the evaluation of risk of stroke in patients with atherosclerosis of the internal carotid artery bifurcation, carotid siphon, and carotid terminus and surrounding branches. It can also help evaluate the risk of subarachnoid hemorrhage second to saccular cerebral aneurysm rupture. However, obtaining fast and accurate non-invasive in-vivo measurements of intracranial arterial WSS has been challenging.

WSS is defined as the derivative of velocity with respect to the distance from the wall, multiplied by the viscosity of the fluid in the vessel. Therefore, WSS can be calculated from velocity measurements from phase contrast velocimetry, ultrasound, and other techniques. However, calculated WSS is only an estimate of physiologic WSS as it is not a parameter that can be measured in vivo. Investigators have used computational fluid dynamics (CFD) and the Navier-Stokes equations to estimate WSS in computerized high-resolution models of vessels of interest using velocity measurements acquired using PC-MRA or ultrasound, however these techniques are time-consuming and typically require a hemodynamic model to be created for patients of interest. PC-MRA and automated spline interpolation can be used to estimate WSS, but a limitation of prior investigations of WSS using MRA is the lack of sufficient spatial resolution necessary to visualize the boundary zone within clinically-useful scan times.⁶

We have implemented a highly accelerated 3D-radial technique called PC HYPRFlow that includes a 3D- radial phase contrast acquisition (PC-VIPR)^7,8 with velocity encoding. PC HYPRFlow is composed of two different scans: 1) a time series of lower resolution whole-brain images during the first pass of a contrast bolus and 2) a phase contrast velocity encoded scan with excellent spatial resolution (0.68×0.68×0.68mm³). The total scan time is 5 minutes. In this report we focus on the velocity data that are obtained as part of the PC HYPRFlow exam from the phase contrast acquisition which is called PC-VIPR (Phase Contrast Vastly-undersampled Projection Reconstruction).⁸ We have also implemented a similar phase contrast technique called PC-SOS⁹ (Phase Contrast Stack Of Stars) that has even higher in-plane spatial resolution (0.4mm×0.4mm in plane x 1mm out of plane) using radial imaging in-plane and Cartesian in the z direction that has slightly longer, but still clinically useful scan times, (8 minutes) but a smaller field of view. Higher spatial resolution allows better visualization of the boundary zone at the edge of the vessel, allowing more precise velocity measurements and more accurate WSS calculations. Another challenge in WSS calculation is the selection of the analysis method to estimate WSS. We have collaborated with the research group at the University of Freiburg, Germany, to apply a spline interpolation algorithm that, when combined with our high-resolution imaging techniques, can generate WSS measurements closer to values acquired using CFD with a total processing time of approximately 30 minutes per vessel.^6,10 In this study, we compare the results of WSS analysis of the middle cerebral arteries in healthy volunteers with both PC-VIPR and PC-SOS to examine the effects of spatial resolution on WSS.

MATERIALS AND METHODS

Volunteer studies were performed in compliance with HIPAA regulations and using a protocol approved by the local Institutional Review Board (IRB). 10 healthy volunteers (6 female, 4 male) ranging in age from 19-58, were imaged with a clinical 3T MR system (HD 750 GE Healthcare, Waukesha, WI) with an 8 channel head coil (Excite HD Brain Coil, Waukesha, WI). Following bolus contrast injection, serial whole brain lower resolution scans were acquired for the time-resolved multi-echo 3D radial acquisition (CE-VIPR).¹¹ Immediately after the serial imaging, velocity encoding was performed using a high-resolution dual-echo 3D radial phase contrast acquisition (PC-VIPR). The PC-VIPR data were used as the composite image (angiographic constraint) for HYPR-LR reconstruction of the dynamic phase images and for hemodynamic evaluation.⁷ Similarly, the process was repeated with CE-VIPR, followed by PC-SOS, which is also used as a composite image. Cutplanes were made using Ensight in the middle cerebral arteries of both the PC-VIPR and PC-SOS datasets and imported into a custom Matlab runtime environment developed in cooperation with researchers at the University of Freiburg, Germany.⁶ Points were selected around the boundaries of the vessels of interest on magnitude images with velocity images side by side (Figure 1a-b) then the software automatically calculates axial WSS using Green’s Theorem and B-spline interpolation.

Figure 1.

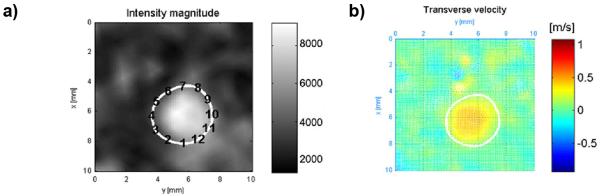
a) points being selected around the left MCA on a amgnitude image of the left MCA. b) velocity image of the left MCA.

RESULTS

Time average axial WSS was 1.069 N/m² (95% confidence interval: 0.8628 < x < 1.276) in the left and right middle cerebral arteries of the 10 healthy volunteers (n=20) when scanned by PC-IPR, and 1.670 N/m² when scanned by PC-SOS (95% confidence interval: 1.395 < x < 1.946). This difference in means was statistically significant (p < 0.002). WSS maps of larger areas, including the axial whole-brain were also acquired using an in-house Matlab tool. Figure 2a shows a WSS map of the left carotid terminus (LCT), Figure 2b shows a segmentation of the LCT, and Figure 2c shows a targeted maximum intensity projection of the axial whole-brain and detail view of the LCT.

Figure 2.

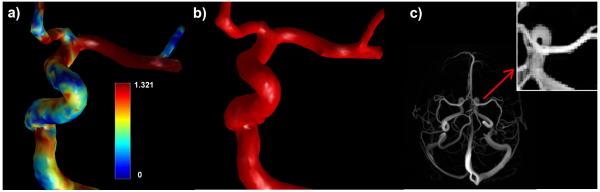
a) left: WSS map of the left carotid terminus generated using velocity data from PC-VIPR. b) middle: PC-VIPR segmentation of the LCT. c) right: angiogram of the axial whole brain from PC-VIPR and detail of LCT.

DISCUSSION

In this report, we show that highly accelerated high-resolution radial PC MRA is capable of acquiring whole-brain velocity-encoded images with sufficient resolution to acquire WSS data that is consistent with values found in the literature.^12,13 We have previously demonstrated that 3D-radial techniques are capable of acquiring whole-brain images of diagnostic quality in medium and large size intracranial vessels¹⁴ and velocity data comparable to transcranial Doppler ultrasound and 2D phase contrast MRA.¹⁵ The combination of velocity data, morphologic images, and WSS data can be used to delineate both normal and pathologic flow conditions.¹⁶ Figure 3a shows a segmentation of the left anterior circle of Willis showing a stenosis in the left MCA. Figure 3b shows a targeted maximum intensity projection of the same stenosis from PC-VIPR, and Figure 3c shows a WSS map of the stenosis. Note increased WSS proximal to the stenosis and decreased WSS distal to the stenosis, indicating plaque progression.

Figure 3.

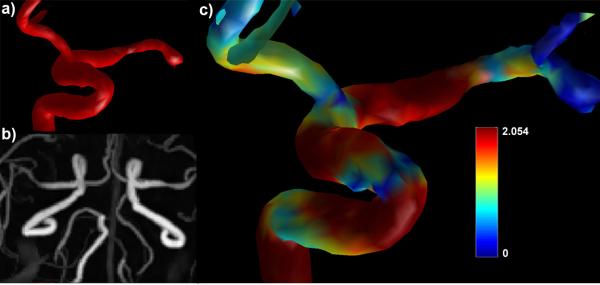
a) Top left: Segmentation of stenosis in the left MCA. b) bottom left: PC-VIPR MIP of a left MCA stenosis. c) right: WSS map of a left MCA stenosis.

Investigating flow conditions in the circle of Willis region is necessary in order to understand pathologic flow features that may lead to the development of arterial stenosis. Hemodynamic studies of the intracranial arteries may also provide insight into the relationship between flow conditions and the formation and rupture of intracranial aneurysms. Multiple studies of the flow within the circle of Willis have shown that branch points have flow alterations that contribute to the development of pathologic changes in the vessels.^17-21

Four dimensional phase contrast MRA has also been used to study the arterial flow in normal subjects.^22-23 Sforza et al,²⁴ emphasized that models of flow and clinical imaging demonstrate non-uniform distribution of WSS with increased and decreased zones at arterial bifurcations and curving arterial segments. Helical flow and recirculating flow patterns are particularly important due to their impact on local WSS. Investigations of computer generated models based on clinical exams have shown a wide variety of flow patterns within and around aneurysms. These studies have also shown that the flow patterns are highly dependent on the vascular geometry which will differ from patient to patient. The flow patterns vary from a simple recirculating vortex to complex flow with inflow jets that increase during systole producing a focal increase in WSS.^25-29

It is interesting to note that both low and high WSS have been implicated in regarding the development and progression of intracranial aneurysms. Some authors note that the dome of an aneurysm is usually the site of rupture and the dome typically has low WSS.¹³ Other authors have noted that patient specific models demonstrate that the point of impact of the inflow jet is usually found in the dome or body of the aneurysm and that WSS is elevated in these regions (although the spatial average WSS may be lower than the parent artery).^{13, 30-32}

Accurate estimates of WSS using PC MRA can only be obtained if the spatial resolution is capable of accurately visualizing the boundary zone. Previous investigators have found that higher spatial resolution results in higher WSS measurements³³ because smaller voxel size results in fewer partial volume effects. This was true in our study as well. In this study, we found that PC-SOS has significantly higher spatial resolution than PC-VIPR and this followed in the WSS measurements. However, PC-VIPR demonstrated a much larger (whole-brain) field of view, as well as faster scan times (5 minutes compared to 8 minutes) and isotropic resolution. We propose to use PC-SOS to evaluate smaller structures, such as blood vessels and aneurysms as small as 3 mm in diameter, and PC-VIPR to evaluate larger and more complex structures, such as arteriovenous malformations.

We recognize that wall shear stress is a parameter that cannot be measured precisely in-vivo. However, our work has shown that areas with pathologic flow conditions have WSS measurements with clinically significant differences from areas without pathology.¹⁶ Another challenge is selecting the appropriate velocity encoding. If the velocity encoding is too high the signal intensity from slow blood flow may be very low and some aneurysms may be difficult to detect. We have recently implemented 5-point velocity encoding³⁴ and dual-venc techniques to help deal with these challenging flow conditions. Additionally, a well recongnized limitation of using PC-MRA to measure velocity is that areas of complex flow may exhibit signal loss due to intravoxel dephasing. In these instances the velocity fields cannot always be accurately calculated. However, a combination of different techniques including morphologic images, magnitude images, velocity information, and velocity derivatives allows can lead to improved characterization of vascular pathology.

To date, much of the published data using PC HYPRFlow and our other 3D-radial PC-MRA techniques have been from a dataset of healthy volunteers.¹⁵ However, we have implemented accelerated PC-MRA methods on our clinical scanners and we are expanding our investigations of WSS to include patients with stenoses, aneurysms, vasospasm, and arteriovenous malformations.¹⁶ We will also determine how these data compare to theoretical models of flow pathophysiology found in the literature in order to create a tool with prognostic value in identifying areas vulnerable to pathologic flow conditions. Additionally, we have begun to implement post-processing techniques that provide clinicians a robust set of visualization options that are useful in assessing neurovascular disease. Velocity data from phase contrast velocimetry can be used to generate streamlines and pathlines that help delineate the nature of flow physiology in areas of complex or pathologic flow. Streamlines give clinicians a more intuitive understanding of flow physiology that may help them with treatment considerations. Pressure measurements also have utility in characterizing areas of complex flow. Identifying flow patterns has prognostic value in determining development of pathologic flow conditions.

CONCLUSION

High resolution 3D-radial PC-MRA is capable of acquiring morphologic images, velocity measurements and derivative calculations (WSS) in brain vascular structures as small as 3 mm within 5-8 minutes. Higher spatial resolution allows WSS calculations to be performed more accurately because of increased precision near the vessel boundary. These techniques may be useful in assessing the pathologic grade of stenoses, identifying areas vulnerable to atherosclerotic disease and aneurysms, and providing potential prognostic information for areas with aneurysms, stenoses, and arteriovenous malformations. A fast, non-invasive tool for assessing neurovascular disease will provide clinicians an alternative to invasive methods such as DSA.