Modeling Controlled Photodegradation in Optically Thick Hydrogels

Abstract

There is a growing interest in developing dynamically responsive hydrogels whose material properties are modulated by environmental cues, including with light. These photoresponsive hydrogels afford spatiotemporal control of material properties through an array of photoaddition and photodegradation reactions. For photoresponsive hydrogels to be utilized most effectively in a broad range of applications, the photoreaction behavior should be well understood, enabling the design of dynamic materials with uniform or anisostropic material properties. Here, a general statistical-kinetic model has been developed to describe controlled photodegradation in hydrogel polymer networks containing photolabile crosslinks. The heterogeneous reaction rates that necessarily accompany photochemical reactions were described by solving a system of partial differential equations that quantify the photoreaction kinetics in the material. The kinetics were coupled with statistical descriptions of network structure in chain polymerized hydrogels to model material property changes and mass loss that occur during the photodegradation process. Finally, the physical relevance of the model was demonstrated by comparing model predictions with experimental data of mass loss and material property changes in photodegradable, PEG-based hydrogels.

INTRODUCTION

Hydrogels comprise a class of hydrophilic, crosslinked polymers that are useful in a broad range of applications owing to their facile synthesis, biocompatibility, tailorability for transport of both low and high molecular weight molecules, as well as robust physical properties.¹ Currently, there is an interest in developing dynamically responsive hydrogels whose material properties can be modulated in time by environmental cues, enabling complex spatial and temporal control of the chemistry and structure of the gels. Responsive hydrogel networks are being exploited to engineer improved drug delivery vehicles,² cell culture scaffolds for regenerative medicine,^3,4 biosenors,⁵ and actuators in microfluidic devices.⁶ Within this paradigm, researchers have developed a unique class of photoresponsive hydrogels that provide the experimenter with spatiotemporal control over the chemical and physical properties of the gels through photoaddition and photodegradation reactions.^7–15

Degradation reactions are employed to modulate physical properties of hydrogels in time and is achieved most typically through the incorporation of hydrolytically or enzymatically degradable moieties within the hydrogel network backbone.16 Cleavage of the degradable moieties breaks elastically active strands within the network, forms soluble degradation products, and, ultimately, causes erosion of the gel. As a general characterization, each bond that is degraded within the network leads to a decrease in the local crosslinking density with a concomitant decrease in modulus and an increase in water swelling. Once a sufficient fraction of local crosslinks is degraded, erosion occurs within the network resulting in mass loss and changes in the geometry of the gel. Throughout this article, the terms degradation and erosion arise frequently; degradation refers to the reaction that cleaves an individual covalent bond, while erosion refers to the local depletion of mass from the network caused by degradation.17,18

Hydrolytically and enzymatically degradable hydrogels are both effective in a broad range of applications,¹⁹ but they are limited in that the degradation kinetics are governed by the initial chemistry and offer little control over material property evolution post-fabrication. As an alternative approach that enables new opportunities for dynamic material property control, photodegradable hydrogels have been engineered to contain photolabile bonds within the network crosslinks, which can be cleaved upon absorbance of light. This unique approach to hydrogel fabrication allows the experimenter to modulate the physical properties of the gel in both space and time exogenously through controlled irradiation. On the molecular level, hydrogels are rendered photodegradable by incorporating specific photocleavable moieties (e.g., nitrobenzyl ether or coumarin) into the macromolecular precursors that comprise the gel network. After formation, these photoactive moieties reside in the network backbone and can be cleaved irreversibly when photons of the appropriate wavelength are absorbed. Through this process, light is employed to degrade bonds within the material, leading to changes in the gel’s modulus and swelling ratio, and, ultimately, to erode the gel. Such systems afford opportunities for innovative experiments to better understand how hydrogel degradation influences desired material properties, as well as offering unprecedented spatiotemporal control of the network structure in real-time.

Several photodegradable hydrogels have been developed^7,8 and employed as cell culture platforms,^9–13,20,21 drug delivery vehicles,^15,22,23 and photolithographic materials.¹⁴ Initially, Turro and coworkers synthesized photodegradable polymer networks via click-chemistry demonstrating the utility of light to tune material properties.^7,8 Anseth and coworkers and Wang and coworkers extended this paradigm to demonstrate that light can be used to tune the modulus of photolabile hydrogels in real time to control fibroblast activation²¹ or migration¹¹, as well as mesenchymal stem cell morphology.^12,20 Further, Kasko and coworkers utilized photodegradable hydrogels as photolithographic materials^.24 A separate class of photodegradable gels has been developed that are comprised of photolabile bonds, which are reversible with low wavelength UV light (λ = 254 nm), and these gels have been applied for drug delivery.^25,26 In each of these investigations, thorough characterization of the material in use allowed the experimenters to describe the light induced changes to the hydrogel’s properties via controlled light presentation.

However, for photoresponsive hydrogels to be utilized most effectively in a broad range of applications, the degradation behavior should be described a priori. A general class of statistical-kinetic models for degradation in hydrolytically and enzymatically degradable hydrogels has been developed that integrates cleavage kinetics with network structural information to predict material property changes during degradation.^17,18,27,28 The goal of the current investigation is to develop a generalized and comprehensive, statistical-kinetic model of hydrogel photodegradation to provide a method to describe and predict light induced changes in the properties of photodegradable hydrogels. In this manner, the concomitant alterations in material properties caused by irradiation can be better understood, predicted, and manipulated to accelerate the design of unique cell culture scaffolds, delivery vehicles, high performance elastomers, and more complex photoresponsive hydrogels.

EXPERIMENTAL

Materials and Methods

All chemical reagents were purchased from Sigma Aldrich except as otherwise noted.

Synthesis of photolabile crosslinker (PEGdiPDA)

The photolabile moiety, ethyl 4-(4-(1-hydroxyethyl)-2-methoxy-5-nitrophenoxy)butanoic acid was prepared as previously described.²⁹ The photolabile moiety was then acrylated as previously described to synthesize the acrylated photolabile moiety (PDA).²⁹ The photolabile crosslinker (PEGdiPDA) was synthesized as previously described by coupling PDA to PEG bisamine (M_n ~3400 Da; Laysan Bio.) using standard peptide coupling reagents.²⁹

Synthesis of photolabile hydrogels

Stock solutions of the redox initiator ammonium persulfate (AP), base catalyst tetramethylethylenediamine (TEMED), co-monomer poly(ethylene glycol) monoacrylate (PEGA; M_n ~ 400 Da; Monomer-Polymer and Dajac Labs), and photolabile crosslinker (PEGdiPDA) were formed in water at 2 M, 2M, 40 wt%, and 20 wt%, respectively. Solutions were prepared from these stocks to produce a total of 15 wt% total polymer in water and 0.2 M AP. In experiments where imaging was necessary, a methacrylated rhodamine (300 µm) was added to the pre-hydrogel solution. The pre-hydrogel solution was vortexed while TEMED (0.1 M) was added and quickly transferred to the gelforming mold. The liquid solution was polymerized for 5 minutes, which corresponds to complete polymerization as determined by rheometry. Gels were polymerized between rubber gaskets at varying thickness from 100 µm to 1500 µm or on a parellal plate rheometer (TA, Ares) with a thickness of 50 µm.

Measurement of molar absorptivities

The molar absorptivities of the o-nitrobenzyl ether (NBE) and the nitrosobenzyl cleavage product (NBP) were calculated using a UV-visible spectrophotometer (Lambda 40 UV/Vis Spectrometer, Perkin Elmer) in a 3:1 mixture by volume of DI water and dimethyl sulfoxide (DMSO). The molar absorptivity of NBE was measured prior to irradiation. The sample was then irradiated (λ = 365 nm; I₀ = 10 mW/cm²) and the molar absorptivity of NBP was measured.

Measurement of quantum yield via photorheometry

To determine the kinetic constants of photolysis in PEGdiPDA hydrogels, thin films (z = 50 µm) were polymerized in situ on a parallel plate photorheometer (TA, Ares). After complete polymerization, the hydrogel was surrounded by water to maintain hydration and then photodegraded (λ = 365 nm or 405 nm; I₀ = 10 mW/cm² or 25 mW/cm², respectively). The shear component of the gel’s storage modulus (G′) was measured as a function of irradiation time, t. A characteristic kinetic constant for photolysis, k, was determined by linear regression of this data (0.5 ≤ G′/G′₀ ≤ 1) based on gel mechanical theories, degradation kinetics, and photolysis kinetics.^10,20,29 The following was used to calculate k:

$$\text{ln}\left(\frac{G^{\prime }}{G_0^{\prime }}\right)=-2kt$$

where t is the irradiation time; G′₀ is the initial shear component of the gel’s storage modulus; and the factor of 2 arises from the structure of the monomer containing two photolabile linkers (a thorough description of this relationship is provided in Supporting Information). The quantum yield, φ, can be calculated from the characteristic kinetic constant as

$$\phi ={10}^6\frac{k{N}_{A}hc}{\epsilon \lambda I_0}$$

where N_A is Avagadro’s constant; h is Planck’s constant; c is the speed of light; ɛ is the molar absorptivity of the NBE at the wavelength of irradiation; λ is the wavelength of irradiation; and I₀ is the irradiation intensity.³⁰

Measurement of quantum yield via NMR

To confirm the quantum yield measurements for 365 nm irradiation, the quantum yield was also determined by NMR analysis of degradation of the NBE moiety. Characteristic ring peaks in the NBE shift dramatically upon degradation, which can be quantified to track the kinetics of degradation as a function of time. Dilute PEGdiPDA solutions were irradiated (λ = 365 nm; I₀ = 10 mW/cm²) for 1, 2, 3, 5, 10, 20, and 30 minutes each. A characteristic kinetic constant for photolysis, k, was determined by linear regression of the intact NBE concentration versus time. The following was used to calculate k:

$$\text{ln}\left(\frac{C}{C_0}\right)=-kt$$

where C is the concentration of NBE moieties; C₀ is the initial concentration of NBE moieties; and t is the irradiation time. As before, the quantum yield, φ, can be calculated from the characteristic kinetic constant as

$$\phi ={10}^6\frac{k{N}_{A}hc}{\epsilon \lambda I_0}$$

where N_A is Avagadro’s constant; h is Planck’s constant; c is the speed of light; ɛ is the molar absorptivity of the NBE at the wavelength of irradiation; λ is the wavelength of irradiation; and I₀ is the irradiation intensity. For practical purposes solution NMR studies of the degradation rate were employed to model degradation rates in the gel network, but as the PEGdiPDA molecule resides in a highly swollen polymer network mobility constraints should not strongly influence the quantum yield and solution studies should approximate in gel reaction kinetics.

Fractional mass loss of PEGdiPDA hydrogels

Data for the fractional mass loss of PEGdiDPA hydrogels exposed to 365 nm irradiation (Fig. 5a) was reported previously in ref. 20, and new results at 405 nm irradiation are added to this data. For fractional mass loss, PEGdiPDA hydrogels ([NBE] = 0.04 or 0.058 M; z = 1500 µm) were placed in a solution of PBS within a chamber between glass slides and exposed to collimated surface irradiation (λ = 365 or 405 nm; I₀ = 20.0 ± 1.0 or 25.0 ± 1.0 mW cm⁻², respectively). At each time point, five gels were taken from the chamber to remove them from the light and the PBS was completely replaced with fresh PBS to limit the accumulation of degradation products in the light path. The gels were then lyophilized and weighed. Fractional mass loss was calculated as the normalized mass at each time point.²⁰

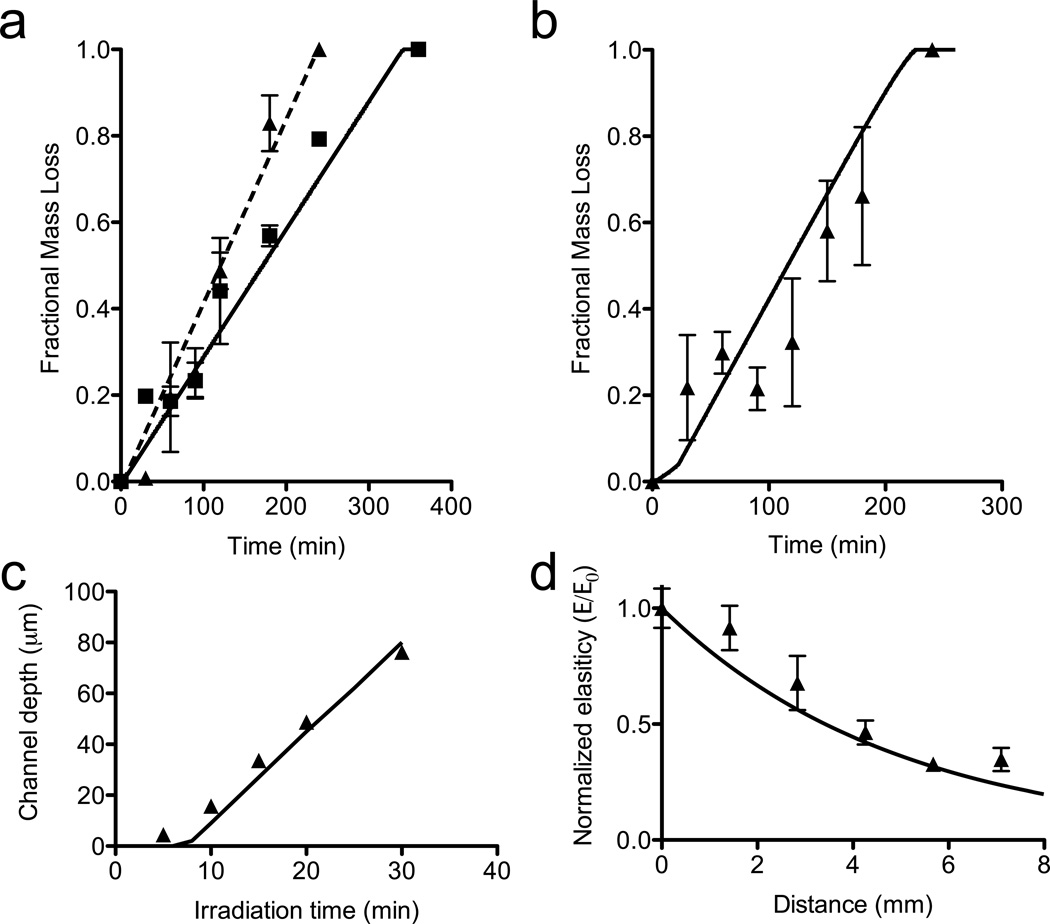
Figure 5. Model predictions compared to experimental degradation of PEGdiPDA hydrogels.

The photodegradation model was employed to predict mass loss and material property changes in chain polymerized, PEGdiPDA hydrogels. (a) Fractional mass loss for two formulations ([NBE] = 0.04 M; z = 1500 µm; triangles – experimental, previously reported data found in ref. 20; dashed line – prediction and [NBE] = 0.058 M; z = 1500 µm; squares – experimental, previously reported data found in ref. 20; solid line – prediction) in response to irradiation (λ = 365 nm; I₀ = 20 mW/cm²) was predicted by the statistical-kinetic mass loss model. (b) Fractional mass loss for PEGdiPDA hydrogels ([NBE] = 0.04 M) in response to irradiation (λ = 405 nm at I₀ = 25 mW/cm²) also compared well with predictions. (triangles – experimental; solid line – prediction) (c) The depth of channels patterned into the surface of PEGdiPDA hydrogels ([NBE] = 0.04 M; λ = 365 nm; I₀ = 10 mW/cm²) was predicted, except at short irradiation times. (triangles – experimental, previously reported data found in ref. 20; solid line – prediction) (d) A gradient in surface elasticity generated by photomasking was also predicted by the statistical-kinetic model. (triangles – experimental, previously reported data found in ref. 21; solid line – prediction, line connects discrete model predictions) For all model calculations, N = 20.

Channel patterning in PEGdiPDA hydrogels

Data for the channel patterning in PEGdiPDA hydrogels (Fig. 5c) was reported previously in ref. 20. Briefly, channels were generated in PEGdiPDA hydrogels ([NBE] = 0.04 M; z = 500 µm) via photolightography (λ = 365 nm; I₀ = 10.0 ± 0.5 mW cm⁻²; 400 µm wide black lines separated by 400 µm wide transparent lines; Mask Aligner, Optical Associates Inc., Model J500) for different times (5 – 30 min) to form channels within the gel through photoerosion. Irradiation was conducted with the gel just below the photomask and surrounded by PBS to facilitate dissolution of erosion products into a surrounding sink during degradation. Channels were measured quantitatively via profilometry (Style Profiler, Dektak 6M) and visually confirmed via confocal LSM (Zeiss 710 NLO LSM) on cross-sections of the gel.²⁰

Surface gradient patterning in PEGdiPDA hydrogels

Data for the gradient in the elastic modulus (Young’s modulus, E) along the surface of PEGdiPDA (Fig. 5d) was reported previously in ref. 20. Briefly, the gradient was generated by exposing the surface of a PEGdiPDA hydrogel ([NBE] = 0.04 M; z ~ 200 µm) to collimated irradiation (λ = 365 nm; I₀ = 10.0 ± 0.5 mW cm⁻²) in a gradient fashion. The gradient of light was achieved by continuously occluding the hydrogel surface with an opaque substrate from the initial side (0 mm) to the final side (9 mm) linearly over the course of 5 minutes. The surface gradient was then measured with AFM (PicoPlusTM scanning probe microscope; Molecular Imaging, Inc.; pyramidal silicon nitride tip with force constant 0.12 N/m, radius = 10 nm, height = 2.5–3.5 nm, and angle of pyramid = 35°) and fitting data to a Hertz model with ν ~ 0.2 for the surface of PEG hydrogel.²⁰

Model calculations

The model was written and executed in MATLAB (Mathworks) with a spatial step size, Δz, of 100 nm and a temporal step size, Δt, of 10 ms. At each temporal node, the z-dependent light intensity profile was solved by Euler integration of the Beer-Lambert law (Eq. 1) over the whole spatial grid. Then, the extent of cleavage of o-nitrobenzyl ether and extent of generation of the nitrosobenzyl cleavage product were calculated through Euler integration of Eqs. 2 & 3, utilizing the light intensity profile for the current temporal node, to update the concentration profiles for the photoactive species. This iterative numerical method was repeated to generate the spatiotemporally varying light intensity and concentration profiles through the depth of the gel at each discrete time step. The fidelity of the numerical method was verified in the manner of Miller et al.31 by comparing calculations to analytic solutions from Wegscheider.^32,33

Model Development

Modeling Light Intensity and Photoactive Species Profiles

A statistical-kinetic model of photodegradation was developed that combines the kinetics of photocleavage reactions with statistical, mean-field descriptions of network connectivity to calculate mass loss in chain polymerized, photodegradable networks. The photodegradation process relies on photochemical reactions whose rates are heterogeneous in both space and time,³³ making descriptions of light-induced material property changes difficult. This hallmark of photochemical reactions occurs because the local reaction rate is proportional to the product of the local concentration of the photoactive species and the local intensity of light.³³ Since photons must be absorbed for reaction to occur, light intensity becomes optically attenuated in photoresponsive networks, causing intensity to be a function of position. Furthermore, the products of most photodegradation reactions possess different molar extinction coefficients than the reactants while erosion of the material removes absorbers from the light path. Both of these phenomena alter the absorptivity of the light path as the reaction progresses, modulating the light intensity profile and, thus, the reaction rate with time. In this manner, optical attenuation produces both spatial and temporal variation in the light intensity profiles, local photodegradation rates, and species concentration profiles.

To model these heterogeneities, one needs to solve a system of coupled partial differential equations that describes the local light intensity and local photoactive species concentrations as functions of both space and time. The Beer-Lambert law was employed to quantify the spatiotemporally varying light intensity profile.

$$\frac{\partial \mathrm{I}(z,t)}{\partial z}=-2.3\mathrm{I}(z,t){\mathrm{\Sigma }}_i{\epsilon }_i[{\mathrm{C}}_{\mathrm{i}}](z,t)$$ (Eq. 1)

Here, I(z,t) is the local irradiation intensity (W cm⁻²) at a given depth in the gel, z, and a given time, t; ɛ_i is the molar absorptivity (L mol⁻¹ cm⁻¹) of the i-th photoactive species in the system for the wavelength of degradation; and [C_i] is the local concentration (mol L⁻¹) of the i-th photoactive species in the system. The incident irradiation was assumed to be constant throughout the time course of degradation so that

$$\mathrm{I}(0,t)={\mathrm{I}}_0$$

The photocleavage reaction was modeled with first-order kinetics such that the local rate of photoreaction and concentration of photoactive species, [C_i](z,t), is described by

$$\frac{\partial [{\mathrm{C}}_i](z,t)}{\partial t}=-\frac{\phi {\epsilon }_i\lambda }{N_{A}hc}[{\mathrm{C}}_{\mathrm{i}}](z,t)\mathrm{I}(z,t)$$ (Eq. 2)

In this equation, φ is the quantum yield (unitless) for the cleavage reaction of i-th photoactive species for the wavelength of irradiation; ɛ_i is the molar absorptivity (L mol⁻¹ cm⁻¹) of i-th photoactive species for the wavelength of irradiation; N_A is Avagadro’s number (mol⁻¹); h is the Planck constant (m² kg s⁻¹); c is the speed of light (m s⁻¹); and λ is the wavelength of irradiation (m). For every cleavage event there is a one-to-one generation of cleavage product(s) described by

$$\frac{\partial [{\mathrm{C}}_j](z,t)}{\partial t}=-\frac{\phi {\epsilon }_i\lambda }{N_{A}hc}[{\mathrm{C}}_{\mathrm{i}}](z,t)\mathrm{I}(z,t)$$ (Eq. 3)

Here, [C_j](z,t) is the concentration (mol L⁻¹) of the j-th cleavage product corresponding to the i-th photoactive species. The rate of generation of the cleavage product(s) is equal and opposite to the consumption of the photoactive species. Note that the molar absorptivity of the cleavage products must be taken into account in Eq. 1 as they can contribute significantly to the attenuation of light. It was assumed that all photoactive species concentrations were initially uniform throughout the material and that all photoactive species were initially intact, so that

$$[{\mathrm{C}}_i](z,\mathit{0})={\mathrm{C}}_{\mathrm{i},0}[{\mathrm{C}}_{\mathrm{j}}](z,\mathit{0})=0$$

Eqs. 1–3 and the corresponding boundary conditions comprise a set of coupled partial differential equations that describe the kinetics of photodegradation as a function of both space and time.^8,31,33 To calculate the light intensity and concentration profiles at each point in space and time, finite element methods were employed to solve this system of coupled equations numerically. Previous studies in optically thick films have presented models of non-uniform photochemical reactions in both bleaching photopolymerizations and photorelease of small molecules.^21,22,31,33 These analyses similarly accounted for the complex dynamics between light attenuation and photochemical reactions by solving a similar series of partial differential equations that describe the attenuation of light and the kinetics of photoreactions. This work uniquely extends this framework to model material property changes and mass loss in chain polymerized photodegradable hydrogels.^10,11

PEGdiPDA photodegradable hydrogels

The purpose of this work is to describe a general framework to model photodegradation in swollen hydrogels using a minimum number of measurable parameters that describe the system of interest. In this manner, the methodology can be extended to a range of photodegradable hydrogels or non-swollen networks for which the governing physical parameters can be determined. In this work, a general photodegradation model is developed and applied to describe the degradation and erosion behavior for a specific photodegradable hydrogel, originally presented by Kloxin et al.^10,12,20,29 Further, model predictions are compared to experimental results to demonstrate the physical relevance of the model.

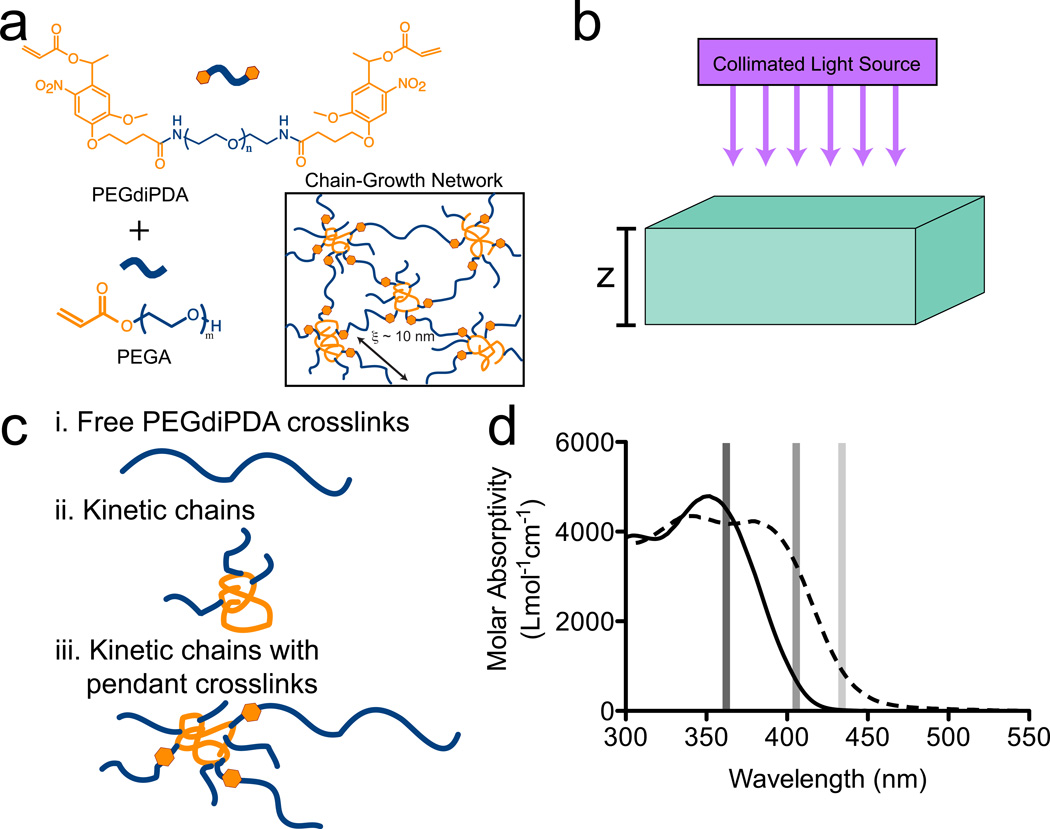
Poly(ethylene glycol) diphotodegradable acrylate (PEGdiPDA) hydrogels were formed through a redox-initiated, free-radical chain polymerization of the crosslinker, PEGdiPDA, with PEGA (poly(ethylene glycol) monoacrylate) under aqueous conditions (Figure 1a). The incorporation of an o-nitrobenzyl ether (NBE) into the crosslinking molecule PEGdiPDA renders the hydrogels photodegradable, as the NBE is susceptible to irreversible cleavage in response to one-photon (λ ~ 320–436nm) or two-photon (λ ~ 740nm) irradiation.^25,26,29

Figure 1. Photodegradable hydrogel system.

(a) Photodegradable PEG based hydrogels were formed through redox-initiated free radical polymerization of the photodegradable crosslinker (PEGdiPDA) with a co-monomer (PEGA). (b) Upon exposure to collimated irradiation, these gels degrade as the photolabile o-nitrobenzyl ether (NBE) cleaves leading to mass loss and, ultimately, erosion. (c) Mass loss results from the release of cleavage products from the network that predominantly fall into three categories: i. free PEGdiPDA crosslinks, ii. kinetic chains, and iii. kinetic chains with pendant crosslinks. Once a sufficient fraction of NBE moieties are cleaved in a local region, the gel undergoes reverse gelation where the polymers no longer form an infinite molecular weight network and the local material erodes from the gel. (d) Photodegradation can be achieved at wavelengths where NBE absorbs light (solid line). In this work, 365 nm, 405 nm, and 436 nm were employed for degradation. The mechanism of mass loss of the gels was dictated by the total absorptivity of the degradable hydrogels, which depends on the molar absorptivity of NBE (solid line), the molar absorptivity of the cleavage product (NBP; dashed line), the concentrations of photoactive species, the thickness of the gel, and the wavelength of irradiation. Molar absorptivity data previously reported in ref. 29.

For the PEGdiPDA hydrogel system, there are only two photoactive species, NBE and the single nitrosobenzyl cleavage product NBP. The molar absorptivity of each of these compounds was quantified previously over the range of irradiation wavelengths (Figure 1c).^{17,18,27–29} Eq. 2 governed the rate of photocleavage and concentration profile of the single photolabile moiety, NBE. As the NBE species was cleaved, there was a one-to-one generation of the cleavage product, NBP, governed by Eq. 3. It was assumed that the NBE species concentration was initially uniform throughout the hydrogel and that all NBE moieties were initially intact, so that

$$[\text{NBE}](z,\mathit{0})={[\text{NBE}]}_0[\text{NBP}](z,\mathit{0})=0$$

Statistical model of degradation, mass loss, and erosion in the gel

To extend this kinetic modeling to predict mass loss and erosion from PEGdiPDA gels, light intensity profiles (Eq. 1) and reaction kinetics (Eqs. 2 & 3) were employed to quantify the concentration of intact NBE species at any point in space and time. The concentration of intact NBE moieties was then combined with statistical descriptions of network connectivity to model the crosslinking density, mass loss, and erosion in the gel during the degradation process. Since this work focuses on modeling degradation in PEGdiPDA networks that are formed from the chain polymerization of telechelic monomers, the appropriate statistical descriptions of chain polymerized hydrogels are employed.^17,18,27,29 However, the general approach is broad, and the model presented here can be extended to describe photodegradable gels that are formed by step-growth or mixed-mode polymerizations by incorporating the appropriate statistical descriptions of these networks, described elsewhere.^18,28,29

To predict network property evolution in PEGdiPDA hydrogels, the spatially and temporally varying concentration profile of intact NBE, [NBE](z,t), calculated by the iterative numerical method, was combined with a statistical description of chain polymerized network connectivity. This approach relied on a mean-field approximation and fundamental probability statements that correlate cleavage of NBE moieties with the degradation of crosslinks in the gel, release of network fragments, and, ultimately, erosion of the material. The probability that a given NBE moiety has been cleaved, P(z,t), was related to the local fraction of intact NBE species

$$P(z,t)=1-\frac{[\text{NBE}](z,t)}{{[\text{NBE}]}_0}$$ (Eq. 4)

where [NBE]₀ is the initial concentration of NBE in the network. Mass loss was approximated in this model by calculating the probability that specific species were released, which is no longer bound to the gel backbone, based on the probability of NBE cleavage (Eq. 4) and a mathematical description of the hydrogel network structure. While a wide range of different molecular weight species can be released from the gel during mass loss, it was approximated that the dominant mass loss would be from three main erosion products, following the work of Metters et al. and Reddy et al.^17,18,29 The three dominant erosion products, for which release was explicitly modeled were (i) free PEGdiPDA crosslinks, (ii) poly(acrylate) kinetic chains, and (iii) poly(acrylate) kinetic chains with pendant PEGdiPDA crosslinks (Figure 1c).

As Metters et al. demonstrated, it is convenient to calculate the state of the crosslinks to model the release of the erosion products from these chain polymerized hydrogels.10,17,20,29 Each PEGdiPDA crosslink can exist in one of three states: (1) an intact crosslink, in which both NBE moieties are intact, (2) a crosslink dangling from a poly(acrylate) kinetic chain, in which one NBE moiety is cleaved and the other intact, and (3) free crosslink, in which both NBE moieties have been cleaved. The fraction of PEGdiPDA crosslinks in each of these three states was calculated from the probability that a given NBE moiety has been cleaved, P(z,t).

1. Fraction of intact crosslinks

   $${\mathrm{f}}_1(z,t)={(1-P(z,t))}^2$$ (Eq. 5)
2. Fraction of dangling crosslinks

   $${\mathrm{f}}_2(z,t)=2P(z,t)(1-P(z,t))$$ (Eq. 6)
3. Fraction of free crosslinks

   $${\mathrm{f}}_3(z,t)=P{(z,t)}^2$$ (Eq. 7)

Note that f₁(z,t) can be used to calculate the crosslinking density (ρ_x) as a function of space and time directly: ρ_x(z,t) = f₁(z,t)•ρ_x,0.

The fractional populations of PEGdiPDA crosslinks, Eqs 5–7, were combined with the connectivity of the network to predict mass loss from the network. For chain-growth hydrogels, the key connectivity parameter is the average number, N, of crosslinks per kinetic chain. It is important to note that crosslinks can exist as loops or dangling ends in the initial gel formation and N only accounts for the number of fully intact crosslinks per kinetic chain. For a poly(acrylate) kinetic chain to be released directly from the network as a type (ii) or (iii) erosion product, all of the crosslinks connected to it must exist in state (2) or (3), i.e., none of the crosslinks attached to the kinetic chain remain intact.^17,18,30

As mentioned above, this assumes that larger molecular weight species, such as a PEGdiPDA molecule with two kinetic chains at both ends, were not released from the material. While these other species can have high molecular weights and contribute significantly to mass loss when released, release only occurs appreciably at late time points in the degradation, and their release is captured by the reverse gelation condition, described below. Therefore, under these assumptions, a kinetic chain connected to N crosslinks has a fractional probability of being released from the network, F_kc,N(z,t):

$${\mathrm{F}}_{\text{kc},\mathrm{N}}(z,t)={({\mathrm{f}}_2(z,t)+{\mathrm{f}}_3(z,t))}^{\mathrm{N}}={(2P(z,t)(1-P(z,t)+P{(z,t)}^2))}^{\mathrm{N}}$$ (Eq. 8)

Once F_kc,N(z,t) is known, the fraction of PEGdiPDA crosslinks released, F_xl(z,t), was calculated by summing the fraction of free crosslinks, f₃(z,t), with the fraction of dangling crosslinks that are released with kinetic chains, F_kc,N(z,t);f₂(z,t)/2. Therefore, F_xl(z,t) can be calculated as:

$${\mathrm{F}}_{\text{xl}}(z,t)={\mathrm{F}}_{\text{kc},\mathrm{N}}(z,t)\frac{{\mathrm{f}}_2(z,t)}{2}+{\mathrm{f}}_3(z,t)={\mathrm{F}}_{\text{kc},\mathrm{N}}(z,t)P(z,t)(1-P(z,t))+P{(z,t)}^2$$ (Eq. 9)

Given the fractions of the eroded products, F_kc,N(z,t) and F_xl(z,t), as functions of space and time, the fractional mass loss for the corresponding locale was calculated by summing the products of the weight fraction of the gel in each of the eroded species by the fraction of each species that is released.

$$\text{ML}(z,t)=({\mathrm{W}}_{\text{kc}}{\mathrm{F}}_{\text{kc},\mathrm{N}}(z,t)+{\mathrm{W}}_{\text{xl}}{\mathrm{F}}_{\text{xl}}(z,t))$$ (Eq. 10)

Here, W_kc and W_xl represent the weight fraction of the gel in the kinetic chains and the PEGdiPDA crosslinks, respectively.

As photodegradtion proceeds, individual NBE moieties cleave, degrading PEGdiPDA crosslinks, and, ultimately, causing the release of erosion products and mass loss of the gel. This process eventually reaches a limit, the reverse gelation point, where the network components no longer form an infinite molecular weight gel locally. The reverse gelation point is reached when a sufficient fraction of NBE moieties are cleaved, P_c, and the local network is then transformed into highly branched soluble polymer chains. At this point, the local network is entirely soluble and the fractional mass loss is assumed to approach 1, ML(z,t) = 1. A recursive approach, originally developed by Miller and Macosko,^20,34,35 was used to determine the critical fraction of cleaved NBE moieties that leads to reverse gelation.18 In this work a monodisperse N was assumed such that all kinetic chains were attached to exactly N PEGdiPDA crosslinks. In reality, a distribution of N crosslinks per kinetic chain exists, and while this can be investigated in future work, previous work in similar systems has shown a modest effect of the distribution of N on the mass loss profile.¹⁸ From this approach, the critical fraction of intact NBE moieties, P_c, at which reverse gelation occurs is given by:

$$P_c=1-\frac{1}{\sqrt{\mathrm{N}-1}}$$ (Eq. 11)

Therefore, the function describing the local fractional mass loss is described by Eq. 10 when P > P_c and is equal to unity once P ≤ P_c. The average number of crosslinks per kinetic chain, N, is a free parameter of the model unless it is determined experimentally through measurements of the masses of soluble erosion products or estimated from the time to reach reverse gelation. In this work, N was assumed to be 20 for all systems (more details are included in the Supporting Information).

The kinetic description of photodegradation, Eqs 1–4, was solved numerically to calculate P(z,t), and at each time point, P(z,t) was combined with Eqs. 5–11 to determine ML(z,t). ML(z,t) was summed over the spatial nodes to determine the total fractional mass loss of the gel, ML(t).

$$\text{ML}(t)=\frac{{\sum }_{i=1}^{{\mathrm{N}}_2}\text{ML}(i,t)}{N_z}$$ (Eq. 12)

where N_z is the number of spatial nodes in the system.

RESULTS AND DISCUSSION

A statistical-kinetic model characterizing photodegradation of hydrogel networks (Eqs. 1–12) is developed based solely on physical parameters of the system. This approach combined model equations that describe heterogeneous photochemical reactions with a mean-field, statistical description of network connectivity for hydrogels formed via chain polymerization of telechelic polymers. In this manner, the methodology could be extended to a broad range of photodegradable hydrogels for which statistical descriptions of network connectivity are known, including polymeric hydrogel networks formed via chain-growth, step-growth, or mixed-mode polymerizations.^18,28

Further, the general form of the model can be applied to photodegradable hydrogels that are based on any photolytic molecule for which the molar absorptivities, ɛ_i, and quantum yields, φ_i, can be measured for the irradiation wavelengths of interest. In this work, application of the photodegradation model focused on hydrogels formed from the chain co-polymerization of a PEGdiPDA crosslinker, originally developed by Kloxin et al.¹⁰ These gels photodegrade on account of the o-nitrobenzyl ether (NBE) moieties in the PEGdiPDA crosslinkers, which undergo an irreversible cleavage to the by-product, NBP, in response to single-photon irradiation (λ = 320–436 nm).

The photophysical parameters for NBE and NBP were measured for the irradiation wavelengths of interest, with a specific focus on 365, 405, and 436 nm irradiation, bands readily available with a mercury arc lamp. The molar absorptivities of NBE, ɛ_NBE, and NBP, ɛ_NBP, were calculated previously for 320 – 436 nm light (Figure 1d).²⁹ At 365 nm, ɛ_NBE = 4300 L mol⁻¹ cm⁻¹ while ɛ_NBP = 4200 L mol⁻¹ cm⁻¹, indicating minimal bleaching upon photoreaction. At 405nm, ɛ_NBE = 720 L mol⁻¹ cm⁻¹ while ɛ_NBP = 3300 L mol⁻¹ cm⁻¹, indicating a red shift in the absorptivity of the NBE upon photoreaction. At 436nm, ɛ_NBE = 16 L mol⁻¹ cm⁻¹ while ɛ_NBP = 800 L mol⁻¹ cm⁻¹, similarly red shifting upon cleavage. The quantum yields for NBE photocleavage were found experimentally to be φ_NBE = 0.027 and φ_NBE = 0.017 for 365 and 405 nm irradiation, respectively. The quantum yield at 436 nm was found previously as φ_NBE = 0.23.²²

PEGdiPDA hydrogels were fabricated via redox-initiated, free-radical chain polymerization at two disparate macromer concentrations, 10 mol% PEGdiPDA:90 mol% PEGA and 25 mol% PEGdiPDA:75 mol% PEGA of a total 15 wt% polymer gel (Figure 1a). These gels possessed concentrations of NBE, [NBE], of 0.040 M and 0.058 M, respectively, and both were assumed to possess an average number of crosslinks per kinetic chain, N, of 20. The average number of crosslinks per kinetic chain may vary between the two gel systems; however, N was not calculated experimentally for either system and the N of 20 resulted in reasonable predictions of the mass loss behavior for both gel systems. Gels were polymerized with a thickness, z, ranging from 100 µm to 1500 µm and, subsequently, irradiated with a collimated light source incident on the surface of the gel (Figure 1b) leading to attenuation and spatially varying degradation rates in the z-dimension.

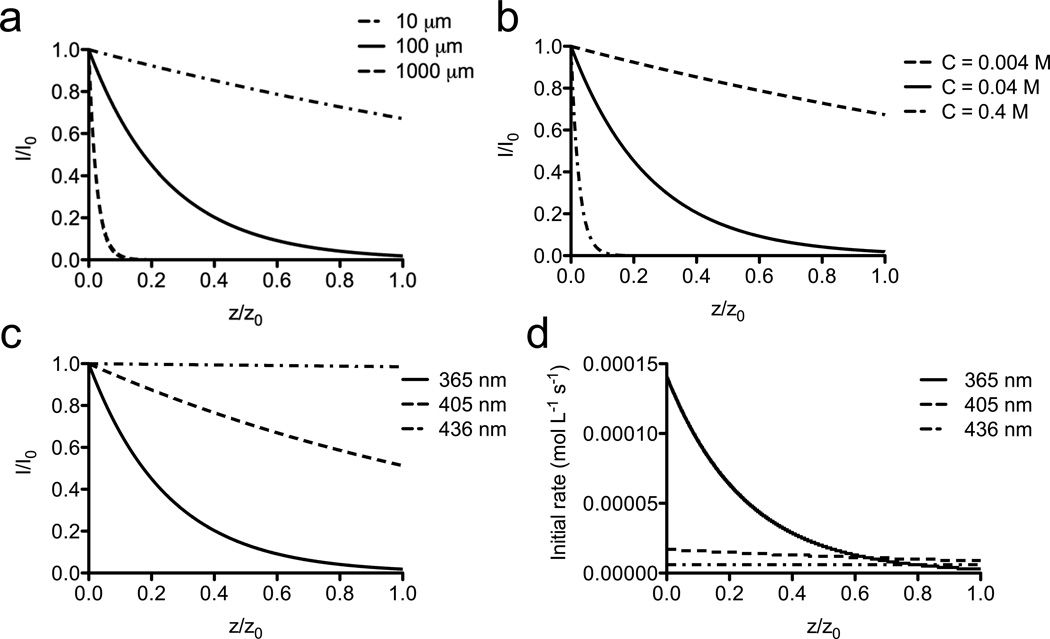
The governing equations of the photodegradation model (Eqs. 1–14) were solved numerically to predict the spatially and temporally varying profiles for the irradiation intensity, concentration of NBE, crosslinking density, and fractional mass loss for these PEGdiPDA hydrogels. The light intensity profiles followed a distinct decay that is indicative of attenuation in the material, which depends on the absorptivity of the particular hydrogel formulation (Figure 2). The absorptivity of the material is related directly to the thickness of the gel, the concentration of the photoactive species, and the molar absorptivity of the photoactive species at the irradiation wavelength as described by the Beer-Lambert Law (Eq. 1). For discussion, the initial absorbance is defined as A = ɛ_NBE•[NBE]•z. Predicted light attenuation profiles at t = 0 for λ = 365 nm, I₀ = 10 mW/cm² irradiation in PEGdiDPA hydrogels ([NBE] = 0.04 M) with z = 10, 100, 1000 µm demonstrated that the fractional penetration depth of the light is dependent on the thickness of the gel (Figure 2a). The light intensity was nearly uniform through the depth of a 10 µm gel (A = 0.17), while only a small volume near the surface of a 1000 µm (A = 17) gel receives significant light at t = 0.

Figure 2. Model predictions of light intensity profiles and kinetic rates.

The incident irradiation is attenuated in the hydrogel on account of the absorbing NBE within the PEGdiPDA hydrogels. (a) Increased thickness of the hydrogel ([NBE] = 0.04 M; λ = 365 nm; I₀ = 10 mW cm⁻²) leads to decreased penetration depth of the light through the gel (z = 10 µm, dash-dot line; z = 100 µm, solid line; z = 1000 µm, dashed line). (b) Similarly, increased concentration of the NBE moieties in the gel (z = 100 µm; λ = 365 nm; I₀ = 10 mW cm⁻²) leads to decreased penetration depth of the light through the gel ([NBE] = 0.004M, dashed line; [NBE] = 0.04M, solid line; [NBE] = 0.4M, dash-dot line). (c) The penetration depth of the light in the gel is also dependent on the wavelength of incident irradiation ([NBE] = 0.04 M; z = 100 µm; I₀ = 10 mW cm⁻²). Here, 365 nm irradiation (solid line) is strongly attenuated owing to the high molar absorptivity of NBE at 365 nm (ɛ_NBE = 4300 L mol⁻¹ cm⁻¹). 405 nm irradiation (dashed line) leads to increased penetration depth (ɛ_NBE = 720 L mol⁻¹ cm⁻¹) while 436 nm irradiation (dash-dot line) is nearly uniform through the depth of the gel (ɛ_NBE = 16 L mol⁻¹ cm⁻¹). (d) The initial photocleavage rate as a function of depth is dependent on the local light intensity and the wavelength of irradiation, through changes in absorbance and quantum yield. ([NBE] = 0.04 M; I₀ = 10 mW cm⁻²; z = 100 µm; λ = 365 nm, solid line; λ = 405 nm, dashed line; λ = 436 nm, dash-dot line)

Similarly, varying the concentration of NBE within the PEGdiPDA gels (z = 100 µm) modulated the light attenuation profile (λ = 365 nm; I₀ = 10 mW/cm²) through the gel (Figure 2b). At a low concentration, ([NBE] = 0.004 M; A = 0.17), light is able to penetrate through the full depth of the gel with only a small amount of attenuation, as the lower concentration of NBE decreases the absorptivity of the gel. As the concentration of NBE, and thus the absorptivity, increases, less light is able to penetrate the full thickness of the gel, creating a steeper gradient in light intensity throughout the depth of the gel.

Irradiating the gel at different wavelengths of light further modified the penetration of light through the gel in a manner that correlates with the absorptivity of the material (Figure 2c). The molar extinction coefficient of NBE (Figure 1c) at the different wavelengths of interest governed the total absorbance of the PEGdiPDA hydrogels ([NBE] = 0.04 M; z = 100 µm). Since 436 nm is only weakly absorbed by NBE moieties (ɛ_NBE = 16 L mol⁻¹ cm⁻¹), incident irradiation at this wavelength penetrates the full depth of the gel uniformly (A = 0.0064). However, as the molar absorptivity of NBE increases at lower wavelengths of light, the incident irradiation becomes attenuated more strongly as evidenced by the model light intensity profiles for 405 nm (ɛ_NBE = 720 L mol⁻¹ cm⁻1; A = 0.29) and 365 nm (ɛ_NBE = 4300 L mol⁻¹ cm¹; A = 1.7). In general, the uniformity of light through the sample is governed by the initial absorbance of the material such that A ≤ 0.1 allows relatively uniform light penetration, whereas A ≥ 10 caused light to be confined primarily to a thin surface region.

Since the photocleavage rate is directly proportional to the local light intensity (Eq. 2), the initial cleavage rate profiles (t = 0) were defined by the attenuated light intensity profiles. In this manner, the rate profiles can be tuned by modulating the absorptivity of the material by altering the thickness of the material (z) or the concentration of the photoactive species ([NBE]). Tuning the wavelength of irradiation also modulates the rate profile as the gel absorbance strongly depends on the wavelength of light; however, the quantum yield is also a function of wavelength and an important parameter in determining the ultimate rate of photocleavage (Eq. 2). Thus, varying the wavelength of light modifies both the uniformity and magnitude of the degradation rate profiles (Figure 2d). For 436 nm irradiation, the rate profile was nearly uniform throughout the depth of the PEGdiPDA gel ([NBE] = 0.04 M; z = 100 µm) on account of the small absorbance (A = 0.0064), but the initial rate at the surface (t = 0; z = 0) was only 5.6 × 10⁻⁶ mol L⁻¹ s⁻¹. In comparison, for 365 nm irradiation ([NBE] = 0.04 M; z = 100 µm) there was significant heterogeneity in the initial rate profile through the gel owing to the high absorbance (A = 1.7), but the initial rate at the surface is much higher, 1.4 × 10⁻⁴ mol L⁻¹ s⁻¹.

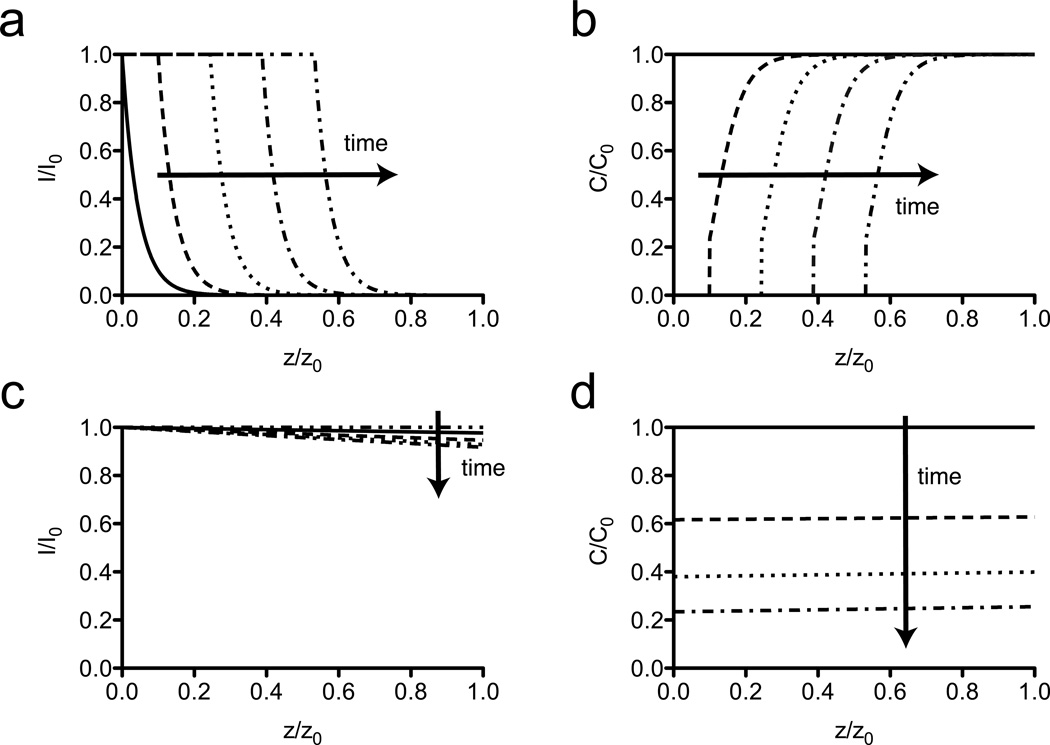
As explained in the model development, the absorptivity of the photodegradable gel changes as the photodegradation proceeds on account of cleavage of NBE to NBP, each possessing different molar absorptivities, and mass loss that occurs at later time points. Therefore, it is necessary to track the evolution of both the light intensity profiles and intact photoactive species concentration profiles in time to better understand the evolution of material properties (Figure 3). Here, two conditions were investigated, one that primarily involved surface erosion of a gel ([NBE] = 0.23 M; z = 100 µm; λ = 365 nm; I₀ = 10 mW/cm2; A = 10) and one that led to a more uniform, bulk degradation of the gel ([NBE] = 0.0056 M; z = 25 µm; λ = 405 nm; I₀ = 10 mW/cm2; A = 0.01). Surface erosion occurs when light is confined to the surface of the gel, concentrating the photocleavage and, thus, the mass loss to this local region (Figure 3a,b). As time progressed the light was able to move through the gel in a wave-like fashion, owing to mass loss at the surface that removes light attenuating material from the light path. Reverse gelation of the material occurs when [NBE]/[NBE]_o ≤ .23, and it was assumed that the erosion products rapidly diffused out of the light path, which is typically reasonable for highly swollen hydrogels. When mass loss occurs, light is able to penetrate further into the gel, resulting in a continual sloughing away of the surface of the gel. The assumption of rapid diffusion of erosion products breaks down for systems in which the degradation occurs more rapidly than the diffusion time scales.

Figure 3. Model predictions of surface and bulk erosion of photodegradable hydrogels.

Surface erosion and bulk degradation are both observed in silico for photodegradable hydrogels depending on the total absorbance of the material. (a) PEGdiPDA hydrogels with high absorbance (A = 10; [NBE] = 0.23 M; z = 100 µm) severely attenuate the incident irradiation (λ = 365 nm; I₀ = 10 mW cm⁻²), which leads to a front of light moving through the depth of the material as degradation proceeds. (arrows indicate the direction of increasing time; t = 0 min, solid line; t = 22.5 min, dashed line; t = 45 min, dotted line; t = 67.5 min, dash-dot line; t = 90 min, dash-double dot line) (b) Photodegradation erodes the surface of the material, where light remains at a high intensity. Erosion is indicated by C/C₀ = 0. In this surface erosion case, the strongly coupled equations (Eqs. 1 – 3) lead to a propagation of light and mass loss through the depth of the gel with time. (t = 0 min, solid line; t = 22.5 min, dashed line; t = 45 min, dotted line; t = 67.5 min, dash-dot line; t = 90 min, dash-double dot line) (c) PEGdiPDA hydrogels with low absorbance (A = 0.01; [NBE] = 0.0056 M; z = 25 µm) allow incident irradiation (λ = 405 nm; I₀ = 25 mW cm⁻²) to penetrate through the full depth of the gel uniformly, which results in bulk degradation of the material. (t = 0 min, solid line; t = 7.5 min, dashed line; t = 15 min, dotted line; t = 22.5 min, dash-dot line; t = 30 min, dash-double dot line) (d) As light penetrates the material uniformly, the reaction rate is uniform through the depth of the gel, which results in an even decrease in [NBE] through the depth of the gel, which is indicative of bulk degradation. At late time points, the whole material erodes. (t = 0 min, solid line; t = 7.5 min, dashed line; t = 15 min, dotted line; t = 22.5 min, dash-dot line; t = 30 min, dash-double dot line) For all model calculations N = 20.

In contrast, bulk degradation occurs whenever the light is more uniformly distributed through the depth of the material (A ≤ 0.1), leading to a similar photocleavage rate throughout the depth of the gel. As time progresses, the light intensity profile is altered slightly as the NBP degradation product absorbs light at 405 nm more strongly than the intact NBE (Figure 3c). Concomitantly, the concentration profile was altered by a near uniform decrease in intact NBE units ([NBE]/[NBE]₀) with depth until the reverse gelation point is reached and the entire gel solubilizes (Figure 3d).

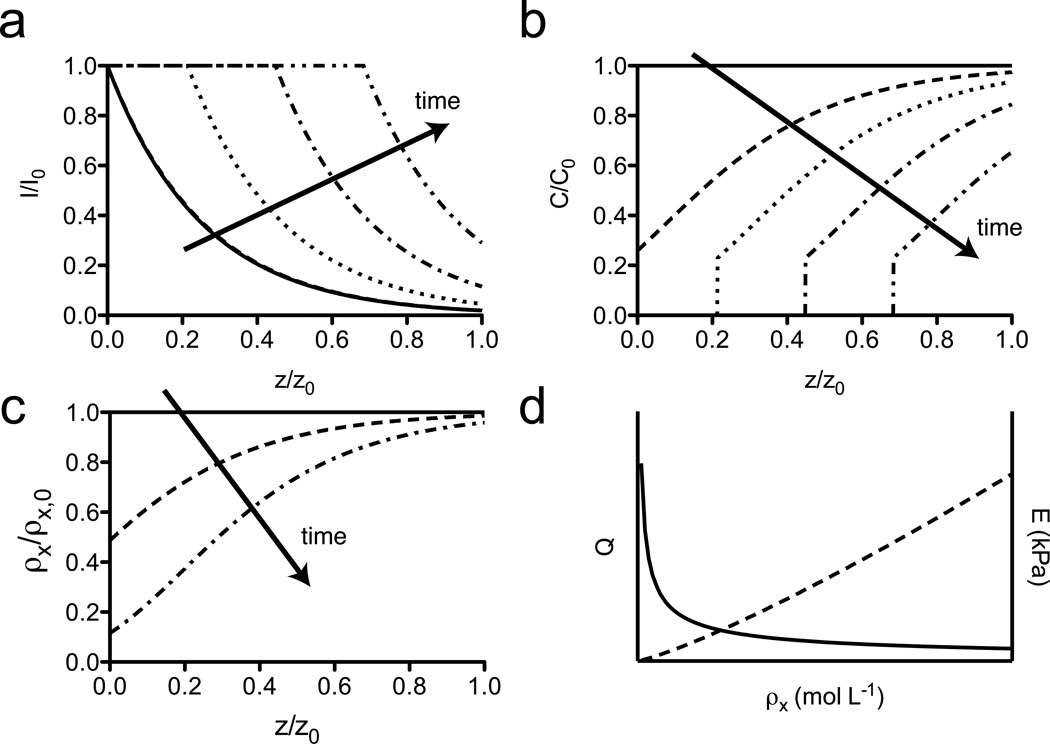
Photodegradation of physically relevant gels often resides in a complex regime that is a blend of the surface erosion and bulk degradation phenomena. Pure bulk degradation only occurs in materials that can be approximated as optically thin films, i.e., A ≤ 0.1. Typical photodegradable hydrogels are 100–1000 µm thick and contain 1–10 wt% photodegradable polymer, which corresponds to A ~ 0.1–10. In such systems, much of the incident light is confined to the surface of the gel owing to attenuation, but a fraction of the light is able to penetrate through the full thickness of the gel, causing non-negligible cleavage of crosslinks (Figure 4a). This results in a surface-eroding wave moving through the gel preceded by a degradation gradient (Figure 4b). Such complex degradation processes are more difficult to conceptualize and model, but can also lead to particularly interesting, anisotropic materials.

Figure 4. Model predictions of photodegradation in PEGdiPDA hydrogels.

For PEGdiPDA hydrogels with intermediate absorbance (A ~ 0.1 – 10), degradation is observed to be a mixture of surface erosion and bulk degradation. (a) In these materials, light is mostly confined to the surface volume of the gel, while a portion of the light is able to penetrate the full thickness, leading to non-neglibile cleavage of NBE moieties. (b) As time progresses the light front moves through the gel surface, eroding the material while anisotropically patterning the full depth of the gel. (arrows indicate the direction of increasing time; t = 0 min, solid line; t = 7.5 min, dashed line; t = 15 min, dotted line; t = 22.5 min, dash-dot line; t = 30 min, dash-double dot line) (c) The anisotropic patterning caused by this phenomenon is predicted to generate materials with gradients in crosslinking density as a function of depth. (t = 0 min, solid line; t = 2 min, dashed line; t = 6 min, dashed-dot line) (d) Since the volumetric swelling ratio, Q, and Young’s modulus, E, of PEG hydrogels depend on the crosslinking density, ρ_x, anisotropies in crosslinking density are readily generated to create spatially varying materials, that can be difficult to synthesize through traditional fabrication routes. For all model calculations, N = 20; [NBE] = 0.04 M; z = 100 µm; λ = 365 nm; I₀ = 10 mW cm⁻²; A = 1.7.

Once the degradation profiles and mass loss behavior are better understood and quantified, this experimental space can be an attractive degradation regime and exploited to generate materials with gradients in crosslinking density through the z-dimension of the material (Figure 4c). Crosslinking density controls many important material properties, including both the volumetric swelling ratio, Q ~ ρ_x^−3/5, and Young’s modulus, E ~ ρ_x^6/5, for PEG hydrogels (Figure 4d).³⁶ As such, gradients in crosslinking density created through photodegradable materials can provide a simple method to fabricate materials with anisotropic properties, which can be difficult to fabricate by traditional methods.

From a modeling perspective, the generation of materials with anisotropic materials is not trivial. Since the photodegradation process alters the crosslinking density, ρ_x, and ultimately, swelling ratio, Q, the hydrogel geometry and concentration of photoactive species within the gel can change as a function of time. For this work, it was assumed that swelling does not influence the concentration of photoactive species during the degradation process, as the initial equilibrium water content of the gels is relatively high (i.e., 85–95% water). However, degradation-induced swelling may introduce dimensional changes into the material. For example, if Q were to increase from 10 to 20 in a bulk degrading hydrogel with isotropic swelling (a large swelling change that one would observe only at late stages of degradation), the sample thickness would change by a factor of 1.26. This version of the photodegradation model does not account for dimensional changes in the material, but future investigations could account for this by incorporating floating boundary conditions that account for dynamic swelling during degradation.

The PEGdiPDA chain polymerized hydrogels developed in previous studies and modeled in this work ([NBE] = 0.04 or 0.058 M; z = 100 – 1500 µm; A ≈ 0.3 – 39) fall primarily in the range of intermediate degradation (a mixture of surface erosion and bulk degradation) with λ = 365 and 405 nm. To demonstrate the physical relevance of this model and the ability that it offers to predict complex degradation and mass loss profiles, the model was applied to described mass loss and erosion of previously studied PEGdiPDA gels. Specifically, the mass loss profiles of thick gels (z = 1500 µm; [NBE] = 0.04 or 0.06 M; A ≈ 26 – 39) exposed to 365 nm irradiation at 20 mW/cm² were modeled and compared to experimental erosion profiles (Figure 5a).20 The model predicted the linear mass loss profile as a function of time in both cases, as expected from surface erosion driven degradation that was expected for these gels. Similar mass loss experiments were conducted with PEGdiPDA hydrogels exposed to 405 nm irradiation at 25 mW/cm² (z = 500 µm; [NBE] = 0.04; A ≈ 1.4; Figure 5b). The model predicted the experimental trends and data well, yet there are some deviations to note in these experiments. Part of this deviation could be caused by an inaccurate determination of N, the average number of crosslinks per kinetic chain, or the assumption that mass diffused out of the path of the light instantly upon reverse gelation. For experiments where the timescale of diffusion, τ_D, is much less than the timescale of degradation, τ_PD, this is a fair assumption. However not all experiments are in this regime, as τ_D/τ_PD ~ 0.1 – 1 for a 100 µm diffusion distance for these gels assuming a diffusion coefficient on the order of 10⁻⁶ cm²/s, which is reasonable for small molecules in water. To improve on this possible error, future iterations of mass loss models in photodegradable hydrogels might focus on better modeling diffusion of degradation and erosion products.

The surface erosion phenomenon was further modeled PEGdiPDA hydrogels ([NBE] = 0.04 M; z = 250 µm; A = 0.7 – 4.3) in which channels were formed using a photomask with 365 nm irradiation at I₀ = 10 mW/cm².²⁰ Similar to the fractional mass loss, the model predicted the progression of channel depth as a function of time, except for some small deviation at short time scales (Figure 5c). However, there is also a degradation gradient that evolves behind the channel growth, as predicted by the mixed-mode degradation. This gradient was indicative of the complex surface erosion and bulk degradation properties of these gels and has been exploited to generate functional materials with gradients in elasticity in both the z-dimension²⁰ and the x-y dimension.^20,21 The photodegradation model was employed to predict an x-y gradient (Figure 5d) generated with this material in a previous study.²⁰

In all, the model of photodegradation presented herein should facilitate and improve the design of hydrogel compositions for desired applications. With this model, physically relevant gels can be designed that preferentially bulk degrade or undergo surface erosion based on material composition. Furthermore, complex, anisotropic materials can be predicted and subsequently engineered using the insight gained from of the mass loss models. In this manner, the model of photodegradation is an enabling tool in the design and use of photoresponsive hydrogels.

CONCLUSIONS

A statistical-kinetic model of photodegradation was presented that predicts photodegradation rates and concomitant changes in material properties as functions of space and time for photolabile hydrogels. The model accounted for the complexity of photodegradation caused by the inherent heterogeneity of the photoreaction as a result of light attenuation within the material. The initial absorbance of the material was used to predict whether the system would undergo bulk degradation and mass loss or surface erosion based on the uniformity or non-uniformity of light in each case. The model methodology is general and can be applied to a broad range of photoresponsive hydrogels whose material properties are connected to photoreactions within the material. In this work, kinetic modeling that combined the Beer-Lambert Law and kinetic expressions to described the photocleavage reaction was combined with statistical descriptions of mass loss in chain polymerized networks, which facilitated the prediction of material property changes in a model PEGdiPDA hydrogel system. In all cases, the predictions compared well with experimental data. In all, a method for modeling photodegradation has been presented that will prove useful in the design and fabrication of photoresponsive networks for cell culture experiments, anisotropic material synthesis, and drug delivery vehicles.