Abstract
A thermodynamic model is used to investigate the conditions under which clathrin triskelions form polyhedral baskets. The analysis, which is similar to classical methods used to study micelle formation, relates clathrin basket energetics to system parameters linked to triskelial rigidity, the natural curvature of an isolated triskelion, and interactions between triskelial legs in the assembled polyhedra. Mathematical theory predicts that a minimal (“critical”) clathrin concentration, CC, needs to be surpassed in order for basket polymerization to occur, and indicates how CC, and the amount of polymerized material, depend on the chosen parameters. Analytical expressions are obtained to indicate how changes in the parameters affect the sizes of the polyhedra which arise when the total clathrin concentration exceeds CC. A continuum analytic approximation then is used to produce numerical results that illustrate the derived dependences.
INTRODUCTION
Protein-coated lipid vesicles are extensively used in eukaryotic cells to transfer materials between membranous organelles, and to and from membrane-delimited cell compartments. Well established examples are intracellular transport between the endoplasmic reticulum (ER) and the Golgi apparatus, and the internalization of cargo at the plasma membrane (and selective transport from the Golgi to the cell surface). Both processes involve vesicle biogenesis mediated by the formation of distinct protein lattices with which other proteins associate to form the outer coats of the vesicles.1, 2 The first utilizes a CopII coat, of which the elemental lattice is a cuboctahedral “cage” built from the Sec13/Sec31 protein complex (MW ca. 339 kDa). In these cages the intrinsic vertex valency is four.3 In the second, more extensively studied, case, the underlying structural lattice is constructed of clathrin, which is a heterodimeric protein composed of a ca. 180–190 kDa heavy chain and an associated light chain of variable, ca. 23–30 kDa, MW.4, 5, 6
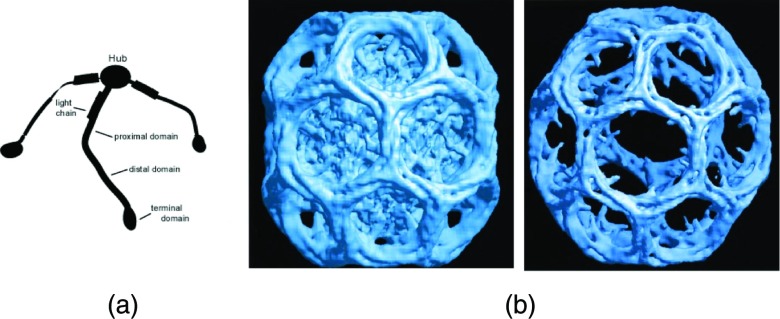
The basic building block of the protein lattices in such clathrin-coated vesicles (CCVs) is a three-legged “triskelion” containing three clathrin molecules whose identical, species specific, heavy chains are non-covalently joined at a common hub (Fig. 1a). The vertex valence of the clathrin lattice everywhere is three, and the cages (also referred to as “baskets”) predominantly contain hexagonal and pentagonal faces. The total length of a leg, which contains bends, is approximately 50 nm, and the diameter of a CCV typically ranges between 80 and 200 nm. Various proteins bind to clathrin within a cell.7, 8, 9 Some have a role in joining the coat to specific lipid components of, e.g., the plasma membrane and/or to receptors and other membrane-embedded entities. Other coat components stimulate the formation of the clathrin lattice or are involved in the release of CCVs from the membrane. Yet others are implicated in the dissolution of the coat prior to the delivery of cargo to endosomes. Among these is the heterotetrameric “adaptor complex,” AP-2, that links clathrin at the plasma membrane to various macromolecular cell constituents, including transmembrane receptors for extra-cellular ligands.9, 10 These adaptors, as well as certain other proteins (e.g., AP1, AP180/CALM, Hip1R), also facilitate the in vitro polymerization of clathrin triskelions (“triskelia”) into closed polyhedral baskets, and therefore sometimes have been called “assembly proteins” (herein referred to, generically, as “APs”). Such baskets retain the overall geometric characteristics of the closed lattices that surround CCVs.
Figure 1.
Clathrin structures. (a) Schematic diagram of a triskelion, showing three heavy chains joined at a common hub, each heavy chain carrying a single bound light chain. (b) CryoEM image of a clathrin basket assembled in the presence of AP2 adaptors. Left-most figure shows entire structure, including APs which are located on the interior of the basket; figure on the right is the same structure, electronically processed to remove the APs. Adapted from Ref. 13.
Structural features of clathrin triskelia and clathrin baskets have been known for many years.11, 12 More recently, cryoelectron microscopy has yielded exquisite images showing how sections of four heavy chains on neighboring triskelions (two distal and two proximal segments) interwind (Fig. 1b) to form the struts of the baskets6, 13, 14, 15 Clathrin baskets self-assemble in vitro in the absence of APs, but readily do so only at low pH and low salt concentrations (e.g., 0.1 M MES buffer, pH ⩽6.4). The rate of polymerization and total amount of clathrin incorporated into baskets are pH dependent, being close to zero at neutral pH but increasing markedly as the pH of the buffer is lowered. At pH 6.0, the assembly of baskets occurs very rapidly and almost all triskelia are incorporated into higher-order structures. In the presence of APs, clathrin assembly occurs even at physiological pH (i.e., pH 7.0), yielding distributions that are highly enriched in smaller baskets.16
In addition to other functions, clathrin structures may play a direct mechanical role in vesicle biogenesis. Clathrin triskelia have an intrinsic curvature in solution, similar to,5, 17 though differing from,18 that assumed by the triskelia when they are incorporated into baskets. Thus, it is possible that if the triskelia form a rigid curved lattice in a cell, they help bend a region of relatively flat plasma membrane into a CCV, whose typical diameter is of the order of 100 nm.19 However, the situation is more complicated, as an analysis of triskelial shapes suggests that the triskelia are rather flexible, and that the bending rigidity of a bare clathrin lattice is close to that of an equivalently-sized patch of plasma membrane.20 This result is substantiated by small angle neutron scattering data21 and by analyzing size distributions of reconstituted clathrin baskets.22 The latter investigation also indicates that APs strengthen the linkage between the legs of the triskelia when they come together to form the struts of the cages, causing an increase in cage rigidity consistent with CCV rigidity determined by atomic force microscopy.23 Moreover, the binding of APs favors assembly of clathrin lattices by increasing the association energy of the lattice, thereby lowering its overall energy.22 This mechanism also can affect the tendency for CCVs to assemble,19 acting along with other factors such as modification of membrane structure by clathrin-binding proteins containing BAR domains.9
We now examine how mechanical and other energetic factors can affect the assembly of clathrin baskets in vitro, particularly if the clathrin concentration is low. By modifying classical thermodynamic theories of micelle formation,24, 25 we predict that there is a critical concentration, CC, below which baskets will not form. Experimental evidence supporting the existence of a critical concentration for in vitro assembly was published over three decades ago.11 Additionally, using protocols in which cellular clathrin concentrations were reduced by RNAi techniques, it was shown that CCV formation is thwarted in vivo when the clathrin concentration falls below a minimal level,26 suggesting that the notion of a critical concentration for assembly may be important for understanding cell function. Indeed, critical concentration biophysics may be used in cellular control functions. For example, when auxilin in down regulated, structures having the appearance of clathrin baskets arise in the cytoplasm of tissue culture cells,27 one interpretation being that auxilin normally binds to triskelions to lower the free clathrin concentration below the CC pertaining to the cellular milieu. Moreover, clathrin is involved in various aspects of mitosis, including interactions with microtubule binding proteins during kinetochore formation,28 and it is likely that, in certain instances, depletion of cytosolic clathrin by mitosis suppresses clathrin mediated endocytosis.29 Other cellular activities also compete for clathrin.30
In Sec. 2, we describe the model adopted for this study, which is analogous to classical models of micelle formation by amphipathic molecules. We derive in the following analysis an approximate, but rather general, expression for the critical concentration pertaining to basket formation in vitro, viz., , where is the free energy change that occurs when triskelia assemble into baskets of maximal prevalence. Consequently, we conclude that CC is lowered by factors that increase basket stability. This approach is based on a purely thermodynamic treatment and, thus, is only an approximate treatment (see the Discussion, below). However, it provides a means to relate the critical behavior to such system parameters as the intrinsic curvature and mechanical rigidity of a triskelion, as well as the energetics of clathrin-clathrin associations. By comparing the dependence of CC on the system parameters, we infer that CC is most sensitive to changes in inter-leg associations. We also derive an analytical approximation that allows us to calculate the mass-weighted distribution of basket size and the dependence of the mean and variance of the distribution as a function of these parameters.
MODEL
The hub where the three legs of a triskelion are joined becomes a vertex of an assembled clathrin lattice. An ideal flat clathrin lattice contains only hexagons and, except for the edges of the lattice, all vertices on average experience the same environment and are identical. In contrast, the essential morphological attribute of clathrin baskets, viz., that they are closed polyhedra, imposes topological constraints31, 32 so, in general, not all of the polyhedral faces are alike. Correspondingly, the vertex angles of such closed structures and the interwinding of neighboring triskelian legs that form the interconnections between vertices are not all identical.11, 15 Nonetheless, when the baskets are sufficiently large, to a first approximation they appear to be almost spherical. In the following, we use a spherical model in which the variable is basket size, measured in terms of the number of constituent triskelia, N.
Utilizing concepts of statistical thermodynamics, one of us previously developed a simple physical theory for interpreting in vitro basket reconstitution experiments.22 The sizes of clathrin baskets were related to parameters describing the rigidity and intrinsic curvature of individual triskelions and, also, a term representing the intermolecular interactions between the legs of neighboring triskelions in the assembled polyhedra. The underlying assumption of that study is that, for baskets to form, favorable attractive energy terms linked to inter-leg associations must offset unfavorable energy terms arising when triskelia are distorted in order to fit into cages of varying sizes. This model produces closed form mathematical expressions for both the basket size of maximal occurrence, N*, and the width of the basket size distribution, W1/2. When applied to experimental data,16 these expressions yielded estimates of the aforementioned parameters. In this earlier theory, the thermodynamic stability of isolated baskets was investigated, but equilibrium among different-sized baskets was not considered.
In the present paper, we assume that thermodynamic principles of self-association apply to the assembly of the baskets. Hence, we adapt a model that has been successfully used to describe micelles and other association colloids such as lipid bilayers and vesicles,24, 25 postulating that at equilibrium the chemical potential of a monomer in a basket of size N triskelions, μN, must be independent of N and equal to the chemical potential of an unpolymerized (i.e., free) triskelion. Thus,
| (1) |
where represents the mean interaction free energy per clathrin triskelion (“monomer”) in a basket of size N, kB is Boltzmann's constant, and T is the absolute temperature. XN signifies the mole fraction of triskelions in baskets of size N. (Strictly speaking, XN is the activity, but we assume that the concentrations of baskets and free triskelia are sufficiently low that the solution is close to “ideal.”) XN is related to the concentration CN of triskelia in baskets of size N in dilute aqueous solutions by XN = CN/55.5, where CN is in molarity and 55.5 is the number of moles of water in 1 liter. If CN is in units of mg/ml, then XN = CN/(55.5M), where M is the net molecular weight of a triskelion assembly, which is taken to be 650 000 Da in the calculations presented below.
By specifying the free energy of the monomer to be the reference energy state, it follows from Eq. 1 that
| (2) |
where β = 1/kBT. In Eq. 2, represents the difference between the free energy of a triskelion in a basket of size N and that of the triskelion when free in solution. Conservation of mass implies
| (3) |
where X represents the total mole fraction of triskelions, both free and polymerized. (Nmin = 20, in accord with topological requirements for closed clathrin baskets containing only pentagons and hexagons.) Given an expression for GN, Eqs. 2, 3 enable the calculation of XN for all values of N if the total mole fraction of triskelia in the solution is known. We remark that XN/N ≡ PN is a relative measure of the number of baskets of size N, which is a quantifiable experimental observable.16, 33 Note that X and X1 must be less than 1. Thus CN is proportional to NPN ∼ Pm, where Pm is the probability of finding a basket of mass m. In systems characterized by Eq. 3, essentially no higher-order (polymerized) structures are formed when C is less than a critical concentration, CC.24, 25 As the concentration is increased beyond CC, formation of polymer (here, clathrin cages) occurs while the monomer concentration remains essentially constant at the value C1 ≈ CC. The existence of a threshold concentration for formation of baskets and the distribution of the basket sizes depend crucially on the N-dependence of GN.
What is the analytic form of the free energy term ? In its simplest form, GN can be expressed as the sum of two terms. First, as before,22 we presume that baskets are stabilized by interactions between legs of neighboring triskelia, viz., , where we recognize that the number of struts within any particular cage equals 3N/2. (By “strut” we mean an edge linking two of the triskelial hubs that lie at the vertices of the polyhedral clathrin cage; note that each hub is linked to three neighbors, and that each strut is shared by two vertices.) As previously mentioned, for baskets formed under normal conditions, b signifies the favorable energy of interaction between the legs of four triskelia (viz., two distal and two proximal segments). Second, we need to account for unfavorable distortion energies linked to the mechanical perturbation of triskelia when located in baskets whose mean curvatures differ from that of a basket of lowest conformational energy. Here we assume that the mechanical distortion of triskelia can be described by a Hooke's Law expression, viz., that the change in free energy associated with leg bending energies may be postulated as
| (4) |
where h is related to the mechanical rigidity of a strut and n−1/2 is a measure of the natural (i.e., intrinsic) curvature of a triskelion. The explicit N-dependence of is motivated by the distortion energy of model membranes. For a closed spherical membrane of radius R, the distortion energy is given, to first order, by34
| (5) |
where R0 is the radius of the spontaneous curvature and κ is the bending modulus of the membrane. By taking 1/R0 as the natural (averaged) curvature of the triskelia and 1/R as the average curvature of a basket of size N, becomes as given by Eq. 4, where the proportionality (R2 ∼ N) between the average surface area of the basket and the number of triskelia on the basket has been recognized. h of Eq. 4 is actually 8πκ and n of Eq. 4 is proportional to . Equation 4 can also be derived by assuming the bending energy of a strut of length L joining two triskelial hubs to be , where EI(s) is a position-dependent flexural rigidity coefficient and ΔC(s) is the deviation of the curvature of the strut from its natural curvature.20 By taking average (uniform) values for EI and the curvatures, one can relate h and EI as h = 0.015·EI·L·(nm)−2 where L is given in nm, h having the units kBT.35 It must be mentioned that Eqs. 4, 5 are in the Helfrich free energy form34 and differ from the previously used assumption.22
If we add the stabilization energy arising from neighboring triskelia and the distortion energy arising from the mechanical deviations away from the naturally preferred curvature of triskelia, we obtain the following expression for the (enthalpic) energy associated with the formation of a basket of size N:
| (6) |
The combined set of Eqs. 2, 3, 6 allows a complete description of CC and the concentrations of unaggregated triskelia and baskets of any aggregation number N for a given total concentration C of triskelia in the solution. Results are given in terms of the three parameters h, b, and n.
ANALYSIS
Phenomenology
Few quantitative studies of the sizes of reconstituted clathrin baskets have been published, and even fewer determinations have been made of the minimum concentration at which clathrin will polymerize. Zaremba and Keen16 used electron microscopy to measure the sizes of clathrin baskets formed in the presence and absence of a mixture of assembly proteins (“APs”) containing AP-2 adaptor complexes and, probably, other constituents that facilitate basket formation. Figure 2a shows the distribution of baskets determined for a purified clathrin sample maintained at pH 6.5 in MES buffer to which an equal mass of APs had been added. Note the sharpness of the size distribution, for which the full width at half maximum, W1/2 ≈ 11, is less than 20% of the value N* ≈ 64 for which the distribution is maximal. These data were obtained at a clathrin concentration of 0.16 mg/ml, which is several times greater than the minimal concentration, CC, at which polymerization is likely to occur. The latter, commented on by Zaremba and Keen, is less than 0.06 mg/ml for such buffer.16 This value is of the same order of magnitude as the value of 0.05 mg/ml put forth by Crowther and Pearse11 for the assembly of purified clathrin in pH 6.2 MES buffer. Crowther and Pearse not only measured the polymerized fraction and showed that it vanished at CC, but they also demonstrated that the amount of unpolymerized clathrin did not increase as C increased beyond CC (see Fig. 2b). Based on knowledge that lower pH and the presence of APs both favor increased basket formation, we take CC ≈ 0.02 mg/ml as a representative value for the illustrative calculations that appear below.
Figure 2.
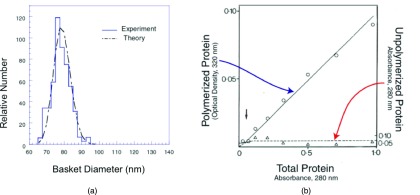
Experimental aspects of clathrin basket polymerization. (a) Relative number of baskets of a given size, PN, assembled along with APs (after Zaremba and Keen16). Theory curve is obtained by data fitting described in Ref. 22, from which this figure was obtained. (b) Polymerized protein and non-polymerized residual when baskets are assembled from purified clathrin lacking APs. (Data taken from Crowther and Pearse.11) Note the existence of a critical concentration, CC, below which baskets will not form.
General theoretical results
The essential characteristics of the experimental observations summarized above are captured by the set of Eqs. 2, 3, 6. Details of calculations based on these equations are discussed below, following Eq. 19; here we note the qualitative features arising from the theory. Figure 3a exhibits a predicted critical concentration CC for the formation of baskets. For C < CC, almost all triskelia are in the unaggregated state and C1, which represents the concentration of free triskelions, is very close to C. For C > CC, the concentration of unaggregated triskelia essentially stays at the same value, C1 ≈ CC, while the concentration of triskelia in the various baskets, (C − C1), increases linearly with the total concentration C. These properties mimic those of the data shown in Fig. 2b. [The dependence of CC on system parameters is discussed in Secs. 3C, 3D.]
Figure 3.
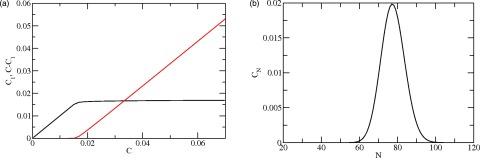
Assembly predicted by the model. (a) Polymerized and free clathin concentrations, CP = C − C1 and C1 (mg/ml), obtained by solving Eq. 10 for b = bs = 21.15 kBT, h = hs = 335 kBT, and n = ns = 90 as a function of C. Triskelion “monomer” at a concentration of 10−6 M corresponds to approximately 0.6 mg/ml clathrin. Here, CP represents the concentration of triskelions in clathrin baskets, and C1 is the free clathrin remaining in solution. CC ≈ 0.02 mg/ml is the critical concentration. Note that C1 is approximately equal to CC when C ≫ CC (c.f. Tanford24 and Israelachvili25). (b) Mass weighted distribution of baskets, CN (relative units), computed for C = 0.5 × 10−6 M and the parameter values used to obtain Fig. 3a.
The distribution of basket sizes for C > CC is illustrated in Fig. 3b. The shape of the distribution is analogous to that observed experimentally (Fig. 2a). The mass distribution, Pm, can be characterized by the basket size of maximal occurrence, width Wm, 1/2 at half maximum, average size ⟨Nm⟩ of the baskets, and the variance . The averages ⟨Nm⟩ and are defined by
| (7) |
and
| (8) |
Similar quantities can be used to describe the characteristics of the number distribution, PN.
As is illustrated in Fig. 3b, for values of C > CC the occurrence of small baskets far below N* is negligible. This feature allows us to extend the lower limit in the sums to zero. Further, an integral (i.e., continuum) approximation to the sum in Eq. 3 yields
| (9) |
For the functional form for GN given by Eq. 6, this integral can readily be performed (see the Appendix) and the continuum approximation provides an analytical form for the equation of conservation of triskelia in the system,
| (10) |
where μ = β[(h/n) − b − ln (X1)], , and is the error function.36 Formulas for ⟨Nm⟩ and obtained from this analysis are given in the Appendix.
Dependence of CC on energy parameters
How is the critical concentration, CC related to the parameters of the model? A simple analytical relationship can be obtained from Eq. 3 if the total concentration of clathrin is several times greater than the critical concentration, i.e., C ≫ CC. In this case, Eq. 3 is given as
| (11) |
where we understand X1 to be close to Xc. If, in accord with Fig. 2a, we further assume that the basket size distribution is narrow, then the sum appearing in Eq. 11 can be approximated by , where N* is the size of the most prevalent basket and α is a constant whose value approximates the width of the distribution. From Eq. 11 we thus find . But, because N* is a large number, the term on the r.h.s. of this equation tends to 1, from which we infer
| (12) |
As described earlier, the mole fractions X and XC are related to the concentrations C and CC by a constant multiplicative factor. Here, is the depth of the energy well associated with the most prevalent (i.e., most stable) baskets. Hence, we immediately see that conditions favoring basket formation and stability also lower the critical concentration.
Upon substituting the expression for GN from Eq. 6, we find the form of CC to be
| (13) |
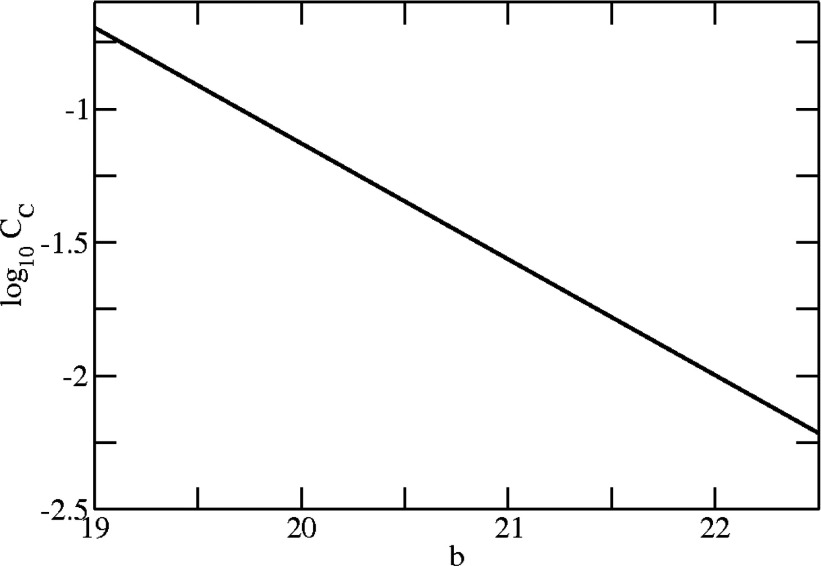
This equation readily allows us to infer that an increase in the rigidity of the triskelions, as represented by the parameter h, raises the critical concentration while an increase in the inter-leg interaction energy, b, lowers CC. Numerical analysis shows that CC is more sensitive to changes in b than to changes in h or n. In fact, for many purposes, CC probably can be approximated to be e−βb.
Size distributions and their linkage to energy parameters
The experimental observable presented in Fig. 2a is the relative number of baskets of a given size, which is proportional to the distribution PN. From Eqs. 1, 2, this quantity may be written as
| (14) |
where A is a normalization constant. Therefore, by incorporating the explicit form of GN given in Eq. 6, we find
| (15) |
where is defined as
| (16) |
In the earlier treatment22 an expression similar to Eq. 15 was obtained except that, instead of , the symbol b (which we now refer to as bold) was used. The other difference is that (1/N − 1/n)2 was used in the earlier treatment22 instead of in Eq. 15. It was noted then that bold contained, in addition to an enthalpic term, an entropic component which in the present treatment is explicitly given as β−1ln X1. Correspondence with the previous treatment is clear if we make the association , except that depends nontrivially on bold through the b-dependence of X1. Here, b signifies only the enthalpic term. The term represents the change in free energy occurring when triskelions leave solution to form closed baskets.
For the model that yields Eq. 15, it is easy to show (see the Appendix) that the size N* at which the number distribution has a maximum is written as
| (17) |
with the full width at half maximum, W1/2, being given as
| (18) |
Similarly, one can obtain an expression for the basket size, , for which the mass distribution {XN} = {NPN} has its maximal value, viz.,
| (19) |
Based on a fit of Eqs. 17, 18 to the number size distribution measured for baskets assembled in the presence of APs and the assumption that GN = 0 where Pn → 0, we choose h = hs = 335 kBT, and kBT as“standard values.” (These were obtained by the procedure described in Ref. 22, but for the free energy parameterization presented in Eq. 6, see Ref. 35.) We also take n = ns = 90 which, while somewhat arbitrary, approximates the size of a typical large basket. By taking the critical concentration to be CC ≈ 0.02 mg/ml ≈ 0.033 × 10−6 M, Eq. 16 yields bs ≈ 21.2 kBT, which is a measure of the enthalpic energy per triskelion needed to dissociate a basket in the low salt, pH 6.5 buffer to which the above-stated standard values pertain.16, 22 [As illustrated by Eq. 16, is the difference between the enthalpic and entropic free energy changes occurring when a triskelion is incorporated into a basket.] Interestingly, this value ( approx 20 kBT) suggests that, in accord with recently published results.37 approximately 1 ATP molecule is hydrolyzed for each triskelion when baskets are dissociated enzymatically. The value for CC used here in the calculations is somewhat less than the value CC ≈ 0.05 mg/ml noted by Crowther and Pearse11 for purified clathrin, but Eq. 16 indicates that the inferred value of b depends only weakly on CC through a logarithmic term, so for present purposes knowing the precise value of CC is of limited importance. Parenthetically, we note that these values satisfy the requirement , in accord with Eqs. 6, 16, and the necessity that the sum in Eq. 3 converges.
We illustrate some of the properties of the model in Figs. 345. When needed in the calculations, we chose the value of the clathrin concentration to be C = 0.3 mg/ml ≈ 0.5 × 10−6 M, which is typical of in vitro assembly conditions and assures that C ≫ CC. (The precise values of these parameters are not really important, as they principally are used merely to show trends.) Figure 3a shows the free clathrin concentration, C1, obtained by solving Eq. 10 with the standard values for h, b, and n, after converting to concentrations according to CN(mg/ml) = 55.5MXN, where M = 650 kDa is taken to be the molecular weight of a triskelion. As previously indicated, in accord with classical theory of micelle formation24, 25 clathrin remains in monomeric form (single triskelions) until a critical concentration is reached, thereafter remaining more-or-less constant while an increasing amount of material is found in baskets. The dependence of CC on the variable b is shown in Fig. 4. To obtain this figure we used the approximate expression given by Eq. 13, but similar results can be obtained by evaluating Eq. 10 (or Eq. 3) directly. It is seen that the critical concentration is a strong function of b, while over the range of variables chosen for the analysis it is almost unaffected by changes in h and n (results not shown). The critical concentration decreases with b as CC ∼ e−βb and increases with h or n, although when the latter exceed certain values their variations seem to have little effect on CC.
Figure 4.
Dependence of the critical concentration, CC, on the interaction energy, b. (h = 335 kBT, n = 90.)
Figure 5.
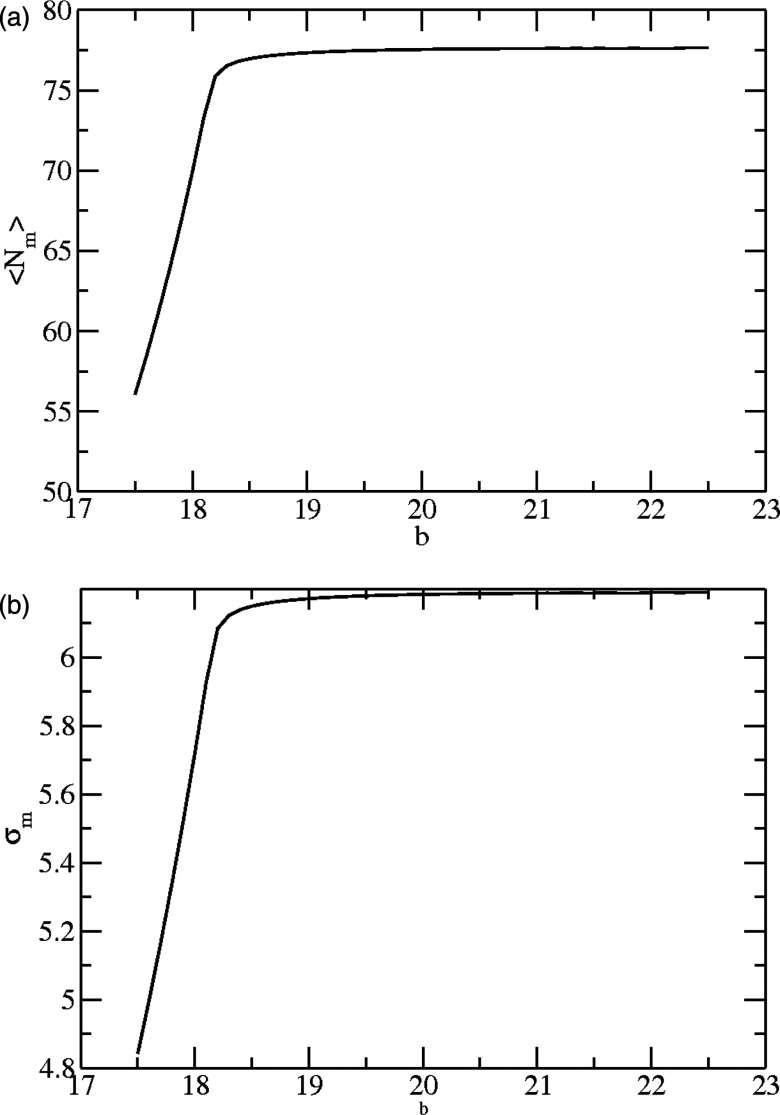
Dependence of basket size on leg-leg association energy. (a) Mean mass-weighted size, ⟨Nm⟩, calculated according to Eq. A8 (h = 335 kBT, n = 90). (b) Variance, , calculated according to Eqs. A8, A9. Note that the mean and variance change in like manner.
In principle, quantities connected with the mass distribution can be related to parameters measured by optical methods such as dynamic light scattering (DLS) or fluorescence correlation spectroscopy (FCS). From Eq. 7 we find that the average size ⟨Nm⟩ varies only weakly with b, generally increasing as b increases (Fig. 5a). Similar behavior holds for , as well as the equivalent quantities for the number size distribution PN (results not shown). This behavior also is apparent in the expression for N* given by Eq. 17, where it also is seen that larger baskets form when the triskelions are very flexible. However, as the rigidity of the legs increases, the basket size is closer to that commensurate with the natural curvature of the individual triskelia. Also, concordant with Eq. 17, the average basket size increases as the natural triskelial curvature, n−1, decreases. In Fig. 5b we plot the variance, as a function of b, noting that if the baskets on average become smaller, their size distribution becomes narrower (and vice versa). The behavior seen in Fig. 5 suggests that entropic factors might favor the formation of many baskets of modest size, rather than the assembly of a few large baskets. These entropic factors predominate, no matter the magnitude of b once a threshold value is surpassed which undoubtedly depends on the values of the other system parameters, h and n.
DISCUSSION
The minimal model used here to describe the energetics of basket formation gives rise to mathematically tractable analysis and provides good fits to experimental basket size distributions.22 It also is found to be in accord with a diverse set of measurements of the physical properties of isolated triskelions.18, 20, 21, 22, 23, 38 The fundamental difference between the current treatment and the earlier study22 is that we now explicitly account for the fact that there may be a critical clathrin concentration, CC, below which basket assembly will not occur. Our analysis predicts that this critical concentration depends much more sensitively on the inter-leg association energy, b, than on the rigidity parameter, h, or the curvature parameter, n−1/2, and that a lowering of CC occurs if b increases. Interestingly, we found, independently, that the strength of the inter-leg associations are significantly greater when APs are present than when clathrin, alone, is allowed to assemble.22
Our assumption that the assembly of clathrin baskets is analogous to the assembly of classical lipid micelles in thermodynamic equilibrium needs to be viewed with some caution. In the case of lipids, it usually is assumed that the micelles can readily exchange their constituents with free lipid molecules in solution without regard to the location of the lipids in the micelle complex, and that the micelles can readily adjust their structure to accommodate changes in molecular number. Except under certain conditions, clathrin exchange probably is more restricted. However, the use of simple thermodynamics, as in our earlier analyses of basket reconstitution, can be rationalized by assuming that during the early steps of polymerization a basket rapidly and freely exchanges its subunits with triskelions from the environment, on a time scale commensurate with the establishment of local thermodynamic equilibrium. Initially the geometry of a basket can fluctuate, but beyond a certain point (perhaps when the cage approximates a hemisphere) the emergent mechanical attributes of the partially assembled polyhedral structure determine the final shape and overall size of the basket. (Partially formed cages are likely to be loose and flexible until a minimal number of triskelions are inserted.)
den Otter et al. have simulated the assembly of triskelion-like entities into closed polyhedral cages,39, 40 indeed noting the existence of small nuclei that constantly arise and dissociate before baskets proceed to completion.39 A recent simulation study of virus assembly41 also shows that the assembly proceeds by successive addition of basic triangular building blocks to a growing curved lattice and that a critical protein concentration is required for assembly. In various aspects, this view is like that of Shraiman,42 who explained basket assembly in terms of a kinetic polymerization model in which pentagonal faces arise by trial and error but then are fixed in place at specific locations as the baskets grow. (An energetic analysis of fullerene shapes43 shows that particular geometries are favored and symmetrical structures generally are more stable.) den Otter et al. postulate that the triskelions are rigid and, like the results reported herein, their computer models indicate a critical triskelion concentration below which the cages do not form, finding that the association of triskelions into higher order structures depends strongly on the magnitude of the energies of inter-leg interactions.39 Their simulations also demonstrate a notable dependence on intrinsic triskelion pucker. In a related publication,44 these authors also used thermodynamic theory to show a critical concentration for basket assembly. However, their study, which neglected the free energy penalty for deviations from spontaneous curvature of the clathrin basket and its dependence on physical variables such as triskelial rigidity, provided an estimate of about 42kBT for the binding energy. This is a factor of two higher than our estimate of 21.2kBT, which is closer to the value of 23kBT estimated from the simulations. A major advantage of performing mathematical calculations is that, as we have shown, dependences on well-defined physical variables are explicitly apparent.
Even if the addition and subtraction of triskelions to a growing basket primarily occurs at its perimeter, because the partially formed baskets themselves constitute an ensemble, their growth kinetics in essence recapitulate the exchange that would occur in completed baskets if the triskelions could add anywhere in the structure (although the values of the energies would differ somewhat). Depending on the pH, salt concentrations, and other solution conditions, completed baskets may resist dissociation once they form unless acted upon by Hsc70 or other biological ATPases, as noted for clathrin structures on CCVs.45 In general, when assembly starts from dissociated triskelia, the free clathrin concentration decreases as baskets are completed. However, as long as the concentration of free triskelions is considerably higher than the critical concentration, the remaining triskelions assemble with identical size distribution until the free clathrin concentration falls to a value very close to CC. At this point the distribution of newly completed baskets changes to a smaller average size24, 25 but, if the starting concentration of triskelions was high relative to CC, these smaller baskets constitute an inconsequential portion of the total basket population.
The forces determining basket structure may be more complicated than represented here (e.g., the energy of leg twisting may be significant), but such details are implicitly subsumed by other aspects of our model. The central theme is that inter-leg associations counteract the forces working against triskelial distortion, a notion that also has been used, analogously, to quantify aspects of sickle cell hemoglobin aggregation.46 We seem to be able to take the baskets as being quasi-spherical (ignoring, e.g., asymmetric structures), which probably reflects the fact that a subset of relatively strain free, spherically symmetric baskets predominates.43, 47
In part, we chose Eq. 6 to describe the free energy change that drives basket formation because it gives rise to mathematically-tractable analytic expressions. However, Eq. 6 fails to reflect the expected divergent increase in free energy linked to mechanical distortion of triskelia if incorporated into a basket whose curvature is significantly greater than the natural curvature. (The first term on the r.h.s. of Eq. 6 tends to a constant value whereas, by using a slightly different analytical form, in Ref. 22 it varies in proportion to N−1.) Moreover, strictly speaking the N dependence of the association energy should vary, to first order, as (N − 1)b rather than Nb. And, our treatment neglects possible small intermediates (incomplete baskets) which are implicitly considered to be unstable and short-lived. In principle each of these concerns can be handled by an extension of the model engendered in Eq. 6, but for this investigation such considerations are unnecessary, as the numerical results of the present calculations should be taken as qualitative indications of the assembly process rather than precise numbers.
As first pointed out by Crowther and Pearse,11 cellular clathrin concentrations might be close to a critical value CC when in the cytoplasm. In this case, the formation of the clathrin polyhedra that appear in the coats of CCVs could be easily regulated by the action of cellular factors that change CC. Our analysis indicates that factors that increase the strength of stabilizing interactions between triskelions tend to lower CC. Studies of the biogenesis of clathrin lattices at the plasma membrane (“coated pits”) indicate that such factors also play an important role in determining whether clathrin coats that nucleate on the surfaces of mammalian cells proceed to complete CCVs.19
ACKNOWLEDGMENTS
This work was supported in part by intramural research funds from the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health. Acknowledgement is also made to the National Institutes of Health (NIH Grant No. R01HG002776-10), National Science Foundation (NSF Grant No. 1105029), Air Force Office of Scientific Research (AFOSR Grant No. FA9550-10-1-0159), and the Materials Research Science and Engineering Center at the University of Massachusetts, Amherst.
APPENDIX: THE CONTINUUM APPROXIMATION
In this section we derive the expressions that have been used to generate Figs. 345. To simplify the presentation, we here suppress the term β by expressing h and b in units of kBT.
Use of the expression for GN from Eq. 6 in Eq. 9 yields
| (A1) |
By writing as an exponential and combining all arguments of the exponential terms, we then obtain
| (A2) |
where μ = (h/n) − b − ln (X1). The integral in Eq. A2 can be rewritten in a more convenient form, by changing the integration variable N to t2, as
| (A3) |
The r.h.s is evaluated by noting that
| (A4) |
where
| (A5) |
The integral in Eq. A5 is readily obtained in terms of the error function,33
| (A6) |
where . Substitution of Eq. A6 into Eq. A4 yields
| (A7) |
Combining Eqs. A2, A3, A7, we get the result given by Eq. 10.
By a similar procedure, the calculations of the mass-weighted quantities ⟨Nm⟩ and involve ∂I/∂μ and ∂2I/∂μ2, leading to the analytical forms
| (A8) |
and
| (A9) |
where I is given by Eq. A7.
Expressions for N* and W1/2, the value of N at which the number density is maximal and the width at half-maximum of that distribution, can be written as follows (cf., also, Ref. 22). First, we recall that, according to Eqs. 6, 14, PN may be written as
| (A10) |
Hence, the expression for N*, given by Eq. 17, is obtained by taking the derivative of the exponent in Eq. A10 with respect to N, setting the resulting expression equal to zero, and then identifying N as N*. It then follows that
| (A11) |
Thus, to find the width W1/2 ≡ (N+ − N−) (determined from ), we solve the quadratic equation 2χ − ψχ2 = −h−1ln 2 + 1/ψ, where χ± ≡ (N±/n)1/2 and . The roots of this equation yield
| (A12) |
from which the expression for W1/2 appearing in Eq. 18 then follows.
References
- Alberts B., Johnson A., Lewis J., Raff M., Roberts K., and Walter P., Molecular Biology of the Cell, 5th ed. (Garland Science, New York, 2007). [Google Scholar]
- Smith C., Science 311, 182 (2006). 10.1126/science.1123754 [DOI] [PubMed] [Google Scholar]
- Stagg S. M., Gürkan C., Fowler D. M., LaPointe P., Foss T. R., Potter C. S., Carragher B., and Balch W. E., Nature (London) 439, 234 (2006). 10.1038/nature04339 [DOI] [PubMed] [Google Scholar]
- Ungewickell E. and Branton D., Nature (London) 289, 420 (1981). 10.1038/289420a0 [DOI] [PubMed] [Google Scholar]
- Kirchhausen T., Annu. Rev. Biochem. 69, 699 (2000). 10.1146/annurev.biochem.69.1.699 [DOI] [PubMed] [Google Scholar]
- Brodsky F. M., Chen C-Y., Knuehl C., Towler M. C., and Wakeham D. E., Annu. Rev. Cell Dev. Biol. 17, 517 (2001). 10.1146/annurev.cellbio.17.1.517 [DOI] [PubMed] [Google Scholar]
- Lafer E. M., Traffic 3, 513 (2002). 10.1034/j.1600-0854.2002.30801.x [DOI] [PubMed] [Google Scholar]
- Blondeau F., Ritter B., Allaire P. D., Wasiak S., Girard M., Hussain N. K., Angers A., Legendre-Guillemin V., Roy L., Boismenu D., Kearney R. E., Bell A. W., Bergeron J. J. M., and McPherson P. S., Proc. Natl. Acad. Sci. U.S.A. 101, 3833 (2004). 10.1073/pnas.0308186101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMahon H. T. and Boucrot E., Nat. Rev. Mol. Cell Biol. 12, 517 (2011). 10.1038/nrm3151 [DOI] [PubMed] [Google Scholar]
- Reider A. and Wendland B., J. Cell. Sci. 124, 1613 (2011). 10.1242/jcs.073395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowther R. A. and Pearse B. M. F., J. Cell Biol. 91, 790 (1981). 10.1083/jcb.91.3.790 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heuser J. and Kirchhausen T., J. Ultrastruct. Res. 92, 1 (1985). 10.1016/0889-1605(85)90123-5 [DOI] [PubMed] [Google Scholar]
- Smith C. J., Grigorieff N., and Pearse B. M. F., EMBO J. 17, 4943 (1998). 10.1093/emboj/17.17.4943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mousavi S. A., Malerod L., Berg R., and Kjeken R., Biochem. J. 377, 1 (2004). 10.1042/BJ20031000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fotin A., Cheng Y. F., Sliz P., Grigorieff N., Harrison S. C., Kirchhausen T., and Walz T., Nature (London) 432, 573 (2004). 10.1038/nature03079 [DOI] [PubMed] [Google Scholar]
- Zaremba S. and Keen J. H., J. Cell Biol. 97, 1339 (1983). 10.1083/jcb.97.5.1339 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirchhausen T., Harrison S. C., and Heuser J., J. Ultrastruct Mol. Struct. Res. 94, 199 (1986). 10.1016/0889-1605(86)90067-4 [DOI] [PubMed] [Google Scholar]
- Ferguson M. L., Prasad K., Sackett D. L., Boukari H., Lafer E. M., and Nossal R., Biochemistry 45, 5916 (2006). 10.1021/bi052568w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee A., Berezhkovskii A. M., and Nossal R., Biophys. J. 102, 2725 (2012). 10.1016/j.bpj.2012.05.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin A. J. and Nossal R., Biophys. J. 78, 1183 (2000). 10.1016/S0006-3495(00)76676-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson M. L., Prasad K., Boukari H., Sackett D. L., Krueger S., Lafer E. M., and Nossal R., Biophys. J. 95, 1945 (2008). 10.1529/biophysj.107.126342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nossal R., Traffic 2, 138 (2001). 10.1034/j.1600-0854.2001.020208.x [DOI] [PubMed] [Google Scholar]
- Jin A. J., Prasad K., Smith P. D., Lafer E. M., and Nossal R., Biophys. J. 90, 3333 (2006). 10.1529/biophysj.105.068742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanford C., The Hydrophobic Effect: Formation of Micelles and Biological Membranes, 2nd ed. (John Wiley and Sons, New York, 1980). [Google Scholar]
- Israelachvili J. N., Intermolecular and Surface Forces, with Applications to Colloidal and Biological Systems (Academic Press, San Diego, CA, 1985). [Google Scholar]
- Moskowitz H. S., Yokoyama C. T., and Ryan T. A., Mol. Biol. Cell 16, 1769 (2005). 10.1091/mbc.E04-08-0739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirst J., Sahlender D. A., Li S., Lubben N. B., Borner G. H., and Robinson M. S., Traffic 8, 135 (2008). 10.1111/j.1600-084.2008.00764.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu W., Jiang Q., and Zhang C., Cell. Res. 21, 1655 (2011). 10.1038/cr.2011.106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fielding A. B., Willox A. K., Okeke E., and Royle S. J., Proc. Natl. Acad. Sci. U.S.A. 109, 6572 (2012). 10.1073/pnas.1117401109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodsky F. M., Annu. Rev. Cell Dev. Biol. 28, 309 (2012). 10.1146/annurev-cellbio-101011-155716 [DOI] [PubMed] [Google Scholar]
- Kanaseki T. and Kadota K., J. Cell Biol. 42, 202 (1969). 10.1083/jcb.42.1.202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin A. J. and Nossal R., Biophys. J. 65, 1523 (1993). 10.1016/S0006-3495(93)81189-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao W., Luo Z., Zheng L., Prasad K., and Lafer E. M., J. Biol. Chem. 274, 22785 (1999). 10.1074/jbc.274.32.22785 [DOI] [PubMed] [Google Scholar]
- Helfrich W., Z. Naturforsch. C 28, 693 (1973). [DOI] [PubMed] [Google Scholar]
- Nossal R., Macromol. Symp. 227, 17 (2005). 10.1002/masy.200550902 [DOI] [Google Scholar]
- Abramowitz M. and Stegun I. A., Handbook of Mathematical Functions, Applied Mathematics Series No. 55 (U.S. Government Printing Office, Washington, D.C., 1964). [Google Scholar]
- Bocking T., Aguet F., Harrison S. C., and Kirchhausen T., Nat. Struct. Mol. Biol. 18, 295 (2011). 10.1038/nsmb.1985 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeham D. E., Chen C. Y., Greene B., Hwang P. K., and Brodsky F. M., EMBO J. 22, 4980 (2003). 10.1093/emboj/cdg511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- den Otter W. K., Renes M. R., and Briels W. J., J. Phys.: Condens. Matter 22, 104103 (2010). 10.1088/0953-8984/22/10/104103 [DOI] [PubMed] [Google Scholar]
- den Otter W. K., Renes M. R., and Briels W. J., Biophys. J. 99, 1231 (2010). 10.1016/j.bpj.2010.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahalik J. P. and Muthukumar M., J. Chem. Phys. 136, 135101 (2012). 10.1063/1.3698408 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shraiman B. I., Biophys J. 72, 953 (1997). 10.1016/S0006-3495(97)78729-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schein S., Sands-Kidner M., and Friedrich T., Biophys. J. 94, 938 (2008). 10.1529/biophysj.107.110833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- den Otter W. K. and Briels W. J., Traffic 12, 1407 (2011). 10.1111/j.1600-0854.2011.01241.x [DOI] [PubMed] [Google Scholar]
- Wu X. F., Zhao X. H., Baylor L., Kaushal S., Eisenberg E., and Greene L. E., J. Cell Biol. 155, 291 (2001). 10.1083/jcb.200104085 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner M. S., Briehl R. W., Ferrone F. A., and Josephs R., Phys. Rev. Lett. 90, 128103 (2003). 10.1103/PhysRevLett.90.128103 [DOI] [PubMed] [Google Scholar]
- Katsura I., J. Theor. Biol. 103, 63 (1983). 10.1016/0022-5193(83)90199-6 [DOI] [PubMed] [Google Scholar]