Abstract
Purpose: To analyze the frequency domain characteristics of the signal in mammography images and breast tomosynthesis projections with patient tissue texture due to detected scattered x-rays.
Methods: Acquisitions of x-ray projection images of 19 different patient breasts were simulated using previously acquired volumetric patient images. Acquisition of these images was performed with a dedicated breast CT prototype system, and the images were classified into voxels representing skin, adipose, and glandular tissue with a previously validated automated algorithm. The classified three dimensional images then underwent simulated mechanical compression representing that which is performed during acquisition of mammography and breast tomosynthesis images. The acquisition of projection images of each patient breast was simulated using Monte Carlo methods with each simulation resulting in two images: one of the primary (non-scattered) signal and one of the scatter signal. To analyze the scatter signal for both mammography and breast tomosynthesis, two projections images of each patient breast were simulated, one with the x-ray source positioned at 0° (mammography and central tomosynthesis projection) and at 30° (wide tomosynthesis projection). The noise power spectra (NPS) for both the scatter signal alone and the total signal (primary + scatter) for all images were obtained and the combined results of all patients analyzed. The total NPS was fit to the expected power-law relationship NPS(f) = k/f^β and the results were compared with those previously published on the power spectrum characteristics of mammographic texture. The scatter signal alone was analyzed qualitatively and a power-law fit was also performed.
Results: The mammography and tomosynthesis projections of three patient breasts were too small to analyze, so a total of 16 patient breasts were analyzed. The values of β for the total signal of the 0° projections agreed well with previously published results. As expected, the scatter power spectrum reflected a fast drop-off with increasing spatial frequency, with a reduction of four orders of magnitude by 0.1 lp/mm. The β values for the scatter signal were 6.14 and 6.39 for the 0° and 30° projections, respectively.
Conclusions: Although the low-frequency characteristics of scatter in mammography and breast tomosynthesis were known, a quantitative analysis of the frequency domain characteristics of this signal was needed in order to optimize previously proposed software-based x-ray scatter reduction algorithms for these imaging modalities.
Keywords: mammography, tomosynthesis, breast, x-ray scatter, noise power spectrum, Monte Carlo
INTRODUCTION
The inclusion of the x-ray scatter signal in mammography and breast tomosynthesis has been shown to result in loss of contrast and accuracy.1, 2, 3 In mammography, an antiscatter grid is used to preferentially absorb scattered x-rays before they are detected. Although failure of the grid motion system may result in image artifacts,4 this solution to reducing the scatter signal in mammography is the standard in most, if not all, clinical mammography systems. However, in breast tomosynthesis, the motion of the x-ray source with respect to the detector results in a varying incidence angle for the primary (non-scattered) x-rays. This makes the use of the traditional antiscatter grid very challenging for this new breast imaging modality. As a result, none of the breast tomosynthesis systems available for clinical use incorporate the grid as a solution for reduction of the x-ray scatter signal.5 Furthermore, to the best of our knowledge, no other x-ray scatter reduction or correction technique is currently used in clinical breast tomosynthesis systems. As a potential alternative, post-acquisition software-based algorithms to reduce the x-ray scatter signal in breast tomosynthesis images have been proposed.1, 6 For optimal performance of some of these algorithms, it is necessary to have an in-depth understanding of the frequency domain characteristics of the x-ray scatter signal that is being addressed. Although it is well known that this signal only includes low spatial frequency components,7, 8, 9 exactly how fast the power content of the signal falls with increasing spatial frequency has not been characterized. Boone et al. estimated the point spread function (PSF) and modulation transfer function (MTF) of the scatter signal for homogeneous polymethyl methacrylate (PMMA) slabs of various thicknesses with a radiographic x-ray tube and an image intensifier, showing that the MTF approaches zero at approximately 0.2 lp/cm.7 Although that study included PMMA thicknesses relevant to mammography and breast tomosynthesis imaging, it did not include the potential impact of the adipose and glandular tissue texture present in patient breasts and the varying breast thickness towards the skin line of the compressed breast. Finally, that study characterized the scatter PSF and resulting MTF for a narrow beam, rather than the scatter power spectrum during acquisition of a full field image. Other studies have investigated in depth how the scatter PSF and the magnitude of scatter, characterized by the scatter-to-primary ratio (SPR), vary for different parameters, such as x-ray energy, homogeneous breast composition, breast thickness, etc. in both mammography and breast tomosynthesis.8, 9, 10 These studies also used metrics such as the scatter PSF and SPR to characterize these effects. Diaz et al. recently proposed an improvement on the convolution method to estimate the scatter field in a whole image, resulting in an improvement in the accuracy of the scatter signal estimate with a considerable reduction in computing time compared to conventional Monte Carlo simulations.11 However, none of these studies characterized the scatter signal in breast imaging from the point of view of its power spectrum.
To characterize qualitatively and quantitatively the frequency domain characteristics of the x-ray scatter signal in mammography and breast tomosynthesis, this study uses Monte Carlo simulations of image acquisition with patient breast volumes obtained with dedicated breast CT (BCT) imaging. The automated classification and mechanical compression of patient breasts imaged with this novel imaging modality allow for the realistic simulation of human breast tissue distributions undergoing projection imaging. These representations of the human breast allow for the inclusion of a realistic pattern of the tissue texture due to the heterogeneous mix of adipose and glandular tissue in the human breast. As opposed to previous studies on x-ray scatter in mammography and breast tomosynthesis, this work is focused on the frequency domain characteristics of this signal, so the results of the Monte Carlo simulations were analyzed in the frequency domain both qualitatively and quantitatively using the power-law relationship in the noise power spectrum (NPS) described by NPS(f) = k/f^β, as is usual in breast tissue texture analysis.12, 13, 14, 15, 16, 17, 18 The information on the scatter NPS for patient breast texture will be useful to more accurately estimate the x-ray scatter signal when performing post-acquisition software-based scatter correction of mammographic and especially breast tomosynthesis projections.
METHODS AND MATERIALS
To analyze the frequency domain characteristics of the x-ray scatter signal in mammography and breast tomosynthesis projections, the acquisition of these images was simulated using Monte Carlo methods performed with automatically classified and mechanically compressed, three-dimensional patient breast images that were acquired with a dedicated breast CT system. The patient BCT images and the processing they underwent are the same as those described previously.19 The details of this process are nevertheless described below.
Dedicated breast computed tomography acquisitions
The BCT images for all 19 patients were acquired for ongoing IRB-approved clinical studies after informed consent was obtained from the patients. As part of the consent, the patients released these images for use in other research projects after anonymization.
All 19 patient BCT images were acquired using a BCT prototype system (Koning Corp., West Henrietta, NY) installed at Emory University. The characteristics of the BCT system have been previously discussed.20, 21, 22, 23 In summary, the system consists of a patient table on which the patient lies prone, with an opening for the breast to be imaged to suspend through. Under the patient table a digital flat panel detector and an x-ray tube rotate around a vertical axis located at the patient's breast while acquiring 300 projections in 10 s. The x-ray beam is emitted by a tungsten target with a tube voltage of 49 kVp with an added aluminum filter, resulting in an x-ray spectrum with a first half value layer of 1.39 mm Al.24 The projections are combined using the FDK reconstruction algorithm, yielding a three dimensional (3D) image with voxels of 0.273 mm in each side.
Tissue classification
The acquired BCT images were classified into air, skin, adipose, and glandular tissue voxels. This was performed automatically using a previously discussed and validated classification algorithm.25 The algorithm achieves this through four steps: (a) cupping correction to reduce this artifact in the BCT reconstructions;26, 27, 28 (b) a multiscale bilateral filter29 to reduce noise in the images; (c) a modified fuzzy C-means classification method to differentiate adipose and glandular tissues; and (d) a morphological method to identify the skin voxels.
The main impact of the x-ray scatter signal present in the acquired BCT projections is the introduction of cupping in the reconstructed image. This cupping is corrected during the first step in this classification algorithm, so we do not believe that the presence of x-ray scatter in the BCT images impacts significantly the subsequent analysis and results on the frequency domain characteristics of scatter in mammography and breast tomosynthesis.
Mechanical compression simulation
Since the breast remains uncompressed during BCT image acquisition, the classified images had to undergo simulated mechanical compression to replicate the positioning of the breast during acquisition of mammographic and tomosynthesis images. For this, a previously discussed method was applied to all 19 patient breast images, which uses a linear spring model.30 In short, this algorithm divides the breast volume into “model elements,” each comprised of 27 voxels, which are assumed connected to each other with springs of linear and isotropic modulus of elasticity. Tissue incompressibility (constant total volume) is imposed by defining variable equilibrium lengths for the springs. The modulus of elasticity of the skin, adipose, and glandular tissue was assumed to be 88.0, 1.0, and 10.0 kPa, respectively.31 Each breast was compressed to match the thickness of the corresponding breast during its last craniocaudal (CC) view screening mammogram.
Monte Carlo simulations
To estimate the primary and scatter signals in mammography and breast tomosynthesis projections of the classified and compressed breasts, a previously developed and validated Monte Carlo simulation of these imaging modalities for voxelized breast representations was used.9, 19, 32 The simulation is based on version 9.5 patch 1 of the Geant4 toolkit, and it used the Livermore electromagnetic physics library.
The simulations represented the x-ray source as an isotropic point source, which emits x-rays only at a 24 × 29 cm ideal energy integrating detector with a source to detector distance of 70 cm. The detector could discriminate between the primary x-rays and the scattered x-rays. No discrimination was made among Compton, Rayleigh, and multiple scattered x-rays. Given the known low frequency content of the scatter signal, and to reduce the simulation time to acceptable levels while obtaining adequate statistics, the pixel size of the detector was set at 1 mm in each side.
The detector setup included the breast compression, breast support, and detector cover plates. The air gap between the bottom of the breast volume and the detector was 2.5 cm, and the breast volume was located in the mammographic position, i.e., at the centerline in the lateral direction and at the chest wall edge of the detector. The central ray was also placed at the centerline of the detector at the exact edge of the detector on the chest wall side. Posterior to the breast voxelized volume a water cuboid was placed to include any backscatter from the patient body. The simulated x-ray spectrum was the one used during acquisition of the last CC view screening mammogram of each patient, with a probability density function defined using the spectral models published by Boone.33 The composition of the breast tissues was defined using the description in Hammerstein et al.34
For the mammography image acquisition simulation, which also represents the 0° breast tomosynthesis projection simulation, the x-ray source was located with the central ray normal to the detector, at the centerline of the detector. To study the variability of the x-ray scatter signal characteristics at different projection angles, the acquisition of a large angle (30°) breast tomosynthesis projection was also simulated. This was accomplished by rotating the x-ray point source about the detector, assuming that the isocenter is located at the detector surface.
To minimize the presence of random white noise in the results due to the statistical nature of the simulations, each simulation involved the following of 2 × 1011 x-rays, until they were completely absorbed or escaped the simulation volume. For the simulation of a projection image taken at 30° for the thickest breast, the mean and maximum uncertainty in the scatter signal within the area of the projected breast was 0.4% and 0.7%, respectively. To complete these simulations in an acceptable timeframe, the Emory Ellipse high performance compute cluster consisting of 1024 computing cores was used. Given the relatively short start-up times of these simulations, the total computing time scales almost linearly with the number of cores used, so a speed-up of a factor of approximately 1000× was experienced by the use of this cluster.
Analysis of simulation results
The power spectrum analysis of both the total (primary + scatter) and scatter only simulated images was performed in the same manner as that described by various other groups.12, 13, 14, 15, 16, 17, 18 Specifically, for each image to be analyzed the logarithm of the image was computed and 1000 regions of interest (ROI) with a size of 64 × 64 pixels were automatically and randomly selected from within the projection of the breast tissue. Only ROIs that are located completely within the projected breast area, i.e., excluding the open field, were generated. The mean signal from each ROI was subtracted, and then the square of the magnitude of the Fourier transform of the ROI was calculated. To minimize spectral leakage, a Hanning window was first applied to the ROI in the spatial domain. The two-dimensional (2D) power spectrum was then obtained by averaging the result of this process of all 1000 ROIs and normalizing by the pixel size. The one-dimensional (1D) power spectrum was then computed by radially averaging the 2D power spectrum and binning the result into bins with spacing of 0.015625 cycles/mm as resulting from the ROI and pixel sizes.
The total and scatter only power spectra for all patients for both the 0° and 30° projections were obtained by averaging the values of each individual patient's corresponding power spectrum. The linear (in a log-log scale) section of the resulting power spectra was fit to a power law distribution described by the equation NPS(f) = k/f^β. The number of points to include in the fit was selected so as to maximize the correlation coefficient of the fit, as is usual in this type of analyses.16, 18
To compensate for the effect of the relatively large detector pixel size used in the Monte Carlo simulations, all power spectra were divided by the square of the sinc function of the pixel aperture and the power law fit was repeated.
As validation of the method, the resulting value of β for the total signal of the 0° projection was compared to those previously published by other groups.12, 13, 14, 15, 16, 17, 18
RESULTS
Of the 19 patient breast images analyzed, the simulated mammographic and tomosynthesis projections of three were less than 64 pixels wide, so no ROIs could be fit within the projection of the breast tissue. Therefore, all results reported are for a total of 16 patient breasts.
Total power spectrum
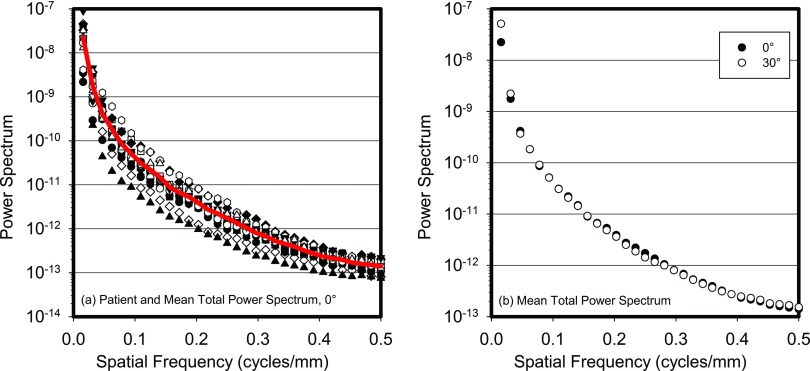
Figure 1 shows each patient's total (primary + scatter) power spectrum for the 0° projection and the resulting total power spectrum averaged for all patients, all before division by the square of the sinc function. This figure also shows a plot of the total power spectrum averaged for all patients for both the 0° and 30° projection angles. Virtually no difference in the power spectra between projection angles can be seen.
Figure 1.
(a) Power spectra of the total (primary + scatter) signal for all 16 patients studied (symbols) and the result of averaging across all patients (line). (b) Average across all patients of the total power spectra for the 0° and 30° projections. All power spectra are before division by the sinc function.
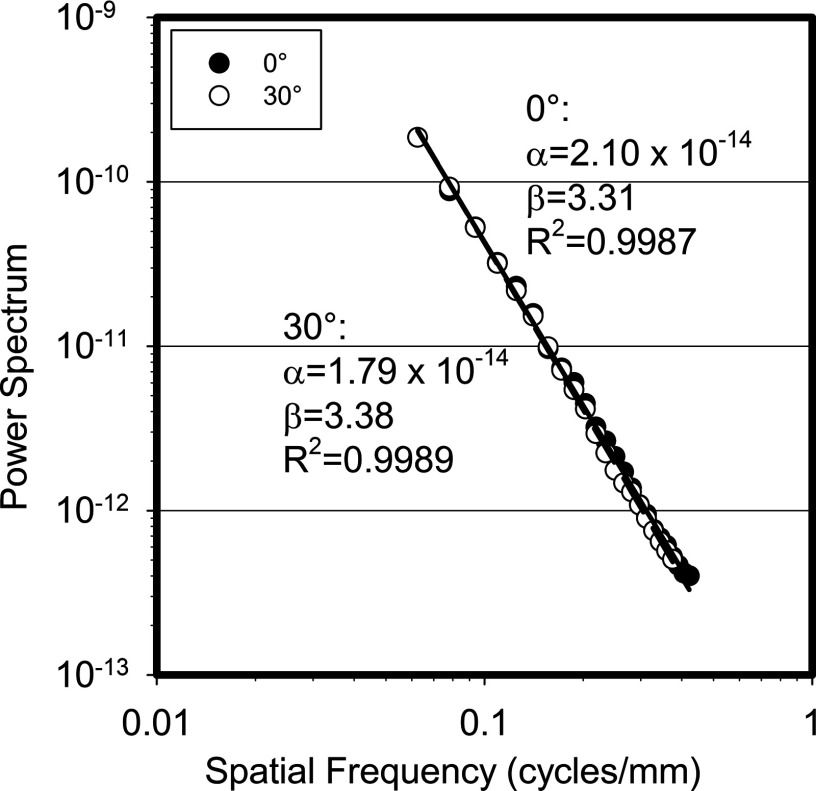
Figure 2 shows the power law fit for both the 0° and the 30° total power spectra averaged for all patients, with their corresponding power law fit coefficients. These spectra include the division by the sinc function. As can be seen, the β value for the total power spectrum for the 0° projection obtained in this study for these 16 patient breasts is 3.31. This compares well to the values of β previously published, which, for real mammographic and tomosynthesis images, both screen-film and digital, have ranged from 2.8 to 3.235,12, 14, 15, 16, 17, 18 while Bochud et al. found it to vary from 3.4 to 4.0.13 Perhaps the β value found in this study for the total signal is higher than those mostly reported due to the use of a simulated voxelized representation of the breast tissues with a voxel size of 0.273 mm, compared to using actual patient breasts during acquisition of real images, as was the case in the studies noted above. In addition, a very small difference in the values of β was found between the two projection angles, consistent with the findings of Engstrom et al., who reported that on a per case basis, the variation in β among the different projection angles in complete real tomosynthesis projection sets was minimal (<2% coefficient of variation).17
Figure 2.
Power law fit for the 0° and 30° total power spectra after division by the sinc function of the pixel aperture.
Scatter power spectrum
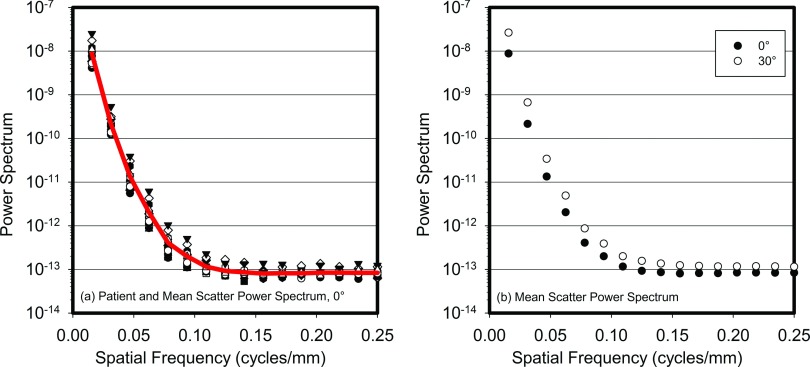
Figure 3 shows each patient's scatter only power spectrum for the 0° projection and the resulting average power spectrum, before division by the sinc function. As can be seen, the power spectrum falls rapidly with increasing spatial frequency, with a reduction of approximately two orders of magnitude by less than 0.05 cycles/mm and almost five orders of magnitude by 0.1 cycles/mm, beyond which point the white noise from the Monte Carlo simulations dominates the signal. This rapid fall off in signal strength indicates that the use of pixels with a size of 1.0 mm in the Monte Carlo simulations did not affect the results in a substantial manner, since the value of the sinc function corresponding to the pixel aperture at 0.1 cycles/mm is still >0.98. This figure also shows a plot of the patient averaged scatter power spectrum for the 0° and 30° tomosynthesis projection angles, demonstrating a minor variation in the scatter power spectrum with projection angle.
Figure 3.
(a) Power spectra of the scatter signal for all 16 patients studied (symbols) and the result of averaging across all patients (line). (b) Average across all patients of the scatter power spectra for the 0° and 30° projections. All power spectra are before division by the sinc function.
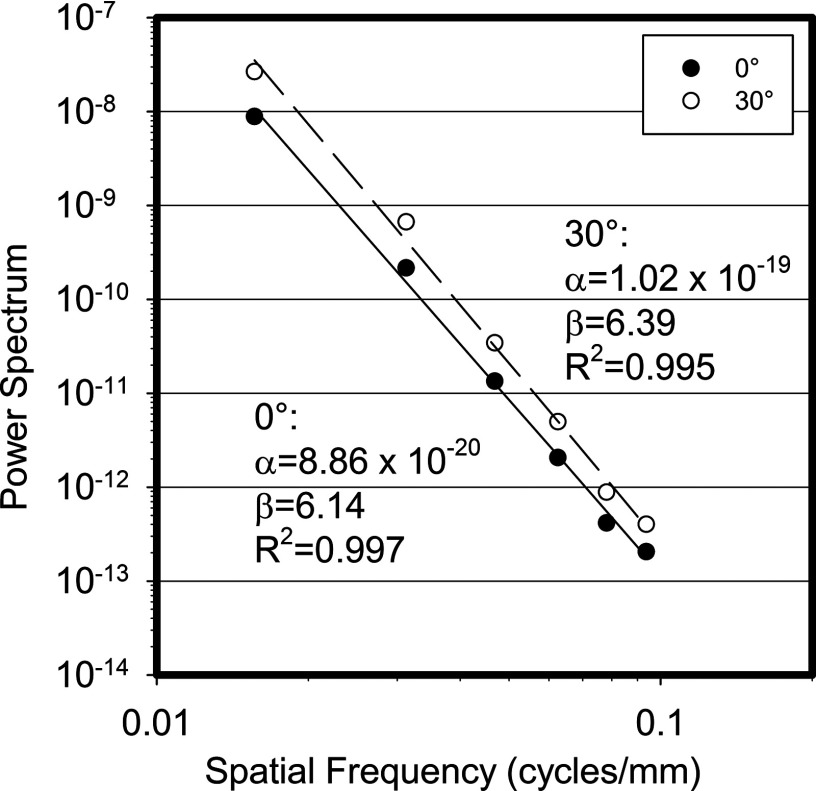
Figure 4 shows the power law fit for both the 0° and 30° scatter power spectra and their fit coefficients. As shown in the figure, the β values for the fits of the 0° and 30° angles are 6.14 and 6.39, respectively. As expected from the very fast drop off seen in the power spectra, the β values for the scatter signal are substantially higher than those for the total power spectra.
Figure 4.
Power law fit for the 0° and 30° scatter power spectra after division by the sinc function of the pixel aperture.
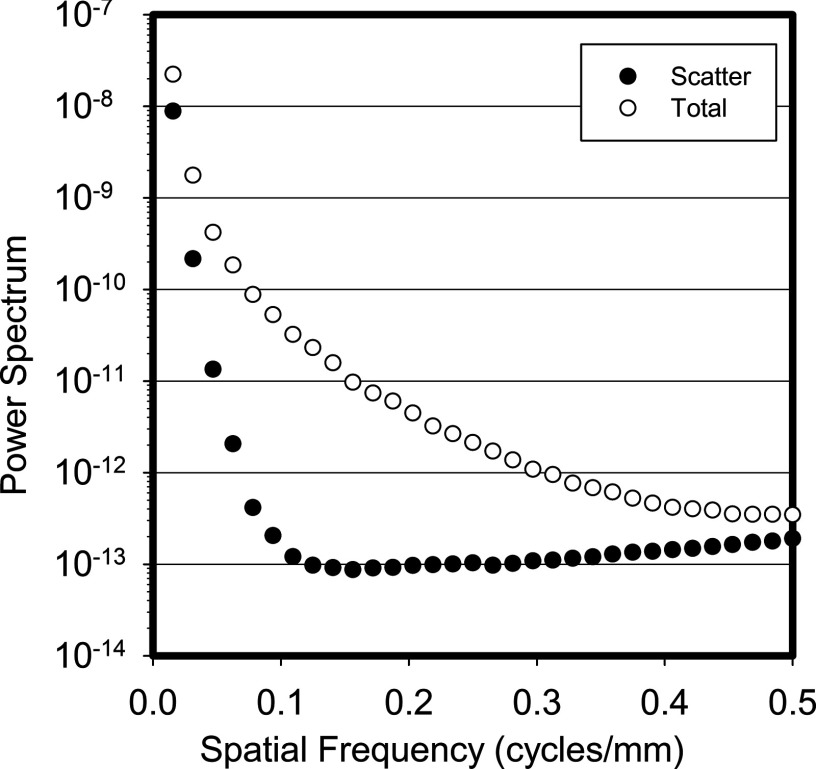
Finally, Fig. 5 shows the total and scatter power spectra for the 0° projection after division by the square of the sinc function, where the difference in the frequency characteristics of both signals is apparent.
Figure 5.
Power spectrum averaged for all patients and divided by the square of the sinc function of the pixel aperture, for the 0° projection for both the scatter only and the total signal. The difference in spatial frequency components of the two signals is evident in this plot.
DISCUSSION
Although it is well known that the scatter signal in mammography and breast tomosynthesis is concentrated at low spatial frequencies,7, 8, 9 to the best of our knowledge the spatial frequency characteristics of x-ray scatter in breast imaging have not been studied extensively before. Having quantitative information on how the magnitude of the scatter signal varies with spatial frequency can aid in the development and performance evaluation of certain post-acquisition, software-based scatter correction algorithms. For example, in an algorithm previously proposed by our group,6 one of the stages involves the use of a low pass filter to isolate only the low frequencies present in the acquired image that include the scatter signal. The knowledge gained in this study provides the information necessary to set the cutoff frequency for that low pass filter.
Qualitative evaluation of the power spectrum of the x-ray scatter signal in mammography and tomosynthesis projections showed that the magnitude of this signals falls very rapidly with increasing spatial frequency, with approximately a drop of five orders of magnitude by 0.1 cycles/mm. This was further shown by the value of β in the power law fit equation NPS(f) = k/f^β, which for the scatter signal was shown to be >6.0.
Validation of the process performed in this study was achieved by comparing the value of β for the total signal of the 0° projection (equivalent to mammography) to that of previously published studies. It was found that this study resulted in a somewhat higher value for β, a fact that could be explained by the discrete nature of the breast tissue representation used in the simulations of image acquisition.
The present study is limited mainly by the low number of cases and, as stated above, the discrete representation of the imaged breast tissues, with voxel sizes that, though small, could have introduced some impact on some of the results. It is important to note that this impact, however, is most probably limited to only the spectral characteristics of the total signal, which was only used for validation, and not of the scatter only signal, which was the real topic of interest in this study, given the latter's already greatly diminished power at spatial frequencies corresponding to the pixel and voxel sizes used in the study. In addition, this study simulated only the CC view acquisitions, ignoring the mediolateral oblique (MLO) view. However, since the simulated compressed breasts used in this study were generated from BCT images, which do not include similar coverage of the pectoralis muscle and the axilary tail as in compressed breast projections, it is challenging to simulate this view from BCT data. According to Chen et al., the value for β for the power law fit for the power spectrum of the total signal is statistically different between the CC and MLO views in mammography, but the difference is not large.18 Therefore, it could be expected that if there is any difference in the spectral characteristics of the scatter only signal for the MLO view compared to the CC view, the difference is most likely to be small.
CONCLUSIONS
This study involved a qualitative and quantitative evaluation of the spatial frequency characteristics of x-ray scatter in mammography and breast tomosynthesis. As expected, it was found that the x-ray scatter signal drops off rapidly with increasing spatial frequency, with a reduction in the power spectrum of approximately five orders of magnitude by 0.1 cycles/mm. This is further demonstrated by the large value for β, the power law fit to the power spectrum, which was found to have values above 6.0 for both projection angles studied, 0° and 30°. The knowledge gained in this study will aid in the development of post-acquisition, software-based scatter reduction algorithms for breast tomosynthesis imaging.
ACKNOWLEDGMENTS
The project described was partially supported by Grant Nos. P50CA128301, R01CA156775, and R01CA163746 from the National Cancer Institute and a grant from the Georgia Cancer Coalition. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Georgia Cancer Coalition, National Cancer Institute or the National Institutes of Health.
References
- Liu B., Wu T., Moore R. H., and Kopans D. B., “Monte Carlo simulation of x-ray scatter based on patient model from digital breast tomosynthesis,” Proc. SPIE 6142, 61421N–61429N (2006). 10.1117/12.650193 [DOI] [Google Scholar]
- Wu G., Mainprize J. G., Boone J. M., and Yaffe M. J., “Evaluation of scatter effects on image quality for breast tomosynthesis,” Proc. SPIE 6510, 65101T–65109T (2007). 10.1117/12.708531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu G., Mainprize J. G., Boone J. M., and Yaffe M. J., “Evaluation of scatter effects on image quality for breast tomosynthesis,” Med. Phys. 36, 4425–4432 (2009). 10.1118/1.3215926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogge J. P., Palmer C. H., Muller C. C., Little S. T., Smith D. C., Fatouros P. P., and de Paredes E. S., “Quality assurance in mammography: Artifact analysis,” Radiographics 19, 503–522 (1999). [DOI] [PubMed] [Google Scholar]
- Sechopoulos I., “A review of breast tomosynthesis. Part I. The image acquisition process,” Med. Phys. 40, 014301 (12pp.) (2013). 10.1118/1.4770279 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng S. S. J. and Sechopoulos I., “A software-based x-ray scatter correction method for breast tomosynthesis,” Med. Phys. 38, 6643–6653 (2011). 10.1118/1.3659703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boone J. M., Arnold B. A., and Seibert J. A., “Characterization of the point spread function and modulation transfer function of scattered radiation using a digital imaging system,” Med. Phys. 13, 254–256 (1986). 10.1118/1.595906 [DOI] [PubMed] [Google Scholar]
- Boone J. M., Lindfors K. K., V. N.Cooper3rd, and Seibert J. A., “Scatter/primary in mammography: Comprehensive results,” Med. Phys. 27, 2408–2416 (2000). 10.1118/1.1312812 [DOI] [PubMed] [Google Scholar]
- Sechopoulos I., Suryanarayanan S., Vedantham S., D’Orsi C. J., and Karellas A., “Scatter radiation in digital tomosynthesis of the breast,” Med. Phys. 34, 564–576 (2007). 10.1118/1.2428404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dance D. R. and Day G. J., “The computation of scatter in mammography by Monte Carlo methods,” Phys. Med. Biol. 29, 237–247 (1984). 10.1088/0031-9155/29/3/003 [DOI] [PubMed] [Google Scholar]
- Díaz O., Dance D. R., Young K. C., Elangovan P., Bakic P. R., and Wells K., “A fast scatter field estimator for digital breast tomosynthesis,” Proc. SPIE 8313, 831305–831305 (2012). 10.1117/12.911494 [DOI] [Google Scholar]
- Burgess A. E., “Mammographic structure: Data preparation and spatial statistics analysis,” Proc. SPIE 3661, 642–653 (1999). 10.1117/12.348620 [DOI] [Google Scholar]
- Bochud F., Abbey C., and Eckstein M., “Statistical texture synthesis of mammographic images with super-blob lumpy backgrounds,” Opt. Express 4, 33–42 (1999). 10.1364/OE.4.000033 [DOI] [PubMed] [Google Scholar]
- Burgess A. E., Jacobson F. L., and Judy P. F., “Human observer detection experiments with mammograms and power-law noise,” Med. Phys. 28, 419–437 (2001). 10.1118/1.1355308 [DOI] [PubMed] [Google Scholar]
- Heine J. J. and Velthuizen R. P., “Spectral analysis of full field digital mammography data,” Med. Phys. 29, 647–661 (2002). 10.1118/1.1445410 [DOI] [PubMed] [Google Scholar]
- Metheany K. G., Abbey C. K., Packard N., and Boone J. M., “Characterizing anatomical variability in breast CT images,” Med. Phys. 35, 4685–4694 (2008). 10.1118/1.2977772 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engstrom E., Reiser I., and Nishikawa R., “Comparison of power spectra for tomosynthesis projections and reconstructed images,” Med. Phys. 36, 1753–1758 (2009). 10.1118/1.3116774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L., Abbey C. K., Nosrateih A., Lindfors K. K., and Boone J. M., “Anatomical complexity in breast parenchyma and its implications for optimal breast imaging strategies,” Med. Phys. 39, 1435–1441 (2012). 10.1118/1.3685462 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sechopoulos I., Bliznakova K., Qin X., Fei B., and Feng S. S. J., “Characterization of the homogeneous tissue mixture approximation in breast imaging dosimetry,” Med. Phys. 39, 5050–5059 (2012). 10.1118/1.4737025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ning R., Conover D., Yu Y., Zhang Y., Cai W., Betancourt-Benitez R., and Lu X., “A novel cone beam breast CT scanner: System evaluation,” Proc. SPIE 6510, 651030–651039 (2007). 10.1117/12.710340 [DOI] [Google Scholar]
- Betancourt-Benitez R., Ning R., Conover D., and Liu S., “NPS characterization and evaluation of a cone beam CT breast imaging system,” J. X-Ray Sci. Technol. 17, 17–40 (2009). 10.3233/XST-2009-0213 [DOI] [PubMed] [Google Scholar]
- Betancourt-Benitez R., Ning R., Conover D., and Liu S., “Composite modulation transfer function evaluation of a cone beam computed tomography breast imaging system,” Opt. Eng. 48, 117002–117011 (2009). 10.1117/1.3258348 [DOI] [Google Scholar]
- O’Connell A., Conover D. L., Zhang Y., Seifert P., Logan-Young W., Lin C.-F. L., Sahler L., and Ning R., “Cone-beam CT for breast imaging: Radiation dose, breast coverage, and image quality,” Am. J. Roentgenol. 195, 496–509 (2010). 10.2214/AJR.08.1017 [DOI] [PubMed] [Google Scholar]
- Sechopoulos I., Feng S. S. J., and D’Orsi C. J., “Dosimetric characterization of a dedicated breast computed tomography clinical prototype,” Med. Phys. 37, 4110–4120 (2010). 10.1118/1.3457331 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X., Wu S., Sechopoulos I., and Fei B., “Cupping artifact correction and automated classification for high-resolution dedicated breast CT images,” Med. Phys. 39, 6397–6406 (2012). 10.1118/1.4754654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwan A. L. C., Boone J. M., and Shah N., “Evaluation of x-ray scatter properties in a dedicated cone-beam breast CT scanner,” Med. Phys. 32, 2967–2975 (2005). 10.1118/1.1954908 [DOI] [PubMed] [Google Scholar]
- Liu B., Glick S. J., and Groiselle C., “Characterization of scatter radiation in cone beam CT mammography,” Proc. SPIE 5745, 818–827 (2005). 10.1117/12.595396 [DOI] [Google Scholar]
- Shikhaliev P. M., “Beam hardening artefacts in computed tomography with photon counting, charge integrating and energy weighting detectors: A simulation study,” Phys. Med. Biol. 50, 5813 (2005). 10.1088/0031-9155/50/24/004 [DOI] [PubMed] [Google Scholar]
- Tomasi C. and Manduchi R., “Bilateral filtering for gray and color images,” in Proceedings of the Sixth International Conference on Computer Vision (Bombay, India, 1998), pp. 839–846.
- Zyganitidis C., Bliznakova K., and Pallikarakis N., “A novel simulation algorithm for soft tissue compression,” Med. Biol. Eng. Comput. 45, 661–669 (2007). 10.1007/s11517-007-0205-y [DOI] [PubMed] [Google Scholar]
- Kellner A. L., Nelson T. R., Cervino L. I., and Boone J. M., “Simulation of mechanical compression of breast tissue,” IEEE Trans. Biomed. Eng. 54, 1885–1891 (2007). 10.1109/TBME.2007.893493 [DOI] [PubMed] [Google Scholar]
- Sechopoulos I., Suryanarayanan S., Vedantham S., D’Orsi C., and Karellas A., “Computation of the glandular radiation dose in digital tomosynthesis of the breast,” Med. Phys. 34, 221–232 (2007). 10.1118/1.2400836 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boone J. M., Fewell T. R., and Jennings R. J., “Molybdenum, rhodium, and tungsten anode spectral models using interpolating polynomials with application to mammography,” Med. Phys. 24, 1863–1874 (1997). 10.1118/1.598100 [DOI] [PubMed] [Google Scholar]
- Hammerstein G. R., Miller D. W., White D. R., Masterson M. E., Woodard H. Q., and Laughlin J. S., “Absorbed radiation dose in mammography,” Radiology 130, 485–491 (1979). 10.1148/130.2.485 [DOI] [PubMed] [Google Scholar]