Nonlinear Scaling of Surface Water Diffusion with Bulk Water Viscosity of Crowded Solutions

Abstract

The translational hydration dynamics within 0.5-1.5 nanometers (nm) of the surface of a DPPC liposome – a model biomacromolecular surface – is analyzed by the recently developed Overhauser dynamic nuclear polarization (ODNP) technique. We find that dramatic changes to the bulk solvent cause only weak changes in the surface hydration dynamics. Specifically, both a >10-fold increase in bulk viscosity and the restriction of diffusion by confinement on a multiple-nm length-scale change the local translational diffusion coefficient of the surface water surrounding the lipid bilayer by less than 2.5-fold. By contrast, previous ODNP studies have shown that changes to the biomacromolecular surface induced by folding, binding, or aggregation can cause local hydration dynamics to vary by factors of up to 30.^1,2 We suggest that the surface topology and chemistry at the ≤ 1.5 nm scale, rather than the characteristics of the bulk fluid, nearly exclusively determine the surface hydration dynamics of aqueous macromolecular solutes.

Most structural biology and biochemistry studies analyze biomolecules dissolved in simple and dilute buffers. However, in nature, a complex mixture of macromolecules and small molecular constituents crowd the cytoplasm. Macromolecules alone occur at concentrations of 300-400 g/L in E. Coli.³ The crowded environment dramatically alters not only the kinetics of biomolecular function, but also the thermodynamic activity of various conformational states, as many studies have clearly demonstrated and rationalized.^4–7 The compartmentalization and nanoscale confinement of the cytoplasm by lipid membranes plays a similarly important role throughout biology.^8–10

Curiously, biochemical studies in dilute buffer solutions still serve as good and representative models of many biologically important processes that occur in the crowded cell. Even more so, proteins tolerate a broad range of perturbations to the bulk solvent – many proteins can recover near complete function with the addition of only a 40% weight ratio of water.^11,12 This broad tolerance would seem to imply an intimate link between the properties and function of the macromolecule itself and the macromolecule’s “surface also,” water broadly termed “hydration water.” Therefore, we seek to analyze the properties of this hydration water in the highly viscous and sometimes opaque conditions implied by crowding and, in particular, to compare the surface hydration water dynamics in crowded and confined environments to that of bulk water in a dilute solution environment.

Here, we successfully utilize ODNP (Overhauser Effect Dynamic Nuclear Polarization) – an emerging and novel magnetic resonance technique – to compare the surface hydration dynamics of high-viscosity solutions to those of low-viscosity solutions. The ODNP tool has now been used in several studies^1,2,13–20 to perform highly localized measurements of translational diffusivity. It is a hybrid of ESR (electron spin resonance) and NMR (nuclear magnetic resonance) that reads out the self- and cross-relaxivities of water molecules near a specifically attached nitroxide moiety, which functions as a “spin label” – i.e. a stable organic radical that provides an unpaired electron spin for ESR and that can be attached to biomacromolecular surfaces. The ODNP measurement and subsequent analysis approximate a correlation time, τ_c, which gives the timescale it takes for the proton spin of the water to pass within the magnetic field generated by the spin label, which extends outwards for 0.5-1.5 nm.¹⁴ The value of τ_c is inversely proportional to the diffusivity of the water.¹⁴ Since this measure of water diffusivity is specific to water molecules passing through the magnetic field generated by the spin label, i.e. within a 0.5-1.5 nm distance of the spin label, we denote it as the “local” diffusivity. Here, we compare this value of τ_c, e.g., against the reference value for a small nitroxide molecule freely dissolved in water, which we denote as τ_c,w. The value of τ_c,w, which picks out the diffusivity of the relatively un-perturbed²¹ bulk water (2.3×10⁻⁹ m²s⁻¹) around the small spin label, is 33.3 ps.²² We calculate translational retardation factors, e.g. τ_c/τ_c,w, which can be approximated as the ratio between bulk water diffusion dynamics and local surface water. In this study, we examine such retardation factors in order to directly analyze the impact of confinement and macromolecular crowding on the local translational diffusivity of the first several water layers, i.e. within 0.5-1.5 nm distances of the surface of biomolecules.

The model system presented here consists of a 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) lipid bilayer that displays a low (3 mol %) concentration of covalently attached spin labels. These are positioned ~0.6-0.8 nm above the level of the phosphate in the phosphatidylcholine head group. Thus, ODNP probes the surface dynamics of a few water layers, within ~2.1-2.3 nm above the phosphate level (well above the DPPC head group), broadly termed “hydration” or “biological” water.^16,20

Our experimental results indicate that the diffusion of hydration water near the lipid membrane surfaces is largely decoupled from the diffusion of the crowded bulk solution, i.e. from the bulk viscosity of the solution. In fact, it is astonishing that biomacromolecules can preserve similar structure, dynamics, and function in the exceedingly crowded cytoplasmic environment as in a dilute buffer solution. We suggest that this is because the characteristic and crucial hydration shell remains relatively decoupled from its bulk environment, and is preserved.

The DPPC bilayer system displays several desirable properties for ODNP analysis. The dynamics of water associated with lipid vesicle surfaces have been shown by FCR (i.e. field cycling relaxometry) to adhere well to the force-free hard sphere (FFHS)²⁵ model (i.e. assuming translational diffusion as the main contributor to cross relaxation) as employed in the standard ODNP analysis.^14,26,27 Furthermore, the DPPC bilayer is in a lipid gel phase at room temperature, and therefore presents less lipid dynamics and a smoother surface than in the liquid crystalline phase. Finally, we are able to prepare the vesicles to generate both 200 nm diameter large unilamellar vesicles (LUVs), where nanoscale confinement should not affect the hydration dynamics, as well as multilamellar vesicles (MLVs), which could exhibit additional changes in dynamics as a result of confinement within the inter bilayer volume.

An analysis of the ODNP data shows that the water near the surface of the DPPC lipid bilayer vesicles translates about 5.8 times slower than it translates in the bulk (see Tab. 1). Previous studies² reported a retardation factor of the same order for water diffusion on lipid vesicle surfaces; specifically yielding a τ_c,DPPC value of 248 ps, corresponding to a retardation factor (τ_c,DPPC/τ_c,w) of 7.4, for water near the surface of DPPC lipid vesicles. Experimental variations or improvements to the methodology that have been made since the previous publication might explain the differences in the two values. Importantly, both results overall agree in showing that the hydration dynamics at the surface of the lipid bilayer is significantly slowed.

Interestingly, the additional slowdown of the hydration dynamics on MLV surfaces that are predominantly sandwiched between bilayers vs. on LUV surfaces that are entirely exposed to bulk water is surprisingly small. This is a particularly unintuitive result, given that DPPC MLV systems are reported to exhibit a close repeat distance of about 6.40 nm, of which the bilayer thickness is 4.96 nm, implying that water diffuses within a confined space encompassing an inter bilayer distance of only 1.44 nm.²⁸ Despite this dramatic confinement, the hydration dynamics on the surface of the LUV are only 20% faster than at the interfacial locations on the MLV, as shown in Tab. 1. Before returning to analyze this observation, the next study investigates the effect of controlled crowding.

As has been thoroughly discussed in the literature, Ficoll and sucrose do not substantially interact with the surface of proteins. Among others, the group of Timosheff has shown that sucrose is actively excluded from the vicinity of proteins, thus stabilizing protein structures,^29,30 i.e. acting as a “protecting osmolyte.”^6,31,32 Ficoll, a branched sucrose polymer, has been shown to similarly avoid interactions with proteins.^33,34 In particular, the group of Pielak has shown that proteins will engage in non-specific, but clearly measurable, interactions with protein-based crowding agents, while they exhibit little to no interaction with Ficoll.^35,36 For this reason, both Ficoll and sucrose are commonly used as viscogens, which facilitate ESR lineshape analysis by slowing down the overall tumbling of the biomolecule in order to highlight the more local spin label dynamics and environment. By dissolving in the buffer, these viscogens are thought to generate a viscous, crowded bulk solvent without introducing any substantial interactions with the biomolecular surfaces.^5,37–39 We follow this lead for analyzing the surface hydration properties of lipid bilayer vesicles.

As described in the Supporting Information, both Ficoll and sucrose have been added to increase the bulk viscosity of the solution by 10-fold, as described in the literature. The Stokes-Einstein relationship then allows one to define and compare this to the local viscosity at the surface of DPPC vesicles, as measured by ODNP. Specifically, if a molecule undergoes non-anomalous Brownian diffusion, it will exhibit a diffusion constant as follows^36,40–43

$$D=\frac{k_{B}T}{6\pi \eta R_H},$$ (1)

where k_B is Boltzmann’s constant, T the absolute temperature, R_H the effective radius of the diffusing particle (here, a water molecule), and η the viscosity of the bulk solution. It is worth noting that certain studies have claimed that the diffusion of small tracer molecules (i.e. fluorophores) in the presence of crowding agents or viscogens such as Ficoll or sucrose is entirely non-anomalous, following Gaussian Brownian motion,⁴³ while other studies have clearly presented diffusion of biomolecules (e.g. proteins) that does not follow a Stokes-law behavior when either synthetic polymers or protein-based crowding agents are present in the solution.^35,36 However, even under situations where the diffusion is anomalous (i.e. non-Gaussian), as has been predicted and demonstrated for small molecules in the presence of large crowders,^36,43 we can define an “effective” local viscosity, η, based on the Stokes-Einstein relationship with the local diffusivity, D, determined from ODNP. As stated previously, the correlation times for translational diffusion should be inversely proportional to the local diffusivity of the water, i.e. (where we designate values for two different samples as primed and unprimed)

$$\frac{{\tau }_c^{\prime }}{{\tau }_c}\approx \frac{D}{D^{\prime }}.$$ (2)

The relative retardation factor, i.e. the ratio of the correlation times under different conditions, should then reflect the ratio of the effective local viscosities,

$$\frac{{\tau }_c^{\prime }}{{\tau }_c}\approx \frac{{\eta }^{\prime }}{\eta },$$ (3)

(from eq. 1-2). Thus far we have discussed one retardation factor, that of the local environment relative to bulk water, i.e. ${\tau }_c^{\prime }∕{\tau }_c={\tau }_c∕{\tau }_{c,w}$. We can now use ODNP to ask the question of whether or not this effective local viscosity couples to the viscosity of the bulk solvent, i.e. whether the viscosity at the LUV surface remains unchanged at 5.8 times greater than the bulk viscosity, or whether it is further retarded as the bulk viscosity increases. In other words we can analyze the retardation relative to the uncrowded DPPC solution, i.e. ${\tau }_c^{\prime }∕{\tau }_c={\tau }_c∕{\tau }_{c,\mathit{DPPC}}$.

We make the surprising observation, as shown in Table 1, that the coupling between the dynamics at the surface of our unconfined bio-macromolecular model system (the DPPC LUV samples) and the bulk viscosity is extremely weak. The addition of the crowding agents slows the translational dynamics of the hydration water by a factor of less than 2, i.e. less than 1/5^th of the increase in the 10-fold bulk viscosity.

Table 1.

Experimental hydration dynamics data from ODNP and NMR relaxation measurements are presented here. The experimental design controls for viscosity that is depressed by confinement (LUV vs. MLV), as well as crowding-induced viscosity, η. The values k_σs_max, k_low, and ξ are derived from fundamental ODNP relaxation rates, as further described in the Supplementary Information. The translational correlation, τ_c, refers to the correlation time at the surface of the aqueous sample listed in a particular row, while τ_c,DPPC refers to the correlation time at the surface of DPPC in pure buffer (i.e. without any viscogens). The translational correlation time of a small nitroxide in pure water, the t_c,w referred to in the penultimate column, is 33.3 ps– as measured elsewhere. ^23,24 The final column calculates the slowdown of the water relative to the surface dynamics of the DPPC LUV system. These last two columns clearly present the nonlinear scaling of the diffusion dynamics of surface hydration vs. bulk water. Additionally, as discussed further in the text, the observed changes are small relative to the changes observed during structural and most conformational changes of the solute itself.

	composition	η/η H2O	kσsmax/ s−1M−1	klow/ s−1M−1	ξ/0.01	τc/τc,w	τc/τc,DPPC
LUV	DPPC	1	18.1±1.2	320±120	9.2±2.2	5.8±1.2	–
	DPPC + Ficoll	10	21.9±0.7	490±260	8.6±4.2	6.1±2.4	1.05±0.41
	DPPC + sucrose	10	14±5	1600±1600	3.9±3.0	10.9±5.7	1.9±1.0
MLV	DPPC	1	15.7±2.9	330±100	7.7±1.9	6.7±1.3	1.15±0.23
	DPPC + Ficoll	10	17.9±6.2	420±220	8.6±4.5	6.1±2.6	1.07±0.45
	DPPC + sucrose	10	17.7±1.6	1170±470	2.9±1.3	13.2±3.9	2.26±0.68
benchmark for structural change:							3.5–4.5

The relatively small change of the local dynamics is not an artifact of the ODNP analysis or experiment, which can and does see very large modulation in the local dynamics due to interactions and structural rearrangements. For instance, a previous study analyzed various sites of apomyoglobin in the folded and unfolded form with ODNP to find values of τ_c ranging from 178 ps to >1000 ps, corresponding to retardation factors of between 5.3 and 30. On transitioning from an unfolded to native folded conformation, the translational hydration dynamics of apomyoglobin slow down by factors in the range of 4.15±2.9 (here, the ±2.9 indicates the standard de viation across different residues).¹ Similarly, tau-187, a short amyloid peptide, exhibits retardation factors of 4.3 and 15.3 before and after aggregation, respectively (144 ps and 511 ps, respectively), exhibiting a 3.5-fold change in local hydration dynamics upon aggregation.² Based on these studies, we can designate a slow-down by a factor of 3.5-4.5 as typical for the retardation of hydration dynamics that accompanies actual structural changes; therefore this value is denoted as a “benchmark for structural change” in Table 1. None of the decreases in water mobility induced by either crowding or confinement, as presented in Table 1, is as dramatic as the slowdown accompanying the structural changes that have been observed in bio-macromolecular systems.

Table 1 also presents that crowding with a viscous sucrose solution reduces the water mobility at the DPPC surface measurably more than a viscous solution of Ficoll of the same nominal bulk viscosity. Sucrose has a thermodynamic activity much greater than the activity of an isoviscous solution of Ficoll 400, as it exhibits an osmolality about an order of magnitude greater¹.⁷ The activity of a sucrose solution should similarly (though to a slightly lesser extent) exceed the activity of an isoviscous solution of Ficoll 70. On the most rudimentary level, the smaller activities needed to achieve the same level of viscosity express the fact that Ficoll is larger than the sucrose (see fig. 1). However, on a deeper level, the larger activity coefficient required of the sucrose states that a sucrose-water solution needs to release a greater free energy before the solution viscosity will increase appreciably. Therefore, the slightly greater perturbation of the surface hydration dynamics exerted by sucrose may be an indication of this increased free energy, part of which may be due to interactions between the sucrose and the water.

Figure 1.

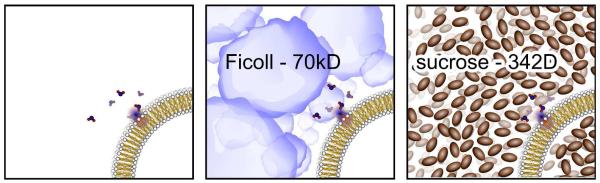
A schematic of the three LUV samples employed in this study. Plain DPPC (left), DPPC + Ficoll 70 (center), DPPC + sucrose (right) are all dissolved in PBS buffer (to enforce a constant pH). Ficoll 70 has a radius of 5.5 nm (and at these concentrations, the different Ficoll molecules likely interact with each other).⁴⁴ Sucrose exhibits an effective hydrodynamic radius of between 0.44 nm and 0.52 nm, depending on the method of determination⁴⁵

Not surprisingly, when the effects of confinement inside the MLV layers and the effects of crowding induced by sucrose act together, they lead to the largest retardation of translational water mobility observed here. Likely, this arises from intercalation of sucrose into the inter-lamellar space of the MLV, which could create obstructions preventing the free passage of water on nanometer length-scales. This hypothesis is supported by the fact that k_low changes more dramatically than for the other samples, where k_low is a parameter that increases along with the population of “bound” water molecules that remain stationary on a timescale of near 6 ns. In other words, k_low signifies the contribution of slowly moving, bound, water (see Supporting Information). Still, even in the sucrose-crowded and MLV-confined interface, the local hydration dynamics decreases only by an additional factor of 2.3 – much less than the 10-fold increase in bulk viscosity.

This is the first direct observation of site localized translational hydration dynamics in crowded environments of different viscosities. In fact, the hydration water probed here actually represents a very small fraction of the total water content of the solutions analyzed. Despite the different nature of this method, a reanalysis of previous ODNP results and a comparison to results acquired by other methods find that the decoupling of the surface vs. bulk water dynamics is compatible with previous observations in the literature. One crowding agent that has been studied by ODNP is PEG (polyethylene glycol). After the addition of 20% PEG, the surface dynamics of a DOPC lipid has been shown to slow down by a factor of only 1.7,² even though the viscosity of a 20% PEG 8000 solution² has a viscosity 20-fold greater than water,⁴⁶ implying decoupled surface and bulk dynamics. We can infer from this that any interaction between PEG polymers and the surface of the lipid vesicle is limited. In a different study, Robinson et. al.⁴⁷ have presented ESR data showing that the rotational diffusion of small nitroxide-based spin label molecules in glucose follows a power-law dependence on the bulk viscosity, rather than obeying the Stokes-Einstein relationship. This again likely reflects effects of volume exclusion due to size or (less likely) the existence of specific interactions between the rotating nitroxide probe and glucose.

At first, the variations we present might seem odd. The dynamics at the surface of the DPPC bilayer are decoupled from the bulk dynamics, but by no means immobilized; water at the surface only moves at about 20% of the typical diffusion rate and exhibits insensitivity to changes in the bulk viscosity. Interestingly, the same 1 nm length-scale that the ODNP approach probes corresponds to the correlation length of water, which determines the length-scale of structural and dynamic changes of the fluid.^48–50 This suggests that the DPPC surface itself controls the dynamics of local water molecules within 1 nm of the lipid vesicle surface, while Ficoll or sucrose controls the dynamics of water molecules in the bulk solvent or those located a few nm away from the DPPC surface, in the bulk solvent.

While it might be intuitive that changes in dynamics several nanometers away might propagate up to the spin label and affect the ODNP measurement, the results presented here show that even dramatic (10-fold) changes in the bulk viscosity can lead to less than a 2-fold change in the local dynamics observed by ODNP. Therefore, a crucially important consequence of this discussion is that when ODNP measures modulation in hydration dynamics that exceed a factor of 2.5, this clearly implies either a change in the local structure or the local chemistry within 1-2 nm of the spin label, or genuinely cooperative effects affecting the hydrogen bonding interaction between the macromolecular surface and hydration water. These observations also emphasizes the importance and the potential impact of comparing ODNP measurements to studies based on other experimental methodologies that might be able to quantify the length-scale of the crossover between bulk and surface dynamics. For instance, the dynamic surface force apparatus has measured viscous forces near both the hydrophilic and hydrophobic surfaces of DPPC mono- and bi-layers.⁵¹ While the typical analysis assigns a location to the hydrodynamic no-slip boundary condition, results like those presented here and elsewhere encourage re-considering such results as a means for extracting the transitions between variable rates of diffusion near the surface. Furthermore, measurements of the zeta potential under different salt conditions give an estimate of the slipping plane, which might allow insight into how far these viscosity effects penetrate into the bulk solvent.⁵² Finally, observations made with Quasi-Elastic Neutron Scattering (QENS)^53,54 observe a sharp increase in translational water mobility on moving away from the surface of a model peptide: the retardation of the water’s translational diffusion decreases from 3.1 to 1.8 to 1.4 (i.e. diffusion coefficients of 0.75, 1.26, 1.65×10⁻⁹ m²s⁻¹) as the concentration of the model peptide, NALMA, in water scales from 2.0 M (which corresponds to approximately one hydration shell) to 1 M to 0.5 M, respectively.⁵⁴ In contrast, ODNP can resolve the nanometer-level differences in hydration dynamics of dilute biomolecular systems in the full presence of bulk water. With these and complementary methods to analyze both detailed local dynamics and the longer-range transition between dynamic regimes, a powerful toolbox will begin to materialize.

As a concluding note, the decoupling of the surface and bulk dynamics may prove important to the function of biomolecular systems in cellular environments. Proteins and cell membranes can gather a soft shell of hydrating water molecules. They provide a microenvironment that remains relatively unperturbed by the surrounding crowded environment and is likely crucial for maintaining structure and function. Even in the incredibly crowded cytoplasm, where macromolecules occupy 20-30% of the volume,⁴ these results imply that water at the surface of the macromolecule will display relatively unperturbed properties, unless interactions occur that penetrate into and perturb this microenvironment at the nanometer scale. This perspective could explain a variety of phenomena, most importantly the concept that the first few layers of water molecules appear sufficient, yet also indispensible, for ensuring the proper function of a folded protein,^11,12 the concept that crowding and confinement might allow compartmentalization of the cell without impacting the fundamental properties of proteins,⁴ and the concept that the properties of the hydration water might be tied to the functions of proteins on a fundamental level.⁵⁵